多项式

Chivas-Regal

#

# 多项式乘法

# 洛谷P1919_A*BProblem升级版

# 🔗

# 💡

我们可以把A转变为一个多项式
$A=A(x)=a_0x^0+a_1x^1+...+a_nx^n$
B同理
此时我们想求出两者的积，也就是把A(x)*B(x)
然后得到的C(x)，对系数转换10进制即可

# ✅

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>

using namespace std;

const int N = 3000010;
const double PI = acos(-1.0);

int n, m;
struct Complex { // 复数结构体
        double x, y;
        Complex friend operator + ( Complex a, Complex b ) { return {a.x + b.x, a.y + b.y}; }
        Complex friend operator - ( Complex a, Complex b ) { return {a.x - b.x, a.y - b.y}; }
        Complex friend operator * ( Complex a, Complex b ) { return { a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x}; }
} a[N], b[N];
int rev[N];
int bit, tot;
int res[N];

inline void FFT ( Complex a[], int inv ) {
        for ( int i = 0; i < tot; i ++ ) if ( i < rev[i] ) swap(a[i], a[rev[i]]);
        for ( int mid = 1; mid < tot; mid <<= 1 ) { 
                Complex w1 = {cos(PI / mid), inv * sin(PI / mid)};
                for ( int i = 0; i < tot; i += mid * 2 ) {
                        Complex wk = {1, 0}; 
                        for ( int j = 0; j < mid; j ++, wk = wk * w1 ) {
                                Complex x = a[i + j], y = wk * a[i + j + mid];
                                a[i + j] = x + y, a[i + j + mid] = x - y;
                        }
                }
        }
}

int main() {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
#endif
        string sa, sb;
        cin >> sa >> sb; n = sa.size() - 1, m = sb.size() - 1;
        for ( int i = 0; i <= n; i ++ ) a[i].x = sa[n - i] - '0'; // 每一位拆出来给实部
        for ( int i = 0; i <= m; i ++ ) b[i].x = sb[m - i] - '0';
        while ( (1 << bit) < n + m + 1 ) bit ++;
        tot = 1 << bit;
        for ( int i = 0; i < tot; i ++ ) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
        FFT( a, 1 ); FFT( b, 1 );
        for ( int i = 0; i < tot; i ++ ) a[i] = a[i] * b[i];
        FFT( a, -1 );
        
        int nxt = 0;
        for ( int i = 0; i <= n + m + 1; i ++ ) {
                res[i] = (nxt + (int)(a[i].x / tot + 0.5)) % 10;
                nxt = (nxt + (int)(a[i].x / tot + 0.5)) / 10;
        }
        int i = n + m + 1;
        while ( res[i] == 0 ) i --;
        for ( ; i >= 0; i -- ) cout << res[i]; // 整合给res输出
        return 0;
}
        
/*
FFT:            1524157891004055895123067864200200646789061868481059858831257643955833850367278502666927131954920793240938240966819899216931602390126499790993189428688835402911622011521694514727469596012471524
BigInteger:
        1524157891004055895125653722788645091233506312925504303275702088400278294811722947111371576399365237685382685411264343661376046834570944235437633873133279847355807870107294514727469596012471524
*/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

# 洛谷P3321_序列统计

# 🔗

# 💡

首先写一个递推式：用 $dp[i][j]$ 表示选 $i$ 个数，乘积模 $m$ 为 $j$ 的方案数
则有转移 $dp[2\times i][c]=\sum\limits_{a\times b\% m=c}dp[i][a]\times dp[i][b]$
可以看到如果连加符下面是 $a+b$ 相关的话就可以直接卷积了，乘法变加法考虑替换为指数
令 $g$ 为 $m$ 的原根，这样的话对于任意的 $i,j\in[0,m-2],i\neq j$ 都能满足 $g^i\neq g^j$
令 $a=g^A,b=g^B,c=g^C\quad\rightarrow\quad A=log_ga,B=log_gb,C=log_gc$ ，则

\begin{aligned} dp[2\times i][C]=&\sum\limits_{g^A\times g^B \% m=g^C}dp[i][A]dp[i][B]\\ =&\sum\limits_{g^{(A+B)\%(m-1)=g^{C}}}dp[i][A]dp[i][B]\\ =&\sum\limits_{(A+B)\%(m-1)=C}dp[i][A]dp[i][B] \end{aligned}

这样看起来已经圆满了，把公式弄清晰一点
令 $f[C]=\sum\limits_{A+B=C}dp[i][A]dp[i][B]$
则 $dp[i][C]=f[C]+f[C+m-1]$
这样答案就成了 $f^n[log_gx]$

注意我们特判掉输入的 $\{S\}$ 中模 $m$ 为 $0$ 的数后，对每一个 $f[s[i]\%m]$ 都要 $+1$ 成为方案数
然后计算 $f$ 的幂可以使用快速幂多项式乘法

# ✅

const int mod = 1004535809;

int n, m, x, sz;
int lg[10004];
int g;

namespace Number {
        inline int Ksm (int a, int b, int mod) {
                int res = 1;
                while (b) {
                        if (b & 1) res = 1ll * res * a % mod;
                        a = 1ll * a * a % mod;
                        b >>= 1;
                }
                return res;
        }
        inline int Inv (int x) {
                return Ksm(x, mod - 2, mod);
        }
        inline int Phi (int x) {
                int res = x;
                for (int i = 2; 1ll * i * i <= x; i ++) {
                        if (x % i == 0) {
                                res = res / i * (i - 1);
                                while (x % i == 0) x /= i;
                        }
                }
                if (x > 1) res = res / x * (x - 1);
                return res;
        }
        
        vector<ll> sep;
        inline void Seperator (int x) {
                x = Phi(x);
                for (int i = 2; i * i <= x; i ++) {
                        if (x % i == 0) sep.push_back(i);
                        while (x % i == 0) x /= i;
                }
                if (x > 1) sep.push_back(x);
        }
        inline bool Check (int x, int n) {
                int phin = Phi(n);
                if (Ksm(x, phin, n) != 1) return 0;
                for (int i = 0; i < sep.size(); i ++) if (Ksm(x, phin / sep[i], n) == 1) return 0;
                return 1;
        }
        inline int Root (int x) {
                sep.clear(); Seperator(x);
                for (int i = 1; i <= x; i ++) if (Check(i, x)) return i;
                return 0;
        }
}
namespace Poly {
        const int N = 3e4 + 10;
        int bit, tot, rev[N];
        int F[N];
        inline void Init () {
                bit = 0; while ((1 << bit) < (m << 1)) bit ++; tot = 1 << bit;
                for (int i = 0; i < tot; i ++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
        }
        inline void NTT (int a[], int op) {
                for (int i = 0; i < tot; i ++) if (i < rev[i]) swap(a[i], a[rev[i]]);
                for (int mid = 1; mid < tot; mid <<= 1) {
                        int g1 = Number::Ksm(3, (mod - 1) / (mid << 1), mod);
                        if (op == -1) g1 = Number::Inv(g1);
                        for (int i = 0; i < tot; i += mid << 1) {
                                int gk = 1;
                                for (int j = 0; j < mid; j ++, gk = 1ll * gk * g1 % mod) {
                                        int x = a[i + j], y = 1ll * gk * a[i + mid + j] % mod;
                                        a[i + j] = (x + y) % mod;
                                        a[i + j + mid] = ((x - y) % mod + mod) % mod;
                                }
                        }
                }
                if (op == -1) {
                        int iv = Number::Inv(tot);
                        for (int i = 0; i < tot; i ++) a[i] = 1ll * a[i] * iv % mod;
                }
        }
        inline void Mul (int A[], int B[], int C[]) {
                int a[N], b[N];
                for (int i = 0; i < tot; i ++) a[i] = A[i], b[i] = B[i];
                NTT(a, 1); NTT(b, 1);
                for (int i = 0; i < tot; i ++) a[i] = 1ll * a[i] * b[i] % mod;
                NTT(a, -1);
                for (int i = 0; i < m - 1; i ++) C[i] = (a[i] + a[i + m - 1]) % mod;
        }
        int res[N];
        inline void Ksm (int A[], int b) {
                res[0] = 1;
                while (b) {
                        if (b & 1) Mul(res, A, res);
                        Mul(A, A, A);
                        b >>= 1;
                }
        }
}

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        cin >> n >> m >> x >> sz;
        g = Number::Root(m); 
        for (int i = 0; i < m - 1; i ++) lg[Number::Ksm(g, i, m)] = i;
        for (int i = 0; i < sz; i ++) {
                int num; cin >> num; num %= m;
                if (num) Poly::F[lg[num]] ++;
        }
        Poly::Init();
        Poly::Ksm(Poly::F, n);
        cout << Poly::res[lg[x]] << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113

# 洛谷P3338_力

# 🔗

# 💡

首先回顾多项式卷积公式
令 $f(x)$ 为多项式， $f[i]$ 为其指数为 $i$ 的系数
$f(x)*g(x)=\sum\limits_{i=0}^nf[i]g[n-i]$

化简式子
$\begin{aligned} E_i=&\frac{F_i}{q_i}\\ =&\frac{\sum\limits_{j=1}^i\frac{q_iq_j}{(i-j)^2}-\sum\limits_{j=i}^n\frac{q_iq_j}{(i-j)^2}}{q_i}\\ =&\sum\limits_{j=1}^i\frac{q_j}{(i-j)^2}-\sum\limits_{j=i}^n\frac{q_j}{(i-j)^2} \end{aligned}$
可以发现对于一块也就是 $\frac{q_j}{(i-j)^2}$ 这是两个部分并且上面是 $j$ 下面是 $i-j$ ，那么令 $f[i]=q_i,g[i]=\frac1{i^2}$
则原式 $=\sum\limits_{j=1}^if[i]g[i-j]-\sum\limits_{j=i}^nf[i]g[i-j]$
前面成卷积的形式了，展开一下后面看看： $\sum\limits_{j=i}^nf[i]g[i-j]=f[i]g[0]+f[i+1]g[1]+...=\sum\limits_{j=0}^{n-i}f[i+j]g[j]$
令 $t=n-i,\;f'[\alpha]=f[n-\alpha]=f[t+i-\alpha]$
则后者 $=\sum\limits_{j=0}^tf'[t-j]g[j]$ 成了
所以原式 $=\sum\limits_{j=1}^if[i]g[i-j]-\sum\limits_{j=0}^tf'[t-j]g[j]$
令 $f[0]=g[0]=0$
则原式 $=\sum\limits_{j=0}^if[i]g[i-j]-\sum\limits_{j=0}^tf'[t-j]g[j]$

固定任务
设多项式 $A(x)=\sum\limits_{i=0}^nf[i],\;B(x)=\sum\limits_{i=0}^ng[i],\;C(x)=\sum\limits_{i=0}^nf'[i]$
则原式 $=(A*B)(x)[i]-(B*C)(x)[n-i]$
用 $FFT$ 优化即可

# ✅

const int N = 3e5 + 10;
const double PI = acos(-1.0);

struct Complex {
        double x, y;
        inline friend Complex operator + (Complex a, Complex b) { return {a.x + b.x, a.y + b.y}; }
        inline friend Complex operator - (Complex a, Complex b) { return {a.x - b.x, a.y - b.y}; }
        inline friend Complex operator * (Complex a, Complex b) { return {a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x}; }
} a[N], b[N], c[N];
int tot, bit, rev[N];

inline void FFT (Complex a[], int inv) {
        for (int i = 0; i < tot; i ++) 
                if (i < rev[i])
                        swap(a[i], a[rev[i]]);
        for (int mid = 1; mid < tot; mid <<= 1) {
                Complex w1 = {cos(PI / mid), inv * sin(PI / mid)};
                for (int i = 0; i < tot; i += mid << 1) {
                        Complex wk = {1, 0};
                        for (int j = 0; j < mid; j ++, wk = wk * w1) {
                                Complex x = a[i + j], y = wk * a[i + j + mid];
                                a[i + j] = x + y, a[i + j + mid] = x - y;
                        }
                }
        }
        if (inv == -1) {
                for (int i = 0; i < tot; i ++) a[i].x = a[i].x / tot;
        }
}

int n;
double p[N];

int main () {
        scanf("%d", &n);
        for (int i = 1; i <= n; i ++) scanf("%lf", &p[i]);
        
        while ((1 << bit) < n + n + 1) bit ++; tot = 1 << bit;
        for (int i = 0; i < tot; i ++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));

        for (int i = 1; i <= n; i ++) {
                a[i].x = p[i];
                b[i].x = 1.0 / i / i;
                c[n - i].x = p[i];
        }

        FFT(a, 1); FFT(b, 1); FFT(c, 1);
        for (int i = 0; i < tot; i ++) a[i] = a[i] * b[i], b[i] = b[i] * c[i];
        FFT(a, -1); FFT(b, -1);

        for (int i = 1; i <= n; i ++) {
                printf("%.3f\n", a[i].x - b[n - i].x);
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

# 洛谷P3702_序列计数

# 🔗

# 💡

很多限制，考虑容斥
首先数都是不超过 $m$ 的正整数这个要求是帮我们固定了枚举系数的范围，如果没有别的要求，我们把 $1\rightarrow m$ 扫一遍
然后看到让和为 $p$ 的倍数，幂乘法本来就是指数加，这样的话让序列这个位置 $[0,p-1]$ 每一个数作为指数，可选的方案数作为系数，通过转化为余数为 $0$ 可以知道，我们的指数只需要用到 $[0,p-1]$ ，那么扫 $[1,m]$ 时所有的数的时候也要转换成对 $p$ 的余数来计算

这个长度为 $n$ 的序列每一个位置下都有一套指数对应系数的可选性，而我们扫 $1\rightarrow m$ 做出来的初始多项式设为 $f(x)$ ，那么答案就让求 $(f(x))^n$ 在 $x$ 的指数为 $0$ 时的系数

而对于容斥掉的部分，是我们所有位置都不用质数的情况，那么做初始多项式扫指数的时候，如果指数是质数，就直接将这一位的方案数也就是系数设置为 $0$ 即可

让两个多项式求完 $n$ 次幂后 $0$ 位置相减就是答案

多项式的幂可以写一个乘法函数然后用快速幂去计算， $p$ 小的离谱，乘法函数暴力写都行

# ✅

const int mod = 20170408;

int n, m, p;

namespace Number {
        const int N = 2e7 + 10;
        int ntp[N];
        vector<int> prime;
        inline void Sieve () {
                ntp[0] = ntp[1] = 1;
                for (int i = 2; i < N; i ++) {
                        if (!ntp[i]) prime.push_back(i);
                        for (int j = 0; j < prime.size() && 1ll * i * prime[j] < N; j ++) {
                                ntp[i * prime[j]] = 1;
                                if (i % prime[j] == 0) break;
                        }
                }
        }
}

namespace Poly {
        const int N = 1e3;
        int F[N];
        int res[N];
        inline void Init () {
                memset(F, 0, sizeof F);
                memset(res, 0, sizeof res);
        }
        inline void Mul (int A[], int B[], int C[]) {
                int c[N] = {0};
                for (int i = 0; i < p; i ++) 
                        for (int j = 0; j < p; j ++)
                                c[(i + j) % p] = (1ll * c[(i + j) % p] + 1ll * A[i] * B[j] % mod) % mod;
                for (int i = 0; i < p; i ++) C[i] = c[i];
        }
        inline void Ksm (int a[], int b) {
                res[0] = 1;
                while (b) {
                        if (b & 1) Mul(res, a, res);
                        Mul(a, a, a);
                        b >>= 1;
                }
        }
}

inline int Solve_all () {
        Poly::Init();
        for (int i = 1; i <= m; i ++) {
                Poly::F[i % p] ++;
        }
        Poly::Ksm(Poly::F, n);
        return Poly::res[0];
}
inline int Solve_del () {
        Poly::Init();
        for (int i = 1; i <= m; i ++) {
                if (Number::ntp[i]) Poly::F[i % p] ++;
        }
        Poly::Ksm(Poly::F, n);
        return Poly::res[0];
}

int main () {
        ios::sync_with_stdio(false);
        cin.tie(0);

        Number::Sieve();

        cin >> n >> m >> p;
        cout << ((Solve_all() - Solve_del()) % mod + mod) % mod << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

# 洛谷P3723_礼物

# 🔗

# 💡

公式转化一下就是
$\begin{aligned} &\sum\limits_{i=1}^n(a_i-b_i+x)^2\\ =&\sum\limits_{i=1}^n(a_i^2+2a_ix-2a_ib_i+x^2-2xb_i+b_i^2)\\ =&\sum\limits_{i=1}^n(a_i^2+b_i^2)+(2x\sum\limits_{i=1}^na_i-2x\sum\limits_{i=1}^nb_i)+(nx^2)-(2\sum\limits_{i=1}^na_ib_i) \end{aligned}$
除了 $x$ ，前三部分都可以预处理出来，但由于可以移动位置，那么最后一个 $\sum\limits_{i=1}^na_ib_i$ 就需要套路地对 $b$ 翻转后与 $[a]$ 凑卷积形式
处理出来每一个之后对每一个位置的匹配（也就是卷积后的指数）去扫 $x$ ，维护最小值即可

注意这里匹配成环，环化作链，让 $a[i+n]=a[i]$ 即可

# ✅

const int N = 300005;
const double PI = acos(-1.0);

int n, m;
struct Complex {
        double x, y;
        inline friend Complex operator + (Complex a, Complex b) { return {a.x + b.x, a.y + b.y}; }
        inline friend Complex operator - (Complex a, Complex b) { return {a.x - b.x, a.y - b.y}; }
        inline friend Complex operator * (Complex a, Complex b) { return {a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x}; }
} a[N], b[N];
int bit, tot, rev[N];

inline void FFT (Complex a[], int op) {
        for (int i = 0; i < tot; i ++) if (i < rev[i]) swap(a[i], a[rev[i]]);
        for (int mid = 1; mid < tot; mid <<= 1) {
                Complex w1 = {cos(PI / mid), op * sin(PI / mid)};
                for (int i = 0; i < tot; i += mid << 1) {
                        Complex wk = {1, 0};
                        for (int j = 0; j < mid; j ++, wk = wk * w1) {
                                Complex x = a[i + j], y = wk * a[i + j + mid];
                                a[i + j] = x + y, a[i + j + mid] = x - y;
                        }
                }
        }
        if (op == -1) for (int i = 0; i < tot; i ++) a[i].x = (int)(a[i].x / tot + 0.5);
}


int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        cin >> n >> m;
        vector<int> ina(n + 1), inb(n + 1);
        for (int i = 1; i <= n; i ++) {
                cin >> ina[i];
                a[i].x = a[i + n].x = ina[i];
        }
        for (int i = 1; i <= n; i ++) {
                cin >> inb[i];
                b[n - i + 1].x = inb[i];
        }

        while ((1 << bit) < (n + n + n)) bit ++; tot = 1 << bit;
        for (int i = 0; i < tot; i ++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));

        FFT(a, 1); FFT(b, 1);
        for (int i = 0; i < tot; i ++) a[i] = a[i] * b[i];
        FFT(a, -1);

        int res1 = 0;
        for (int i = 1; i <= n; i ++) res1 += ina[i] * ina[i] + inb[i] * inb[i];
        int res2 = 0;
        for (int i = 1; i <= n; i ++) res2 += ina[i] - inb[i]; res2 *= 2;
        int res3 = n;
        int res4 = 2;

        int RES = 0x3f3f3f3f;
        for (int i = n + 1; i <= 2 * n; i ++) {
                for (int x = -m; x <= m; x ++) {
                        RES = min(RES, res1 + x * res2 + res3 * x * x - res4 * (int)a[i].x);
                }
        }
        cout << RES << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

# 洛谷P3763_DNA

# 🔗

# 💡

看到这个先把其中一个序列转义一下
那么问题就变成了，从多少个位置开始匹配两个字符串，不相似度可以 $\le 3$ ，这种字符串匹配下相似度的问题，可以直接用 $fft$ 实现

相似度可以转化为所有字符的重合度
对于匹配字符 $a$ 的重合度
将模式串字符是不是 $a$ 作为系数，下标翻转后作为指数传入，那么如果从主串的 $i$ 位置开始匹配，则匹配方式为：
$\begin{aligned} &i &i+1 &i+2 &i+3 \dots\\ &m-1 &m-2 &m-3 &m-4 \dots \end{aligned}$
这样下来，匹配出来相似度的所有结果将会存入 $m-1+i$ 这个指数的系数上
我们对四个字符做多项式乘，那么从每一个位置开始匹配的相似度就可以加出来
如果这个值超过 $m-3$ 那么就说明不相似度满足了

# ✅

const int N = 5e5 + 10;
const double PI = acos(-1.0);

struct Complex {
        double x, y;
        inline friend Complex operator + (Complex a, Complex b) { return {a.x + b.x, a.y + b.y}; }
        inline friend Complex operator - (Complex a, Complex b) { return {a.x - b.x, a.y - b.y}; }
        inline friend Complex operator * (Complex a, Complex b) { return {a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x}; }
} a1[N], a2[N], t1[N], t2[N], c1[N], c2[N], g1[N], g2[N];
int bit, tot, rev[N];
int same[N];

inline void FFT (Complex a[], int inv) {
        for (int i = 0; i < tot; i ++) if (i < rev[i]) swap(a[i], a[rev[i]]);
        for (int mid = 1; mid < tot; mid <<= 1) {
                Complex w1 = {cos(PI / mid), inv * sin(PI / mid)};
                for (int i = 0; i < tot; i += mid << 1) {
                        Complex wk = {1, 0};
                        for (int j = 0; j < mid; j ++, wk = wk * w1) {
                                Complex x = a[i + j], y = wk * a[i + mid + j];
                                a[i + j] = x + y;
                                a[i + j + mid] = x - y;
                        }
                }
        }
        if (inv == -1) {
                for (int i = 0; i < tot; i ++) same[i] += (int)(a[i].x / tot + 0.5);
        }
}

inline void Solve () {
        for (int i = 0; i < N; i ++) a1[i] = a2[i] = t1[i] = t2[i] = c1[i] = c2[i] = g1[i] = g2[i] = {0, 0}, same[i] = 0;

        string a, b; cin >> a >> b;
        int n = a.size(), m = b.size();
        n --, m --;
        reverse(b.begin(), b.end());

        bit = 0; while ((1 << bit) < n + m + 1) bit ++; tot = 1 << bit;
        for (int i = 0; i < tot; i ++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));

        for (int i = 0; i <= n; i ++) {
                a1[i].x = a[i] == 'A';
                t1[i].x = a[i] == 'T';
                c1[i].x = a[i] == 'C';
                g1[i].x = a[i] == 'G';
        }
        for (int i = 0; i <= m; i ++) {
                a2[i].x = b[i] == 'A';
                t2[i].x = b[i] == 'T';
                c2[i].x = b[i] == 'C';
                g2[i].x = b[i] == 'G';
        }
        FFT(a1, 1); FFT(t1, 1); FFT(c1, 1); FFT(g1, 1);
        FFT(a2, 1); FFT(t2, 1); FFT(c2, 1); FFT(g2, 1);
        for (int i = 0; i < tot; i ++) {
                a1[i] = a1[i] * a2[i];
                t1[i] = t1[i] * t2[i];
                c1[i] = c1[i] * c2[i];
                g1[i] = g1[i] * g2[i];
        }
        FFT(a1, -1); FFT(t1, -1); FFT(c1, -1); FFT(g1, -1);

        int res = 0;
        for (int i = m; i <= n; i ++) {
                if (same[i] >= m - 2) res ++;
        }
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

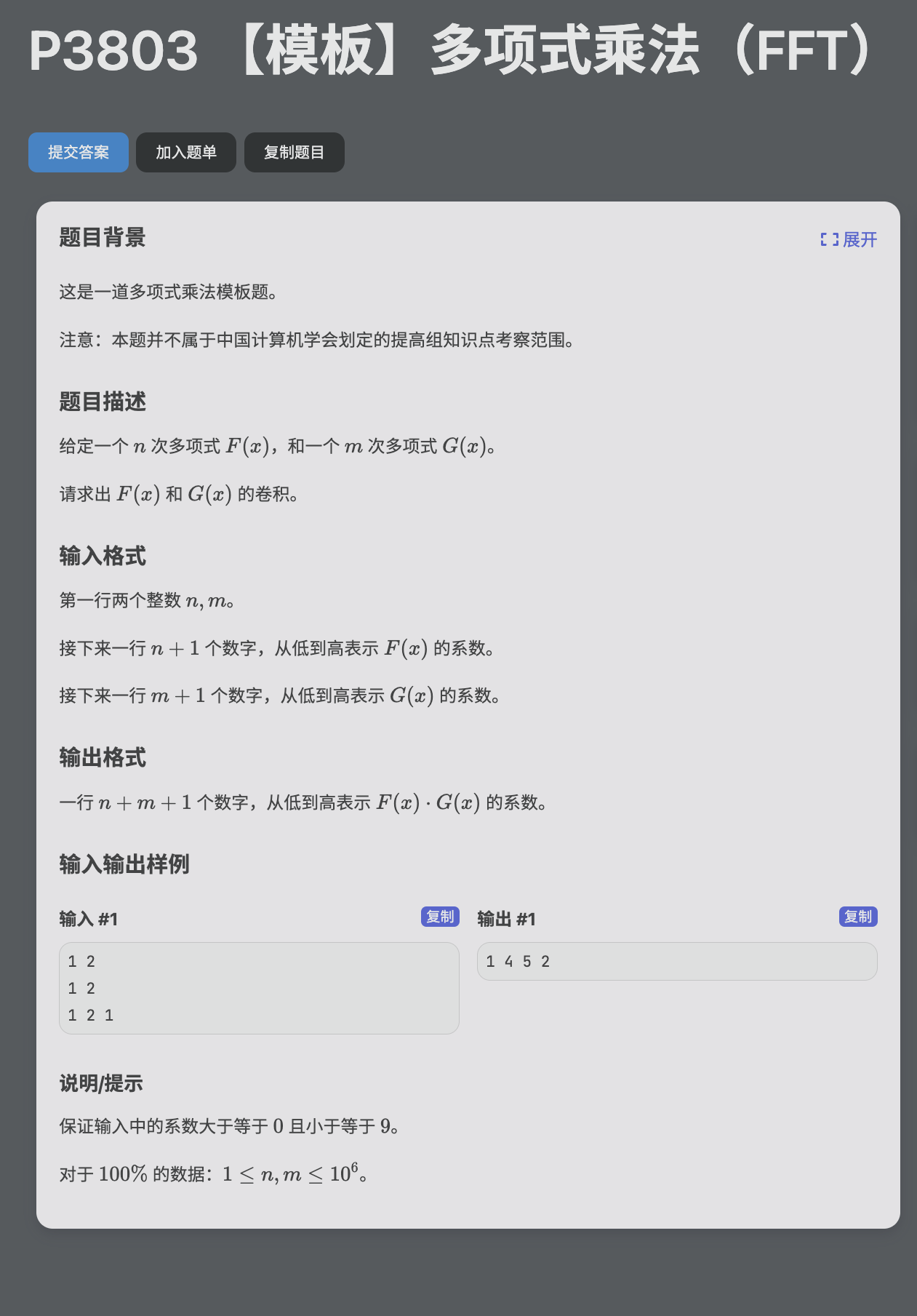
# 洛谷P3803_【模板】多项式乘法（FFT）

# 🔗

# 💡

Blog--例题讲解

# ✅

const int N = 3000010;
const double PI = acos(-1.0);

int n, m;
struct Complex { // 复数结构体
        double x, y;
        Complex friend operator + ( Complex a, Complex b ) { return {a.x + b.x, a.y + b.y}; }
        Complex friend operator - ( Complex a, Complex b ) { return {a.x - b.x, a.y - b.y}; }
        Complex friend operator * ( Complex a, Complex b ) { return { a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x}; }
} a[N], b[N]; // 两个多项式的点表示
int rev[N];   // 分治时候的二进制表示对应的结果二进制表示，即反过来了
int bit, tot; // 二进制上的位数，总个数

inline void FFT ( Complex a[], int inv ) {
        for ( int i = 0; i < tot; i ++ ) if ( i < rev[i] ) swap(a[i], a[rev[i]]); // 变成正确的分治结果位置（只能换一半，防止换回来
        for ( int mid = 1; mid < tot; mid <<= 1 ) { // 枚举分块的块长度
                Complex w1 = {cos(PI / mid), inv * sin(PI / mid)}; // 这也是把整个单位圆平均切成mid个后出现的 \omega^1
                for ( int i = 0; i < tot; i += mid * 2 ) { // 两个两个块向后跳，枚举每一段
                        Complex wk = {1, 0}; // w(n, 0)单位一开始
                        for ( int j = 0; j < mid; j ++, wk = wk * w1 ) { // 把区间里面数枚举一遍，且wk要往上跑一格
                                Complex x = a[i + j], y = wk * a[i + j + mid]; // x把左边提出，y把右边提出
                                a[i + j] = x + y, a[i + j + mid] = x - y;      // 左边和右边重构
                        }
                }
        }
}

int main() {
        cin >> n >> m;
        for ( int i = 0; i <= n; i ++ ) cin >> a[i].x; // 把输入的系数塞入实部
        for ( int i = 0; i <= m; i ++ ) cin >> b[i].x; // 把输入的系数塞入虚部
        while ( (1 << bit) < n + m + 1 ) bit ++; // 次数最多到n+m+1，所以利用n+m+1记录二进制位数
        tot = 1 << bit; // 在二进制位数下计算刚好达不到的那个位数的数
        for ( int i = 0; i < tot; i ++ ) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1)); // 每个rev[i]初始化为i的二进制逆转
        FFT( a, 1 ); FFT( b, 1 ); // 完成a和b的点表示
        for ( int i = 0; i < tot; i ++ ) a[i] = a[i] * b[i]; // 点表示法内完成两方程合并
        FFT( a, -1 ); // 逆向做一遍得到系数表示
        for ( int i = 0; i <= n + m; i ++ ) cout << (int)(a[i].x / tot + 0.5) << " "; // 防止精度丢失，要向上0.5再强转扔精度
        return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

# 洛谷P4173_残缺的字符串

# 🔗

# 💡

含有通配符， $KMP$ 难以做到
如果让通配符为 $0$ ，他乘任何的数都是 $0$ ，那么可以用字符串乘法操作
不仅与通配符有关，还与两个字符有关
那么我们令 $dis(s,t)=\sum\limits_{i=0}^{m-1}(s_i-t_i)^2s_it_i$ ，完全匹配意味着 $dis=0$
令 $i$ 表示 $s$ 与 $t$ 进行匹配的开始位置
则

\begin{aligned} f_i=&dis_i(s_{[i,i+m-1]},t)\\ =&\sum\limits_{j=0}^{m-1}(s_{i+j}-t_j)s_{i+j}t_j\\ =&\sum\limits_{j=0}^{m-1}s_{i+j}^3t_{j}-2\times\sum\limits_{j=0}^{m-1}s_{i+j}^2t_j^2+\sum\limits_{j=0}^{m-1}s_{i+j}t_j^3 \end{aligned}

发现每一部分都可以成为卷积，那么套路地翻转字符串 $t$ ，公式变为

\sum\limits_{j=0}^{m-1}s_{i+j}^3t_{m-1-j}-2\sum\limits_{j=0}^{m-1}s_{i+j}^2t_{m-1-j}^2+\sum\limits_{j=0}^{m-1}s_{i+j}t_{m-1-j}^3

卷积形式，将下标视作指数，下标相加 $=i+j+m-1-j=i+m-1$
$i\in[0,n-m]$ ，对应上面相加后的幂为 $[m-1,n-1]$
即对应 $f[m-1,n-1]$ 中为 $0$ 的位置表示全部匹配
即扫描 $i\in[m-1,n-1]$ 如果匹配了输出 $i-m+2$

（屑题卡常开个 $O2$ ）

# ✅

const int N = 2000006;
const double PI = acos(-1.0);

struct Complex {
        double x, y;
        inline friend Complex operator + (Complex a, Complex b) { return {a.x + b.x, a.y + b.y}; }
        inline friend Complex operator - (Complex a, Complex b) { return {a.x - b.x, a.y - b.y}; }
        inline friend Complex operator * (Complex a, Complex b) { return {a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x}; }
        inline friend Complex operator * (Complex a, double b)  { return {a.x * b, a.y * b}; }
} a1[N], a2[N], a3[N], b1[N], b2[N], b3[N], c[N];
int bit, tot, rev[N];

inline void FFT (Complex a[], int op) {
        for (int i = 0; i < tot; i ++) if (i < rev[i]) swap(a[i], a[rev[i]]);
        for (int mid = 1; mid < tot; mid <<= 1) {
                Complex w1 = {cos(PI / mid), op * sin(PI / mid)};
                for (int i = 0; i < tot; i += mid << 1) {
                        Complex wk = {1, 0};
                        for (int j = 0; j < mid; j ++, wk = wk * w1) {
                                Complex x = a[i + j], y = wk * a[i + j + mid];
                                a[i + j] = x + y, a[i + j + mid] = x - y;
                        }
                }
        }
}

char a[300005], b[300005];
int res[300005], idx;

int main () {
        int n, m; scanf("%d%d", &m, &n);
        scanf("%s%s", b, a);
        n --, m --;

        while ((1 << bit) < (n + m)) bit ++; tot = 1 << bit;
        for (int i = 0; i < tot; i ++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));

        for (int i = 0; i <= n; i ++) {
                if (a[i] != '*')
                        a1[i].x = (a[i] - 'a' + 1),
                        a2[i].x = (a[i] - 'a' + 1) * (a[i] - 'a' + 1),
                        a3[i].x = (a[i] - 'a' + 1) * (a[i] - 'a' + 1) * (a[i] - 'a' + 1);
        }
        for (int i = 0; i <= m; i ++) {
                if (b[m - i] != '*') 
                        b1[i].x = (b[m - i] - 'a' + 1),
                        b2[i].x = (b[m - i] - 'a' + 1) * (b[m - i] - 'a' + 1),
                        b3[i].x = (b[m - i] - 'a' + 1) * (b[m - i] - 'a' + 1) * (b[m - i] - 'a' + 1);
        }
        
        FFT(a1, 1); FFT(a2, 1); FFT(a3, 1);
        FFT(b1, 1); FFT(b2, 1); FFT(b3, 1);
        for (int i = 0; i < tot; i ++) 
                c[i] = a3[i] * b1[i] - a2[i] * b2[i] * 2 + a1[i] * b3[i];
        FFT(c, -1);


        for (int i = m; i <= n; i ++) {
                if (fabs((int)(c[i].x / tot + 0.5)) < 1e-3) {
                        res[idx ++] = i - m + 1;
                }
        }

        printf("%d\n", idx);
        for (int i = 0; i < idx; i ++) printf("%d ", res[i]);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

# 洛谷P4986_逃离

# 🔗

# 💡

根据勾股定理，令 $F(x)=A(x)^2+B(x)^2-C(x)^2=0$ 时即相等
那么我们先用 $FFT$ 求出 $F(x)$ 的表示
我们要求 $F(x)=0$ 时候的 $x$
发现这个指数为整数的多项式是一个一阶可导函数，我们对其求导为 $f'(x)$ ，然后使用牛顿迭代法 (opens new window) 求 $[l,r]$ 范围内的零点即可
初始点可以设置为 $\left\lfloor\frac{l+r}2\right\rfloor$

# ✅

const int N = 4e5 + 10;
const double PI = acos(-1.0);

struct Complex {
        double x, y;
        inline friend Complex operator + (Complex a, Complex b) { return {a.x + b.x, a.y + b.y}; }
        inline friend Complex operator - (Complex a, Complex b) { return {a.x - b.x, a.y - b.y}; }
        inline friend Complex operator * (Complex a, Complex b) { return {a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x}; }
} A[N], B[N], C[N];
int tot, bit, rev[N];
int F[N], f1[N], n;

inline void FFT (Complex a[], int op) {
        for (int i = 0; i < tot; i ++) if (i < rev[i]) swap(a[i], a[rev[i]]);
        for (int mid = 1; mid < tot; mid <<= 1) {
                Complex w1 = {cos(PI / mid), op * sin(PI / mid)};
                for (int i = 0; i < tot; i += mid << 1) {
                        Complex wk = {1, 0};
                        for (int j = 0; j < mid; j ++, wk = wk * w1) {
                                Complex x = a[i + j], y = wk * a[i + j + mid];
                                a[i + j] = x + y;
                                a[i + j + mid] = x - y;
                        }
                }
        }
        if (op == -1) {
                for (int i = 0; i < tot; i ++) a[i].x = (int)(a[i].x / tot + 0.5);
        }
}
inline double _F (double x) {
        double res = 0, cur = 1;
        for (int i = 0; i <= n; i ++) {
                res += cur * F[i];
                cur = cur * x;
        } 
        return res;
}
inline double _f1 (double x) {
        double res = 0, cur = 1;
        for (int i = 0; i < n; i ++) {
                res += cur * f1[i];
                cur = cur * x;
        }
        return res;
}

inline double Newton_Iteration (double x, int tim, const double l, const double r) {
        while (tim --) {
                if (fabs(_F(x)) < 1e-9) return x;
                x -= _F(x) / _f1(x);
                x = max(x, l); x = min(x, r);
        }
        return -4;
}

int main () {
        int a, b, c; scanf("%d%d%d", &a, &b, &c);
        double l, r; scanf("%lf%lf", &l, &r);
        n = max({a, b, c}) << 1;
        bit = 0; while ((1 << bit) <= n) bit ++; tot = 1 << bit;
        for (int i = 0; i < tot; i ++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));

        for (int i = 0; i <= a; i ++) scanf("%lf", &A[i].x);
        FFT(A, 1); for (int i = 0; i < tot; i ++) A[i] = A[i] * A[i]; FFT(A, -1);
        for (int i = 0; i <= b; i ++) scanf("%lf", &B[i].x);
        FFT(B, 1); for (int i = 0; i < tot; i ++) B[i] = B[i] * B[i]; FFT(B, -1);
        for (int i = 0; i <= c; i ++) scanf("%lf", &C[i].x);
        FFT(C, 1); for (int i = 0; i < tot; i ++) C[i] = C[i] * C[i]; FFT(C, -1);

        for (int i = 0; i < tot; i ++) F[i] = (int)(A[i].x + 0.5) + (int)(B[i].x + 0.5) - (int)(C[i].x + 0.5);
        for (int i = 0; i + 1 < tot; i ++) f1[i] = F[i + 1] * (i + 1);
        
        double res = Newton_Iteration((l + r) / 2, 30, l, r);
        if (res > l) printf("%.10f", res);
        else puts("Inconsistent!");
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76

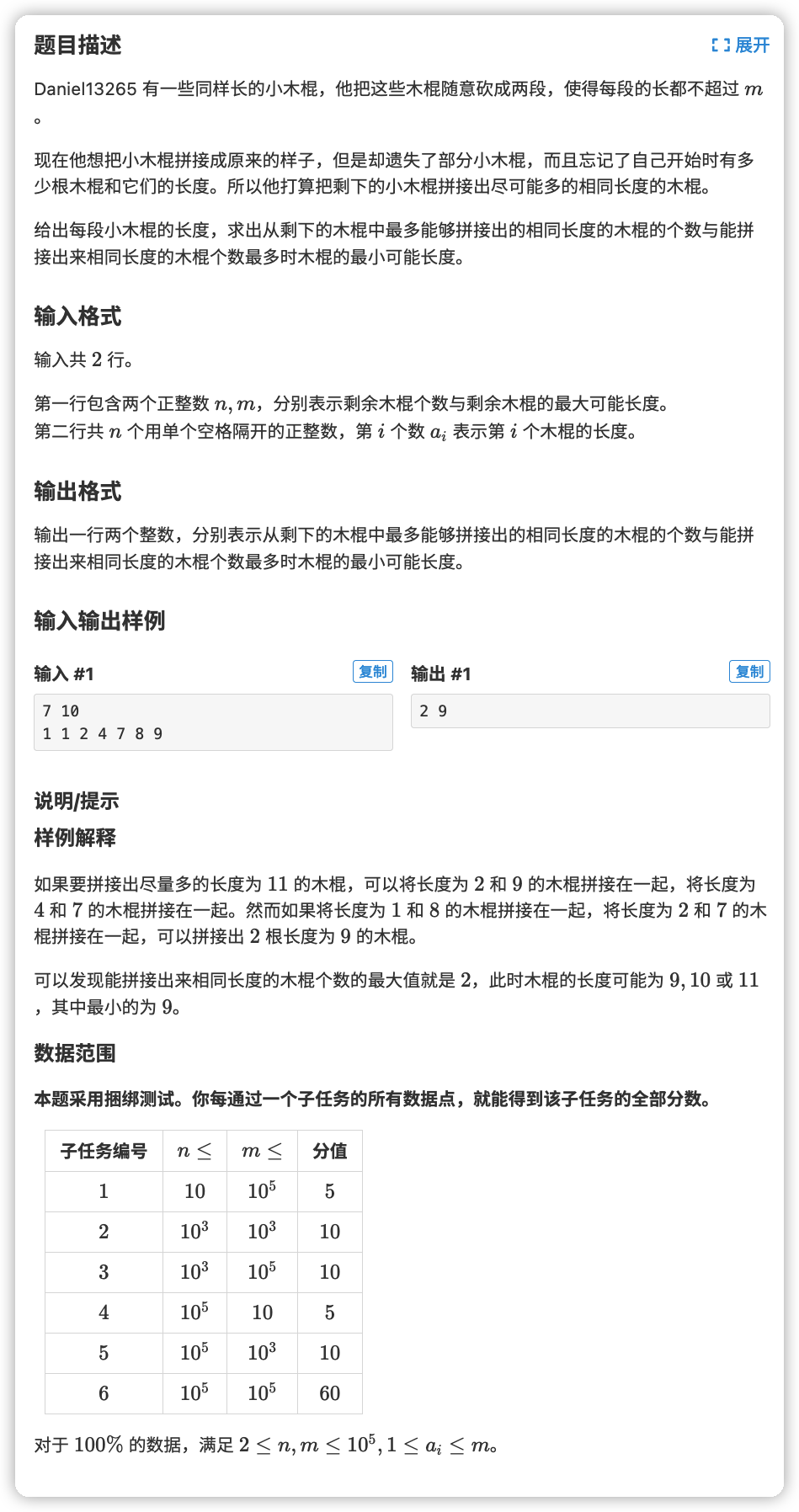
# 洛谷P6300_悔改

# 🔗

# 💡

首先把这个问题换成一个式子
令 $a_i$ 为长度为 $i$ 的木棍个数
拼成 $k$ 的方案数为 $f_k=\left\lfloor\frac{\sum\limits_{i+j=k}\min(a_i,a_j)}2\right\rfloor$
其中去掉 $(i,j)$ 和 $(j,i)$ 这种因顺序不同导致的重复与两个相同的木棍拼成 $k$ 的方案数，所以要除 $2$ 下取整

那么注意到上面这一块也就是 $\sum\limits_{i+j=k}\min(a_i,a_j)$ 是一个类似于卷积形式的卷 $\min$
考虑如何将这一部分转化为卷积

\begin{aligned} &\sum\limits_{i+j=k}\min(a_i,a_j)\\ =&\sum\limits_{i+j=k}\sum\limits_{d=1}[a_i\ge d][a_j\ge d]\\ =&\sum\limits_{d=1}\sum\limits_{i+j=k}[a_i\ge d][a_j\ge d] \end{aligned}

这样枚举 $d$ 后面就是一个卷积了

但是如果 $d$ 是暴力 $[1,2m]$ 了话时间复杂度还是过不去，注意到这都是 $\ge$ ，考虑区间跳跃优化
我们将所有出现的次数存入一个数组 $b$ ，将其排序去重
我们 $d$ 只枚举 $b$ 中的元素
如果当前枚举到 $b_d$ ，如果卷出来系数不为 $0$ 的地方，那么对于 $b_d-b_{d-1}$ 这一部分是我们之前没有计算到的地方也是这一次卷积满足的地方，就要让系数乘上 $b_d-b_{d-1}$ 累加入这一位的计数数组 $[res]$ 中
最后从小往大枚举指数 $i$ ，找最大的且是第一次出现的 $\left\lfloor\frac{res_i}2\right\rfloor$ 即可

# ✅

const int N = 4e5 + 10;
const int mod = 998244353;
inline ll ksm (ll a, ll b) { ll res = 1; while (b) { if (b & 1) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv (ll x) { return ksm(x, mod - 2); }

int f[N], rev[N], tot, bit;
int res[N];
inline void NTT (int a[], int op) {
        for (int i = 0; i < tot; i ++) if (i < rev[i]) swap(a[i], a[rev[i]]);
        for (int mid = 1; mid < tot; mid <<= 1) {
                int g1 = ksm(3, (mod - 1) / (mid << 1));
                if (op == -1) g1 = inv(g1);
                for (int i = 0; i < tot; i += mid << 1) {
                        int gk = 1;
                        for (int j = 0; j < mid; j ++, gk = 1ll * gk * g1 % mod) {
                                int x = a[i + j], y = 1ll * gk * a[i + j + mid] % mod;
                                a[i + j] = (x + y) % mod;
                                a[i + j + mid] = ((x - y) % mod + mod) % mod;
                        }
                }
        }
        if (op == -1) {
                int iv = inv(tot);
                for (int i = 0; i < tot; i ++) a[i] = 1ll * a[i] * iv % mod;
        }
}

int main () {
        ios::sync_with_stdio(false);
        cin.tie(0);

        int n, m; cin >> n >> m;
        vector<int> a(m * 2 + 1, 0), b(m * 2 + 1, 0);
        for (int i = 0; i < n; i ++) {
                int x; cin >> x;
                a[x] ++;
                b[x] = a[x];
        }
        sort(b.begin(), b.end());
        b.erase(unique(b.begin(), b.end()), b.end());

        while ((1 << bit) < (m << 1)) bit ++; tot = 1 << bit;
        for (int i = 0; i < tot; i ++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));

        for (int d = 1; d < b.size(); d ++) {
                memset(f, 0, sizeof f);
                for (int i = 1; i <= m * 2; i ++) f[i] = a[i] >= b[d];
                NTT(f, 1);
                for (int i = 0; i < tot; i ++) f[i] = 1ll * f[i] * f[i] % mod;
                NTT(f, -1);
                for (int i = 1; i <= m * 2; i ++) res[i] += 1ll * (b[d] - b[d - 1]) * f[i] % mod;
        }
        
        pair<int, int> RES = {0, 0x3f3f3f3f};
        for (int i = 1; i <= m * 2; i ++) {
                if (RES.first < res[i] / 2) RES = {res[i] / 2, i};
        }
        cout << RES.first << " " << RES.second << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

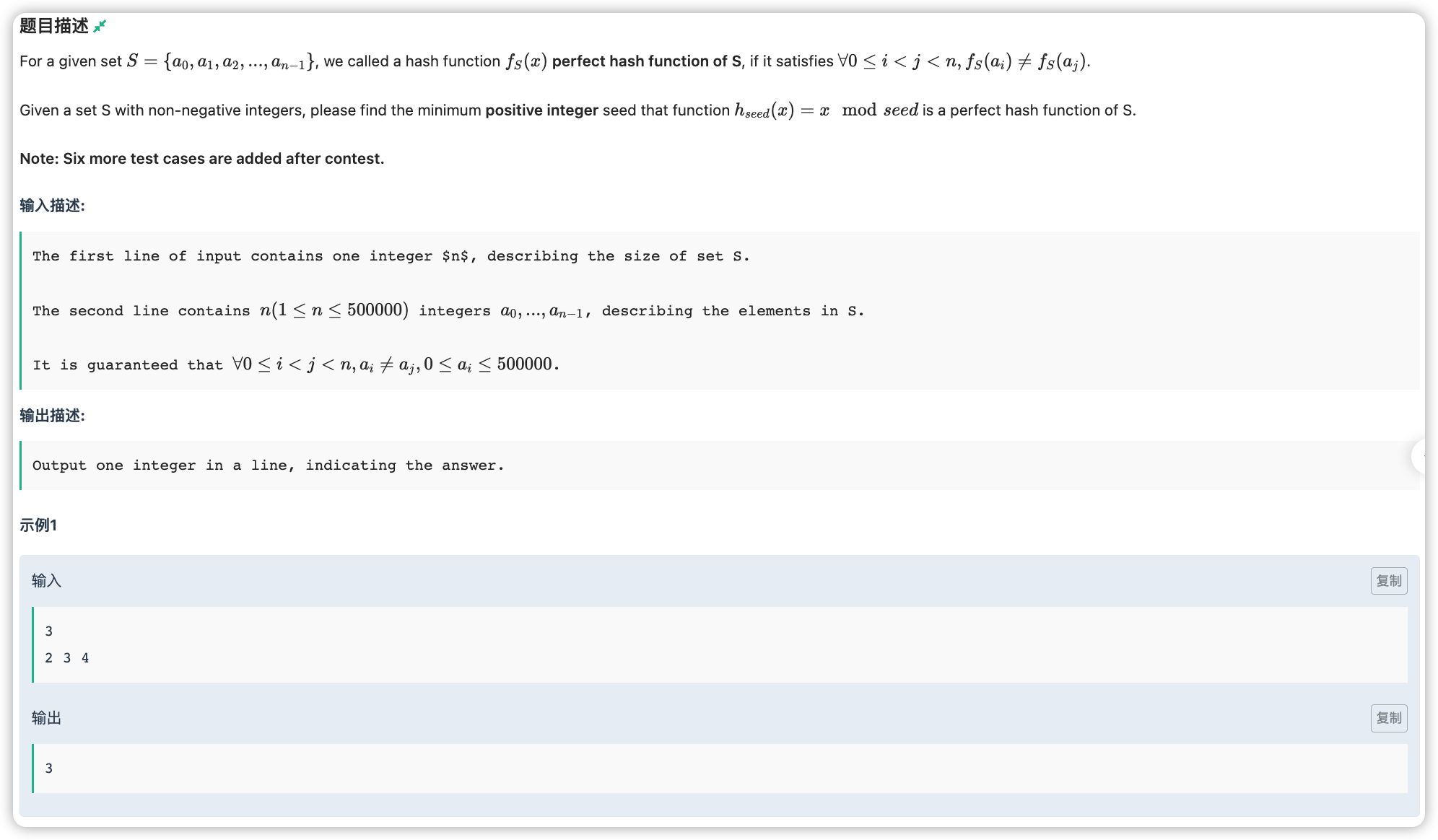
# 牛客2021多校(1)H_HashFunction

# 🔗

# 💡

数学题肯定要先转化为数学公式啦，即找到一个 $seed$ 满足
$\forall i,j\in[1,n],i\neq j,a_i\not\equiv a_j(mod\;seed)$
转化一下变成 $a_i-a_j\not\equiv0(mod\;seed)$
这就意味着两两之间的差的因数都不能作为 $seed$
如果能获取出来所有的两两差，直接判定的话就行了
这种两两之间的问题可以转化为两个多项式相乘，这里作为判定的话就给出现元素赋系数为 $1$ 即可，令数值作为指数，卷一下就有了所有的两两数值关系，但是注意到这里存在减法而我们需要加法才能卷，可以 $a_i+(5\times 10^5-a_j)-5\times 10^5$
即读入 $x$ 时两个多项式一个对指数为 $x$ 的系数标 $1$ ，一个对指数为 $5\times 10^5-x$ 的系数标 $1$ ，卷完之后让所有系数不为零且指数大于 $5\times 10^5$ 的指数减去 $5\times 10^5$ ，就可以获取到所有满足条件的减法最终值了，最多只到 $5\times 10^5$ （这也是为什么上面用 $5\times 10^5-$ 代替减法的原因）
然后用埃氏筛的思想跑所有数，然后看其倍数是否存在 $1$ ，如果没有倍数存在的话那就是这个因数了

# ✅

const int N = 5e6 + 10;
const int mod = 998244353;

inline ll Ksm (ll a, ll b) { ll res = 1; while (b) { if (b & 1) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll Inv (ll x) { return Ksm(x, mod - 2); }

int bit, tot;
int rev[N];

inline void NTT (int a[], int inv) {
    for (int i = 0; i < tot; i ++) if (i < rev[i]) swap(a[i], a[rev[i]]);
    for (int mid = 1; mid < tot; mid <<= 1) {
        int g1 = Ksm(3, (mod - 1) / (mid << 1));
        for (int i = 0; i < tot; i += mid << 1) {
            int gk = 1;
            for (int j = 0; j < mid; j ++, gk = 1ll * gk * g1 % mod) {
                int x = a[i + j], y = 1ll * gk * a[i + j + mid] % mod;
                a[i + j] = (x + y) % mod;
                a[i + j + mid] = (x - y + mod) % mod;
            }
        }
    }
    if (inv == -1) {
        reverse(a + 1, a + tot);
        int iv = Ksm(tot, mod - 2);
        for (int i = 0; i < tot; i ++) a[i] = 1ll * a[i] * iv % mod;
    }
}


int n;
int vis[N];
int a[N], b[N];

int main () {
    scanf("%d", &n);
    int mxa = 0, mxb = 0;
    for (int i = 1; i <= n; i ++) {
        int x; scanf("%d", &x);
        a[x] = 1;
        b[500000 - x] = 1;
        mxa = max(mxa, x);
        mxb = max(mxb, 500000 - x);
    }

    while ((1 << bit) < mxa + mxb - 1) bit ++; tot = 1 << bit;
    for (int i = 0; i < tot; i ++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));

    NTT(a, 1); NTT(b, 1);
    for (int i = 0; i < tot; i ++) a[i] = 1ll * a[i] * b[i] % mod;
    NTT(a, -1);


    for (int i = 500000; i <= 1000000; i ++) {
        if (a[i]) {
            vis[i - 500000] = 1;
        }
    }

    for (int d = 1; d < N; d ++) {
        bool flag = true;
        for (int i = d; i < N; i += d) {
            if (vis[i]) flag = false;
            if (!flag) break;
        }
        if (flag) {
            printf("%d\n", d);
            return 0;
        }
    }
}

# CodeForces608B_HammingDistanceSum

# 🔗

# 💡

求每一步匹配不上的数量
也就是不相似度的累加和
我们可以求一下相似度，然后
用所有都相似的相似度减去我们求到的相似度累加和就是不相似度的累加和

# ✅

#include <iostream>
#include <algorithm>
#include <map>
#include <cmath>
#include <vector>
using namespace std;
#define ll long long

const ll N = 1000010;
const double PI = acos(-1.0);
ll res[N];

ll n, m;
struct Complex {
        double x, y;
        Complex friend operator + ( Complex a, Complex b ) { return {a.x + b.x, a.y + b.y}; }
        Complex friend operator - ( Complex a, Complex b ) { return {a.x - b.x, a.y - b.y}; }
        Complex friend operator * ( Complex a, Complex b ) { return { a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x}; }
} a[N], b[N];
ll rev[N];
ll bit, tot; 
string sa, sb;

inline void FFT ( Complex a[], ll inv ) {
        for ( ll i = 0; i < tot; i ++ ) if ( i < rev[i] ) swap(a[i], a[rev[i]]);
        for ( ll mid = 1; mid < tot; mid <<= 1 ) {
                Complex w1 = {cos(PI / mid), inv * sin(PI / mid)};
                for ( ll i = 0; i < tot; i += mid * 2 ) {
                        Complex wk = {1, 0};
                        for ( ll j = 0; j < mid; j ++, wk = wk * w1 ) {
                                Complex x = a[i + j], y = wk * a[i + j + mid];
                                a[i + j] = x + y, a[i + j + mid] = x - y;
                        }
                }
        }
}

inline void Solve ( char c ) {
        for ( ll i = 0; i < N; i ++ ) a[i] = b[i] = {0, 0};
        for ( ll i = 0; i < n; i ++ ) a[i].x = (sa[i] == c);
        for ( ll i = 0; i < m; i ++ ) b[i].x = (sb[m - i - 1] == c);
        FFT(a, 1); FFT(b, 1);
        for ( ll i = 0; i < tot; i ++ ) a[i] = a[i] * b[i];
        FFT(a, -1);  
        for ( ll i = m - 1; i <= n + m - 2; i ++ ) {
                res[i] += (ll)(a[i].x / tot + 0.5);
        }
}

int main () {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif

        cin >> sb >> sa;
        n = sa.size(), m = sb.size();
        while ( (1ll << bit) <= n + m - 2 ) bit ++; tot = 1ll << bit;
        for ( ll i = 0; i < tot; i ++ ) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));

        Solve('1'); Solve('0');
        ll RES = (n - m + 1) * m; // 都完美匹配上的情况
        for ( ll i = m - 1; i <= n - 1; i ++ ) RES -= res[i]; // 减去相似度
        cout << RES << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

# HDU2022多校（5）7_CountSet

# 🔗

# 💡

根据 $2-sat$ 思想，选谁就不能选谁是一条边，互相制约的关系建边后，可以形成一张图。
这里是全排列，其置换环为建图后的环，可以提出来。
一个环上我们可以选任意个数，而我们只要保证所有环中选出数量的总和等于 $k$ 即可。
首先看内层的计数：一个长度为 $n$ 的环上选 $k$ 个数，互相不相邻，将选出的一个数的长度视作 $2$ ，不选的视作 $1$ ，可以保证每个选中的数会在同一个方向上多覆盖一个数，来保证不相邻。如果是在序列上的问题那么得到 $\binom{n-k}{k}$ ，但这是一个环，考虑将环从某个位置劈开就是一个序列问题了。但如果有一个长度为 $2$ 的块要放在序列首和尾，那么剩下的 $k-1$ 个块有 $n-k-1$ 个位置可以放，两者加起来为 $\binom{n-k}{k}+\binom{n-k-1}{k-1}$ 。
再看外层的计数：首想计数 $dp$ ，也是多重计数背包，但这样复杂度为 $O(nklogk)$ ，时间过不去，但是这种问题也是一种生成函数问题，转移为多项式求解，令 $ax^b$ 表示选 $b$ 个的方案数为 $a$ ，利用 $NTT$ 最后要得到的为 $x^k$ 的系数，多个多项式累乘，使用 $NTT$ 的启发式合并或者分治即可，复杂度为 $O(nlognlogk)$

整体设计如下：
首先划分出每个置换环大小 $r$ ，求出其选 $i$ 个数的方案数 $b_i=\binom{r-i}{i}+\binom{r-i-1}{i-1}$ ，构建出生成函数 $y=\sum\limits_{i=0}^{min(k,\left\lceil\frac{r+1}{2}\rceil\right)}b_ix^i$ 。
使用启发式/分治 $NTT$ 快速得到这些环的生成函数的卷积。
输出卷积 $x^k$ 的系数。

由于 $NTT$ 取模运算和乘法中复刻数组的常数复杂度很大，我们预处理出来原根对应每一个 $mid$ 的值与其逆元，并且将多项式乘法转换成新运算，用引用传递数组。

# ✅

const int N = 1e6 + 10;
const int mod = 998244353;

inline int ksm (int a, int b) { int res = 1; while (b) { if (b & 1) res = 1ll * res * a % mod; a = 1ll * a * a % mod; b >>= 1; } return res; }
inline int inv (int x) { return ksm(x, mod - 2); }
inline int C (int n, int m) { if (n < 0 || n < m || m < 0) return 0; return f[n] * ivf[m] % mod * ivf[n - m] % mod; }


vector<int> rols; // 所有置换环的大小
int n, k;

ll f[N], ivf[N];
vector<int> rev;
int bit, tot;
vector<vector<int> > gk[2]; // 原根的幂
inline void pre_Mul (int _n) { // 优化：乘之前处理一次
        while ((1 << bit) > _n) bit --;
        while ((1 << bit) <= _n) bit ++; tot = 1 << bit;
        rev.resize(tot);
        for (int i = 0; i < tot; i ++) rev[i] = 0;
        for (int i = 0; i < tot; i ++) {
                rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
        }
}

struct Poly { // 多项式
        vector<int> a;
        int len;
        inline void resizePoly (int _n) {
                while ((1 << bit) >  _n) bit --;
                while ((1 << bit) <= _n) bit ++; 
                tot = 1 << bit;
                a.resize(tot);
                len = _n;
        }
        inline void NTT (int op) {
                for (int i = 0; i < tot; i ++) if (i < rev[i]) swap(a[i], a[rev[i]]);
                for (int mid = 1, w = 0; mid < tot; mid <<= 1, ++ w) {
                        for (int i = 0; i < tot; i += mid << 1) {
                                for (int j = 0; j < mid; j ++) {
                                        int x = a[i + j], y = 1ll * gk[op == 1 ? 1 : 0][w][j] * a[i + j + mid] % mod;
                                        a[i + j] = x + y; if (a[i + j] >= mod) a[i + j] -= mod;
                                        a[i + j + mid] = x - y; if (a[i + j + mid] < 0) a[i + j + mid] += mod;
                                }
                        }
                }
                if (op == -1) {
                        int iv = inv(tot);
                        for (int i = 0; i < tot; i ++) a[i] = 1ll * a[i] * iv % mod;
                }
        }      
        inline friend bool operator < (Poly x, Poly b) {
                return x.len > b.len;
        }
        Poly &operator *= (Poly &B) {
                int newlen = min(k, len + B.len);
                pre_Mul(newlen);
                resizePoly(newlen);
                B.resizePoly(newlen);
                NTT(1); B.NTT(1);
                for (int i = 0; i < tot; i ++) a[i] = 1ll * a[i] * B.a[i] % mod;
                NTT(-1);
                return *this;
        }
};


priority_queue<Poly> pque; // 启发式合并，按多项式长度排序，小的在顶
inline void Solve () {
        rols.clear();
        while (!pque.empty()) pque.pop();

        scanf("%d%d", &n, &k);
        vector<int> p(n + 1); for (int i = 1; i <= n; i ++) scanf("%d", &p[i]);
        vector<int> vis(n + 1, 0);

        for (int i = 1; i <= n; i ++) {
                int num = 0;
                int ii = i;
                while (!vis[ii]) {
                        num ++;
                        vis[ii] = 1;
                        ii = p[ii];
                }
                if (num > 1) rols.push_back(num);
        }
        if (k == 0) {puts("1"); return;}
        else if (rols.size() == 0) {puts("0"); return;}
        sort(rols.begin(), rols.end());

        int all = 0;
        for (int r : rols) { // 构建生成函数
                all += (r + 1) / 2;
                Poly pol;
                pol.resizePoly(min(r, k));
                pol.a[0] = 1;
                for (int i = 1; i <= min(r, k); i ++) pol.a[i] = (C(r - i, i) + C(r - i - 1, i - 1)) % mod;
                pque.push(pol);
        }
        while (pque.size() > 1) { // 启发式合并：每次提两个短的多项式
                Poly f = pque.top(); pque.pop();
                Poly s = pque.top(); pque.pop();
                f *= s;
                pque.push(f);
        }
        printf("%d\n", pque.top().a[k]);
}

int main () {

        f[0] = 1;
        for (int i = 1; i < N; i ++) f[i] = f[i - 1] * i % mod;
        ivf[N - 1] = inv(f[N - 1]);
        for (int i = N - 2; i >= 0; i --) ivf[i] = ivf[i + 1] * (i + 1) % mod;
        gk[1].resize(30);
        gk[0].resize(30);
        for (int g1, i = 0, mid = 1; mid < N; ++i, mid <<= 1) {
                gk[1][i].resize(mid);
                gk[0][i].resize(mid);
                gk[1][i][0] = 1; g1 = ksm(3, (mod - 1) / (mid << 1));
                gk[0][i][0] = 1;
                for (int j = 1; j < mid; j ++) gk[1][i][j] = 1ll * g1 * gk[1][i][j - 1] % mod, gk[0][i][j] = inv(gk[1][i][j]);
        }

        int cass; scanf("%d", &cass); while ( cass -- ) {
                Solve ();
        }
}

# HDUOJ1028_IgnatiusandthePrincessIII

# 🔗

# 💡

本题就是一个母函数的模板题
这里使用FFT优化

1.构造本问题的生成函数
$(1+x+x^2+...+x^n)*(1+x^2+x^4+...+x^{\left\lfloor\frac n2\right \rfloor * 2})*(1+x^3+x^6+...+x^{\left\lfloor\frac n3\right \rfloor * 3}) *...$

2.转移为多项式问题
$(1+1x+1x^2+...+1x^n)*(1+0x^1+1x^2+0x^3+1x^4+...+1x^{\left \lfloor \frac n2\right \rfloor*2})*....$

每次合并创建的多项式给a
对b不断地重启与清零，a在求得后对虚部与某些实部清零

PS:小数据不推荐使用FFT，常数较大有些吃亏

# ✅

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>

using namespace std;

const int N = 30010;
const double PI = acos(-1.0);

int n, m, num;
struct Complex { // 复数结构体
        double x, y;
        Complex () {}
        Complex ( double _x, double _y ) : x(_x), y(_y) {}
        Complex friend operator+(Complex a, Complex b) { return {a.x + b.x, a.y + b.y}; }
        Complex friend operator-(Complex a, Complex b) { return {a.x - b.x, a.y - b.y}; }
        Complex friend operator*(Complex a, Complex b) { return {a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x}; }
} a[N], b[N];
int rev[N];
int bit, tot;

inline void FFT(Complex a[], int inv) {
        for ( int i = 0; i < tot; i ++ ) if (i < rev[i]) swap(a[i], a[rev[i]]);
        for ( int mid = 1; mid < tot; mid <<= 1) {
                Complex w1 = {cos(PI / mid), inv * sin(PI / mid)};
                for ( int i = 0; i < tot; i += mid * 2 ) {
                        Complex wk = {1, 0};
                        for (int j = 0; j < mid; j++, wk = wk * w1) {
                                Complex x = a[i + j], y = wk * a[i + j + mid];
                                a[i + j] = x + y, a[i + j + mid] = x - y;
                        }
                }
        }
}

int main(){
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
#endif
        num = 120;
        for ( int i = 0; i <= num; i ++ ) a[i].x = 1;
        n = num;
        for ( int k = 2; k <= num; k ++ ){
                m = num / k * k;
                
                while ( (1 << bit) < n + m + 1 ) bit ++;
                tot = 1 << bit;
                
                // b的重启读入
                for ( int i = 0; i <= m; i ++ ) b[i].x = (i % k == 0), b[i].y = 0; // k的倍数为1，否则为0。 虚部固定为0
                for ( int i = m + 1; i < tot; i ++ ) b[i].x = 0, b[i].y = 0; // 后面的实部和虚部也要为0

                // rev数组的更新
                for ( int i = 0; i < tot; i ++ ) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1)); // 二进制反转
                
                FFT(a, 1); FFT(b, 1);
                for ( int i = 0; i < tot; i ++ ) a[i] = a[i] * b[i];
                FFT(a, -1);
                
                // a的重启读入
                for ( int i = 0; i <= n + m; i ++ ) a[i] = {(double)(int)(a[i].x / tot + 0.5), 0}; // 读入后虚部重启为0
                for ( int i = n + m + 1; i <= N; i ++ ) a[i] = {0, 0}; // 实部虚部重启为0
                
                n += m; // 第一个多项式扩到n + m
        }
        
        while ( scanf("%d", &num) == 1 ){
                printf("%d\n", (int)(a[num].x + 0.5));
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

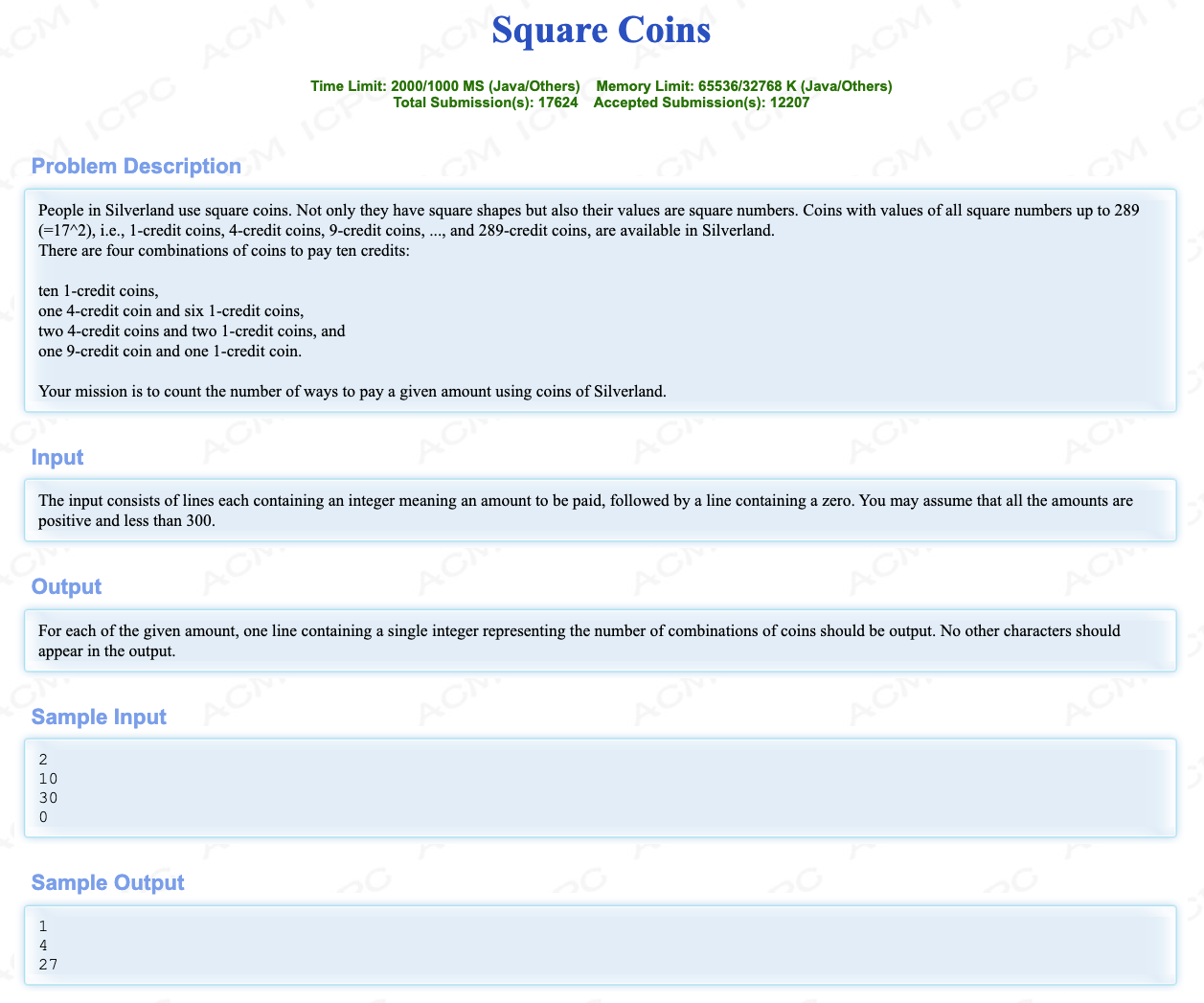
# HDUOJ1398_SquareCoins

# 🔗

# 💡

与FFT加速母函数一样，这里构造的多项式的系数为1的条件是i%(kk)==0
同样的，在枚举下一个括号的最后一个1时，使用m=num/(kk)(kk)

# ✅

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>

using namespace std;

const int N = 10210;
const double PI = acos(-1.0);

int n, m, num;
struct Complex { // 复数结构体
        double x, y;
        Complex () {}
        Complex ( double _x, double _y ) : x(_x), y(_y) {}
        Complex friend operator+(Complex a, Complex b) { return {a.x + b.x, a.y + b.y}; }
        Complex friend operator-(Complex a, Complex b) { return {a.x - b.x, a.y - b.y}; }
        Complex friend operator*(Complex a, Complex b) { return {a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x}; }
} a[N], b[N];
int rev[N];
int bit, tot;

inline void FFT ( Complex a[], int inv ) {
        for ( int i = 0; i < tot; i ++ ) if ( i < rev[i] ) swap(a[i], a[rev[i]]);
        for ( int mid = 1; mid < tot; mid <<= 1 ) {
                Complex w1 = {cos(PI / mid), inv * sin(PI / mid)};
                for ( int i = 0; i < tot; i += mid * 2 ) {
                        Complex wk = {1, 0};
                        for ( int j = 0; j < mid; j ++, wk = wk * w1 ) {
                                Complex x = a[i + j], y = wk * a[i + j + mid];
                                a[i + j] = x + y, a[i + j + mid] = x - y;
                        }
                }
        }
}

int main(){
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
#endif
        num = 300;
        for ( int i = 0; i <= num; i ++ ) a[i].x = 1;
        n = num;
        for ( int k = 2; k <= 17; k ++ ){
                m = num / (k * k) * (k * k);
                
                while ( (1 << bit) < n + m + 1 ) bit ++;
                tot = 1 << bit;
                
                // b的重启读入
                for ( int i = 0; i <= m; i ++ ) b[i].x = (i % (k * k) == 0), b[i].y = 0; // k的倍数为1，否则为0。 虚部固定为0
                for ( int i = m + 1; i < tot; i ++ ) b[i].x = 0, b[i].y = 0; // 后面的实部和虚部也要为0

                // rev数组的更新
                for ( int i = 0; i < tot; i ++ ) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1)); // 二进制反转
                
                FFT(a, 1); FFT(b, 1);
                for ( int i = 0; i < tot; i ++ ) a[i] = a[i] * b[i];
                FFT(a, -1);
                
                // a的重启读入
                for ( int i = 0; i <= n + m; i ++ ) a[i] = {(double)(int)(a[i].x / tot + 0.5), 0}; // 读入后虚部重启为0
                for ( int i = n + m + 1; i <= N; i ++ ) a[i] = {0, 0}; // 实部虚部重启为0
                
                n += m; // 第一个多项式扩到n + m
        }
        
        while ( scanf("%d", &num) == 1 && num ){
                printf("%d\n", (int)(a[num].x + 0.5));
        }
}





/*

int elem[18] = {0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289};

*/

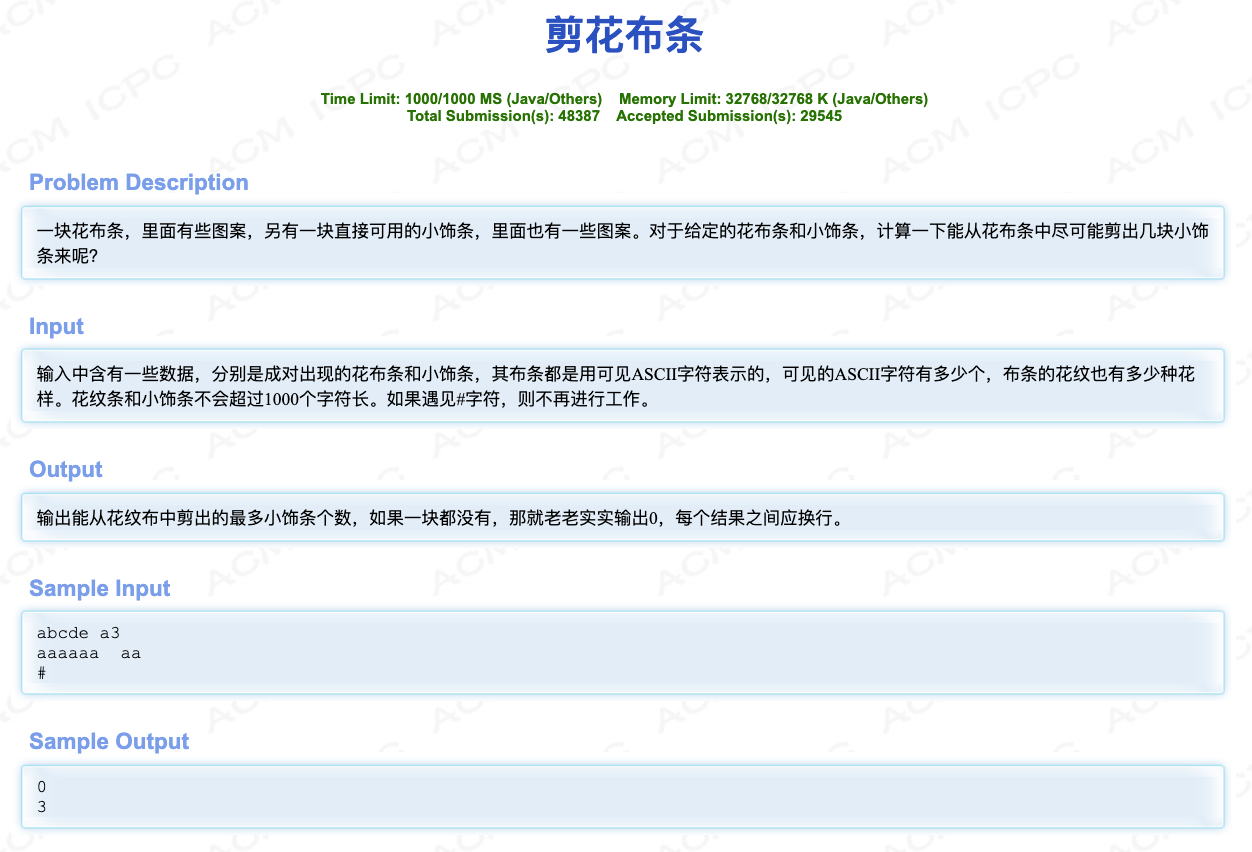
# HDUOJ2087_剪花布条

# 🔗

# 💡

本题可以使用fft去写
对每个字符c建立一个多项式，系数表示当前位是不是c，如果是为1，不是为0
b字符串反着建之后，每一次匹配可以与a的每一位形成一个固定的指数
然后直接访问指数得到c字符的贡献值即可
如果贡献值满m，那么就匹配成功，指针向后移动m位
否则匹配不成功，指针移动一位

# ✅

#include <iostream>
#include <map>
#include <algorithm>
#include <string>
#include <cstring>

using namespace std;


const int N = 3010;
const double PI = acos(-1.0);

int n, m;
struct Complex {
        double x, y;
        Complex friend operator + ( Complex a, Complex b ) { return {a.x + b.x, a.y + b.y}; }
        Complex friend operator - ( Complex a, Complex b ) { return {a.x - b.x, a.y - b.y}; }
        Complex friend operator * ( Complex a, Complex b ) { return { a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x}; }
} a[N], b[N]; 
int rev[N]; 
int bit, tot; 

inline void FFT ( Complex a[], int inv ) {
        for ( int i = 0; i < tot; i ++ ) if ( i < rev[i] ) swap(a[i], a[rev[i]]);
        for ( int mid = 1; mid < tot; mid <<= 1 ) { 
                Complex w1 = {cos(PI / mid), inv * sin(PI / mid)}; 
                for ( int i = 0; i < tot; i += mid * 2 ) {
                        Complex wk = {1, 0}; 
                        for ( int j = 0; j < mid; j ++, wk = wk * w1 ) { 
                                Complex x = a[i + j], y = wk * a[i + j + mid]; 
                                a[i + j] = x + y, a[i + j + mid] = x - y;      
                        }
                }
        }
}

string sa, sb;
int res[N];

inline void Solve ( char c ) {
        for ( int i = 0; i < N; i ++ ) a[i] = b[i] = {0, 0};
        for ( int i = 0; i < n; i ++ ) a[i].x = sa[i] == c;
        for ( int i = 0; i < m; i ++ ) b[m - i - 1].x = sb[i] == c;
        FFT(a, 1); FFT(b, 1);
        for ( int i = 0; i <= m + n - 2; i ++ ) a[i] = a[i] * b[i];
        FFT(a, -1);
        for ( int i = m - 1; i <= n - 1; i ++ ) res[i] += (int)(a[i].x / tot + 0.5);
}

int main () {

#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif

        while ( cin >> sa && sa != "#" ) { cin >> sb;
                
                memset( res, 0, sizeof res ); // 重启一下res数组
                memset( rev, 0, sizeof rev ); 
                tot = 0, bit = 0;
                
                n = sa.size(), m = sb.size();
                // 搭建rev数组
                while ( (1ll << bit) <= n + m - 2 ) bit ++; tot = 1ll << bit;
                for ( int i = 0; i <= n + m - 2; i ++ ) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
                
                // 把出现的字符扔进去
                map<char, int> chr;
                for ( int i = 0; i < n; i ++ ) chr[sa[i]] ++;
                for ( int i = 0; i < m; i ++ ) chr[sb[i]] ++;
                for ( auto i : chr ) Solve(i.first); // 各跑一遍积累贡献值
                
                int RES = 0;
                int id = m - 1; while ( id <= n - 1 ) {
                        if ( res[id] == m ) id += m, RES ++;
                        else id ++;
                }
                cout << RES << endl;

        }
}

# HDU2021多校(3)C_ForgivingMatching

# 🔗

# 💡

一看就是一个通配符下的字符串匹配问题
只需要对所有的字符分开考虑即可，就是正常的多项式然后一个式子反过来
求出从每一个位置作为开始的不相似度为多少，（m-匹配度）注意由于通配符的存在如果遇见两个通配符对应了话会重复多算九次，因此要以通配符为匹配符再扣一次 $9$ 就好了
最后求一下所有不相似度对应起始下标个数的前缀和，就是答案

# ✅

int n, m;
char s[N], t[N];

struct Complex {
    double x, y;
    Complex friend operator + ( Complex a, Complex b ) { return {a.x + b.x, a.y + b.y}; }
    Complex friend operator - ( Complex a, Complex b ) { return {a.x - b.x, a.y - b.y}; }
    Complex friend operator * ( Complex a, Complex b ) { return { a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x}; }
} a[N], b[N];
int rev[N], bit, tot;

inline void fft (Complex a[], int op) {
    for (int i = 0; i < tot; i ++) {
        if (i < rev[i]) swap(a[i], a[rev[i]]);
    }
    for (int mid = 1; mid < tot; mid <<= 1) {
        Complex w1 = {cos(PI / mid), op * sin(PI / mid)};
        for (int i = 0; i < tot; i += mid << 1) {
            Complex wk = {1, 0};
            for (int j = 0; j < mid; j ++, wk = wk * w1) {
                Complex x = a[i + j], y = wk * a[i + j + mid];
                a[i + j] = x + y, a[i + j + mid] = x - y;
            }
        }
    }
}

int res[N], cnt[N];

inline void Work (char c, int v) {
    for (int i = 0; i < tot; i ++) a[i] = b[i] = {0, 0};
    for (int i = 0; i < n; i ++) a[i].x = s[i] == c || s[i] == '*';
    for (int i = 0; i < m; i ++) b[i].x = t[m - i - 1] == c || t[m - i - 1] == '*';

    fft(a, 1); fft(b, 1);
    for (int i = 0; i < tot; i ++) a[i] = a[i] * b[i];
    fft(a, -1);
    
    for (int i = m - 1; i <= n + m - 2; i ++) 
        res[i - m + 1] += (int)(a[i].x / tot + 0.5) * v;
}

inline void Solve () {
    scanf("%d%d", &n, &m);
    scanf("%s%s", s, t);

    for (int i = 0; i <= n; i ++) cnt[i] = res[i] = 0;
    bit = 0; while ((1 << bit) < n + m - 1) bit ++; tot = 1 << bit;
    for (int i = 0; i < tot; i ++) rev[i] = rev[i >> 1] >> 1 | ((i & 1) << (bit - 1));

    for (char i = '0'; i <= '9'; i ++) Work(i, 1);
    Work('*', -9);

    for (int i = 0; i < n - m + 1; i ++) cnt[m - res[i]] ++;
    for (int i = 1; i <= m + 1; i ++) cnt[i] += cnt[i - 1];


    for (int i = 0; i <= m; i ++) printf("%d\n", cnt[i]);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

# ICPC2021大田H_RockPaperScissors

# 🔗

# 💡

本题是用于解决字符串匹配相似度的
本题最朴素的写法就是暴力匹配，然后时间是O(nm)，稳T
最显眼的还是只有三个字符，字符串在一位一位匹配的时候，很像多项式卷积的过程，用到一位对应一位求解
那么其实可以反转一下b串，让这个对应刚好使得指数为定值
那么我们也可以利用多项式卷积，把一个字符串以某个字符匹配时的相似度做一个多项式
即我们在以字符c匹配时令一个位置的系数为[s[i]=c]
那么可以构造出这样一个多项式
$\begin{aligned}&a_0x^0+a_1x^1+a_2x^2+a_3x^3\\&b_0x^2+x_1x^1+x_2x^0 \end{aligned}$
这样在第一次匹配时，即寻找指数为2的卷积结果。第二次匹配时寻找指数为3的卷积结果...

# ✅

#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;

const int N = 300010;
const double PI = acos(-1.0);
int res[N];

int n, m;
struct Complex { // 复数结构体
        double x, y;
        Complex friend operator + ( Complex a, Complex b ) { return {a.x + b.x, a.y + b.y}; }
        Complex friend operator - ( Complex a, Complex b ) { return {a.x - b.x, a.y - b.y}; }
        Complex friend operator * ( Complex a, Complex b ) { return { a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x}; }
} a[N], b[N];
int rev[N];
int bit, tot; 
string sa, sb;

inline void FFT ( Complex a[], int inv ) {
        for ( int i = 0; i < tot; i ++ ) if ( i < rev[i] ) swap(a[i], a[rev[i]]);
        for ( int mid = 1; mid < tot; mid <<= 1 ) {
                Complex w1 = {cos(PI / mid), inv * sin(PI / mid)};
                for ( int i = 0; i < tot; i += mid * 2 ) {
                        Complex wk = {1, 0};
                        for ( int j = 0; j < mid; j ++, wk = wk * w1 ) {
                                Complex x = a[i + j], y = wk * a[i + j + mid];
                                a[i + j] = x + y, a[i + j + mid] = x - y;
                        }
                }
        }
}

inline void Solve ( char c ) {
        for ( int i = 0; i < N; i ++ ) a[i] = b[i] = {0, 0};
        for ( int i = 0; i < n; i ++ ) a[i].x = (sa[i] == c);
        for ( int i = 0; i < m; i ++ ) b[i].x = (sb[m - i - 1] == c);
        FFT(a, 1); FFT(b, 1);
        for ( int i = 0; i < tot; i ++ ) a[i] = a[i] * b[i];
        FFT(a, -1);  
        for ( int i = m - 1; i <= n + m - 2; i ++ ) {
                res[i] += (int)(a[i].x / tot + 0.5);
        }
}

int main () {
        cin >> n >> m >> sa >> sb;
        for ( int i = 0; i < m; i ++ ) {
                if ( sb[i] == 'S' ) sb[i] = 'P';
                else if ( sb[i] == 'P' ) sb[i] = 'R';
                else sb[i] = 'S';
        }
        while ( (1ll << bit) <= n + m - 2 ) bit ++; tot = 1ll << bit;
        for ( int i = 0; i < tot; i ++ ) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));

        Solve('R'); Solve('S'); Solve('P');
        int RES = 0;
        for ( int i = m - 1; i <= n + m - 2; i ++ ) RES = max ( RES, res[i] );
        cout << RES << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

# 洛谷P5339_唱、跳、rap和篮球

# 🔗

# 💡

正着考虑要 $dp$ ，要枚举四种人的人数状态，比较麻烦，正难则反考虑至少有一组的情况
一组为 $[1,2,3,4]$ ，那么对于 $i$ 组，还剩下 $n-4i$ 个散点，共 $n-3i$ 个点，选择 $i$ 个位置为组，方案数为 $\binom{n-3i}{i}$
那么这四种分别剩下 $a-i,b-i,c-i,d-i$
如果各用 $a',b',c',d'$ 组成 $n-4i$ ，那么方案数为 $\frac{(n-4i)!}{(a')!(b')!(c')!(d')!}$
总方案依然是不能枚举，但是可以从上面的得到启发，公式为
$\sum\limits_{a'=1}^{a-i}\sum\limits_{b'=1}^{b-i}\sum\limits_{c'=1}^{c-i}\sum\limits_{d'=1}^{d-i}\frac{(n-4i)!}{(a')!(b')!(c')!(d')!}[a'+b'+c'+d'=n-4i]$
这个式子就是一个卷积式
故提出四个多项式把它们乘一下就可以了（令乘出来的多项式为 $g$ ，第 $i$ 位的系数为 $g[i]$ ）
则在容斥下，最终方案等于 $\sum\limits_{i=0}^{min(a,b,c,d,\left\lfloor\frac n4\right\rfloor)}(-1)^i\binom{n-3i}{i}g[n-4i]$

# ✅

const int mod = 998244353;
inline int ksm (int a, int b) { int res = 1; while (b) { if (b & 1) res = (ll)res * a % mod; a = (ll)a * a % mod; b >>= 1; } return res; }
inline int inv (int x)  {return ksm(x, mod - 2);}

const int N = 1e4 + 10;
int f[N], ivf[N];
inline int C (int n, int m) { return (ll)f[n] * ivf[n - m] % mod * ivf[m] % mod; }

int bit, tot, rev[N];
inline void initPoly (int n) {
    bit = 0;
    while ((1 << bit) <= n) bit ++;
    tot = 1 << bit;
    for (int i = 0; i < tot; i ++) 
        rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
}
inline void Ntt (int *a, int op) {
    for (int i = 0; i < tot; i ++) if (i < rev[i]) swap(a[i], a[rev[i]]);
    for (int mid = 1; mid < tot; mid <<= 1) {
        int g1 = ksm(3, (mod - 1) / (mid << 1));
        if (op == -1) g1 = inv(g1);
        for (int i = 0; i < tot; i += mid << 1) {
            int gk = 1;
            for (int j = 0; j < mid; j ++, gk = (ll)gk * g1 % mod) {
                int x = a[i + j], y = (ll)a[i + j + mid] * gk % mod;
                a[i + j] = (x + y) % mod;
                a[i + j + mid] = (x - y + mod) % mod;
            }
        }
    }
    if (op == -1) {
        int iv = inv(tot);
        for (int i = 0; i < tot; i ++) a[i] = (ll)a[i] * iv % mod;
    }
}
inline void Mul (int *a, int *b) {
    Ntt(a, 1); Ntt(b, 1);
    for (int i = 0; i < tot; i ++) a[i] = (ll)a[i] * b[i] % mod;
    Ntt(a, -1);
}

int n, a, b, c, d;
int ma[N], mb[N], mc[N], md[N];
inline int Sol (int blk) {
    memset(ma, 0, sizeof ma);
    memset(mb, 0, sizeof mb);
    memset(mc, 0, sizeof mc);
    memset(md, 0, sizeof md);
    for (int i = 0; i <= min(n - 4 * blk, a - blk); i ++) ma[i] = ivf[i];
    for (int i = 0; i <= min(n - 4 * blk, b - blk); i ++) mb[i] = ivf[i];
    for (int i = 0; i <= min(n - 4 * blk, c - blk); i ++) mc[i] = ivf[i];
    for (int i = 0; i <= min(n - 4 * blk, d - blk); i ++) md[i] = ivf[i];
    initPoly((n - 4 * blk) * 4);

    Ntt(ma, 1); Ntt(mb, 1); Ntt(mc, 1); Ntt(md, 1);
    for (int i = 0; i < tot; i ++) ma[i] = (ll)ma[i] * mb[i] % mod * mc[i] % mod * md[i] % mod;
    Ntt(ma, -1);
    return (ll)f[n - 4 * blk] * ma[n - 4 * blk] % mod;
}

int main () {
    f[0] = 1;
    for (int i = 1; i < N; i ++) f[i] = (ll)f[i - 1] * i % mod;
    ivf[N - 1] = inv(f[N - 1]);
    for (int i = N - 2; i >= 0; i --) ivf[i] = (ll)ivf[i + 1] * (i + 1) % mod;

    int res = 0;
    scanf("%d%d%d%d%d", &n, &a, &b, &c, &d);
    for (int i = 0; i <= min({a, b, c, d, n / 4}); i ++) {
        if (i & 1) res -= (ll)C(n - 3 * i, i) * Sol(i) % mod;
        else       res += (ll)C(n - 3 * i, i) * Sol(i) % mod;
        res = (res % mod + mod) % mod;
    }
    printf("%d\n", res);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

# 拉格朗日插值

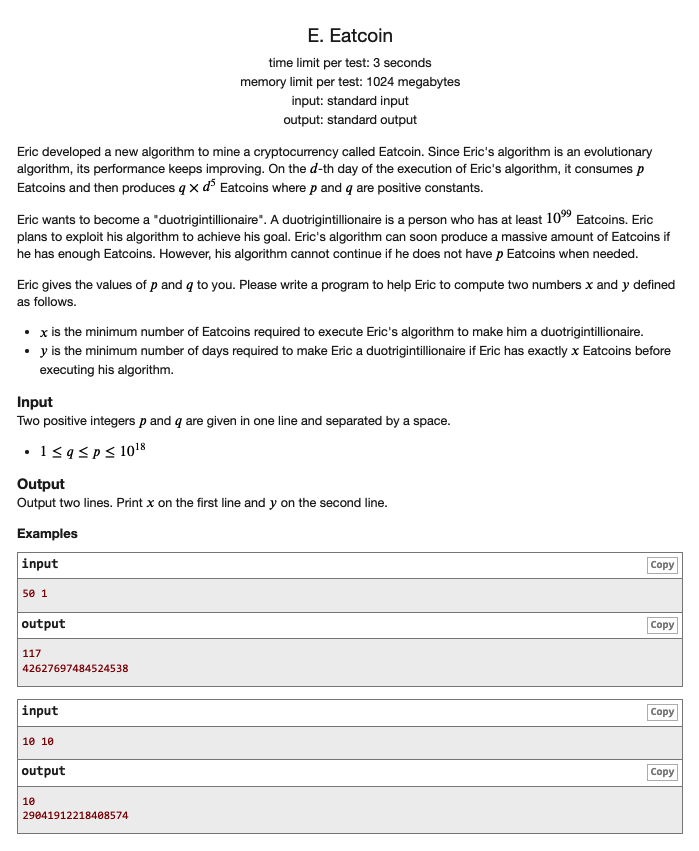
# ICPC2021台湾省赛E_EatCoin

# 🔗

# 💡

首先我们化简一下问题
第 $\inline d$ 天算法会消耗 $\inline p$ ，获得 $\inline qd^5$
也就是若算法可以执行，那么将获得 $\inline -p+qd^5$
若开始前有 $\inline x$ ，执行 $\inline y$ 天后会成为 $\inline x-py+q\sum\limits_{i=1}^yi^5$
我们要让这个值 $\inline \ge10^{99}$
同时要保证 $\inline \forall&space;j\in[0,y],x-pj+q\sum\limits_{i=1}^ji^5\ge&space;p$ ，不然就继续不了算法了，（左侧如果开始上升那么就可以保证了

我们求 $\inline \sum\limits_{i=1}^ji^5$ 可以用求自然数幂和 (opens new window)的方式进行拉格朗日插值，这里 $\inline k$ 不大，所以就是常数复杂度
我们求 $\inline x$ 可以使用第二个限制进行二分
求 $\inline y$ 可以使用第一个进行二分

数很大，开java的BigInteger

# ✅

public class Main{
        static int N = 100;
        static BigInteger zero = BigInteger.ZERO;
        static BigInteger one = BigInteger.ONE;
        static BigInteger two = BigInteger.valueOf(2);
        static BigInteger six = BigInteger.valueOf(6);
        static BigInteger ten = BigInteger.TEN;
        static BigInteger five = BigInteger.valueOf(5);

        static BigInteger ksm ( BigInteger a, BigInteger b ) {
                BigInteger res = one;
                while ( b.compareTo(zero) == 1 ) {
                        if ( b.mod(two).compareTo(one) == 0 ) {
                                res = res.multiply(a);
                        } a = a.multiply(a);
                        b = b.divide(two);
                } return res;
        }
        static BigInteger[] fac = new BigInteger[N];
        static BigInteger[] pre = new BigInteger[N];
        static BigInteger[] suf = new BigInteger[N];
        static BigInteger pownk ( BigInteger n, int k ) {
                BigInteger y = zero, up = zero, down = zero, res = zero;
                fac[0] = pre[0] = suf[k + 3] = one;
                for ( int i = 1; i <= k + 2; i ++ ) {
                        pre[i] = pre[i - 1].multiply(n.subtract(BigInteger.valueOf(i)));
                        fac[i] = fac[i - 1].multiply(BigInteger.valueOf(i));
                }
                for ( int i = k + 2; i >= 1; i -- ) {
                        suf[i] = suf[i + 1].multiply(n.subtract(BigInteger.valueOf(i)));
                }
                for ( int i = 1; i <= k + 2; i ++ ) {
                        y = y.add(ksm(BigInteger.valueOf(i), BigInteger.valueOf(k)));
                        up = pre[i - 1].multiply(suf[i + 1]);
                        down = fac[i - 1].multiply(fac[k + 2 - i]).multiply(((k - i) & 1) > 0 ? zero.subtract(one) : one);
                        res = res.add(y.multiply(up).divide(down));
                }
                return res;
        }
        static BigInteger q, p;
        static BigInteger x, y;

        static boolean check ( BigInteger j ) {
                BigInteger a = x.subtract(p.multiply(j)).add(q.multiply(pownk(j, 5)));
                BigInteger b = ksm(ten, BigInteger.valueOf(99));
                if ( a.compareTo(b) >= 0 ) return true;
                return false;
        }
        static boolean chk_x ( BigInteger xx ) {
                boolean flg = false;
                for ( Long i = Long.valueOf(0);; i ++ ) {
                        if ( xx.subtract(p.multiply(BigInteger.valueOf(i))).add(q.multiply(pownk(BigInteger.valueOf(i), 5))).compareTo(p) == -1 ) break;
                        if ( i > Long.valueOf(0) && xx.subtract(p.multiply(BigInteger.valueOf(i))).add(q.multiply(pownk(BigInteger.valueOf(i), 5))).compareTo(xx.subtract(p.multiply(BigInteger.valueOf(i - 1))).add(q.multiply(pownk(BigInteger.valueOf(i - 1), 5)))) == 1 ) { flg = true; break;}
                }
                return flg;
        }

        public static void main (String[] args) {
                Scanner input = new Scanner(System.in);
                p = input.nextBigInteger();
                q = input.nextBigInteger();
                x = p;
                y = zero;
                
                BigInteger l = zero, r = ksm(ten, BigInteger.valueOf(20));
                while ( l.compareTo(r) == -1 ) {
                        BigInteger mid = l.add(r).divide(two);
                        if ( chk_x(mid) ) r = mid;
                        else l = mid.add(one);
                }
                x = l;

                l = zero; r = ksm(ten, BigInteger.valueOf(30));
                while ( l.compareTo(r) == -1 ) {
                        BigInteger mid = l.add(r).divide(two);
                        if ( check(mid) ) r = mid;
                        else l = mid.add(one);
                }
                y = l;
                System.out.println(x + "\n" + y);
        }
}

莫比乌斯反演置换群