结论
Chivas-Regal
#
# 牛客2021多校(1)F_Find3-friendlyIntegers
# 🔗
https://ac.nowcoder.com/acm/contest/11166/F
# 💡
这种数字类问题，可以先想利用前缀求区间
但是这一题发现
在二位数还勉强可以构造
在三位数不管如何构造，也构造不出来一个不能"模三"的数
所以在100以内暴力查询
100以外就直接计算有多少个数即可
# ✅
/*
________ _ ________ _
/ ______| | | | __ | | |
/ / | | | |__| | | |
| | | |___ _ _ _ ___ _ _____ | ___| ______ _____ ___ _ | |
| | | __ \ |_| | | | | | _\| | | ____| | |\ \ | __ | | _ | | _\| | | |
| | | | \ | _ | | | | | | \ | | \___ | | \ \ | |_/ _| | |_| | | | \ | | |
\ \______ | | | | | | \ |_| / | |_/ | ___/ | | | \ \ | /_ \__ | | |_/ | | |
Author : \________| |_| |_| |_| \___/ |___/|_| |_____| _________|__| \__\ |______| | | |___/|_| |_|
____| |
\_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF
#define ll long long
#define ull unsigned long long
#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'
#define CHIVAS_ int main()
#define _REGAL exit(0)
#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
//#define map unordered_map
#define _int(a) int a; cin >> a
#define _ll(a) ll a; cin >> a
#define _char(a) char a; cin >> a
#define _string(a) string a; cin >> a
#define _vectorInt(a, n) vector<int>a(n); cin >> a
#define _vectorLL(a, b) vector<ll>a(n); cin >> a
#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cass = inputInt(); cass; cass--)
#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1
using namespace std;
template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
template<typename T> vector<T>& operator-- (vector<T> &v){for (auto& i : v) --i; return v;}
template<typename T> vector<T>& operator++ (vector<T> &v){for (auto& i : v) ++i; return v;}
template<typename T> istream& operator>>(istream& is, vector<T> &v){for (auto& i : v) is >> i; return is;}
template<typename T> ostream& operator<<(ostream& os, vector<T> v){for (auto& i : v) os << i << ' '; return os;}
inline int inputInt(){int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);}
inline void outInt(int X){if(X<0) {putchar('-'); X=~(X-1);}int s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline ll inputLL(){ll X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1); }
inline void outLL(ll X){if(X<0) {putchar('-'); X=~(X-1);}ll s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline bool calc(ll x){
if(x / 10 == 0){
if(x % 3 == 0) return true;
else return false;
}
if(x % 3 == 0 || x % 10 % 3 == 0 || x / 10 % 3 == 0) return true;
return false;
}
CHIVAS_{
int cass;
EACH_CASE(cass){
ll L, R; cin >> L >> R;
ll res = 0;
ll i = L;
for(; i <= MIN(99ll, R); i ++) res += calc(i);//暴力查询
if(i <= R) res += (R - i + 1);//超100的数
cout << res << endl;
}
_REGAL;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
# CodeForces1629D_PeculiarMoviePreferences
# 🔗
# 💡
对于不超过三个字符的串，这是一个突破口
如果一个串长度为 或者自成回文串，那么就一定是 YES
那么剩下的就是长度 的串了
他们需要和别的串组合
可以想到的是，如果一个拼接串回文，那么它第一个串一定和最后一个串对应
因此如果你可以造出来回文串，那么两个就可以
问题就简单了
对于串长我们找 、 、 、 的串就可以了
拿个 map 标记一下遍历
# ✅
inline void Solve () {
int n; cin >> n;
vector<string> vec;
map<string, int> mp;
bool flag = false;
for ( int i = 0; i < n; i ++ ) {
string s; cin >> s;
vec.push_back(s); mp[s] ++;
if ( s.size() == 1 ) {
flag = true;
} else if ( s.size() == 2 ) {
if ( s[0] == s[1] ) flag = true;
} else if ( s.size() == 3 ) {
if ( s[0] == s[2] ) flag = true;
}
}
if ( flag ) {
cout << "YES" << endl;
return;
}
for ( int i = 0; i < n; i ++ ) {
mp[vec[i]] --;
string rev = vec[i]; reverse(rev.begin(), rev.end());
if ( mp[rev] ) {
cout << "YES" << endl;
return;
}
if ( vec[i].size() == 2 ) {
for ( char c = 'a'; c <= 'z'; c ++ ) {
string cur = vec[i] + c;
reverse(cur.begin(), cur.end());
if ( mp[cur] ) {
cout << "YES" << endl;
return;
}
}
} else {
rev = rev.substr(1, 2);
if ( mp[rev] ) {
cout << "YES" << endl;
return;
}
}
}
cout << "NO" << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
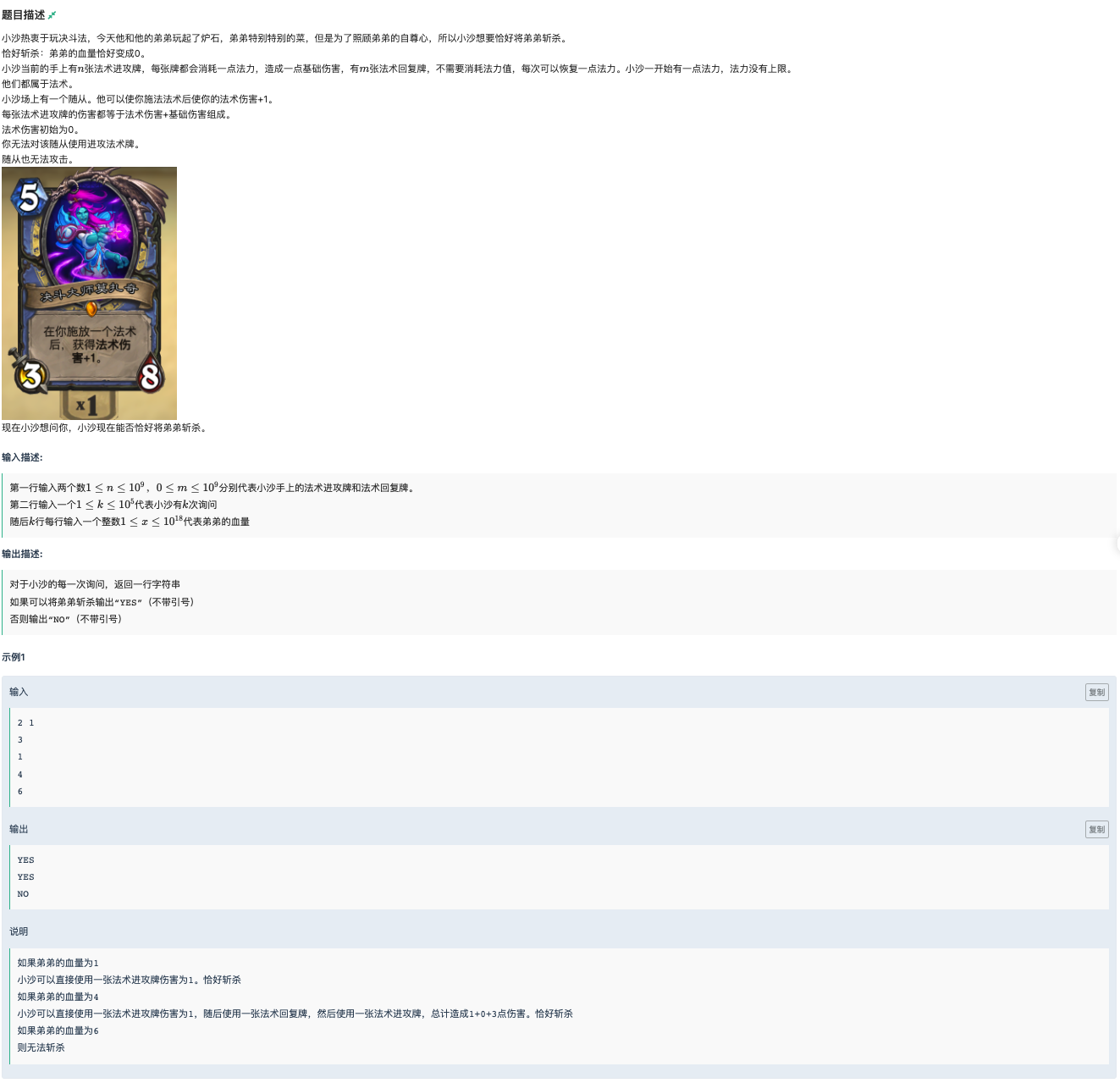
# 牛客2022寒假算法基础集训营2A_小沙的炉石
# 🔗
# 💡
我们多次计算不难发现一个性质，就是在使用同样数量的攻击卡、插入回蓝时，所造成的伤害是固定的
那么我们设置我们使用 次攻击
最小的伤害是一次攻击一次恢复一次攻击....一次恢复一次攻击
最大的伤害是恢复完 次之后再全部攻击
那么伤害是处在 之间，化简最小值为
我们要找到最大 满足 ，因为再大就超了就不能完美击败了
那么就是 ，对于这个 我们带入公式去求最大值 mx
看看最大值是否
# ✅
int main () {
ios::sync_with_stdio(false);
ll n, m; cin >> n >> m;
ll k; cin >> k;
while ( k -- ) {
ll hp; cin >> hp;
ll a = min(n, m + 1);
a = min(a, (ll)sqrt(hp));
if ( (2 * m + a + 1) * a / 2 >= hp ) cout << "YES" << endl;
else cout << "NO" << endl;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
2
3
4
5
6
7
8
9
10
11
12
13
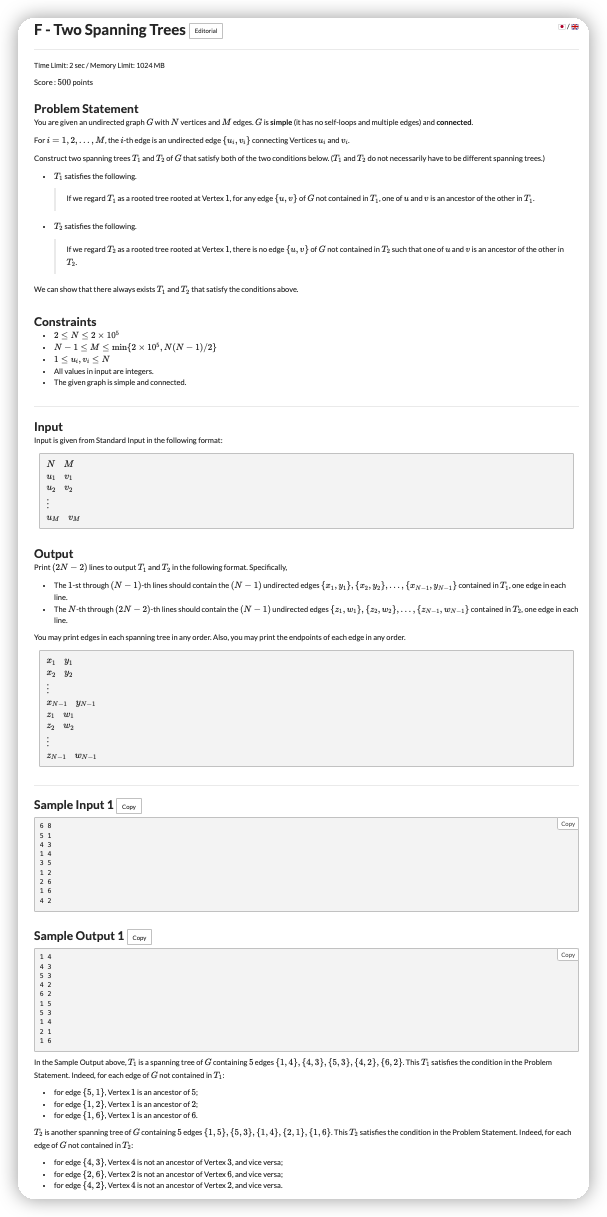
# ABC251F_TwoSpanningTrees
# 🔗
# 💡
第一问中，让我们删去的边在生成树中为祖孙关系，那么就是要一条链
在构造的时候肯定也是希望尽可能是一条链最好（如果不是一条链那就再加一条链），这样的话如果删去的边肯定会连接一条链的某两个点，也就能满足要求
就是一条路走到尽头的方法，就直接上 即可
与之相对的，第二问肯定希望越浅越好，那就上
# ✅
const int N = 2e5 + 10;
int n, m;
vector<pair<int, int> > graph;
const int M = 4e5 + 10;
struct Edge {
int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to) {
edge[++cnt] = {head[from], to};
head[from] = cnt;
}
int vis[N];
vector<pair<int, int> > res1;
inline void dfs (int u) {
if (vis[u]) return; vis[u] = 1;
for (int i = head[u]; i; i = edge[i].nxt) {
int v = edge[i].to;
if (!vis[v])
res1.push_back({u, v}),
dfs(v);
}
}
vector<pair<int, int> > res2;
inline void bfs (int u) {
memset(vis, 0, sizeof vis);
queue<int> que;
que.push(u); vis[u] = 1;
while (!que.empty()) {
int u = que.front(); que.pop();
for (int i = head[u]; i; i = edge[i].nxt) {
int v = edge[i].to;
if (!vis[v])
res2.push_back({u, v}),
que.push(v),
vis[v] = 1;
}
}
}
int main () {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
graph = vector<pair<int, int> >(m);
for (auto &[x, y] : graph)
cin >> x >> y,
add_Edge(x, y), add_Edge(y, x);
dfs(1);
for (auto [x, y] : res1) cout << x << " " << y << "\n";
bfs(1);
for (auto [x, y] : res2) cout << x << " " << y << "\n";
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
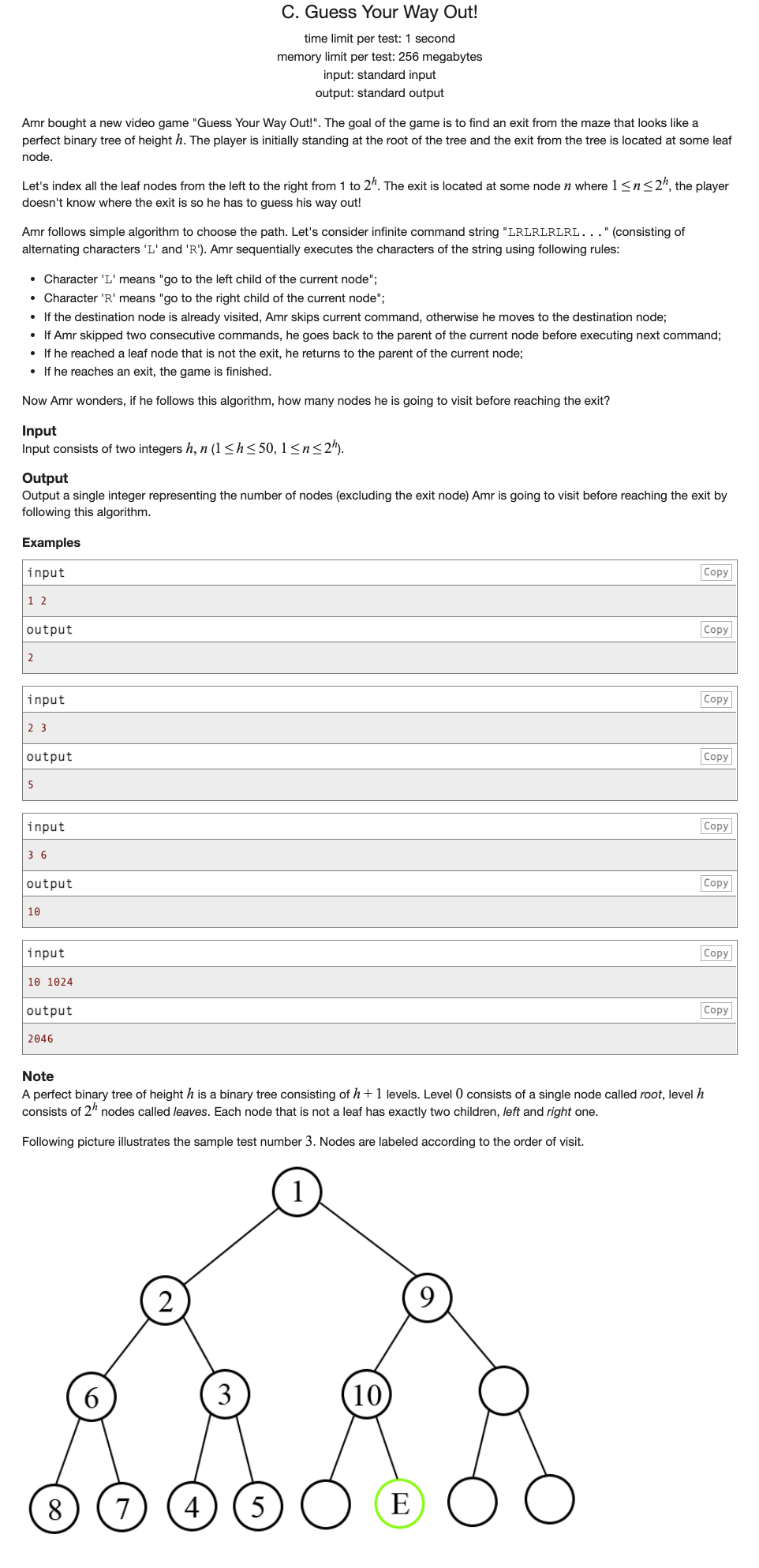
# CodeForces507C_GuessYourWayOut
# 🔗
# 💡
这道题刚开始可能没有什么思路，在纸上画一下一个比较大的树的遍历顺序并把值写上去
发现在把叶子分为两部分时，左区间的右端点与右区间的左端点的差值为，再进一步划分就是
每一个区间的左右端点差值也有类似的性质
一个节点的左儿子的树在中间两个数是递增的，右儿子中间两个数是递减的
把所有的可以用的性质挖出来之后
我们发现可以二分查找地推出来我们找的序号的值
设变量l,r是左右总区间端点序号，l1,r1是左区间的两个端点序号，l2,r2是右区间的两个端点序号
val_l1,val_r1是左区间的两个端点值，val_l2,val_r2是右区间的两个端点值
并建立一个VAL_L用来继承上一步求得的val_l1或者val_l2（具体是哪个要根据我们选择的是左区间还是右区间
推到最后l=r时停止
# ✅
#include <iostream>
#include <cmath>
#include <algorithm>
#define ll long long
using namespace std;
ll h, n;
int main () {
#ifndef ONLINE_JUDGE
freopen("in.in", "r", stdin);
freopen("out.out", "w", stdout);
#endif
cin >> h >> n;
ll l = 1, r = (1ll << h);
ll l1, r1, l2, r2;
ll val_l1 = (1ll << h), val_r1, val_l2, val_r2 = (1ll << (h + 1)) - 1;
ll dep = (1ll << h); // 两端点差值
ll val_l = (1ll << h);
bool flag = true; // 选左儿子false, 选右儿子true
while ( l != r ) {
// 8个变量的值根据结论进行推
l1 = l, r1 = l1 + dep / 2 - 1,
l2 = r1 + 1, r2 = r;
val_l1 = val_l;
val_r1 = val_l1 - dep / 2 + 1;
if ( flag )
val_l2 = val_r1 + dep - 1;
else
val_l2 = val_r1 - dep + 1;
val_r2 = val_l2 + dep / 2 - 1;
if ( l1 <= n && n <= r1 ) // 进入左区间
l = l1, r = r1,
val_l = val_l1,// 继承左区间的左端点
flag = false;
else // 进入右区间
l = l2, r = r2,
val_l = val_l2,// 继承右区间的左端点
flag = true;
dep /= 2;
}
cout << val_l - 1 << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# CodeForces1634B_FortuneTelling
# 🔗
# 💡
本题在不深入了解异或与加法的关系时，需要猜结论
首先题目确保只有一个人能赢， 与 的不同之处有一个是奇偶性且 一定是奇偶中的一个
所以考虑奇偶性
一个易得的性质：加法和异或奇偶性相同
即：
那么我们让 和 看看哪个奇偶性和 相同就是谁赢
# ✅
inline void Solve () {
ll n, x, y; cin >> n >> x >> y;
vector<ll> a(n + 5);
ll sum = 0;
for ( int i = 0; i < n; i ++ ) {
cin >> a[i];
sum += a[i];
}
ll ali = x;
ll bob = x + 3;
ali += sum;
bob += sum;
if ( ali % 2 == y % 2 ) cout << "Alice" << endl;
else cout << "Bob" << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# CodeForces1638B_OddSwapSort
# 🔗
# 💡
那么交换位置只可以发生在两个奇偶性不同的数之间
意味着后面的奇数不可能跨越前面的奇数，偶数一样
所以我们只需要看偶数序列和奇数序列是否排序好了就行了
# ✅
inline void Solve () {
int n; cin >> n;
vector<int> odd, eve;
for ( int i = 0; i < n; i ++ ) {
int x; cin >> x;
if ( x & 1 ) odd.push_back(x);
else eve.push_back(x);
}
if (is_sorted(odd.begin(), odd.end()) && is_sorted(eve.begin(), eve.end())) cout << "Yes" << endl;
else cout << "No" << endl;
}
int main () {
ios::sync_with_stdio(false);
int cass; cin >> cass; while ( cass -- ) {
Solve ();
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# HDU2021多校(5)3_VCisAllYouNeed
# 🔗
# 💡
画一个图
发现基础的二维控制在三个点以内就行
后面每多一维其实是有给出一个边去分割
此时也就是点数<=维度+1即可
# ✅
int main () {
ios::sync_with_stdio(false);
int cass;
for ( cin >> cass; cass; cass -- ) {
ll n, k; cin >> n >> k;
if ( n - k < 2 ) cout << "Yes" << endl;
else cout << "No" << endl;
}
}
1
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
# HDU2021多校(5)7_BanZhuan
# 🔗
# 💡
首先看最大费用
就是不仅很坦诚地造出来一个n阶方块
同时还要每个都从最高的位置往下落
那么就是
再看看最小费用
每一个都是刚好放上去而不让它落下，然后能缺的就缺
下面的一层正常放
画一个二阶发现最划算的是在x=1和y=1的两侧构造一面墙
同时交界处不放方块
那么就是
数很大还要取模，直接开BigInteger
# ✅
public class Main {
static BigInteger m = BigInteger.valueOf(1000000007);
static BigInteger one = BigInteger.ONE;
static BigInteger two = BigInteger.valueOf(2);
static BigInteger zero = BigInteger.ZERO;
static BigInteger six = BigInteger.valueOf(6);
static BigInteger ksm ( BigInteger a, BigInteger b ) {
BigInteger res = BigInteger.ONE;
while ( b.compareTo(BigInteger.ZERO) == 1 ) {
if ( b.mod(two).compareTo(BigInteger.ONE) == 0 ) res = res.multiply(a).mod(m);
a = a.multiply(a).mod(m);
b = b.divide(two);
}
return res;
}
public static void main ( String[] args ) {
boolean flag = true;
Scanner input = new Scanner(System.in);
int cass = input.nextInt(); while ( cass -- > 0 ) {
BigInteger n = input.nextBigInteger();
BigInteger resBig = n.multiply(n).multiply(n).multiply(n);
resBig = resBig.multiply(n.add(one)).multiply(n.add(one));
resBig = resBig.multiply(n.multiply(two).add(one));
resBig = resBig.divide(six).divide(two).mod(m);
BigInteger resSml = n.multiply(n);
resSml = resSml.multiply(n.add(one)).multiply(n.add(one));
resSml = resSml.multiply(n.multiply(two).add(one));
resSml = resSml.divide(six).divide(two).mod(m);
BigInteger tmp1 = two.add(n).multiply(n.subtract(one)).divide(two);
BigInteger tmp2 = n.multiply(n.add(one)).multiply(n.multiply(two).add(one)).divide(six).subtract(one);
tmp2 = tmp2.multiply(tmp1);
tmp1 = tmp1.multiply(tmp1);
resSml = resSml.add(tmp2).add(tmp1).mod(m);
System.out.println(resSml);
System.out.println(resBig);
flag = false;
}
input.close();
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43