主席树

#

---

洛谷P1972_HH的项链

🔗

💡

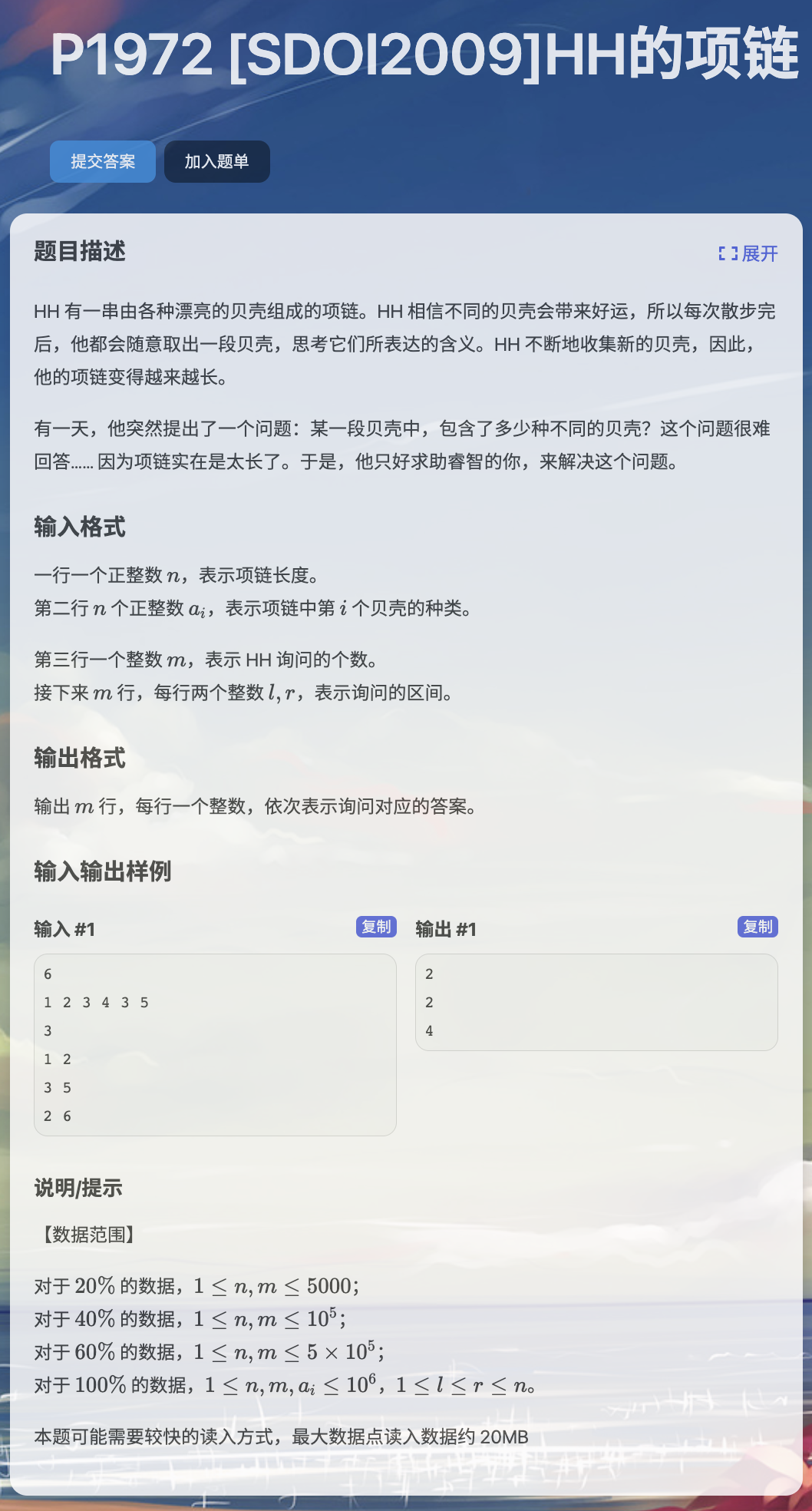
一道主席树查找区间不同数的个数的模板题
对于每个数，就算出现很多次，我们在求的时候实际关注的还是最右侧的位置
那么在本题里面可以用主席树构建前缀数列中每一个数出现的最右侧的位置
这样我们就可以在很少的修改下，将一个数列的每个前缀数列中的每个数出现的最右侧位置记录下来了
也可以做到对于一个位置要么是 $0$ 要么是 $1$ ，可以实现直接地区间查询
那么还是两步

$1.$插入
在 $a[i]$ 插入时以上一个版本删掉之前 $a[i]$ 出现过的位置，在当前版本加入 $i$ 这个位置
$2.$查询
输入 $l, r$
对于版本 $r$，查询数列中 $l$ 位置之后的数的出现个数
若pos <= mid，那么我们该向左固定区间，同时得知右一半的区间均满足，则 res += query () + sgtr[sgtr[rt].r].sum
若pos > mid，那么我们该向右固定区间，就还是正常的查询 res += query()

✅

#include <iostream>
#include <vector>
#include <algorithm>
#define ll long long

using namespace std;

const int N = 1e6 + 10;
int a[N], n, m;
struct node {
        int l, r, sum;
} sgtr[N * 40];
int root[N], tot;
int lastPos[1000010];

inline void insert ( int l, int r, int pre, int &now, int p, int op ) {
        sgtr[++tot] = sgtr[pre];
        now = tot;
        sgtr[now].sum += op;

        if ( l == r ) return;

        int mid = (l + r) >> 1;
        if ( p <= mid ) insert ( l, mid, sgtr[pre].l, sgtr[now].l, p, op );
        else insert ( mid + 1, r, sgtr[pre].r, sgtr[now].r, p, op );
}

inline int query ( int l, int r, int rt, int pos ) {
        if ( l == r ) return sgtr[rt].sum;
        int res = 0, mid = (r + l) >> 1;
        if ( pos <= mid ) res += query ( l, mid, sgtr[rt].l, pos ) + sgtr[sgtr[rt].r].sum;
        else res += query ( mid + 1, r, sgtr[rt].r, pos );
        return res;
}

int main () {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif
        scanf("%d", &n);
        for ( int i = 1; i <= n; i ++ ) 
                scanf("%d", &a[i]);

        for ( int i = 1; i <= n; i ++ ) {
                if ( lastPos[a[i]] ) {
                        insert ( 1, n, root[i - 1], root[i], lastPos[a[i]], -1 );
                        insert ( 1, n, root[i], root[i], i, 1 );
                } else {
                        insert ( 1, n, root[i - 1], root[i], i, 1 );
                }
                lastPos[a[i]] = i;
        }

        scanf("%d", &m);
        while ( m -- ) {
                int l, r; scanf("%d%d", &l, &r);
                printf("%d\n", query(1, n, root[r], l) );
        }
}

---

洛谷P4137_RmqProblemMex

🔗

💡

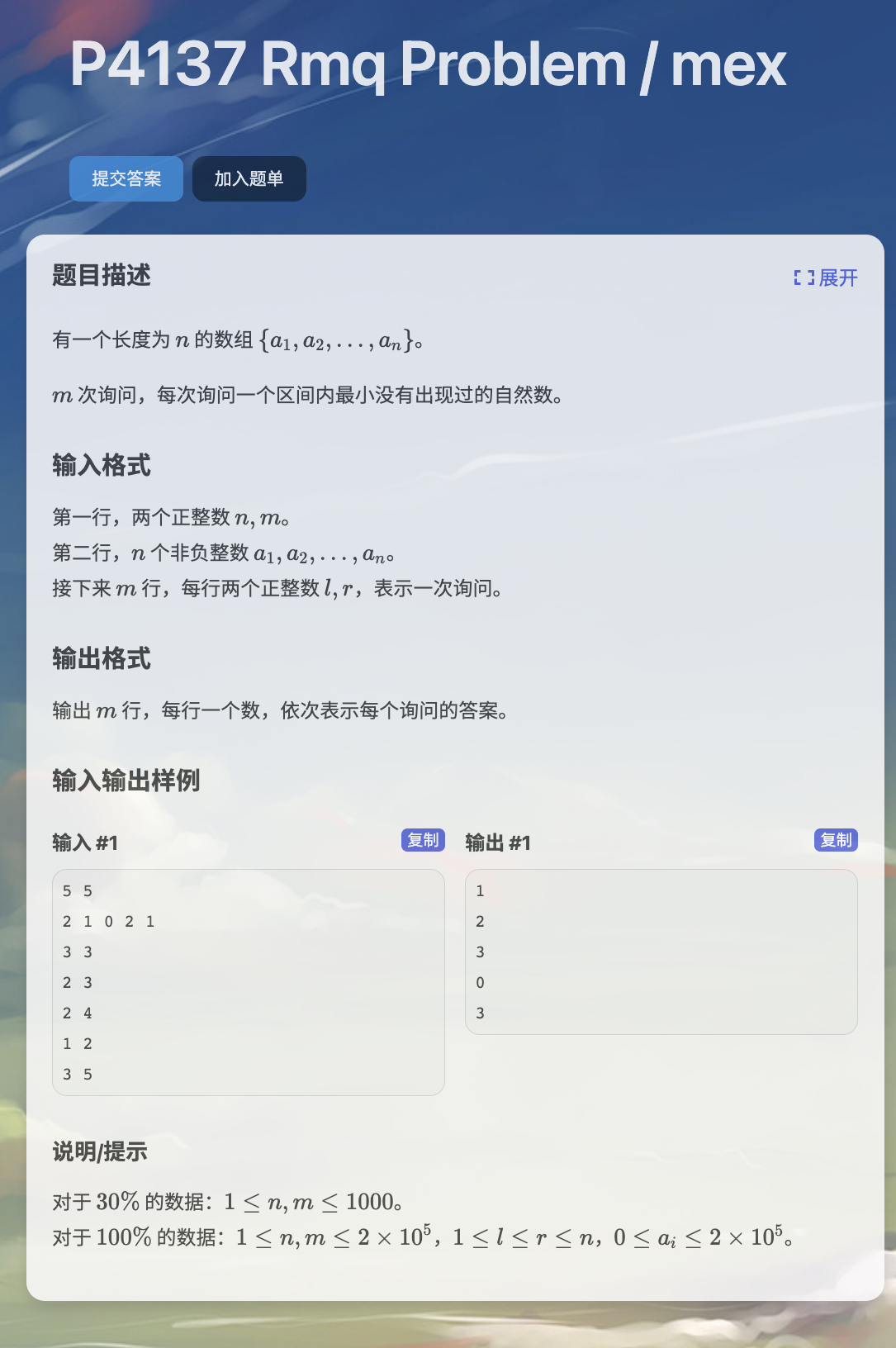
我们可以对每个数存一个最右端位置
然后维护一下这个前缀版本区间内的最小下标
在查询[l,r]的时候，只需要查询在root[r]的版本下，下标没有出现在l后的最小的数
那么每次就是对左右子树分别查看，这个最小下标是否可以出现在子树内，来决定递归哪一个
肯定优先递归左子树，所以只有左子树的val>=pos的时候，才做右子树

✅

#include <iostream>
#include <vector>
#include <algorithm>
#define ll long long

using namespace std;

const int N = 3e5 + 10;
struct node {
        int l, r;
        int val; // 维护当前区间内每个数最右侧下标的最小值
} sgtr[N * 40];
int root[N], tot;
int n, a[N], m, x, y;

inline void insert ( int l, int r, int pre, int &now, int p, int c ) { // p是数值，c是新下标
        sgtr[++tot] = sgtr[pre];
        now = tot;
        if ( l == r ) { // 更新
                sgtr[now].val = c;
                return;
        }
        int mid = (l + r) >> 1;
        if ( p <= mid ) // 新数值改变左子树
                insert ( l, mid, sgtr[pre].l, sgtr[now].l, p, c ); 
        else 
                insert ( mid + 1, r, sgtr[pre].r, sgtr[now].r, p, c );
        sgtr[now].val = min ( sgtr[sgtr[now].l].val, sgtr[sgtr[now].r].val ); // 更新一下最小值（pushup）
}

inline int query ( int l, int r, int rt, int pos ) { // 查询 MEX
        if ( l == r ) return l;
        int mid = (l + r) >> 1;
        if ( sgtr[sgtr[rt].l].val >= pos ) // 若左子树右侧下标最小值都出现在[L,R]区间内，就查询右子树 
                return query ( mid + 1, r, sgtr[rt].r, pos );
        else                               // 否则查询左子树
                return query ( l, mid, sgtr[rt].l, pos );
}


int main () {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif
        scanf("%d%d", &n, &m);
        for ( int i = 1; i <= n; i ++ ) 
                scanf("%d", &a[i]);

        for ( int i = 1; i <= n; i ++ ) {
                insert ( 0, 1e9, root[i - 1], root[i], a[i], i ); // ai插入主席树并将ai位置更新为i
        } 
        while ( m -- ) {
                int l, r; scanf("%d%d", &l, &r);
                printf("%d\n", query ( 0, 1e9, root[r], l ) );
        }
}

---

牛客NC21758_LittleWAndDiscretization

🔗

💡

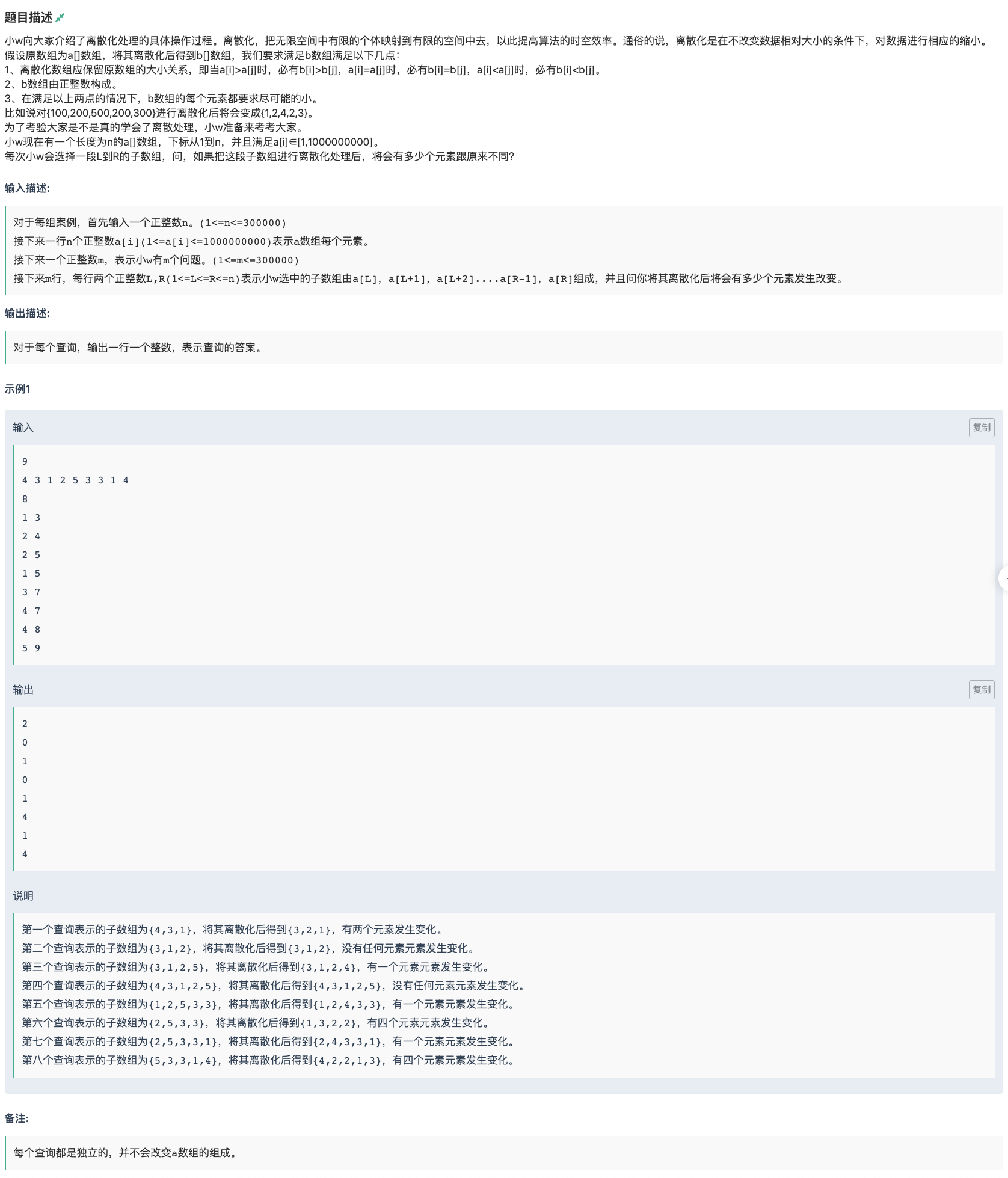
首先分析，在离散化的时候，哪些数会发生改变
若中间空了一个数，后面的数皆会改变
空的也就是mex，所以取出mex，然后求出这个区间内比mex大的有多少个数

求mex
我们可以对每个数存一个最右端位置
然后维护一下这个前缀版本区间内的最小下标
在查询[l,r]的时候，只需要查询在root[r]的版本下，下标没有出现在l后的最小的数
那么每次就是对左右子树分别查看，这个最小下标是否可以出现在子树内，来决定递归哪一个
肯定优先递归左子树，所以只有左子树的val>=pos的时候，才做右子树

求比mex大的数
存主席树时，也存一个该区间内数的个数
求出来mex后，在两个版本前缀主席树相减下，求出这个区间[mex+1, 1e9]的权值和

✅

const int N = 3e5 + 10;
struct node {
        int l, r;
        int val; // 维护当前区间内每个数最右侧下标的最小值
        int sum; // 维护当前区间内有多少个数
} sgtr[N * 40];
int root[N], tot;
int n, a[N], m, x, y;

inline void insert ( int l, int r, int pre, int &now, int p, int c ) { // p是数值，c是新下标
        sgtr[++tot] = sgtr[pre];
        now = tot;
        sgtr[now].sum ++;
        if ( l == r ) { // 更新
                sgtr[now].val = c;
                return;
        }
        int mid = (l + r) >> 1;
        if ( p <= mid ) // 新数值改变左子树
                insert ( l, mid, sgtr[pre].l, sgtr[now].l, p, c ); 
        else 
                insert ( mid + 1, r, sgtr[pre].r, sgtr[now].r, p, c );
        sgtr[now].val = min ( sgtr[sgtr[now].l].val, sgtr[sgtr[now].r].val ); // 更新一下最小值（pushup）
}

inline int query ( int l, int r, int rt, int pos ) { // 查询 MEX
        if ( l == r ) return l;
        int mid = (l + r) >> 1;
        if ( sgtr[sgtr[rt].l].val >= pos ) // 若左子树右侧下标最小值都出现在[L,R]区间内，就查询右子树 
                return query ( mid + 1, r, sgtr[rt].r, pos );
        else                               // 否则查询左子树
                return query ( l, mid, sgtr[rt].l, pos );
}

inline int getSum ( int l, int r, int L, int R, int pos ) { // 区间减出>=pos的所有数的个数
        if ( l == r ) return sgtr[R].sum - sgtr[L].sum;
        int mid = (l + r) >> 1;
        int res = 0;
        if ( pos <= mid ) 
                res += getSum ( l, mid, sgtr[L].l, sgtr[R].l, pos ) + sgtr[sgtr[R].r].sum - sgtr[sgtr[L].r].sum; // 如果pos在左子树则右子树全部满足
        else 
                res += getSum ( mid + 1, r, sgtr[L].r, sgtr[R].r, pos );
        return res;
}


int main () {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif
        scanf("%d", &n);
        for ( int i = 1; i <= n; i ++ ) 
                scanf("%d", &a[i]);

        for ( int i = 1; i <= n; i ++ ) {
                insert ( 1, 1e9, root[i - 1], root[i], a[i], i ); // ai插入主席树并将ai位置更新为i
        } 
        scanf("%d", &m);
        while ( m -- ) {
                int l, r; scanf("%d%d", &l, &r);
                int mex = query ( 1, 1e9, root[r], l ); // 取出区间mex
                printf ( "%d\n", getSum ( 1, 1e9, root[l - 1], root[r], mex + 1 ) ); // 找比mex大的数的个数
        }
}

---

CCPC2022浙江省赛F_EasyFix

🔗

💡

考虑在交换 $p_l,p_r$ 时，有哪些值会变
即下标在 $[l,r]$ 内，权值在 $[p_l,p_r]$ 内的
这里两个偏序关系使用主席树
考虑变化量，若 $p_l<p_r$ ，那么这里的 $a-b+$
若 $p_l>p_r$ ，那么这里的 $a+b-$
那么可以直接算出两个维度的 $\sum min(a,b),\sum min(a-1,b+1),\sum min(a+1,b-1)$
然后在主席树内区间查询即可
然后注意到 $p_l,p_r$ 交换后这两个点的权值也会变化，可以直接求左侧右侧有几个小于它的数，还要注意 $\min(p_l,p_r)$ 对 $\max(p_l,p_r)$ 也有贡献

✅

const int N = 1e5 + 10;
# define int long long

int tr[N]; 
inline int lowbit (int x) { return x & -x; }
inline void _update (int id, int c) {while (id < N) {tr[id] += c; id += lowbit(id);}}
inline int _query (int id) {int res = 0; while (id) res += tr[id], id -= lowbit(id); return res;}
int n, m, a[N], b[N], p[N];

struct node {
    int l, r;
    int sum[3];
    int s;
} t[N * 40];
int root[N], tot;

inline void insert (int l, int r, int pre, int &now, int p, int i) {
    t[++tot] = t[pre];
    now = tot;
    t[now].s ++;
    if (l == r) {
        t[now].sum[0] = min(a[i], b[i]);
        t[now].sum[1] = min(a[i] - 1, b[i] + 1);
        t[now].sum[2] = min(a[i] + 1, b[i] - 1);
        return;
    }
    int mid = (l + r) >> 1;
    if (p <= mid) insert(l, mid, t[pre].l, t[now].l, p, i);
    if (p > mid)  insert(mid + 1, r, t[pre].r, t[now].r, p, i);
    t[now].sum[0] = t[t[now].l].sum[0] + t[t[now].r].sum[0];
    t[now].sum[1] = t[t[now].l].sum[1] + t[t[now].r].sum[1];
    t[now].sum[2] = t[t[now].l].sum[2] + t[t[now].r].sum[2];
}
inline int query (int nml, int nmr, int idl, int idr, int l, int r, int i) {
    if (nml > nmr) return 0;
    if (nml <= l && r <= nmr) {
        if (0 <= i && i < 3) return t[idr].sum[i] - t[idl].sum[i];
        else return t[idr].s - t[idl].s;
    }
    int mid = (l + r) >> 1;
    int res = 0;
    if (nml <= mid) res += query(nml, nmr, t[idl].l, t[idr].l, l, mid, i);
    if (nmr > mid)  res += query(nml, nmr, t[idl].r, t[idr].r, mid + 1, r, i);
    return res;
}   

inline void Solve () {
    scanf("%lld", &n);
    int sum = 0;
    for (int i = 1; i <= n; i ++) scanf("%lld", &p[i]);
    for (int i = 1; i <= n; i ++) {
        a[i] = _query(p[i]);
        _update(p[i], 1);
    }
    for (int i = 1; i <= n; i ++) _update(p[i], -1);
    for (int i = n; i >= 1; i --) {
        b[i] = _query(p[i]);
        sum += min(a[i], b[i]);
        _update(p[i], 1);
    }

    for (int i = 1; i <= n; i ++) {
        insert(1, n, root[i - 1], root[i], p[i], i);
    } 

    scanf("%lld", &m);
    while (m --) {
        int l, r; scanf("%lld%lld", &l, &r);
        if (l > r) swap(l, r);
        int res = 0;

        if (p[l] < p[r]) {
            res = sum;
            res -= query(p[l] + 1, p[r] - 1, root[l], root[r - 1], 1, n, 0);
            res += query(p[l] + 1, p[r] - 1, root[l], root[r - 1], 1, n, 1);
            res -= min(a[l], b[l]) + min(a[r], b[r]);
            if (p[r] != 1) res += min(query(1, p[r] - 1, root[0], root[l - 1], 1, n, 3), query(1, p[r] - 1, root[l], root[n], 1, n, 3) + 1);
            if (p[l] != 1) res += min(query(1, p[l] - 1, root[0], root[r - 1], 1, n, 3), query(1, p[l] - 1, root[r], root[n], 1, n, 3));
        } else if (p[l] > p[r]) {
            res = sum;
            res -= query(p[r] + 1, p[l] - 1, root[l], root[r - 1], 1, n, 0);
            res += query(p[r] + 1, p[l] - 1, root[l], root[r - 1], 1, n, 2);
            res -= min(a[l], b[l]) + min(a[r], b[r]);
            if (p[r] != 1) res += min(query(1, p[r] - 1, root[0], root[l - 1], 1, n, 3), query(1, p[r] - 1, root[l], root[n], 1, n, 3));
            if (p[l] != 1) res += min(query(1, p[l] - 1, root[0], root[r - 1], 1, n, 3) + 1, query(1, p[l] - 1, root[r], root[n], 1, n, 3));
        } else {
            res = sum;
        }
        printf("%lld\n", res);
    }
}

signed main () {
    cin.tie(0);

    int cass = 1; while (cass --) {
        Solve ();
    }
}

---

CodeForces1227D2_OptimalSubsequences（Hard Version）

🔗

💡

首先每个数转换为第几个选很容易，就是首先数值要大，其次位置要靠前。
对于第一个样例可以转换为：

a	10	20	10
b	2	1	3

那么问题就是：在 $[b]$ 中所有小于等于 $k$ 的位置中，找到第 $r$ 靠前的位置
很容易想到二分，但是二分了话我们需要的单调性因素就是：前面小于等于 $k$ 的个数
这里有两个条件：前面、数，即下标、数值。
数值可以权值线段树，下标之前就是前缀，一个前缀权值线段树就是主席树
那么构建出一棵主席树，然后对于一次查询 $k,p$ ，开启二分，在 $mid$ 处查询主席树中以 root[mid] 为根的主席树中有多少个小于等于 $k$ 的数，如果 $\ge p$ 就维护一下答案然后继续向前找，否则答案在后面，往后找。

能过，但时间不尽人意（马上就 $T$ 了）
调换一下解法
其实也可以用 $[b]$ 排序后当根的前缀建树

a	20	10	10
b	1	2	3
c	2	1	3

在以 root[k] 中找下标第 $p$ 小
这就很板了，而且时间也快了不少（因为直接在查询的时候二分了）

✅

// 初步解法 ---------------------------------------------------------------
const int N = 2e5 + 10;
int n, m, b[N], a[N];
pair<int, int> tmp[N];
 
struct node {
        int l, r, sum;
} t[N * 40];
int tot, root[N];
 
inline void Insert (int l, int r, int pre, int &now, int p) {
        t[++ tot] = t[pre];
        now = tot;
        t[now].sum ++;
        if (l == r) return;
 
        int mid = (l + r) >> 1;
        if (p <= mid) Insert(l, mid, t[pre].l, t[now].l, p);
        else Insert(mid + 1, r, t[pre].r, t[now].r, p);
}
inline int Query (int id, int l, int r, int rt) { // [1,id]
        if (r <= id) return t[rt].sum;
        if (l > id) return 0;
        int mid = (l + r) >> 1;
        return Query(id, l, mid, t[rt].l) + Query(id, mid + 1, r, t[rt].r);
}
 
int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);
 
        cin >> n;
        for (int i = 1; i <= n; i ++) {
                cin >> a[i];
                tmp[i].first = a[i];
                tmp[i].second = i;
        }
 
        sort(tmp + 1, tmp + 1 + n, [&](pair<int, int> x, pair<int, int> y) {
                if (x.first != y.first) return x.first > y.first;
                return x.second < y.second;
        });
        for (int i = 1; i <= n; i ++) b[tmp[i].second] = i;
        for (int i = 1; i <= n; i ++) Insert(1, n, root[i - 1], root[i], b[i]);
 
        cin >> m;
        while (m --) {
                int k, p; cin >> k >> p;
                int l = 1, r = n, res = n;
                while (l <= r) {
                        int mid = (l + r) >> 1;
                        int pre_lowk = Query(k, 1, n, root[mid]);
                        if (pre_lowk >= p) res = mid, r = mid - 1;
                        else l = mid + 1;
                }
                cout << a[res] << endl;
        }
 
}

// 优化解法----------------------------------------------------------------
const int N = 2e5 + 10;
int n, m, a[N];
pair<int, int> tmp[N];

struct node {
        int l, r, sum;
} t[N * 40];
int tot, root[N];

inline void Insert (int l, int r, int pre, int &now, int p) {
        t[++ tot] = t[pre];
        now = tot;
        t[now].sum ++;
        if (l == r) return;

        int mid = (l + r) >> 1;
        if (p <= mid) Insert(l, mid, t[pre].l, t[now].l, p);
        else Insert(mid + 1, r, t[pre].r, t[now].r, p);
}
inline int Query (int l, int r, int rt, int k) { 
        if (l == r) return l;
        int mid = (l + r) >> 1;
        int cnt = t[t[rt].l].sum;
        if (k <= cnt) return Query(l, mid, t[rt].l, k);
        else return Query(mid + 1, r, t[rt].r, k - cnt);
}

int main () {
        scanf("%d", &n);
        for (int i = 1; i <= n; i ++) {
                scanf("%d", &a[i]);
                tmp[i].first = a[i];
                tmp[i].second = i;
        }

        sort(tmp + 1, tmp + 1 + n, [&](pair<int, int> x, pair<int, int> y) {
                if (x.first != y.first) return x.first > y.first;
                return x.second < y.second;
        });
        for (int i = 1; i <= n; i ++) Insert(1, n, root[i - 1], root[i], tmp[i].second); // 省略了 [b] ，排完序直接建

        scanf("%d", &m);
        while (m --) {
                int k, p; scanf("%d%d", &k, &p);
                printf("%d\n", a[Query(1, n, root[k], p)]);
        }
}

---