筛法

Chivas-Regal

#

# 埃氏筛

# 牛客NC228910_PrimeDistance

# 🔗

# 💡

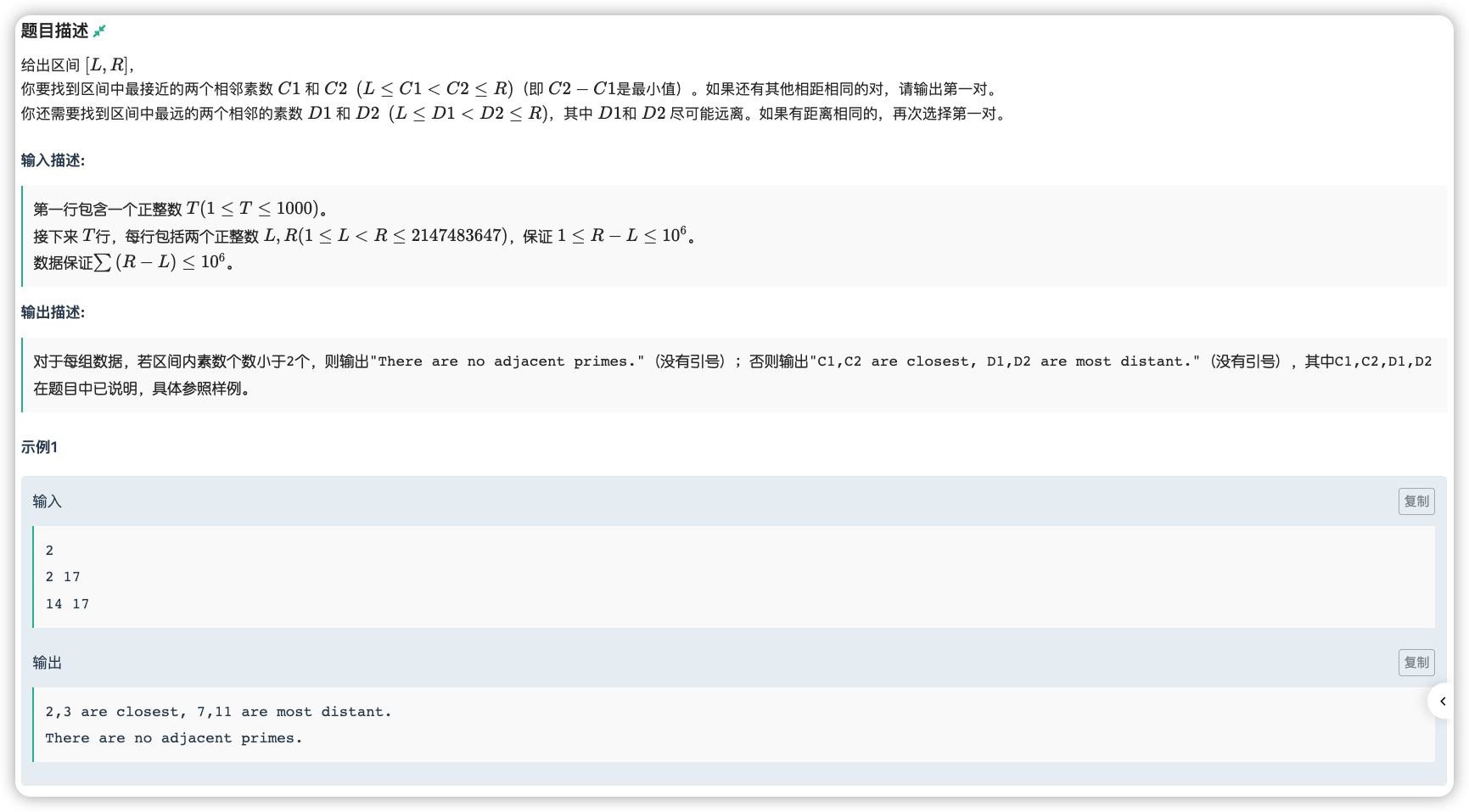
根据素数判定的 $2\le i\le \sqrt{x}$ 可生推论
若要筛去所有 $[l,r]$ 的合数，他们最小的素因数一定小于等于 $\sqrt{r}$ ，因为若存在一个大于 $\sqrt{r}$ 的素因数，那么必然存在一个小于 $\sqrt{r}$ 的素因数
所以用 $\sqrt{r_{max}}$ 的素数用埃氏筛去将 $[l,r]$ 内的合数全筛出来，然后枚举两两素数之间的距离即可
注意这本身是 $O(nlogn)$ 如果再加一个 $logn$ 存一个数是不是合数可能跑不过去，这里可以将 $x$ 映射为 $x-l$ ，使用数组查询即可

# ✅

const int N = 1e5 + 10;
bool ntp[N];
vector<int> pr;
inline void Sieve () {
    ntp[0] = ntp[1] = 1;
    for (int i = 2; i < N; i ++) {
        if (!ntp[i]) pr.push_back(i);
        for (int j = 0; j < pr.size() && i * pr[j] < N; j ++) {
            ntp[i * pr[j]] = 1;
            if (i % pr[j] == 0) break;
        }
    }
}
int book[1000006];
inline void Solve () {
    int l, r; scanf("%d%d", &l, &r);

    vector<int> now_prime;
    vector<int> now_not_prime;
    for (int i : pr) {
        for (ll j = (1ll * l + i - 1) / i * i; j <= r; j += i) {
            if (j == i) continue;
            book[j - l] = 1;
            now_not_prime.push_back(j - l);
        }
    }
    for (int i = l; i <= r; i ++) {
        if (i == 1 || i == 0) continue;
        if (!book[i - l]) now_prime.push_back(i);
    }
    if (now_prime.size() <= 1) {
        puts("There are no adjacent primes.");
    } else {
        pair<int, int> mindis = {0, 0x3f3f3f3f}, maxdis = {1, 0};
        for (int i = 1; i < now_prime.size(); i ++) {
            if (now_prime[i] - now_prime[i - 1] < mindis.second - mindis.first) mindis = {now_prime[i - 1], now_prime[i]};
            if (now_prime[i] - now_prime[i - 1] > maxdis.second - maxdis.first) maxdis = {now_prime[i - 1], now_prime[i]};
        }
        printf("%d,%d are closest, %d,%d are most distant.\n", mindis.first, mindis.second, maxdis.first, maxdis.second);
    }

    for (int i : now_not_prime) book[i] = 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

# ABC249D_IndexTrio

# 🔗

# 💡

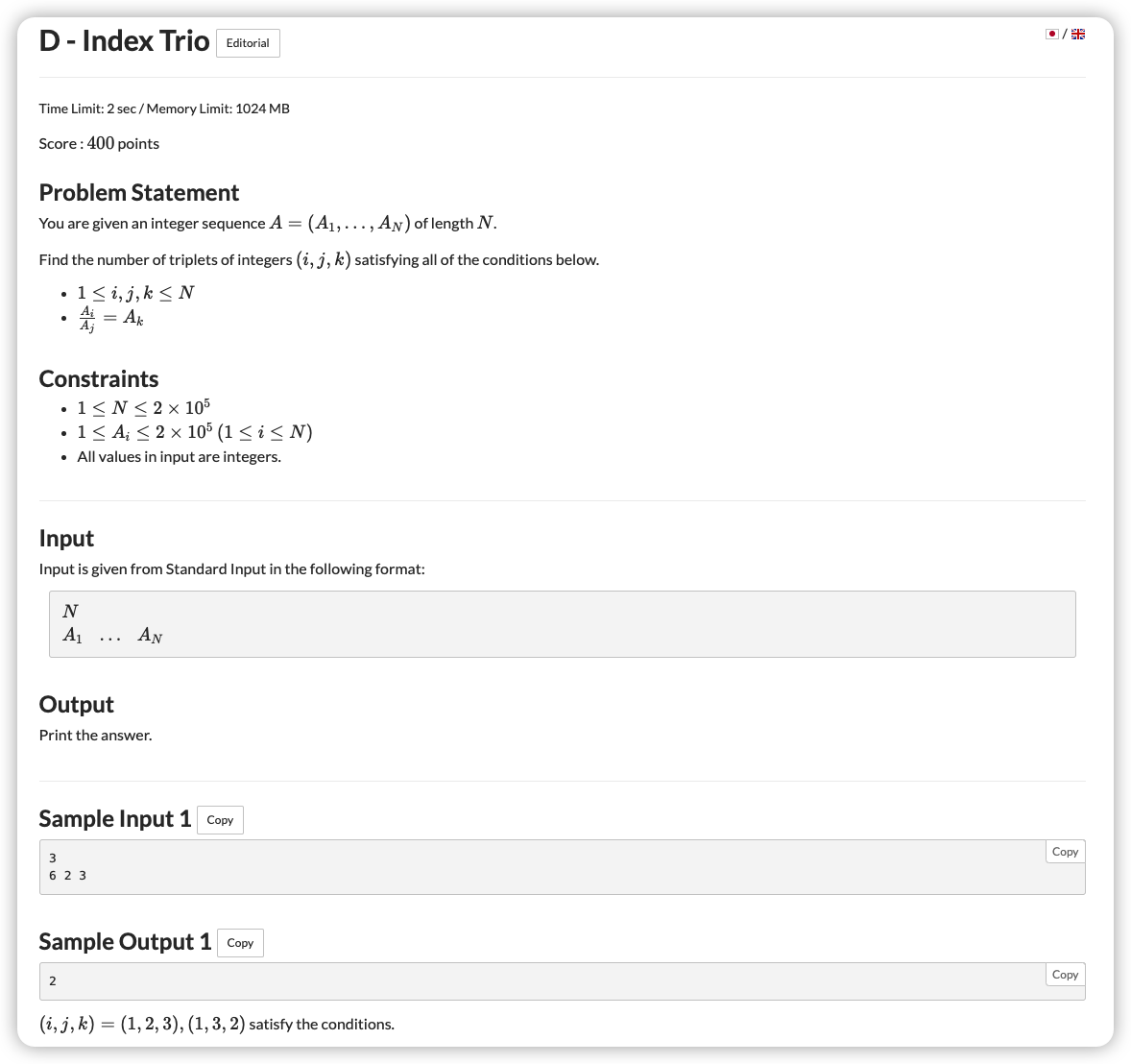
化简柿子

\frac {A_i}{A_j}=A_k=A_kA_j=A_i

发现三元组的通用解法（一边存一边统计）似乎并没有合适的进展
但是可以看到 $A_i$ 是 $A_k$ 的 $A_j$ 倍
对于这种倍数计数问题，可以放前面考虑就是埃氏筛
我们先统计完所有的数的出现情况，然后用埃氏筛去枚举每一个数与其倍数，这样三个数都出来了，那么就累加计算一下这三个数出现次数的乘积即可

# ✅

const int N = 200005;

int num[N];

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        int n; cin >> n;
        for (int i = 0; i < n; i ++) {
                int x; cin >> x;
                num[x] ++;
        }
        ll res = 0;
        for (int i = 1; i < N; i ++) {
                if (!num[i]) continue;
                for (int j = i; j < N; j += i) {
                        int k = j / i;
                        res += 1ll * num[i] * num[j] * num[k];
                }
        }
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# CodeForces1512G_ShortTask

# 🔗

# 💡

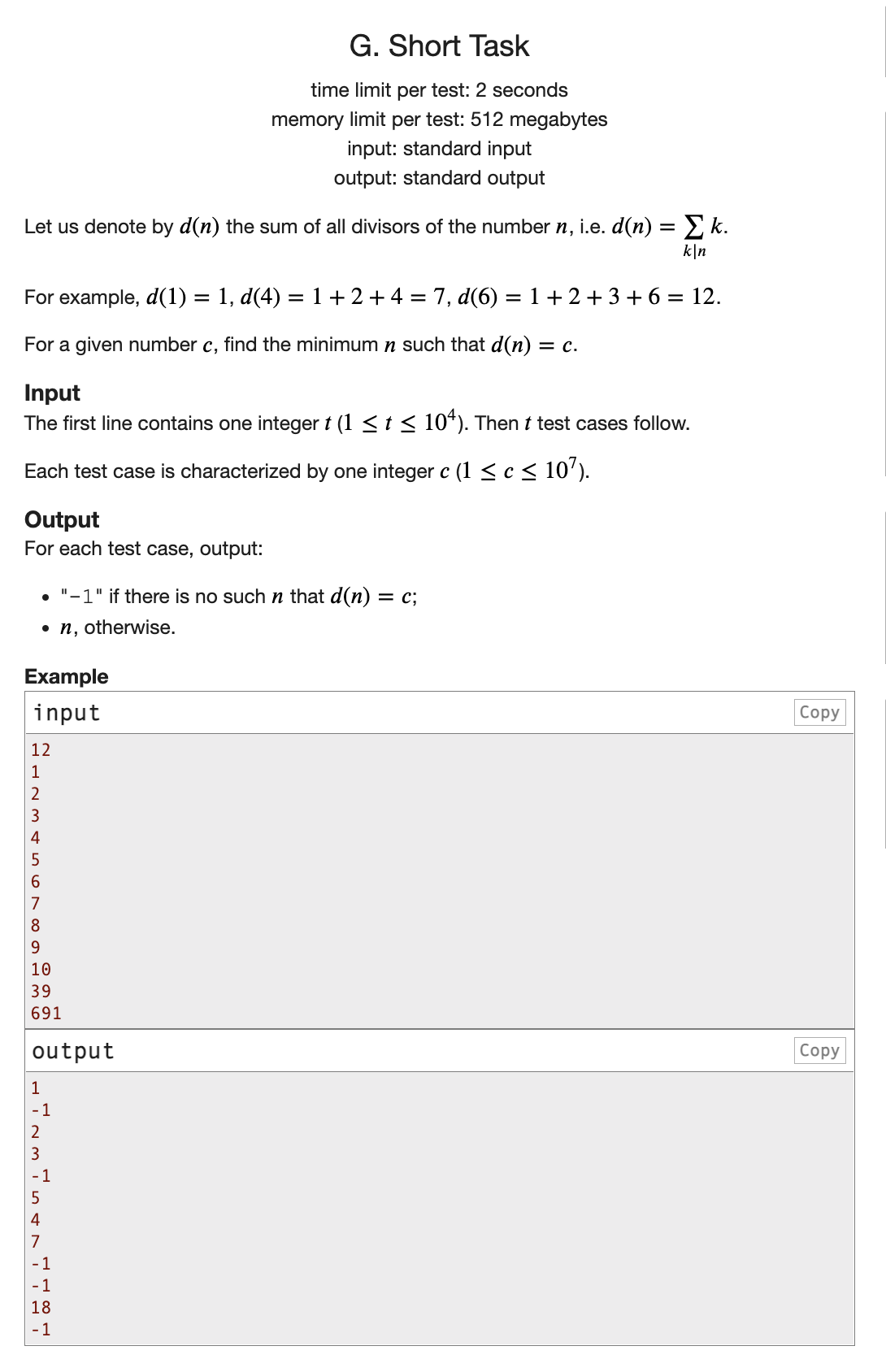
每个数的因数都要算一遍，那么我们就需要用到埃氏筛的重复筛的性质
给了两秒，可以支持O(nlogn)
那么我们直接开埃氏筛存数即可

# ✅

#include <iostream>

using namespace std;

const int N = 1e7 + 10;
int mark[N], res[N], n;

inline void Get () {
	for ( int i = 1; i < N; i ++ )
		for ( int j = i; j < N; j += i )
			mark[j] += i; // 每个数的因子和都要记录一下
	for ( int i = 1; i < N; i ++ ) 
		if ( mark[i] < N && !res[mark[i]] )
                        res[mark[i]] = i; // 第一个出现的存进去
}

int main () {
	Get(); int cass, x;
	for ( cin >> cass; cass; cass -- )
		cin >> x, cout << (res[x] == 0? -1 : res[x])<< endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# CodeForces1627D_NotAdding

# 🔗

# 💡

可以简单的得到，其实就是每次选任意多任意的位置上的数，将它们的 $\inline gcd$ 放进数组
那么我们可以枚举这个 $\inline gcd$ ，将数组中所有是它的倍数的数求一下 $\inline gcd$ ，如果这些数的 $\inline gcd$ 就是我们当前枚举的 $\inline gcd$ 并且该 $\inline gcd$ 没有在原数组内出现过，那么我们就可以加入

枚举所有的倍数，埃氏筛就可以实现

# ✅

const int N = 1e6 + 1;
int vis[N];
 
inline int gcd ( int a, int b ) {
        return b ? gcd(b, a % b) : a;
}
 
int main () {
        ios::sync_with_stdio(false);
 
        int n; cin >> n;
        for ( int i = 0; i < n; i ++ ) {
                int x; cin >> x;
                vis[x] = 1;
        }
        int res = 0;
        for ( int i = 1; i < N; i ++ ) {
                if ( vis[i] ) continue;
                int g = 0;
                for ( int j = i; j < N; j += i ) {
                        if ( vis[j] ) g = gcd(g, j);
                }
                res += g == i;
        }
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

# CodeForces1646E_PowerBoard

# 🔗

# 💡

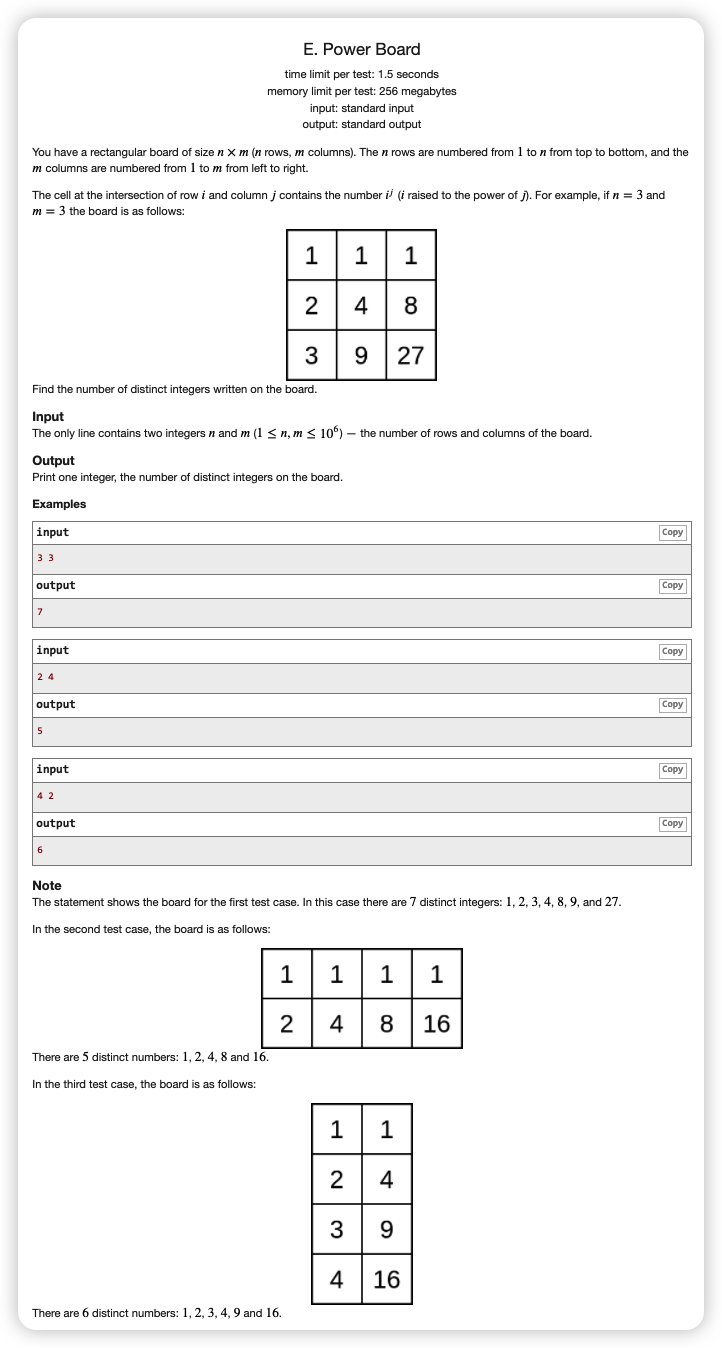
思考一下什么时候会出现重复， $2^4=4^2=16^1$
那么我们考虑一下分组
对于一个正整数 $x$ ，令所有以 $x^k$ 开始的行归为一组 $Group(x)$
即:

Group(x)=\left\{\begin{aligned} k=1,\quad &x,x^2,x^3,\dots\newline k=2,\quad &x^2,x^4,x^6,\dots\newline k=3,\quad &x^3,x^6,x^9,\dots\newline \dotso \end{aligned}\right\}

显然，同一组内不同行不同列可能存在相同数，而 $x\neq y\Longrightarrow Group(x)\cap Group(y)=\empty$
那么对于每一组行为 $i$ ，列为 $j$ ，我们需要统计 $i\times j$ 的个数然后不同组进行累加即可

枚举 $x$ ，要想 $x^k\le n$ ，那么 $k\lt 20$
对于 $x$ 看它在 $n$ 内的 $max\_k$ ，也就意味着可以形成一个 $max\_k$ 行 $m$ 列矩阵
那么我们可以先处理出来 $n\_dif[i]$ 表示在一组内，一个 $i$ 行 $m$ 列矩阵的不同 $i\times j$ 的数量，这个可以用埃氏筛枚举倍数实现
然后在枚举 $x$ 计算完 $max\_k$ 后累加 $n\_dif[max\_k]$ 即可

# ✅

const int N = 1e6 + 10;
int n, m;
bool vis[N * 25];
ll n_dif[25];

int main () {
        ios::sync_with_stdio(false);

        cin >> n >> m;

        for ( int i = 1; i <= 20; i ++ ) {
                n_dif[i] += n_dif[i - 1];
                for ( int j = 1; j <= m; j ++ ) {
                        if ( !vis[i * j] ) 
                                vis[i * j] = true,
                                n_dif[i] ++;
                }
        }

        memset(vis, 0, sizeof vis);

        ll res = 1;
        for ( int x = 2; x <= n; x ++ ) {
                int row = 0;
                for ( ll pw = x; pw <= n; pw *= x ) {
                        if ( vis[pw] ) continue; vis[pw] = true;
                        row ++;
                }
                res += n_dif[row];
        }
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

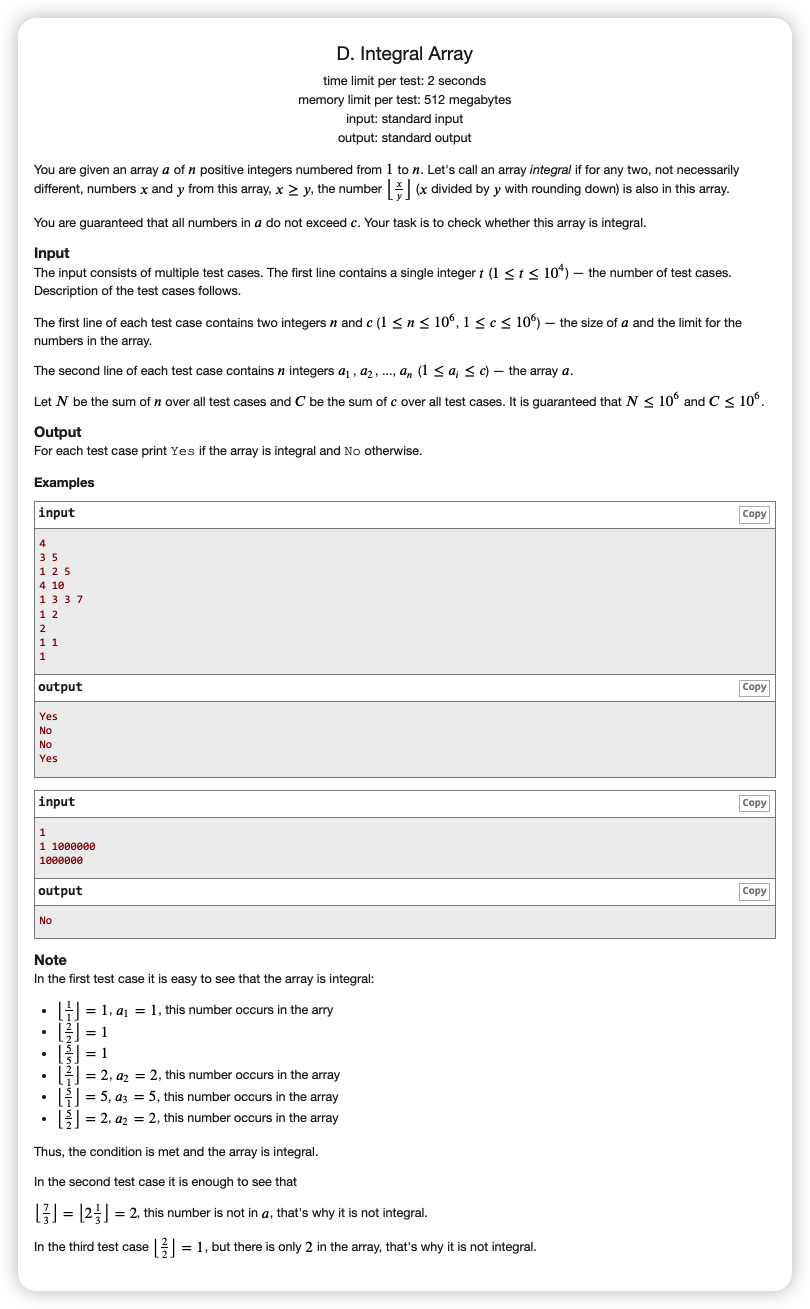
# CodeForces1649D_IntegralArray

# 🔗

# 💡

分两步考虑了
由于 $a=\left\lfloor\frac xy\right\rfloor$ 要看对于 $y:1\to x$ 看其中每一个 $a$ 出现的情况，这些是会有很多重复的情况，那么我们可以开数论分块
对每一个出现过的 $a_i$ 数论分块，看一个块内 $y\in[l,r]\;(\left\lfloor\frac xl\right\rfloor=\left\lfloor\frac xr\right\rfloor)$ 是否有出现过数，出现过的话那么 $\left\lfloor\frac xl\right\rfloor$ 也必然要出现，这个如果没有出现就是 No 了
这个复杂度就是 $O(n\sqrt{m})$ ，是会超的

既然我们可以对分母分块，那么也自然可以用埃氏筛枚举倍数的方式对分子分块
枚举分母 $a$ ，再枚举 $a$ 的倍数 $i$ ，那么一个块 $[l,r]=[a\times i,a\times(i+1)-1]$ 那么 $\left\lfloor\frac la\right\rfloor=\left\lfloor ra\right\rfloor=i$
如果 $[l,r]$ 出现过且 $i$ 每出现就是 No
复杂度均摊 $O(mlogm)$

# ✅

int sum[1000005]; // 记录区间数字个数
int cnt[1000005]; // 记录单点数字个数
 
inline void Solve () {
        int n, c; cin >> n >> c; a.clear();
        
        for ( int i = 0; i <= c; i ++ ) sum[i] = cnt[i] = 0;
        for ( int i = 0; i < n; i ++ ) {
                int x; cin >> x;
                sum[x] ++;
                cnt[x] = 1;
        }
        for ( int i = 1; i <= c; i ++ ) sum[i] += sum[i - 1];
 
 
        for ( int i = 1; i <= c; i ++ ) {
                if ( !cnt[i] ) continue;
                for ( int j = 1; j * i <= c; j ++ ) {
                        int L = j * i, R = min(j * i + i - 1, c);
                        if ( sum[R] - sum[L - 1] && !cnt[j] ) {
                                cout << "No" << endl;
                                return ;
                        } 
                }
        }
        cout << "Yes" << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# ICPC吉林站2020G_Matrix

# 🔗

# 💡

一个埃氏筛的思想
从 $\inline 1$ 枚举 $\inline i$ 然后改变 $\inline i$ 的倍数的话
每个数有多少个因数就会被筛几次

我们设 $\inline dv[i]$ 表示 $\inline i$ 的因数个数
那么一个位置在 $\inline (i,j)$ 的元素会被筛 $\inline dv[i]\times&space;dv[j]$ 次
为了使一个位置的元素筛奇数次，则 $\inline i$ 和 $\inline j$ 都具有奇数个因数才可以
性质：具有奇数个因数的数都是完全平方数
所以我们计算 $\inline \left\lfloor\sqrt[]{n}\right\rfloor\times\left\lfloor\sqrt{m}\right\rfloor$ 即可

# ✅

int main () {
        ios::sync_with_stdio(false);
        int cass; cin >> cass; while ( cass -- ) {
                ll n, m; cin >> n >> m;
                cout << (ll)sqrt(n) * (ll)sqrt(m) << endl;
        }
}

1
2
3
4
5
6
7

# LOJ10199_轻拍牛头

# 🔗

# 💡

题目任务转化是让求整个数列有多少个数是a[i]的因数
那么我们可以直接对每个数用埃氏筛的思想把倍数统计一遍
但是一个个统计会超时，因为如果都是1的话一个个会超大的重复量
所以我们可以使用一个数组统计一下每个数出现的次数
只需要把数枚举一遍即可

# ✅

#include <unordered_map>
#include <iostream>

using namespace std;

const int N = 1e6 + 10;
unordered_map<int, int> mark;
int res[N], n, a[N];

inline void Get () {
        for ( auto i : mark )
                for ( int j = i.first; j < N; j += i.first )
                        res[j] += i.second;
}

int main () {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
#endif
        cin >> n;
        for ( int i = 0; i < n; i ++ ) cin >> a[i], mark[a[i]] ++;
        Get();
        for ( int i = 0; i < n; i ++ ) cout << res[a[i]] - 1 << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# 杜教筛

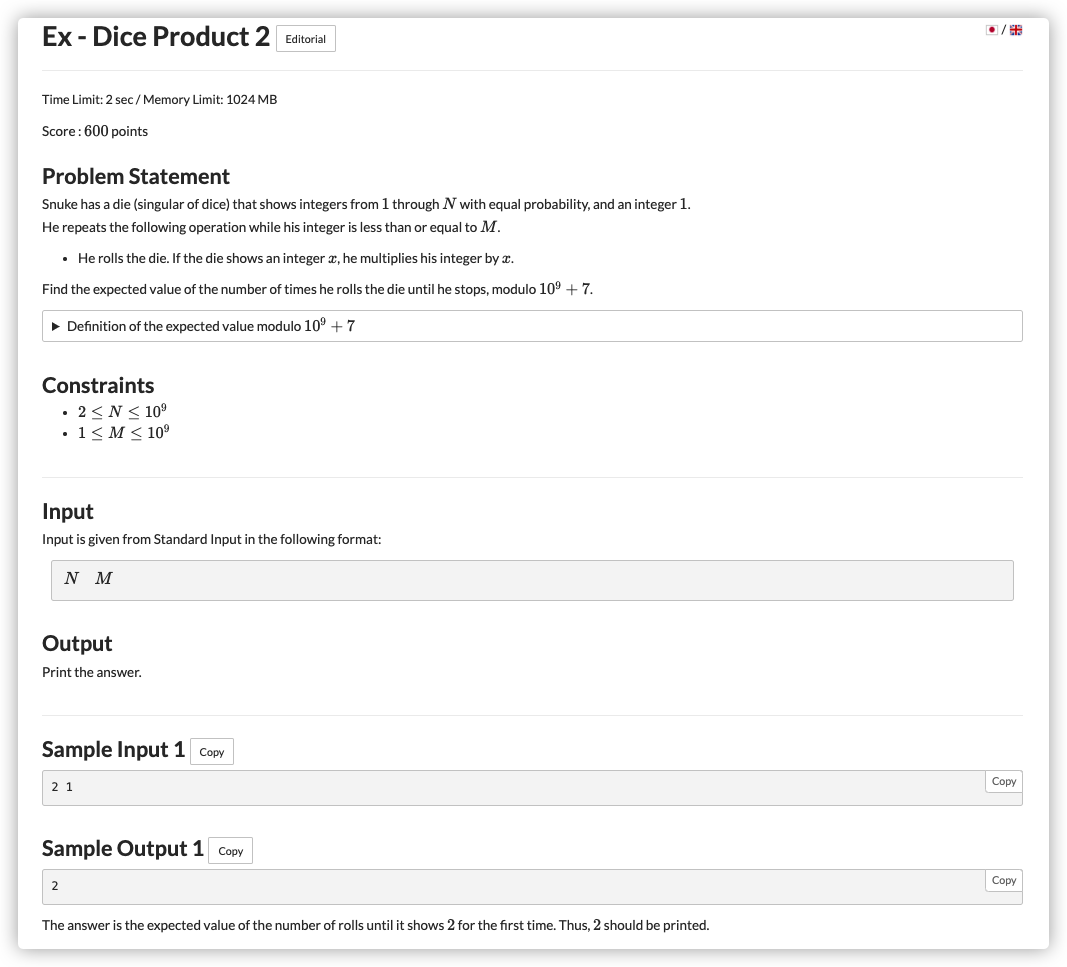
# ABC239Ex_DiceProduct2

# 🔗

# 💡

转化成 $dp$ 去考虑
在 $N$ 下，设 $dp_x$ 表示 $M=x$ 时的期望
则

dp_x=1+\frac1N\sum\limits_{i=1}^Ndp_{\frac xi}

由于 $i=1$ 时不影响 $x$ ， $1$ 会贯彻从而可以让答案 $\times\frac{N}{N-1}$

例如

$1+\frac12+\frac14+\frac18+\dots=2$
$1+\frac13+\frac19+\frac1{27}+\dots=3$
$\dots$

那么原式为

\begin{aligned} &\frac N{N-1}(1+\frac1N\sum\limits_{i=2}^Nf_{\left\lfloor\frac xi\right\rfloor})\\ =&\frac{N+\sum\limits_{i=2}^Nf_{\left\lfloor\frac xi\right\rfloor}}{N-1} \end{aligned}

发现内部有 $\left\lfloor\right\rfloor$ 可以使用杜教筛进行整除分块

# ✅

const int mod = 1e9 + 7;
inline ll ksm ( ll a, ll b ) { ll res = 1; while ( b ) { if ( b & 1 ) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv ( ll x ) { return ksm(x, mod - 2); }

ll N, M, invnsub1;
inline ll g ( ll k, ll x ) { return k / (k / x); }
unordered_map<ll, ll> mp;
inline ll duSieve ( ll x ) {
        if ( mp[x] ) return mp[x];
        ll res = 0;
        for ( int L = 2, R; L <= min(N, x); L = R + 1 ) {
                R = min(N, g(x, L));
                res += duSieve(x / L) * (R - L + 1) % mod;
                res %= mod;
        }
        return mp[x] = (N + res) * invnsub1 % mod;
}

int main () {
        ios::sync_with_stdio(false);

        cin >> N >> M;
        invnsub1 = inv(N - 1);
        cout << duSieve(M) << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

置换群计算几何