后缀自动机

Chivas-Regal

#

# 洛谷P4070_生成魔咒

# 🔗

# 💡

子串问题，考虑使用 $sam$
新加入一个字符 $i$ ，则说明新增的串只在 $s[1],s[1..2],s[1..3],...,s[1..i]$ 中
在 $sam$ 中， $fail$ 指的是最长后缀，也是前面出现过的后缀（子串）中的一个，在插入新字符然后建好后，比其 $len[fail[i]]$ 更长的后缀一定是都没有出现过的，不然 $fail[i]$ 会指向那一个串
比如 $fail["1234567"]="4567"$ ，如果 $"34567"$ 存在于 $i$ 之前的前缀串的后缀中，比如假设 $"034567"$ 为之前出现过的某一个前缀，那么在 $"3456"$ 会产生 $7$ 分支到两个地方，不满足自动机规则后会出现一个合并后的 $"34567"$ 成为两者父节点
所以比 $len[fail[i]]$ 更长的 $s[1..i]$ 后缀一定是之前没出现过的子串，故每插入一次后答案累加 $len[ed]-len[fa[ed]]$ 即可

# ✅

ll res = 0;
const int N = 1e6 + 10;
struct SuffixAutoMaton {
    int ed, ct;
    int fa[N], len[N];
    map<int, int> to[N];
    inline SuffixAutoMaton () { ed = ct = 1; }
    inline void insert (int c, int l) {
        int v = ed;
        ed = ++ct;
        len[ed] = l;
        for (; v && !to[v].count(c); v = fa[v]) to[v][c] = ed;
        if (!v) {
            fa[ed] = 1;
        } else if (len[v] + 1 == len[to[v][c]]) {
            fa[ed] = to[v][c];
        } else {
            int np = ++ct;
            int p = to[v][c];
            for (auto it : to[p]) to[np][it.first] = it.second;
            len[np] = len[v] + 1;
            fa[np] = fa[p];
            fa[p] = fa[ed] = np;
            for (int i = v; to[i].count(c) && to[i][c] == p; i = fa[i]) to[i][c] = np;
        }   
        res += len[ed] - len[fa[ed]];
    }
} sam;

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n; cin >> n;
    for (int i = 1; i <= n; i ++) {
        int x; cin >> x;
        sam.insert(x, i);
        cout << res << endl;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

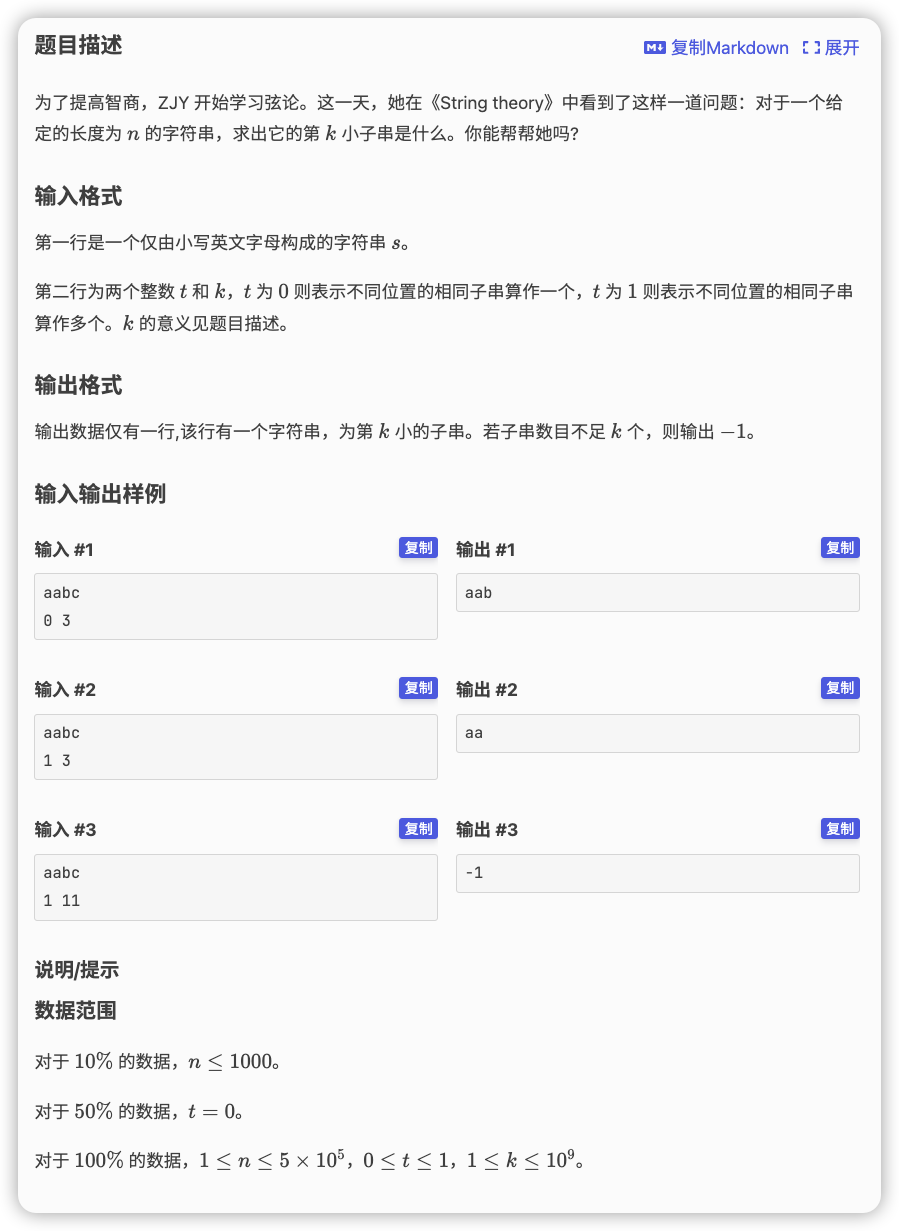
# 洛谷P3975_弦论

# 🔗

# 💡

想一下在二叉树中找第 $k$ 大的方式，既然保证了左子树比右子树小，那么如果左子树的大小小于等于 $k$ 的话进入左子树，否则进入右子树，且让 $k-size[lson]$
这里同理，注意到自动机是一个 $16$ 叉树，那么我们就在这十六叉上遍历哪个让 $k$ 小于等于 $size[c]$ 即可，如果大于，和二叉树上的思想一样让 $k$ 减去 $size[c]$ 就行了
大体思路有了，开始细化
一个子串出现的次数也就是一个节点出现的次数，和模板题一样，就是让平层上的点的 $size$ 为 $1$ ，然后在 $fail$ 树上累加即为前缀的后缀出现的次数。而如果 $t$ 是零的话，那么就让所有的 $size$ 为 $1$ 即可
然后处理一个子树上的 $size$ 和，记作 $dp$ ，用来判断 $k$ 是否小于等于从而是否进入该子树，要注意的是， $sam$ 并不是一棵树，而是一个 $dag$ 图，所以使用记忆化搜索来求
最后找答案就模拟二叉树的方式进行输出即可

还有一个地方需要考虑，即 $size[1]$ 和 $dp[1]$ 都是空的，应该设为 $0$

# ✅

const int N = 2e6 + 10;
int dp[N];
struct SuffixAutoMaton {
    int ed, ct;
    int fa[N], to[N][26], len[N], size[N];
    inline SuffixAutoMaton () { ed = ct = 1; }
    inline void insert (int c, int l) {
        int v = ed;
        ed = ++ct;
        len[ed] = l;
        size[ed] = 1;
        for (; v && to[v][c] == 0; v = fa[v]) to[v][c] = ed;
        if (!v) {
            fa[ed] = 1;
        } else if (len[v] + 1 == len[to[v][c]]) {
            fa[ed] = to[v][c];
        } else {
            int np = ++ct;
            int p = to[v][c];
            for (int i = 0; i < 26; i ++) to[np][i] = to[p][i]; fa[np] = fa[p];
            len[np] = len[v] + 1;
            fa[p] = fa[ed] = np;
            for (int i = v; to[i][c] == p; i = fa[i]) to[i][c] = np;
        }
    }
} sam;
struct Edge {
    int nxt, to;
} edge[N];
int head[N], cnt;
inline void add_Edge (int from, int to) {
    edge[++cnt] = {head[from], to};
    head[from] = cnt;
}

inline void dfs_Size (int u) {
    for (int i = head[u]; i; i = edge[i].nxt) {
        int v = edge[i].to;
        if (v) {
            dfs_Size(v);
            sam.size[u] += sam.size[v];
        }
    }
    dp[u] = sam.size[u];
}
int vis[N];
inline int dfs_sumDp (int u) {
    if (vis[u]) return dp[u]; vis[u] = 1;
    for (int i = 0; i < 26; i ++) {
        int v = sam.to[u][i];
        if (v) dp[u] += dfs_sumDp(v);
    }
    return dp[u];
}
inline void print_Res (int u, int k) {
    if (k > dp[u]) {
        cout << "-1\n"; exit(0);
    }
    if (k <= sam.size[u]) return;
    k -= sam.size[u];
    for (int i = 0; i < 26; i ++) {
        int v = sam.to[u][i];
        if (!v) continue;
        if (k > dp[v]) {
            k -= dp[v];
        } else {
            cout << char(i + 'a');
            print_Res(v, k);
            return;
        }
    }
}

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    string s; cin >> s;
    int t, k; cin >> t >> k;
    for (int i = 0; i < s.size(); i ++) sam.insert(s[i] - 'a', i + 1);
    for (int i = 2; i <= sam.ct; i ++) add_Edge(sam.fa[i], i);   
    
    if (!t) {
        for (int i = 1; i <= sam.ct; i ++) dp[i] = sam.size[i] = 1;
    } else {
        dfs_Size(1);
    }

    sam.size[1] = dp[1] = 0;
    dfs_sumDp(1); 
    print_Res(1, k);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92

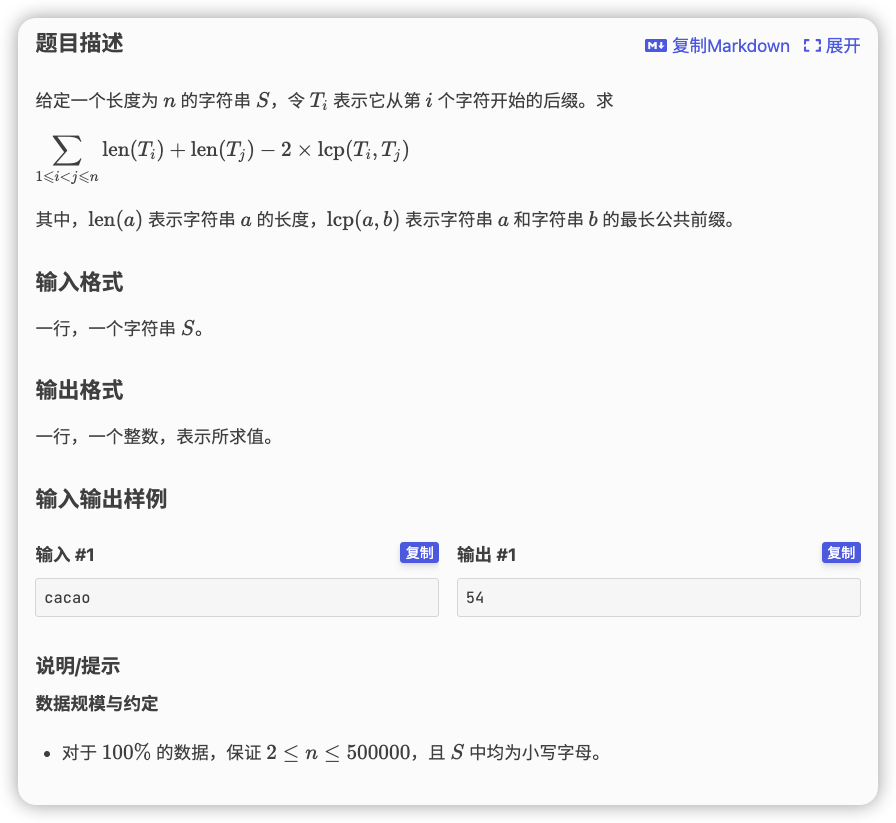
# 洛谷P4248_差异

# 🔗

# 💡

式子前两项提出合并一下，变为 $\frac{(n-1)n(n+1)}{2}-2\sum\limits_{1\le i<j\le n}lcp(T_i,T_j)$
后缀的最长公共前缀，有后缀有前缀，试着转化为 $sam$ 的问题， $sam$ 是解决前缀的后缀，那么就把字符串翻一下，变成求前缀的最长公共后缀
由于 $sam$ 的 $fail$ 树上的每个叶子节点存的是前缀字符串，注意到这就是 $sam$ 的 $fail$ 树上的非叶子节点，任意两个的 $lcs$ 就是他们的 $lca$ 所表示的字符串，一个这样的节点会被计算的数量为任意选两个不同的子树上的节点的数量
通过一边累加之前的子树大小和，一边用之前的子树大小和乘上该子树的大小，表示前面的任意一个节点与该子树上任意一个点配对，然后令方案数乘上该分支节点的长度即可

# ✅

const int N = 1e6 + 10;
struct SuffixAutoMaton {
    int ed, ct;
    int fa[N], to[N][26], len[N];
    int size[N];
    inline SuffixAutoMaton () { ed = ct = 1; }
    inline void insert (int c, int l) {
        int v = ed;
        ed = ++ct;
        len[ed] = l;
        size[ed] = 1;
        for (; v && to[v][c] == 0; v = fa[v]) to[v][c] = ed;
        if (!v) {
            fa[ed] = 1;
        } else if (len[v] + 1 == len[to[v][c]]) {
            fa[ed] = to[v][c];
        } else {
            int np = ++ct;
            int p = to[v][c];
            for (int i = 0; i < 26; i ++) to[np][i] = to[p][i];
            len[np] = len[v] + 1;
            fa[np] = fa[p];
            fa[p] = fa[ed] = np;
            for (int i = v; to[i][c] == p; i = fa[i]) to[i][c] = np;
        }
    }
} sam;
struct Edge {
    int nxt, to;
} edge[N];
int head[N], cnt;
inline void add_Edge (int from, int to) {
    edge[++cnt] = {head[from], to};
    head[from] = cnt;
}

ll res = 0;
inline void dfs (int u) {
    int sum = 0;
    int del = 0;
    for (int i = head[u]; i; i = edge[i].nxt) {
        int v = edge[i].to;
        dfs(v);
        res -= (ll)sam.size[u] * sam.size[v] * sam.len[u] * 2;
        sam.size[u] += sam.size[v];
    }
}

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    string s; cin >> s;
    reverse(s.begin(), s.end());
    int n = s.size();

    for (int i = 0; i < s.size(); i ++) sam.insert(s[i] - 'a', i + 1);
    for (int i = 2; i <= sam.ct; i ++)  add_Edge(sam.fa[i], i);

    res = (ll)(n - 1) * n * (n + 1) / 2;
    dfs(1);
    cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

后缀数组