打表、找规律

#

---

牛客2021多校(3)E_Math

🔗

💡

看柿子，好乱啊，而且是最没有什么性质可言的可约符
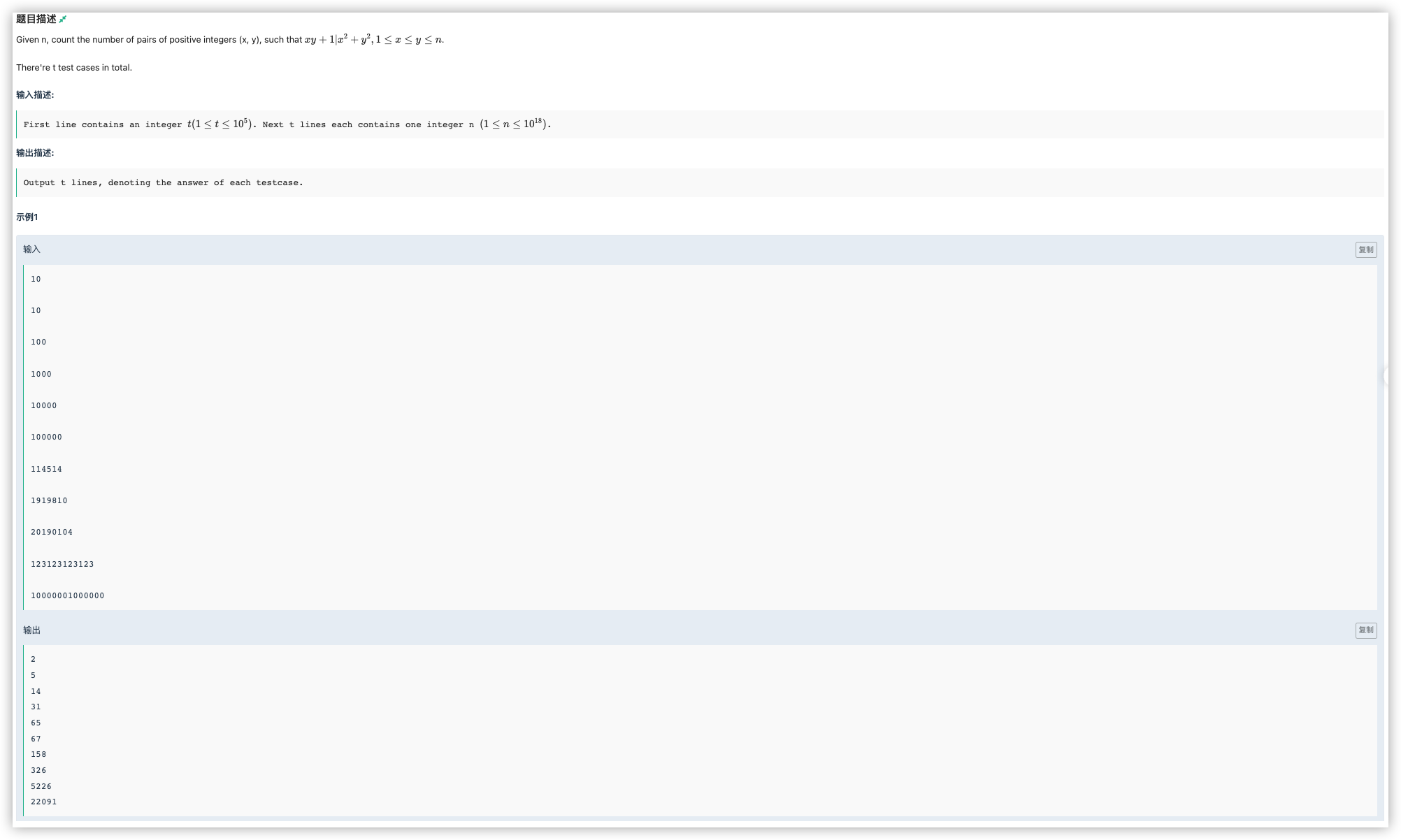
看样例，数不多啊，打个表看一下都是谁
首先发现 $(x,x^4)$ 是满足的
然后发现出现在一组里面第二个的，也会出现在别的组里面第一个
挖出来一条链看一下性质：
$2\;8\;30\;112\;418\;1560\;5822...$
$8$ 到 $30$ 最接近是乘 $4$ ，然后减 $2$ ，用同乘规律试一下
$8\times 4-2=30\\30\times 4-8=112\\112\times 4-30=418\\...$
然后再看
$3\;27\;240\;2133\;18957\;168480...$
$27$ 到 $240$ 最接近是乘 $9$ ，然后减 $3$ ，同样同乘试一试
$27\times 9-3=240\\240\times 9-27=2133\\...$
也满足，然后发现乘的都是第一个数的二次幂，试一下第一个数 $4$ 的情况，也满足，那太好了
于是我们可以通过这种链处理出来所有 $1\le x\le y\le 10^{18}$ 的二元组，也不多

在得答案时不能一个个找，毕竟如果 $n=10^{18}$ ，那么 $10^6$ 个答案还是至少有的，结合 $T$ ，就会超时
但是用 $x\le y$ 来看，我们只要保证 $y\le n$ ，故将所有的二元组 $(x,y)$ 以 $y$ 的大小排序，然后最后统计一下不大于 $(n,n)$ 的数量即可，lower_bound

✅

struct node {
    ll x, y;
    inline node (ll _x, ll _y) {x = _x; y = _y;}
    inline friend bool operator < (node a, node b) {
        return a.y < b.y;
    }
};
vector<node> res;

inline void Solve () {
    ll n; cin >> n;
    cout << upper_bound(res.begin(), res.end(), node(n, n)) - res.begin() << endl;
}

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    res.push_back({1, 1});
    for (ll x = 2; x <= 1000000; x ++) {
        res.push_back({x, x * x * x});
        vector<ll> a; 
        a.push_back(x); a.push_back(x * x * x);
        while (1) {
            __int128_t nxt = (__int128_t)a.back() * x * x - a[a.size() - 2];
            if (nxt <= 1000000000000000000) 
                res.push_back({a.back(), (ll)nxt}),
                a.push_back(nxt);
            else 
                break;
        }
    }
    sort(res.begin(), res.end());

    int cass; cin >> cass; while ( cass -- ) {
        Solve ();
    }
}

---