位运算

Chivas-Regal

#

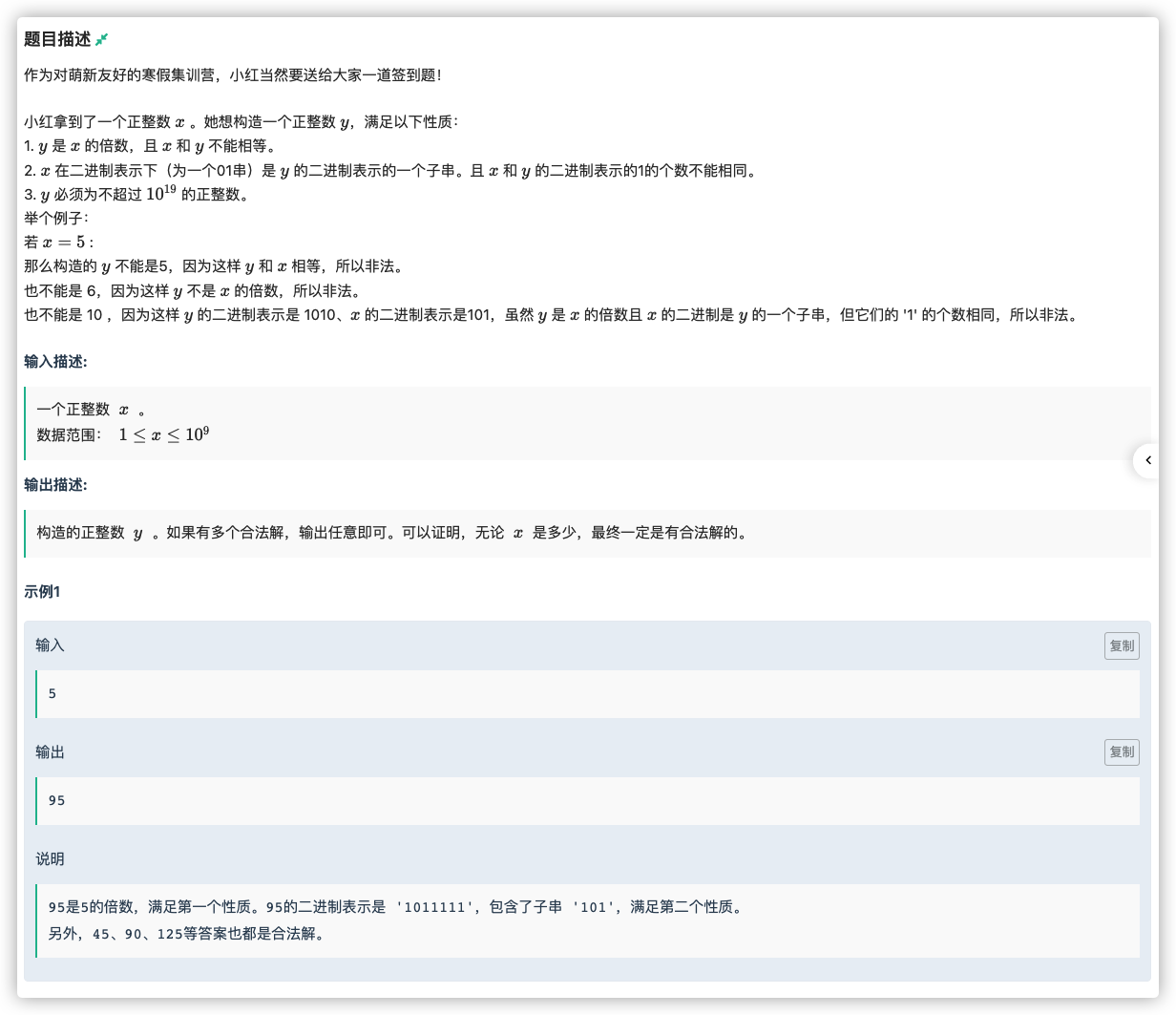
# 牛客2022寒假算法基础集训营4K_小红的真真假假签到题题

# 🔗

# 💡

要求子串，且 $1$ 的个数不同
那么我们让 $x$ 化为 $01$ 串后两段 $x$ 拼在一起即可
方便下其实左移 $30$ 为后腾出充足的位置在补上 $x$ 即可

# ✅

x = int(input())
print(x << 30 | x)

1
2

# ABC238D_ANDandSUM

# 🔗

# 💡

首先 $\&$ 下两个数在 $a$ 含 $1$ 的位置上都至少是 $1$ ，所以 $s$ 至少是 $a+a$
这是首先的特判
多出来的部分我们设置为 $dir$ ， $dir$ 可以通过 $x$ 或 $y$ 都是 $0$ 的位置让其中一个变成 $1$ 但是不能都变，不然 $\&$ 就会改变，当然 $1$ 的位置是变不了的
所以只要 $dir$ 和 $a$ 不存在有一位两者都为 $1$ 即可
即 $dir\&a=0$

# ✅

inline void Solve () {
        ll a, s; cin >> a >> s;
        if ( a + a > s ) cout << "No" << endl;
        else {
                ll dir = s - (a + a);
                if ( dir & a ) cout << "No" << endl;
                else           cout << "Yes" << endl;
        }
}

1
2
3
4
5
6
7
8
9

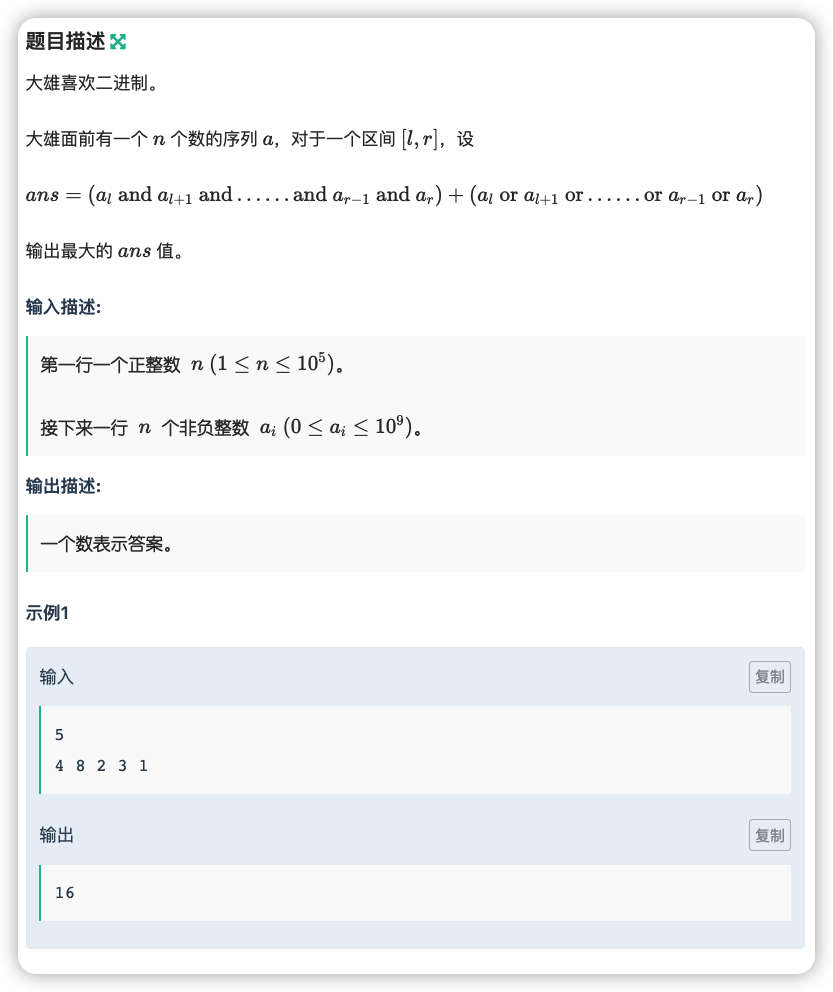
# 牛客练习赛97B_野比大雄的作业

# 🔗

# 💡

注意到对于两个数的一位
如果同为 $1$ ，那么这两位在与和且的时候都同为 $1$
如果一个 $0$ 一个 $1$ ，那么这两位在与和且的时候会变成 $0$ 和 $1$
如果同为 $0$ ，那么这两位会变成 $0$ 和 $0$
发现并没有数量上的增多减少，那么就选一个就行了

# ✅

int main () {
        ios::sync_with_stdio(false);

        int n; cin >> n;
        vector<int> a(n);
        int res = 0;
        for ( int i = 0; i < n; i ++ ) cin >> a[i], res = max(res, a[i] * 2);
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9

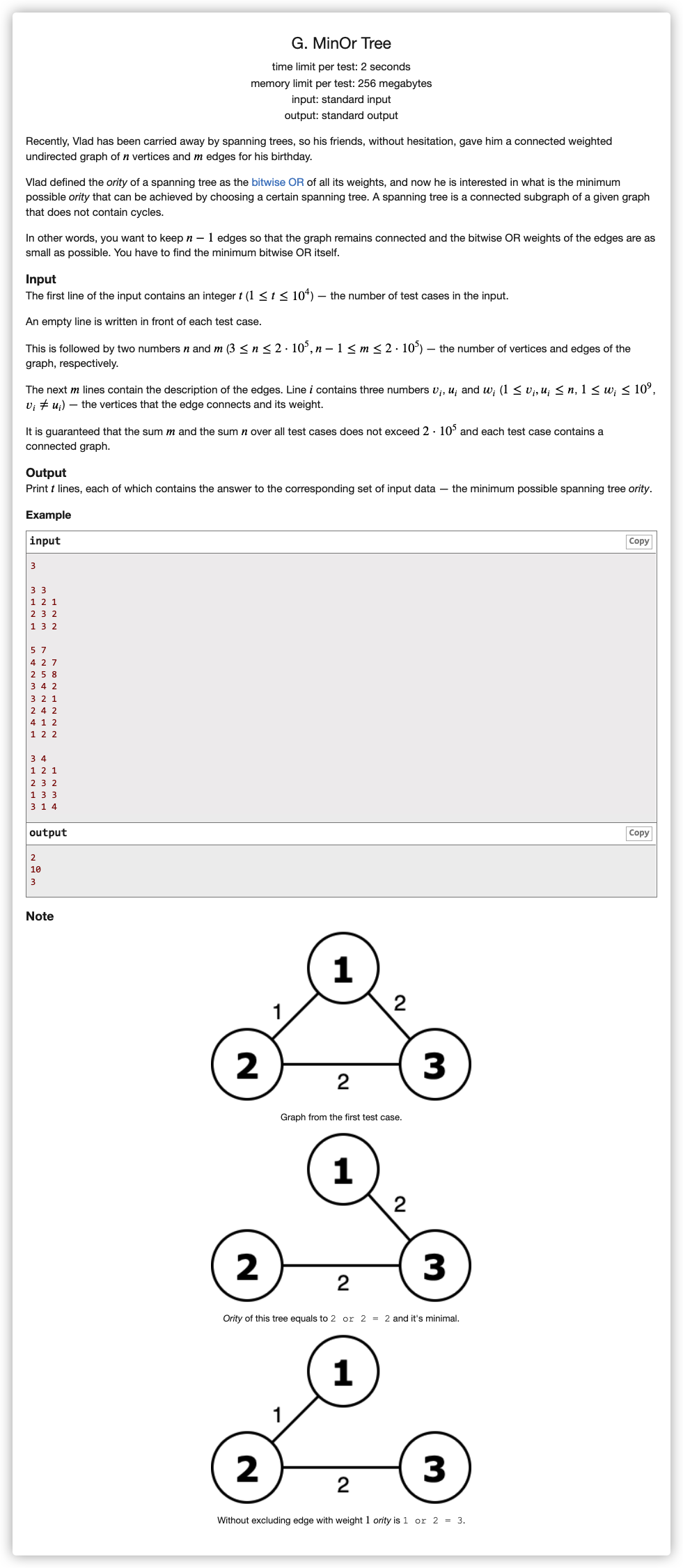
# CodeForces1624G_MinOrTree

# 🔗

# 💡

考虑或的性质
我们想让或出来的尽可能小
那么很高的位我们肯定要尽可能不选
从 $30$ 向下枚举二进制位数
对于这一位为 $1$ 的边，如果可以拆掉我们肯定想去拆掉，但是判是否为割边十分麻烦，不如反向思考一下
如果可以不计算这一位的 $1$ 意味着所有这一位非 $0$ 的边能把 $n$ 个点组成一个整的连通块（这一步可以用并查集实现，原本 $n$ 个块每真正意义上合并一次都会让连通块个数 $-1$ ）
这样的话所有的 $1$ 边都可以删掉了
否则我们既然要计算，那还不如不删，就保留下来，并让 $res$ 这一位为 $1$

# ✅

const int N = 2e5 + 10;

struct Edge {
	int u, v, c, id;
	inline friend bool operator < ( Edge a, Edge b ) {
		return a.id < b.id;
	}
}; set<Edge> st;
int n, m, nblk;

int nod[N];
inline void Init () { for ( int i = 0; i <= n; i ++ ) nod[i] = i; }
inline int Find ( int x ) { return nod[x] == x ? x : nod[x] = Find(nod[x]); }
inline void Merge ( int x, int y ) { 
	int fx = Find(x), fy = Find(y); 
	if ( fx != fy ) {
		nblk --;
		nod[fx] = fy;
	}
}


inline void Solve () {
	scanf("%d%d", &n, &m); 
	st.clear();
	for ( int i = 0; i < m; i ++ ) {
		int u, v, c; scanf("%d%d%d", &u, &v, &c);
		st.insert({u, v, c, i});
	}
	int res = 0;
	for ( int bit = 30; bit >= 0; bit -- ) {
		Init(); nblk = n;
		for ( auto e : st ) {
			if ( (e.c & (1 << bit)) ) continue;
			Merge(e.u, e.v);
		}
		if ( nblk > 1 ) res |= (1 << bit);
		else {
			vector<Edge> del;
			for ( auto e : st ) {
				if ( e.c & (1 << bit) ) del.push_back(e);
			}
			for ( auto e : del ) st.erase(e);
		}
	}
	printf("%d\n", res);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

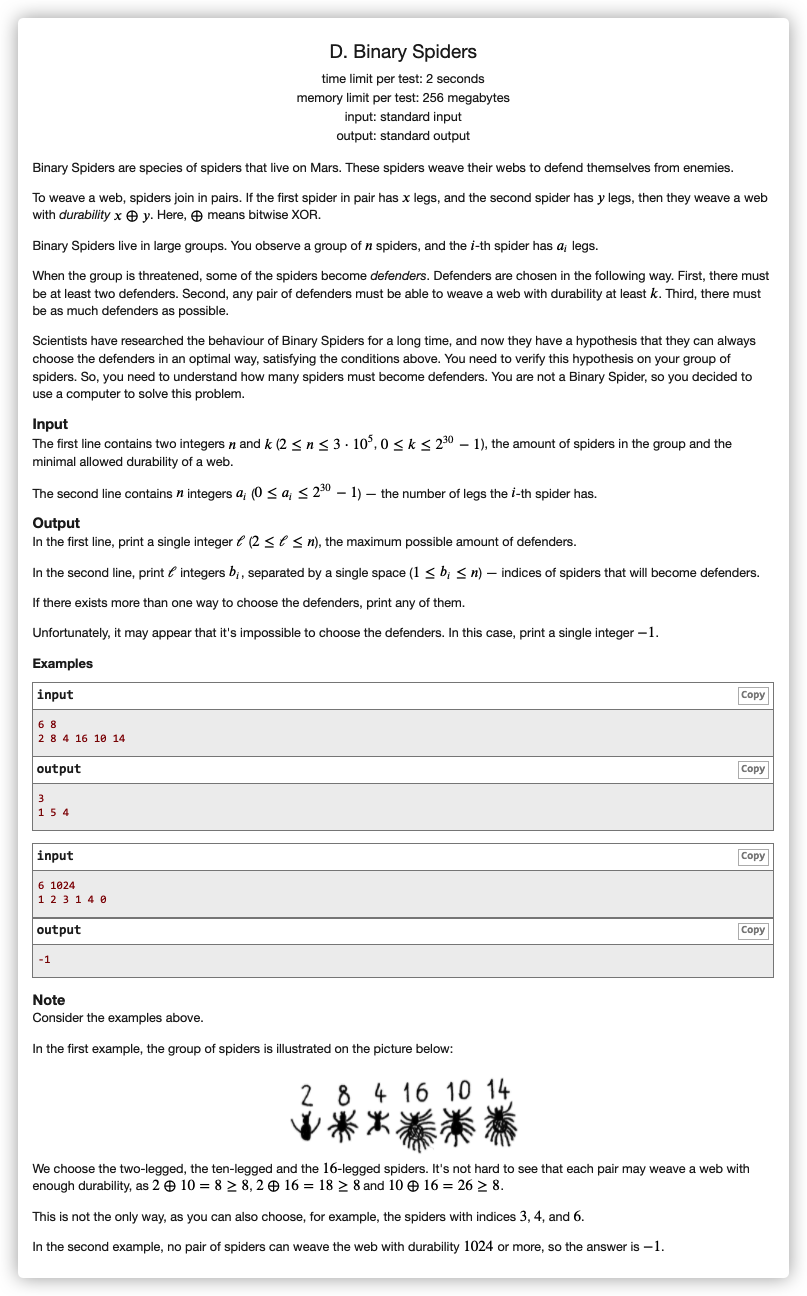
# CodeForces1625D_BinarySpiders

# 🔗

# 💡

考虑 $k$ 有 $m$ 位，若一对数 $m$ 以上的位存在不同的，那么必然可以
若一对数 $m$ 以上的位相同，那么去检查相同的内部是否存在两者 $\oplus\ge k$
那么存 $m$ 以上的前缀

不同，随便选
相同，考虑 $a\oplus b\ge k,a\oplus c\ge k\Longrightarrow a_m\neq b_m,a_m\neq c_m\Longrightarrow b_m=c_m\Longrightarrow b\oplus c\lt k$ ，所以此时最多可以选两个，但至少可以选一个

同前缀内可以用 $Trie$ 数去查每个数的最大异或

# ✅

const int N = 3e5 + 10;

int n, k, m;
map<int, int> id;
map<int, vector<int> > pres;

inline int Bits ( int x ) {
        int res = 0;
        while ( x ) x >>= 1, res ++;
        return res;
}

namespace Trie {
        int t[N * 30][2], idx;
        inline void Init () { memset(t, 0, sizeof (int) * 2 * (idx + 1)); idx = 0; }
        inline void Insert ( int x ) {
                int p = 0;
                for ( int i = 30; i >= 0; i -- ) {
                        int u = x >> i & 1;
                        if ( !t[p][u] ) t[p][u] = ++ idx;
                        p = t[p][u];
                }
        }
        inline int Query ( int x ) {
                int res = 0, p = 0;
                for ( int i = 30; i >= 0; i -- ) {
                        int u = x >> i & 1;
                        if ( !t[p][!u] ) {
                                res = res << 1 | u;
                                p = t[p][u];
                        } else {
                                res = res << 1 | (!u);
                                p = t[p][!u];
                        }
                }
                return res;
        }
}

int main () {
        ios::sync_with_stdio(false);

        cin >> n >> k; m = Bits(k);
        for ( int i = 1; i <= n; i ++ ) {
                int x; cin >> x;
                pres[x >> m].push_back(x);
                id[x] = i;
        }
        if ( k == 0 ) {
                cout << n << endl;
                for ( int i = 1; i <= n; i ++ ) cout << i << " ";
                return 0;
        }
        vector<int> res; 
        for ( auto pre : pres ) {
                bool flag = false;
                Trie::Init();
                for ( auto x : pre.second ) {
                        int t = Trie::Query(x);
                        if ( (t ^ x) >= k ) {
                                res.push_back(id[t]);
                                res.push_back(id[x]);
                                flag = true;
                                break;
                        }
                        Trie::Insert(x);
                }
                if ( !flag ) res.push_back(id[pre.second[0]]);
        }
        if ( res.size() <= 1 ) cout << "-1" << endl;
        else {
                cout << res.size() << endl;
                for ( auto i : res ) cout << i << " ";
                cout << endl;
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76

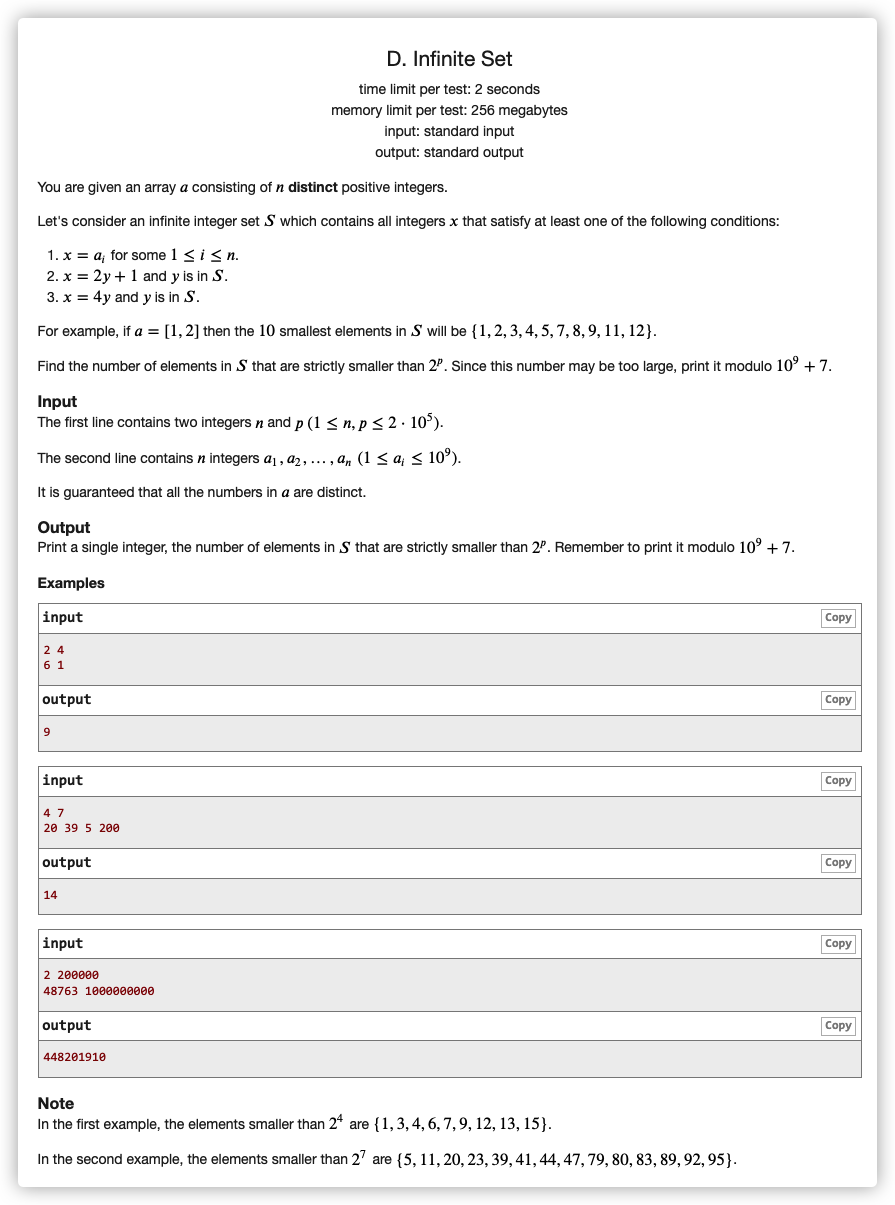
# CodeForces1635D_InfiniteSet

# 🔗

# 💡

$2x+1$ 为奇， $4x$ 为偶
若 $a<b$ ， $a\in[a]$ 且 $b\in[a]$ 且 $a$ 可变为 $b$ ，删去 $b$ ，称为去重
去重操作从大到小，对数的奇偶性进行向下修正，直到为偶数且模 $4$ 不为 $0$ 停止，如果向下修正时当前数已经存在，那么需要删掉
去重后，剩下的所有在变化中将毫不相干

注意 $2^p$ 说明是一个二进制问题
考虑一下，对于

1_2\left\{\begin{aligned} &\stackrel{\times2+1}{\longrightarrow}11_2\\ &\stackrel{\times4}{\longrightarrow}100_2 \end{aligned}\right.

可以看出，一个 $x$ 位的数可以推到 $x+1$ 位与 $x+2$ 位
阶梯问题，所以是 $fibonacci$
那么对于一个有 $sz$ 位的数，可以变化出 $p$ 位以下的有 $p-sz+1$ 位
即 $fibonacci$ 前缀和 $sum[p-sz+1]$
对去重后的所有数累加即可

# ✅

const int N = 2e5 + 10;
const int mod = 1e9 + 7;
ll n, p;
set<ll> st;
vector<ll> a;

ll fibo[N];

int main () {
        ios::sync_with_stdio(false);
        fibo[1] = fibo[2] = 1;
        for ( int i = 3; i < N; i ++ ) fibo[i] = (fibo[i - 1] + fibo[i - 2]) % mod;
        for ( int i = 2; i < N; i ++ ) fibo[i] = (fibo[i] + fibo[i - 1]) % mod; // fibonacci 前缀和

        cin >> n >> p;
        for ( int i = 0; i < n; i ++ ) {
                ll x; cin >> x;
                st.insert(x);
                a.push_back(x);
        }
        // 去重
        sort ( a.begin(), a.end(), greater<ll>() );
        a.erase(unique(a.begin(), a.end()), a.end());
        for ( int i = 0; i < a.size(); i ++ ) {
                if ( *st.lower_bound(a[i]) != a[i] ) continue;

                ll cur = a[i];
                bool flag = false;
                while ( cur ) {
                        if ( cur & 1 ) cur = (cur - 1) / 2; // 反式 *2+1
                        else {
                                if ( cur % 4 ) break; // 化不下去了
                                else cur /= 4; // 反式 *4
                        }
                        if ( *st.lower_bound(cur) == cur ) { // [a]内存在
                                flag = true;
                                break;
                        }
                }
                if ( flag ) st.erase(a[i]);
        }
        // 逐个累加
        ll res = 0;
        for ( auto i : st ) {
                ll tmp = i;
                ll sz = 0; while ( tmp ) sz ++, tmp /= 2; 
                if ( p >= sz ) (res += fibo[p - sz + 1]) %= mod;
        }
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

# CodeForces1658D1_388535（Easy Version）

# 🔗

# 💡

虽然样例很具迷惑性要猜结论，但是这里要考虑位运算
注意到 $l=0$
将前几位数分解了

\begin{aligned} &0=&0000\\ &1=&1000\\ &2=&0100\\ &3=&1100\\ &4=&0010\\ &5=&0011 \end{aligned}

注意到每一位上前缀 $0$ 的个数 $\ge$ $1$ 的个数
又考虑一下对于一位上异或 $1$ 的性质：结果 $01$ 反转
那么对于给出的 $r-l+1$ 个数，我们将其拆分，看看所有数在每一位上 $01$ 的个数，如果 $0$ 的个数 $\lt$ $1$ 的个数那么就意味着要反转，即让答案这一位变为 $1$

# ✅

inline void Solve() {
        int l, r; cin >> l >> r;
        vector<int> dir10(30, 0);
        for ( int i = l; i <= r; i ++ ) {
                int x; cin >> x;
                for ( int j = 0; j < 30; j ++ ) {
                        dir10[j] += x >> j & 1;
                        dir10[j] -= !(x >> j & 1);
                }
        }
        int res = 0;
        for ( int i = 0; i < 30; i ++ ) {
                if ( dir10[i] > 0 ) res |= 1 << i;
        }
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

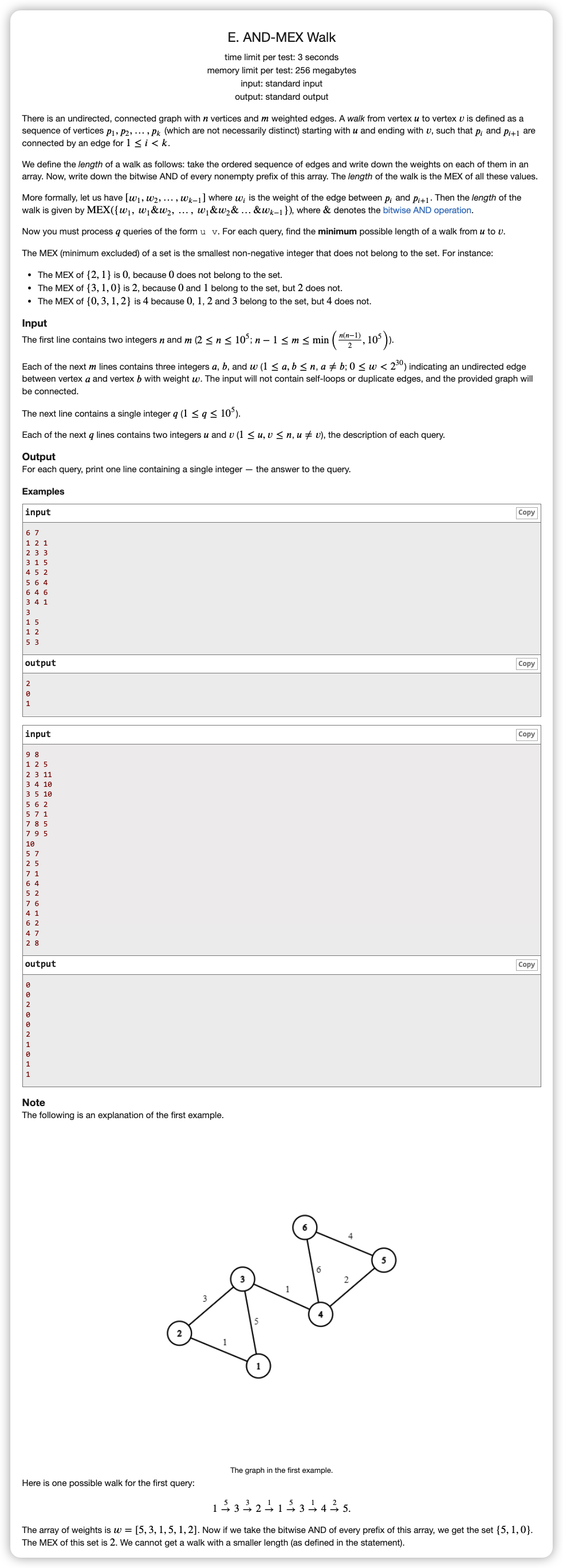
# CodeForces1659E_AND-MEXWalk

# 🔗

# 💡

首先从样例中猜测答案不会大于 $2$ ，证明一下发现在与操作中， $10_2$ 是不可能变成一个完全相反的数的即 $01_2$ ，那么也就是说 $1$ 和 $2$ 不会同时出现在数列的前缀与中的

那么答案就变成了三种情况： $0,1,2$
首先看一下 $0$ 的情况：
考虑一下与操作的特性：全 $1$ 则 $1$ ，否则为 $0$
要想为 $0$ ，首先保证最后一个数不为 $0$
这也就意味着必须要有一位从头到尾都出现
这个判断可以通过对每一位维护一个连通块，如果存在一位的连通块能把 $u,v$ 都连接起来，就说明答案为 $0$
然后看一下 $1$ 的情况：
这就是说我们要从一个大于 $1$ 的数直接跳到 $0$
可以在不为 $1$ 的时候通过一个偶数将第 $0$ 位关闭
这个就意味着我们在遇见第一个偶数的时候，答案还不为 $0$
化简一下任务，也就是说我们在存在除了第 $0$ 位以外别的位为 $1$ 的时候，突然出现一个偶数把第 $0$ 位为 $1$ 的可能性关闭了
这样可以先标记一下哪些点的邻边为偶数
然后用这些点去标记除了 $0$ 位之外每一位连通块中的每一个点（其实就更新该连通块内的首点即可）
意味着这些点完全可以走到我们一开始标记的点来关闭掉出现 $1$ 的可能性，然后再继续它的任务走到 $v$
除此之外也就是 $2$ 了

# ✅

const int N = 1e5 + 10;

struct DSU {
        std::vector<int> f;
        DSU (int n) : f(n) { std::iota(f.begin(), f.end(), 0); }
        inline int leader (int x) { return x == f[x] ? x : f[x] = leader(f[x]); }
        inline bool same (int x, int y) { return leader(x) == leader(y); }
        inline void merge (int x, int y) {
                x = leader(x);
                y = leader(y);
                if (x == y) return;
                f[y] = x;
        }
};

int main () {
        std::ios::sync_with_stdio(false);
        std::cin.tie(nullptr);

        int n, m; std::cin >> n >> m;

        std::vector dsu(30, DSU(n + 1));
        std::vector near_eve(n + 1, false);

        for (int i = 0; i < m; i ++) {
                int u, v, w; std::cin >> u >> v >> w;
                if (w % 2 == 0) {
                        near_eve[u] = near_eve[v] = true;
                }
                for (int j = 0; j < 30; j ++) {
                        if (w >> j & 1) {
                                dsu[j].merge(u, v);
                        }
                }
        }

        std::vector close0(30, std::vector<bool>(n + 1));
        for (int i = 1; i <= n; i ++) {
                if (near_eve[i]) {
                        for (int j = 1; j < 30; j ++) {
                                close0[j][dsu[j].leader(i)] = true;
                        }
                }
        }

        int q; std::cin >> q;
        while (q --) {
                int u, v; std::cin >> u >> v;
                int res = 2;
                for (int i = 0; i < 30; i ++) if (dsu[i].same(u, v)) res = std::min(res, 0);
                for (int i = 1; i < 30; i ++) if (close0[i][dsu[i].leader(u)]) res = std::min(res, 1);
                std::cout << res << "\n";
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

万能头文件手动添加二分