树形DP

Chivas-Regal

#

# 洛谷P2899_CellPhoneNetworkG

# 🔗

# 💡

由于一个节点可以被自己给信号，可以被儿子给信号，可以被父亲给信号
所以我们设置 $dp[i][0/1/2]$ 表示 $i$ 节点被 $[$ 自己 $/$ 儿子 $/$ 父亲 $]$ 给信号需要的节点数

若被自己给信号
那么它的儿子被谁给信号都可以
$dp[u][0]+=min(dp[v][0],dp[v][1],dp[v][2])$

若被父亲给信号
那么说明儿子 $v$ 一定没法从 $u$ 身上获得信号
$dp[u][2]+=min(dp[v][0],dp[v][1])$

若被儿子给信号
那么还是上面这种
但是要注意，我们只有一个父亲，但可能有很多个儿子
所以在众多儿子中我们需要保证至少选一个 $dp[v][0]$
那么可以先把 $dp[v][0]$ 都选了，然后对所有儿子的 $dp[v][1]-dp[v][0]$ 进行排序
然后在前儿子个数 $-1$ 个儿子内看看哪些可以替换为 $dp[v][1]$
即

$dp[u][1]+=\sum\limits_{son}dp[son][0]\\ \textbf{sort}(son,\{dp[son][1]-dp[son][0],\textbf{<}\})\\ \textbf{for}\;son\;\textbf{in}\;sons\;\;\textbf{\&}\;\;son\neq endson:\\ \qquad \textbf{if}\;dp[son][1]-dp[son][0]<0:\\ \qquad\qquad dp[u][1]+=dp[son][1]-dp[son][0];\\ \qquad \textbf{else}\\ \qquad\qquad \textbf{break};\\$

统计答案
由于根节点无父亲，所以最后取 $min(dp[rt][0],dp[rt][1])$

# ✅

// 有上述转移，此处就不放置代码了

# 洛谷P3174_[HAOI2009]毛毛虫

# 🔗

# 💡

维护每一个点向下走链的最大值，即 $dp[fa]=max(dp[son]+numson_{fa})$
然后我们知道一个链可以从上到下，也可以跨过一个点再折下去
从上到下就是 $dp[i]$
第二种情况则是对于一个点 $u$ ，找到两个儿子 $v1,v2$ ，该毛毛虫为 $dp[v1]+dp[v2]+deg_u-1$
故我们跑 $dfs$ 维护 $dp$ ，然后每次维护 $max(dp[i]$ ,两个最大儿子 $dp$ 的和加上 $deg_u-1)$

# ✅

const int N = 300010;
const int M = N << 1;
const int mod = 1e9 + 7;
struct Edge {
    int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to) {
    edge[++cnt] = {head[from], to};
    head[from] = cnt;
}

map<pair<int, int>, bool> mp;

int dp[N], du[N];
int res = 0;
inline void dfs (int u, int fa) {
    int son = 0;
    vector<int> vec;
    for (int i = head[u]; i; i = edge[i].nxt) {
        int v = edge[i].to;
        if (v == fa) continue;
        son ++;
        dfs(v, u);
        vec.push_back(dp[v]);
    }
    sort(vec.begin(), vec.end(), greater<int>());
    if (!son) {
        dp[u] = 1;
    } else {
        dp[u] = vec[0] + son;
    }

    res = max(res, dp[u]);
    if (son > 1) {
        res = max(res, vec[0] + vec[1] + du[u] - 1);
    }
}

int main () {
    int n, m; scanf("%d%d", &n, &m);
    for (int i = 0; i < m; i ++) {
        int u, v; scanf("%d%d", &u, &v);
        if (mp.count({u, v}) || mp.count({v, u})) continue;
        mp[{u, v}] = 1;
        add_Edge(u, v);
        add_Edge(v, u);
        du[u] ++; du[v] ++;
    }
    dfs(1, 1);
    printf("%d\n", res);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

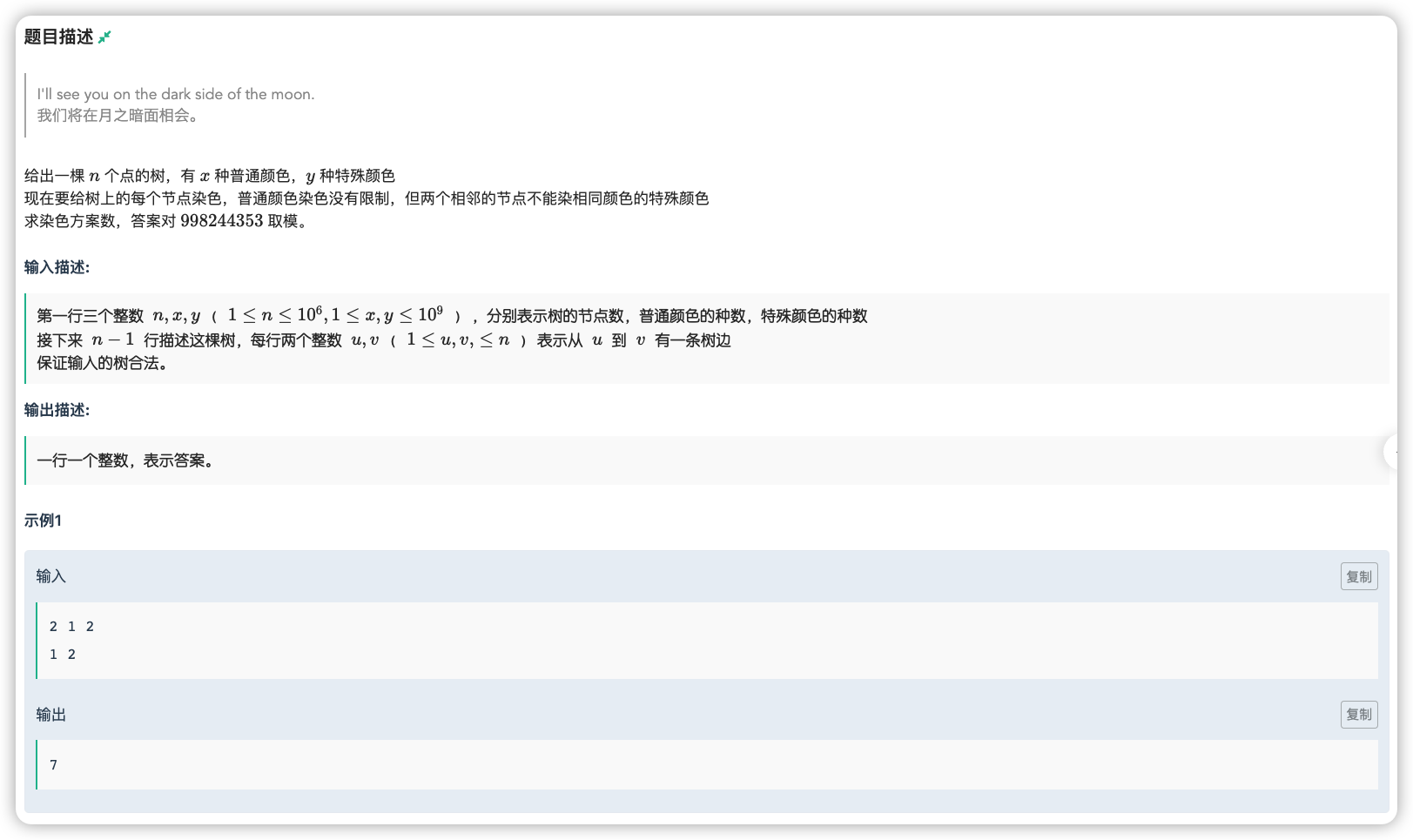
# 牛客练习赛97D_月之暗面

# 🔗

# 💡

对于每一个点选择同类别的每一个颜色的方案数都是相同的
那么我们就对于一个点固定下来一个颜色后，利用儿子进行转移
其在选普通颜色时儿子为哪一种颜色都可以
选特殊颜色时儿子的特殊颜色只能选 $y-1$ 种
向上转移最后 $dp[1][0]\times x+dp[1][1]\times y$ 就是答案了

# ✅

int n, x, y;
modint dp[N][2];
inline void DFS ( int u, int father ) {
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == father ) continue;
                DFS(v, u);
                dp[u][0] *= dp[v][0] * x + dp[v][1] * y;
                dp[u][1] *= dp[v][0] * x + dp[v][1] * (y - 1);
        }
}

int main () {
        cin.tie(0)->sync_with_stdio(0);
        cin.exceptions(cin.failbit);

        cin >> n >> x >> y;
        for ( int i = 1; i < n; i ++ ) {
                int u, v; cin >> u >> v;
                add_Edge(u, v);
                add_Edge(v, u);
        }

        for ( int i = 1; i <= n; i ++ ) dp[i][0] = dp[i][1] = 1;

        DFS(1, 0);

        cout << dp[1][0] * x + dp[1][1] * y << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

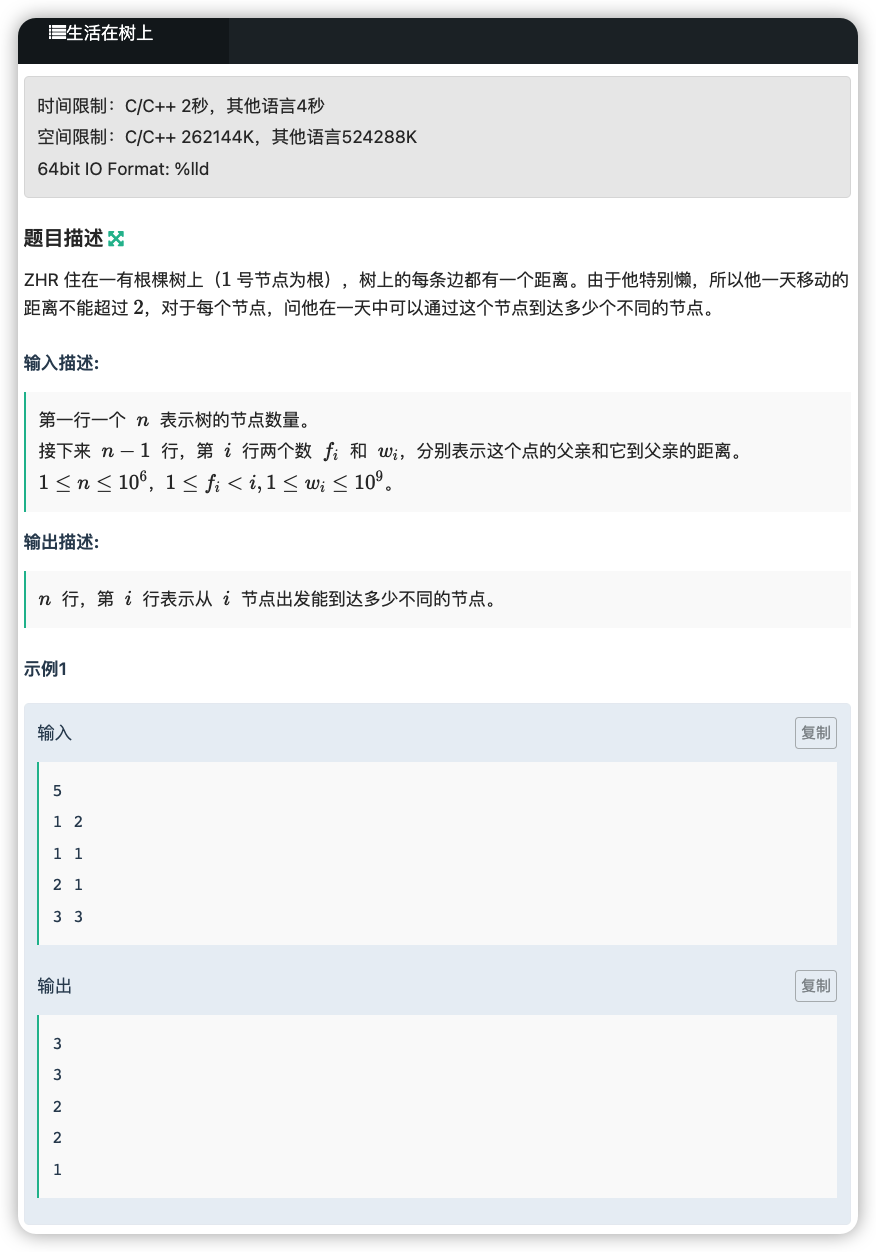
# 牛客小白月赛46D_生活在树上

# 🔗

# 💡

注意到一天移动的距离不超过 $2$
且边权 $\ge 1$
那么最多可以经过两条边转移
考虑可以到达点 $x$ 的点 $y$ 位置的三种可能性：
$1.$ $y$ 在 $x$ 的爷节点或者父节点
$2.$ $y$ 在 $x$ 的子节点或者孙节点
$3.$ $y$ 与 $x$ 同一个父亲且与父亲的边权都为 $1$

第三种情况我们每个节点记录一下每一个距离为 $1$ 的儿子然后对儿子的第三个答案统一赋值
第二钟情况我们用两个记录数组（距离为 $1$ 的个数，距离为 $2$ 的个数）去往上回溯
第三种情况与第二种情况类似，往下推就行了

最后答案是这三个加起来再加一

# ✅

const int N = 1e6 + 10;
const int M = 2e6 + 10;

struct Edge {
        int nxt, to;
        ll val;
} edge[M];
int head[N], cnt;
inline void add_Edge ( int from, int to, ll val ) {
        edge[++cnt] = { head[from], to, val };
        head[from] = cnt;
}

ll res_down1[N], res_down2[N];
ll res_samefather[N];
ll res_up1[N], res_up2[N];

inline void DFS ( int u, int fa ) {
        int num1 = 0;
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fa ) continue;

                if ( edge[i].val == 1 ) res_down1[v] ++, res_down2[v] += res_down1[u];
                else if ( edge[i].val == 2 ) res_down2[v] ++;
                DFS(v, u);
                if ( edge[i].val == 1 ) res_up2[u] += res_up1[v], res_up1[u] ++;
                else if ( edge[i].val == 2 ) res_up2[u] ++;

                num1 += edge[i].val == 1;
        }
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fa || edge[i].val != 1 ) continue;
                res_samefather[v] += num1 - 1;
        }
}
int main () {
        int n; scanf("%d", &n);
        for ( int i = 2; i <= n; i ++ ) {
                int f, w; scanf("%d%d", &f, &w);
                add_Edge(i, f, w);
                add_Edge(f, i, w);
        }

        DFS(1, 0);
        for ( int i = 1; i <= n; i ++ ) printf("%lld\n", 1 + res_down1[i] + res_down2[i] + res_samefather[i] + res_up1[i] + res_up2[i]);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

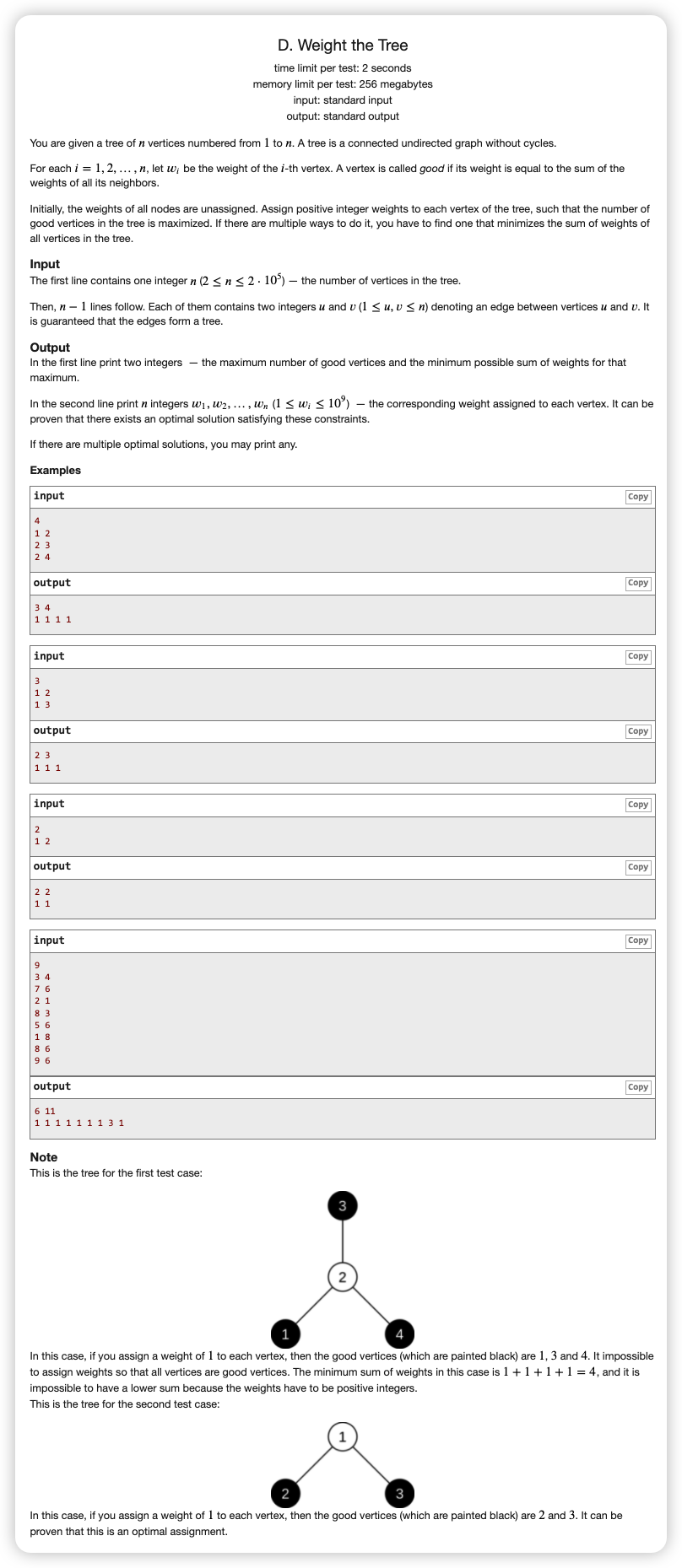
# CodeForces1646D_WeightTheTree

# 🔗

# 💡

考虑一下如何让 $sum\{w\}$ 最小：不选的节点为 $1$ ，选的节点为 $du$
用 $dp$ 转移出来最大独立集
但是在有多个最大独立集时我们想让我们的 $sum\{w\}$ 最小
那么我们要设置两个关键字 $\{$ 独立集个数贡献， $-w$ 贡献 $\}$
令每一个节点存在两个 $dp$ 状态， $0/1$ 即不选与选
在 $dp$ 转移的时候 $dp[u][0]$ 可以通过 $dp[v][0],dp[v][1]$ 转移，累加其中最大的即可
$dp[u][1]$ 只可以通过 $dp[v][0]$ 转移

那么我们可以向下 $DFS$ ，看这一位要是否选就让两个答案加上 $dp[u][0/1]$ ，并给 $w[u]$ 赋值
同时走子节点时，若这一位选了 $1$ 或者 $dp[v][0]>dp[v][1]$ ，那么子节点都要选 $0$
否则选 $1$

# ✅

const int N = 2e5 + 10;
const int M = 4e5 + 10;
 
int n, du[N];
struct Edge {
        int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge ( int from, int to ) {
        edge[++cnt] = { head[from], to };
        head[from] = cnt;
}
 
pair<int, int> dp[N][2];
 
inline void DFS ( int u, int fa ) {
        dp[u][1] = {1, -du[u]};
        dp[u][0] = {0, -1};
 
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fa ) continue;
                DFS(v, u);
                dp[u][1].first += dp[v][0].first;
                dp[u][1].second += dp[v][0].second;
                pair<int, int> mx = max(dp[v][0], dp[v][1]);
                dp[u][0].first += mx.first;
                dp[u][0].second += mx.second;
        }
}
 
int res1, res2;
 
int w[N];
inline void Solve ( int u, int fa, int op ) {
        if ( op ) {
                w[u] = du[u];
                res1 ++;
                res2 += du[u];
        } else {
                w[u] = 1;
                res2 ++;
        }
 
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fa ) continue;
                if ( op == 1 || dp[v][0] > dp[v][1]) {
                        Solve (v, u, 0);
                } else {
                        Solve (v, u, 1);
                }
        }
}
 
int main () {
        scanf("%d", &n);
        for ( int i = 1; i < n; i ++ ) {
                int u, v; scanf("%d%d", &u, &v);
                add_Edge(u, v);
                add_Edge(v, u);
                du[u] ++;
                du[v] ++;
        }
        if ( n == 2 ) {
                printf("%d %d\n%d %d", 2, 2, 1, 1);
                return 0;
        }
 
        DFS(1, 0);
 
        Solve (1, 0, dp[1][0] < dp[1][1]);
 
        printf("%d %d\n", res1, res2);
        for ( int i = 1; i <= n; i ++ ) printf("%d ", w[i]);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76

# gym103145C_VertexDeletion

# 🔗

# 💡

一个树形dp的比较经典的模型
由于本题设计两个点存在问题：存在、存在且与另一个存在相连
再带上一个不存在的问题，所以设计三个状态
dp[x][0]：不存在
dp[x][1]：存在但不连子节点
dp[x][2]：存在且连了子节点

分类讨论一下：
0--不存在：除了不连子节点的点以外，其余状态点都可以连
$dp[x][0] = \prod(dp[y][0]+dp[y][2])$
1--存在但不连子节点：连上所有不存在的点
$dp[x][1] = \prod dp[y][0]$
2--存在且连了子节点：除了子节点都不存在以外，别的方式都可以连
$dp[x][2] = \prod(dp[y][0] + dp[y][1] + dp[y][2]) - \prod dp[y][0]$

最后不能选存在且不连子节点的祖先，这样是一个被孤立的点，所以我们计算
$dp[1][0] +dp[1][2]$

# ✅

#include <iostream>
#define ll long long
using namespace std;

const int N = 1e5 + 10,
	  M = 2e5 + 10,
	  mod = 998244353;

struct Edge {
	int nxt, to;
}edge[M];

int head[M], cnt;
ll dp[N][3];
int vis[N];
int n;

inline void Init () {
	for ( int i = 0; i < n * 2 + 5; i ++ ) 
		head[i] = -1;
	for ( int i = 0; i < n + 5; i ++ ) 
		vis[i] = 0,  
		dp[i][0] = dp[i][1] = dp[i][2] = 1;
	cnt = 0;
}

inline void Add_Edge ( int from, int to ) {
	edge[++cnt] = { head[from], to };
	head[from] = cnt; 
}

inline void DFS ( int x ) {
	vis[x] = 1;
	for ( int i = head[x]; ~i; i = edge[i].nxt ) {
		int to = edge[i].to;
		if ( vis[to] ) continue;
		DFS ( to );

		dp[x][0] = dp[x][0] * ( dp[to][0] + dp[to][2] ) % mod;
		dp[x][1] = dp[x][1] * dp[to][0] % mod;	
		dp[x][2] = dp[x][2] * ( dp[to][0] + dp[to][1] + dp[to][2] ) % mod;
	}
	dp[x][2] = ((dp[x][2] + mod - dp[x][1]) % mod + mod) % mod;
}

int main () {
#ifndef ONLINE_JUDGE
	freopen("in.in", "r", stdin);
	freopen("out.out", "w", stdout);
#endif
	int cass;
	for ( scanf("%d", &cass); cass; cass -- ) {
		scanf("%d", &n); Init(); 
		for ( int i = 1; i < n; i ++ ) {
			int a, b; scanf("%d%d", &a, &b); 
			Add_Edge ( a, b );
			Add_Edge ( b, a );
		}
		DFS (1);
		printf("%lld\n",( dp[1][0] + dp[1][2] ) % mod);
	}
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

# HDUOJ2412_PartyatHali-Bula

# 🔗

https://acm.hdu.edu.cn/showproblem.php?pid=2412

# 💡

选了上司就不能选员工了
所以我们设dp[i][0]表示不选根节点i时的最大选数，dp[i][1]表示选根节点i时的最大选数
dp[i][0]了话，员工选不选都行，就对每个子节点求最优即可
dp[i][1]了话，员工不能选，+dp[son[i]][0]

在选使用哪个子状态时，使用的那个子状态如果是多解，那么此时父状态也是多解
最后还要判断一下总问题的两种可能性是不是相同

# ✅

#include <unordered_map>
#include <iostream>
#include <cstdio>
#include <string>

using namespace std;

const int N = 205;
struct Edge {
        int nxt; string to;
        inline Edge () {}
        inline Edge ( int _nxt, string _to ) : nxt(_nxt), to(_to) {}
} edge[2 * N];
unordered_map <string, int> head, vis, num;
unordered_map <string, pair<int, int> > dp, f; 
int cnt, n;
string stt; 

inline void Init () {
        head.clear();
        vis.clear();
        num.clear();
        cnt = 0;
}
inline void Add_edge ( string from, string to ) { edge[++cnt] = Edge(head[from], to); head[from] = cnt; }
inline void DFS ( string x ) {
        if ( !num[x] ) { dp[x] = make_pair(0, 1); f[x] = make_pair(0, 0); return; }
        vis[x] = 1;
        dp[x] = make_pair(0, 1);
        f[x] = make_pair(0, 0);
        for ( int i = head[x]; i; i = edge[i].nxt ) {
                string to = edge[i].to;
                if ( !vis[to] ) DFS ( to );

                if ( dp[to].first == dp[to].second ) { // 看看通过哪个推最优解，如果子阶段是多解，那么它对应的
                        dp[x].first += dp[to].first;
                        f[x].first = 1;
                } else if ( dp[to].first > dp[to].second ) {
                        dp[x].first += dp[to].first;
                        if ( f[to].first ) f[x].first = 1;
                } else if ( dp[to].first < dp[to].second ) {
                        dp[x].first += dp[to].second;
                        if( f[to].second ) f[x].first = 1;
                }
                dp[x].second += dp[to].first;
                if ( f[to].first ) f[x].second = 1;
        }
}

int main () {
        while ( cin >> n, n ) {
                Init();
                cin >> stt;
                for ( int i = 0; i < n - 1; i ++ ) {
                        string a, b; cin >> a >> b;
                        Add_edge( b, a ); num[b] ++;
                }
                DFS ( stt );
                if ( dp[stt].first > dp[stt].second ) { // 看看利用哪个得到最优解
                        cout << dp[stt].first << " " << (f[stt].first ? "No" : "Yes") << endl;
                } else if ( dp[stt].first < dp[stt].second ) {
                        cout << dp[stt].second << " " << (f[stt].second ? "No" : "Yes") << endl;
                } else {
                        cout << dp[stt].first << " " << "No" << endl;
                }
        }
        return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

# ICPC2018银川站G_Factories

# 🔗

# 💡

这个就是类似于树背包的问题，我们要看每一个节点选了多少个叶子结点
分析一下点间距离的计算方式， $dis(i,j)=deep_i+deep_j-2\times deep_{lca(i,j)}$ ，换算到这里 $deep_u$ 表示的就是之前的路径和
令 $dp[u][i]$ 表示节点 $u$ 选了 $i$ 个叶子结点
放进 $dp$ 里面，就是先处理加操作，即将每一个叶子节点 $u$ ，它的 $dp[u][0]=0,dp[u][1]=deep[u]*(k-1)$ ，乘上 $k-1$ 意味着这个点要和别的 $k-1$ 个点各匹配一次，然后在一个节点上操作时，对于扫描到的子节点 $v$ ，我们设前面的儿子一共选了 $i$ 个叶子节点，该子树选了 $j$ 个叶子结点，则要更新 $u$ 选 $i+j$ 个叶子结点的位置，当然不可以直接更新到当前位置，不然可能会使得子树利用子树
就是 $tmp[i+j]=dp[u][j]+dp[v][i]-2\times i\times j\times deep_u$
最后算根节点的 $dp[][k]$ 即可
不过有特判的地方，就是 $n=2$ 时要分开 $k=1$ 和 $k=2$ 两种情况直接算，还有根节点不能度为 $1$ ，要选一个不可以作为叶子的根节点

# ✅

const int N = 1e5 + 10;
vector<pair<int, int> > g[N];
inline void add_Edge (int from, int to, int val) {
    g[from].push_back({to, val});
    g[to].push_back({from, val});
}
 
int n, k;
 
ll tmp[210];
ll pre[N];
ll dp[N][210];
int sz[N];
inline void dfs (int u, int fa) {
    dp[u][0] = 0;
    for (auto [v, w] : g[u]) if (v == fa) pre[u] = pre[fa] + w;
    if (g[u].size() == 1 && g[u][0].first == fa) {
        dp[u][1] = 1ll * (k - 1) * pre[u];
        sz[u] = 1;
        return;
    }
    sz[u] = 0;
    for (auto [v, w] : g[u]) {
        if (v == fa) continue;
        dfs(v, u);
        for (int i = 0; i <= k; i ++) tmp[i] = 2e18;
        for (int i = 0; i <= sz[u]; i ++) {
            for (int j = 0; j <= sz[v] && i + j <= k; j ++) {
                tmp[i + j] = min(tmp[i + j], dp[u][i] + dp[v][j] - 2ll * i * j * pre[u]);
            }
        }
        sz[u] += sz[v];
        for (int i = 0; i <= k; i ++) dp[u][i] = min(dp[u][i], tmp[i]);
    }
}
inline void Solve () {
    scanf("%d%d", &n, &k);
    for (int i = 1; i <= n; i ++) g[i].clear();
    for (int i = 1; i < n; i ++) {
        int u, v, w; scanf("%d%d%d", &u, &v, &w);
        add_Edge(u, v, w);
    }
    if (n == 2) {
        printf("%d\n", (k == 2) * g[1][0].second);
        return;
    }
    for (int i = 1; i <= n; i ++) for (int j = 0; j <= k; j ++) dp[i][j] = 2e18;
 
    int root = 1;
    while (root <= n && g[root].size() == 1) root ++;
    dfs(root, 0);
    printf("%lld\n", dp[root][k]);
}
int main () {
    int cass; scanf("%d", &cass);
    for (int i = 1; i <= cass; i ++) {
        printf("Case #%d: ", i);
        Solve();
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

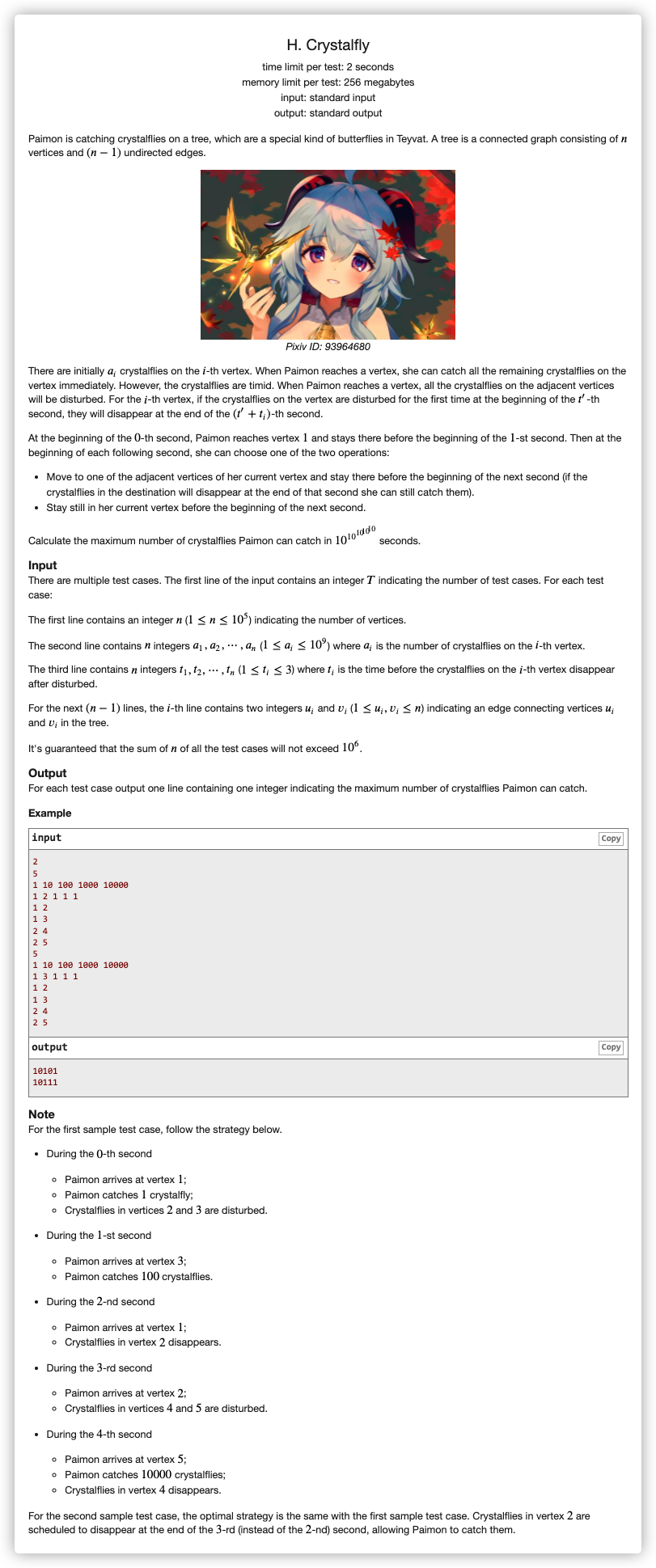
# ICPC2021南京站H_Crystalfly

# 🔗

# 💡

考虑到有两种决策

对着 $u$ 的一个子节点 $v$ 走下去，别的子节点舍弃
刚碰到 $u$ 的一个字节点 $v$ 立马掉头去碰 $t=3$ 的另一个子节点 $w$ ， $v$ 的子节点不管了

我们设置 $dp_i$ 表示 $i$ 节点上已经失效，但 $i$ 的子节点们 $\{son_i\}$ 还未激活
令 $sum_u=\sum\limits_{v\in\{son_u\}}dp_v$
则对于一个节点的两种决策

$c_{u1}=\underset{v\in\{son_u\}}{max}(sum_u+a_u)$
$c_{u2}=\underset{v\in\{son_u\},\;v\neq w,\;t_w=3}{max}(sum_u+a_v+a_w+sum_v-dp_v)$

对于第二种决策我们找出最大的 $a_w$ 后让其更新所有同级点，同时为保正确性也让所有同级点更新它从而获得 $c_{u2}$
那么最后 $dp_u$ 取其中最大值即可

最后答案就根据状态来， $a_1+dp_1$

# ✅

const int N = 1e5 + 10,
	  M = 2e5 + 10;
int n, t[N]; ll a[N];

struct Edge {
        int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge ( int from, int to ) {
        edge[++cnt] = { head[from], to };
        head[from] = cnt;
}

ll dp[N], sum[N];

inline void DFS ( int u, int fa ) {
	if ( edge[head[u]].nxt == 0 && fa != u ) return;
	for ( int i = head[u]; i; i = edge[i].nxt ) {
		int v = edge[i].to;
		if ( v == fa ) continue;
		DFS(v, u);
		sum[u] += dp[v];
	}

	ll t1 = 0, t2 = 0;

	for ( int i = head[u]; i; i = edge[i].nxt ) {
		int v = edge[i].to;
		if ( v == fa ) continue;
		t1 = max(t1, sum[u] + a[v]);
	}

	ll mxw = 0; int w = 0;
	for ( int i = head[u]; i; i = edge[i].nxt ) {
		int v = edge[i].to;
		if ( v == fa || t[v] < 3 ) continue;
		if ( a[v] > mxw ) mxw = a[v], w = v;
	}

	if ( w ) {
		for ( int i = head[u]; i; i = edge[i].nxt ) {
			int v = edge[i].to;
			if ( v == fa || v == w ) continue;
			t2 = max(t2, sum[u] - dp[v] + a[v] + sum[v] + a[w]);
		}
		for ( int i = head[u]; i; i = edge[i].nxt ) {
			int v = edge[i].to;
			if ( v == fa || v == w || t[v] < 3 ) continue;
			t2 = max(t2, sum[u] - dp[w] + a[w] + sum[w] + a[v]);
		}
	}

	dp[u] = max(t1, t2);
}

inline void Solve () {
	scanf("%d", &n);
	for ( int i = 1; i <= n; i ++ ) head[i] = -1, dp[i] = sum[i] = 0; cnt = 0;
	for ( int i = 1; i <= n; i ++ ) scanf("%lld", &a[i]);
	for ( int i = 1; i <= n; i ++ ) scanf("%d", &t[i]);
	for ( int i = 1; i < n; i ++ ) {
		int u, v; scanf("%d%d", &u, &v);
		add_Edge(u, v);
		add_Edge(v, u);
	}
	DFS(1, 1);
	printf("%lld\n", dp[1] + a[1]);
}

int main () {
	int cass; scanf("%d", &cass); while ( cass -- ) {
		Solve ();
	}

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

状压DP 组合数学