树上问题

#

---

树的重心

POJ1655_BalancingAct

🔗

💡

本题是让输出树的值最小的重心和这个重心的重量
算是模板题

回溯求得
我们要求的每个树的子树大小然后进行比较，得到一个初步的重量
拿这个初步的重量和另一端的重量进行比较，也就是n-sz[x]
得到后，根据重心的性质：如果重量小于等于n/2，那么可以成为树的重心
在这个条件下进行比较当前点是否满足，满足的话比较一下数值大小

最后输出重心和重量

✅

const int N = 2e4 + 10, M = 5e4;
int n;

namespace TreeMap {
        struct Edge { int nxt, to; } edge[M];
        int head[M], cnt;
        inline void Init () {
                for ( int i = 0; i < M; i ++ ) head[i] = -1;
                cnt = 0;
        }
        inline void add_Edge ( int from, int to ) {
                edge[ ++ cnt ] = { head[from], to };
                head[from] = cnt;
        }
} using namespace TreeMap;


namespace TreeWeightCenter {
        int sz[N], weight[N], center;
        inline void Init () {
                for ( int i = 0; i < N; i ++ ) 
                        sz[i] = 1, 
                        weight[i] = 0;
                center = 1e9;
        }
        inline void dfs ( int x, int fath ) {
                for ( int i = head[x]; ~i; i = edge[i].nxt ) {
                        int to = edge[i].to;
                        if ( to == fath ) continue;
                        dfs ( to, x );
                        sz[x] += sz[to]; // 子树大小
                        weight[x] = max ( weight[x], sz[to] ); // 重量选择最大子树大小
                }
                weight[x] = max ( weight[x], n - sz[x] ); // 还要和另一端的子树对比一下
                if ( weight[x] <= n / 2 ) center = min ( center, x ); // 可以作为重心
        }
} using namespace TreeWeightCenter;


int main () {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif
        int cass; scanf("%d", &cass); while ( cass -- ) {
                TreeMap::Init(); TreeWeightCenter::Init();
                scanf("%d", &n);
                for ( int i = 1, a, b; i < n; i ++ )
                        scanf("%d%d", &a, &b),
                        add_Edge(a, b),
                        add_Edge(b, a);
                dfs ( 1, 1 );
                printf("%d %d\n", center, weight[center]);
        }
}

---

树链剖分

洛谷P3384_【模板】轻重链剖分树链剖分

🔗

💡

板子，包含了路径修改查询，子树修改查询

✅

const ll N = 1e5 + 10;
const ll M = 2e5 + 10;

ll a[N], n, m, r, p;

namespace Map {
        struct Edge {
                ll nxt, to;
        } edge[M];
        ll cnt, head[M];

        inline void add_Edge ( ll from, ll to ) {
                edge[ ++cnt ] = { head[from], to };
                head[from] = cnt;
        }

} using namespace Map;

namespace TreeDivid {
        ll top[N], fa[N], son[N], sz[N], dep[N];
        ll dfn[N], id[N], idx;
        inline void DFS1 ( ll x, ll fath ) {
                sz[x] = 1; dep[x] = dep[fath] + 1;
                son[x] = 0, fa[x] = fath;
                for ( ll i = head[x]; i; i = edge[i].nxt ) {
                        ll to = edge[i].to; if ( to == fath ) continue;
                        DFS1 ( to, x );
                        sz[x] += sz[to];
                        if ( sz[son[x]] < sz[to] ) son[x] = to;
                }
        }
        inline void DFS2 ( ll x, ll topx ) {
                top[x] = topx;
                dfn[ ++ idx ] = x; id[x] = idx;
                if ( son[x] ) DFS2 ( son[x], topx );
                for ( ll i = head[x]; i; i = edge[i].nxt ) {
                        ll to = edge[i].to;
                        if ( to == fa[x] || to == son[x] ) continue;
                        DFS2 ( to, to );
                }
        }
} using namespace TreeDivid;

namespace SegmentTree {
        struct Sgtr {
                ll val, lazy;
        }sgtr[ N << 2 ];
        inline void pushUp ( ll rt ) {
                sgtr[rt].val = (sgtr[rt << 1].val + sgtr[rt << 1 | 1].val) % p;
        }
        inline void pushDown ( ll l, ll r, ll rt ) {
                if ( !sgtr[rt].lazy ) return;
                auto &now = sgtr[rt], &lson = sgtr[rt << 1], &rson = sgtr[rt << 1 | 1];
                ll mid = (l + r) >> 1;
                lson.lazy += now.lazy; lson.val += now.lazy * (mid - l + 1);
                rson.lazy += now.lazy; rson.val += now.lazy * (r - mid);
                now.lazy = 0;
        }
        inline void Build ( ll l, ll r, ll rt ) {
                sgtr[rt].lazy = 0;
                if ( l == r ) { sgtr[rt].val = a[dfn[l]]; return; }
                ll mid = (l + r) >> 1;
                Build ( l, mid, rt << 1 );
                Build ( mid + 1, r, rt << 1 | 1);
                pushUp ( rt );
        }
        inline void Update ( ll a, ll b, ll c, ll l, ll r, ll rt ) {
                if ( a <= l && r <= b ) { sgtr[rt].val = (sgtr[rt].val + c * (r - l + 1) % p) % p; sgtr[rt].lazy = (sgtr[rt].lazy + c) % p; return; }
                if ( a > r || b < l ) return;
                ll mid = (l + r) >> 1;
                pushDown ( l, r, rt );
                Update ( a, b, c, l, mid, rt << 1 );
                Update ( a, b, c, mid + 1, r, rt << 1 | 1);
                pushUp ( rt );
        }
        inline ll Query ( ll a, ll b, ll l, ll r, ll rt ) {
                if ( a <= l && r <= b ) return sgtr[rt].val;
                if ( a > r || b < l ) return 0;
                ll mid = (l + r) >> 1;
                pushDown ( l, r, rt );
                return (Query ( a, b, l, mid, rt << 1 ) + Query ( a, b, mid + 1, r, rt << 1 | 1)) % p;
        }
} using namespace SegmentTree;

inline void Change ( ll x, ll y, ll c ) {
        while ( top[x] != top[y] ) {
                if ( dep[top[x]] < dep[top[y]] ) swap ( x, y );
                Update ( id[top[x]], id[x], c, 1, n, 1 );
                x = fa[top[x]];
        }
        if ( dep[x] > dep[y] ) swap ( x, y );
        Update ( id[x], id[y], c, 1, n, 1 );
}
inline ll Get ( ll x, ll y ) {
        ll res = 0;
        while ( top[x] != top[y] ) {
                if ( dep[top[x]] < dep[top[y]] ) swap ( x, y );
                res = (res + Query ( id[top[x]], id[x], 1, n, 1 )) % p;
                x = fa[top[x]];
        }
        if ( dep[x] > dep[y] ) swap ( x, y );
        return (res + Query ( id[x], id[y], 1, n, 1 )) % p;
}

int main () {
        ios::sync_with_stdio(false);
        cin >> n >> m >> r >> p;
        for ( ll i = 1; i <= n; i ++ ) cin >> a[i];
        for ( ll i = 1, x, y; i < n; i ++ ) {
                cin >> x >> y;
                add_Edge ( x, y );
                add_Edge ( y, x );
        }
        DFS1 ( r, 0 ); DFS2 ( r, r ); Build (1, n, 1);
        while ( m -- ) {
                ll op; cin >> op;
                if ( op == 1 ) {        // 路径操作
                        ll x, y, z; cin >> x >> y >> z;
                        Change ( x, y, z );
                } else if ( op == 2 ) { // 路经查询
                        ll x, y; cin >> x >> y;
                        cout << Get ( x, y ) << endl;
                } else if ( op == 3 ) { // 子树操作
                        ll x, z; cin >> x >> z;
                        Update ( id[x], id[x] + sz[x] - 1, z, 1, n, 1 );
                } else {                // 子树查询
                        ll x; cin >> x;
                        cout << Query ( id[x], id[x] + sz[x] - 1, 1, n, 1 ) << endl;
                }
         }
}

---

CodeForces1702G2_PassablePath（Hard Version）

🔗

💡

思考什么时候会出现 NO 的情况，即题目问的，如果点集不在一条路径上就是 NO ，当然转换一下，如果我们确定出来了一条路径（当然是所能走到极限的路径）
一个有根树，两个点在一条路路径上，有两种情况：1.在同一条竖链上，2.不在同一条竖链上
先看第二种情况，这种情况是主要的问题
可以先对给定的点集按深度排一个序，保证如果在同一条链上了话， $a[i]$ 是 $a[i-1]$ 的祖先
由于我们要走极限路径，所以如果在同一条链上了话，将 $a[i]=a[i-1]$ ，即为保留这条链上的最深点
如果出现 $a[i]$ 不是 $a[i-1]$ 的祖先的情况，意味着这两个点位于两条链上的最深点，那么 $a[i-1]\rightarrow lca\rightarrow a[i]$ 即为一条极限路径，我们查这条路径上有多少个我们选中的点，如果数量是点集大小的话就说明这条极限路径能把点集中所有的点都包含进去，也就意味着这些点在同一条路径上，YES。如果不是就说明包含不了，就是 NO。
如果一直没有出现这种情况，说明它们在同一条链上，输出 YES 即可
那么问题在于如何快速求得路径上选中点的数量，这是基本的路径查询，可以用树剖+线段树实现

✅

const int N = 2e5 + 10;
const int M = 4e5 + 10;
struct Edge {
        int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to) {
        edge[++cnt] = {head[from], to};
        head[from] = cnt;
}
int num[N];
int n, nn;
namespace TreeDivid {
        ll top[N], fa[N], son[N], sz[N], dep[N];
        ll dfn[N], id[N], idx;
        inline void DFS1 ( ll x, ll fath ) {
                sz[x] = 1; dep[x] = dep[fath] + 1;
                son[x] = 0, fa[x] = fath;
                for ( ll i = head[x]; i; i = edge[i].nxt ) {
                        ll to = edge[i].to; if ( to == fath ) continue;
                        DFS1 ( to, x );
                        sz[x] += sz[to];
                        if ( sz[son[x]] < sz[to] ) son[x] = to;
                }
        }
        inline void DFS2 ( ll x, ll topx ) {
                top[x] = topx;
                dfn[ ++ idx ] = x; id[x] = idx;
                if ( son[x] ) DFS2 ( son[x], topx );
                for ( ll i = head[x]; i; i = edge[i].nxt ) {
                        ll to = edge[i].to;
                        if ( to == fa[x] || to == son[x] ) continue;
                        DFS2 ( to, to );
                }
        }
} using namespace TreeDivid;

namespace SegmentTree {
        struct Sgtr {
                ll val, lazy;
        }sgtr[ N << 2 ];
        inline void pushUp ( ll rt ) {
                sgtr[rt].val = (sgtr[rt << 1].val + sgtr[rt << 1 | 1].val);
        }
        inline void pushDown ( ll l, ll r, ll rt ) {
                if ( !sgtr[rt].lazy ) return;
                auto &now = sgtr[rt], &lson = sgtr[rt << 1], &rson = sgtr[rt << 1 | 1];
                ll mid = (l + r) >> 1;
                lson.lazy += now.lazy; lson.val += now.lazy * (mid - l + 1);
                rson.lazy += now.lazy; rson.val += now.lazy * (r - mid);
                now.lazy = 0;
        }
        inline void Update ( ll a, ll b, ll c, ll l, ll r, ll rt ) {
                if ( a <= l && r <= b ) { sgtr[rt].val = (sgtr[rt].val + c * (r - l + 1)); sgtr[rt].lazy = (sgtr[rt].lazy + c); return; }
                if ( a > r || b < l ) return;
                ll mid = (l + r) >> 1;
                pushDown ( l, r, rt );
                Update ( a, b, c, l, mid, rt << 1 );
                Update ( a, b, c, mid + 1, r, rt << 1 | 1);
                pushUp ( rt );
        }
        inline ll Query ( ll a, ll b, ll l, ll r, ll rt ) {
                if ( a <= l && r <= b ) return sgtr[rt].val;
                if ( a > r || b < l ) return 0;
                ll mid = (l + r) >> 1;
                pushDown ( l, r, rt );
                return (Query ( a, b, l, mid, rt << 1 ) + Query ( a, b, mid + 1, r, rt << 1 | 1));
        }
} using namespace SegmentTree;

inline void Change ( ll x, ll y, ll c ) {
        while ( top[x] != top[y] ) {
                if ( dep[top[x]] < dep[top[y]] ) swap ( x, y );
                Update ( id[top[x]], id[x], c, 1, n, 1 );
                x = fa[top[x]];
        }
        if ( dep[x] > dep[y] ) swap ( x, y );
        Update ( id[x], id[y], c, 1, n, 1 );
}
inline ll Get ( ll x, ll y ) {
        ll res = 0;
        while ( top[x] != top[y] ) {
                if ( dep[top[x]] < dep[top[y]] ) swap ( x, y );
                res = (res + Query ( id[top[x]], id[x], 1, n, 1 ));
                x = fa[top[x]];
        }
        if ( dep[x] > dep[y] ) swap ( x, y );
        return (res + Query ( id[x], id[y], 1, n, 1 ));
}
inline int LCA(int x, int y){
        while(top[x] != top[y]){                   
                if(dep[top[x]] < dep[top[y]]) swap(x, y);
                x = fa[top[x]];  
        }
        return dep[x] < dep[y] ? x : y;
}


inline void Solve () {
        scanf("%d", &n);
        cnt = 0;
        for (int i = 1; i <= n; i ++) head[i] = num[i] = 0;
        for (int i = 0; i < n - 1; i ++) {
                int u, v; scanf("%d%d", &u, &v);
                add_Edge (u, v);
                add_Edge (v, u);
        }
        DFS1(1, 0); DFS2(1, 1);
        int m; scanf("%d", &m);
        while (m --) {
                scanf("%d", &nn);
                vector<int> a(nn);
                vector<int> b(nn);
                for (int i = 0; i < nn; i ++) scanf("%d", &a[i]), Change(a[i], a[i], 1), b[i] = a[i];
                sort(a.begin(), a.end(), [&](int x, int y) {
                        return dep[x] > dep[y];
                });
                for (int i = 1; i < nn; i ++) {
                        int lca = LCA(a[i - 1], a[i]);
                        if (lca != a[i]) {
                                if (nn != Get(a[i], a[i - 1])) {
                                        puts("NO");
                                } else {
                                        puts("YES");
                                }
                                goto end;
                        } else {
                                a[i] = a[i - 1];
                        }
                }
                puts("YES");
                end:;
                for (int i = 0; i < nn; i ++) Change(b[i], b[i], -1);
        }
}

---

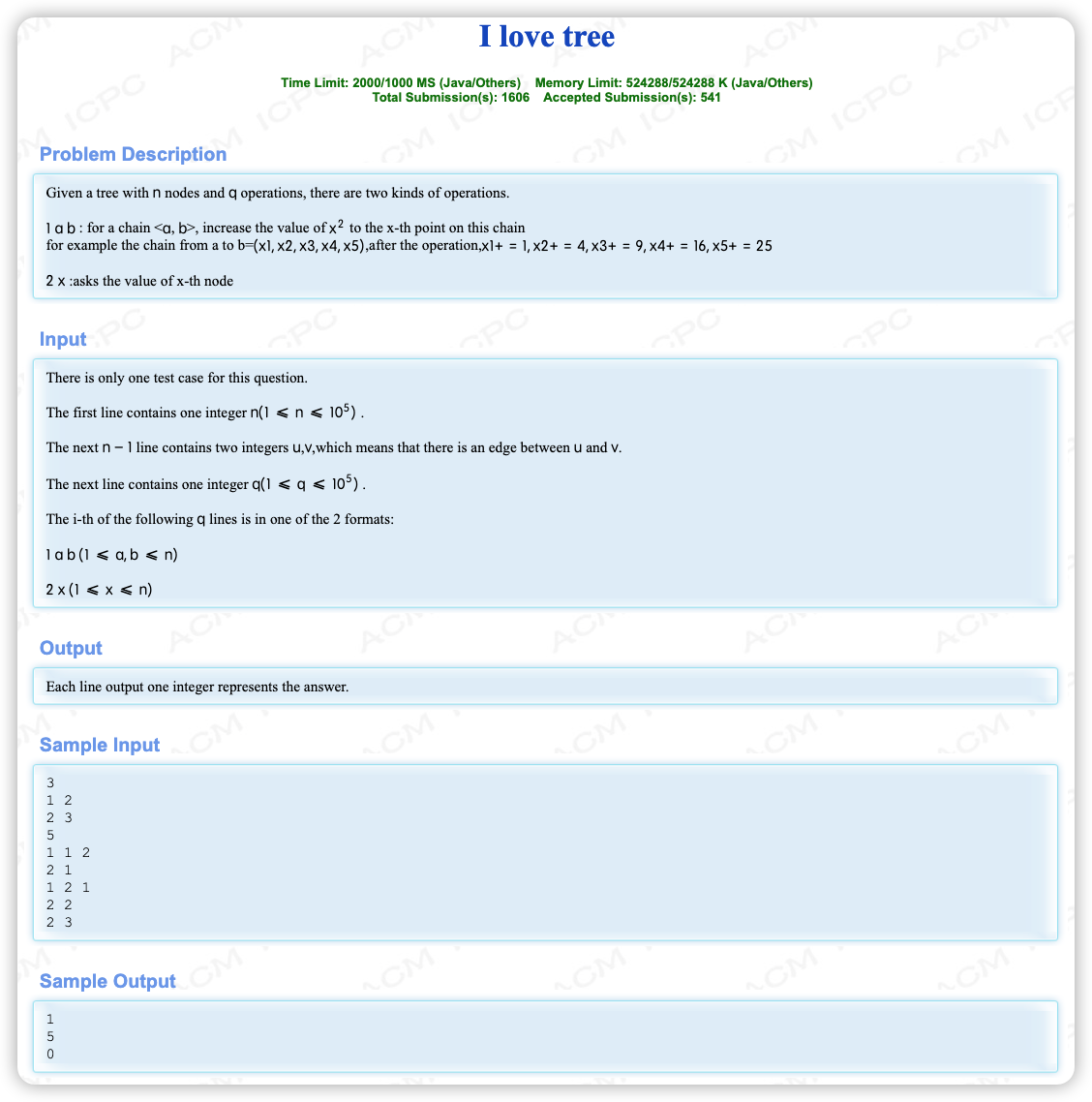
HDU2021多校(2)B_ILoveTree

🔗

💡

这就很板啊...路径更新，单点查询，裸的树剖+线段树吧
如果什么都不考虑的情况下，树剖完就和 这道题 一模一样了
但是关键就在，树剖后更新的时候，对左端点和右端点的决策
一个路径 $x\to y$ 会转化为 $x\to lca\to y$ ，且树剖更新下总是高的对应的线性位置更小，故都是高的到低的更新
所以在第一段时，$x$ 是一次更新的右端点，$top[x]$ 是一次更新的左端点，那么越靠左要加的越多，这样就应该用 $i\in [id[topx],id[x]],+((r+1)-i)^2$ ，也就是 $i^2+2(r+1)i+(r+1)^2$
而在 $lca\to y$ 时，顺序就是正常的，就 $i\in [id[topx],id[x]],+(i-(l-1))^2$ ，也就是 $i^2+2(l-1)i+(l-1)^2$
且左右端点应该随着更新次数的增加越来越偏离更新区间，比如已经更新了 $num$ 个点了，那么我再用它作为 $l$ 更新的时候应该是 $i^2+2(l-num-1)i+(l-num-1)^2$ ，右端点同理要加

从下到上再到从上到下这是两种不同的更新方式，所以要分两次更新，且每次更新时要提出所有的更新区间然后分别按深度降序排序和深度升序排序
但是还有问题就是考虑到 $lca$ 这个位置会被更新两次且第二段整体左端点会偏移，所以只需要第一段记完 $num$ 后第二段再用时是 $num-1$ 开始的，然后让最后答案 $res[lca]-num*num$ 即可

✅

const int N = 2e5 + 10;
const int M = 2 * N;
struct Edge {
    int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to) {
    edge[++cnt] = {head[from], to};
    head[from] = cnt;
}

int top[N], fa[N], son[N], sz[N], dep[N];
int dfn[N], id[N], idx;
inline void Dfs1 (int u, int fath) {
    sz[u] = 1; dep[u] = dep[fath] + 1;
    son[u] = 0; fa[u]= fath;
    for (int i = head[u]; i; i = edge[i].nxt) {
        int v = edge[i].to;
        if (v == fath) continue;
        Dfs1(v, u);
        sz[u] += sz[v];
        if (sz[son[u]] < sz[v]) son[u] = v;
    }
}
inline void Dfs2 (int u, int topu) {
    top[u] = topu;
    dfn[++idx] = u; id[u] = idx;
    if (son[u]) Dfs2(son[u], topu);
    for (int i = head[u]; i; i = edge[i].nxt) {
        int v = edge[i].to;
        if (v == fa[u] || v == son[u]) continue;
        Dfs2(v, v);
    }
}


int n;
int q;
struct Sgtr {
    ll sum2, sum1, sum0; // 三个系数实值
    ll laz2, laz1, laz0; // 三个系数懒标记
    bool haslaz = false;
} t[N << 2];

inline void pushup (int rt) {
    int ch = rt << 1;
    t[rt].sum0 = t[ch].sum0 + t[ch | 1].sum0;
    t[rt].sum1 = t[ch].sum1 + t[ch | 1].sum1;
    t[rt].sum2 = t[ch].sum2 + t[ch | 1].sum2;
}
inline void pushdown (int l, int r, int rt) {
    if (!t[rt].haslaz) return;
    int ch = rt << 1; 
    t[ch].sum0 += t[rt].laz0; t[ch | 1].sum0 += t[rt].laz0;
    t[ch].sum1 += t[rt].laz1; t[ch | 1].sum1 += t[rt].laz1;
    t[ch].sum2 += t[rt].laz2; t[ch | 1].sum2 += t[rt].laz2;
    t[ch].laz0 += t[rt].laz0; t[ch | 1].laz0 += t[rt].laz0;
    t[ch].laz1 += t[rt].laz1; t[ch | 1].laz1 += t[rt].laz1;
    t[ch].laz2 += t[rt].laz2; t[ch | 1].laz2 += t[rt].laz2;
    t[rt].laz0 = t[rt].laz1 = t[rt].laz2 = t[rt].haslaz = 0;
    t[ch].haslaz = t[ch | 1].haslaz = 1;
}
inline void update (int basl, int a, int b, int l = 1, int r = 2 * n, int rt = 1) {
    if (a <= l && r <= b) {
        t[rt].sum2 ++;
        t[rt].sum1 += 2 * (basl - 1);
        t[rt].sum0 += (basl - 1) * (basl - 1);
        t[rt].laz2 ++;
        t[rt].laz1 += 2 * (basl - 1);
        t[rt].laz0 += (basl - 1) * (basl - 1);
        t[rt].haslaz = true;
        return;
    }
    pushdown(l, r, rt);
    int mid = (l + r) >> 1;
    if (a <= mid) update(basl, a, b, l, mid, rt << 1);
    if (b > mid) update(basl, a, b, mid + 1, r, rt << 1 | 1);
    pushup(rt);
}
inline ll query (int id, int l = 1, int r = 2 * n, int rt = 1) {
    if (l == r) {
        return t[rt].sum0 - t[rt].sum1 * l + t[rt].sum2 * l * l;
    }
    int mid = (l + r) >> 1;
    pushdown(l, r, rt);
    if (id <= mid) return query(id, l, mid, rt << 1);
    else return query(id, mid + 1, r, rt << 1 | 1);
}
inline int Change (int num, int x, int y, int op) {
    vector<pair<int, int> > v_upd; // 所有更新区间
    while (top[x] != top[y]) {
        if (dep[top[x]] < dep[top[y]]) swap(x, y);
        v_upd.push_back({top[x], x});
        x = fa[top[x]];
    }
    if (dep[x] > dep[y]) swap(x, y);
    v_upd.push_back({x, y});

    int num_upd = num;
    if (op == 0) {
        sort(v_upd.begin(), v_upd.end(), [&](pair<int, int> a, pair<int, int> b) { return dep[a.first] > dep[b.first]; });
        for (int i = 0; i < v_upd.size(); i ++) {
            int l = v_upd[i].first;
            int r = v_upd[i].second;
            update(id[r] + 2 + num_upd, id[l], id[r]); // 由于右端点要记录+1，故+2-1 = +1
            num_upd += id[r] - id[l] + 1;
        }
    } else {
        sort(v_upd.begin(), v_upd.end(), [&](pair<int, int> a, pair<int, int> b) { return dep[a.first] < dep[b.first]; });
        for (int i = 0; i < v_upd.size(); i ++) {
            int l = v_upd[i].first;
            int r = v_upd[i].second;
            update(id[l] - num_upd, id[l], id[r]);
            num_upd += id[r] - id[l] + 1;
        }
    }
    return num_upd;
}
inline int Lca (int x, int y) {
    while (top[x] != top[y]) {
        if (dep[top[x]] < dep[top[y]]) swap(x, y);
        x = fa[top[x]];
    }
    if (dep[x] > dep[y]) swap(x, y);
    return x;
}

int neddel[N];

signed main () {
    scanf("%lld", &n);
    for (int i = 1; i < n; i ++) {
        int u, v; scanf("%lld%lld", &u, &v);
        add_Edge(u, v);
        add_Edge(v, u);
    }
    Dfs1(1, 0); Dfs2(1, 1);
    int q; scanf("%lld", &q);
    while (q --) {
        int op; scanf("%lld", &op);
        if (op == 1) {
            int x, y; scanf("%lld%lld", &x, &y);
            int lca = Lca(x, y);   

            if (x == lca) {
                Change(0, x, y, 1);
            } else if (y == lca) {
                Change(0, x, y, 0);
            } else {
                int num = Change(0, x, lca, 0);
                neddel[lca] += num * num;
                Change(num - 1, lca, y, 1);
            } 
        } else {
            int x; scanf("%lld", &x);
            printf("%lld\n", query(id[x]) - neddel[x]);
        }
    }
}

---

虚树

洛谷P2495_消耗战

🔗

💡

首先想到树形dp向上转移
对于i，当前儿子是to，预处理出来1到每个节点的最短距离minv[i]
如果to是关键点：dp[i] += minv[i]
如果to不是关键点：dp[i] += min ( minv[i], dp[to] )

而题目中询问的是总和
那么我们其实就可以算出来影响到的点和边的dp最优解
有很多没受到影响的其实不必要跑dp，时间承担不了
对需要的跑dp，可以想到构建一棵虚树
再虚树上跑

就对关键点和交汇点建立虚树即可

✅

#include <iostream>
#include <map>
#include <vector>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <queue>

#define ll long long
using namespace std;

const int N = 500500;
const int M = 10000;


int n, q, num;

namespace Map {
        struct Edge {
                int nxt, to;
                ll val;
        }edge[N << 1], vedge[N << 1]; // 主树边，虚树边
        int  head[N << 1],  cnt = 0;  // 主树指针
        int vhead[N << 1], vcnt = 0;  // 虚树指针
        inline void add_Edge ( int from, int to, ll val ) { // 添加主树
                edge[ ++ cnt ] = (Edge){ head[from], to, val };
                head[from] = cnt;
        }
        inline void add_vEdge ( int from, int to ) {        // 添加虚树 
                vedge[ ++ vcnt ] = (Edge){ vhead[from], to };
                vhead[from] = vcnt;
        }
} using namespace Map;

namespace VirtualTree {
        int dfscnt = 1, dfn[N]; // dfs序
        int dep[N];             // 深度
        int fa[N][25];          // 父亲st表
        int mxFa[N];            // 优化 -> i最多有mxFa[i]层祖先
        ll  minv[N];             // 1到i的最小边权是minv[i]
        
        // 预处理fa[][]，dfn[]，minv[]
        inline void dfs ( int pos ) {
                int k;
                for ( k = 0; fa[pos][k]; k ++ ) fa[pos][k + 1] = fa[fa[pos][k]][k];
                mxFa[pos] = k;
                dfn[pos] = dfscnt ++;
                for ( int i = head[pos]; i; i = edge[i].nxt ) {
                        int to = edge[i].to;
                        if ( !dfn[to] ) 
                                dep[to] = dep[pos] + 1,
                                minv[to] = min ( minv[pos], edge[i].val ),
                                fa[to][0] = pos,
                                dfs ( to );
                }
        }

        // st求LCA
        inline int LCA ( int x, int y ) {
                if ( dep[x] < dep[y] ) swap ( x, y );
                for ( int i = mxFa[x]; i >= 0; i -- ) if ( dep[fa[x][i]] >= dep[y] ) x = fa[x][i];
                if ( x == y ) return x;
                for ( int i = mxFa[x]; i >= 0; i -- ) if ( fa[x][i] != fa[y][i] ) x = fa[x][i],
                                                                                  y = fa[y][i];
                return fa[x][0];
        }
        int stk[N], top; // 单调栈
        int lst[N];      // 查询的一套关键点
        inline void build () {
                sort ( lst + 1, lst + num + 1, [&]( int x, int y ) { return dfn[x] < dfn[y]; } ); // 按dfs序排序
                stk[top = 1] = lst[1]; // 此时stk[0] = 0，dep[0] = 0，深度最小的哨兵
                for ( int i = 2; i <= num; i ++ ) {
                        int now = lst[i];
                        int lca = LCA ( now, stk[top] );
                        while ( 1 ) {
                                if ( dep[lca] >= dep[stk[top - 1]] ) { // lca已在下面，应作为右链元素了
                                        if ( lca != stk[top] ) {       // top要删掉了
                                                add_vEdge ( lca, stk[top] );
                                                if ( lca != stk[top - 1] ) stk[top] = lca; // lca加入
                                                else                       top --;         // lca已有
                                        }
                                        break;
                                } else { // 一直弹直到lca在下面
                                        add_vEdge ( stk[top - 1], stk[top] );
                                        top --;
                                }
                        }
                        stk[ ++ top ] = now;
                }
                while ( --top ) add_vEdge ( stk[top], stk[top + 1] );
        }
} using namespace VirtualTree;

bool query[N];
inline ll dp ( int pos ) {
        ll sum = 0, res;
        for ( int i = vhead[pos]; i; i = vedge[i].nxt ) sum += dp ( vedge[i].to );
        if ( query[pos] ) res = minv[pos];
        else              res = min ( minv[pos], sum );
        // 实时清空
        query[pos] = false;
        vhead[pos] = 0;
        return res;
}

int main () {
        minv[1] = 1e18;
        scanf("%d", &n);
        for ( ll i = 0, x, y, val; i < n - 1; i ++ ) 
                scanf("%lld%lld%lld", &x, &y, &val),
                add_Edge ( x, y, val ),
                add_Edge ( y, x, val );
        dfs ( 1 );
        scanf("%d", &q);
        while ( q -- ) {
                scanf("%d", &num);
                for ( int i = 1; i <= num; i ++ ) scanf("%d", &lst[i]), query[lst[i]] = true;
                build();
                printf("%lld\n", dp(stk[1]));
                vcnt = 0;
        }
} 

---

洛谷P3320_寻宝游戏

🔗

💡

可以观察到每一次的值都是虚树的边权和的两倍
但是这棵虚树我们不需要完整地造出来
因为我们只是求它的边权和，并没有转移
所以可以用STL实现点的删除和增加（这里用的是set

预处理LCA，每一次加点其实就是计算改变的边权
改变的是这个插入的点和它dfs序内两个相邻虚点的距离
两点距离 = dist[i] + dist[j] - dist[lca] * 2
求相邻的两个点可以直接使用set.lower_bound-1和upper_bound实现

最后如果虚树不为空还要加上两个哨兵之间的距离
（这里弄了一个大哨兵和一个小哨兵）

✅

namespace Map {
        struct Edge {
                int nxt, to;
                ll val;
        } edge[M];
        int cnt = 0;
        int head[M];
        inline void add_Edge ( int from, int to, ll val ) {
                edge [ ++ cnt ] = (Edge){ head[from], to, val };
                head[from] = cnt;
        } 
} using namespace Map;

namespace ProblemOnTree {
        int dep[N], fa[N][25], mxFa[N];
        ll  dist[N];
        int dfn[N], dfsid = 0, nfd[N];
        inline void dfs ( int pos, int fath ) {
                int k;
                for ( k = 0; fa[pos][k]; k ++ ) fa[pos][k + 1] = fa[fa[pos][k]][k];
                mxFa[pos] = k;
                dfn[pos] = ++dfsid, nfd[dfsid] = pos;
                for ( int i = head[pos]; i; i = edge[i].nxt ) {
                        int to = edge[i].to;
                        if ( to == fath ) continue;
                        dep[to] = dep[pos] + 1;
                        fa[to][0] = pos;
                        dist[to] = dist[pos] + edge[i].val;
                         dfs ( to, pos );
                }
        }
        inline int LCA ( int x, int y ) {
                if ( dep[x] < dep[y] ) swap ( x, y );
                for ( int i = mxFa[x]; i >= 0; i -- ) if ( dep[fa[x][i]] >= dep[y] ) x = fa[x][i];
                if ( x == y ) return x;
                for ( int i = mxFa[x]; i >= 0; i -- ) if ( fa[x][i] != fa[y][i] ) x = fa[x][i], y = fa[y][i];
                return fa[x][0];
        }
        inline ll Dis ( int x, int y ) {
                return dist[x] + dist[y] - dist[LCA(x, y)] * 2;
        }
} using namespace ProblemOnTree;

int n, m; 
ll res;
int x, y, z;
set<int> st;

int main () {
        scanf("%d%d", &n, &m);
        for ( int i = 1; i < n; i ++ ) {
                scanf("%d%d%d", &x, &y, &z);
                add_Edge ( x, y, z );
                add_Edge ( y, x, z );
        }
        dfs ( 1, 1 );
        st.insert(-1); st.insert(99999999);
        for ( int i = 0, x, op; i < m; i ++ ) {
                scanf("%d", &x);
                if ( *st.lower_bound(dfn[x]) == dfn[x] )  op = -1, st.erase(dfn[x]); 
                else                                      op = 1,  st.insert(dfn[x]);
                
                int l = *--st.lower_bound(dfn[x]), r = *st.upper_bound(dfn[x]);

                if ( l != -1 )                  res += Dis ( nfd[l], x ) * op;
                if ( r != 99999999 )            res += Dis ( x, nfd[r] ) * op;
                if ( l != -1 && r != 99999999 ) res -= Dis ( nfd[l], nfd[r] ) * op;

                printf("%lld\n", res + (st.size() == 2 ? 0 : Dis(nfd[*++st.begin()], nfd[*--st.lower_bound(99999999)])) );
        }
}

---

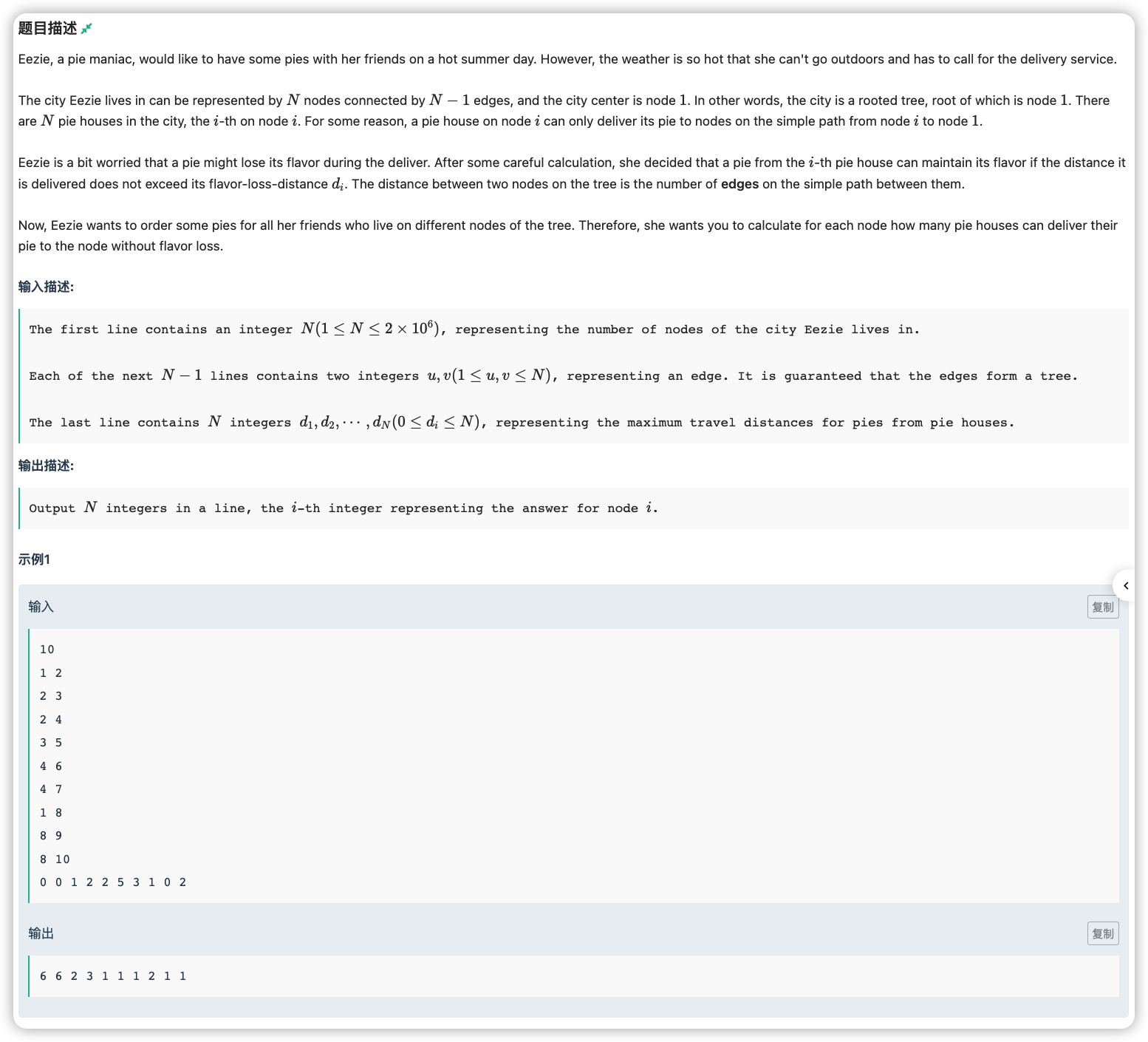
子树问题

牛客2022多校（6）B_EezieAndPie

🔗

💡

路径操作，查询统计都在下面，那么直接树上差分就行。
对于每一个点 $i$ ，它的路径结束位置在它向上 $d_i$ 的位置上，这里倍增求一下结束位置在哪（$j$），然后就对 $val_i+1$ ，$val_{fa[j]}-1$
做完标记之后 $dfs$ 合并一下就结束了。

✅

const int N = 2e6 + 10;
struct node {
        int v, nxt;
} g[N << 1];
int head[N], idx;
int val[N];
int d[N], f[N][25], dep[N];
 
void add (int u, int v) {
        g[++idx] = {v, head[u]};
        head[u] = idx;
}
void dfs (int u, int p) {
        dep[u] = dep[p]+1;
        f[u][0] = p;
        for (int i = 1; i <= 23; i ++)
                f[u][i] = f[f[u][i - 1]][i - 1];
        for (int i = head[u]; i; i = g[i].nxt) {
                int v = g[i].v;
                if (v == p) continue;
                dfs(v, u);
        }
}
int get (int u) {
        int dp = dep[u] - d[u];
        for (int i = 23; i >= 0; i --)
                if (dep[f[u][i]] >= dp) u = f[u][i];
        return u;
}
void dfs1 (int u,int p) {
        for (int i = head[u]; i; i = g[i].nxt) {
                int v = g[i].v;
                if (v == p) continue;
                dfs1(v, u);
                val[u] += val[v];
        }
}
signed main () {
        int n;
        scanf("%d", &n);
        for (int i = 1; i < n; i ++) {
                int u,v;
                scanf("%d%d",&u, &v);
                add(u, v),add(v, u);
        }
        for (int i = 1;i <= n;i ++)  scanf("%d", &d[i]);
        dfs(1, 0);
        for (int i = 1; i <= n; i ++) {
                val[i] ++;
                int v = get(i);
                if(v != 1) val[f[v][0]] --;
        }
        dfs1(1, 0);
        for (int i = 1; i <= n; i ++) printf("%d ", val[i]);
}

---

ABC239E_SubtreeK-thMax

🔗

💡

这个题的突破口在于是否能快速注意到数据范围 $k\le 20$
注意到这个就很好做了
每个点维护一个子树权值的小顶堆，装入子树下最大的 $20$ 个点权
用 $DFS$ 回溯维护
每次查询就跑一下这个堆即可

✅

const int N = 1e5 + 10;
const int M = 2e5 + 10;
priority_queue<int, vector<int>, greater<int> > pque[N];
int n, q;
struct Edge {
        int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge ( int from, int to ) {
        edge[++cnt] = { head[from], to };
        head[from] = cnt;
}
int val[N];
 
inline void DFS ( int x, int fa ) {
        pque[x].push(val[x]);
        for ( int i = head[x]; i; i = edge[i].nxt ) {
                int y = edge[i].to;
                if ( y == fa ) continue;
                DFS(y, x);
                priority_queue<int> tmp;
                while ( pque[y].size() ) {
                        tmp.push(pque[y].top());
                        if ( pque[x].size() < 20 ) pque[x].push(pque[y].top());
                        else {
                                if ( pque[y].top() > pque[x].top() ) pque[x].pop(), pque[x].push(pque[y].top());
                        }
                        pque[y].pop();
                }
                while ( tmp.size() ) pque[y].push(tmp.top()), tmp.pop();
        } 
}
 
int main () {
        scanf("%d%d", &n, &q);
        for ( int i = 1; i <= n; i ++ ) scanf("%d", &val[i]);
        for ( int i = 0; i < n - 1; i ++ ) {
                int a, b; scanf("%d%d", &a, &b);
                add_Edge(a, b);
                add_Edge(b, a);
        }
        DFS(1, 1);
        while ( q -- ) {
                int v, k; scanf("%d%d", &v, &k);
                priority_queue<int> tmp;
                while ( pque[v].size() ) tmp.push(pque[v].top()), pque[v].pop();
                int idx = 0;
                while ( tmp.size() ) {
                        idx ++;
                        if ( idx == k ) printf("%d\n", tmp.top());
                        pque[v].push(tmp.top()); tmp.pop();
                }
        }
}

---

CCPC2022河南省赛J_MexTree

🔗

💡

这个编号建图，权值 $mex$ 太奇怪了，建图的时候直接用它们的权值当编号建吧，即对于权值 $v[]$ 数组，连边 $(u,v)$ ，直接 add_Edge(v[u], v[v])

分析情况：
若 $mex=i$ 说明小于 $i$ 的都要有，且不能包含 $i$
在朴素情况下说明只能选一棵以 $i$ 为分割的几棵子树之一，这棵子树必须包含 $[0,i-1]$

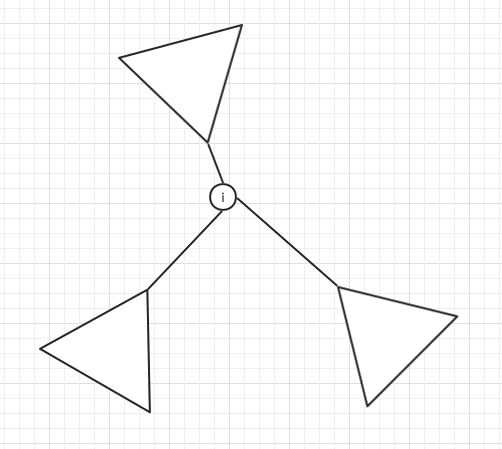
就是选其中之一

假设总树是建的一棵有根树，那么这三棵树分别代表着：除了以 $i$ 为根的子树之外的节点构成的连通块、以 $i$ 的儿子为根构成的子树

• $1.$ 如果前者可以成为我们选择的连通块，说明 $i$ 的子树中不含 $[0,i-1]$ 的任意一个权值，这样的话我们直接取 $n-sz[i]$ 即可
• $2.$ 如果后者是我们要选择的连通块，说明 $i$ 的其中一棵儿子子树一定包含了 $[0,i-1]$ 的所有点，直接取其这棵子树的 $sz$ 即可
• $3.$ 都不满足，那么就是 $0$

情况 $1$ 的判定方式为，$i$ 的子树最小值等于 $i$ ，就说明 $[0,i-1]$ 都不在 $i$ 的子树种
情况 $2$ 的判定方式为，$[0,i-1]$ 的 $lca$ 的深度比 $i$ 小，就说明其 $lca$ 是 $i$ 的子孙之一。$[0,i-1]$ 的 $lca$ 求法为其区间 $dfs$ 序最小值的点和最大值的点构成的 $lca$ ，这两个点在递进 $i$ 的时候维护一下就行。在 $i$ 的哪棵子树的求法为用倍增跑到 $lca$ 的一个父亲 $f$ 满足 $dep[f]=dep[i]-1$
情况 $3$ 的判定方式为，else

特殊情况

• $0$ 的答案：以 $0$ 为根建图，那就是找最大的子树
• $n+1$ 的答案：选全部，就是 $n$

✅

// 这里拿权值从 [1,n] 开始了，写着方便
const int N = 1e6 + 10;
const int M = N << 1;
struct Edge {
    int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to) {
    edge[++cnt] = {head[from], to};
    head[from] = cnt;
}
int n, v[N], mn[N]; // 点数，权值，子树最小值
int sz[N], fa[N][25], dep[N]; // 子树大小，父亲倍增表，深度
int dfn[N], df_idx; // dfs序
inline void dfs (int u, int father) { // 预处理上面的信息
    fa[u][0] = father;
    dep[u] = dep[father] + 1;
    sz[u] = 1;
    mn[u] = u;
    dfn[u] = ++df_idx;
    for (int i = head[u]; i; i = edge[i].nxt) {
        int v = edge[i].to;
        if (v == father) continue;
        dfs(v, u);
        sz[u] += sz[v];
        mn[u] = min(mn[u], mn[v]);
    }
}
inline int Lca (int x, int y) {
    if (dep[x] < dep[y]) swap(x, y);
    for (int i = 20; i >= 0; i --) {
        if (fa[x][i] && dep[fa[x][i]] > dep[y]) x = fa[x][i];
    }
    if (x == y) return x;
    for (int i = 20; i >= 0; i --) {
        if (fa[x][i] && fa[y][i] && fa[x][i] != fa[y][i]) {
            x = fa[x][i];
            y = fa[y][i];
        }
    }
    return fa[x][0];
}

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n;
    for (int i = 1; i <= n; i ++) {
        cin >> v[i], mn[i] = 0x3f3f3f3f;
        v[i] ++; // 令权值整体上升1，在建图的时候好建
    }
    // 用权值建图，操作起来方便
    for (int i = 2; i <= n; i ++) {
        int fa; cin >> fa;
        add_Edge(v[fa], v[i]);
        add_Edge(v[i], v[fa]);
    }

    dfs(1, 1);
    for (int j = 1; j <= 20; j ++) {
        for (int i = 1; i <= n; i ++) fa[i][j] = fa[fa[i][j - 1]][j - 1];
    }

    // 0 的答案，也就是对应我的建图里面的 1 的答案
    int res1 = 0;
    for (int i = head[1]; i; i = edge[i].nxt) 
        res1 = max(res1, sz[edge[i].to]);
    cout << res1 << " ";

    // 维护两个dfs序的最值点
    pair<int, int> mndfn = {dfn[1], 1};
    pair<int, int> mxdfn = {dfn[1], 1};
    for (int i = 2; i <= n; i ++) {
        if (mn[i] == i) { // 上面
            cout << n - sz[i] << " "; 
        } else { // 子树中
            int lca = Lca(mndfn.second, mxdfn.second);
            if (dep[lca] <= dep[i]) cout << "0 "; // 不在同一棵子树中
            else {
                while (dep[lca] <= dep[i] - 1) { // 跑到 i 的一个儿子
                    for (int j = 20; j >= 0; j --) {
                        if (dep[fa[lca][j]] <= dep[i] - 1) {
                            lca = fa[lca][j];
                            break;
                        }
                    }
                }
                cout << sz[lca] << " ";
            }
        }
        if (mndfn.first > dfn[i]) mndfn = {dfn[i], i};
        if (mxdfn.first < dfn[i]) mxdfn = {dfn[i], i};
    }

    // n+1 的答案
    cout << sz[1] << endl;
}

---

CCPC2022河南省赛K_复合函数

🔗

💡

注意到每一个点的出度为 $1$ ，这就像一个向父边延伸的点。画一下易得每一个点最后会进入一个环中
且这个图由很多这样的连通块组成，每一个连通块也就是一个根为环的基环树
考虑问题： $f^a(x)=f^b(x),\;(a<b)$

• $a=b$ 时这是绝对成立的，
• 令 $c$ 为一棵基环树的环大小，如果 $a\equiv b(mod\;c)$ 说明它们如果进环会走到同一个点，也就是 $c|(b-a)$ ，但是要保证能进环也就是 $dep[x]\le a$ 的点们

这样还是很难处理，因为可能有很多基环树
但它们的环大小会有很多是相同的，最多不同大小环的基环树数量为 $\sqrt{n}$
故直接合并环长相同的信息 （深度小于等于 $i$ 的点数，通过前缀和实现），然后枚举环长，便可以在 $O(n\sqrt n)$ 的复杂度下解决这件事情

那么如何分出来一个个基环树与获取他们的环长呢

• 在除了根环之外还有点的基环树，可以直接通过从入度为 $0$ 且没有遍历过的点进入递归遍历，设置一个点可以被遍历两次，那么所有被遍历两次的点就会形成一个环，且第一个遍历两遍就是他们的根。然后从根向下遍历对这棵树的点都打上标记同时处理出来每一个点的 $dep[]$
• 在只有根环的基环树上，可以在扫完上述条件后对每一个没有遍历过的点进行遍历，只允许访问一次，一次遍历到的点数就是这个基环树的环长

✅

const int N = 1e5 + 10;
int n;
vector<int> sumd[N]; // 同环长合并后的信息
// 不同的环长
vector<int> set_rolsz;
int vis_stsz[N];

int fa[N], in[N];
vector<int> son[N];

vector<int> rol;
int rol_size;
int vis[N], dep[N];

int root, inrol[N];
inline void dfs_findTree (int u) { // 找基环树的根和环长
    if (vis[u] > 1) { // 第一次遍历两次的点就是根
        root = u;
        return;
    }
    if (vis[u] == 1) { // 第二次遍历的就是根环
        rol_size ++;
        inrol[u] = 1;
    } else { // 第一次遍历都记录下来
        rol.push_back(u);
    } vis[u] ++;
    dfs_findTree(fa[u]);
}
inline void dfs_rolTree (int u, int father) { // 顺着根向下走挖出所有的树点
    if (vis[u]) return;
    vis[u] = 1;
    rol.push_back(u);
    if (u != father) dep[u] = dep[father] + 1;
    for (auto v : son[u]) dfs_rolTree(v, u);
}

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n;
    for (int i = 1; i <= n; i ++) {
        cin >> fa[i];
        if (fa[i] != i) in[fa[i]] ++;
        son[fa[i]].push_back(i);
    }

    // 第一种情况
    for (int i = 1; i <= n; i ++) {
        if (!in[i] && !vis[i]) {
            rol_size = 0;
            rol.clear();
            dfs_findTree(i);
            for (int it : rol) vis[it] = 0; // 重启这个树上点的遍历次数
            rol.clear();
            dfs_rolTree(root, root); 
            if (!vis_stsz[rol_size]) {
                vis_stsz[rol_size] = 1;
                set_rolsz.push_back(rol_size);
            }
            for (int it : rol) {
                if (inrol[it]) dep[it] = 0;
                if (sumd[rol_size].size() < dep[it] + 1) sumd[rol_size].resize(dep[it] + 1);
                sumd[rol_size][dep[it]] ++;
            }
        }
    }
    for (int i = 1; i <= n; i ++) if (inrol[i]) vis[i] = 1;
    // 第二种情况
    for (int i = 1; i <= n; i ++) {
        if (!vis[i]) {
            rol_size = 0;
            dfs_findTree(i);
            if (!vis_stsz[rol_size]) {
                vis_stsz[rol_size] = 1;
                set_rolsz.push_back(rol_size);
            }
            if (sumd[rol_size].size() == 0) sumd[rol_size].resize(1);
            sumd[rol_size][0] += rol_size;
        }
    }

    // 前缀和预处理
    for (int i : set_rolsz) {
        for (int j = 1; j < sumd[i].size(); j ++) {
            sumd[i][j] += sumd[i][j - 1];
        }
    }

    int q; cin >> q;
    while (q --) {
        ll a, b; cin >> a >> b;
        if (a == b) cout << n << endl;
        else {
            if (b < a) swap(a, b);
            int res = 0;
            for (int i : set_rolsz) {
                if ((b - a) % i == 0) {
                    res += sumd[i][min((ll)sumd[i].size() - 1, a)];
                }
            }
            cout << res << endl;
        }
    }
}

---

CodeForces1307E_1TreesAndQueries

🔗

💡

设添加边为 $(a,b)$ ，起始点与终点为 $(x,y)$
我们如果到 $y$ 的时候距离是 $s'$ ，为了到达 $s$ 我们从 $y$ 向邻点进行折返跑，每次 $+2$ ，这样的话也就是说如果 $s'$ 与 $s$ 奇偶性相同且 $s'\le s$ 那么就是可以的
注意到添加了一条边后 $x\rightarrow y$ 有三条路径，分别是：
$x\rightarrow y$ ，对应距离为 $dis(x,y)$
$x\rightarrow a\rightarrow b\rightarrow y$ ，对应距离为 $dis(x,a)+1+dis(y,b)$
$x\rightarrow b\rightarrow a\rightarrow y$ ，对应距离为 $dis(x,b)+1+dis(y,a)$
至于 $dis(i,j)$ 的快速求法可以利用深度，但是这可能是两条链，所以处理出来 $lca(i,j)$ 即可，$lca$ 和他们都是同一条链，则 $dis(i,j)=dep_i+dep_j-2dep_{lca}$
三条路径得到的 $s'$ 都以上面说的判断格式判断一下即可

✅

const int N = 2e5 + 10;
const int M = 4e5 + 10;
struct Edge {
        int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to) {
        edge[++cnt] = {head[from], to};
        head[from] = cnt;
}
 
int n, m;
 
namespace TreeDivid {
        ll top[N], fa[N], son[N], sz[N], dep[N];
        ll dfn[N], id[N], idx;
        // 树剖 lca 
        inline void DFS1(int x, int fath);
        inline void DFS2(int x, int topx);
        inline int LCA(int x, int y);
} using namespace TreeDivid;
 
inline int dis (int a, int b) {
        int lca = LCA(a, b);
        return abs(dep[lca] * 2 - dep[a] - dep[b]);
}
 
inline void Solve () {
        scanf("%d", &n);
        for (int i = 1; i < n; i ++) {
                int u, v; scanf("%d%d", &u, &v);
                add_Edge(u, v);
                add_Edge(v, u);
        }
        DFS1(1, 0); DFS2(1, 1);
        scanf("%d", &m);
        while (m --) {
                int a, b, x, y, s; scanf("%d%d%d%d%d", &a, &b, &x, &y, &s);
                vector<int> dis_xy;
                dis_xy.push_back(dis(x, y));
                dis_xy.push_back(dis(a, x) + dis(b, y) + 1);
                dis_xy.push_back(dis(a, y) + dis(b, x) + 1);
                for (int i : dis_xy) {
                        if (i % 2 == s % 2 && i <= s) {
                                puts("YES");
                                goto end;
                        }
                }
                puts("NO");
                end:;
        }
}

---

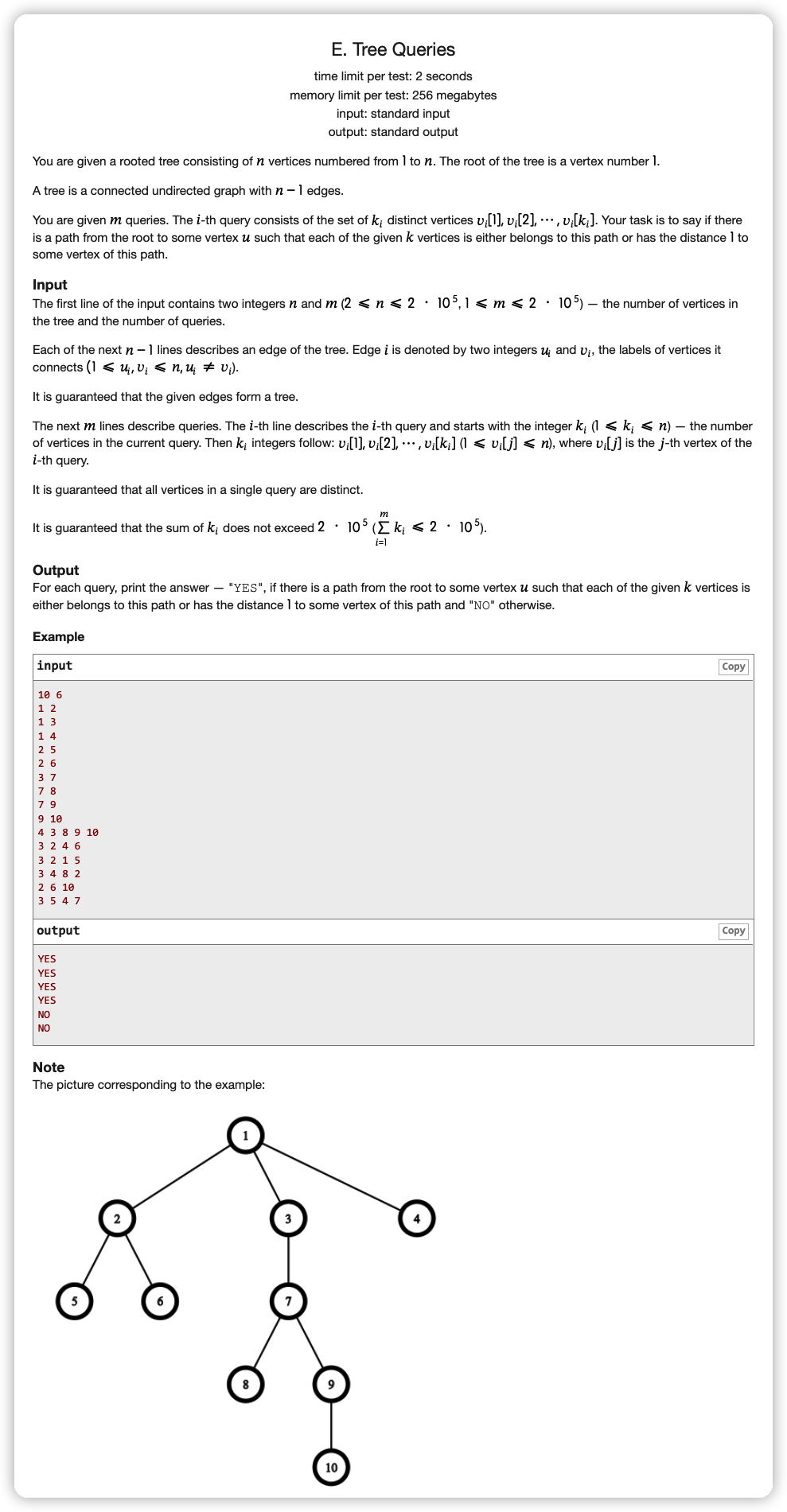
CodeForces1328E_TreeQueries

🔗

💡

要确定路，首先要确定 $u$ ，发现 $u$ 一定是输入点集中最深的点，深度相同的取谁都一样，要么是兄弟节点不影响答案，要么不是兄弟节点就是 NO ，所以深度相同取谁都行
开始想着让所有的点都对邻点贡献一次，但是如果是菊花图，每次查询都有中心点，那么一次询问就是 $O(n)$ 的，吃不消吃不消
但是能发现，其实没必要对子节点做贡献，毕竟如果能到达子节点那必定经过它自己，所以只考虑父节点即可
这样任务就变成了：从 $1$ 到查询中最深的点 $u$ 构成的路径，查询点集中是否满足要么是在路径上，要么是父节点。
那么就从 $u$ 往上走，按深度排序，从最深的点出发。
第一种情况： $lca(a[i-1],a[i])=a[i]$
第二种情况： $lca(a[i-1],a[i])$ 要么是 $a[i]$ 的父节点要么是 $a[i-1]$ 的父节点
这样 check 完所有的点就行了

新奇思路

其实这个新奇思路是我一开始想的，并且实现出来 $AC$ 了，只不过复杂度高了一个 $log$
可以用树剖+线段树，每次查询一个点是否在这条路径上
即扫描所有的点 $x$ ，对于 $x_i$ ，如果将对应位置的线段树数值 $+1$ 会让这条路径（$1\rightarrow u$）的总值 $+1$ ，说明在这条路径上，否则不在
如果不在的话，看看它的父节点在不在，同样的操作插入 $fa[x_i]$ 。如果父节点不在的话，就说明这个询问要输出 NO 了
代码就不给了，思路比较直观

✅

const int N = 2e5 + 10;
const int M = 4e5 + 10;
struct Edge {
        int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to) {
        edge[++cnt] = {head[from], to};
        head[from] = cnt;
}
int num[N];
int n, m, nn;
namespace TreeDivid {
        ll top[N], fa[N], son[N], sz[N], dep[N];
        ll dfn[N], id[N], idx;
        inline void DFS1 ( ll x, ll fath ) {
                sz[x] = 1; dep[x] = dep[fath] + 1;
                son[x] = 0, fa[x] = fath;
                for ( ll i = head[x]; i; i = edge[i].nxt ) {
                        ll to = edge[i].to; if ( to == fath ) continue;
                        DFS1 ( to, x );
                        sz[x] += sz[to];
                        if ( sz[son[x]] < sz[to] ) son[x] = to;
                }
        }
        inline void DFS2 ( ll x, ll topx ) {
                top[x] = topx;
                dfn[ ++ idx ] = x; id[x] = idx;
                if ( son[x] ) DFS2 ( son[x], topx );
                for ( ll i = head[x]; i; i = edge[i].nxt ) {
                        ll to = edge[i].to;
                        if ( to == fa[x] || to == son[x] ) continue;
                        DFS2 ( to, to );
                }
        }
} using namespace TreeDivid;

inline int LCA(int x, int y){
        while(top[x] != top[y]){                   
                if(dep[top[x]] < dep[top[y]]) swap(x, y);
                x = fa[top[x]];  
        }
        return dep[x] < dep[y] ? x : y;
}


inline void Solve () {
        scanf("%d", &n);
        scanf("%d", &m);
        cnt = 0;
        for (int i = 1; i <= n; i ++) head[i] = num[i] = 0;
        for (int i = 0; i < n - 1; i ++) {
                int u, v; scanf("%d%d", &u, &v);
                add_Edge (u, v);
                add_Edge (v, u);
        }
        DFS1(1, 0); DFS2(1, 1);
        while (m --) {
                scanf("%d", &nn);
                vector<int> a(nn);
                for (int i = 0; i < nn; i ++) scanf("%d", &a[i]);
                sort(a.begin(), a.end(), [&](int x, int y) {
                        return dep[x] > dep[y];
                });
                for (int i = 1; i < nn; i ++) {
                        int lca = LCA(a[i], a[i - 1]);
                        if (lca != fa[a[i]] && lca != fa[a[i - 1]] && lca != a[i]) {
                                puts("NO");
                                goto end;
                        }
                }
                puts("YES");
                end:;
        }
}

---

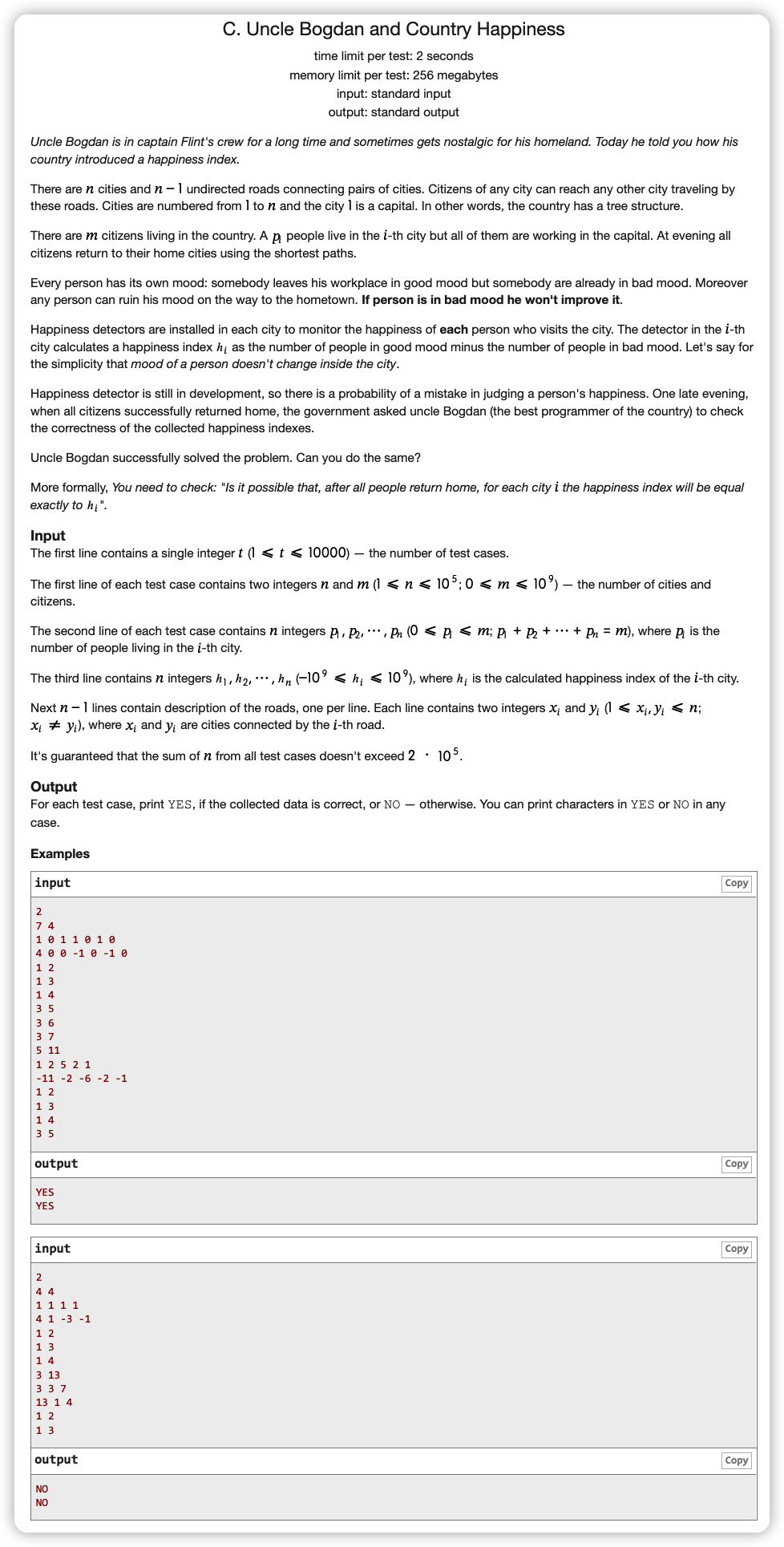
CodeForces1388C_UncleBogdanAndCountryHappiness

🔗

💡

根据题意，一个人路径上的心情状态可能是这样的 $...1111(-1)(-1)(-1)...$ ，那么我们可以思考他们在哪个位置心态变化了
由于给定的是一个固定的，我们先做出来一个每个点的参考数值，在参考数值上进行修改会比较简单
所以先让每个人一直都是 $(-1)$ 的状态，这样每个点的值就是其子树中 $[a]$ 数值和的相反数，得到数组 $[t]$
由于我们让所有人的心情都是最低，所以给定 $[h]$ 在每一个位置上都应该大于等于 $[t]$ ，且注意到如果对于 $i$ 位置上 $h_i>t_i$ ，那么我们可以在 $fa[i]\rightarrow i$ 的路径上选择 $x=\frac{h_i-t_i}{2}$ 个人 ，让他们在经过 $i$ 之后心情才变差，这样我们就可以让 $t_i$ 补到 $h_i$ 的高度
考虑到这样操作有一种局限性：如果 $i$ 的子树中确定出来了 $x$ 个 $1$ ，那么 $i$ 是一定至少被提升了 $2x$ 的，因为为了保证子树中节点的成立性，它所用的 $1$ 一定是穿过其祖先的
那么这一条就可以用作判断，维护一个数组 $[chg]$ 表示子树中总共被修改了多少个人，由于我们无法降低参考值，如果在 $i$ 位置上原本的参考值 $t_i$ 加上子树中被修改的量 $chg_i$ 乘 $2$ 大于了我们的目标值 $h_i$ ，就肯定是不行了，就要输出 NO 了 ，当然结合前面的判断情况输出 NO 的还有参考值 $t_i$ 将所有的人都变成 $1$ 即 $t_i+2sz_i$ 都无法达到目标值 $h_i$ ，也是不行的，（当然由于修改是修改偶数，所以要保证参考值和目标值的差的奇偶性相同）

✅

const int N = 1e5 + 10;
const int M = N << 1;
struct Edge {
        int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to) {
        edge[++cnt] = {head[from], to};
        head[from] = cnt;
}
int n, m;
ll a[N], h[N], t[N], sz[N], chg[N];

inline void dfs_T (int u, int fa) {
        sz[u] = a[u];
        for (int i = head[u]; i; i = edge[i].nxt) {
                int v = edge[i].to;
                if (v == fa) continue;
                dfs_T(v, u);
                sz[u] += sz[v];
        }
        t[u] = -sz[u];
}

bool flag = true;
inline void dfs_Check (int u, int fa) {
        if (!flag) return;
        for (int i = head[u]; i; i = edge[i].nxt) {
                int v = edge[i].to;
                if (v == fa) continue;
                dfs_Check(v, u);
                chg[u] += chg[v];
        }
        if (t[u] + chg[u] * 2 > h[u] || t[u] + sz[u] * 2 < h[u] || (h[u] - t[u]) % 2 != 0) {
                flag = false;
                return;
        }
        chg[u] += (h[u] - t[u] - chg[u] * 2) / 2;
}

inline void Solve () {
        scanf("%d%d", &n, &m);
        for (int i = 1; i <= n; i ++) scanf("%lld", &a[i]);
        for (int i = 1; i <= n; i ++) scanf("%lld", &h[i]);
        for (int i = 1; i <= n; i ++) head[i] = chg[i] = 0; cnt = 0;
        for (int i = 1; i < n ; i ++) {
                int u, v; scanf("%d%d", &u, &v);
                add_Edge(u, v);
                add_Edge(v, u);
        }
        dfs_T(1, 1);
        flag = true;
        dfs_Check(1, 1);
        if (flag) puts("YES");
        else puts("NO");
}

---

CodeForces1399E1_WeightsDivision（Easy Version）

🔗

💡

这个是对边进行操作的，每条边的贡献次数为其子树上的叶子结点数
令 $i$ 子树上的叶子结点数为 $son\_leaves_i$ ，如果对 $i$ 操作一次，那么总体减的值为 $\left\lceil\frac{val_i}{2}\right\rceil\times son\_leaves_i$
且这个操作是不影响别的边的贡献次数与值的，所以每次应该选能减的量最大的
然后将其减过之后，重新放入堆中排序
所以先预处理出来子树中叶子结点的数量，然后建立一个优先队列，里面存的都是下标，排序规则为减得多的在前
每次挑选出来堆顶，减完之后重新放入堆中，并判断是否当前值小于 $S$ ，如果小了直接退出

✅

const int N = 2e5 + 10;
const int M = 4e5 + 10;
struct Edge {
        int nxt, to;
        int val;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to, int val) {
        edge[++cnt] = {head[from], to, val};
        head[from] = cnt;
}
 
ll son_leaves[N];
ll fa_edge[N];
 
inline void dfs_Son (int u, int fa) {
        bool is_leaf = true;
        for (int i = head[u]; i; i = edge[i].nxt) {
                int v = edge[i].to;
                if (v == fa) {
                        fa_edge[u] = edge[i].val;
                        continue;
                }
                dfs_Son(v, u);
                is_leaf = false;
                son_leaves[u] += son_leaves[v];
        }
        son_leaves[u] += is_leaf;
}
 
struct node {
        int id;
        inline friend bool operator < (node a, node b) {
                return (fa_edge[a.id] + 1) / 2 * son_leaves[a.id] < (fa_edge[b.id] + 1) / 2 * son_leaves[b.id];
        }
};
 
int n; ll m;
inline void Solve () {
        scanf("%d%lld", &n, &m);
        for (int i = 1; i <= n; i ++) head[i] = son_leaves[i] = 0; cnt = 0;
        for (int i = 1; i < n; i ++) {
                int u, v, w; scanf("%d%d%d", &u, &v, &w);
                add_Edge(u, v, w);
                add_Edge(v, u, w);
        }
        dfs_Son(1, 1);
 
        ll sum = 0, res = 0;
        priority_queue<node> pque;
        for (int i = 2; i <= n; i ++) {
                pque.push({i});
                sum += fa_edge[i] * son_leaves[i];
        }
        while (!pque.empty()) {
                if (sum <= m) break;
                res ++;
                int id = pque.top().id; pque.pop();
                sum -= (fa_edge[id] + 1) / 2 * son_leaves[id];
                fa_edge[id] /= 2;
                pque.push({id});
        }
 
        printf("%lld\n", res);
}

---

CodeForces1399E2_WeightsDivision（Hard Version）

🔗

💡

这个和第一个题差不多，但是难的地方在于操作的花费有的是 $1$ 有的是 $2$
这两者混在一起进行排序非常难做，因为有的地方用了 $2$ 是浪费，而有的地方必须用 $2$ 才够贪，并且考虑到最后的结果一定是操作了 $x$ 次 $1$ 和操作了 $y$ 次 $2$ ，所以尝试将两者分开处理
分开处理可以得到在光操作需要花费 $c$ 的边的时候，操作 $i$ 次后这些边的 $sum$ 最少变成 $v_i$ ，由于每条边花费相同，处理方式和简单版一样
两种花费，处理后得到两个数组 $[v1],[v2]$ ，枚举“操作需要花费 $1$ 的边”的次数 $num1$ ，动态减小“操作需要花费 $2$ 的边”的次数 $num2$
在满足 $v1[num1]+v2[num2]\le S$ 的情况下，维护 $num1+2\times num2$

✅

const int N = 2e5 + 10;
const int M = 4e5 + 10;
struct Edge {
        int nxt, to;
        int val;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to, int val) {
        edge[++cnt] = {head[from], to, val};
        head[from] = cnt;
}
 
ll son_leaves[N];
ll fa_edge[N];
 
inline void dfs_Son (int u, int fa) {
        bool is_leaf = true;
        for (int i = head[u]; i; i = edge[i].nxt) {
                int v = edge[i].to;
                if (v == fa) {
                        fa_edge[u] = edge[i].val;
                        continue;
                }
                dfs_Son(v, u);
                is_leaf = false;
                son_leaves[u] += son_leaves[v];
        }
        son_leaves[u] += is_leaf;
}
 
struct node {
        int id;
        inline friend bool operator < (node a, node b) {
                return (fa_edge[a.id] + 1) / 2 * son_leaves[a.id] < (fa_edge[b.id] + 1) / 2 * son_leaves[b.id];
        }
};
 
int n; ll m;
inline void Solve () {
        scanf("%d%lld", &n, &m);
        for (int i = 1; i <= n; i ++) head[i] = son_leaves[i] = 0; cnt = 0;
        for (int i = 1; i < n; i ++) {
                int u, v, w; scanf("%d%d%d", &u, &v, &w);
                add_Edge(u, v, w);
                add_Edge(v, u, w);
        }
        dfs_Son(1, 1);
 
        ll sum = 0, res = 0;
        priority_queue<node> pque;
        for (int i = 2; i <= n; i ++) {
                pque.push({i});
                sum += fa_edge[i] * son_leaves[i];
        }
        while (!pque.empty()) {
                if (sum <= m) break;
                res ++;
                int id = pque.top().id; pque.pop();
                sum -= (fa_edge[id] + 1) / 2 * son_leaves[id];
                fa_edge[id] /= 2;
                pque.push({id});
        }
 
        printf("%lld\n", res);
}

---

CodeForces1626E_BlackAndWhiteTree

🔗

💡

如果一个点只有它的两侧各有一个点，那么它是可以动的，但仍会选另一个点导致弹回原位，我们把它视作动不了
我们考虑什么样的边可以保证通过（并且不弹回来）
对于 以 为根的子树有多于两个黑点，那么我们可以借用一个黑点走到 然后再借用另一个往里走，这个是不会弹回来的，所以这条边是可以走的
如果 黑点， 只需要一步就可以走到他想去的点，所以也可以视作能走

如果对于每个方向都求一次 那么时间肯定不允许
但是由于子树的性质：
如果整棵树以 为根
的子树 为
子树 为

利用这个性质，我们遍历一次 DFS 即可
然后我们根据上面对“边是否能走”的判断来建一个新图
如果 可以走，那么我们建一条 的边，这样的话我们从所有黑点多源 BFS 即可走出所有能到达黑点的点

✅

const int M = 6e5 + 10;
const int N = 3e5 + 10;
struct Edge {
        int nxt, to;
} edge[2][M];
int head[2][N], cnt[2];
inline void add_Edge ( int from, int to, int id ) {
        edge[id][++cnt[id]] = { head[id][from], to };
        head[id][from] = cnt[id];
}
int n, c[N];
int fa[N];
int num[N];

inline void DFS ( int x, int fath ) {
        fa[x] = fath;
        num[x] += c[x];
        for ( int i = head[0][x]; i; i = edge[0][i].nxt ) {
                int y = edge[0][i].to;
                if ( y == fath ) continue;
                DFS(y, x);
                num[x] += num[y];
        }
}

int main () {
        scanf("%d", &n);
        for ( int i = 1; i <= n; i ++ ) scanf("%d", &c[i]);
        for ( int i = 0; i < n - 1; i ++ ) {
                int a, b; scanf("%d%d", &a, &b);
                add_Edge(a, b, 0);
                add_Edge(b, a, 0);
        }        
        DFS(1, -1);

        for ( int x = 1; x <= n; x ++ ) {
                for ( int i = head[0][x]; i; i = edge[0][i].nxt ) {
                        int y = edge[0][i].to;
                        if ( c[x] ) {
                                add_Edge(x, y, 1);
                        } else {
                                if ( fa[y] == x && num[1] - num[y] > 1 ) add_Edge(x, y, 1);
                                else if ( fa[x] == y && num[x] > 1 )     add_Edge(x, y, 1);
                        }
                }
        }

        queue<int> que;
        for ( int i = 1; i <= n; i ++ ) if ( c[i] ) que.push(i);
        while ( que.size() ) {
                int x = que.front(); que.pop();
                for ( int i = head[1][x]; i; i = edge[1][i].nxt ) {
                        int y = edge[1][i].to;
                        if ( !c[y] ) 
                                c[y] = 1,
                                que.push(y);
                }
        }
        for ( int i = 1; i <= n; i ++ ) printf("%d ", c[i]);
}

---