莫队

#

---

普通莫队

CodeForces617E_XORAndFavoriteNumber

🔗

💡

由于异或的性质，反复异或等于0
所以求a[l]^a[l+1]^...^a[r]时
可以将a[i]标记为前缀和，然后求a[l-1]^a[r]即可
那么问题转化为记录区间里面a[l-1]^a[r]=k的个数
那么对于每个a[r]我们求一下a[r]^k的个数累加即可

✅

#include <iostream> 
#include <algorithm> 
#include <cmath> 
#include <queue>
#include <cstring>
#include <vector>
#include <unordered_map>
#include <map>
#define ll long long

using namespace std;

const ll N = 1e5 + 10;

struct Q{
	ll l, r, id;
}q[N];// 查询
ll a[N], res[N], RES, pos[N]; // 数列，记录答案，当前答案，块编号
ll cnt[5000010]; // 统计出现过的数的个数
ll n, m, k, len;

int main () {
	ios::sync_with_stdio(false);
#ifndef ONLINE_JUDGE
	freopen("in.in", "r", stdin);
	freopen("out.out", "w", stdout);
#endif

	auto add = [&] ( ll id ) {
		RES += cnt[a[id] ^ k]; // 利用区间内出现数的个数求一下当前RES
		cnt[a[id]] ++;  // 前缀和出现个数++
	};
	auto sub = [&] ( ll id ) {
		cnt[a[id]] --;
		RES -= cnt[a[id] ^ k];
	}; 

	cin >> n >> m >> k; len = sqrt(n);

	for ( ll i = 1; i <= n; i ++ ) {
		cin >> a[i]; a[i] ^= a[i - 1];
		pos[i] = i / len;
	}

	for ( ll i = 0; i < m; i ++ ) {
		cin >> q[i].l >> q[i].r;
		q[i].id = i;
	}

	sort ( q, q + m, []( Q a, Q b ) {
		if ( pos[a.l] != pos[b.l] ) return pos[a.l] < pos[b.l];
		return a.r < b.r;		
	});

	ll l = 1, r = 0; cnt[0] = 1;
	for ( ll i = 0; i < m; i ++ ) {
		while ( l > q[i].l ) add ( -- l - 1 );
		while ( r < q[i].r ) add ( ++ r );
		while ( l < q[i].l ) sub ( l ++ - 1 );
		while ( r > q[i].r ) sub ( r -- );
		res[q[i].id] = RES; 
	}
	for ( ll i = 0; i < m; i ++ ) {
		cout << res[i] << endl;
	}
	return 0;
}

---

洛谷P3674_小清新人渣的本愿

🔗

💡

一道莫队维护bitset的好题
bitset是一个很妙的STL容器，可以实现很多优化
是否有两个数的差为，只需要判断是否存在1即可

是否有两个数的和为
可以推导一下

那么我们建立一个存放的bst2，然后查一下中是否存在1即可

是否有两个数的积为
直接暴力枚举因数然后查一下在不在就行了

✅

#include <iostream>
#include <cstring>
#include <cstdio>
#include <vector>
#include <algorithm>
#include <cmath>
#include <map>
#include <bitset>
#define ll long long

using namespace std;

const int N = 1e5 + 10;
int n, m, len;
int a[N];
struct Q {
        int id, l, r;
        int tgt, opt;
} q[N];
bitset<N> bst1, bst2;
int res[N], vis[N];

inline void add ( int x ) {
        if ( !(vis[x] ++) ) bst1[x] = bst2[N - x] = true;
}
inline void del ( int x ) {
        if ( !(-- vis[x]) ) bst1[x] = bst2[N - x] = false;
}


inline int get ( int x ) {
        return x / len;
}

int main () {
        ios::sync_with_stdio(false);
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif
        cin >> n >> m; len = sqrt ( n );
        for ( int i = 1; i <= n; i ++ ) cin >> a[i];
        for ( int i = 0; i < m; i ++ ) {
                int opt, l, r, x; cin >> opt >> l >> r >> x;
                q[i] = {i, l, r, x, opt};
        }
        sort ( q, q + m, [&](Q a, Q b){
                if ( get(a.l) != get(b.l) ) return get(a.l) < get(b.l);
                return a.r < b.r;
        });
        for ( int L = 1, R = 0, i = 0; i < m; i ++ ) {
                
                while ( L < q[i].l ) del ( a[ L ++ ] );
                while ( L > q[i].l ) add ( a[ -- L ] );
                while ( R > q[i].r ) del ( a[ R -- ] );
                while ( R < q[i].r ) add ( a[ ++ R ] );

                if ( q[i].opt == 1 ) {
                        res[q[i].id] = (bst1 & (bst1 << q[i].tgt)).any();
                } else if ( q[i].opt == 2 ) {
                        res[q[i].id] = (bst1 & (bst2 >> (N - q[i].tgt))).any();
                } else {
                        for ( int j = 1; j * j <= q[i].tgt; j ++ ) {
                                if ( q[i].tgt % j == 0 && bst1[j] && bst1[q[i].tgt / j] ) {
                                        res[q[i].id] = true;
                                        break;
                                }
                        }
                }
        }
        for ( int i = 0; i < m; i ++ ) {
                puts(res[i] ? "hana" : "bi");
        }
}

---

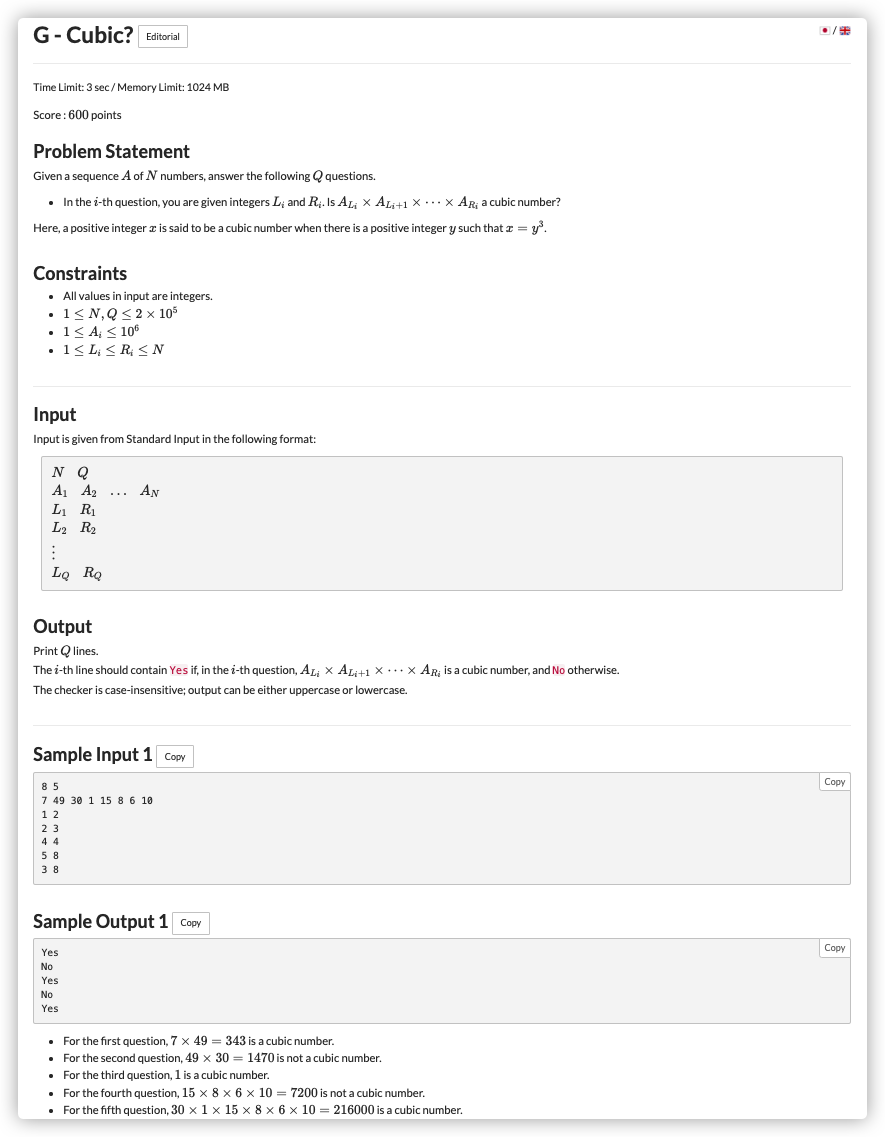
ABC238G_Cubic?

🔗

💡

注意一下立方数的性质：分解质因数后每个质因数出现至少三的倍数次
仅有区间查询，我们可以使用莫队
对每一次移动的数，都对其质因数进行统计，如果出现操作后变得不是三的倍数，就使计数变量 $+1$ ，相反的情况是 $-1$
当然如果我们移动的时候都求一次，会超时
那么我们可以先对每一个位置打一个质因数表
移动的时候直接遍历这个位置的质因数表即可
带上奇偶优化，勉强卡过去

✅

const int N = 1e6 + 10;

namespace Number {
        bool not_prime[N];
        vector<ll> prime;
        inline void Sieve () {
                not_prime[0] = not_prime[1] = 1;
                for ( int i = 2; i < N; i ++ ) {
                        if ( !not_prime[i] ) prime.push_back(i);
                        for ( ll j = 0; j < prime.size() && i * prime[j] < N; j ++ ) {
                                not_prime[i * prime[j]] = 1;
                                if ( i % prime[j] == 0 ) break;
                        }
                }
        }
        inline vector<pair<ll, ll> > get_Div ( ll x ) {
                vector<pair<ll, ll> > res;
                for ( ll p : prime ) {
                        if ( p * p > x ) break;
                        if ( !not_prime[x] ) break;
                        ll num = 0;
                        while ( x % p == 0 ) x /= p, num ++;
                        if ( num ) res.push_back({p, num});
                }
                if ( x > 1 ) res.push_back({x, 1});
                return res;
        }
}

int stsz;
int cnt[N];
vector<pair<ll, ll> > divid[N];


inline void add ( int id ) {
        for ( pair<ll, ll> pr : divid[id] ) {
                int pre = cnt[pr.first];
                cnt[pr.first] += pr.second;
                int thn = cnt[pr.first];
                if ( pre % 3 == 0 && thn % 3 != 0 ) stsz ++;
                else if ( pre % 3 != 0 && thn % 3 == 0 ) stsz --;
        }
}
inline void del ( int id ) {
        for ( pair<ll, ll> pr : divid[id] ) {
                int pre = cnt[pr.first];
                cnt[pr.first] -= pr.second;
                int thn = cnt[pr.first];
                if ( pre % 3 == 0 && thn % 3 != 0 ) stsz ++;
                else if ( pre % 3 != 0 && thn % 3 == 0 ) stsz --;
        }
}

int n, q;
int a[N];
int len;
inline int pos ( int x ) {
        return x / len;
}
struct Query {
        int l, r;
        int id;
        inline friend bool operator < ( Query a, Query b ) {
                if ( pos(a.l) != pos(b.l) ) return pos(a.l) < pos(b.l);
                if ( pos(a.l) % 2 ) return a.r > b.r;
                else return a.r < b.r;
        }
} qry[N];
int res[N];

int main () {
        Number::Sieve();

        scanf("%d%d", &n, &q); len = sqrt(n);
        for ( int i = 1; i <= n; i ++ ) 
                scanf("%d", &a[i]),
                divid[i] = Number::get_Div(a[i]);
        for ( int i = 0; i < q; i ++ ) 
                scanf("%d%d", &qry[i].l, &qry[i].r), 
                qry[i].id = i;
        sort(qry, qry + q);

        int L = 1, R = 0;
        for ( int i = 0; i < q; i ++ ) {
                while ( L < qry[i].l ) del(L ++);
                while ( L > qry[i].l ) add(-- L);
                while ( R > qry[i].r ) del(R --);
                while ( R < qry[i].r ) add(++ R);
                if ( stsz ) res[qry[i].id] = 0;
                else res[qry[i].id] = 1;
        }
        for ( int i = 0; i < q; i ++ ) {
                if ( res[i] ) puts("Yes");
                else puts("No");
        }
}

---

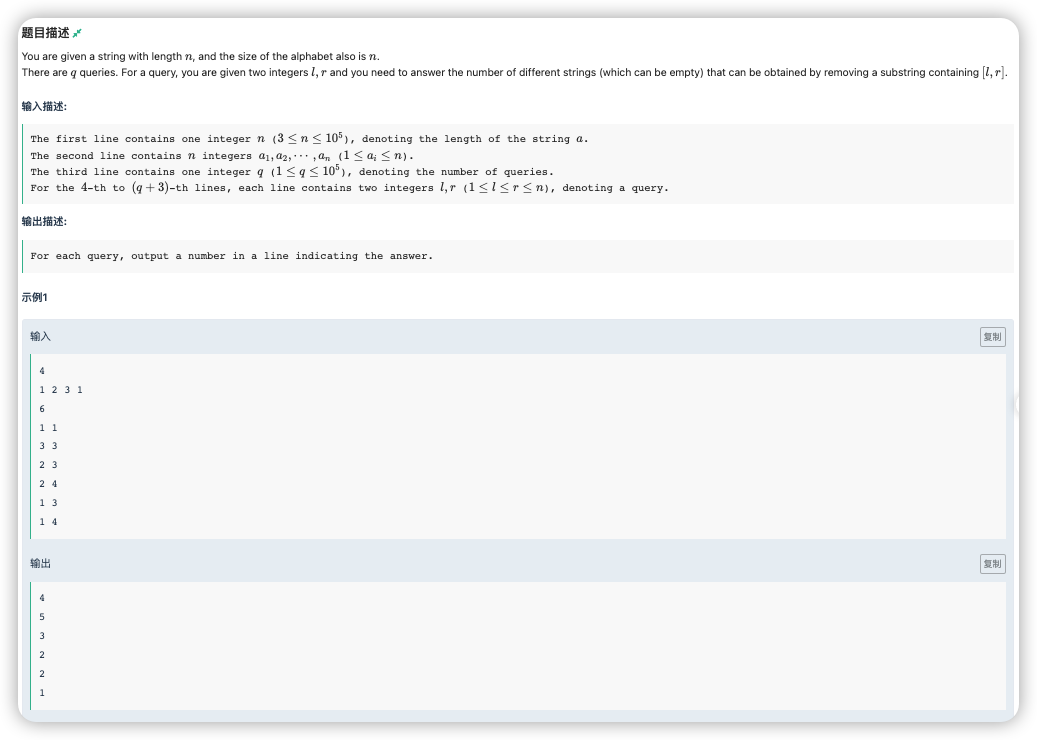
ICPC2022昆明E_EasyStringProblem

🔗

💡

$10^5$ 的区间问题，考虑莫队
看看在递进区间时，我们可以通过一个点得到什么需要维护的信息
要得到删去后不同串的数量比较难，正难则反，可以看看删去后相同的串的数量
删去的剩下的要相等，如果一个串两侧剩下相同的那么留谁都可以，所以定义 $numr[i]$ 为右侧字符 $i$ 的数量，$numl[i]$ 为左侧字符 $i$ 的数量，选取区间剩余相同的数量为 $\sum\limits_{i}numl[i]numr[i]$
所以用这个来维护莫队的动态加点删点即可

✅

const int N = 1e5 + 10;
struct Query {int l, r, i;} qry[N];
int n, q, sq;
int a[N];
ll res[N];

ll _res;
int num[2][N];
inline void add (int x, int op) {
    num[op][a[x]] ++;
    _res += num[!op][a[x]];
}
inline void del (int x, int op) {
    num[op][a[x]] --;
    _res -= num[!op][a[x]];
}

inline int p (int x) { return x / sq; }

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n;
    for (int i = 1; i <= n; i ++) cin >> a[i];
    sq = sqrt(n);
    cin >> q;
    for (int i = 1; i <= q; i ++) cin >> qry[i].l >> qry[i].r, qry[i].i = i;

    sort(qry + 1, qry + 1 + q, [&](Query a, Query b) {
        if (p(a.l) != p(b.l)) return a.l < b.l;
        if (p(a.l) & 1) return a.r < b.r;
        return a.r > b.r;
    });
    
    int L = 1, R = n;
    for (int i = 1; i <= q; i ++) {
        while (L < qry[i].l) del(L ++, 0);
        while (L > qry[i].l) add(-- L, 0);
        while (R < qry[i].r) add(++ R, 1);
        while (R > qry[i].r) del(R --, 1);
        res[qry[i].i] = 1ll * L * (n - R + 1) - _res;
    }
    for (int i = 1; i <= q; i ++) cout << res[i] << endl;
}

---

HDU2021多校(2)D_ILoveCounting

🔗

💡

看到 $x\oplus y\le z$ 这类二进制的比大小，可以联想到按位比，第一个不同即出大小，那么用字典树贴着 $x\oplus c=b$ 跑就行了，然后能小于的时候过去看一眼累加一下值再接着往下走
但是如果我们字典树中存的是子树的下标集然后在上面二分出 $[l,r]$ 之间的数了话，很难去保证里面都是不同的，但是如果我们对于区间相同的数只插入一个的话就会方便很多，直接加就行了
区间保证只插一个的做法很经典可以用莫队来实现，开一个 $num$ 数组，减的时候就如果减到零了在字典树中删除，加的时候如果加成一了就在字典树中插入 $(TLE)$
分析一下没太大的复杂度问题，优化常数
数组下标访问很慢，且看到每一个数小于 $10^5$ ，字典树换成二叉树来跑，即左子树为 $0$ 边，右子树为 $1$ 边，在这个二叉树上做字典树的操作就能优化很多下标常数了

✅

int t[10000007];

inline void Insert (int x, int c) {
    int root = 1;
    for (int i = 18; i >= 0; i --) {
        root = (root << 1) + (x >> i & 1);
        t[root] += c;
    }
}
inline int Query (int a, int b) {
    int root = 1, res = 0;
    for (int i = 18; i >= 0; i --) {
        int ca = a >> i & 1;
        int cb = b >> i & 1;
        if (cb == 1) {
            res += t[root << 1 | ca];
            root = root << 1 | (!ca);
        } else {
            root = root << 1 | ca;
        }
    }
    return res + t[root];
}

int num[100005];
int a[100005];

inline void add (int x) {
    if (!num[x]) Insert(x, 1);
    num[x] ++;
}
inline void del (int x) {
    num[x] --;
    if (!num[x]) Insert(x, -1);
}

int n, q, sq;
inline int get (int x) {return x / sq;}
struct query {
    int l, r, a, b, id;
    inline friend bool operator < (query a, query b) {
        if (get(a.l) != get(b.l)) return get(a.l) < get(b.l);
        if (get(a.l) & 1) return a.r > b.r;
        return a.r < b.r;
    }
} qry[100005];
int res[100005];

int main () {
    scanf("%d", &n); sq = sqrt(n);
    for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);
    scanf("%d", &q);
    for (int i = 1; i <= q; i ++) {
        int l, r, a, b; scanf("%d%d%d%d", &l, &r, &a, &b);
        qry[i] = {l, r, a, b, i};
    }
    sort(qry + 1, qry + 1 + q);

    for (int L = 1, R = 0, i = 1; i <= q; i ++) {
        while (L < qry[i].l) del(a[L ++]);
        while (L > qry[i].l) add(a[-- L]);
        while (R < qry[i].r) add(a[++ R]);
        while (R > qry[i].r) del(a[R --]);
        res[qry[i].id] = Query(qry[i].a, qry[i].b);
    }
    for (int i = 1; i <= q; i ++) printf("%d\n", res[i]);
}

---

HDU2021多校(1)J_zoto

🔗

💡

::: tips 解前 $PS$ 两种偏序关系，使用可持久化线段树造区间线段树吧，写了一会儿发现不行，带减法，意思是要减之后还存在的 $y$ 的不同的数量，维护不了...
那么 $CDQ$ 分治的儿子纯树状数组，离线所有的点做二维前缀和，不行还是带减法...
（以上思路想和实现一共用了三个小时...）
:::

在做不了前缀减得区间的情况下，思考另一种跑 $RMQ$ 的方式：莫队
线段树动态维护所有的 $y$ ，$cnt[y_i]$ 为零该加时插入，$cnt[y_i]$ 为 $1$ 该减时删去，对于查询求一下线段树里面 $[l_y,r_y]$ 的区间和即可（TLE）
虽然它有 $10^5$ ，但它是 $2.5$ 秒耶，线段树 $T$ 了，试试树状数组（AC）....
（我是笨瓜）

✅

const int N = 2e5 + 10;
int cnt[N];

int t[N];
inline int lowbit (int x) {return x & -x;}
inline void update (int id, int va) { while (id < N) t[id] += va, id += lowbit(id);}
inline int query (int id) { int ret = 0; while (id) ret += t[id], id -= lowbit(id); return ret; }
inline int query (int l, int r) { return query(r) - query(l - 1); }



int sq;
inline int pos (int x) {return x / sq;}
struct Query {
    int l, r, l1, r1, id;
    inline friend bool operator < (Query a, Query b) {
        if (pos(a.l) != pos(b.l)) return a.l < b.l;
        if (pos(a.l) & 1) return a.r > b.r;
        return a.r < b.r;
    }
} qry[N];
inline void add (int x) {
    if (!cnt[x]) update(x, 1);
    cnt[x] ++;
}
inline void del (int x) {
    cnt[x] --;
    if (!cnt[x]) update(x, -1);
}

int a[N];
int res[N];
inline void Solve () {
    memset(cnt, 0, sizeof cnt);
    memset(t, 0, sizeof t);

    int n, q; scanf("%d%d", &n, &q);
    sq = sqrt(n);
    for (int i = 1; i <= n; i ++) {
        scanf("%d", &a[i]);
        a[i] += 2;
    }
    for (int i = 0; i < q; i ++) {
        scanf("%d%d%d%d", &qry[i].l, &qry[i].l1, &qry[i].r, &qry[i].r1), qry[i].id = i;
        qry[i].l1 += 2;
        qry[i].r1 += 2;
    }
    sort(qry, qry + q);

    for (int L = 1, R = 0, i = 0; i < q; i ++) {
        while (L < qry[i].l) del(a[L ++]);
        while (R > qry[i].r) del(a[R --]);
        while (L > qry[i].l) add(a[-- L]);
        while (R < qry[i].r) add(a[++ R]);
        res[qry[i].id] = query(qry[i].l1, qry[i].r1);
    }
    for (int i = 0; i < q; i ++) printf("%d\n", res[i]);
}

---

带修莫队

黑暗爆炸2120_数颜色

🔗

💡

带修莫队的模板题
add和sub也就是普通的记录一下出现次数就行
关键在于对第三个指针（时间戳）的记录

✅

#include <iostream>
#include <cmath>
#include <algorithm>

using namespace std;


const int N = 133350, M = 1e6 + 10;
int cnt[M], a[N], res[N];
int n, m, len;
int nq, nm, RES;
struct Q{
	int l, r, t, id;
}qry[N];
struct M{
	int x, y;
}mdf[N];

inline void add ( int x ) {
	RES += ! cnt[x] ++;
}
inline void sub ( int x ) {
	RES -= ! -- cnt[x];
}
inline int get ( int id ) {
	return id / len;
}

int main () {
	scanf("%d%d", &n, &m);
	for ( int i = 1; i <= n; i ++ )
		scanf("%d", &a[i]);
	for ( int i = 1; i <= m; i ++ ) {
		char op[2]; int x, y;
		scanf("%s%d%d", op, &x, &y);
		if ( op[0] == 'Q' ) ++ nq, qry[nq] = { x, y, nm, nq };
		else                ++ nm, mdf[nm] = { x, y };
	} 
	len = cbrt ((double)n * nm) + 1;
	sort ( qry + 1, qry + 1 + nm, [&]( Q a, Q b ){
		if ( get(a.l) != get(b.l) ) return get(a.l) < get(b.l);
		if ( get(a.r) != get(b.r) ) return get(a.r) < get(b.r);
		if ( get(a.r) & 1 ) return a.t > b.t;
		return a.t < b.t;		
	});
	
	for ( int L = 1, R = 0, T = 0, k = 1; k <= nq; k ++ ) {
		while ( L < qry[k].l ) sub ( a[L ++] );
		while ( L > qry[k].l ) add ( a[-- L] );
		while ( R < qry[k].r ) add ( a[++ R] );
		while ( R > qry[k].r ) sub ( a[R --] );
		while ( T != qry[k].t ) {
			if ( T < qry[k].t ) T ++;
			if ( L <= mdf[T].x && mdf[T].x <= R ) 
				sub ( a[mdf[T].x] ),
				add ( mdf[T].y );
			swap ( a[mdf[T].x], mdf[T].y );
			if ( T > qry[k].t ) T --;
		}
		res[qry[k].id] = RES;
	}
	for ( int i = 1; i <= nq; i ++ ) 
		printf("%d\n", res[i]);
	return 0;
}

---