计算几何

Chivas-Regal

#

# 牛客2021多校(1)B_BallDropping

# 🔗

https://ac.nowcoder.com/acm/contest/11166/B

# 💡

一个数学几何推导
在梯形尖端拼出一个三角形
利用三角形相似求解
⚠️：一定等公式化简完了再解，不然duoble会有精度丢失

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'

#define CHIVAS_ int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
//#define map unordered_map

#define _int(a) int a; cin >> a
#define  _ll(a) ll a; cin >> a
#define _char(a) char a; cin >> a
#define _string(a) string a; cin >> a
#define _vectorInt(a, n) vector<int>a(n); cin >> a
#define _vectorLL(a, b) vector<ll>a(n); cin >> a

#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cass = inputInt(); cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
template<typename T>             vector<T>& operator--            (vector<T> &v){for (auto& i : v) --i;            return  v;}
template<typename T>             vector<T>& operator++            (vector<T> &v){for (auto& i : v) ++i;            return  v;}
template<typename T>             istream& operator>>(istream& is,  vector<T> &v){for (auto& i : v) is >> i;        return is;}
template<typename T>             ostream& operator<<(ostream& os,  vector<T>  v){for (auto& i : v) os << i << ' '; return os;}
inline int inputInt(){int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);}
inline void outInt(int X){if(X<0) {putchar('-'); X=~(X-1);}int s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline ll inputLL(){ll X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1); }
inline void outLL(ll X){if(X<0) {putchar('-'); X=~(X-1);}ll s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}



CHIVAS_{
        double r, a, b, h;
        cin >> r >> a >> b >> h;
        if(4 * h * h + a * a - 2 * a * b + b * b < 0 ||
           a == b || (r * sqrt(4 * h * h + a * a - 2 * a * b + b * b) - h * b ) / (a - b) < 0){
                cout << "Drop" << endl;
        }else{
                cout << "Stuck" << endl;
                printf("%.10f", (r * sqrt(4 * h * h + a * a - 2 * a * b + b * b) - h * b) / (a - b));
        }
        _REGAL;
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98

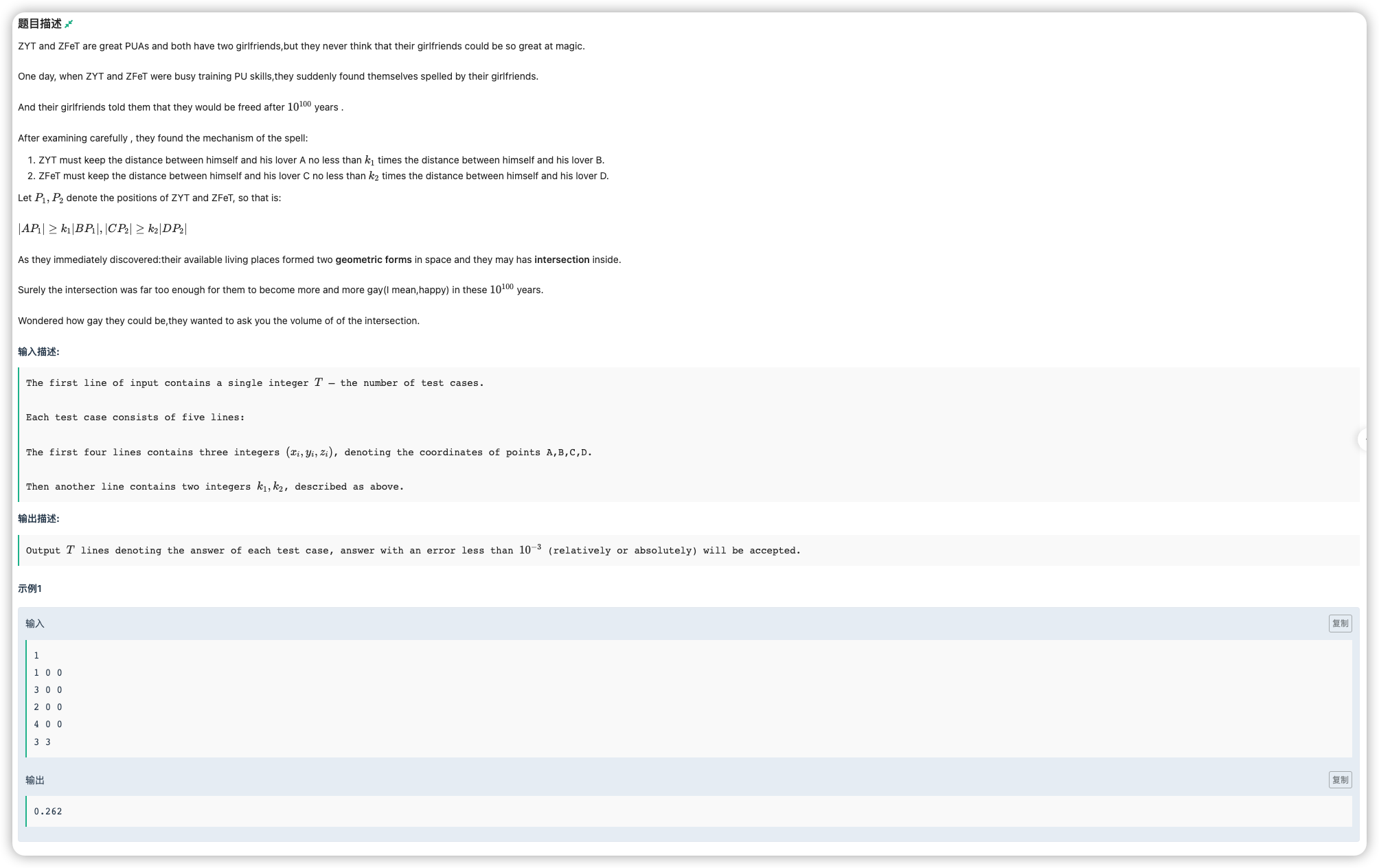
# 牛客多校2021(2)F_Girlfriend

# 🔗

# 💡

先看一个人，他可以活动的位置设为 $P$ ，两个女朋友在 $A,B$ ，距离倍数为 $k$ 写一下式子
$(a_x-p_x)^2+(a_y-p_y)^2+(a_z-p_z)^2\ge k^2((b_x-p_x)^2+(b_y-p_y)^2+(b_z-p_z)^2)$
$\left.\begin{aligned}+a_x^2-2p_xa_x+p_x^2\\+a_y^2-2p_ya_y+p_y^2\\+a_z^2-2p_za_z+p_z^2\end{aligned}\right\}\ge\left\{\begin{aligned}+k^2b_x^2+2k^2p_xb_x+k^2p_x^2\\+k^2b_y^2+2k^2p_yb_y+k^2p_y^2\\+k^2b_z^2+2k^2p_zb_z+k^2p_z^2\end{aligned}\right.$
$\left.\begin{aligned}+p_x^2(1-k^2)+p_y^2(1-k^2)+p_z^2(1-k^2)\\+2p_x(k^2b_x-a_x)+2p_y(k^2b_y-a_y)+2p_z(k^2b_z-a_z)\\+a_x^2+a_y^2+a_z^2-k^2b_x^2-k^2b_y^2-k^2b_z^2\end{aligned}\right\}\ge 0$
发现这是一个球，算出其中心点、半径
然后算球的体积交即可

# ✅

const double PI = acos(-1.0);

struct Point { double x, y, z; };
struct Ball { Point p; double r2, r; };

inline Ball person (Point a, Point b, double k) {
    Ball res;
    double down = 1 - k * k;
    double _a = (k * k * b.x - a.x) / down;
    double _b = (k * k * b.y - a.y) / down;
    double _c = (k * k * b.z - a.z) / down; 
    double _d = (a.x * a.x + a.y * a.y + a.z * a.z - k * k * b.x * b.x - k * k * b.y * b.y - k * k * b.z * b.z) / down;
    res.p = {-_a, -_b, -_c};
    res.r2 = _a * _a + _b * _b + _c * _c - _d;
    res.r = sqrt(res.r2);
    return res;
}
inline double distance (Point a, Point b) {
    return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y) + (a.z - b.z) * (a.z - b.z));
}
inline double distance2 (Point a, Point b) {
    return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y) + (a.z - b.z) * (a.z - b.z);
}
inline double in (Ball a, Ball b) {
    double dis2 = distance2(a.p, b.p);
    double dis = distance(a.p, b.p);
    if (dis >= a.r + b.r) return 0;
    else if (dis + a.r <= b.r) return PI * a.r * a.r * a.r * 4 / 3;
    else if (dis + b.r <= a.r) return PI * b.r * b.r * b.r * 4 / 3;
    
    double h1 = a.r - (a.r2 + dis2 - b.r2) / (dis * 2);
    double h2 = b.r - (b.r2 + dis2 - a.r2) / (dis * 2);
    double V = PI * h1 * h1 * (a.r - h1 / 3) + PI * h2 * h2 * (b.r - h2 / 3);
    return V;
}

int main () {
    int t; scanf("%d", &t); while (t --) {
        Point a, b;
        scanf("%lf%lf%lf%lf%lf%lf", &a.x, &a.y, &a.z, &b.x, &b.y, &b.z);
        Point c, d;
        scanf("%lf%lf%lf%lf%lf%lf", &c.x, &c.y, &c.z, &d.x, &d.y, &d.z);
        double k1, k2 ;scanf("%lf%lf", &k1, &k2);
        printf("%.3f\n", in(person(a, b, k1), person(c, d, k2)));
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

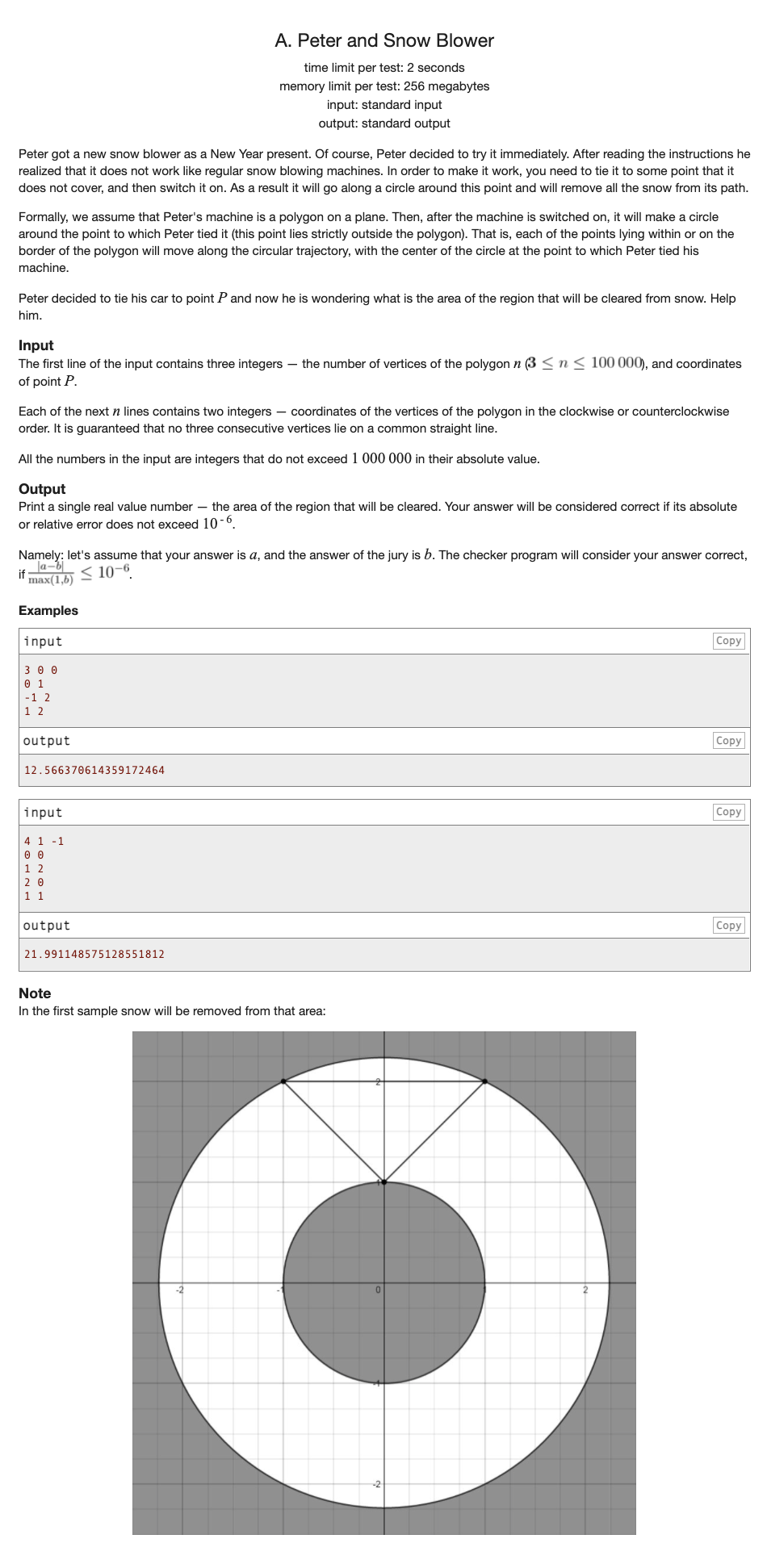
# CodeForces613A_PeterAndSnowBlower

# 🔗

# 💡

一个计算几何问题
首先我们考虑外围圆半径R，就是离圆心最远的直接就可以从点中找到
但是考虑内圈圆半径r的时候，我们需要寻找圆心到边的最近距离即可（计算几何板子扔上去）
最后答案就是 ( R * R - r * r ) * PI

# ✅

#include <iostream>
#include <algorithm>
#include <map>
#include <cmath>
#include <vector>
#include <cstring>
#include <list>
using namespace std;
#define ll long long
const ll mod = 998244353;
const double PI = acos(-1.0);
const double eps = 1e-9;

inline ll sgn ( double x ) {
        if ( x < -1e-9 ) return -1;
        else if ( x > 1e-9 ) return 1;
        return 0;
}

struct point {
        double x, y;
        point () {}
        point ( double a, double b ) : x(a), y(b) {}
        point operator + ( point b ) const {
                return point ( x + b.x, y + b.y );
        }
        point operator - ( point b ) const {
                return point ( x - b.x, y - b.y );
        }
        double operator * ( point b ) const {
                return x * b.x + y * b.y;
        }
        double operator ^ ( point b ) const {
                return x * b.y - y * b.x;
        }
};

inline point proj ( point a, point k1, point k2 ) {
        point res;
        double dx = k1.x - k2.x;
        double dy = k1.y - k2.y;
        double u = (a.x - k1.x) * (k1.x - k2.x) + (a.y - k1.y) * (k1.y - k2.y);
        u = u / ((dx * dx) + (dy * dy));
        res.x = k1.x + u * dx;
        res.y = k1.y + u * dy;
        return res;
}

inline bool OnSeg ( point p, point a, point b ) {
        return sgn ( ( a - p ) ^ ( b - p ) ) == 0 &&
        sgn ( (p.x - a.x) * (p.x - b.x) ) <= 0 &&
        sgn ( ( p.y - a.y ) * (p.y - b.y) );
}

inline double dist ( point a, point b ) {
        double dirx = a.x - b.x;
        double diry = a.y - b.y;
        return sqrt ( dirx * dirx + diry * diry );
}

inline point PointLine ( point p, point a, point b ) {
        point result;
        double t = ( ( p - a ) * ( b - a ) ) / ( ( b - a ) * ( b - a ));
        if ( t >= 0 && t <= 1 ) {
                result.x = a.x + (b.x - a.x) * t;
                result.y = a.y + (b.y - a.y) * t;
        } else {
                if ( dist ( p, a ) < dist ( p, b ) ) result = a;
                else result = b;
        }
        return result;
}

int main () {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif
        ll n;
        double X, Y; 
        cin >> n >> X >> Y;
        point PT = {X, Y};
        vector<point> pt;
        double r = 10000000000000000, R = 0;
        for ( ll i = 0; i < n; i ++ ) {
                double a, b; cin >> a >> b;
                pt.push_back({a, b});
                if ( dist(PT, pt.back()) - R > eps ) R = dist(PT, pt.back());
        }
        for ( int i = 0; i < n; i ++ ) {
                point near = PointLine ( PT, pt[i], pt[(i + 1) % n]);
                if ( r - dist(PT, near) > eps ) r = dist(PT, near);
        }

        printf("%.10f\n", (R * R - r * r) * PI);
}

# ICPC上海站2020I_SkyGarden

# 🔗

# 💡

这些点的排布有规律，所以我们分析一下所有可能的点对距离

同圈：看看走直线和走曲线哪个更近，由于是等分，所以这两个都很好求出
异圈：外圈的先走到小圈，然后看看走直线和走曲线哪个更近

易知道，同圈上一个点访问该圈所有的点求出之后设为 $\inline cur$ ，外圈上一个点访问这圈所有点在这圈上走的距离是 $\inline dir\times2\times&space;m+cur$
所以这道题的关键就在于遍历每一圈，求出这圈上一个点访问所有点的距离，然后用外圈所有的点套这个距离就行了

那么我们就可以把问题分为“圈上选择走法”和“直线走法”
圈上选择走法：
从内圈向外遍历圈数，第 $\inline i$ 圈求出 $\inline cur$ ，该圈互相访问需要 $\inline \frac{cur}{2}$ ，比这圈层数大的点的个数为 $\inline 2\times&space;m$ ，去访问这所有点在圈上选择走法总距离为 $\inline$

直线走法：
每一次外圈要访问该圈所有点都要先走到这圈，那么每一个点到这个圈的距离为 $\inline 1,2,\dots,n-dp$ ，每个点访问这圈所有点要走 $\inline n$ 次
总距离就是 $\inline 2\times&space;m\times\frac{(1+n-dp)(n-dp)}{2}\times2\times&space;m$

注意，当分割线数量不为 $\inline 1$ 时，还有个所有点到圆心的距离
也就是 $\inline 2\times&space;m\times\frac{(1+n)n}{2}$

C++ 精度一直出问题，所以换成 Java 来做

# ✅

public class Main{
        static BigDecimal  mysol(int n, int m) {
                BigDecimal res1 = BigDecimal.ZERO, res2 = BigDecimal.ZERO; // 圈上选择，直接直线
                for ( int dp = 1; dp <= n; dp ++ ) { // 枚举第几圈
                        BigDecimal line = BigDecimal.valueOf(dp).multiply(BigDecimal.valueOf(2)).multiply(BigDecimal.valueOf(m)); // 走直线的话需要的步数
                        BigDecimal one_arc = BigDecimal.valueOf(dp).multiply(BigDecimal.valueOf(Math.PI)); // 一个弧
                        
                        BigDecimal cur = BigDecimal.ZERO; // 圈上每个点到该圈所有点的距离和
                        for ( int i = 1; i < m; i ++ ) {
                                if ( line.compareTo(one_arc.multiply(BigDecimal.valueOf(i))) == 1 ) cur = cur.add(one_arc.multiply(BigDecimal.valueOf(i)));
                                else cur = cur.add(line);
                        }
                        cur = cur.multiply(BigDecimal.valueOf(2));
                        cur = cur.add(line);
        
                        res1 = res1.add(cur.multiply(BigDecimal.valueOf(n).subtract(BigDecimal.valueOf(dp))).multiply(BigDecimal.valueOf(2))).add(cur); // 外圈和该圈所有点在该圈上移动的距离和
                        res2 = res2.add(BigDecimal.valueOf(m).multiply(BigDecimal.valueOf(1 + n - dp)).multiply(BigDecimal.valueOf(n - dp)).multiply(BigDecimal.valueOf(2 * m))); // 外圈到该圈需要的距离和
                }
                if ( m != 1 ) res2 = res2.add(BigDecimal.valueOf(m * n * (n + 1))); // 有圆心，要加所有点到圆心的距离和
                return res1.add(res2);
        }
        public static void main(String[] args) {
                Scanner input = new Scanner(System.in);
                int n = input.nextInt(), m = input.nextInt();
                String res =  String.format("%.10f", mysol(n, m));
                System.out.println(res);
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

筛法强连通分量