牛顿迭代法

简介

牛顿迭代法是由牛顿和拉弗森提出的，用于在复数域或实数域上求一阶可导函数的根或者二阶可导函数的极值的近似值。
由于其具有二阶收敛性，能相对于二分更快地逼近我们想要的答案。

迭代式

首先看一个 $wiki$ 上面的动画

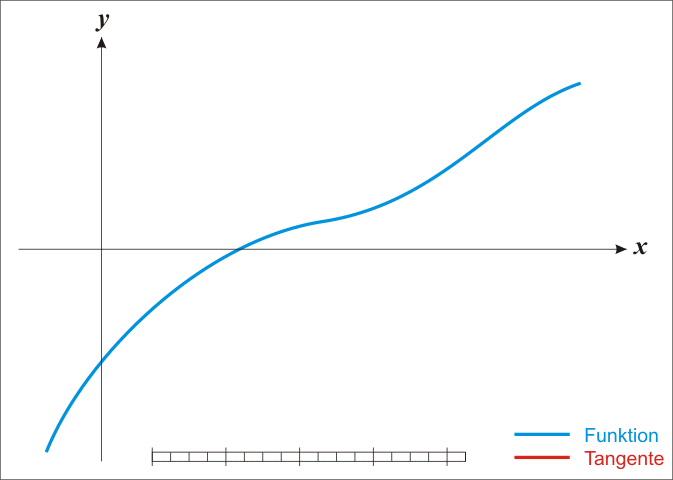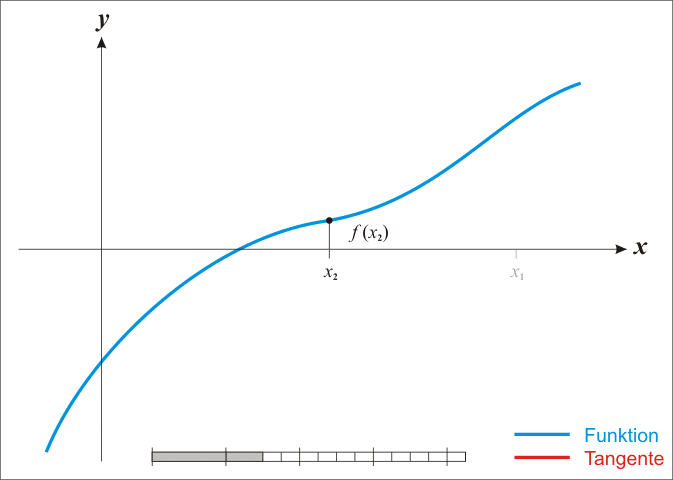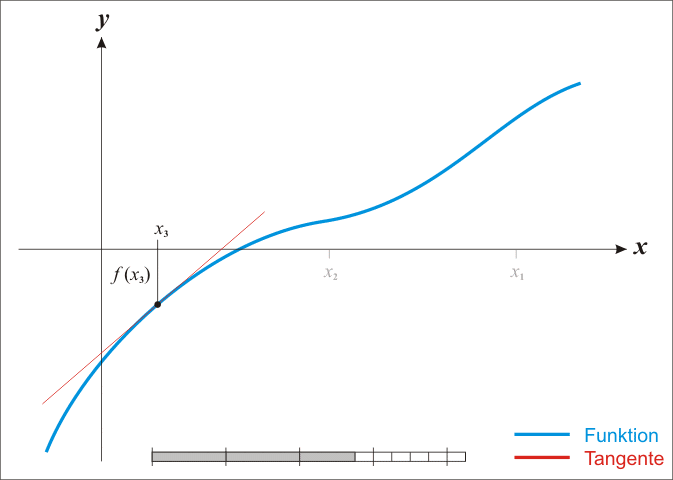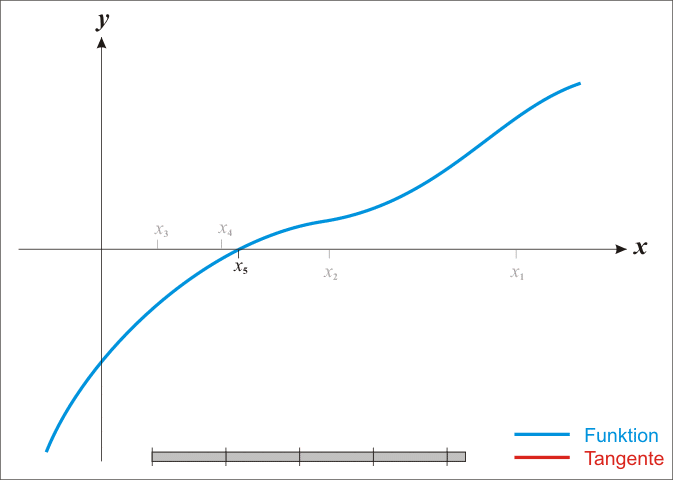
过程是

• 首先取一个最初的 $x_1$
• 对 $(x_1,f(x_1))$ 做切线 $l$
• $l$ 交 $x$ 轴于 $x_2$

重复上述步骤便可逐渐趋近于零点
通过这个动画也可以观察到迭代式

$$x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)}$$

证明

这里用到泰勒公式： $f(x)=f(x_0)+\frac{f'(x_0)}{1!}(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+\dots+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+R_n$
由于是近似值，我们省去二次项之后的项，可有 $f(x)\approx f(x_0)+f'(x_0)(x-x_0)$
则对于 $f(x)=0$ 的根 $x$
$\begin{aligned} f(x_0)+f'(x_0)(x-x_0)&\approx 0\\ x=x_0&\approx-\frac{f(x_0)}{f'(x_0)}\\ x&\approx x_0-\frac{f(x_0)}{f'(x_0)} \end{aligned}$
由此便可构造出迭代式 $x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)}$

应用

求多项式 $F(x)$ 的零点
我们首先计算出 $f'(x)$ 的各个系数
设置一个迭代次数，每次使用上面的迭代式让 $x$ 逼近零点

inline double F (double x) { /*...*/ } // F(x)
inline double f1 (double x) { /*...*/ } // f(x)

inline double Newton_Iteration (double x, int tim) { // 初始参数 与 迭代次数
        while (tim --) {
                if (fabs(F(x)) < 1e-9) return x;
                x -= F(x) / f1(x);
        }
        return -inf; // 达不到零点
}

缺点

驻点

驻点处 $f'(x)=0$ ，与 $x$ 轴平行无交点，所以得不到下一次的迭代的 $x$

逐渐远离的不收敛

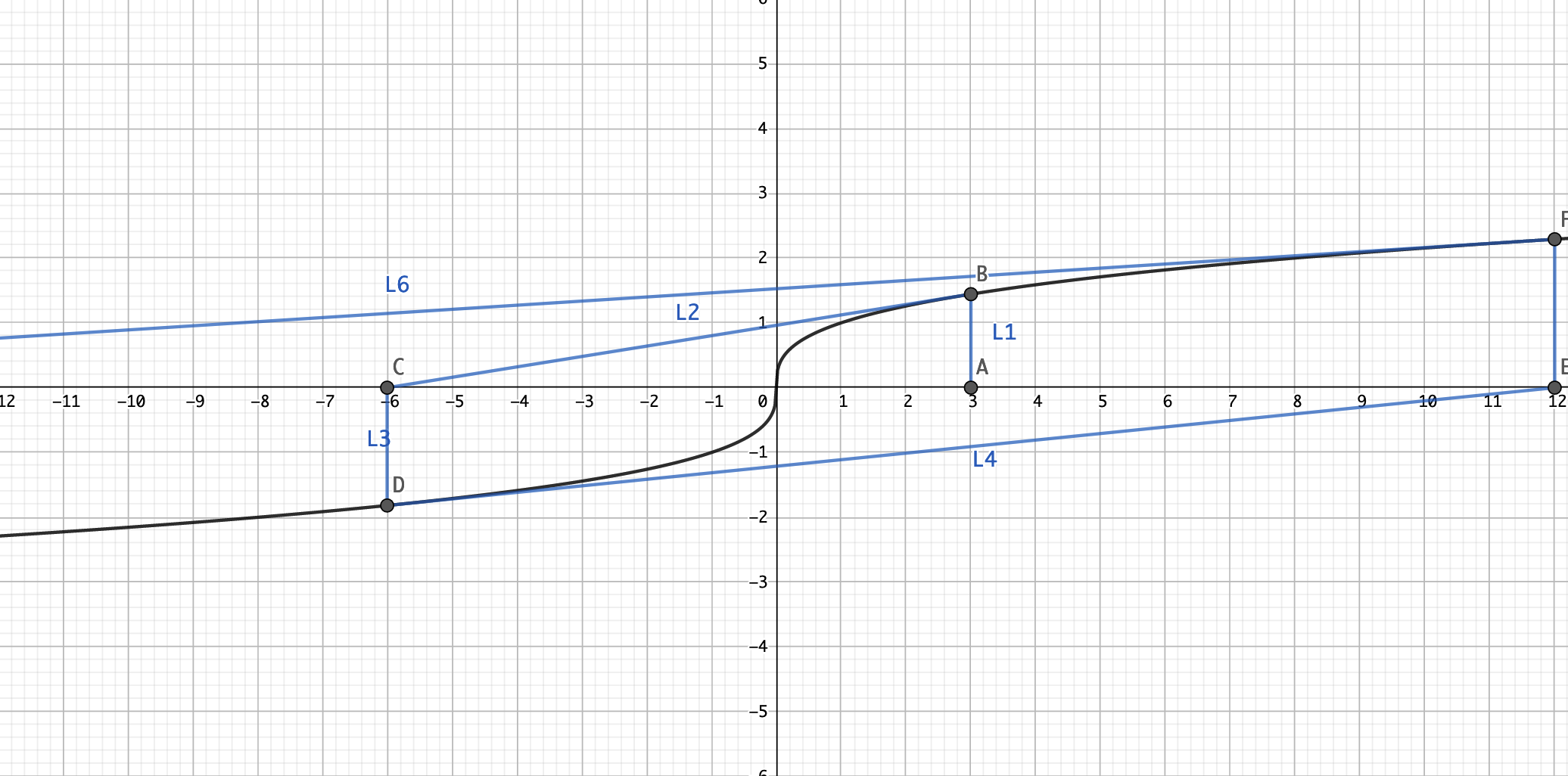
这是一个 $f(x)=x^{\frac13}$ 的函数
此时进入公式中： $x_k-\frac{f(x_k)}{f'(x_k)}=x_k-\frac{x_k^{\frac13}}{\frac13x_k^{-\frac23}}=-2x_k$
这种会导致迭代出来的 $x$ 越来越远离零点

震荡循环的不收敛

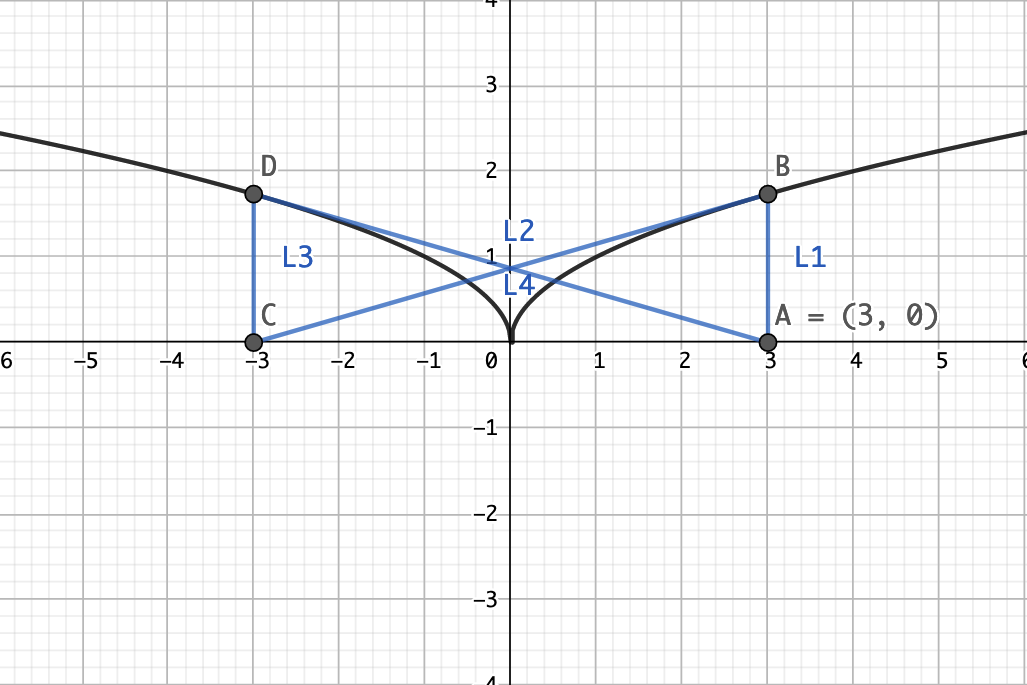这是一个 $f(x)=|x|^{\frac12}$ 的函数
由于对称，会导致经过两次迭代就走回原位置了

所有的根

对于一些有多个根的多项式，如果选择离驻点更近的 $x$ 作为起始点，那么切线斜率很小，会走向更远的点
此时我们就没办法确定离当前点最近的零点