差分约束

Chivas-Regal

#

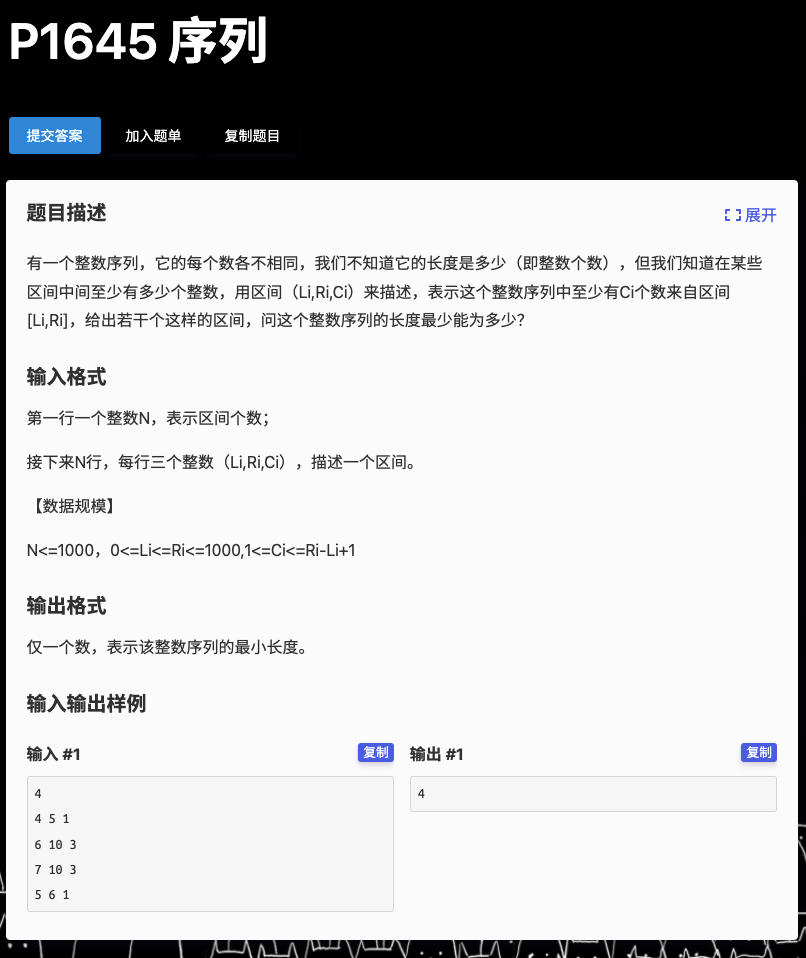
# 洛谷P1645_序列

# 🔗

# 💡

槽点

这个蓝题竟然是洛谷P1250 (opens new window) 这个橙题的数据简化版
本意可能是贪心（虽然贪心 $tag$ 难度也不够），过了之后看了眼题解差分约束（好久没做差分约束了感知力下降了很多）

我们用前缀和入手
设 $vis[i]$ 为 $bool$ 型变量的 $i$ 是否被选择
$s[i]$ 为 $vis$ 的前缀和
那么我们可以得到约束条件

$s[b]-s[a-1]\ge c$
$1\ge s[i+1]-s[i]\ge 0\left\{\begin{aligned}&s[i+1]-s[i]\ge 0\\&s[i]-s[i+1]\ge-1\end{aligned}\right.$
由于是问最小值，所以我们化成 $\ge$ 后求最长路

# ✅

const int N = 1100;
const int M = 3100;

struct Edge {
        int nxt, to;
        int val;
} edge[M];
int head[N], cnt;
inline void add_Edge ( int from, int to, int val ) {
        edge[++cnt] = { head[from], to, val };
        head[from] = cnt;
}

int dis[N], vis[N];
inline void SPFA () {
        for ( int i = 0; i < N; i ++ ) dis[i] = -0x3f3f3f3f;
        queue<int> que;
        que.push(0); vis[0] = 1; dis[0] = 0;
        while ( que.size() ) {
                int x = que.front(); que.pop();
                vis[x] = 0;
                for ( int i = head[x]; i; i = edge[i].nxt ) {
                        int y = edge[i].to;
                        if ( dis[y] < dis[x] + edge[i].val ) {
                                dis[y] = dis[x] + edge[i].val;
                                if ( !vis[y] ) vis[y] = 1, que.push(y);
                        }
                }
        }
}

int n;
int main () {
        ios::sync_with_stdio(false);
        cin >> n;
        int mx = 0;
        for ( int i = 0; i < n; i ++ ) {
                int a, b, c; cin >> a >> b >> c;
                add_Edge(a - 1, b, c);
                mx = max(mx, b);
        }
        for ( int i = 0; i < mx; i ++ ) {
                add_Edge(i, i + 1, 0);
                add_Edge(i + 1, i, -1);
        }
        SPFA();
        cout << dis[mx] << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

# CCPC2022上海省赛B_BracketQuery

# 🔗

# 💡

给定的区间做一下公式让它更清晰
令 $num0/num1$ 为区间内左/右括号数量，则有 $num0-num1=c,num0+num1=r-l+1$
化简可得 $num0=\frac{r-l+1+c}{2}$ ，这个是区间的数量，让相对变得绝对，换成前缀和问题
令 $s_i$ 表示 $[0,i]$ 的左括号数量 ~~（比赛的时候用左右括号数量差的前缀和做，麻烦的要死...最终没 $A$ ）~~
则有 $s_r-s_{l-1}=\frac{r-l+1+c}{2}$ （必须保证 $r-l+1+c$ 是偶数）
给定一大堆前缀和之间的差值关系，就是比较明显的并查集或者差分约束，但是并查集只可以解决是否成立的问题，构造合法解还是得差分约束
则第一个约束已经出来了： $s_r-s_{l-1}=\frac{r-l+1+c}{2}$
这是给定的，按照常理一个位置不可能出两个左括号，故第二个约束 $0\le s_i-s_{i-1}\le 1$
还有一个问题没有加进去，那就是最终解是一个合法括号序列，那么这就有关于每一个 $s_i$ 的上下界
最多的时候前面都是左括号（不能超过 $n/2$ ），故 $min(i,n/2)$
最少的时候前面尽可能成对，即 $\left\lceil\frac i2\right\rceil$
故第三个约束为 $\left\lceil\frac i2\right\rceil\le s_i-s_0\le min(i,n/2)$

上面的三个约束条件统一化为 $\le$ 求最短路
$s_r-s_l\le \frac{r-l+1+c}{2}\\s_l-s_r\le -\frac{r-l+1+c}{2}\\s_i-s_{i-1}\le 1\\s_{i-1}-s_i\le 0\\s_i-s_0\le min(i,n/2)\\s_0-s_i\le -\left\lceil\frac i2\right\rceil$

$spfa$ 判断是否合法。
求出来一组 $dis$ 后，我们要判断是否和我们已知的 $<l,r,c>$ 成立，即在给定的时候记录 $dif[l][r]=c$ ，求完 $dis$ 扫描 $ij$ ，看 $dis[j]-dis[i-1]$ 是否等于 $\frac{j-i+1+dif[i][j]}{2}$
最后输出时由于我们 $dis$ 数组最多差 $1$ ，且是一组合法的前缀和，那么如果 $dis[i]>dis[i-1]$ 说明 $i$ 多了一个 $'('$ ，否则是一个 $')'$

# ✅

const int M = 1e6 + 10;
const int N = 3e3 + 10;
struct Edge {
    int nxt, to, val;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to, int val) {
    edge[++cnt] = {head[from], to, val};
    head[from] = cnt;
}

int n, q;

int dis[N], vis[N], ct[N];
inline bool spfa () {
    for (int i = 0; i <= n; i ++) dis[i] = 0x3f3f3f3f, vis[i] = ct[i] = 0;
    deque<int> q; q.push_back(1); vis[1] = true; dis[1] = 0;
    while (q.size()) {
        int u = q.front(); q.pop_front();
        vis[u] = false;
        for (int i = head[u]; i; i = edge[i].nxt) {
            int v = edge[i].to;
            if (dis[v] > dis[u] + edge[i].val) {
                dis[v] = dis[u] + edge[i].val;
                ct[v] = ct[u] + 1;
                if (ct[v] > n) return false;
                if (!vis[v]) {
                    vis[v] = true;
                    if (q.size() && dis[v] > dis[q.front()]) q.push_back(v);
                    else q.push_front(v);
                }
            }
        }
    }
    return true;
}

# define NOOOOOO {puts("?");return 0;}

int nod[N];
inline int find (int x) { return x == nod[x] ? x : nod[x] = find(nod[x]); }
inline bool is_link (int x, int y) {
    x = find(x), y = find(y);
    if (x == y) return true;
    nod[x] = y;
    return false;
}
int dif[N][N];

int main () {
    for (int i = 0; i < N; i ++) {
        nod[i] = i;
        for (int j = 0; j < N; j ++) dif[i][j] = 0x3f3f3f3f;
    }

    scanf("%d%d", &n, &q);
    for (int i = 0; i < q; i ++) {
        int l, r, c; scanf("%d%d%d", &l, &r, &c);
        if ((r - l + 1 + c) % 2) NOOOOOO
        dif[l][r] = c;
        if (!is_link(l - 1, r)) {
            add_Edge(l - 1, r, (r - l + 1 + c) / 2);
            add_Edge(r, l - 1, -(r - l + 1 + c) / 2);
        }
    }
    for (int i = 1; i <= n; i ++) {
        add_Edge(i - 1, i, 1);
        add_Edge(i, i - 1, 0);
    }
    for (int i = 0; i <= n; i ++) {
        add_Edge(0, i, min(n / 2, i));
        add_Edge(i, 0, -(i + 1) / 2);
    }

    if (spfa()) {
        for (int i = 1; i <= n; i ++) {
            for (int j = i; j <= n; j ++) {
                if (dif[i][j] == 0x3f3f3f3f) continue;
                if ((j - i + 1 + dif[i][j]) / 2 != dis[j] - dis[i - 1]) NOOOOOO
            }
        }
        printf("! ");
        for (int i = 1; i <= n; i ++) {
            printf("%c", "()"[dis[i] == dis[i - 1]]);
        }
    } else NOOOOOO
}

# HDUOJ3592_WorldExhibition

# 🔗

https://acm.dingbacode.com/showproblem.php?pid=3592

# 💡

一个比较明显的差分约束题型

前x个：a[i] b[i] c[i]
表示：b[i] - a[i] <= c[i]
后y个：a[i] b[i] c[i]
表示：b[i] - a[i] >= c[i]

求最大值，所以要跑最短路，标准化一下不等式得
x: b[i] - a[i] <= c[i]
y: a[i] - b[i] <= -c[i]
使用Bellman-Ford
1.距离无限大，-1
2.有负环，-2
3.不是1.2.就输出

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'

#define CHIVAS_ int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
//#define map unordered_map

#define _int(a) int a; cin >> a
#define  _ll(a) ll a; cin >> a
#define _char(a) char a; cin >> a
#define _string(a) string a; cin >> a
#define _vectorInt(a, n) vector<int>a(n); cin >> a
#define _vectorLL(a, b) vector<ll>a(n); cin >> a

#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cass = readInt(); cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
template<typename T>             vector<T>& operator--            (vector<T> &v){for (auto& i : v) --i;            return  v;}
template<typename T>             vector<T>& operator++            (vector<T> &v){for (auto& i : v) ++i;            return  v;}
template<typename T>             istream& operator>>(istream& is,  vector<T> &v){for (auto& i : v) is >> i;        return is;}
template<typename T>             ostream& operator<<(ostream& os,  vector<T>  v){for (auto& i : v) os << i << ' '; return os;}
inline int readInt(){int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);}
inline int writeInt(int X){if(X<0) {putchar('-'); X=~(X-1);}int s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline ll readLL(){ll X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1); }
inline int writeLL(ll X){if(X<0) {putchar('-'); X=~(X-1);}ll s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}

const int N = 1100, M = 21000;
int fr[M], to[M], vl[M];
int dis[N];
int n, x, y;

inline void Init(){
        for(int i = 0; i < N; i ++) dis[i] = 1e9;
}
inline void DrawMap(){
        n = readInt(); x = readInt(); y = readInt();
        for(int i = 0; i < x; i ++) fr[i] = readInt(), to[i] = readInt(), vl[i] = readInt();
        for(int i = 0; i < y; i ++) to[i + x] = readInt(), fr[i + x] = readInt(), vl[i + x] = -readInt();
}
inline void Bellman_Ford(){
        dis[1] = 0;
        for(int k = 1; k < n; k ++){
                for(int i = 0; i < x + y; i ++){
                        dis[to[i]] = MIN(dis[fr[i]] + vl[i], dis[to[i]]);
                }
        }
        if (dis[n] == 1e9) { puts("-2"); return; }//到不了，无限远
        for(int i = 0; i < x + y; i ++){
                if(dis[to[i]] > dis[fr[i]] + vl[i]){
                        puts("-1"); return;//还能松弛，有负环
                }
        }
        writeInt(dis[n]); puts("");
}


CHIVAS_{
        int cass;
        EACH_CASE(cass){
                Init();
                DrawMap();
                Bellman_Ford();
        }
        _REGAL;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123

# 洛谷2294_狡猾的商人

# 🔗

# 💡

对于给定的a,b,c
可以使用前缀和，(b)-(a-1)=c
那么就建边:
(b)-(a-1)<=c
(a-1)-(b)<=-c

即然检查正确性，那么就跑图，对于每个连通块看一下有没有负环

# ✅

const ll N = 1e2 + 10, M = 2e3 + 10;

int stt[M], tgt[M], val[M], cnt;
int dis[N], vis[N];
int n, m;

inline bool Bellman_Ford ( int x ) {
        memset ( dis, 0x3f3f3f, sizeof dis ); dis[x] = 0;
        for ( int k = 0; k < n - 1; k ++ ) 
                for ( int i = 0; i < cnt; i ++ )
                        dis[tgt[i]] = min ( dis[tgt[i]], dis[stt[i]] + val[i] ), 
                        vis[tgt[i]] = 1;
        for ( int i = 0; i < cnt; i ++ )
                if ( dis[tgt[i]] > dis[stt[i]] + val[i] ) 
                        return false;
        return true;
}

int main () {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif 
        int cass;
        for ( scanf("%d", &cass); cass; cass -- ) {
                scanf("%d%d", &n, &m);
                cnt = 0; memset ( vis, 0, sizeof vis );
                for ( int i = 0, a, b, c; i < m; i ++ ) 
                        scanf("%d%d%d", &a, &b, &c),
                        stt[cnt] = a - 1, tgt[cnt] = b, val[cnt ++] = c,
                        stt[cnt] = b, tgt[cnt] = a - 1, val[cnt ++] = -c;
                dis[0] = 0;
                
                bool flag = true;
                for ( int i = 0; i <= n; i ++ ) {
                        if ( !vis[i] && !Bellman_Ford( i ) ) { flag = false; break; }
                }
                if ( flag ) puts("true");
                else        puts("false");
        }
        return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

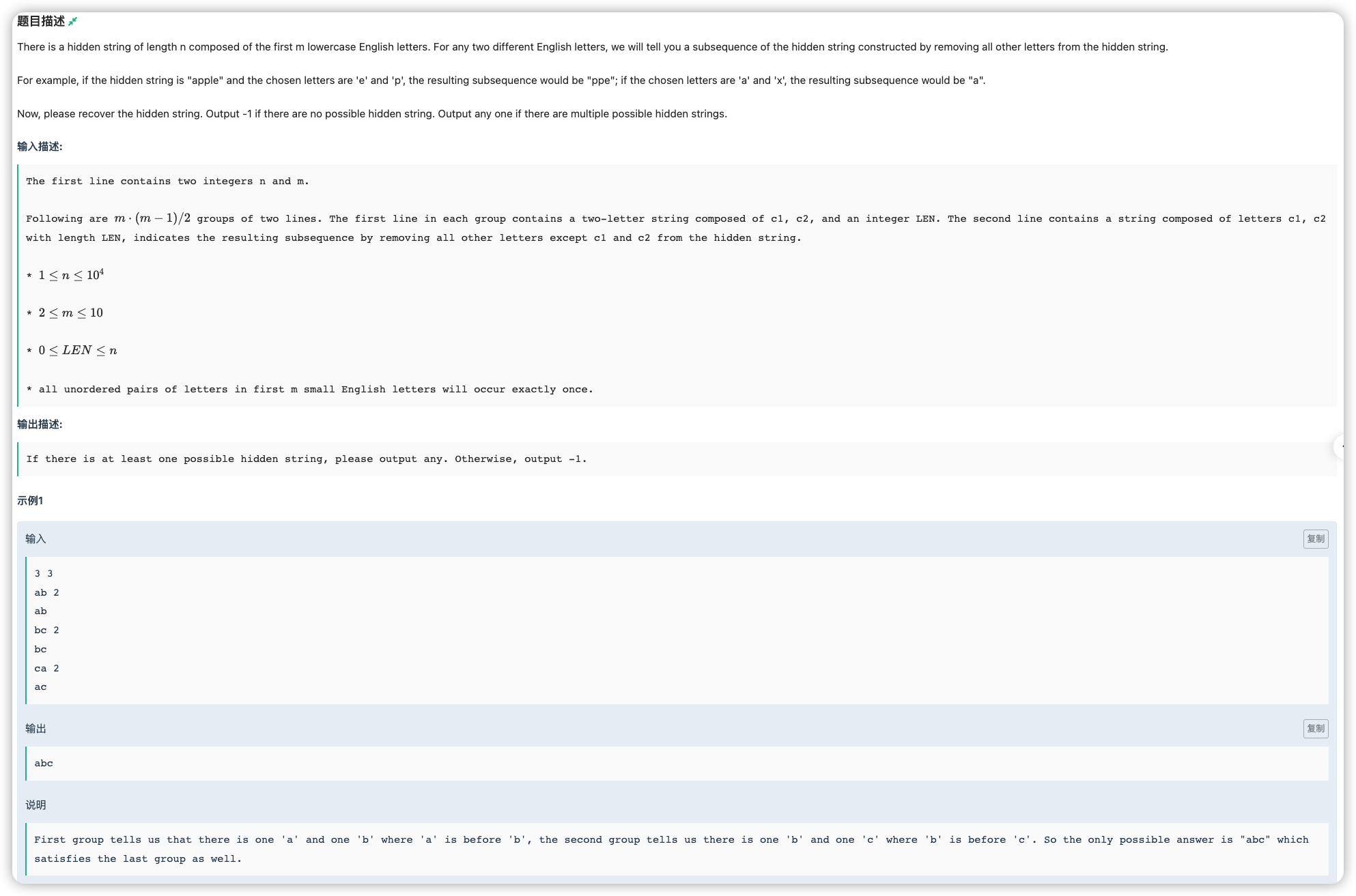
# 牛客2022国庆集训派对day3H_Subsequence2

# 🔗

# 💡

看一下给定的东西包含什么信息

一种字符的数量个数
两种字符的每一个字符的相对位置

这个相对位置就很灵性了，如果将 $a$ 的第 $x$ 个字符的位置映射到 $a_x$
在给定 $aaba$ 的意义下，就意味着 $a_1<a_2,\;a_2<b_1,\;b_1<a_3$
这就是一个差分约束系统啊，如果 $x<y$ 说明 $x-y<0$
那就用 $x-y\le -1$ 建图就好了，对于将每一个字符每一次出现的位置映射成一个点，在跑完最短路获取到 $dis[]$ 后将每个点按 $dis$ 进行排序，依次输出这个点是哪个字符

但是这个 $n$ 很大 $m$ 与 $n$ 同级，跑个 $spfa$ 大概率寄掉，但是注意到每一个边权都是 $-1$ ，故直接跑一个拓扑排序维护最短路就行了

# ✅

inline void cgets (char *s) { // 读取一行字符串
    char ch;
    int i = 0;
    while (scanf("%c", &ch) != EOF && ch != '\n') {
        s[i++] = ch;
    }
    s[i] = '\0';
}

const int N = 1e4 + 10;
const int M = N * 26 * 10;

int in[N * 26];
int idchar[N * 26], idx; // 第 idx 个点是哪个字符
int charid[26][N], char_num[26]; // charid[i][j]:i字符出现的第j个对应哪个点 ，char_num[i]:i字符的个数
struct Edge {
    int nxt, to, val;
} edge[M];
int head[N * 26], cnt;
inline void add_Edge (int from, int to, int val) {
    edge[++cnt] = {head[from], to, val};
    head[from] = cnt;
    in[to] ++;
}

int n, m; 

int dis[N * 26];
inline bool topSort () {
    for (int i = 0; i < N * 26; i ++) {
        dis[i] = 0x3f3f3f3f;
    }
    
    queue<int> que;
    for (int i = 1; i <= n; i ++) {
        if (!in[i]) {
            que.push(i);
            dis[i] = 0;
        }
    }
    while (!que.empty()) {
        int u = que.front();
        que.pop();
        for (int i = head[u]; i; i = edge[i].nxt) {
            int v = edge[i].to;
            in[v] --;
            dis[v] = min(dis[v], dis[u] + edge[i].val);
            if (!in[v]) {
                que.push(v);
            }
        }
    }

    for (int i = 1; i <= n; i ++) if (dis[i] == 0x3f3f3f3f) return false;
    
    return true;
}

char t[4];
char s[N];

int main () {
    scanf("%d%d", &n, &m); 
    for (int i = 0; i < m * (m - 1) / 2; i ++) {
        int len;
        scanf("%s%d", t, &len); 
        getchar(); cgets(s);

        // 如果 t[0] 没获取过信息
        if (!charid[t[0] - 'a'][1]) {
            int id = 0;
            for (int j = 0; j < len; j ++) {
                if (s[j] == t[0]) {
                    charid[t[0] - 'a'][++id] = ++idx;
                    idchar[idx] = t[0] - 'a';
                }
            }
            char_num[t[0] - 'a'] = id;
            // 先是同一个字符内的大小关系
            for (int j = 1; j + 1 <= id; j ++) {
                add_Edge(charid[t[0] - 'a'][j + 1], charid[t[0] - 'a'][j], -1);
            }
        }
        // 如果 t[1] 没获取过信息
        if (!charid[t[1] - 'a'][1]) {
            int id = 0;
            for (int j = 0; j < len; j ++) {
                if (s[j] == t[1]) {
                    charid[t[1] - 'a'][++id] = ++idx;
                    idchar[idx] = t[1] - 'a';
                }
            }
            char_num[t[1] - 'a'] = id;
            for (int j = 1; j + 1 <= id; j ++) {
                add_Edge(charid[t[1] - 'a'][j + 1], charid[t[1] - 'a'][j], -1);
            }
        }

        // 建边，按 s 的顺序搭建
        int id1 = 0, id2 = 0;
        if (s[0] == t[0]) id1 ++; else id2 ++;
        for (int j = 1; j < len; j ++) {
            if (s[j] == t[0]) id1 ++;
            else id2 ++;
            if (s[j] != s[j - 1]) {
                if (s[j - 1] == t[0]) add_Edge(charid[t[1] - 'a'][id2], charid[t[0] - 'a'][id1], -1);
                else add_Edge(charid[t[0] - 'a'][id1], charid[t[1] - 'a'][id2], -1);
            }
        }
    }
    
    if (idx != n) {
        printf("-1\n");
        return 0;
    }

    if (!topSort()) {
        printf("-1\n");
    } else {
        vector<int> v;
        for (int i = 1; i <= idx; i ++) v.push_back(i);
        sort(v.begin(), v.end(), [&](int a, int b) {
            return dis[a] < dis[b];
        });
        for (int i = 0; i < v.size(); i ++) {
            printf("%c", idchar[v[i]] + 'a');
        }
    }

}

强连通分量树上启发式合并