哈希表

Chivas-Regal

#

# hash

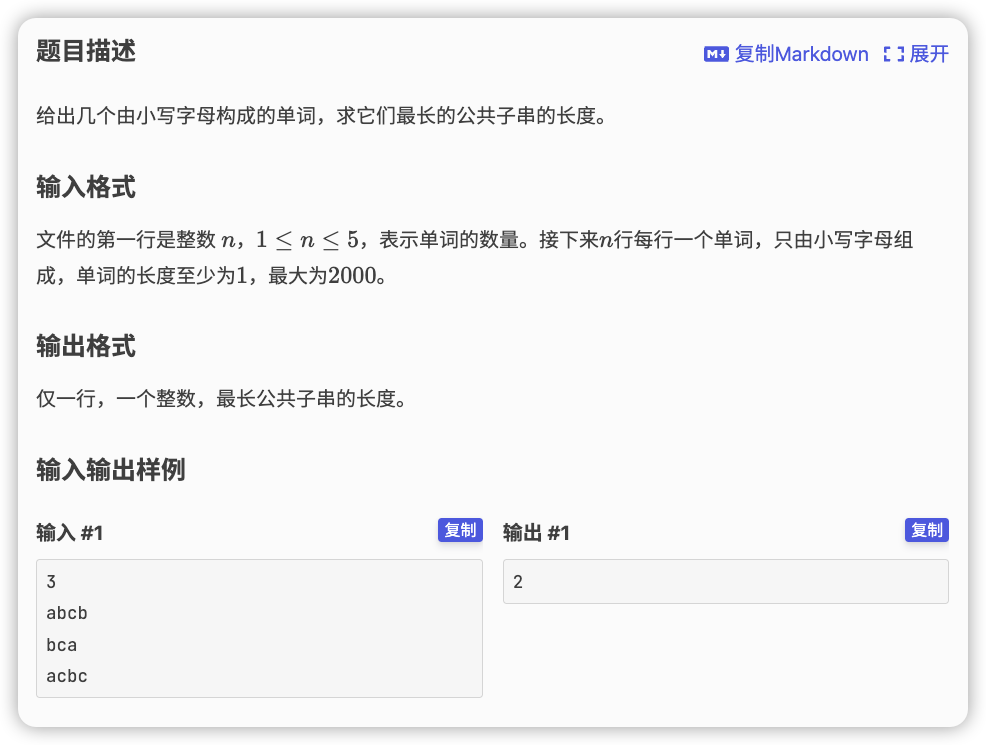
# 洛谷P5546_公共串

# 🔗

# 💡

$2000$ 初始可以想一个高复杂度的
这个数据量看来似乎可以将所有的子串全部枚举出来了
存储的时候如果存储所有子串空间不够，考虑压缩为 $hash$ 数值存储
$n \le 5$ 可以直接用 $map$ 将 $key$ 设置为 $hash$ 值，将 $val$ 设置为二进制表示在哪个字符串中出现过
第 $i$ 个串的所有子串全部与上 $2^i$ 最后扫描所有子串看看是否够 $2^n-1$ ，够的话代表在所有字符串中均出现过，维护最大值
这样分析一下复杂度 $O(5n^2logn)$ 有点大了，优化一下
求最长公共子串应该要注意到这个“最”字，可以看一下是否存在单调性
可以发现，如果 $abcdefg$ 为公共子串，那么 $abcdef$ 也为公共子串
这就证明检查公共子串的长度是否存在是存在 $01$ 单调性的
于是直接二分答案即可，复杂度为 $O(5nlognlogn)$ 的

# ✅

const int N = 2e3 + 10;
const ll mod1 = 2000000011;
const ll mod2 = 3000000019;
const int HASH1 = 20023;
const int HASH2 = 20011;
ll h1[N], h2[N];
ll sum1[10][N], sum2[10][N];
inline ll query1 (int l, int r, int op) {
    return ((sum1[op][r] - sum1[op][l - 1] * h1[r - l + 1] % mod1) % mod1 + mod1) % mod1;
}
inline ll query2 (int l, int r, int op) {
    return ((sum2[op][r] - sum2[op][l - 1] * h2[r - l + 1] % mod2) % mod2 + mod2) % mod2;
}
inline pair<ll, ll> query (int l, int r, int op) {
    return {query1(l, r, op), query2(l, r, op)};
}

int n;
int len[10];
inline bool Check (int x) {
    map<pair<ll, ll>, int> mp;
    for (int i = 0; i < n; i ++) {
        for (int j = 1; j + x - 1 <= len[i]; j ++) {
            mp[query(j, j + x - 1, i)] |= 1 << i;
            if (mp[query(j, j + x - 1, i)] == (1 << n) - 1) return true;
        }
    }
    return false;
}

char str[10][N];
int main () {
    h1[0] = h2[0] = 1;
    for (int i = 1; i < N; i ++) h1[i] = h1[i - 1] * HASH1 % mod1, h2[i] = h2[i - 1] * HASH2 % mod2;

    cin >> n;
    for (int i = 0; i < n; i ++) {
        cin >> (str[i] + 1);
        len[i] = strlen(str[i] + 1);
        for (int j = 1; j <= len[i]; j ++) {
            sum1[i][j] = (sum1[i][j - 1] * HASH1 % mod1 + str[i][j]) % mod1;
            sum2[i][j] = (sum2[i][j - 1] * HASH2 % mod2 + str[i][j]) % mod2;
        }
    }

    int l = 1, r = 2000, res = 0;
    while (l <= r) {
        int mid = (l + r) >> 1;
        if (Check(mid)) res = mid, l = mid + 1;
        else r = mid - 1;
    }
    cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

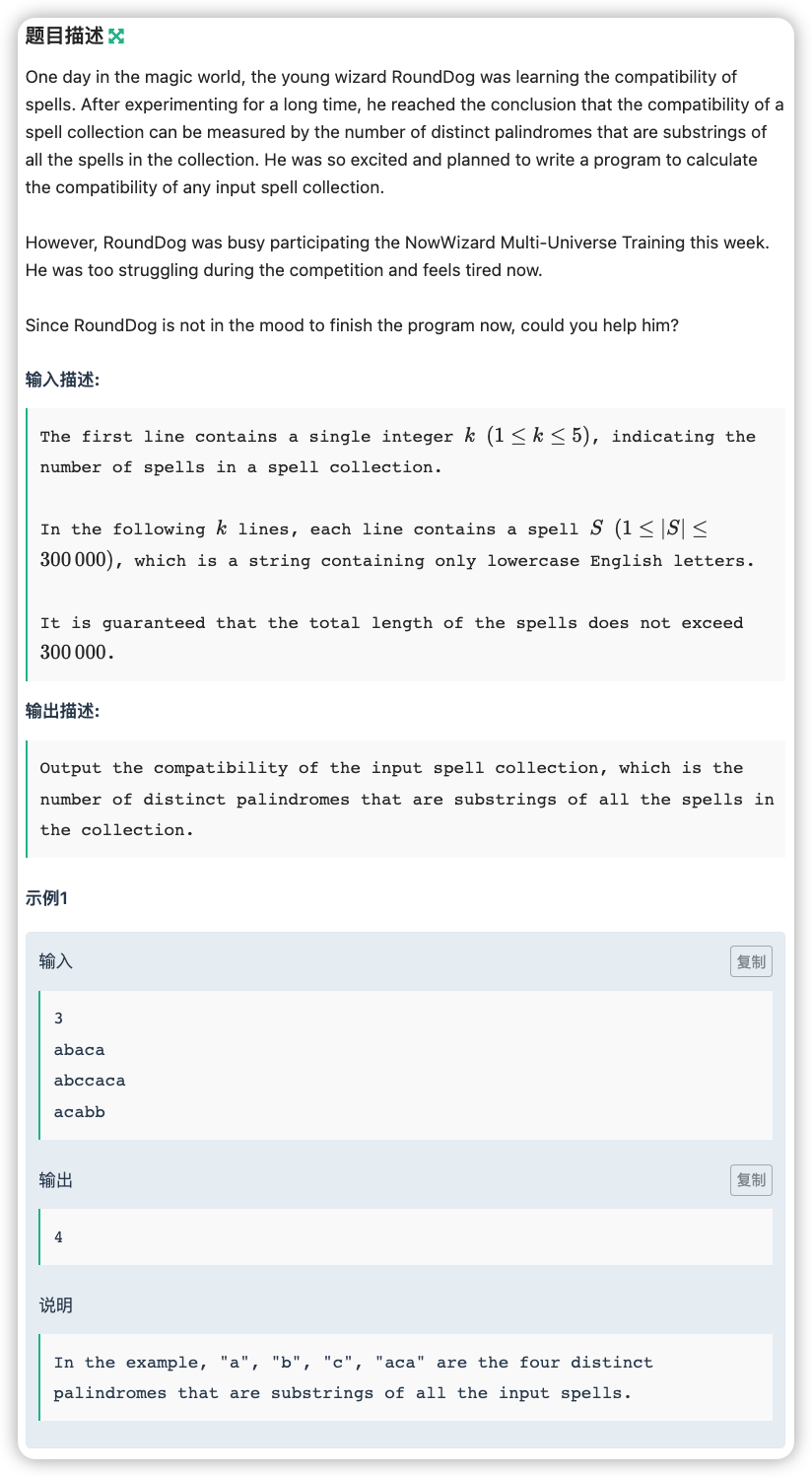
# 牛客2022多校（9）G_MagicSpells

# 🔗

# 💡

回文串，如果硬截取的话，是 $n^2$ 的复杂度，内存也不够
回文串就考虑 $Manacher$ ，注意其中的 $len[]$ 最开始是一个继承的关系，它继承对称中心前面的也就代表 $[i-len_i,i+len_i]$ 这一部分的都已经算过了，只有在扩展的时候 “有可能会出现新的回文串” ，在做统计某个回文串是否出现在这个字符串中的方式可以使用字符串 $Hash$
对第 $i$ 个串的回文串让其权值 $map[hash]$ 与上 $2^i$ ，这样在最后枚举所有的回文串看其权值是否为 $2^k-1$ 即可

注意到本题字符串过多可能会出现冲突的情况，开一个双哈希即可

# ✅

const int N = 1e6 + 10;
const ll mod1 = 2000000011;
const ll mod2 = 3000000019;
const int HASH1 = 20023;
const int HASH2 = 20011;
ll h1[N], h2[N];
ll sum1[N], sum2[N];
inline ll query1 (int l, int r) {
    return ((sum1[r] - sum1[l - 1] * h1[r - l + 1] % mod1) % mod1 + mod1) % mod1;
}
inline ll query2 (int l, int r) {
    return ((sum2[r] - sum2[l - 1] * h2[r - l + 1] % mod2) % mod2 + mod2) % mod2;
}
inline pair<ll, ll> query (int l, int r) {
    return {query1(l, r), query2(l, r)};
}

int n;
char s[N], t[N];
inline void Init () {
    s[0] = '@';
    for (int i = 1; i <= n; i += 2) {
        s[i] = '#';
        s[i + 1] = t[(i + 1) >> 1];
    }
    s[n + 1] = '#', s[n + 2] = '$'; s[n + 3] = '\0';
    sum1[0] = sum2[0] = '@';
    for (int i = 1; i <= n + 2; i ++) {
        sum1[i] = (sum1[i - 1] * HASH1 % mod1 + s[i]) % mod1;
        sum2[i] = (sum2[i - 1] * HASH2 % mod2 + s[i]) % mod2;
    }
}
int len[N];

map<pair<ll, ll>, int> mp;
inline void Manacher (int cur) {
    int p = 0, po = 0;
    for (int i = 1; i <= n; i ++) {
        if (p > i) {
            len[i] = min(len[po * 2 - i], p - i);
        } else {
            len[i] = 0;
        }
        while (s[i + len[i] + 1] == s[i - len[i] - 1]) {
            len[i] ++;
            if (s[i + len[i]] == '#') {
                mp[query(i - len[i], i + len[i])] |= (1 << cur);
            }
        }
        if (i + len[i] > p) {
            p = i + len[i];
            po = i;
        }
    }
}

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    h1[0] = h2[0] = 1;
    for (int i = 1; i < N; i ++) {
        h1[i] = h1[i - 1] * HASH1 % mod1;
        h2[i] = h2[i - 1] * HASH2 % mod2;
    }

    int k; cin >> k;
    for (int i = 0; i < k; i ++) {
        cin >> (t + 1);
        n = strlen(t + 1);
        n <<= 1;
        Init();
        Manacher(i);
    }

    int res = 0;
    for (auto x : mp) {
        if (x.second == (1 << k) - 1) res ++;
    }
    cout << res << endl;
}

# 牛客NC50986_兔子与兔子

# 🔗

https://ac.nowcoder.com/acm/contest/1008/B

# 💡

将字符串定义为一种进制
保证不同的字符串进制一定不同

建立一个hash表映射i位置前的字符串进制

在求区间字符串时只需要求区间进制即可
进制相同就字符串相同，否则不同

# ✅

#pragma region
//#pragma GCC optimize(3,"Ofast","inline")
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define eps 1e-6
#define PI acos(-1.0)
#define ll long long
#define INF 0x7FFFFFFF
#define Regal exit(0)
#define Chivas int main()
#define pb(x) push_back(x)
#define SP system("pause")
#define ull unsigned long long
#define Max(a,b) ((a)>(b)?(a):(b))
#define Min(a,b) ((a)<(b)?(a):(b))
#define IOS ios::sync_with_stdio(false)
#define mm(a, b) memset(a, b, sizeof(a))
#define each_cass(cass) for (cin>>cass; cass; cass--)
#define test(a) cout << "---------" << a << "---------" << '\n'
 
using namespace std;
#pragma endregion

//全局变量
#pragma region
const int maxn = 2e6 + 10;
const int base = 131;
char s[maxn];
int Q;
ull _hash[maxn], sys[maxn];//_hash[i]表示i以前的字符串进制，sys[i]表示base^i
#pragma endregion

//主体-------------------------------------------------------------------
inline void Init_system(){//将字符串每一位化为一个进制数，并初始化这个进制表
    int len = strlen(s + 1);
    _hash[0] = 0, sys[0] = 1;
    for(int i = 1; i <= len; i ++){
        _hash[i] = _hash[i - 1] * base + s[i] - 'a' + 1;
        sys[i] = sys[i - 1] * base;
    }
}

inline ull Get_lr(int l, int r){//求l~r的区间进制
    return _hash[r] - _hash[l - 1] * sys[r - l + 1];//类似于区间和，这里求区间进制
}

Chivas{
    scanf("%s", s + 1);
    Init_system();
    cin >> Q;
    while(Q --){
        int l1, r1, l2, r2;
        cin >> l1 >> r1 >> l2 >> r2;
        cout << (Get_lr(l1, r1) == Get_lr(l2, r2) ? "Yes" : "No") << endl;
    }
    Regal;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

# CCPC2020威海站G_CaesarCipher

# 🔗

# 💡

查询是求两个子串是否相等，判断子串相等考虑哈希，还有修改，使用线段树维护哈希
那么在修改的时候，区间每个数字加 $1$ 意味着这个 $[l,r]$ 区间加 $string(r-l+1,'1')$ ，在取模哈希下，求出所有长度的 $111...$ 的取模后的值 $val[]$
这样区间传烂标记的时候左区间只用加上 $lazy\times val[mid-l+1]$
注意到还有一个地方，就是每一个位置都是循环的，也就是说它如果等于 $65536$ 的话它会立即变成 $0$ ，也就意味着所有的位置都不能大于等于 $65536$ ，这个地方的处理可以记录一个区间的最大值，然后每次查询前看一个区间的最大值是否超过了进制，超过了话进入递归向下走并单点修改，重新搭建这一条区间链
怕被卡，两个线段树，使用双哈希

# ✅

const int N = 5e5 + 10;
const int base = 65536;
const int mod[2] = {1000000009, 1000000007}; 
 
int pwbase[2][N];
int all1[2][N]; // 1 重复 i 次的值
 
struct Sgtr {
    int val, lazy;
    int mxv;
} t[2][N << 2]; 
inline void pushup (int l, int r, int rt) {
    int mid = (l + r) >> 1;
    for (int i = 0; i < 2; i ++) {
        t[i][rt].mxv = max(t[i][rt << 1].mxv, t[i][rt << 1 | 1].mxv);
        t[i][rt].val = ((ll)t[i][rt << 1].val * pwbase[i][r - mid] % mod[i] + t[i][rt << 1 | 1].val) % mod[i];
    }
}
 
inline void pushdown (int l, int r, int rt) {
    int mid = (l + r) >> 1;
    for (int i = 0; i < 2; i ++) {
        if (!t[i][rt].lazy) continue;
        int laz = t[i][rt].lazy;
        (t[i][rt << 1].val += (ll)laz * all1[i][mid - l + 1] % mod[i]) %= mod[i];
        (t[i][rt << 1 | 1].val += (ll)laz * all1[i][r - mid] % mod[i]) %= mod[i];
        t[i][rt << 1].mxv += laz;
        t[i][rt << 1 | 1].mxv += laz;
        t[i][rt << 1].lazy += laz;
        t[i][rt << 1 | 1].lazy += laz;
        t[i][rt].lazy = 0;
    }
}
inline void update (int a, int b, int l, int r, int rt) {
    if (a <= l && r <= b) {
        (t[0][rt].val += all1[0][r - l + 1]) %= mod[0];
        (t[1][rt].val += all1[1][r - l + 1]) %= mod[1];
        t[0][rt].lazy ++; t[1][rt].lazy ++;
        t[0][rt].mxv ++; t[1][rt].mxv ++;
        return;
    }
    pushdown(l, r, rt);
    int mid = (l + r) >> 1;
    if (a <= mid) update(a, b, l, mid, rt << 1);
    if (b > mid)  update(a, b, mid + 1, r, rt << 1 | 1);
    pushup(l, r, rt);
}
inline void new_tree (int l, int r, int rt, int i) {
    if (l == r) {
        t[i][rt].val %= base;
        t[i][rt].mxv = t[i][rt].val;
        return;
    }
    pushdown(l, r, rt);
    int mid = (l + r) >> 1;
    if (t[i][rt << 1].mxv == t[i][rt].mxv) new_tree(l, mid, rt << 1, i);
    if (t[i][rt << 1 | 1].mxv == t[i][rt].mxv) new_tree(mid + 1, r, rt << 1 | 1, i);
    pushup(l, r, rt);
}
inline int query (int a, int b, int l, int r, int rt, int i) {
    if (t[i][rt].mxv >= base) new_tree(l, r, rt, i);
    if (a <= l && r <= b) return (ll)t[i][rt].val * pwbase[i][b - r] % mod[i];
    pushdown(l, r, rt);
    int res = 0, mid = (l + r) >> 1;
    if (a <= mid) res += query(a, b, l, mid, rt << 1, i);
    if (b > mid)  res += query(a, b, mid + 1, r, rt << 1 | 1, i);
    return res % mod[i];
}
 
inline void build (int l, int r, int rt) {
    if (l == r) {
        int x; scanf("%d", &x);
        t[1][rt].val = t[0][rt].val = x;
        t[1][rt].mxv = t[0][rt].mxv = x;
        return;
    }
    int mid = (l + r) >> 1;
    build(l, mid, rt << 1);
    build(mid + 1, r, rt << 1 | 1);
    pushup(l, r, rt);
}
 
int main () {
    int n, q; scanf("%d%d", &n, &q);
 
    all1[0][1] = all1[1][1] = 1;
    for (int i = 2; i < N; i ++) {
        all1[0][i] = ((ll)all1[0][i - 1] * base % mod[0] + 1) % mod[0];
        all1[1][i] = ((ll)all1[1][i - 1] * base % mod[1] + 1) % mod[1];
    }   
    pwbase[0][0] = pwbase[1][0] = 1;
    for (int i = 1; i < N; i ++) 
        pwbase[0][i] = (ll)pwbase[0][i - 1] * base % mod[0],
        pwbase[1][i] = (ll)pwbase[1][i - 1] * base % mod[1];
 
    build(1, n, 1);
    
    while (q --) {
        int op; scanf("%d", &op);
        if (op == 1) {
            int l, r; scanf("%d%d", &l, &r);
            update(l, r, 1, n, 1);
        } else {
            int x, y, l; scanf("%d%d%d", &x, &y, &l);
            pair<int, int> qx = {query(x, x + l - 1, 1, n, 1, 0), query(x, x + l - 1, 1, n, 1, 1)};
            pair<int, int> qy = {query(y, y + l - 1, 1, n, 1, 0), query(y, y + l - 1, 1, n, 1, 1)};
            if (qx == qy) printf("yes\n");
            else printf("no\n");
        }
    }
}

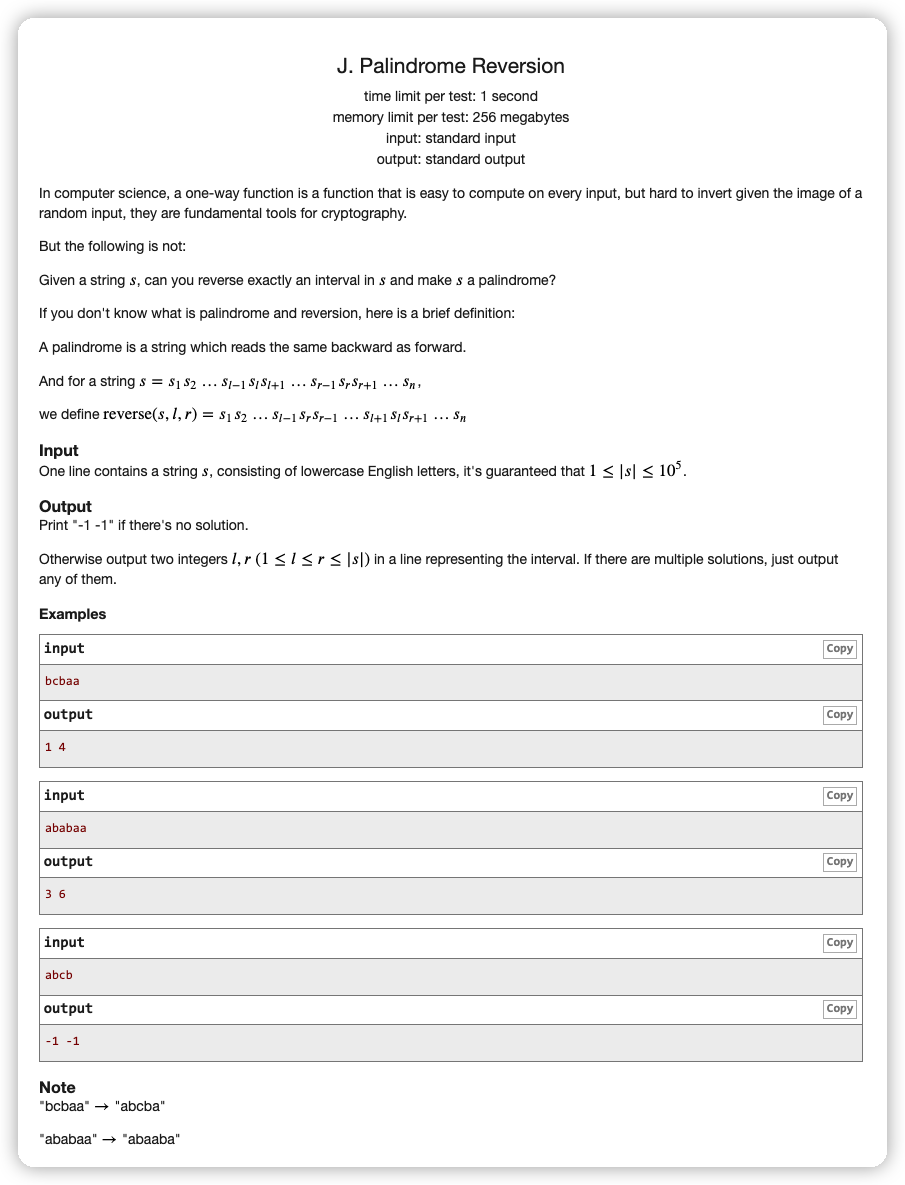
# CCPC湖北省赛J_PalindromeReversion

# 🔗

# 💡

首先可以把首位回文的部分给去掉，如果 $s[1]=s[n]$ 且翻转 $[1,i]$ 可以回文，说明 $s[i]=s[n]=s[1]$ ，那么其实翻转 $[2,i]$ 就可以了
令 $P$ 为回文串
删去回文首尾后，如果出现形如 $abc\;P\;abc$ 这样一个回文串左右两侧子串相同的字符串，那么我们翻转左边或者右边的子串即可，也就是 $cba\;P\;abc$
我们让它更朴素一点，将相同的字符串设置为 $A$ ，那么上面讨论的就是 $APA$ 这样的字符串

既然 $APA\rightarrow \tilde{A}PA$ 可以成立，考虑什么样的字符串也可以变换为这样
即 $PAA$ 通过翻转 $PA$ 也可以实现，以及 $AAP$ 通过翻转 $AP$ 也可以实现

那么具体一下，首先删去首尾回文的部分，开始分讨

$\underline{A}PA$
$\underline{PA}A$
$A\underline{AP}$

第一种情况可以通过从中心往外扩展并保证中间回文，然后检查两侧是否相同
第二种情况可以通过从右端枚举字符串长度，检查相邻左侧同长度的字符串是否和它相等，以及剩下的最左侧的字符串是否回文
第三种情况可以通过从左侧枚举字符串长度，检查相邻右侧同长度字符串是否和它相等，以及剩下的最右侧的字符串是否回文
检查相等和回文都可以使用字符串 $Hash$ 来实现

# ✅

const int base = 131;
const int mod = 1e9 + 7;
const int N = 100005;

inline ll ksm (ll a, ll b) {
        ll res = 1;
        while (b) {
                if (b & 1) res = res * a % mod;
                a = a * a % mod;
                b >>= 1;
        }
        return res;
}
inline ll inv (ll x) {
        return ksm(x, mod - 2);
}

ll h1[N], h2[N];
inline ll get1 (int l, int r) { // 正哈希求区间
        if (l == 0) {
                return h1[r];
        } else {
                return ((h1[r] - h1[l - 1] * ksm(base, r - l + 1) % mod) % mod + mod) % mod;
        }
}
inline ll get2 (int l, int r) { // 反哈希求区间
        return ((h2[l] - h2[r + 1] * ksm(base, r - l + 1) % mod) % mod + mod) % mod;
}

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        string s; cin >> s;
        int n = s.size();

        // 删去首尾回文部分
        int beg_s = 0; for (; beg_s < n; beg_s ++) {
                if (s[beg_s] != s[n - beg_s - 1]) break;
        }
        int end_s = n - beg_s - 1;
        if (beg_s == n) { cout << "1 1\n"; return 0; }
        else s = s.substr(beg_s, end_s - beg_s + 1);

        // 预处理正哈希和反哈希
        for (int i = 0; i < s.size(); i ++) {
                if (i == 0) h1[i] = s[i] - 'a';
                else h1[i] = h1[i - 1] * base % mod + (s[i] - 'a');
                h1[i] %= mod;
        }
        for (int i = s.size() - 1; i >= 0; i --) {
                if (i == s.size() - 1) h2[i] = s[i] - 'a';
                else h2[i] = h2[i + 1] * base % mod + (s[i] - 'a');
                h2[i] %= mod;
        }

        // 开始分讨
        // AA
        if (s.size() % 2 == 0) {
                int l = 0, r = s.size() - 1;
                int mid = (l + r) >> 1;
                if (get1(l, mid) == get1(mid + 1, r)) {
                        cout << beg_s + 1 << " " << beg_s + mid + 1 << endl;
                        return 0;
                }
        }

        // PAA
        for (int i = 0; i < s.size(); i ++) {
                if (get1(0, i) == get2(0, i)) {
                        int l = i + 1, r = s.size() - 1;
                        if (r < l) continue;
                        if ((r - l + 1) & 1) continue;
                        int mid = (l + r) >> 1;
                        if (get1(l, mid) == get1(mid + 1, r)) {
                                cout << beg_s + 1 << " " << beg_s + mid + 1 << endl;
                                return 0;
                        }
                }
        }

        // AAP
        for (int i = s.size() - 1; i >= 0; i --) {
                if (get1(i, s.size() - 1) == get2(i, s.size() - 1)) {
                        int l = 0, r = i - 1;
                        if (r < l) continue;
                        if ((r - l + 1) & 1) continue;
                        int mid = (l + r) >> 1;
                        if (get1(l, mid) == get1(mid + 1, r)) {
                                cout << beg_s + mid + 1 + 1 << " " << beg_s + s.size() - 1 + 1 << endl;
                                return 0;
                        }
                }
        }

        // APA
        for (int i = s.size() / 2 - (s.size() % 2 == 0); i >= 0; i --) {
                if (s[i] != s[s.size() - i - 1]) break;
                if (get1(0, i - 1) == get1(s.size() - i, s.size() - 1)) {
                        cout << beg_s + 1 << " " << beg_s + i - 1 + 1 << endl;
                        return 0;
                }
        }

        cout << "-1 -1\n";
}

# HDUOJ1425_sort

# 🔗

http://acm.hdu.edu.cn/showproblem.php?pid=1425

# 💡

模板题

sort或堆排肯定超时（unordered_map也超时就离谱）
用hash表放位置
输入完即存完

输出时在范围内降序查找即可

# ✅

#pragma region
#pragma GCC optimize(3,"Ofast","inline")
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define eps 1e-6
#define PI acos(-1.0)
#define ll long long
#define INF 0x7FFFFFFF
#define Regal exit(0)
#define Chivas int main()
#define pb(x) push_back(x)
#define SP system("pause")
#define Max(a,b) ((a)>(b)?(a):(b))
#define Min(a,b) ((a)<(b)?(a):(b))
#define IOS ios::sync_with_stdio(false)
#define mm(a, b) memset(a, b, sizeof(a))
#define each_cass(cass) for (cin>>cass; cass; cass--)
#define test(a) cout << "---------" << a << "---------" << '\n'
 
using namespace std;
#pragma endregion

//全局变量
#pragma region
const int maxn = 1e6 + 10;
int mp[maxn];//存输入的某个数的个数
int n, m;
int vec[maxn];//存输入的数
#pragma endregion

//主体-------------------------------------------------------

Chivas{
   while(scanf("%d%d", &n, &m) == 2){

      for(int i = 0, x; i < n; i ++){
         scanf("%d", &vec[i]);
         mp[vec[i] + 500000]++;//"++"是因为可能重复输入，"+500000"是因为输入可能有负数
      }

      bool first_put = false;
      for(int i = 1000000; i >= 0; i--){
         while(m && mp[i]){
            if(first_put) printf(" %d",i - 500000);
            else          printf("%d", i - 500000), first_put = true;
            
            mp[i]--;
            m--;
         }
         if(!m) break;
      }
      printf("\n");
      

      for(int i = 0; i < n; i ++) mp[vec[i] + 500000] = 0;//清除

   }
   Regal;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

# HDUOJ1496_Equetions

# 🔗

http://acm.hdu.edu.cn/showproblem.php?pid=1496

# 💡

1.暴力存三重循环然后查最后一个是否存在
2.用大size存数组，直接把数放进下标内
3.用小size存数组，然后用除余存地址

# ✅

#pragma region
#pragma GCC optimize(3,"Ofast","inline")
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define eps 1e-6
#define PI acos(-1.0)
#define ll long long
#define INF 0x7FFFFFFF
#define Regal exit(0)
#define Chivas int main()
#define pb(x) push_back(x)
#define SP system("pause")
#define Max(a,b) ((a)>(b)?(a):(b))
#define Min(a,b) ((a)<(b)?(a):(b))
#define IOS ios::sync_with_stdio(false)
#define mm(a, b) memset(a, b, sizeof(a))
#define each_cass(cass) for (cin>>cass; cass; cass--)
#define test(a) cout << "---------" << a << "---------" << '\n'
 
using namespace std;
#pragma endregion

//全局变量
#pragma region
const int maxn_solve2 = 2e6 + 10;
const int maxn_solve3 = 5e4 + 10;//100 * 100 最多产生 10000 种可能性
int x[110];//打平方表
int num[maxn_solve3];//该地址存放元素个数
int val[maxn_solve3];//该地址存放的什么元素
int _hash[maxn_solve2];
int a, b, c, d;
#pragma endregion

//主体-------------------------------------------------------------------------

inline int Hash(int x){//除余选址
   int id = x % maxn_solve3;//第一步固定地址范围
   if(id < 0) id += maxn_solve3;//x可能为负数，负数除余出来的地址+maxn就为正了
   while(num[id] && val[id] != x) //前用作存入时的判断，后用于查找时的判断
      id = (id + 1) % maxn_solve3;//环式选址：后面的找不到就去前面找
   return id;
}

inline void solve_1(){
   for(int i = 0; i < 110; i ++) x[i] = i * i;
   while(scanf("%d%d%d%d", &a, &b, &c, &d) == 4){
      if((a > 0 && b > 0 && c > 0 && d > 0) || (a < 0 && b < 0 && c < 0 && d < 0)){
         printf("0\n");
         continue;
      }

      ll res = 0;

      for(int i = 1; i <= 100; i ++){
         for(int j = 1; j <= 100; j ++){
            for(int k = 1; k <= 100; k ++){
               int cur_s = x[i] * a + x[j] * b + x[k] * c;
               int end_be_mod = cur_s % d;
               int end_ans = ( - cur_s) / d;
               if(end_be_mod == 0 && end_ans <= 10000 && end_ans > 0 && (int)sqrt(end_ans) * (int)sqrt(end_ans) == end_ans) 
                  res ++;
            }
         }
      }

      printf("%lld\n", res * 16);
   }
}

inline void solve_2(){
   for(int i = 0; i < 110; i ++) x[i] = i * i;
   while(scanf("%d%d%d%d", &a, &b, &c, &d) == 4){
      if((a < 0 && b < 0 && c < 0 && d < 0) || (a > 0 && b > 0 && c > 0 && d > 0)){
         printf("0\n");
         continue;
      }

      mm(_hash, 0);

      //存入
      for(int i = 1; i <= 100; i ++){
         for(int j = 1; j <= 100; j ++){
            _hash[x[i] * a + x[j] * b + 1000000] ++;//防负数，所以 + 1000000
         }
      }

      ll res = 0;

      //统计
      for(int i = 1; i <= 100; i ++){
         for(int j = 1; j <= 100; j ++){
            res += _hash[ - (c * x[i] + d * x[j]) + 1000000];
         }
      }

      printf("%lld\n", res * 16);
   }
}

inline void solve_3(){
   for(int i = 0; i <= 100; i ++) x[i] = i * i;
   while(scanf("%d%d%d%d", &a, &b, &c, &d) == 4){
      if((a < 0 && b < 0 && c < 0 && d < 0) || (a > 0 && b > 0 && c > 0 && d > 0)){
         printf("0\n");//怎么都不可能为0
         continue;
      }
      mm(num, 0), mm(val, 0);

      //存入 a * x[1]^2 + b * x[2]^2的所有可能性
      for(int i = 1; i <= 100; i ++){
         for(int j = 1; j <= 100; j ++){
            int cur = x[i] * a + x[j] * b;
            int hash_cur = Hash(cur);
            val[hash_cur] = cur, num[hash_cur] ++;
         }
      }

      ll res = 0;

      for(int i = 1; i <= 100; i ++){
         for(int j = 1; j <= 100; j ++){
            int cur = - (x[i] * c + x[j] * d);//查找相反的
            int hash_cur = Hash(cur);
            res += num[hash_cur];//计算该位置存入多少个数
         }
      }

      printf("%lld\n", res * 16);//因为我们只找了[0, 100]，每一个都对称，所以要乘 2^4 = 16

   }
}

Chivas{
   Regal;
}

# HDUOJ4821_String

# 🔗

https://acm.hdu.edu.cn/showproblem.php?pid=4821

# 💡

我们可以考虑把一段 m * l 的子串分成 m 个 l 的子串
然后利用map统计不同的个数

但是我们发现，从 1 步进到 s.size() 明显时间过长，达到 O(n^2)
我们也能发现，这些串都是以 l 为周期进行的，也就是说我们在移动 l 次 1 后，将会锁定与第一次串同周期的区间
那么我们就只需外层遍历 1 ～ l，然后每一次遍历都要直接通道最后。
不同的 m * l 增一个后面的 l 区间，减一个前面的 l 区间，维护这 m * l 的不同l长子串个数

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long
#define INT __int128

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << endl

#define CHIVAS_ inline int MAIN()
#define _REGAL return 0;

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
//#define map unordered_map

#define pbb pair<bool, bool>
#define pii pair<int, int> 
#define pll pair<ll, ll>
#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cass = inputInt(); cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;
inline int inputInt(){int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);}
inline void outInt(int X){if(X<0) {putchar('-'); X=~(X-1);}int s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline ll inputLL(){ll X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1); }
inline void outLL(ll X){if(X<0) {putchar('-'); X=~(X-1);}ll s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}

template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return make_pair(MaxVal, MaxId);}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return make_pair(MinVal, MinId);}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return make_pair(MaxVal, MaxId);}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return make_pair(MinVal, MinId);}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return make_pair(cnt, div);}

namespace Solution_In_Codeforces{
        inline void solve();
        namespace N_cass {
                void Main(){ int cass; for ( cin >> cass; cass; cass -- ) { solve();} };
        }
        namespace One_cass {
                void Main(){ solve(); };
        }
}
inline void Solution_In_Codeforces::solve() {}





unordered_map<ull, int> mp;
int m, l; string s;


const int BASE = 31;
const int N = 1e5  +10;
class StringHash_Implement{
private:
        string s;
        ull HASH[N], amg[N];
public:
        inline StringHash_Implement ( string ss ) { s = ss; }
        inline void Init () {
                HASH[0] = s[0] - 'a';
                amg[0] = 1;
                for ( int i = 1; i < s.size(); i ++ ) {
                        HASH[i] = HASH[i - 1] * BASE + (ull)(s[i] - 'a');
                        amg[i] = amg[i - 1] * BASE;
                }
        }
        inline ull Get ( int l, int len ) {
                int r = l + len - 1;
                if ( l == 0 ) return HASH[r];
                return HASH[r] - HASH[l - 1] * amg[len];
        }
};

inline void Solve ( StringHash_Implement strHsh ) {
        int res = 0;
        for( int j = 0, lft = j, rgt = lft + m * l - 1; j < l && rgt < s.size(); j ++, lft = j, rgt = lft + m * l - 1 ) { // 锁定一下当前枚举的 m * l 的 lft 和 rgt 
                mp.clear();
                for ( int i = 0 ; i < m; i ++ ) mp[strHsh.Get(lft + i * l, l)] ++; // 先对这 m * l 存一下
                if ( mp.size() == m ) res ++;
                while ( rgt + l < s.size() ) { // 向后以 l 为单位地步进
                        lft += l, rgt += l;
                        
                        ull lose = strHsh.Get(lft - l, l);              //即将丢失的串
                        ull obtain = strHsh.Get(rgt - l + 1, l);        //即将获得的串
                        mp[lose] --;
                        if ( !mp[lose] ) mp.erase(lose);
                        mp[obtain] ++;

                        if ( mp.size() == m ) res ++;
                }
        }cout << res << endl;
}


CHIVAS_{
        while ( cin >> m >> l ) {
                cin >> s; 
                StringHash_Implement strHsh = StringHash_Implement(s);
                strHsh.Init(); Solve(strHsh);
        }
        _REGAL;
}









































int main(){

#ifndef ONLINE_JUDGE
freopen("in.in", "r", stdin);
freopen("out.out", "w", stdout);
#endif

        MAIN();

#ifndef ONLINE_JUDGE
cerr    << "\033[1m\033[31m\n" 
        << "\n\n===============================\n" 
        << "|| Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << " s. ||\n" 
        << "===============================" 
        << "\033[0m";
#endif

        exit(0);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208

# NCD2019E_AdnanAndTheBurnedDrivers

# 🔗

# 💡

题目暗示过回文串是正着读和反着读都一样的串
而这里也有改数一样的单点修改和区间查询
那么我们可以用字符串 $\inline Hash$ + 线段树

字符串 $\inline Hash$ 为一个正读 $\inline Hash$ 和一个反渎 $\inline Hash:s_2$ ，将这两个数组作为线段树数组

我们单点修改的时候也就是重启所有连接到这个点的段值，这个处理一个 $\inline pw$ 数组作为 $\inline base$ 的幂
一个修改中

s1[rt] = s1[rt << 1] * pw[r - mid] + s1[rt << 1 | 1] // 正读左边乘base的次数幂
s2[rt] = s2[rt << 1] + s2[rt << 1 | 1] * pw[mid - l + 1] // 反读右边乘base的次数幂

1
2

一个查询中，就和线段树一样要对于查询的段左子树查询右子树查询
和上面注释同理，这里也要正读反读各自乘幂

// 当然如果整个区间在左一半直接递归左半边即可，否则右半边
which ? ( Query ( l, mid, rt << 1, ql, mid, which ) + Query ( mid + 1, r, rt << 1 | 1, mid + 1, qr, which ) * pw[mid - ql + 1] ) % mod
      : ( Query ( l, mid, rt << 1, ql, mid, which ) * pw[qr - mid] + Query ( mid + 1, r, rt << 1 | 1, mid + 1, qr, which )) % mod; // which：0——正读，1——反读

1
2
3

这样操作下来，我们每次查询的时候如果这个段长是奇数，就差 $\inline [l,mid]$ 的正读和 $\inline [mid,r]$ 的反读
否则差 $\inline [l,mid-1]$ 的正和 $\inline [mid+1,r]$ 的反
比较这两个，如果一样的话就是回文

# ✅

const ll mod = 1e9 + 3;
const ll base = 131;
const ll N = 1e5 + 10;

ll n, m;
ll s1[N << 2], s2[N << 2];
char s[N];
ll pw[N];

inline void get_Pw () {
        pw[0] = 1;
        for ( ll i = 1; i < N; i ++ ) pw[i] = pw[i - 1] * base % mod;
}

inline void Update ( ll l, ll r, ll rt, ll id, ll c ) {
        if ( l == r ) {
                s1[rt] = s2[rt] = c;
                return;
        }

        ll mid = (l + r) >> 1;
        if ( id <= mid ) Update(l, mid, rt << 1, id, c);
        else             Update(mid + 1, r, rt << 1 | 1, id, c);
        s1[rt] = (s1[rt << 1] * pw[r - mid] + s1[rt << 1 | 1]) % mod;
        s2[rt] = (s2[rt << 1] + s2[rt << 1 | 1] * pw[mid - l + 1]) % mod;
}

inline ll Query ( ll l, ll r, ll rt, ll ql, ll qr, ll which ) { // 0:正，1:反
         if ( l == ql && r == qr ) return which? s2[rt] : s1[rt];
         ll mid = (l + r) >> 1;
         if ( qr <= mid ) return Query ( l, mid, rt << 1, ql, qr, which );
         else if ( ql > mid ) return Query ( mid + 1, r, rt << 1 | 1, ql, qr, which );
         else return which? ( Query ( l, mid, rt << 1, ql, mid, which ) + Query ( mid + 1, r, rt << 1 | 1, mid + 1, qr, which ) * pw[mid - ql + 1] ) % mod
                          : ( Query ( l, mid, rt << 1, ql, mid, which ) * pw[qr - mid] + Query ( mid + 1, r, rt << 1 | 1, mid + 1, qr, which )) % mod;
}

inline void Solve () {
        scanf("%lld%lld", &n, &m);
        getchar();
        scanf("%s", s + 1);
        for ( ll i = 1; i <= n; i ++ ) Update(1, n, 1, i, s[i]);
        while ( m -- ) {
                ll op; scanf("%lld", &op);
                if ( op == 1 ) {
                        ll id; scanf("%lld", &id); 
                        getchar();
                        char c; scanf("%c", &c);
                        Update ( 1, n, 1, id, c );

                        s[id] = c;
                } else {
                        ll l, r; scanf("%lld%lld", &l, &r);
                        ll mid = (l + r) >> 1;
                        if ( l == r ) {
                                puts("Adnan Wins");
                        } else if ( (r - l + 1) & 1 ) {
                                puts(Query(1, n, 1, l, mid - 1, 0) == Query(1, n, 1, mid + 1, r, 1) ? "Adnan Wins" : "ARCNCD!");
                        } else {
                                puts(Query(1, n, 1, l, mid, 0) == Query(1, n, 1, mid + 1, r, 1) ? "Adnan Wins" : "ARCNCD!");
                        }
                }
        }
}

int main () {
        get_Pw();
        ll cass; scanf("%lld", &cass); while ( cass -- ) {
                Solve ();
        }
}

# 康托展开

# HDUOJ1027_IgnatiusAndThePrincess2

# 🔗

http://acm.hdu.edu.cn/showproblem.php?pid=1027

# 💡

康托逆展开的模板题，需牢记

# ✅

#pragma region
//#pragma GCC optimize(3,"Ofast","inline")
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define eps 1e-6
#define PI acos(-1.0)
#define ll long long
#define INF 0x7FFFFFFF
#define Regal exit(0)
#define Chivas int main()
#define pb(x) push_back(x)
#define SP system("pause")
#define Max(a,b) ((a)>(b)?(a):(b))
#define Min(a,b) ((a)<(b)?(a):(b))
#define IOS ios::sync_with_stdio(false)
#define mm(a, b) memset(a, b, sizeof(a))
#define each_cass(cass) for (cin>>cass; cass; cass--)
#define test(a) cout << "---------" << a << "---------" << '\n'
 
using namespace std;
 
#pragma endregion

//全局变量
#pragma region
int n, m;
vector<int> f;//存阶乘
vector<int> vec;//存当前有多少个数可取（升序）
#pragma endregion

//主体----------------------------------------------------------------------------

void Jie_Cheng(){
    f.push_back(1);
    f.push_back(1);
    for(int i = 2; i < 13; i ++){
        f.push_back(f.back() * i);
    }
}

void Rev_Kangtuo(){
    vector<int> res;
    m --;
    for(int i = 1; i <= n; i ++){
        int id;
        if(n - i > 10) id = 0;//f[n - i]过大，m / f[n - i] = 0， m % f[n - i] = m，没必要
        else           id = m / f[n - i], m %= f[n - i];//加入第除数个，余数接着用
        res.push_back(vec[id]);
        vec.erase(vec.begin() + id);//删去
    }

    for(int i = 0; i < res.size(); i ++){
        printf("%d%c", res[i], i == res.size() - 1 ? '\n' : ' ');
    }
}

Chivas{
    Jie_Cheng();
    while(scanf("%d%d", &n, &m) == 2){
        vec.clear();
        for(int i = 1; i <= n; i ++) vec.push_back(i);
        Rev_Kangtuo();
    }
    Regal;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76

主席树链表