线段树
Chivas-Regal
#
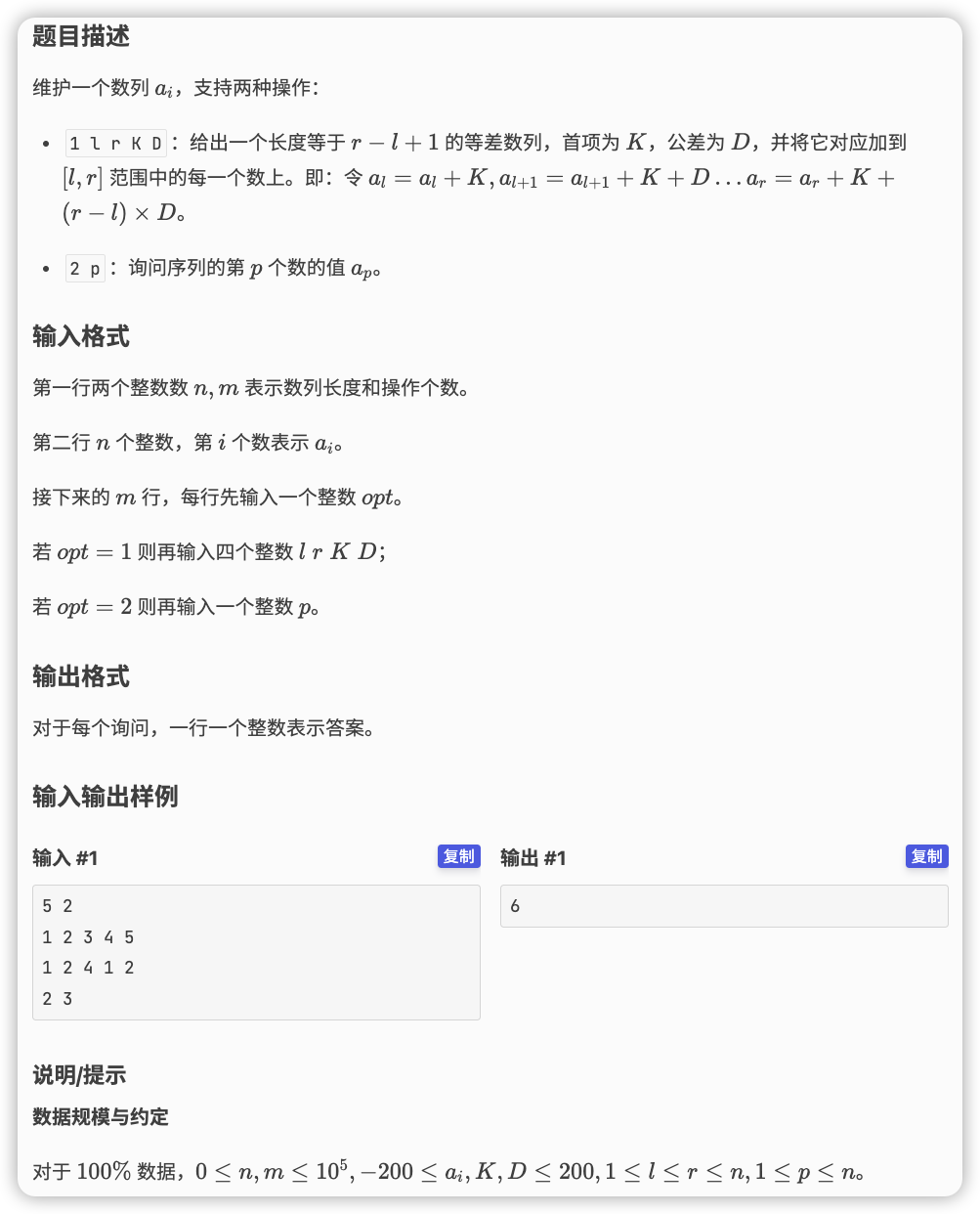
# 洛谷P1438_无聊的数列
# 🔗
# 💡
区间加等差数列的问题，既然等差，也就是等差分
所以线段树转化为差分数组，在每次区间修改时，将 的位置上都加上 ，然后在 的位置上加上 ，在 的位置上减去
查询的时候就是查 的和，也就是差分的前缀和等于位置上的数值
# ✅
const int N = 1e5 + 10;
int n, m;
int a[N], d[N];
struct node {
ll sum;
ll lazy;
} t[N << 2];
inline void pushup (int rt) {
t[rt].sum = t[rt << 1].sum + t[rt << 1 | 1].sum;
}
inline void pushdown (int l, int r, int rt) {
if (!t[rt].lazy) return;
int mid = (l + r) >> 1;
t[rt << 1].sum += t[rt].lazy * (1ll * mid - l + 1);
t[rt << 1 | 1].sum += t[rt].lazy * (1ll * r - mid);
t[rt << 1].lazy += t[rt].lazy;
t[rt << 1 | 1].lazy += t[rt].lazy;
t[rt].lazy = 0;
}
inline void build (int l = 1, int r = n, int rt = 1) {
t[rt].lazy = 0;
if (l == r) {
t[rt].sum = d[l];
return;
}
int mid = (l + r) >> 1;
build(l, mid, rt << 1);
build(mid + 1, r, rt << 1 | 1);
pushup(rt);
}
inline void update (int a, int b, int c, int l = 1, int r = n, int rt = 1) {
if (a <= l && r <= b) {
t[rt].sum += (1ll * r - l + 1) * 1ll * c;
t[rt].lazy += c;
return;
}
pushdown(l, r, rt);
int mid = (l + r) >> 1;
if (a <= mid) update(a, b, c, l, mid, rt << 1);
if (b > mid) update(a, b, c, mid + 1, r, rt << 1 | 1);
pushup(rt);
}
inline ll query (int a, int b, int l = 1, int r = n, int rt = 1) {
if (a <= l && r <= b) return t[rt].sum;
pushdown(l, r, rt);
int mid = (l + r) >> 1;
ll res = 0;
if (a <= mid) res += query(a, b, l, mid, rt << 1);
if (b > mid) res += query(a, b, mid + 1, r, rt << 1 | 1);
return res;
}
int main () {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= n; i ++) cin >> a[i];
for (int i = 1; i <= n; i ++) d[i] = a[i] - a[i - 1];
build();
while (m --) {
int op; cin >> op;
if (op == 1) {
int l, r, k, d; cin >> l >> r >> k >> d;
update(l, l, k);
if (l + 1 <= r) update(l + 1, r, d);
if (r + 1 <= n) update(r + 1, r + 1, -k - (r - l) * d);
} else {
int p; cin >> p;
cout << query(1, p) << endl;
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
# 洛谷P1471_方差
# 🔗
# 💡
首先是区间修改的操作 这个括号放在一起很难处理，考虑将它们独立出来为
同理区间查询方差时提出来为
这样需要的信息就很明显了，一个区间和 一个区间平方和
平方和修改时需要用修改前的区间和为
区间和就正常修改
然后查询时要用区间和求出平均数 ，然后按上面拆出来的内容求 即可
# ✅
const int N = 1e5 + 10;
int n, m;
double a[N];
struct node {
double sum, sum2;
double lazy;
} t[N << 2];
inline void pushup (int rt) {
t[rt].sum = t[rt << 1].sum + t[rt << 1 | 1].sum;
t[rt].sum2 = t[rt << 1].sum2 + t[rt << 1 | 1].sum2;
}
inline void pushdown (int l, int r, int rt) {
if (!t[rt].lazy) return;
int mid = (l + r) >> 1;
t[rt << 1].sum2 += 2 * t[rt].lazy * t[rt << 1].sum + (mid - l + 1) * t[rt].lazy * t[rt].lazy;
t[rt << 1 | 1].sum2 += 2 * t[rt].lazy * t[rt << 1 | 1].sum + (r - mid) * t[rt].lazy * t[rt].lazy;
t[rt << 1].sum += t[rt].lazy * (1ll * mid - l + 1);
t[rt << 1 | 1].sum += t[rt].lazy * (1ll * r - mid);
t[rt << 1].lazy += t[rt].lazy;
t[rt << 1 | 1].lazy += t[rt].lazy;
t[rt].lazy = 0;
}
inline void build (int l = 1, int r = n, int rt = 1) {
t[rt].lazy = 0;
if (l == r) {
t[rt].sum = a[l];
t[rt].sum2 = a[l] * a[l];
return;
}
int mid = (l + r) >> 1;
build(l, mid, rt << 1);
build(mid + 1, r, rt << 1 | 1);
pushup(rt);
}
inline void update (int a, int b, double c, int l = 1, int r = n, int rt = 1) {
if (a <= l && r <= b) {
t[rt].sum2 += 2.0 * c * t[rt].sum + c * c * (r - l + 1);
t[rt].sum += c * (r - l + 1);
t[rt].lazy += c;
return;
}
pushdown(l, r, rt);
int mid = (l + r) >> 1;
if (a <= mid) update(a, b, c, l, mid, rt << 1);
if (b > mid) update(a, b, c, mid + 1, r, rt << 1 | 1);
pushup(rt);
}
inline double query (int a, int b, int l = 1, int r = n, int rt = 1) {
if (a <= l && r <= b) return t[rt].sum;
pushdown(l, r, rt);
int mid = (l + r) >> 1;
double res = 0;
if (a <= mid) res += query(a, b, l, mid, rt << 1);
if (b > mid) res += query(a, b, mid + 1, r, rt << 1 | 1);
return res;
}
inline double query2 (int a, int b, int l = 1, int r = n, int rt = 1) {
if (a <= l && r <= b) return t[rt].sum2;
pushdown(l, r, rt);
int mid = (l + r) >> 1;
double res = 0;
if (a <= mid) res += query2(a, b, l, mid, rt << 1);
if (b > mid) res += query2(a, b, mid + 1, r, rt << 1 | 1);
return res;
}
int main () {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++) scanf("%lf", &a[i]);
build();
while (m --) {
int op; scanf("%d", &op);
if (op == 1) {
int x, y; scanf("%d%d", &x, &y);
double k; scanf("%lf", &k);
update(x, y, k);
} else if (op == 2) {
int x, y; scanf("%d%d", &x, &y);
printf("%.4f\n", query(x, y) / (y - x + 1));
} else {
int x, y; scanf("%d%d", &x, &y);
double q1 = query(x, y);
double q2 = query2(x, y);
double ave = q1 / (y - x + 1);
printf("%.4f\n", (q2 - 2.0 * ave * q1 + ave * ave * (y - x + 1)) / (y - x + 1));
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
# 洛谷P2216_理想正方形
# 🔗
# 💡
转化成对于一个 的 问题为：查询行区间为 且列区间为 的最大值与最小值
可以预处理存 个区间数据结构，每个数据结构都能查找 的最大值最小值信息，其实就是存每一列的信息
注意到这个预处理即可，因为后面只有读取没有更改，那么就用 表，这样后期可以 地查询
然后对于每一行 ，都先设置这一行的所有元素，第 个元素表示第 列区间 的最大值和最小值
对于这一行的每一列 用另一个数据结构区间查询 的最小值最大值，即为这一个 正方形的最小值最大值
一个变量维护其的最小差值即可
# ✅
const int N = 1003;
const int M = N * N;
int a, b, n;
int res[N][N];
int g[N][N];
int RES = 0x3f3f3f3f;
struct ST_Table {
int mx, mn;
} st[N][N][10];
inline void Init () {
int k = 32 - __builtin_clz(a) - 1;
for (int l = 1; l <= b; l ++) {
for (int i = 1; i <= a; i ++) st[l][i][0] = {g[i][l], g[i][l]};
for (int j = 1; j <= k; j ++) {
for (int i = 1; i + (1 << j) - 1 <= a; i ++) {
st[l][i][j].mx = max(st[l][i][j - 1].mx, st[l][i + (1 << (j - 1))][j - 1].mx);
st[l][i][j].mn = min(st[l][i][j - 1].mn, st[l][i + (1 << (j - 1))][j - 1].mn);
}
}
}
}
inline int max_inCol (int l, int r, int col) {
int k = 32 - __builtin_clz(r - l + 1) - 1;
return max(st[col][l][k].mx, st[col][r - (1 << k) + 1][k].mx);
}
inline int min_inCol (int l, int r, int col) {
int k = 32 - __builtin_clz(r - l + 1) - 1;
return min(st[col][l][k].mn, st[col][r - (1 << k) + 1][k].mn);
}
struct SqrtTree {
int mx, mn;
} tr[N << 2];
inline void pushUp_Row (int rt) {
tr[rt].mn = min(tr[rt << 1].mn, tr[rt << 1 | 1].mn);
tr[rt].mx = max(tr[rt << 1].mx, tr[rt << 1 | 1].mx);
}
inline void Update_Row (int id, int mx, int mn, int l, int r, int rt) {
if (l == id && id == r) {
tr[rt] = {mx, mn};
return;
}
int mid = (l + r) >> 1;
if (id <= mid) Update_Row(id, mx, mn, l, mid, rt << 1);
else Update_Row(id, mx, mn, mid + 1, r, rt << 1 | 1);
pushUp_Row(rt);
}
inline int Query_max_Row (int a, int b, int l, int r, int rt) {
if (a <= l && r <= b) return tr[rt].mx;
else if (r < a || b < l) return 0;
int mid = (l + r) >> 1;
int res = 0;
if (a <= mid) res = max(res, Query_max_Row(a, b, l, mid, rt << 1));
if (mid <= b) res = max(res, Query_max_Row(a, b, mid + 1, r, rt << 1 | 1));
return res;
}
inline int Query_min_Row (int a, int b, int l, int r, int rt) {
if (a <= l && r <= b) return tr[rt].mn;
else if (r < a || b < l) return 0x3f3f3f3f;
int mid = (l + r) >> 1;
int res = 0x3f3f3f3f;
if (a <= mid) res = min(res, Query_min_Row(a, b, l, mid, rt << 1));
if (mid <= b) res = min(res, Query_min_Row(a, b, mid + 1, r, rt << 1 | 1));
return res;
}
int main () {
scanf("%d%d%d", &a, &b, &n);
for (int i = 1; i <= a; i ++)
for (int j = 1; j <= b; j ++)
scanf("%d", &g[i][j]);
Init();
for (int i = n; i <= a; i ++) {
for (int j = 1; j <= b; j ++) {
Update_Row(j, max_inCol(i - n + 1, i, j), min_inCol(i - n + 1, i, j), 1, b, 1);
if (j >= n)
RES = min(RES, Query_max_Row(j - n + 1, j, 1, b, 1) - Query_min_Row(j - n + 1, j, 1, b, 1));
}
}
printf("%d\n", RES);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
# 洛谷P2824_排序
# 🔗
# 💡
这个数有点多，缩小一下问题：看一下 串是怎么样排序的
对 升序排序，我们假设其中 的个数有 个，那么排序后 全部是 ， 全部是
对 降序排序，我们假设其中 的个数有 个，那么排序后 全部是 ， 全部是
这个可以利用线段树区间更新去解决
那么回到这个问题，这个问题数有点多，我们可以通过设置一个分界线 来让问题变成 的，即 为 否则为
那么这就是一个二分答案了
二分这个分界线，看排到最后 位置上是否为 即可
# ✅
const int N = 1e5 + 10;
struct node { int op, l, r; };
vector<node> ope;
vector<int> a, s;
int n, m, p;
struct SegmentTree {
int cnt, make;
} t[N << 2];
inline void pushUp (int rt) {
t[rt].cnt = t[rt << 1].cnt + t[rt << 1 | 1].cnt;
}
inline void pushDown (int l, int r, int rt) {
if (!t[rt].make) return;
int mid = (l + r) >> 1;
t[rt << 1].make = t[rt << 1 | 1].make = t[rt].make;
if (t[rt].make == 1) {
t[rt << 1].cnt = mid - l + 1, t[rt << 1 | 1].cnt = r - mid;
} else {
t[rt << 1].cnt = t[rt << 1 | 1].cnt = 0;
}
t[rt].make = 0;
}
inline void Build (int l, int r, int rt) {
t[rt] = {0, 0};
if (l == r) {
t[rt].cnt = s[l] == 1;
return;
}
int mid = (l + r) >> 1;
Build(l, mid, rt << 1);
Build(mid + 1, r, rt << 1 | 1);
pushUp(rt);
}
inline void Update (int a, int b, int l, int r, int rt, int make) {
if (a > r || l > b) return;
if (a <= l && r <= b) {
t[rt].cnt = make * (r - l + 1);
t[rt].make = make ? 1 : -1;
return;
}
int mid = (l + r) >> 1;
pushDown(l, r, rt);
Update(a, b, l, mid, rt << 1, make);
Update(a, b, mid + 1, r, rt << 1 | 1, make);
pushUp(rt);
}
inline int Query (int a, int b, int l, int r, int rt) {
if (a > r || l > b) return 0;
if (a <= l && r <= b) return t[rt].cnt;
int mid = (l + r) >> 1;
pushDown(l, r, rt);
return Query(a, b, l, mid, rt << 1) + Query(a, b, mid + 1, r, rt << 1 | 1);
}
inline bool Check (int x) {
for (int i = 1; i <= n; i ++) s[i] = a[i] >= x;
Build(1, n, 1);
for (auto [op, l, r] : ope) {
int cnt = Query(l, r, 1, n, 1);
if (op == 0) {
Update(l, r - cnt, 1, n, 1, 0);
Update(r - cnt + 1, r, 1, n, 1, 1);
} else {
Update(l, l + cnt - 1, 1, n, 1, 1);
Update(l + cnt, r, 1, n, 1, 0);
}
}
return Query(p, p, 1, n, 1);
}
int main () {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
ope.resize(m); a.resize(n + 1); s.resize(n + 1);
for (int i = 1; i <= n; i ++) cin >> a[i];
for (auto &[op, l, r] : ope) cin >> op >> l >> r;
cin >> p;
int l = 1, r = n, res = 1;
while (l <= r) {
int mid = (l + r) >> 1;
if (Check(mid)) res = mid, l = mid + 1;
else r = mid - 1;
}
cout << res << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
# 洛谷P6327_区间加区间sin和
# 🔗
# 💡
首先看修改，对 加
可以想到和差化积
我们可以看到每次会用到两个值 和
，那么我们线段树维护这两个就行了
可以发现修改也是可以在原有基础上进行 和
的乘法分配律的
所以我们可以正常 维护加的
# ✅
#### include <iostream>
#### include <algorithm>
#### include <cstring>
#### include <vector>
#### include <map>
#### include <cmath>
#### define ll long long
using namespace std;
const int N = 2e5 + 10;
int a[N], n, m;
struct Sgtr {
double sine, cosi;
ll lazy;
}sgtr[N << 2];
inline void Calc ( double &sumsin, double &sumcos, ll x ) {
double tmp_sumsin = sumsin;
double tmp_sumcos = sumcos;
double sinx = sin(x);
double cosx = cos(x);
sumsin = tmp_sumsin * cosx + tmp_sumcos * sinx;
sumcos = tmp_sumcos * cosx - tmp_sumsin * sinx;
}
inline void PushUp ( int rt ) {
sgtr[rt].sine = sgtr[rt << 1].sine + sgtr[rt << 1 | 1].sine;
sgtr[rt].cosi = sgtr[rt << 1].cosi + sgtr[rt << 1 | 1].cosi;
}
inline void PushDown ( int l, int r, int rt ) {
if (!sgtr[rt].lazy) return;
sgtr[rt << 1].lazy += sgtr[rt].lazy;
sgtr[rt << 1 | 1].lazy += sgtr[rt].lazy;
Calc (sgtr[rt << 1].sine, sgtr[rt << 1].cosi, sgtr[rt].lazy);
Calc (sgtr[rt << 1 | 1].sine, sgtr[rt << 1 | 1].cosi, sgtr[rt].lazy);
sgtr[rt].lazy = 0;
}
inline void Build ( int l = 1, int r = n, int rt = 1 ) {
sgtr[rt].lazy = 0;
if (l == r) {
sgtr[rt].cosi = cos(a[l]);
sgtr[rt].sine = sin(a[l]);
return;
}
int mid = (l + r) >> 1;
Build (l, mid, rt << 1);
Build (mid + 1, r, rt << 1 | 1);
PushUp (rt);
}
inline void Update ( int a, int b, ll c, int l = 1, int r = n, int rt = 1 ) {
if (a <= l && r <= b) {
sgtr[rt].lazy += c;
Calc (sgtr[rt].sine, sgtr[rt].cosi, c);
return;
}
if (a > r || b < l) return;
int mid = (l + r) >> 1;
PushDown (l, r, rt);
Update (a, b, c, l, mid, rt << 1);
Update (a, b, c, mid + 1, r, rt << 1 | 1);
PushUp (rt);
}
inline double Query ( int a, int b, int l = 1, int r = n, int rt = 1 ) {
if (a <= l && r <= b) return sgtr[rt].sine;
if (a > r || b < l) return 0;
PushDown (l, r, rt);
int mid = (l + r) >> 1;
return Query (a, b, l, mid, rt << 1) + Query (a, b, mid + 1, r, rt << 1 | 1);
}
int main () {
scanf("%d", &n);
for ( int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
scanf("%d", &m);
Build();
while ( m -- ) {
int op; scanf("%d", &op);
if ( op == 1 ) {
int l, r, v; scanf("%d%d%d", &l, &r, &v);
Update (l, r, v);
} else {
int l, r; scanf("%d%d", &l, &r);
printf("%.1f\n", Query(l, r));
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
# 洛谷P7244_章节划分
# 🔗
# 💡
由于全局最大值一定在贡献中，所以答案一定是全局最大值的约数
枚举约数 ，如果当前 的最大划分区间数量超过 ，那么是可以通过合并区间来缩小的
所以当前就是看 的最大划分区间数量是否能超过
在这种区间中作为最值的问题，首先要处理出来每个位置可以作为最大值的最左侧点，也就是找到左侧第一个比它大的点 （通过单调栈来实现）
要求最大的划分，这种属于类似于最长子序列类型的
令 表示到第 个位置可以划分的最多段数（要满足每一段最大值是 的倍数）
则若 说明它可以作为一个新段的最大值，则
若 ，说明它不可以作为新段的最大值，需要前面与前面比它大的连接成为同一段得到保佑，则
而起始则是
要注意到一个点，就是 且 且 ，说明它无法从 转移过来，并且前面也没有已经被划分的段，这就意味着它自己是抽不动前面的，故 。换句话说，从可以 位置转移为 的位置必须满足它可以从 位置开始自成一段。
这在一个 里面就是一个 的算法，需要优化
我们求的是 ，单单一个区间最大值，拿线段树优化完事儿
# ✅
const int N = 1e6 + 10;
int n, k;
int a[N], mxa;
int l[N];
int t[N << 2];
inline void pushup (int rt) {
t[rt] = max(t[rt << 1], t[rt << 1 | 1]);
}
inline void update (int id, int c, int l = 0, int r = n, int rt = 1) {
if (l == r) {
t[rt] = c;
return;
}
int mid = (l + r) >> 1;
if (id <= mid) update(id, c, l, mid, rt << 1);
else update(id, c, mid + 1, r, rt << 1 | 1);
pushup(rt);
}
inline int query (int a, int b, int l = 0, int r = n, int rt = 1) {
if (a <= l && r <= b) return t[rt];
int mid = (l + r) >> 1;
int res = 0;
if (a <= mid) res = max(res, query(a, b, l, mid, rt << 1));
if (b > mid) res = max(res, query(a, b, mid + 1, r, rt << 1 | 1));
return res;
}
inline int max_Sep (int x) {
update(0, 0, 0);
for (int i = 1; i <= n; i ++) {
if (a[i] % x == 0) {
if (l[i] != 0 && query(l[i], i - 1) == 0) update(i, 0); // 被孤立了
else update(i, query(l[i], i - 1) + 1); // 跨越一下
} else {
update(i, query(l[i], l[i])); // 与左边比自己大的放在一段里面
}
}
return query(n, n);
}
int num_mul[N]; // 因数 x 在全局中有几个位置出现了
int main () {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> k;
for (int i = 1; i <= n ;i ++)
cin >> a[i],
mxa = max(mxa, a[i]);
stack<int> stk;
stk = stack<int>();
for (int i = 1; i <= n; i ++) {
while (!stk.empty() && a[stk.top()] <= a[i]) stk.pop();
l[i] = stk.size() ? stk.top() : 0;
stk.push(i);
}
vector<int> div; // 最大值因数
for (int i = 1; i * i <= mxa; i ++) {
if (mxa % i == 0) {
div.push_back(i);
for (int j = 1; j <= n; j ++) if (a[j] % i == 0) num_mul[i] ++;
if (i * i == mxa) continue;
div.push_back(mxa / i);
for (int j = 1; j <= n; j ++) if (a[j] % (mxa / i) == 0) num_mul[mxa / i] ++;
}
}
sort(div.begin(), div.end(), greater<int>());
for (int it : div) {
if (num_mul[it] >= k && max_Sep(it) >= k) {
cout << it << endl;
return 0;
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
# 洛谷T225362_《山茶文具店》
# 🔗
# 💡
在一寒假见了三次线段树维护进制的题且看了《山茶文具店》强烈推荐下
决定出了这样一道最基础写法的题
这道题考的是是否完全弄明白了线段树的结构
对于一个掌管区间 的节点，它的左右子节点掌管的区间分别为 ,
考虑到一个数内，左侧的数位要高于右侧的数位，且从左到右数位是一个下降的阶梯
那么对于这个左右子区间，左侧的区间阶梯要完整的比右侧的区间阶梯高出 层
由于一层对应的是 ，那么 层对应的是
那么在线段树中层层向上便是
在查询的时候我们也应当考虑是否会出现右侧没有数但是我们依旧让左侧台阶往上走很高的情况
就可以采用区间压缩
inline ll Query ( ll a, ll b, ll l, ll r, ll rt ) {
if ( a > r || b < l ) return 0;
if ( l == a && r == b ) return sgtr[rt].val;
ll mid = (l + r) >> 1;
if ( b <= mid ) // 向左压缩
return Query ( a, b, l, mid, rt << 1 );
else if ( a > mid ) // 向右压缩
return Query ( a, b, mid + 1, r, rt << 1 | 1 );
else // 向中间压缩
return Query ( a, mid, l, mid, rt << 1 ) * ksm(10, b - mid) + Query ( mid + 1, b, mid + 1, r, rt << 1 | 1 );
}
1
2
3
4
5
6
7
8
9
10
11
2
3
4
5
6
7
8
9
10
11
注意对递归出口也就是线段树的叶子节点要赋值
毕竟它可没有儿子节点
# ✅
namespace SegmentTree_Num {
ll s[N << 2];
inline ll ksm ( ll a, ll b ) { ll res = 1; while ( b ) { if ( b & 1 ) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline void Build ( ll l, ll r, ll rt ) {
if ( l == r ) {
s[rt] = a[l];
return;
}
int mid = (l + r) >> 1;
Build(l, mid, rt << 1);
Build(mid + 1, r, rt << 1 | 1);
s[rt] = (s[rt << 1] * ksm(10, r - mid) % mod + s[rt << 1 | 1]) % mod;
}
inline void Update ( ll id, ll c, ll l, ll r, ll rt ) {
if ( l > id || r < id ) return;
if ( id == l && r == id ) {
s[rt] = c;
return;
}
ll mid = (l + r) >> 1;
Update(id, c, l, mid, rt << 1);
Update(id, c, mid + 1, r, rt << 1 | 1);
s[rt] = (s[rt << 1] * ksm(10, r - mid) % mod + s[rt << 1 | 1]) % mod;
}
inline ll Query ( ll a, ll b, ll l, ll r, ll rt ) { // 区间压缩的理解下面的题有说
if ( a > r || b < l ) return 0;
if ( l == a && r == b ) return s[rt];
ll mid = (l + r) >> 1;
if ( b <= mid ) return Query ( a, b, l, mid, rt << 1 );
else if ( a > mid ) return Query ( a, b, mid + 1, r, rt << 1 | 1 );
else return (Query ( a, mid, l, mid, rt << 1 ) * ksm(10, b - mid) % mod + Query ( mid + 1, b, mid + 1, r, rt << 1 | 1 )) % mod;
}
}
int main () {
ios::sync_with_stdio(false);
cin >> n >> q;
string s; cin >> s; for ( ll i = 1; i <= n; i ++ ) a[i] = s[i - 1] - '0';
SegmentTree_Num::Build(1, n, 1);
while ( q -- ) {
ll op, x, y; cin >> op >> x >> y;
if ( op == 1 ) {
SegmentTree_Num::Update(x, y, 1, n, 1);
} else {
cout << SegmentTree_Num::Query(x, y, 1, n, 1) << endl;
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
# 牛客2022寒假算法基础集训营4B_进制
# 🔗
# 💡
正解很好想，就是找出区间中最大的数，我们利用的进制就是 mx + 1
问题在于快速求进制和快速求
两个线段树即可
一个区间 一个区间求大数
令 为 进制的线段树数组
那么向上更新时便是左子树多乘进制套着右子树向上走
# ✅
const ll N = 1e5 + 10;
const ll mod = 1e9 + 7;
ll a[N], n, q;
namespace SegmentTree_Max {
ll sgtr[N << 2];
inline void push_Up ( ll rt ) {
sgtr[rt] = max ( sgtr[rt << 1], sgtr[rt << 1 | 1] );
}
inline void Build ( ll l, ll r, ll rt ) {
if ( l == r ) { sgtr[rt] = a[l]; return; }
ll mid = (l + r) >> 1;
Build ( l, mid, rt << 1 );
Build ( mid + 1, r, rt << 1 | 1 );
push_Up ( rt );
}
inline void Update ( ll id, ll c, ll l, ll r, ll rt ) {
if ( l > id || r < id ) return;
if ( l == id && r == id ) { sgtr[rt] = c; return; }
ll mid = (l + r) >> 1;
Update ( id, c, l, mid, rt << 1 );
Update ( id, c, mid + 1, r, rt << 1 | 1 );
push_Up ( rt );
}
inline ll Query ( ll a, ll b, ll l, ll r, ll rt ) {
if ( a <= l && r <= b ) return sgtr[rt];
if ( a > r || b < l ) return 0;
ll mid = (l + r) >> 1;
return max ( Query ( a, b, l, mid, rt << 1 ), Query ( a, b, mid + 1, r, rt << 1 | 1) );
}
}
namespace SegmentTree_Num {
ll s[15][N << 2];
inline ll ksm ( ll a, ll b ) { ll res = 1; while ( b ) { if ( b & 1 ) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline void Build ( ll l, ll r, ll rt ) {
if ( l == r ) {
for ( int i = 2; i <= 10; i ++ )
s[i][rt] = a[l];
return;
}
int mid = (l + r) >> 1;
Build(l, mid, rt << 1);
Build(mid + 1, r, rt << 1 | 1);
for ( int i = 2; i <= 10; i ++ )
s[i][rt] = (s[i][rt << 1] * ksm(i, r - mid) % mod + s[i][rt << 1 | 1]) % mod;
}
inline void Update ( ll id, ll c, ll l, ll r, ll rt ) {
if ( l > id || r < id ) return;
if ( id == l && r == id ) {
for ( int i = 2; i <= 10; i ++ )
s[i][rt] = c;
return;
}
ll mid = (l + r) >> 1;
Update(id, c, l, mid, rt << 1);
Update(id, c, mid + 1, r, rt << 1 | 1);
for ( int i = 2; i <= 10; i ++ )
s[i][rt] = (s[i][rt << 1] * ksm(i, r - mid) % mod + s[i][rt << 1 | 1]) % mod;
}
inline ll Query ( ll a, ll b, ll l, ll r, ll rt, ll bs ) { // 区间压缩的理解下面的题有说
if ( a > r || b < l ) return 0;
if ( l == a && r == b ) return s[bs][rt];
ll mid = (l + r) >> 1;
if ( b <= mid ) return Query ( a, b, l, mid, rt << 1, bs );
else if ( a > mid ) return Query ( a, b, mid + 1, r, rt << 1 | 1, bs );
else return (Query ( a, mid, l, mid, rt << 1, bs ) * ksm(bs, b - mid) % mod + Query ( mid + 1, b, mid + 1, r, rt << 1 | 1, bs )) % mod;
}
}
int main () {
ios::sync_with_stdio(false);
cin >> n >> q;
string s; cin >> s; for ( ll i = 1; i <= n; i ++ ) a[i] = s[i - 1] - '0';
SegmentTree_Max::Build(1, n, 1);
SegmentTree_Num::Build(1, n, 1);
while ( q -- ) {
ll op, x, y; cin >> op >> x >> y;
if ( op == 1 ) {
SegmentTree_Num::Update(x, y, 1, n, 1);
SegmentTree_Max::Update(x, y, 1, n, 1);
} else {
int mx = SegmentTree_Max::Query(x, y, 1, n, 1);
cout << SegmentTree_Num::Query(x, y, 1, n, 1, mx + 1) << endl;
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
# 牛客2022寒假算法基础集训营4G_子序列权值乘积
# 🔗
# 💡
考虑每个数作为 和 出现的次数
作为
对于 ，我们应当找左侧 的数和右侧 的数，但是我们要考虑在相同的数 ，从 抽取子序列和从 抽取子序列会有重复的情况
所以我们右侧找 的数的个数
左侧个数设为 ，右侧个数设为
那么左侧有 个选择方式
右侧有 个选择方式
总共就有 个选择方式
对答案的贡献即为
作为 同理
在找左侧右侧个数的时候我们可以利用权值线段树一边扫描一边实时统计
本题纯组合数学解法请看这里 (opens new window)
# ✅
const int N = 2e5 + 10;
ll a[N], n, b[N];
vector<ll> nums;
const ll mod = 1e9 + 7;
const ll powmod = 1e9 + 6;
inline ll ksm ( ll a, ll b, ll mod = 1e9 + 7 ) { ll res = 1; while ( b > 0 ) { if ( b & 1 ) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
ll t[N << 2];
inline void PushUp ( int rt ) {
t[rt] = t[rt << 1] + t[rt << 1 | 1];
}
inline void Update ( int id, int c = 1, int l = 1, int r = n + 1, int rt = 1 ) {
if ( l > id || id > r ) return;
if ( l == r && l == id ) {
t[rt] += c;
return;
}
int mid = (l + r) >> 1;
Update(id, c, l, mid, rt << 1);
Update(id, c, mid + 1, r, rt << 1 | 1);
PushUp(rt);
}
inline ll Query ( int a, int b, int l = 1, int r = n + 1, int rt = 1 ) {
if ( r < a || b < l ) return 0;
if ( a <= l && r <= b ) return t[rt];
int mid = ( l + r ) >> 1;
return Query(a, b, l, mid, rt << 1) + Query(a, b, mid + 1, r, rt << 1 | 1);
}
int l[N], r[N];
inline ll Calc1 () {
memset(t, 0, sizeof t);
for ( int i = 0; i < n; i ++ ) {
l[i] = Query(1, b[i]);
Update(b[i]);
}
memset(t, 0, sizeof t);
for ( int i = n - 1; i >= 0; i -- ) {
r[i] = Query(1, b[i] - 1);
Update(b[i]);
}
ll res = 1;
for ( int i = 0; i < n; i ++ ) {
res = res * ksm(a[i], ksm(2, l[i], powmod) * ksm(2, r[i], powmod) % powmod) % mod;
}
return res;
}
inline ll Calc2 () {
memset(t, 0, sizeof t);
for ( int i = 0; i < n; i ++ ) {
l[i] = Query(b[i], n + 1);
Update(b[i]);
}
memset(t, 0, sizeof t);
for ( int i = n - 1; i >= 0; i -- ) {
r[i] = Query(b[i] + 1, n + 1);
Update(b[i]);
}
ll res = 1;
for ( int i = 0; i < n; i ++ ) {
res = res * ksm(a[i], ksm(2, l[i], powmod) * ksm(2, r[i], powmod) % powmod) % mod;
}
return res;
}
int main () {
ios::sync_with_stdio(false);
cin >> n;
for ( ll i = 0; i < n; i ++ ) {
cin >> a[i];
nums.push_back(a[i]);
}
sort ( nums.begin(), nums.end() );
nums.erase(unique(nums.begin(), nums.end()), nums.end());
for ( int i = 0; i < n; i ++ ) {
b[i] = lower_bound(nums.begin(), nums.end(), a[i]) - nums.begin() + 2;
}
cout << Calc1() * Calc2() % mod << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
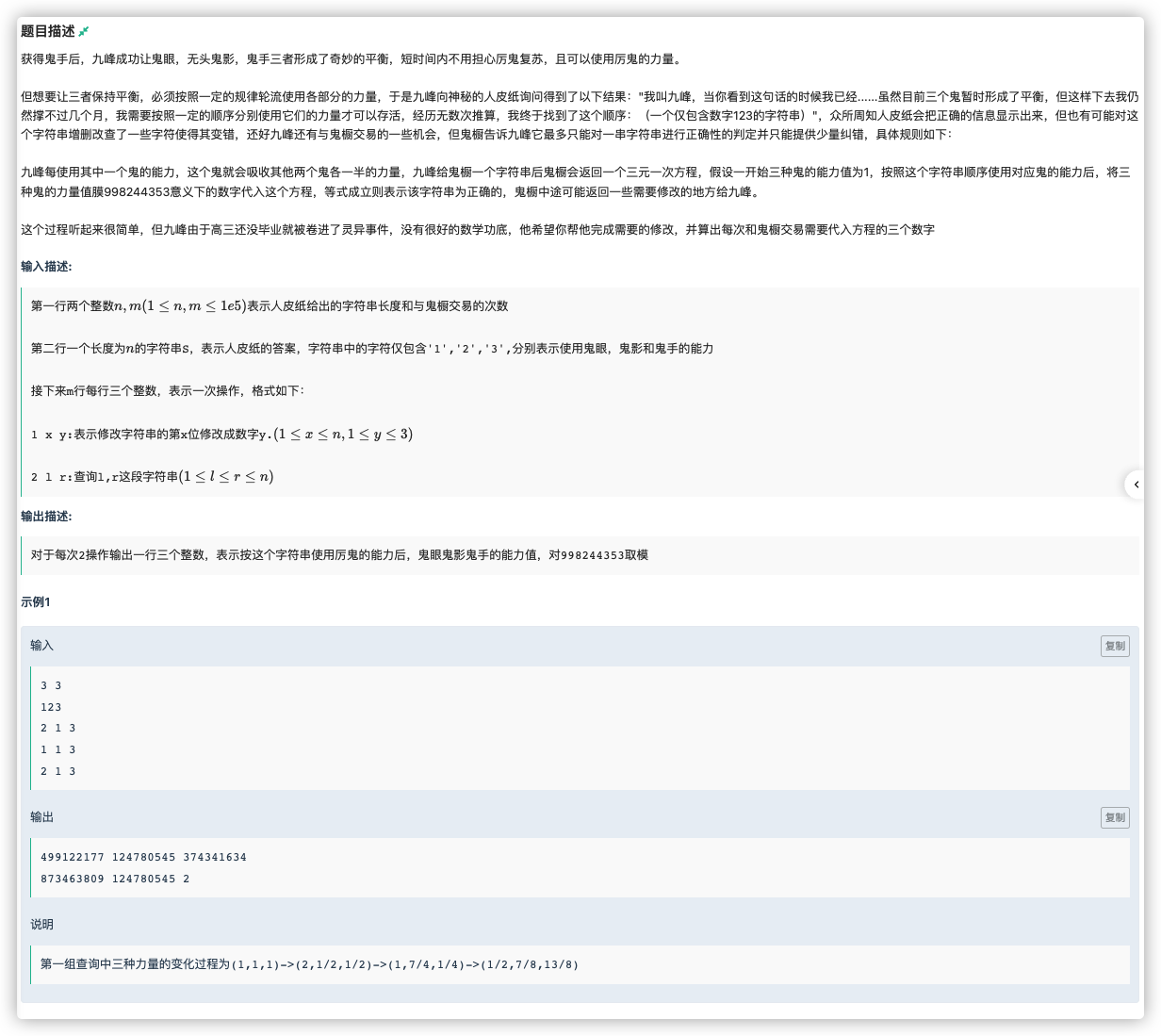
# 牛客2022寒假算法基础集训营5E_复苏小孩
# 🔗
# 💡
先简化一下情况
我们设置当前某个鬼的力量为
那么有两种情况
- 吸收力量：
- 被吸收力量：
那么我们可以将这两种情况抽象成数位关系的进制
即 进制，每个位置要么是 要么是
对于这种修改查询我们可以想到使用线段树维护大数来解决
令 为第 只鬼的线段树数组
那么向上更新时便是左子树多乘进制套着右子树向上走
查询时也与之类似，但要考虑到防止右侧没有数但是左侧仍然进位的情况
我们进行区间压缩
即
// 查询 [a,b] ，第 bs 只鬼
inline ll Query ( ll a, ll b, ll l, ll r, ll rt, ll bs ) {
...
if ( b <= mid ) return Query ( a, b, l, mid, rt << 1, bs ); // 向左压缩
else if ( a > mid ) return Query ( a, b, mid + 1, r, rt << 1 | 1, bs ); // 向右压缩
else return (Query ( a, mid, l, mid, rt << 1, bs ) * ksm(iv2, b - mid) % mod + Query ( mid + 1, b, mid + 1, r, rt << 1 | 1, bs )) % mod; // 向中间压缩
}
1
2
3
4
5
6
7
2
3
4
5
6
7
当然还有一些细节部分
- 开始时力量默认为 ，所以 位要额外 进行求值
- 开始那一位带上了一遍 所以最后要多除一遍
# ✅
const ll N = 1e5 + 10;
const ll mod = 998244353;
ll a[N];
namespace SegmentTree_Num {
ll s[15][N << 2];
inline ll ksm ( ll a, ll b ) { ll res = 1; while ( b ) { if ( b & 1 ) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv ( ll x ) { return ksm(x, mod - 2); }
ll iv2 = inv(2);
inline void Build ( ll l, ll r, ll rt ) {
if ( l == r ) {
for ( ll i = 1; i <= 3; i ++ )
s[i][rt] = 3 * (a[l] == i);
return;
}
ll mid = (l + r) >> 1;
Build(l, mid, rt << 1);
Build(mid + 1, r, rt << 1 | 1);
for ( ll i = 1; i <= 3; i ++ )
s[i][rt] = (s[i][rt << 1] * ksm(iv2, r - mid) % mod + s[i][rt << 1 | 1]) % mod;
}
inline void Update ( ll id, ll c, ll l, ll r, ll rt ) {
if ( l > id || r < id ) return;
if ( id == l && r == id ) {
for ( ll i = 1; i <= 3; i ++ )
s[i][rt] = 3 * (c == i);
return;
}
ll mid = (l + r) >> 1;
Update(id, c, l, mid, rt << 1);
Update(id, c, mid + 1, r, rt << 1 | 1);
for ( ll i = 1; i <= 3; i ++ )
s[i][rt] = (s[i][rt << 1] * ksm(iv2, r - mid) % mod + s[i][rt << 1 | 1]) % mod;
}
inline void Pre ( ll id, ll l, ll r, ll rt ) { // id位+1
if ( l > id || r < id ) return;
if ( id == l && r == id ) {
for ( ll i = 1; i <= 3; i ++ ) s[i][rt] ++;
return;
}
ll mid = (l + r) >> 1;
Pre(id, l, mid, rt << 1);
Pre(id, mid + 1, r, rt << 1 | 1);
for ( ll i = 1; i <= 3; i ++ )
s[i][rt] = (s[i][rt << 1] * ksm(iv2, r - mid) % mod + s[i][rt << 1 | 1]) % mod;
}
inline void Las ( ll id, ll l, ll r, ll rt ) { // id位-1
if ( l > id || r < id ) return;
if ( id == l && r == id ) {
for ( ll i = 1; i <= 3; i ++ ) s[i][rt] --;
return;
}
ll mid = (l + r) >> 1;
Las(id, l, mid, rt << 1);
Las(id, mid + 1, r, rt << 1 | 1);
for ( ll i = 1; i <= 3; i ++ )
s[i][rt] = (s[i][rt << 1] * ksm(iv2, r - mid) % mod + s[i][rt << 1 | 1]) % mod;
}
inline ll Query ( ll a, ll b, ll l, ll r, ll rt, ll bs ) {
if ( a > r || b < l ) return 0;
if ( l == a && r == b ) return s[bs][rt];
ll mid = (l + r) >> 1;
if ( b <= mid ) return Query ( a, b, l, mid, rt << 1, bs );
else if ( a > mid ) return Query ( a, b, mid + 1, r, rt << 1 | 1, bs );
else return (Query ( a, mid, l, mid, rt << 1, bs ) * ksm(iv2, b - mid) % mod + Query ( mid + 1, b, mid + 1, r, rt << 1 | 1, bs )) % mod;
}
}
char s[N];
int main () {
ll n, q; scanf("%lld%lld", &n, &q);
scanf("%s", s);
for ( ll i = 1; i <= n; i ++ ) a[i] = s[i - 1] - '0';
SegmentTree_Num::Build(1, n, 1);
while ( q -- ) {
ll op, x, y; scanf("%lld%lld%lld", &op, &x, &y);
if ( op == 1 ) {
SegmentTree_Num::Update(x, y, 1, n, 1);
a[x] = y;
} else {
SegmentTree_Num::Pre(x, 1, n, 1);
for ( ll i = 1; i <= 3; i ++ ) printf("%lld ", SegmentTree_Num::Query(x, y, 1, n, 1, i) * SegmentTree_Num::iv2 % mod);
puts("");
SegmentTree_Num::Las(x, 1, n, 1);
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
# 牛客练习赛68A_牛牛的mex
# 🔗
https://ac.nowcoder.com/acm/contest/13647/A
# 💡
线段树储存前后缀最小值
从而在区间内未出现的最小数O(1)查询
# ✅
#include <stack>
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <cstring>
#include <cstdio>
#include <map>
#include <set>
#include <queue>
#include <cmath>
#define rep1(i, a, n) for (ll i = a; i <= n; i++)
#define rep2(i, a, n) for (ll i = a; i >= n; i--)
#define mm(a, b) memset(a, b, sizeof(a))
#define each_cass(cass) for (cin >> cass; cass; cass--)
typedef long long ll;
void mc(ll *aa, ll *a, ll len) { rep1(i, 1, len) * (aa + i) = *(a + i); }
const int INF = 0x7FFFFFFF;
const ll LNF = 1e18;
const double G = 10;
const double eps = 1e-6;
const double PI = acos(-1.0);
const int mod = 1e9 + 7;
using namespace std;
const int maxn = 1e5 + 10;
int minn[maxn << 2];
int a[maxn];
void PushUp(int rt) { minn[rt] = min(minn[rt << 1], minn[rt << 1 | 1]); }
void Build(int l, int r, int rt)
{
if (l == r)
{
minn[rt] = a[l];
return;
}
int mid = (l + r) >> 1;
Build(l, mid, rt<<1);
Build(mid + 1, r, rt<<1|1);
PushUp(rt);
}
int Query(int a, int b, int l, int r, int rt)
{
if (a > r || b < l)
return INF;
if (a <= l && b >= r)
return minn[rt];
int mid = (l + r) >> 1;
return min(Query(a, b, l, mid, rt << 1), Query(a, b, mid + 1, r, rt << 1 | 1));
}
int main()
{
int n, q;
cin >> n >> q;
a[0]=a[n+1]=n;
for (int i = 1; i <= n; i++)
cin >> a[i];
Build(0, n+1, 1);
while (q--)
{
int l, r;
cin >> l >> r;
cout << min(Query(0, l-1, 0, n+1, 1), Query(r+1, n+1, 0, n+1, 1)) << endl;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
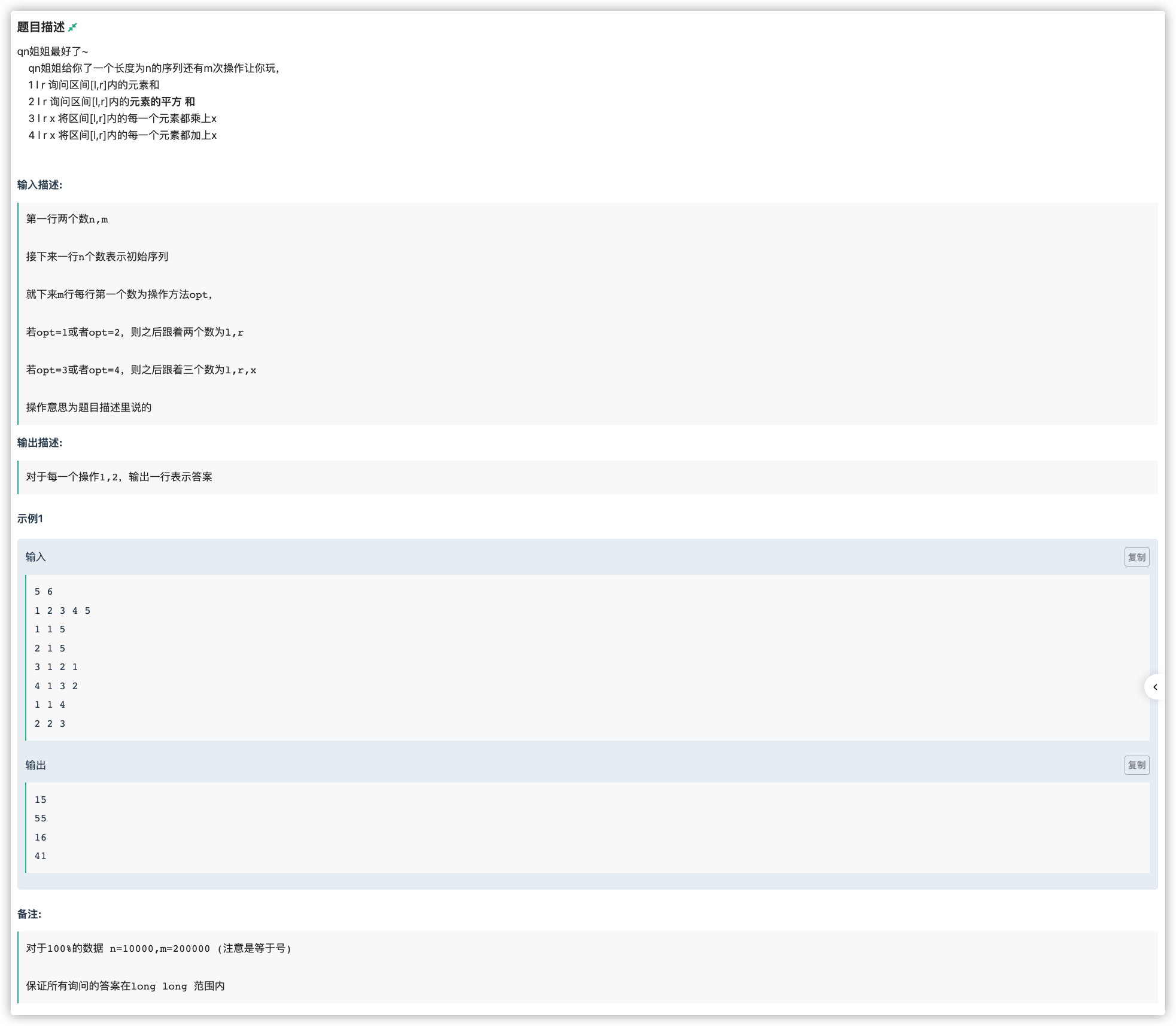
# 牛客NC19246_数据结构
# 🔗
# 💡
区间加和区间乘互相包含且顺序不能混，所以用两个懒标记实现 lazy_add, lazy_mul
区间平方和与区间和也同样，所以用两个记录数值实现 val1, val2
在 PushDown() 内
子点 lazy_add 一定包含在父点的 lazy_mul 内，所以应在推 lazy_mul 时让子点的 lazy_add 也乘上
且先推 lazy_mul 再推 lazy_add
lazy_mul推的时候，除了平方数乘 外别的均乘 （没什么好说的lazy_add推的时候，别的都很简单，但要注意平方数- 这里 就是本身所以
+=即可 - 是以
val2的区间整体乘 - 则是累加了 次
- 所以
ls.val1 += c * c * (mid - l + 1) + 2 * c * ls.val2
- 这里 就是本身所以
在 Update() 内
区间加和上面说的类似
区间乘时要注意之前加过的也就是 lazy_add 也要乘
# ✅
const int N = 1e4 + 10;
int n, m;
ll a[N];
namespace SegmentTree {
struct sgtr {
ll val1, val2;
ll lazy_mul, lazy_plus;
} t[N << 2];
inline void PushUp ( int rt ) {
sgtr &ls = t[rt << 1], &rs = t[rt << 1 | 1], &fa = t[rt];
fa.val1 = ls.val1 + rs.val1;
fa.val2 = ls.val2 + rs.val2;
}
inline void PushDown ( int l, int r, int rt ) {
sgtr &ls = t[rt << 1], &rs = t[rt << 1 | 1], &fa = t[rt];
if ( fa.lazy_mul != 1 ) {
ll k = fa.lazy_mul;
ls.val1 *= k * k; rs.val1 *= k * k;
ls.val2 *= k; rs.val2 *= k;
ls.lazy_mul *= k; rs.lazy_mul *= k;
ls.lazy_plus *= k; rs.lazy_plus *= k;
fa.lazy_mul = 1;
}
if ( fa.lazy_plus != 0 ) {
ll k = fa.lazy_plus;
int mid = (l + r) >> 1;
ls.val1 += k * k * (mid - l + 1) + 2 * k * ls.val2; rs.val1 += k * k * (r - mid) + 2 * k * rs.val2;
ls.val2 += k * (mid - l + 1); rs.val2 += k * (r - mid);
ls.lazy_plus += k; rs.lazy_plus += k;
fa.lazy_plus = 0;
}
}
inline void Build ( int l = 1, int r = n, int rt = 1 ) {
t[rt].lazy_mul = 1, t[rt].lazy_plus = 0;
if ( l == r ) {
t[rt].val1 = a[l] * a[l];
t[rt].val2 = a[l];
return;
}
int mid = (l + r) >> 1;
Build(l, mid, rt << 1);
Build(mid + 1, r, rt << 1 | 1);
PushUp(rt);
}
inline void update ( int a, int b, ll c, int opt, int l = 1, int r = n, int rt = 1 ) {
if ( r < a || b < l ) return;
if ( a <= l && r <= b ) {
if ( opt == 3 ) {
t[rt].val1 *= c * c;
t[rt].val2 *= c;
t[rt].lazy_mul *= c;
t[rt].lazy_plus *= c;
} else {
t[rt].val1 += c * c * (r - l + 1) + 2 * c * t[rt].val2;
t[rt].val2 += c * (r - l + 1);
t[rt].lazy_plus += c;
}
return;
}
int mid = (l + r) >> 1;
PushDown(l, r, rt);
update(a, b, c, opt, l, mid, rt << 1);
update(a, b, c, opt, mid + 1, r, rt << 1 | 1);
PushUp(rt);
}
inline ll Query ( int a, int b, int opt, int l = 1, int r = n, int rt = 1 ) {
if ( r < a || b < l ) return 0;
if ( a <= l && r <= b ) return opt == 1 ? t[rt].val2 : t[rt].val1;
int mid = (l + r) >> 1;
PushDown(l, r, rt);
return Query(a, b, opt, l, mid, rt << 1) + Query(a, b, opt, mid + 1, r, rt << 1 | 1);
}
} using namespace SegmentTree;
int main () {
scanf("%d%d", &n, &m);
for ( int i = 1; i <= n; i ++ ) scanf("%lld", &a[i]);
Build();
while ( m -- ) {
int opt, l, r; scanf("%d%d%d", &opt, &l, &r);
if ( opt <= 2 ) {
printf("%lld\n", Query(l, r, opt));
} else {
ll c; scanf("%lld", &c);
update(l, r, c, opt);
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
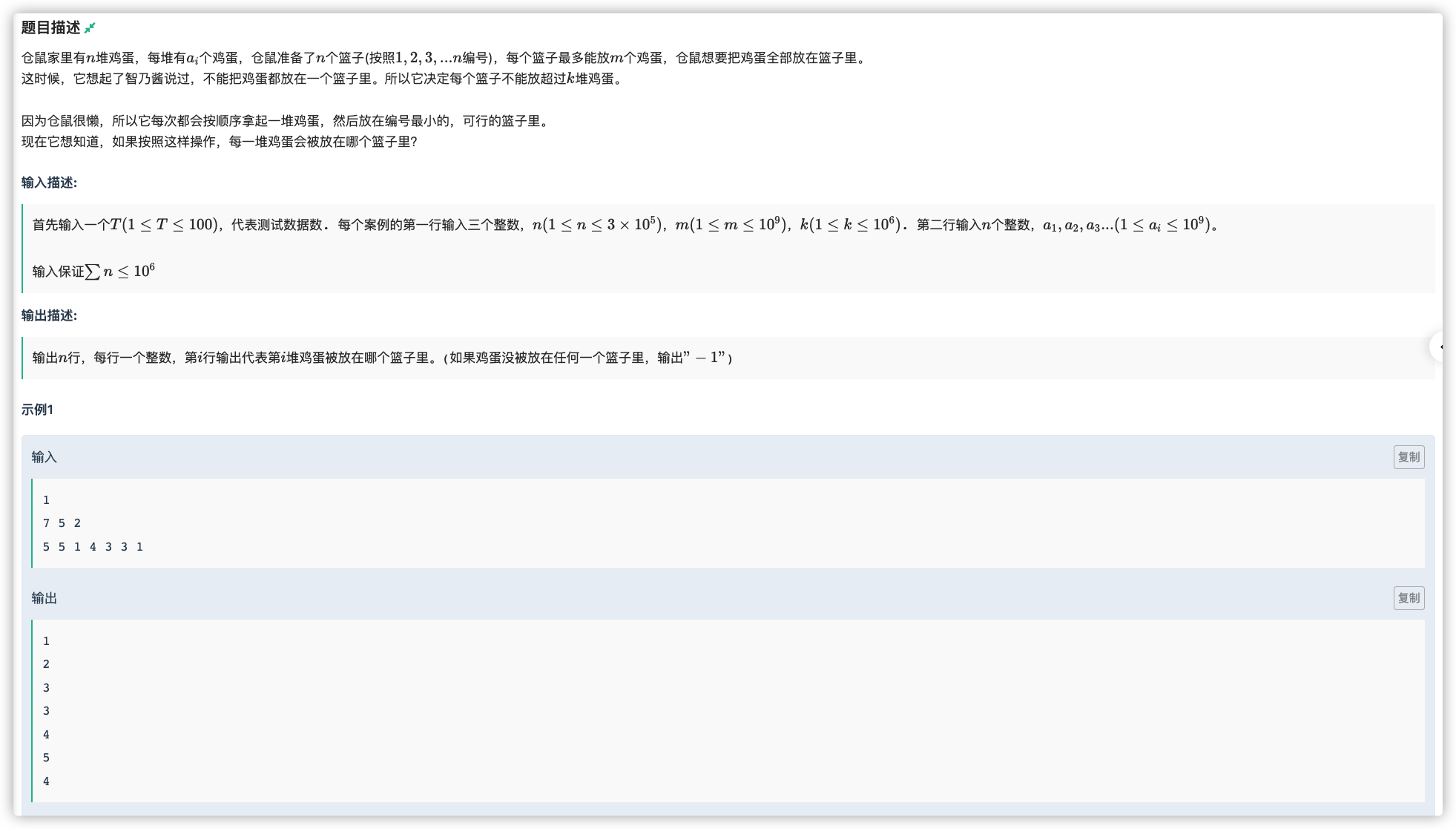
# 牛客NC226170_仓鼠的鸡蛋
# 🔗
# 💡
求篮子中剩余值第一个大于等于 的位置
以篮子做线段树数组
维护区间 ，查询时对 与 进行比较，优先去找左区间
找到单点后答案即为该点，然后单点修改，注意如果种类放完也就是说 那么可放个数 也要变成
# ✅
const int N = 3e5 + 10;
const int mod = 1e9 + 7;
int n, m, k;
int a[N];
struct sgtr {
int cnt_num;
int cnt_kind;
} t[N << 2];
inline void PushUp ( int rt ) {
t[rt].cnt_num = max(t[rt << 1].cnt_num, t[rt << 1 | 1].cnt_num);
}
inline void Build ( int l, int r, int rt ) {
if ( l == r ) {
t[rt] = {m, k};
return;
}
int mid = (l + r) >> 1;
Build(l, mid, rt << 1);
Build(mid + 1, r, rt << 1 | 1);
PushUp(rt);
}
inline void Update ( int id, int c, int l = 1, int r = n, int rt = 1 ) {
if ( l > id || id > r ) return;
if ( l == r ) {
t[rt].cnt_num -= c;
t[rt].cnt_kind --;
if ( t[rt].cnt_kind == 0 ) t[rt].cnt_num = 0;
return;
}
int mid = (l + r) >> 1;
Update(id, c, l, mid, rt << 1);
Update(id, c, mid + 1, r, rt << 1 | 1);
PushUp(rt);
}
inline int Query ( int num, int l = 1, int r = n, int rt = 1 ) {
if ( l == r ) return l;
int mid = (l + r) >> 1;
if ( t[rt << 1].cnt_num >= num ) return Query(num, l, mid, rt << 1);
else return Query(num, mid + 1, r, rt << 1 | 1);
}
inline void Solve () {
scanf("%d%d%d", &n, &m, &k);
for ( int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
Build(1, n, 1);
for ( int i = 1; i <= n; i ++ ) {
if ( t[1].cnt_num < a[i] ) {
puts("-1");
continue;
}
int id = Query(a[i]);
printf("%d\n", id);
Update(id, a[i]);
}
}
int main () {
int cass; scanf("%d", &cass); while ( cass -- ) {
Solve();
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
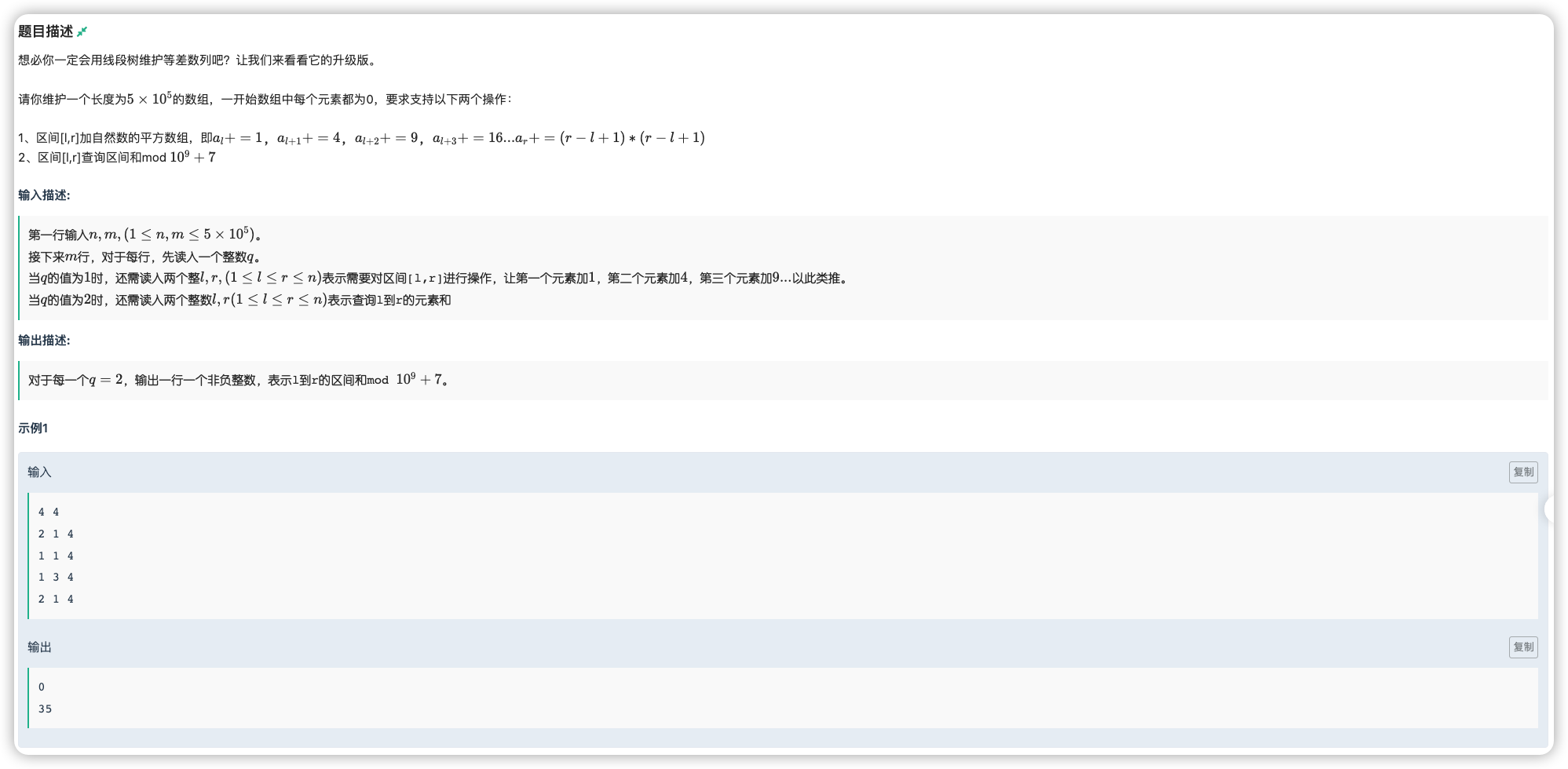
# 牛客NC226172_智乃酱的平方数列
# 🔗
# 💡
三阶前缀和版本的学不会...要被苦恼吃了...
这里是维护多项式版本的
对于区间更新 ，里面所有的点 ，它实际上加的值为 ，发现这个 是死的，故可以用三个 懒记录这三个系数
在传 的时候或者强制更新（ 出口）的时候，思考如何区间更新加和
继续推式子：
也就是这两个等差数列的平方和与一次方和都很好求，在强制更新的时候是要用给定的 算这三个系数然后乘进去，而在传懒标记时要用三个 当这三个项的系数，分别乘 、 、 即可
# ✅
const int N = 5e5 + 10;
const int mod = 1e9 + 7;
struct Sgtr {
ll sum2, sum1, sum0;
ll laz2, laz1, laz0;
bool haslaz = false;
} t[N << 2];
inline ll Sum2 (ll x) {
if (x <= 0) return 0;
return x * (x + 1) * (2 * x + 1) / 6 % mod;
}
inline ll Sum1 (ll x) {
if (x <= 0) return 0;
return (x + 1) * x / 2 % mod;
}
inline void pushup (int rt) {
int ch = rt << 1;
t[rt].sum0 = (t[ch].sum0 + t[ch | 1].sum0) % mod;
t[rt].sum1 = (t[ch].sum1 + t[ch | 1].sum1) % mod;
t[rt].sum2 = (t[ch].sum2 + t[ch | 1].sum2) % mod;
}
inline void pushdown (int l, int r, int rt) {
if (!t[rt].haslaz) return;
int mid = (l + r) >> 1;
int ch = rt << 1;
(t[ch].sum0 += t[rt].laz0 * (mid - l + 1) % mod) %= mod;
(t[ch].sum1 += t[rt].laz1 * (Sum1(mid) - Sum1(l - 1)) % mod) %= mod;
(t[ch].sum2 += t[rt].laz2 * (Sum2(mid) - Sum2(l - 1)) % mod) %= mod;
(t[ch | 1].sum0 += t[rt].laz0 * (r - mid) % mod) %= mod;
(t[ch | 1].sum1 += t[rt].laz1 * (Sum1(r) - Sum1(mid)) % mod) %= mod;
(t[ch | 1].sum2 += t[rt].laz2 * (Sum2(r) - Sum2(mid)) % mod) %= mod;
(t[ch].laz0 += t[rt].laz0) %= mod;
(t[ch].laz1 += t[rt].laz1) %= mod;
(t[ch].laz2 += t[rt].laz2) %= mod;
(t[ch | 1].laz0 += t[rt].laz0) %= mod;
(t[ch | 1].laz1 += t[rt].laz1) %= mod;
(t[ch | 1].laz2 += t[rt].laz2) %= mod;
t[rt].laz0 = t[rt].laz1 = t[rt].laz2 = t[rt].haslaz = 0;
t[ch].haslaz = t[ch | 1].haslaz = 1;
}
inline void update (ll a, int b, int l, int r, int rt) {
if (a <= l && r <= b) {
(t[rt].sum2 += Sum2(r) - Sum2(l - 1)) %= mod;
(t[rt].sum1 += 2ll * (a - 1) * (Sum1(r) - Sum1(l - 1)) % mod) %= mod;
(t[rt].sum0 += (a - 1) * (a - 1) % mod * (r - l + 1) % mod) %= mod;
t[rt].laz2 ++;
(t[rt].laz1 += 2ll * (a - 1) % mod) %= mod;
(t[rt].laz0 += (a - 1) * (a - 1) % mod) %= mod;
t[rt].haslaz = true;
return;
}
pushdown(l, r, rt);
int mid = (l + r) >> 1;
if (a <= mid) update(a, b, l, mid, rt << 1);
if (b > mid) update(a, b, mid + 1, r, rt << 1 | 1);
pushup(rt);
}
inline ll query (int a, int b, int l, int r, int rt) {
if (a <= l && r <= b) return t[rt].sum2 - t[rt].sum1 + t[rt].sum0;
int mid = (l + r) >> 1;
ll res = 0;
pushdown(l, r, rt);
if (a <= mid) res += query(a, b, l, mid, rt << 1);
if (b > mid) res += query(a, b, mid + 1, r, rt << 1 | 1);
return res % mod;
}
int main () {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, q; cin >> n >> q;
while (q --) {
int op, l, r; cin >> op >> l >> r;
if (op == 1) {
update(l, r, 1, n, 1);
} else {
cout << (query(l, r, 1, n, 1) % mod + mod) % mod << endl;
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
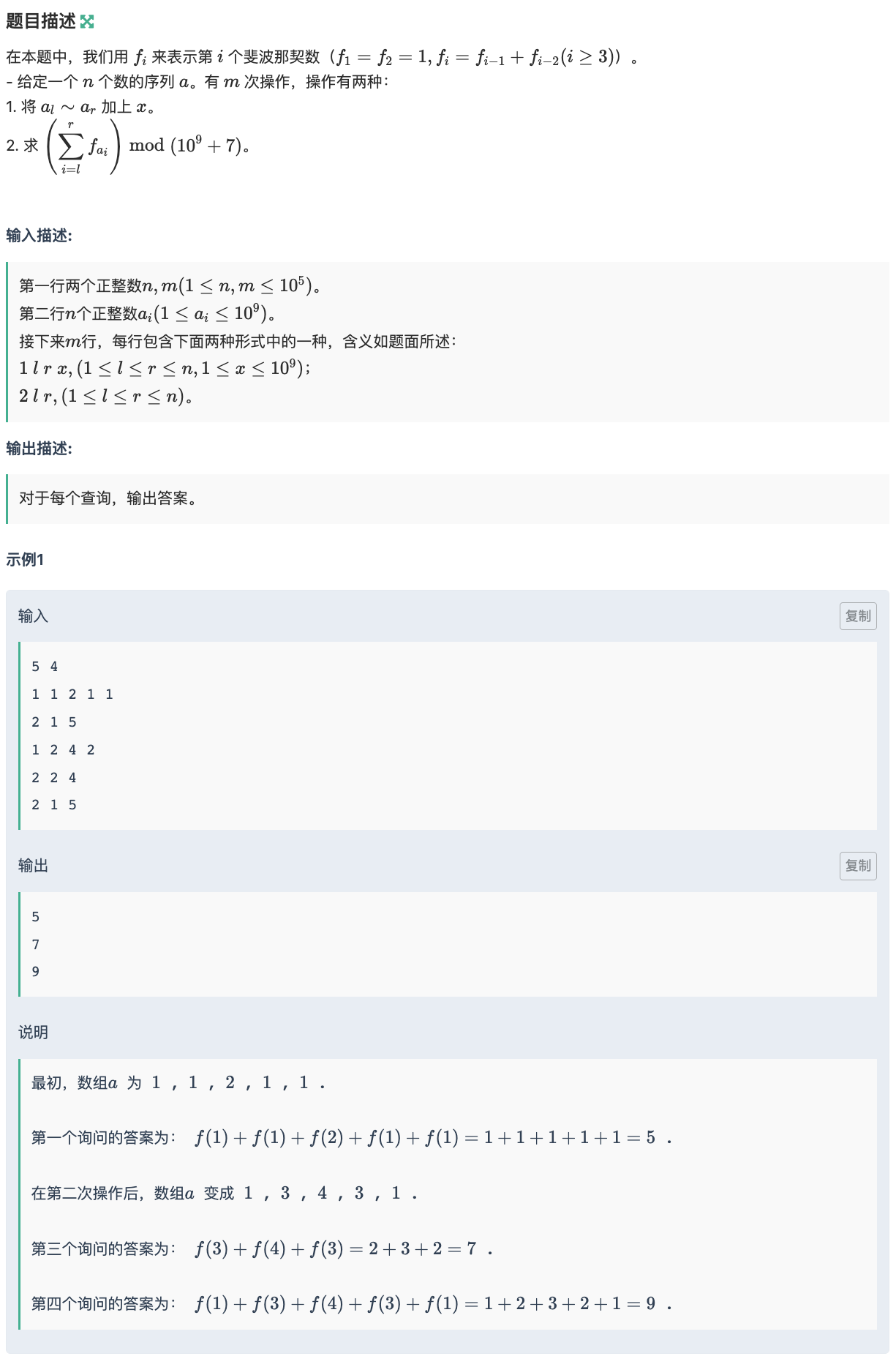
# 牛客NC230082_SashaAndArray
# 🔗
# 💡
一个涉及到区间修改和区间求和的问题
且 到最后会很大，所以想矩阵
，我们设置
矩阵就是
的基础矩阵
那么在矩阵里面区间修改加也就是变成了区间修改乘（区间和矩阵乘上 矩阵的
次方
区间乘可以由乘法分配律满足，所以线段树懒标记就可以实现
而统计的时候就是区间查询加，这个就直接用线段树的区间求和数组计算加后的矩阵
由于满足乘法分配律，我们直接用初始的竖矩阵去乘这个区间和矩阵就行了
# ✅
struct Mat {
ll m[2][2];
inline Mat() {}
inline Mat ( int e ) {
for ( int i = 0; i < 2; i ++ )
for ( int j = 0; j < 2; j ++ )
m[i][j] = e * (i == j);
}
inline Mat operator + ( Mat a ) {
Mat res(0);
for ( int i = 0; i < 2; i ++ )
for ( int j = 0; j < 2; j ++ )
res.m[i][j] = (a.m[i][j] + m[i][j]) % mod;
return res;
}
inline friend Mat operator * ( Mat a, Mat b ) {
Mat res(0);
for ( int i = 0; i < 2; i ++ )
for ( int j = 0; j < 2; j ++ )
for ( int k = 0; k < 2; k ++ )
res.m[i][j] = (res.m[i][j] + a.m[i][k] * b.m[k][j] % mod) % mod;
return res;
}
inline bool operator == ( Mat b ) {
for ( int i = 0; i < 2; i ++ )
for ( int j = 0; j < 2; j ++ )
if ( m[i][j] != b.m[i][j] ) return false;
return true;
}
} base, one(1), zero(0), res(0);
inline Mat ksm ( Mat a, ll b ) { Mat res(1); while ( b ) { if ( b & 1 ) res = res * a; a = a * a; b >>= 1; } return res; }
const int N = 1e5 + 10;
int n, m, a[N];
struct SegmenTree {
Mat val, lazy;
} sgtr[N << 2];
inline void PushUp ( int rt ) { sgtr[rt].val = sgtr[rt << 1].val + sgtr[rt << 1 | 1].val; }
inline void PushDown ( int rt, int l, int r ) {
auto &cur = sgtr[rt], &lson = sgtr[rt << 1], &rson = sgtr[rt << 1 | 1];
if ( cur.lazy == one ) return;
int mid = (l + r) >> 1;
lson.val = lson.val * cur.lazy; lson.lazy = lson.lazy * cur.lazy;
rson.val = rson.val * cur.lazy; rson.lazy = rson.lazy * cur.lazy;
cur.lazy = one;
}
inline void Build ( int l, int r, int rt ) {
sgtr[rt].lazy = one;
if ( l == r ) {
if ( a[l] == 1 ) sgtr[rt].val.m[0][0] = 1;
else if ( a[l] == 2 ) sgtr[rt].val.m[0][0] = sgtr[rt].val.m[0][1] = 1;
else sgtr[rt].val = res * ksm(base, a[l] - 2);
return;
}
int mid = (l + r) >> 1;
Build ( l, mid, rt << 1 );
Build ( mid + 1, r, rt << 1 | 1);
PushUp ( rt );
}
inline void Update ( int a, int b, Mat c, int l, int r, int rt ) {
if ( a <= l && r <= b ) {
sgtr[rt].val = sgtr[rt].val * c;
sgtr[rt].lazy = sgtr[rt].lazy * c;
return;
}
if ( a > r || b < l ) return;
int mid = (l + r) >> 1;
PushDown ( rt, l, r );
Update ( a, b, c, l, mid, rt << 1 );
Update ( a, b, c, mid + 1, r, rt << 1 | 1 );
PushUp ( rt );
}
inline ll Query ( int a, int b, int l, int r, int rt ) {
if ( a <= l && r <= b ) return sgtr[rt].val.m[0][0];
if ( a > r || b < l ) return 0;
PushDown ( rt, l, r );
int mid = (l + r) >> 1;
return (Query ( a, b, l, mid, rt << 1 ) + Query ( a, b, mid + 1, r, rt << 1 | 1 )) % mod;
}
int main () {
base.m[0][0] = base.m[0][1] = base.m[1][0] = 1; base.m[1][1] = 0;
res.m[0][0] = res.m[0][1] = 1;
cin >> n >> m;
for ( int i = 1; i <= n; i ++ ) cin >> a[i];
Build ( 1, n, 1 );
while ( m -- ) {
int op; cin >> op;
if ( op == 1 ) {
int l, r, x; cin >> l >> r >> x;
Update ( l, r, ksm(base, x), 1, n, 1 );
} else {
int l, r; cin >> l >> r;
cout << Query ( l, r, 1, n, 1 ) << endl;
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
# ABC233F_ParenthesisChecking
# 🔗
# 💡
括号匹配的本质是两两相消。
对于每一个位置的点重定义一下它的权值：'(' = 1，')' = -1
在累加过程中，可以和
相消为
，所以计算总贡献
那么可以记录一个权值前缀和
那么对于每一个区间，如果其中的最小值小于 的前缀和的话，那么就一定是不匹配的（最小值的位置前右括号太多了
当然如果本身 的前缀和不等于
的前缀和就也是不匹配的
这里的最小值可以使用线段树进行维护，修改便直接在线段树上修改如果本身是'('，修改后区间-2，否则+2
# ✅
#include <iostream>
#include <vector>
#include <algorithm>
#include <set>
#include <map>
#include <deque>
using namespace std;
#define ll long long
const int N = 2e5 + 10;
char s[N];
int a[N], n, q;
namespace SegmentTree {
struct Sgtr { int val, lazy; } sgtr[N << 2];
inline void push_Up ( int rt ) {
sgtr[rt].val = min ( sgtr[rt << 1].val, sgtr[rt << 1 | 1].val );
}
inline void push_Down ( int l, int r, int rt ) {
if ( !sgtr[rt].lazy ) return;
sgtr[rt << 1].val += sgtr[rt].lazy;
sgtr[rt << 1 | 1].val += sgtr[rt].lazy;
sgtr[rt << 1].lazy += sgtr[rt].lazy;
sgtr[rt << 1 | 1].lazy += sgtr[rt].lazy;
sgtr[rt].lazy = 0;
}
inline void Build ( int l, int r, int rt ) {
if ( l == r ) { sgtr[rt].val = a[l]; return; }
int mid = (l + r) >> 1;
Build ( l, mid, rt << 1 );
Build ( mid + 1, r, rt << 1 | 1 );
push_Up ( rt );
}
inline void Update ( int a, int b, int c, int l, int r, int rt ) {
if ( a <= l && r <= b ) { sgtr[rt].lazy += c, sgtr[rt].val += c; return; }
if ( a > r || b < l ) return;
int mid = (l + r) >> 1;
push_Down ( l, r, rt );
Update ( a, b, c, l, mid, rt << 1 );
Update ( a, b, c, mid + 1, r, rt << 1 | 1 );
push_Up ( rt );
}
inline int Query ( int a, int b, int l, int r, int rt ) {
if ( a <= l && r <= b ) return sgtr[rt].val;
if ( a > r || b < l ) return N;
int mid = (l + r) >> 1;
push_Down ( l, r, rt );
return min ( Query ( a, b, l, mid, rt << 1 ), Query ( a, b, mid + 1, r, rt << 1 | 1) );
}
} using namespace SegmentTree;
int main () {
ios::sync_with_stdio(false);
cin >> n >> q >> (s + 1);
for ( int i = 1; i <= n; i ++ )
if ( s[i] == '(' ) a[i] = a[i - 1] + 1;
else a[i] = a[i - 1] - 1;
Build ( 1, n, 1 );
while ( q -- ) {
int op, l, r; cin >> op >> l >> r;
if ( op == 1 ) {
if ( s[l] == s[r] ) continue;
if ( s[l] == '(' ) Update ( l, r - 1, -2, 1, n, 1 );
else Update ( l, r - 1, 2, 1, n, 1 );
swap ( s[l], s[r] );
} else {
int L = l == 1 ? 0 : Query ( l - 1, l - 1, 1, n, 1 ), R = Query ( r, r, 1, n, 1 );
if ( L != R ) { cout << "No" << endl; continue; }
if ( Query ( l, r, 1, n, 1 ) < L ) { cout << "No" << endl; continue; }
cout << "Yes" << endl;
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
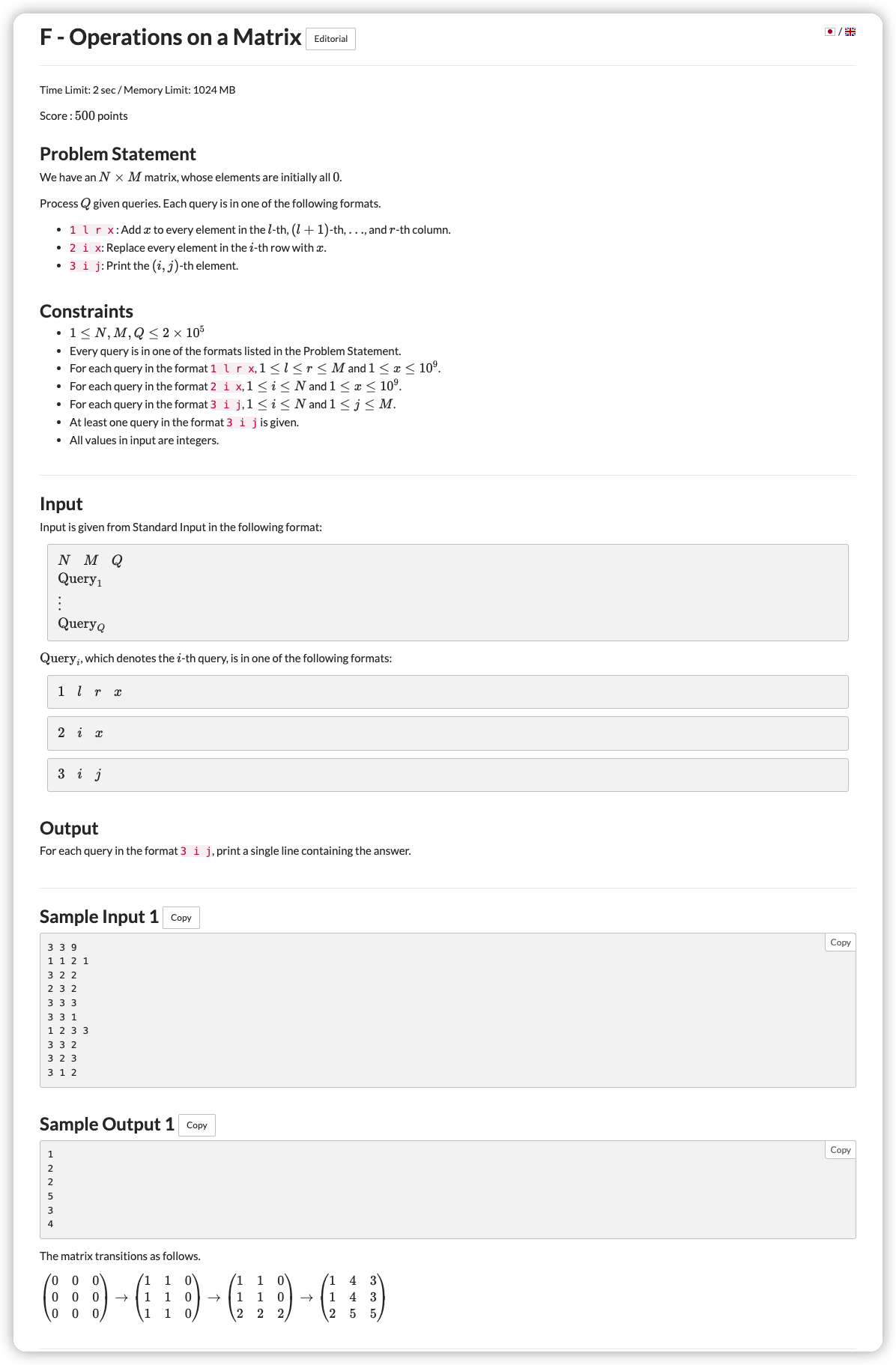
# ABC253F_OperationsOnAMatrix
# 🔗
# 💡
拿到这个题第一反应就是那种记录时间戳的操作，因为修改行相当于直接覆盖
那么问题是，对于查询 ，我最后一次覆盖行 的时间 与查询的时间 之间，对 这一列的修改如何得知
考虑前缀和相减等于区间和，我们在 时令 的查询结果减去对 列的单点查询 ，然后在 时令查询结果加上对 的单点查询 ，那么就可以得到这一个区间的修改，当然结果也要加上我们对 行覆盖的值
所以我们要对每一个查询 获取最后一次覆盖第 行的操作的时间戳，并且对这个时间戳存一个数组，内容为它影响了哪些查询（这里为存入 ）
这样的话我们可以在每一次覆盖时遍历它的数组，令这些时间戳的查询加上 并减去对 的单点查询
如果是查询操作，就加上对 的单点查询并输出结果
# ✅
# define mid ((l + r) >> 1)
const int N = 2e5 + 10;
# define int ll
int n, m, Q;
struct qry {
int op;
int a, b, c;
int res;
} q[N];
pair<int, int> LASTX[N]; // 对于第i个查询(x,y)，最后一次覆盖x的时间戳与值
ll t[N << 2], laz[N << 2];
inline void pushup (int rt) {
t[rt] = t[rt << 1] + t[rt << 1 | 1];
}
inline void pushdown (int l, int r, int rt) {
if (!laz[rt]) return;
t[rt << 1] += laz[rt] * (mid - l + 1);
t[rt << 1 | 1] += laz[rt] * (r - mid);
laz[rt << 1] += laz[rt];
laz[rt << 1 | 1] += laz[rt];
laz[rt] = 0;
}
inline void update (int a, int b, ll c, int l = 1, int r = m, int rt = 1) {
if (a <= l && r <= b) {
t[rt] += c * (r - l + 1);
laz[rt] += c;
return;
}
if (a > r || b < l) return;
pushdown(l, r, rt);
update(a, b, c, l, mid, rt << 1);
update(a, b, c, mid + 1, r, rt << 1 | 1);
pushup(rt);
}
inline ll query (int id, int l = 1, int r = m, int rt = 1) {
if (l == id && id == r) return t[rt];
pushdown(l, r, rt);
if (id <= mid) return query(id, l, mid, rt << 1);
else return query(id, mid + 1, r, rt << 1 | 1);
}
vector<int> ned[N]; // 每一个覆盖真正影响的查询时间戳
signed main () {
scanf("%lld%lld%lld", &n, &m, &Q);
for (int i = 1; i <= Q; i ++) {
scanf("%lld", &q[i].op);
if (q[i].op == 1) {
scanf("%lld%lld%lld", &q[i].a, &q[i].b, &q[i].c);
} else {
scanf("%lld%lld", &q[i].a, &q[i].b);
if (q[i].op == 3) {
q[i].res = LASTX[q[i].a].second;
ned[LASTX[q[i].a].first].push_back(i); // 对这个查询最后一次行覆盖的时间戳，存入这个查询的时间戳
} else {
LASTX[q[i].a] = {i, q[i].b};
}
}
}
for (int i = 0; i < N; i ++) LASTX[i] = {0, 0};
for (int i = 1; i <= Q; i ++) {
if (q[i].op == 1) {
update(q[i].a, q[i].b, q[i].c);
} else {
if (q[i].op == 3) {
q[i].res += query(q[i].b);
printf("%lld\n", q[i].res);
} else {
LASTX[q[i].a] = {i, q[i].b};
for (auto id : ned[i]) {
q[id].res -= query(q[id].b);
}
}
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
# CCPC2020威海站G_CaesarCipher
# 🔗
# 💡
查询是求两个子串是否相等，判断子串相等考虑哈希，还有修改，使用线段树维护哈希
那么在修改的时候，区间每个数字加 意味着这个 区间加 ，在取模哈希下，求出所有长度的 的取模后的值
这样区间传烂标记的时候左区间只用加上
注意到还有一个地方，就是每一个位置都是循环的，也就是说它如果等于 的话它会立即变成 ，也就意味着所有的位置都不能大于等于 ，这个地方的处理可以记录一个区间的最大值，然后每次查询前看一个区间的最大值是否超过了进制，超过了话进入递归向下走并单点修改，重新搭建这一条区间链
怕被卡，两个线段树，使用双哈希
# ✅
const int N = 5e5 + 10;
const int base = 65536;
const int mod[2] = {1000000009, 1000000007};
int pwbase[2][N];
int all1[2][N]; // 1 重复 i 次的值
struct Sgtr {
int val, lazy;
int mxv;
} t[2][N << 2];
inline void pushup (int l, int r, int rt) {
int mid = (l + r) >> 1;
for (int i = 0; i < 2; i ++) {
t[i][rt].mxv = max(t[i][rt << 1].mxv, t[i][rt << 1 | 1].mxv);
t[i][rt].val = ((ll)t[i][rt << 1].val * pwbase[i][r - mid] % mod[i] + t[i][rt << 1 | 1].val) % mod[i];
}
}
inline void pushdown (int l, int r, int rt) {
int mid = (l + r) >> 1;
for (int i = 0; i < 2; i ++) {
if (!t[i][rt].lazy) continue;
int laz = t[i][rt].lazy;
(t[i][rt << 1].val += (ll)laz * all1[i][mid - l + 1] % mod[i]) %= mod[i];
(t[i][rt << 1 | 1].val += (ll)laz * all1[i][r - mid] % mod[i]) %= mod[i];
t[i][rt << 1].mxv += laz;
t[i][rt << 1 | 1].mxv += laz;
t[i][rt << 1].lazy += laz;
t[i][rt << 1 | 1].lazy += laz;
t[i][rt].lazy = 0;
}
}
inline void update (int a, int b, int l, int r, int rt) {
if (a <= l && r <= b) {
(t[0][rt].val += all1[0][r - l + 1]) %= mod[0];
(t[1][rt].val += all1[1][r - l + 1]) %= mod[1];
t[0][rt].lazy ++; t[1][rt].lazy ++;
t[0][rt].mxv ++; t[1][rt].mxv ++;
return;
}
pushdown(l, r, rt);
int mid = (l + r) >> 1;
if (a <= mid) update(a, b, l, mid, rt << 1);
if (b > mid) update(a, b, mid + 1, r, rt << 1 | 1);
pushup(l, r, rt);
}
inline void new_tree (int l, int r, int rt, int i) {
if (l == r) {
t[i][rt].val %= base;
t[i][rt].mxv = t[i][rt].val;
return;
}
pushdown(l, r, rt);
int mid = (l + r) >> 1;
if (t[i][rt << 1].mxv == t[i][rt].mxv) new_tree(l, mid, rt << 1, i);
if (t[i][rt << 1 | 1].mxv == t[i][rt].mxv) new_tree(mid + 1, r, rt << 1 | 1, i);
pushup(l, r, rt);
}
inline int query (int a, int b, int l, int r, int rt, int i) {
if (t[i][rt].mxv >= base) new_tree(l, r, rt, i);
if (a <= l && r <= b) return (ll)t[i][rt].val * pwbase[i][b - r] % mod[i];
pushdown(l, r, rt);
int res = 0, mid = (l + r) >> 1;
if (a <= mid) res += query(a, b, l, mid, rt << 1, i);
if (b > mid) res += query(a, b, mid + 1, r, rt << 1 | 1, i);
return res % mod[i];
}
inline void build (int l, int r, int rt) {
if (l == r) {
int x; scanf("%d", &x);
t[1][rt].val = t[0][rt].val = x;
t[1][rt].mxv = t[0][rt].mxv = x;
return;
}
int mid = (l + r) >> 1;
build(l, mid, rt << 1);
build(mid + 1, r, rt << 1 | 1);
pushup(l, r, rt);
}
int main () {
int n, q; scanf("%d%d", &n, &q);
all1[0][1] = all1[1][1] = 1;
for (int i = 2; i < N; i ++) {
all1[0][i] = ((ll)all1[0][i - 1] * base % mod[0] + 1) % mod[0];
all1[1][i] = ((ll)all1[1][i - 1] * base % mod[1] + 1) % mod[1];
}
pwbase[0][0] = pwbase[1][0] = 1;
for (int i = 1; i < N; i ++)
pwbase[0][i] = (ll)pwbase[0][i - 1] * base % mod[0],
pwbase[1][i] = (ll)pwbase[1][i - 1] * base % mod[1];
build(1, n, 1);
while (q --) {
int op; scanf("%d", &op);
if (op == 1) {
int l, r; scanf("%d%d", &l, &r);
update(l, r, 1, n, 1);
} else {
int x, y, l; scanf("%d%d%d", &x, &y, &l);
pair<int, int> qx = {query(x, x + l - 1, 1, n, 1, 0), query(x, x + l - 1, 1, n, 1, 1)};
pair<int, int> qy = {query(y, y + l - 1, 1, n, 1, 0), query(y, y + l - 1, 1, n, 1, 1)};
if (qx == qy) printf("yes\n");
else printf("no\n");
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
# CodeForces1234D_DistinctCharactersQueries
# 🔗
# 💡
字符串是由 个英文字母组成，查询的时候如果能知道每一个字母对答案的贡献就很好做了
那么构建 棵线段树分别对应每一个字母的出现次数，查询的时候直接查询每棵线段树 里面出现的次数，如果不为 就对答案贡献
# ✅
const int N = 1e5 + 10;
string s;
int t[N << 2][26];
inline void pushup (int rt, int op) {
t[rt][op] = t[rt << 1][op] + t[rt << 1 | 1][op];
}
inline void build (int l, int r, int rt) {
if (l == r) {
t[rt][s[l] - 'a'] = 1;
return;
}
int mid = (l + r) >> 1;
build(l, mid, rt << 1);
build(mid + 1, r, rt << 1 | 1);
for (int i = 0; i < 26; i ++) pushup(rt, i);
}
inline void update (int id, char c, int l, int r, int rt) {
if (l == r) {
t[rt][s[l] - 'a'] = 0;
s[l] = c;
t[rt][s[l] - 'a'] = 1;
return;
}
int mid = (l + r) >> 1;
if (id <= mid) update(id, c, l, mid, rt << 1);
else update(id, c, mid + 1, r, rt << 1 | 1);
for (int i = 0; i < 26; i ++) pushup(rt, i);
}
inline int query (int a, int b, int l, int r, int rt, int op) {
if (a > r || b < l) return 0;
if (a <= l && r <= b) return t[rt][op];
int mid = (l + r) >> 1;
return query(a, b, l, mid, rt << 1, op) + query(a, b, mid + 1, r, rt << 1 | 1, op);
}
int main () {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> s; s = "0" + s;
int n = s.size() - 1;
build(1, n, 1);
int m; cin >> m;
while (m --) {
int op; cin >> op;
if (op == 1) {
int id; char c; cin >> id >> c;
update(id, c, 1, n, 1);
} else {
int l, r; cin >> l >> r;
int res = 0;
for (int i = 0; i < 26; i ++) {
res += query(l, r, 1, n, 1, i) > 0;
}
cout << res << endl;
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
# CodeForces1354D_Multiset
# 🔗
# 💡
两种操作：插入一个数 ，删去第 小的数
这两个操作明显都可以使用权值线段树实现
插入操作就直接在 的位置上
删除操作先找到第 小的数是谁（直接在权值线段树内走二分优化掉一个 ），找到后对它的位置上进行 即可
# ✅
const int N = 1e6 + 10;
int n, m, t[N << 2];
inline void pushup (int rt) {
t[rt] = t[rt << 1] + t[rt << 1 | 1];
}
inline void update (int id, int c, int l = 1, int r = n, int rt = 1) {
if (l == r) {
t[rt] += c;
return;
}
int mid = (l + r) >> 1;
if (id <= mid) update(id, c, l, mid, rt << 1);
if (id > mid) update(id, c, mid + 1, r, rt << 1 | 1);
pushup(rt);
}
inline int query (int b, int l = 1, int r = n, int rt = 1) {
if (r <= b) return t[rt];
if (l > b) return 0;
int mid = (l + r) >> 1;
return query(b, l, mid, rt << 1) + query(b, mid + 1, r, rt << 1 | 1);
}
inline int find_kth (int k, int l = 1, int r = n, int rt = 1) {
if (l == r) return l;
int mid = (l + r) >> 1;
if (t[rt << 1] >= k) return find_kth(k, l, mid, rt << 1);
else return find_kth(k - t[rt << 1], mid + 1, r, rt << 1 | 1);
}
int main () {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m; n ++;
for (int i = 1; i < n; i ++) {
int x; cin >> x;
update(x, 1);
} update(n, 1);
while (m --) {
int x; cin >> x;
if (x < 0) {
update(find_kth(-x), -1);
} else {
update(x, 1);
}
}
int res = find_kth(1);
if (res == n) cout << 0;
else cout << res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
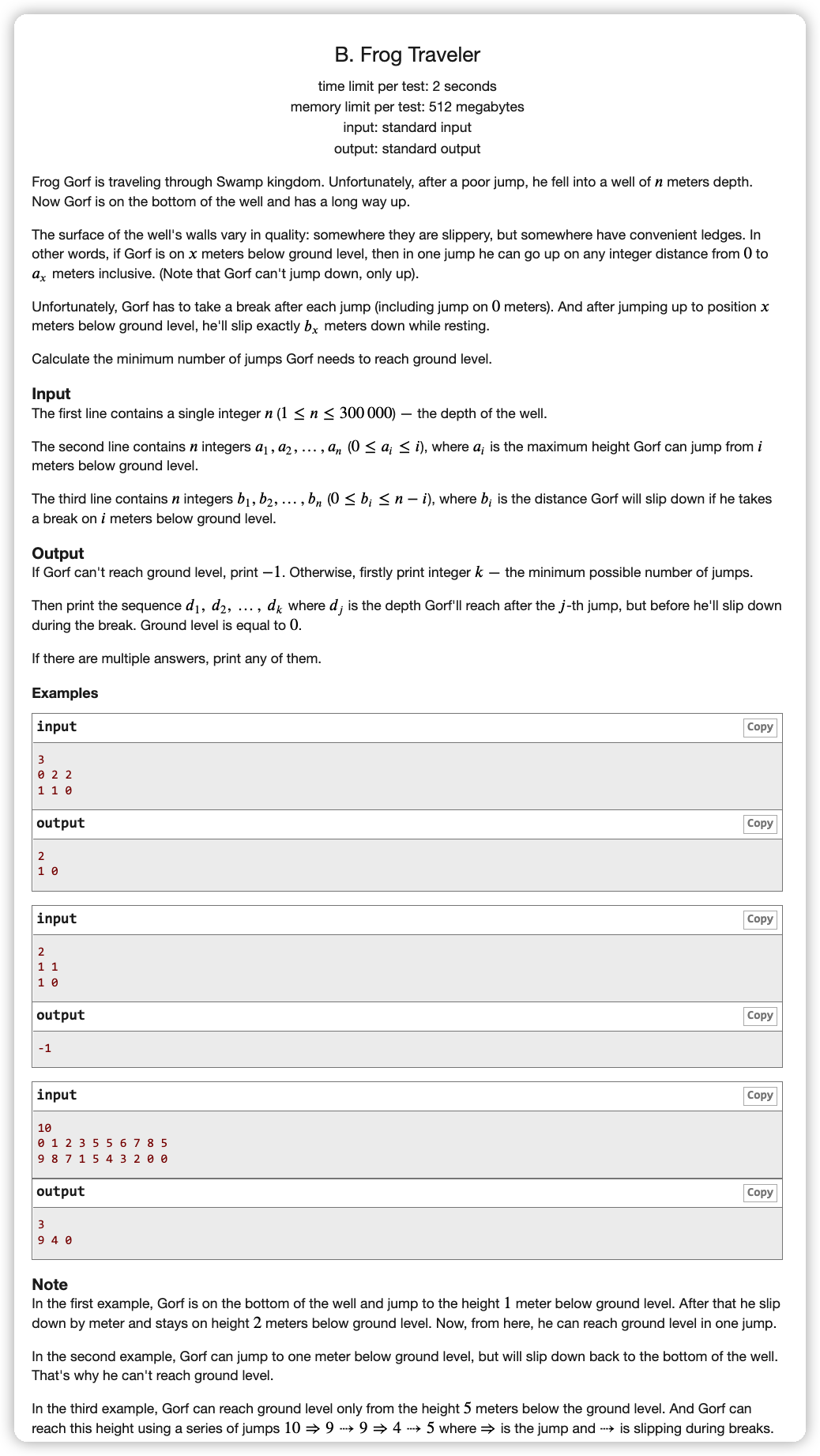
# CodeForces1601B_FrogTraveler
# 🔗
# 💡
分析这个问题
首先这个问题是一个类似于最短路的问题，我们要跳最少的次数到达目的地，需要更新
同时这个问题也要维护路径，需要记录最短路前驱
如果把它按最短路单纯地连边的话，边数可能会到达 ，非常大，时间空间都过不去
注意到一个点可以跑的点是它后面连续的一段点，考虑到其实 就是一个 的转移，那么用线段树区间修改进行这个 的转移操作
但是注意到有一个下滑的过程，由于我们要使用这个连续的下标，我们就要在用 时，用 这个点的最短距离 更新
因为我们路径记录的都是下滑之前的路径点，所以标记这次更新是用 更新的即可
所以我们要有一个双关键字的懒标记，一个关键字是更新的距离，另一个则是更新出第一个关键字的出发点
线段树懒标记往下推的时候，需要考虑需不需要更改这两个关键字，而当子树的 了话，就代表我们推到底了，如果将距离更新为更短了，就要直接修改
# ✅
const int N = 3e5 + 10;
const int inf = 0x3f3f3f3f;
int pre[N]; // 最短路的前驱
struct node {
int val;
pair<int, int> lazy;
} t[N << 2];
inline void pushUp (int rt) {
t[rt].val = max(t[rt << 1].val, t[rt << 1 | 1].val);
}
inline void pushDown (int l, int r, int rt) {
if (t[rt].lazy.first == inf) return;
node &fa = t[rt], &ls = t[rt << 1], &rs = t[rt << 1 | 1];
// 更短的话，更新的原因点也要修改
if (ls.lazy.first > fa.lazy.first) ls.lazy = fa.lazy;
if (rs.lazy.first > fa.lazy.first) rs.lazy = fa.lazy;
int mid = (l + r) >> 1;
// 叶子节点，如果需要更新的话就把 pre 更新了
if (mid - l + 1 == 1) {
if (ls.val > fa.lazy.first) {
pre[l] = fa.lazy.second;
ls.val = fa.lazy.first;
}
} else {
ls.val = min(ls.val, fa.lazy.first);
}
if (r - mid == 1) {
if (rs.val > fa.lazy.first) {
pre[r] = fa.lazy.second;
rs.val = fa.lazy.first;
}
} else {
rs.val = min(rs.val, fa.lazy.first);
}
fa.lazy = {inf, -1};
}
inline void Build (int l, int r, int rt) {
t[rt] = {inf, {inf, -1}};
if (l == r) return;
int mid = (l + r) >> 1;
Build(l, mid, rt << 1);
Build(mid + 1, r, rt << 1 | 1);
}
inline void Update (int a, int b, int c, int id, int l, int r, int rt) {
if (a <= l && r <= b) {
if (t[rt].lazy.first > c) t[rt].lazy = {c, id};
// 同理，叶子结点要看情况直接更新 pre
if (l == r) {
if (t[rt].val > c) {
t[rt].val = c;
pre[l] = id;
}
} else {
t[rt].val = min(t[rt].val, c);
}
return;
}
pushDown(l, r, rt);
int mid = (l + r) >> 1;
if (a <= mid) Update(a, b, c, id, l, mid, rt << 1);
if (b > mid) Update(a, b, c, id, mid + 1, r, rt << 1 | 1);
pushUp(rt);
}
inline int Query (int id, int l, int r, int rt) {
if (l == r) return t[rt].val;
pushDown(l, r, rt);
int mid = (l + r) >> 1;
if (id <= mid) return Query(id, l, mid, rt << 1);
else return Query(id, mid + 1, r, rt << 1 | 1);
}
int a[N], b[N], n;
int main () {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i ++) cin >> a[i];
for (int i = 1; i <= n; i ++) cin >> b[i];
Build(0, n, 1);
Update(n, n, 0, n + 1, 0, n, 1);
for (int i = n; i >= 1; i --) {
int ti = i + b[i];
// 用当前所在点的最短路 去 更新下滑过后的点所能跑到的区间，并记录这次更新是当前所在点更新的
if (a[ti]) Update(ti - a[ti], ti - 1, Query(i, 0, n, 1) + 1, i, 0, n, 1);
}
for (int i = 0; i <= n; i ++) Query(i, 0, n, 1); // 懒标记全推下去
if (t[1].val == inf) {
cout << "-1\n";
return 0;
}
cout << t[1].val << endl;
vector<int> res;
int cur = 0;
while (pre[cur] != n + 1) {
res.push_back(cur);
cur = pre[cur];
}
reverse(res.begin(), res.end());
for (auto i : res) cout << i << " ";
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
# CodeForces1690G_CountTheTrains
# 🔗
# 💡
首先可以得到，只有每一个前缀最小值才会被保留为本身的数
那么我们首先可以将序列变为一个 序列， 表示为前缀最小值， 表示不是前缀最小值
然后用一个答案记录动态修改答案
在一次操作中， 则它可能会变为前缀最小值，即变后小于前缀最小值了
如果变前不是，而变后是，那么就将其赋为 ，同时让答案
并且本次修改之后，向后找到第一个小于它的位置 （可以二分找），那么 里面的 都应该被覆盖为 ，我们减一下区间和，然后区间修改为 即可
二分的操作就是向后找区间最小值即可，第一个 的区间最小值小于修改后的
这其中的需求为：
一个能得到区间 最小值的线段树，支持单点修改、区间查询
一个 的线段树，支持单点修改、区间修改、区间查询
# ✅
const int N = 1e5 + 10;
int n, m, a[N];
int RES;
int t_min[N << 2], t_sum[N << 2], lazy[N << 2];
inline void pushup_min (int rt) { // 最小值线段树上推区间最小值
t_min[rt] = min(t_min[rt << 1], t_min[rt << 1 | 1]);
}
inline void pushup_sum (int rt) { // 01线段树上推区间和
t_sum[rt] = t_sum[rt << 1] + t_sum[rt << 1 | 1];
}
inline void pushdown_sum (int l, int r, int rt) { // 01线段树下推懒标记
if (!lazy[rt]) return;
int mid = (l + r) >> 1;
lazy[rt << 1] = lazy[rt << 1 | 1] = 1;
lazy[rt] = 0;
t_sum[rt << 1] = 0;
t_sum[rt << 1 | 1] = 0;
}
inline void build_min (int l, int r, int rt) { // 最小值线段树建树
t_min[rt] = 0x3f3f3f3f;
if (l == r) {
t_min[rt] = a[l];
return;
}
int mid = (l + r) >> 1;
build_min(l, mid, rt << 1);
build_min(mid + 1, r, rt << 1 | 1);
pushup_min(rt);
}
inline int query_min (int a, int b, int l, int r, int rt) { // 最小值线段树区间查询
if (a <= l && r <= b) return t_min[rt];
if (a > r || b < l) return 0x3f3f3f3f;
int mid = (l + r) >> 1;
return min(query_min(a, b, l, mid, rt << 1), query_min(a, b, mid + 1, r, rt << 1 | 1));
}
inline void build_sum (int l, int r, int rt) { // 01线段树建树
lazy[rt] = 0;
if (l == r) {
if (l == 1) t_sum[rt] = 1;
else t_sum[rt] = (a[l] < query_min(1, l - 1, 1, n, 1));
RES += t_sum[rt];
return;
}
int mid = (l + r) >> 1;
build_sum(l, mid, rt << 1);
build_sum(mid + 1, r, rt << 1 | 1);
pushup_sum(rt);
}
inline int query_sum (int a, int b, int l, int r, int rt) { // 01线段树区间查询
if (a > b) return 0;
if (a <= l && r <= b) return t_sum[rt];
if (a > r || b < l) return 0;
pushdown_sum(l, r, rt);
int mid = (l + r) >> 1;
return query_sum(a, b, l, mid, rt << 1) + query_sum(a, b, mid + 1, r, rt << 1 | 1);
}
inline void update_min (int id, int c, int l, int r, int rt) {
if (l == r) {
t_min[rt] -= c;
return;
}
int mid = (l + r) >> 1;
if (id <= mid) update_min(id, c, l, mid, rt << 1);
if (id > mid) update_min(id, c, mid + 1, r, rt << 1 | 1);
pushup_min(rt);
}
inline void update_sum0 (int a, int b, int l, int r, int rt) { // 01线段树区间赋0
if (a > b) return;
if (a > r || b < l) return;
if (a <= l && r <= b) {
t_sum[rt] = 0;
lazy[rt] = 1;
return;
}
pushdown_sum(l, r, rt);
int mid = (l + r) >> 1;
if (a <= mid) update_sum0(a, b, l, mid, rt << 1);
if (b > mid) update_sum0(a, b, mid + 1, r, rt << 1 | 1);
pushup_sum(rt);
}
inline void update_sum1 (int id, int l, int r, int rt) { // 01线段树单点赋1
if (l == r) {
t_sum[rt] = 1;
return;
}
pushdown_sum(l, r, rt);
int mid = (l + r) >> 1;
if (id <= mid) update_sum1(id, l, mid, rt << 1);
else update_sum1(id, mid + 1, r, rt << 1 | 1);
pushup_sum(rt);
}
inline void Solve () {
RES = 0;
cin >> n >> m;
for (int i = 1; i <= n; i ++) cin >> a[i];
build_min(1, n, 1);
build_sum(1, n, 1);
auto find_first_lowerid = [&](int id) { // < a[id] 的第一个位置
int l = id + 1;
int r = n;
int res = n + 1;
int aid = query_min(id, id, 1, n, 1);
while (l <= r) {
int mid = (l + r) >> 1;
if (query_min(l, mid, 1, n, 1) < aid) {
res = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
return res;
};
while (m --) {
int id, c; cin >> id >> c;
if (id == 1) {
update_min(id, c, 1, n, 1);
int ffl = find_first_lowerid(id); //cout << ffl << endl;
RES -= query_sum(2, ffl - 1, 1, n, 1);
update_sum0(id + 1, ffl - 1, 1, n, 1);
} else {
int pre_min = query_min(1, id - 1, 1, n, 1);
int aid = query_min(id, id, 1, n, 1);
if (aid >= pre_min && aid - c < pre_min) update_sum1(id, 1, n, 1), RES ++;
update_min(id, c, 1, n, 1);
int ffl = find_first_lowerid(id);
RES -= query_sum(id + 1, ffl - 1, 1, n, 1);
update_sum0(id + 1, ffl - 1, 1, n, 1);
}
cout << RES << " ";
} cout << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
# CCPC湖北省赛L_ChthollyAndTheBrokenChronograph
# 🔗
# 💡
一个单点上锁解锁、区间更新、区间查询的问题
区间加我们要知道这个区间有多少个需要被加的点才能快速在进入这个区间后立刻停止
那么就线段树结构体也维护一个区间上锁个数 ，那么对于已经走到并要修改的区间修改 ，我们需要加的为
考虑上锁与解锁都需要将所有的懒标记推下去才可以，但其实可以注意到其实更新就需要每一次都往下推，这就是一个单点更新的过程，在走到点之前就一直往下推懒标记就行了，也就是单点更新更新的是 ，区间更新更新的是
查询就暴力查就行
# ✅
const int N = 1e5 + 10;
struct SegmentTree {
ll val, lazy;
int lock;
} t[N << 2];
int n, q, s[N];
ll a[N];
inline void pushUp (int rt) {
t[rt].val = t[rt << 1].val + t[rt << 1 | 1].val;
t[rt].lock = t[rt << 1].lock + t[rt << 1 | 1].lock;
}
inline void pushDown (int l, int r, int rt) {
if (!t[rt].lazy) return;
int mid = (l + r) >> 1;
t[rt << 1].val += (1ll * mid - l + 1 - t[rt << 1].lock) * t[rt].lazy;
t[rt << 1 | 1].val += (1ll * r - mid - t[rt << 1 | 1].lock) * t[rt].lazy;
t[rt << 1].lazy += t[rt].lazy;
t[rt << 1 | 1].lazy += t[rt].lazy;
t[rt].lazy = 0;
}
inline void Build (int l, int r, int rt) {
t[rt].lazy = 0;
if (l == r) {
t[rt] = {a[l], 0, !s[l]};
return;
}
int mid = (l + r) >> 1;
Build(l, mid, rt << 1);
Build(mid + 1, r, rt << 1 | 1);
pushUp(rt);
}
inline void Update (int a, int b, ll c, int l, int r, int rt) {
if (a <= l && r <= b) {
t[rt].val += (1ll * r - l + 1 - t[rt].lock) * c;
t[rt].lazy += c;
return;
}
if (a > r || b < l) return;
pushDown(l, r, rt);
int mid = (l + r) >> 1;
Update(a, b, c, l, mid, rt << 1);
Update(a, b, c, mid + 1, r, rt << 1 | 1);
pushUp(rt);
}
inline void Lock (int id, int l, int r, int rt) {
if (l == id && id == r) {
t[rt].lock = 1;
return;
}
pushDown(l, r, rt);
int mid = (l + r) >> 1;
if (id <= mid) Lock(id, l, mid, rt << 1);
else Lock(id, mid + 1, r, rt << 1 | 1);
pushUp(rt);
}
inline void unLock (int id, int l, int r, int rt) {
if (l == id && id == r) {
t[rt].lock = 0;
return;
}
pushDown(l, r, rt);
int mid = (l + r) >> 1;
if (id <= mid) unLock(id, l, mid, rt << 1);
else unLock(id, mid + 1, r, rt << 1 | 1);
pushUp(rt);
}
inline ll Query (int a, int b, int l, int r, int rt) {
if (a <=l && r <= b) return t[rt].val;
if (a > r || b < l) return 0;
pushDown(l, r, rt);
int mid = (l + r) >> 1;
return Query(a, b, l, mid, rt << 1) + Query(a, b, mid + 1, r, rt << 1 | 1);
}
int main () {
ios::sync_with_stdio(false);
cin.tie(nullptr);
scanf("%d%d", &n, &q);
for (int i = 1; i <= n; i ++) scanf("%lld", &a[i]);
for (int i = 1; i <= n; i ++) scanf("%d", &s[i]);
Build(1, n, 1);
while (q --) {
int op; scanf("%d", &op);
if (op == 1) {
int x; scanf("%d", &x);
Lock(x, 1, n, 1);
} else if (op == 2) {
int x; scanf("%d", &x);
unLock(x, 1, n, 1);
} else if (op == 3) {
int l, r; ll c; scanf("%d%d%lld", &l, &r, &c);
Update(l, r, c, 1, n, 1);
} else {
int l, r; scanf("%d%d", &l, &r);
printf("%lld\n", Query(l, r, 1, n, 1));
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
# CodeForces1477B_NezzarAndBinaryString
# 🔗
# 💡
我们只能改上一次询问后的内容来让我们下一次询问满足，当然这一次修改可能不只是为了下一次，也可能是下下次...
所以我们没法确定要修改哪一部分，后面的操作太多了
但是注意到每一次询问都要满足，所以每次操作的上一次询问也要满足
出现了更强的关联性就是一次修改只能修改上一次询问的区间，且上一次询问的区间全部相等
那么就可以反过来看：就是从后往前每次修改 字符串，所有的修改都是为了下一次询问能满足且只能修改下一次询问的区间
对于区间是 变 还是 变 ，注意到有一个条件是每次只能修改严格少于一半的数量
可以在下一次修改的区间里面查询 的个数，如果少于一半就只能变 ，如果多于一半就只能变 ，如果等于一半那就说明都改不了，就只能 NO 了
当然还要求了最后两串相等，这些操作都是固定的，所以所有操作走完之后看看是不是每一位都相等即可
需求内需要的工具：支持区间变 变 、可区间查询。那么就使用一个带懒标记的线段树即可
# ✅
const int N = 2e5 + 10;
string a, b;
struct node {
int val;
int lazy;
} t[N << 2];
inline void pushup (int rt) {
t[rt].val = t[rt << 1].val + t[rt << 1 | 1].val;
}
inline void pushdown (int l, int r, int rt) {
if (!t[rt].lazy) return;
if (t[rt].lazy == -1) {
t[rt << 1].val = t[rt << 1 | 1].val = 0;
t[rt << 1].lazy = t[rt << 1 | 1].lazy = -1;
t[rt].lazy = 0;
} else {
int mid = (l + r) >> 1;
t[rt << 1].val = mid - l + 1; t[rt << 1 | 1].val = r - mid;
t[rt << 1].lazy = t[rt << 1 | 1].lazy = 1;
t[rt].lazy = 0;
}
}
inline void build (int l, int r, int rt) {
t[rt].lazy = 0;
if (l == r) {
t[rt].val = b[l] - '0';
return;
}
int mid = (l + r) >> 1;
build(l, mid, rt << 1);
build(mid + 1, r, rt << 1 | 1);
pushup(rt);
}
inline void update (int a, int b, int c, int l, int r, int rt) {
if (a > r || b < l) return;
if (a <= l && r <= b) {
if (c == 0) {
t[rt].val = 0;
t[rt].lazy = -1;
} else {
t[rt].val = r - l + 1;
t[rt].lazy = 1;
}
return;
}
pushdown(l, r, rt);
int mid = (l + r) >> 1;
if (a <= mid) update(a, b, c, l, mid, rt << 1);
if (b > mid) update(a, b, c, mid + 1, r, rt << 1 | 1);
pushup(rt);
}
inline int query (int a, int b, int l, int r, int rt) {
if (a > r || b < l) return 0;
if (a <= l && r <= b) return t[rt].val;
pushdown(l, r, rt);
int res = 0, mid = (l + r) >> 1;
if (a <= mid) res += query(a, b, l, mid, rt << 1);
if (b > mid) res += query(a, b, mid + 1, r, rt << 1 | 1);
return res;
}
inline void Solve () {
int n, m; cin >> n >> m;
cin >> a >> b; a = "0" + a; b = "0" + b;
vector<pair<int, int> > ope(m);
for (auto &[l, r] : ope) cin >> l >> r;
reverse(ope.begin(), ope.end());
build(1, n, 1);
for (auto &[l, r] : ope) {
int num1 = query(l, r, 1, n, 1);
if (num1 * 2 == r - l + 1) {
cout << "NO\n";
return;
} else if (num1 <= (r - l) / 2) {
update(l, r, 0, 1, n, 1);
} else {
update(l, r, 1, 1, n, 1);
}
}
for (int i = 1; i <= n; i ++) {
if (a[i] - '0' != query(i, i, 1, n, 1)) {
cout << "NO\n";
return;
}
}
cout << "YES\n";
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
# CodeForces1668D_OptimalPartition
# 🔗
# 💡
看到这个其实很想维护完前缀和后，对于每个 扫描每个在它之前的 然后按照规则维护 贡献 的最大值
对于规则一和规则三可以两个线段树来实现，将 贡献分开维护，每一个 位置插入为 和 ，这也就是 和 ，这样的话在统计的时候可以把 的贡献加上，边记录边统计
当然因为是线段树区间维护数值可能会到 和负数，所以这里需要离散化一下
在维护最大值的时候对于规则一就查第一棵里面大于 的位置上的最大值 ，第二棵小于 的位置上的最大值
此时规则二要查 相等的里面的最大值，这个用一个数组进行更新即可
# ✅
const int N = 5e5 + 30;
pair<int, int> t[N << 2];
# define mid ((l + r) >> 1)
inline void push_Up (int rt) {
t[rt].first = max(t[rt << 1].first, t[rt << 1 | 1].first);
t[rt].second = max(t[rt << 1].second, t[rt << 1 | 1].second);
}
inline void Build (int l, int r, int rt) {
t[rt] = {-0x3f3f3f3f, -0x3f3f3f3f};
if (l == r) return;
Build(l, mid, rt << 1);
Build(mid + 1, r, rt << 1 | 1);
}
inline void Update (int id, int c1, int c2, int l, int r, int rt) {
if (l == id && id == r) {
t[rt] = {max(t[rt].first, c1), max(t[rt].second, c2)};
return;
}
if (id <= mid) Update(id, c1, c2, l, mid, rt << 1);
else Update(id, c1, c2, mid + 1, r, rt << 1 | 1);
push_Up(rt);
}
inline int Query1 (int a, int b, int l, int r, int rt) {
if (a <= l && r <= b) return t[rt].first;
if (a > r || b < l) return -0x3f3f3f3f;
return max(Query1(a, b, l, mid, rt << 1), Query1(a, b, mid + 1, r, rt << 1 | 1));
}
inline int Query2 (int a, int b, int l, int r, int rt) {
if (a <= l && r <= b) return t[rt].second;
if (a > r || b < l) return -0x3f3f3f3f;
return max(Query2(a, b, l, mid, rt << 1), Query2(a, b, mid + 1, r, rt << 1 | 1));
}
int n;
ll a[N];
ll sum[N];
int dp[N], dp1[N];
inline void Solve () {
cin >> n;
for (int i = 1; i <= n; i ++) cin >> a[i];
for (int i = 1; i <= n; i ++) sum[i] = sum[i - 1] + a[i];
vector<ll> nums; for (int i = 0; i <= n; i ++) nums.push_back(sum[i]);
sort(nums.begin(), nums.end());
nums.erase(unique(nums.begin(), nums.end()), nums.end());
auto id = [&](ll x) { return lower_bound(nums.begin(), nums.end(), x) - nums.begin() + 1; };
int up = nums.size() + 1;
for (int i = 0; i <= n; i ++) dp[i] = -0x3f3f3f3f;
for (int i = 0; i <= up + 1; i ++) dp1[i] = -0x3f3f3f3f;
Build(0, up + 1, 1);
Update(id(0), 0, 0, 0, up + 1, 1); dp1[id(0)] = 0;
for (int i = 1; i <= n; i ++) {
int val = id(sum[i]);
dp[i] = max({Query1(0, val - 1, 0, up + 1, 1) + i, dp1[val], Query2(val + 1, up + 1, 0, up + 1, 1) - i});
Update(val, dp[i] - i, dp[i] + i, 0, up + 1, 1);
dp1[val] = max(dp1[val], dp[i]);
}
cout << dp[n] << endl;
}
int main () {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int cass; cin >> cass; while ( cass -- ) {
Solve ();
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
# HDU2021多校(2)B_ILoveTree
# 🔗
# 💡
这就很板啊...路径更新，单点查询，裸的树剖+线段树吧
如果什么都不考虑的情况下，树剖完就和 这道题 一模一样了
但是关键就在，树剖后更新的时候，对左端点和右端点的决策
一个路径 会转化为 ，且树剖更新下总是高的对应的线性位置更小，故都是高的到低的更新
所以在第一段时， 是一次更新的右端点， 是一次更新的左端点，那么越靠左要加的越多，这样就应该用 ，也就是
而在 时，顺序就是正常的，就 ，也就是
且左右端点应该随着更新次数的增加越来越偏离更新区间，比如已经更新了 个点了，那么我再用它作为 更新的时候应该是 ，右端点同理要加
从下到上再到从上到下这是两种不同的更新方式，所以要分两次更新，且每次更新时要提出所有的更新区间然后分别按深度降序排序和深度升序排序
但是还有问题就是考虑到 这个位置会被更新两次且第二段整体左端点会偏移，所以只需要第一段记完 后第二段再用时是 开始的，然后让最后答案 即可
# ✅
const int N = 2e5 + 10;
const int M = 2 * N;
struct Edge {
int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to) {
edge[++cnt] = {head[from], to};
head[from] = cnt;
}
int top[N], fa[N], son[N], sz[N], dep[N];
int dfn[N], id[N], idx;
inline void Dfs1 (int u, int fath) {
sz[u] = 1; dep[u] = dep[fath] + 1;
son[u] = 0; fa[u]= fath;
for (int i = head[u]; i; i = edge[i].nxt) {
int v = edge[i].to;
if (v == fath) continue;
Dfs1(v, u);
sz[u] += sz[v];
if (sz[son[u]] < sz[v]) son[u] = v;
}
}
inline void Dfs2 (int u, int topu) {
top[u] = topu;
dfn[++idx] = u; id[u] = idx;
if (son[u]) Dfs2(son[u], topu);
for (int i = head[u]; i; i = edge[i].nxt) {
int v = edge[i].to;
if (v == fa[u] || v == son[u]) continue;
Dfs2(v, v);
}
}
int n;
int q;
struct Sgtr {
ll sum2, sum1, sum0; // 三个系数实值
ll laz2, laz1, laz0; // 三个系数懒标记
bool haslaz = false;
} t[N << 2];
inline void pushup (int rt) {
int ch = rt << 1;
t[rt].sum0 = t[ch].sum0 + t[ch | 1].sum0;
t[rt].sum1 = t[ch].sum1 + t[ch | 1].sum1;
t[rt].sum2 = t[ch].sum2 + t[ch | 1].sum2;
}
inline void pushdown (int l, int r, int rt) {
if (!t[rt].haslaz) return;
int ch = rt << 1;
t[ch].sum0 += t[rt].laz0; t[ch | 1].sum0 += t[rt].laz0;
t[ch].sum1 += t[rt].laz1; t[ch | 1].sum1 += t[rt].laz1;
t[ch].sum2 += t[rt].laz2; t[ch | 1].sum2 += t[rt].laz2;
t[ch].laz0 += t[rt].laz0; t[ch | 1].laz0 += t[rt].laz0;
t[ch].laz1 += t[rt].laz1; t[ch | 1].laz1 += t[rt].laz1;
t[ch].laz2 += t[rt].laz2; t[ch | 1].laz2 += t[rt].laz2;
t[rt].laz0 = t[rt].laz1 = t[rt].laz2 = t[rt].haslaz = 0;
t[ch].haslaz = t[ch | 1].haslaz = 1;
}
inline void update (int basl, int a, int b, int l = 1, int r = 2 * n, int rt = 1) {
if (a <= l && r <= b) {
t[rt].sum2 ++;
t[rt].sum1 += 2 * (basl - 1);
t[rt].sum0 += (basl - 1) * (basl - 1);
t[rt].laz2 ++;
t[rt].laz1 += 2 * (basl - 1);
t[rt].laz0 += (basl - 1) * (basl - 1);
t[rt].haslaz = true;
return;
}
pushdown(l, r, rt);
int mid = (l + r) >> 1;
if (a <= mid) update(basl, a, b, l, mid, rt << 1);
if (b > mid) update(basl, a, b, mid + 1, r, rt << 1 | 1);
pushup(rt);
}
inline ll query (int id, int l = 1, int r = 2 * n, int rt = 1) {
if (l == r) {
return t[rt].sum0 - t[rt].sum1 * l + t[rt].sum2 * l * l;
}
int mid = (l + r) >> 1;
pushdown(l, r, rt);
if (id <= mid) return query(id, l, mid, rt << 1);
else return query(id, mid + 1, r, rt << 1 | 1);
}
inline int Change (int num, int x, int y, int op) {
vector<pair<int, int> > v_upd; // 所有更新区间
while (top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]]) swap(x, y);
v_upd.push_back({top[x], x});
x = fa[top[x]];
}
if (dep[x] > dep[y]) swap(x, y);
v_upd.push_back({x, y});
int num_upd = num;
if (op == 0) {
sort(v_upd.begin(), v_upd.end(), [&](pair<int, int> a, pair<int, int> b) { return dep[a.first] > dep[b.first]; });
for (int i = 0; i < v_upd.size(); i ++) {
int l = v_upd[i].first;
int r = v_upd[i].second;
update(id[r] + 2 + num_upd, id[l], id[r]); // 由于右端点要记录+1，故+2-1 = +1
num_upd += id[r] - id[l] + 1;
}
} else {
sort(v_upd.begin(), v_upd.end(), [&](pair<int, int> a, pair<int, int> b) { return dep[a.first] < dep[b.first]; });
for (int i = 0; i < v_upd.size(); i ++) {
int l = v_upd[i].first;
int r = v_upd[i].second;
update(id[l] - num_upd, id[l], id[r]);
num_upd += id[r] - id[l] + 1;
}
}
return num_upd;
}
inline int Lca (int x, int y) {
while (top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]]) swap(x, y);
x = fa[top[x]];
}
if (dep[x] > dep[y]) swap(x, y);
return x;
}
int neddel[N];
signed main () {
scanf("%lld", &n);
for (int i = 1; i < n; i ++) {
int u, v; scanf("%lld%lld", &u, &v);
add_Edge(u, v);
add_Edge(v, u);
}
Dfs1(1, 0); Dfs2(1, 1);
int q; scanf("%lld", &q);
while (q --) {
int op; scanf("%lld", &op);
if (op == 1) {
int x, y; scanf("%lld%lld", &x, &y);
int lca = Lca(x, y);
if (x == lca) {
Change(0, x, y, 1);
} else if (y == lca) {
Change(0, x, y, 0);
} else {
int num = Change(0, x, lca, 0);
neddel[lca] += num * num;
Change(num - 1, lca, y, 1);
}
} else {
int x; scanf("%lld", &x);
printf("%lld\n", query(id[x]) - neddel[x]);
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
# HDU2021多校8D_CountingStars
# 🔗
# 💡
首先看这些操作都有什么影响
操作一 就是消掉最后一位
操作二 就是把最高位再往前推一位
操作二很好维护，令 表示区间的和， 就是区间最高位的和
那么这里既然每一个都是 ，那么在区间上也是一样的
但是操作 怎么搞，其实可以考虑到一共只有 位，那么操作 在保证每一个都成功减的时候，全局也就只会操作 次单点修改，故使用势能优化，势能优化在区间内含 最多的点的含 量为 时，就可以不往下进行了
结合上面的，我们维护的有：
- 区间和
- 区间最高位和
- 区间最多 的数量
- 每一个 的位是几，在减操作时要减去的
- 在操作二时下推的懒标记
在操作一的区间更新下，对于叶子区间那么就是上面说的，推这个懒标记的时候就是 ，也就是 ，而 ，同时注意要将懒标记叠加给两个儿子然后清空自己的
在操作二下，我们单点修改到的叶子节点，要保证路上每一个节点的 都不是 ，然后在叶子结点让 ，同时本 减去 的结尾值，并 掉，注意如果 时直接让 设置为 即可
# ✅
const int N = 1e5 + 10;
const int mod = 998244353;
inline int lowbit (int x) { return x & -x; }
inline ll ksm (int a, int b) { int res = 1; while (b) {if (b & 1) res = (ll)res * a % mod; a = (ll)a * a % mod; b >>= 1;} return res;}
ll pw2[31];
struct node {
ll sumhigh, sumval;
ll mostbit, lessbit;
int lazymul2;
vector<int> bit;
} t[N << 2];
inline void pushup (int rt) {
node &ls = t[rt << 1], &rs = t[rt << 1 | 1], &fa = t[rt];
fa.sumhigh = (ls.sumhigh + rs.sumhigh) % mod;
fa.sumval = (ls.sumval + rs.sumval) % mod;
fa.lessbit = min(ls.lessbit, rs.lessbit);
fa.mostbit = max(ls.mostbit, rs.mostbit);
}
inline void pushdown (int l, int r, int rt) { // 加操作的下推
node &ls = t[rt << 1], &rs = t[rt << 1 | 1], &fa = t[rt];
if (!fa.lazymul2) return;
(ls.sumval += ls.sumhigh * (ksm(2, fa.lazymul2) - 1) % mod) %= mod;
(rs.sumval += rs.sumhigh * (ksm(2, fa.lazymul2) - 1) % mod) %= mod;
(ls.sumhigh *= ksm(2, fa.lazymul2)) %= mod;
(rs.sumhigh *= ksm(2, fa.lazymul2)) %= mod;
ls.lazymul2 += fa.lazymul2; rs.lazymul2 += fa.lazymul2;
fa.lazymul2 = 0;
}
inline void update (int a, int b, int l, int r, int rt) { // 加操作的区间更新
if (!t[rt].mostbit) return;
if (a <= l && r <= b) {
t[rt].lazymul2 ++;
(t[rt].sumval += t[rt].sumhigh) %= mod;
(t[rt].sumhigh *= 2) %= mod;
return;
}
int mid = (l + r) >> 1;
pushdown(l, r, rt);
if (a <= mid) update(a, b, l, mid, rt << 1);
if (b > mid) update(a, b, mid + 1, r, rt << 1 | 1);
pushup(rt);
}
/*
2 10 2 1 1
0 8 0 1 1
*/
inline void update_del (int a, int b, int l, int r, int rt) {
if (t[rt].mostbit == 0) return;
if (l == r) {
t[rt].lessbit = max(0ll, t[rt].lessbit - 1);
t[rt].mostbit --;
if (t[rt].mostbit == 0) {
t[rt].sumhigh = t[rt].sumval = 0;
} else {
(t[rt].sumval -= t[rt].bit.back()) %= mod;
t[rt].bit.pop_back();
}
return;
}
int mid = (l + r) >> 1;
pushdown(l, r, rt);
if (a <= mid) update_del(a, b, l, mid, rt << 1);
if (b > mid) update_del(a, b, mid + 1, r, rt << 1 | 1);
pushup(rt);
}
inline ll query (int a, int b, int l, int r, int rt) {
if (a <= l && r <= b) return t[rt].sumval;
pushdown(l, r, rt);
int mid = (l + r) >> 1; ll res = 0;
if (a <= mid) (res += query(a, b, l, mid, rt << 1)) %= mod;
if (b > mid) (res += query(a, b, mid + 1, r, rt << 1 | 1)) %= mod;
return res;
}
inline void clear (node &x) {
x.bit.clear();
x.lazymul2 = 0;
x.lessbit = 0;
x.mostbit = 0;
x.sumhigh = 0;
x.sumval = 0;
}
inline void build (int l, int r, int rt) {
clear(t[rt]);
if (l == r) {
scanf("%lld", &t[rt].sumval);
ll x = t[rt].sumval;
for (int i = 30; i >= 0; i --) {
if (pw2[i] <= x) {
if (!t[rt].sumhigh) t[rt].sumhigh = pw2[i];
t[rt].bit.push_back(pw2[i]);
x -= pw2[i];
t[rt].lessbit ++; t[rt].mostbit ++;
}
}
return;
}
int mid = (l + r) >> 1;
build(l, mid, rt << 1);
build(mid + 1, r, rt << 1 | 1);
pushup(rt);
}
inline void Solve () {
int n; scanf("%d", &n);
build(1, n, 1);
int q; scanf("%d", &q);
while (q --) {
int op, l, r; scanf("%d%d%d", &op, &l, &r);
if (op == 1) {
printf("%lld\n", (query(l, r, 1, n, 1) + mod) % mod);
} else if (op == 2) {
update_del(l, r, 1, n, 1);
} else {
update(l, r, 1, n, 1);
}
}
}
int main () {
pw2[0] = 1;
for (int i = 1; i <= 30; i ++) pw2[i] = pw2[i - 1] * 2;
int cass; scanf("%d", &cass); while (cass --) {
Solve();
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
# HDU1394_MinimumInversionNumber
# 🔗
http://acm.hdu.edu.cn/showproblem.php?pid=1394
# 💡
# ✅
#include <map>
#include <set>
#include <stack>
#include <queue>
#include <cmath>
#include <string>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define G 10.0
#define LNF 1e18
#define eps 1e-6
#define mod 1e9 + 7
#define ll long long
#define INF 0x7FFFFFFF
#define PI acos(-1.0)
#define pb(x) push_back(x)
#define SP system("pause")
#define mm(a, b) memset(a, b, sizeof(a))
#define fir(i, a, n) for (ll i = a; i <= n; i++)
#define rif(i, a, n) for (ll i = a; i >= n; i--)
#define each_cass(cass) for (scanf("%d", &cass); cass; cass--)
using namespace std;
const int maxn = 5e3 + 10;
struct SegTree
{
int val;
int lazy;
} SegTree[maxn << 2];
int n;
int a[maxn];
void PushUp(int rt);
void PushDown(int l, int r, int rt);
void BuildTree(int l, int r, int rt);
void UpDate(int a, int b, int c, int l, int r, int rt);
ll Query(int a, int b, int l, int r, int rt);
int main()
{
while (scanf("%d", &n) == 1)
{
BuildTree(1, n, 1);
ll cnt = 0;
fir(i, 1, n)
scanf("%d", &a[i]),
UpDate(a[i], a[i], 1, 1, n, 1),
cnt += Query(a[i] + 1, n, 1, n, 1);
ll res = cnt;
fir(i, 1, n)
{
cnt += (n - 1 - a[i]) - a[i];
res = min(res, cnt);
}
printf("%lld\n", res);
}
return 0;
}
void PushUp(int rt)
{
SegTree[rt].val = SegTree[rt << 1].val + SegTree[rt << 1 | 1].val;
}
void PushDown(int l, int r, int rt)
{
if (!SegTree[rt].lazy)
return;
int mid = (l + r) >> 1;
SegTree[rt << 1].val += SegTree[rt].lazy * (mid - l + 1);
SegTree[rt << 1 | 1].val += SegTree[rt].lazy * (r - mid);
SegTree[rt << 1].lazy += SegTree[rt].lazy;
SegTree[rt << 1 | 1].lazy += SegTree[rt].lazy;
SegTree[rt].lazy = 0;
}
void BuildTree(int l, int r, int rt)
{
SegTree[rt].lazy = 0;
if (l == r)
{
SegTree[rt].val = 0;
return;
}
int mid = (l + r) >> 1;
BuildTree(l, mid, rt << 1);
BuildTree(mid + 1, r, rt << 1 | 1);
PushUp(rt);
}
void UpDate(int a, int b, int c, int l, int r, int rt)
{
if (a > r || b < l)
return;
if (a <= l && b >= r)
{
SegTree[rt].val += c * (r - l + 1);
SegTree[rt].lazy += c;
return;
}
PushDown(l, r, rt);
int mid = (l + r) >> 1;
UpDate(a, b, c, l, mid, rt << 1);
UpDate(a, b, c, mid + 1, r, rt << 1 | 1);
PushUp(rt);
}
ll Query(int a, int b, int l, int r, int rt)
{
if (a > r || b < l)
return 0;
if (a <= l && b >= r)
return SegTree[rt].val;
int mid = (l + r) >> 1;
return Query(a, b, l, mid, rt << 1) + Query(a, b, mid + 1, r, rt << 1 | 1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
# NamomoCamp2022春季div1每日一题_子串最大差
# 🔗
# 💡1
和 牛客2022寒假算法基础集训营4G_子序列权值乘积 想法类似
作为最小值
由于这里是子区间，那么我们用 分别维护
- 左侧最大的 的下标，若没有则是
- 右侧最小的 的下标，若没有则是
那么一共可覆盖的范围为 ，这里对答案的贡献为
作为最大值
同理
最后结果让最大值减去最小值即可
两个偏序关系 权值,下标
那么令权值为线段树的根节点，这个可以离散化后实现
令下标为线段树每个根节点表示的权值
在求最大下标和最小下标的时候，我们让线段树维护区间
每次查询 是查询 的区间
每次更新则是在 离散化后的位置上单点更新为
# ✅1
const int N = 5e5 + 10;
int n;
ll a[N];
int b[N], Mx;
vector<ll> nums;
struct Sgtr {
int mx, mn;
} t[N << 2];
inline void PushUp ( int rt ) {
Sgtr &ls = t[rt << 1], &rs = t[rt << 1 | 1], &fa = t[rt];
fa = {max(ls.mx, rs.mx), min(ls.mn, rs.mn)};
}
inline void Update ( int id, int c, int l = 1, int r = Mx, int rt = 1 ) {
if ( r < id || id < l ) return;
if ( l == id && id == r ) {
t[rt] = {max(c, t[rt].mx), min(c, t[rt].mn)};
return;
}
int mid = (l + r) >> 1;
Update(id, c, l, mid, rt << 1);
Update(id, c, mid + 1, r, rt << 1 | 1);
PushUp(rt);
}
inline int Query_Max ( int a, int b, int l = 1, int r = Mx, int rt = 1 ) {
if ( r < a || b < l ) return 0;
if ( a <= l && r <= b ) return t[rt].mx;
int mid = (l + r) >> 1;
return max(Query_Max(a, b, l, mid, rt << 1), Query_Max(a, b, mid + 1, r, rt << 1 | 1));
}
inline int Query_Min ( int a, int b, int l = 1, int r = Mx, int rt = 1 ) {
if ( r < a || b < l ) return 0x3f3f3f3f;
if ( a <= l && r <= b ) return t[rt].mn;
int mid = (l + r) >> 1;
return min(Query_Min(a, b, l, mid, rt << 1), Query_Min(a, b, mid + 1, r, rt << 1 | 1));
}
int l[N], r[N];
inline ll Calc1 () {
for ( int i = 0; i < (N << 2); i ++ ) t[i] = {0, 0x3f3f3f3f};
memset(l, 0, sizeof l);
for ( int i = 1; i <= n; i ++ ) {
l[i] = Query_Max(1, b[i] - 1);
Update(b[i], i);
}
for ( int i = 0; i < (N << 2); i ++ ) t[i] = {0, 0x3f3f3f3f};
memset(r, 0, sizeof r);
for ( int i = n; i >= 1; i -- ) {
r[i] = Query_Min(1, b[i]);
if ( r[i] == 0x3f3f3f3f ) r[i] = n + 1;
Update(b[i], i);
}
ll res = 0;
for ( int i = 1; i <= n; i ++ ) {
ll numl = i - l[i];
ll numr = r[i] - i;
ll num = numl * numr;
res += a[i] * num;
}
return res;
}
inline ll Calc2 () {
for ( int i = 0; i < (N << 2); i ++ ) t[i] = {0, 0x3f3f3f3f};
memset(l, 0, sizeof l);
for ( int i = 1; i <= n; i ++ ) {
l[i] = Query_Max(b[i] + 1, Mx);
Update(b[i], i);
}
for ( int i = 0; i < (N << 2); i ++ ) t[i] = {0, 0x3f3f3f3f};
memset(r, 0, sizeof r);
for ( int i = n; i >= 1; i -- ) {
r[i] = Query_Min(b[i], Mx);
if ( r[i] == 0x3f3f3f3f ) r[i] = n + 1;
Update(b[i], i);
}
ll res = 0;
for ( int i = 1; i <= n; i ++ ) {
ll numl = i - l[i];
ll numr = r[i] - i;
ll num = numl * numr;
res += a[i] * num;
}
return res;
}
int main () {
ios::sync_with_stdio(false);
cin >> n;
for ( int i = 1; i <= n; i ++ ) cin >> a[i], nums.push_back(a[i]);
sort (nums.begin(), nums.end());
nums.erase(unique(nums.begin(), nums.end()), nums.end());
for ( int i = 1; i <= n; i ++ ) {
b[i] = lower_bound(nums.begin(), nums.end(), a[i]) - nums.begin() + 2;
Mx = max(Mx, b[i]);
}
cout << Calc2() - Calc1() << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
# POJ2299_Ultra-QuickSort
# 🔗
http://poj.org/problem?id=2299
# 💡
# ✅
/*
________ _ ________ _
/ ______| | | | __ | | |
/ / | | | |__| | | |
| | | |___ _ _ _ ___ _ _____ | ___| ______ _____ ___ _ | |
| | | __ \ |_| | | | | | _\| | | ____| | |\ \ | __ | | _ | | _\| | | |
| | | | \ | _ | | | | | | \ | | \___ | | \ \ | |_/ _| | |_| | | | \ | | |
\ \______ | | | | | | \ |_| / | |_/ | ___/ | | | \ \ | /_ \__ | | |_/ | | |
Author : \________| |_| |_| |_| \___/ |___/|_| |_____| _________|__| \__\ |______| | | |___/|_| |_|
____| |
\_____/
*/
//#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF
#define ll long long
#define ull unsigned long long
#define INT __int128
#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << endl
#define CHIVAS_ inline int MAIN(){
#define _REGAL return 0;}
#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
//#define map unordered_map
#define pbb pair<bool, bool>
#define pii pair<int, int>
#define pll pair<ll, ll>
#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for ( int cass = inputInt(); cass; cass--)
#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1
using namespace std;
inline int inputInt(){int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);}
inline void outInt(int X){if(X<0) {putchar('-'); X=~(X-1);}int s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline ll inputLL(){ll X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1); }
inline void outLL(ll X){if(X<0) {putchar('-'); X=~(X-1);}ll s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return make_pair(MaxVal, MaxId);}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return make_pair(MinVal, MinId);}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return make_pair(MaxVal, MaxId);}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return make_pair(MinVal, MinId);}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return make_pair(cnt, div);}
namespace Solution_In_Codeforces{
inline void solve();
namespace N_cass {
void Main(){ int cass; for ( cin >> cass; cass; cass -- ) { solve();} };
}
namespace One_cass {
void Main(){ solve(); };
}
}
inline void Solution_In_Codeforces::solve() {}
// ============================================================= BeginCode ==========================================================================================
const int maxn = 5e5 + 15;
struct SegTree{
int lazy;
int val;
} SegTree[maxn << 2];
struct Num{
int id;
int val;
friend bool operator<(Num a,Num b){
return a.val < b.val;
}
} Num[maxn];
int A[maxn];
int n;
inline void Disc();
inline void PushUp(int rt);
inline void PushDown(int l, int r, int rt);
inline void BuildTree(int l, int r, int rt);
inline void UpDate(int a, int b, int c, int l, int r, int rt);
inline ll Query(int a, int b, int l, int r, int rt);
CHIVAS_
while(scanf("%lld",&n)==1,n){
for (int i = 1; i <= n; i++) scanf("%lld", &Num[i].val), Num[i].id = i;
Disc();
ll cnt = 0;
BuildTree(1, n, 1);
for (int i = 1; i <= n; i++){
UpDate(A[i], A[i], 1, 1, n, 1);
cnt += Query(A[i]+1, n, 1, n, 1);
}
printf("%lld\n", cnt);
}
_REGAL
inline void Disc(){
int cnt = 0;
sort(Num + 1, Num + n + 1);
A[Num[1].id] = 1;
cnt=1;
for (int i = 2; i <= n; i++){
if(Num[i].val==Num[i-1].val)
A[Num[i].id] = cnt;
else
A[Num[i].id] = ++cnt;
}
}
inline void PushUp(int rt){
SegTree[rt].val = SegTree[rt << 1].val + SegTree[rt << 1 | 1].val;
}
inline void PushDown(int l, int r, int rt){
if (!SegTree[rt].lazy)
return;
int mid = (l + r) >> 1;
SegTree[rt << 1].val += SegTree[rt].lazy * (mid - l + 1);
SegTree[rt << 1 | 1].val += SegTree[rt].lazy * (r - mid);
SegTree[rt << 1].lazy += SegTree[rt].lazy;
SegTree[rt << 1 | 1].lazy += SegTree[rt].lazy;
SegTree[rt].lazy = 0;
}
inline void BuildTree(int l, int r, int rt){
SegTree[rt].lazy = 0;
if (l == r)
{
SegTree[rt].val = 0;
return;
}
int mid = (l + r) >> 1;
BuildTree(l, mid, rt << 1);
BuildTree(mid + 1, r, rt << 1 | 1);
PushUp(rt);
}
inline void UpDate(int a, int b, int c, int l, int r, int rt){
if (a > r || b < l)
return;
if (a <= l && b >= r){
SegTree[rt].val += c * (r - l + 1);
SegTree[rt].lazy += c;
return;
}
PushDown(l, r, rt);
int mid = (l + r) >> 1;
UpDate(a, b, c, l, mid, rt << 1);
UpDate(a, b, c, mid + 1, r, rt << 1 | 1);
PushUp(rt);
}
inline ll Query(int a, int b, int l, int r, int rt){
if (a > r || b < l)
return 0;
if (a <= l && b >= r)
return SegTree[rt].val;
PushDown ( l, r, rt );
int mid = (l + r) >> 1;
return Query(a, b, l, mid, rt << 1) + Query(a, b, mid + 1, r, rt << 1 | 1);
}
// ============================================================= EndCode ==========================================================================================
int main(){
#ifndef ONLINE_JUDGE
freopen("in.in", "r", stdin);
freopen("out.out", "w", stdout);
#endif
MAIN();
#ifndef ONLINE_JUDGE
cerr << "\033[1m\033[31m\n"
<< "\n\n===============================\n"
<< "|| Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << " s. ||\n"
<< "==============================="
<< "\033[0m";
#endif
exit(0);
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259