分治

#

---

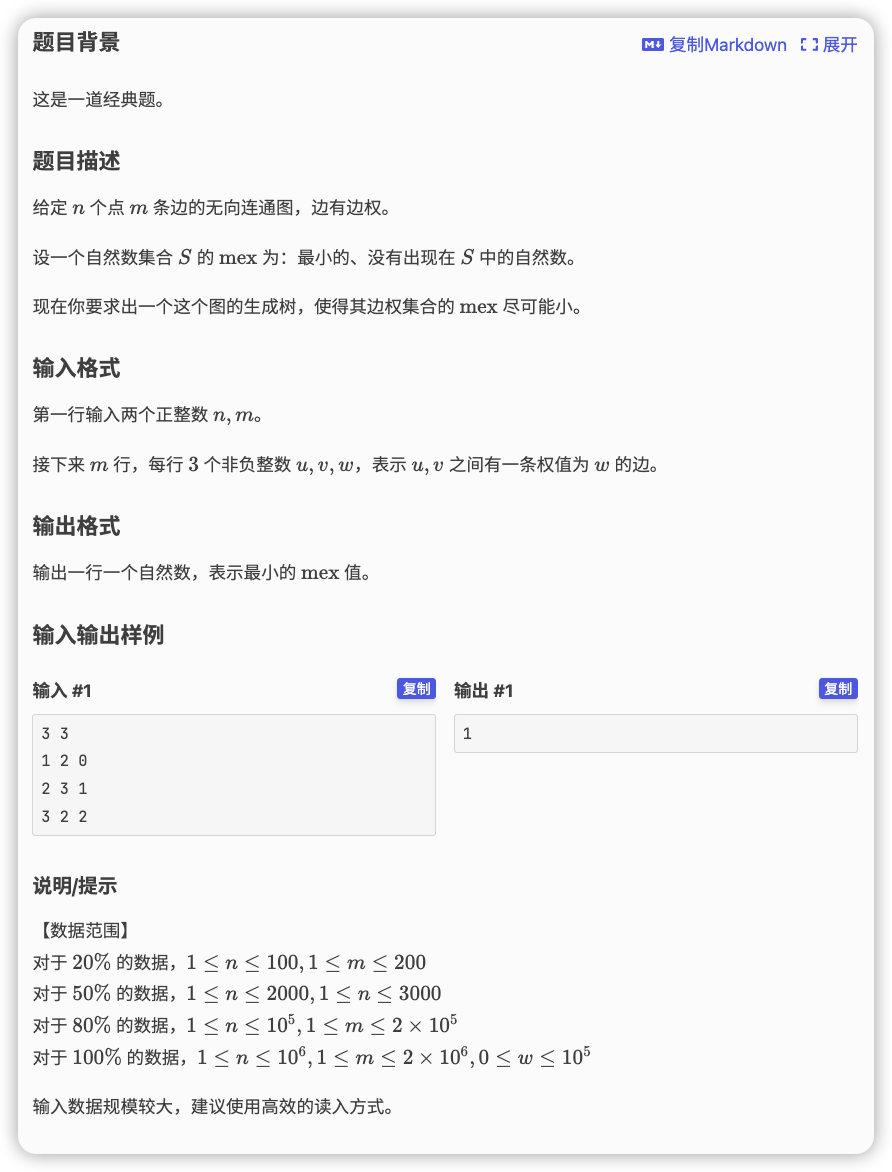
洛谷P5631_最小mex生成树

🔗

💡

如果 $mex=x$ 可以成立，说明将所有权值不为 $x$ 的边对应的邻点并在一起可以使整张图连通
对边权排过序后，对其分治 $l,r$ 表示除了边权在 $[l,r]$ 之外的所有边对应的邻点全部建立并查集

即对于进入权值范围 $l,r$ ，我们要递归 $l,mid$ 的时候将 $mid+1,r$ 范围内的边点相连，然后进入递归退出后再撤销操作
接下来递归 $mid+1,r$ 将范围在 $l,mid$ 内的边点相连，进入递归后退出后再撤销
最后到 $l=r$ 时，说明剩下的就只有边权 $l$ 的边没有用，检查一下 $sz[find(1)]$ 是否为 $n$

由于有撤销操作，这里使用可撤销并查集

✅

struct Edge {
    int u, v, w;
    inline friend bool operator < (Edge a, Edge b) {
        return a.w < b.w;
    }
};

int n, m;
vector<Edge> e;

const int N = 1e6 + 10;
int fa[N], sz[N];
inline int find (int x) {
    return x == fa[x] ? x : find(fa[x]);
}
inline int merge (int x, int y) {
    x = find(x);
    y = find(y);
    if (x == y) return 0;
    if (sz[x] > sz[y]) {
        sz[x] += sz[y];
        fa[y] = x;
        return y;
    } else {
        sz[y] += sz[x];
        fa[x] = y;
        return x;
    }
}
inline void del (int x) {
    sz[fa[x]] -= sz[x];
    fa[x] = x;
}

// 权值范围，边的下标范围
inline void dfs (int l, int r, int idl, int idr) {
    if (l == r) {
        if (sz[find(1)] == n) {
            printf("%d\n", l);
            exit(0);
        }
        return;
    }

    int mid = (l + r) >> 1;
    int tpl = idl, tpr = idr;
    vector<int> v;

    while (idr >= idl && e[idr].w > mid) {
        int mg = merge(e[idr].u, e[idr].v);
        if (mg) v.push_back(mg);
        idr --;
    }
    dfs(l, mid, idl, idr);
    while (!v.empty()) del(v.back()), v.pop_back();

    idl = tpl; idr = tpr;
    while (idl <= idr && e[idl].w <= mid) {
        int mg = merge(e[idl].u, e[idl].v);
        if (mg) v.push_back(mg);
        idl ++;
    }
    dfs(mid + 1, r, idl, idr);
    while (!v.empty()) del(v.back()), v.pop_back();
}

int main () {
    scanf("%d%d", &n, &m);
    e.resize(m);
    for (auto &[u, v, w] : e) scanf("%d%d%d", &u, &v, &w);
    sort(e.begin(), e.end());

    for (int i = 1; i <= n; i ++) sz[i] = 1, fa[i] = i;

    dfs(0, e.back().w + 1, 0, m - 1);
}

---

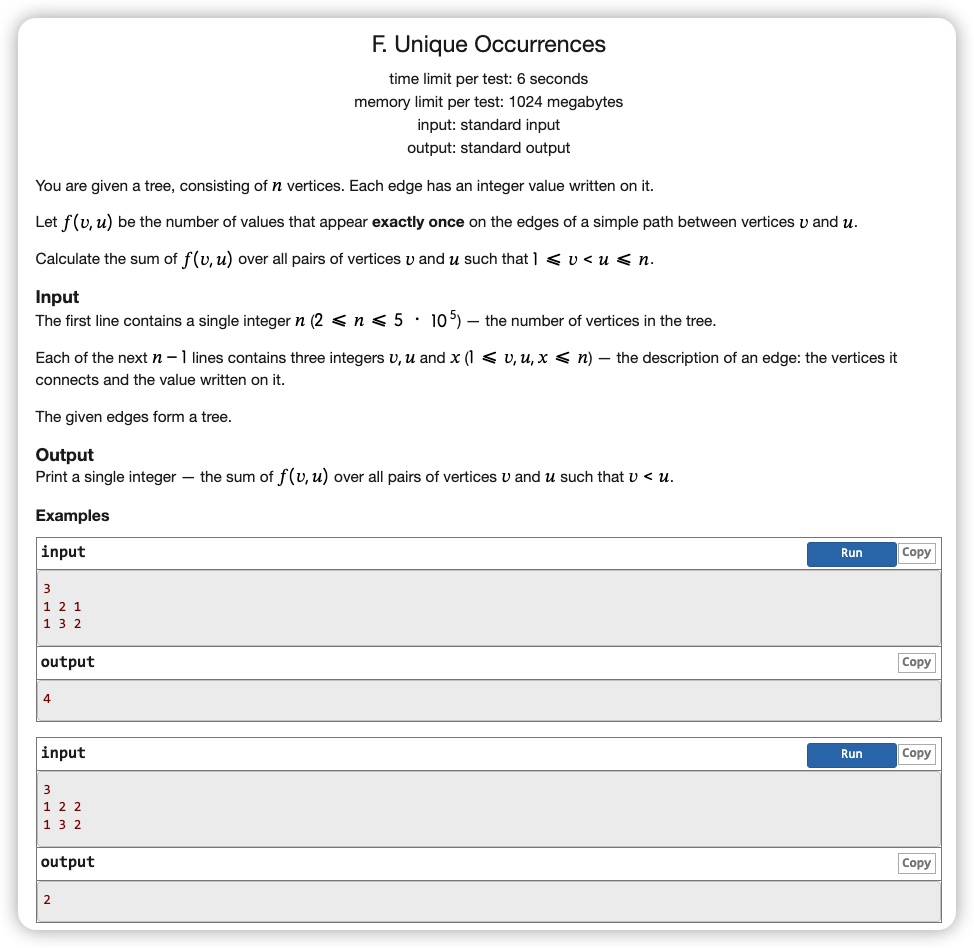
CodeForces1681F_UniqueOccurrences

🔗

💡

考虑将每个边权分开处理贡献
一个边权可以贡献的数量为：不合并此边权的边的情况下，对应边的两点属于的集合大小的乘积
故对边权分治，分治方法和 这道题 一样
最后到 $l=r$ 时扫描一遍以 $l$ 为边权的边，累加两点的集合大小乘积

✅

struct Edge {
    int u, v, w;
    inline friend bool operator < (Edge a, Edge b) {
        return a.w < b.w;
    }
};
vector<Edge> e;

const int N = 5e5 + 10;
int n, m;
int sz[N], fa[N];
inline int find (int x) { return x == fa[x] ? x : find(fa[x]); }
inline int merge (int x, int y) {
    x = find(x);
    y = find(y);
    if (x == y) return 0;
    if (sz[x] < sz[y]) {
        fa[x] = y;
        sz[y] += sz[x];
        return x;
    } else {
        fa[y] = x;
        sz[x] += sz[y];
        return y;
    }
}
inline void ctrlz (int x) {
    sz[fa[x]] -= sz[x];
    fa[x] = x;
}

vector<pair<int, int> > val_e[N];
ll res = 0;
inline void dfs (int l, int r, int idl, int idr) {
    if (l == r) {
        for (auto [x, y] : val_e[l]) {
            res += 1ll * sz[find(x)] * sz[find(y)];
        }
        return;
    }

    int mid = (l + r) >> 1;
    vector<int> v;
    int tpl = idl, tpr = idr;

    while (idl <= idr && e[idr].w > mid) {
        int mg = merge(e[idr].u, e[idr].v);
        if (mg) v.push_back(mg);
        idr --;
    }
    dfs(l, mid, idl, idr);
    idl = tpl, idr = tpr;
    while (!v.empty()) ctrlz(v.back()), v.pop_back();

    while (idl <= idr && e[idl].w <= mid) {
        int mg = merge(e[idl].u, e[idl].v);
        if (mg) v.push_back(mg);
        idl ++;
    }
    dfs(mid + 1, r, idl, idr);
    idl = tpl, idr = tpr;
    while (!v.empty()) ctrlz(v.back()), v.pop_back();
}

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n;
    for (int i = 1; i < n; i ++) {
        int u, v, w; cin >> u >> v >> w;
        e.push_back({u, v, w});
        val_e[w].push_back({u, v});
    }
    sort(e.begin(), e.end());

    for (int i = 1; i <= n; i ++) {
        fa[i] = i;
        sz[i] = 1;
    }
    dfs(e[0].w, e[n - 2].w, 0, n - 2);

    cout << res << endl;
}

---

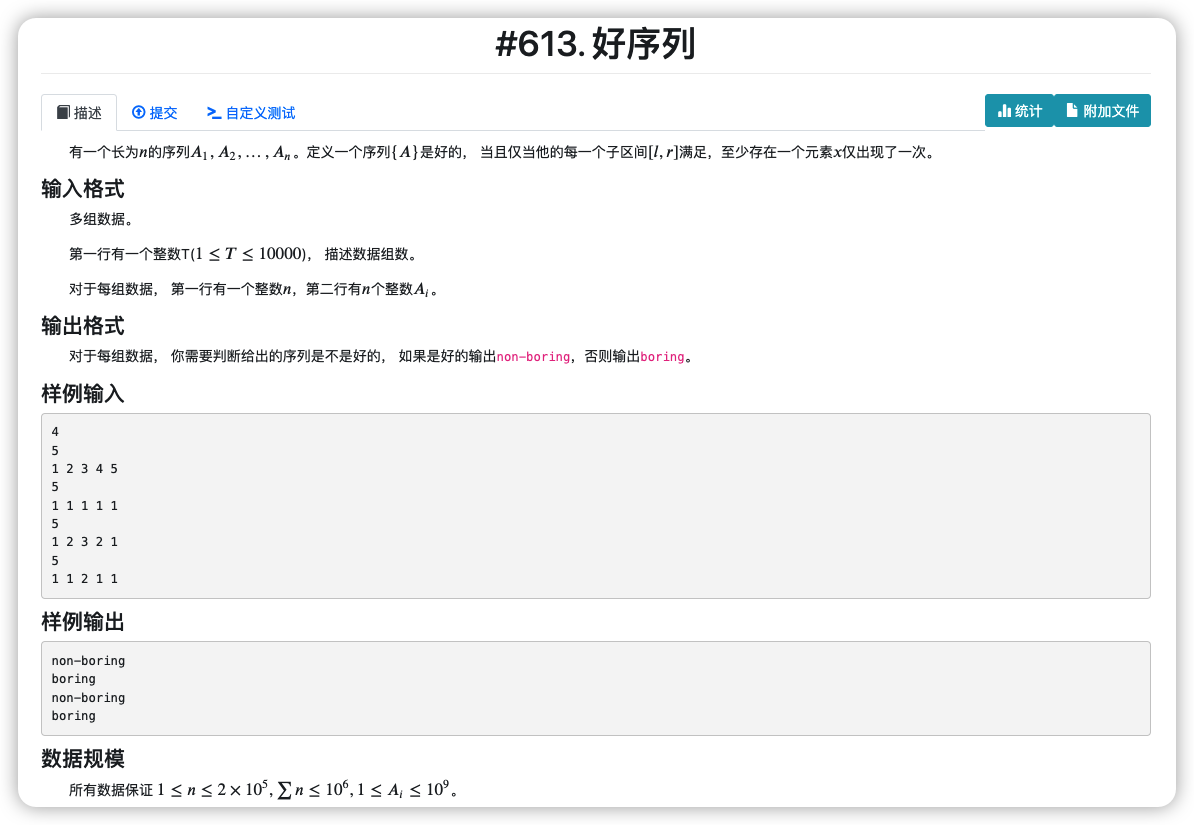
NamomoCamp2022春季div1每日一题_好序列

🔗

💡

看到这种区间要满足一堆信息判断的，先去想分治
发现如果一个区间内有出现 $1$ 次的，那么左边界在这个位置左边，右边界在这个位置右边的子区间均满足
这样涵盖下来，就只剩左右边界都在左侧和都在右侧的情况了
就可以去分治
但是分治内暴力处理一遍每个数出现次数肯定是很不优雅也很费时的
所以我们预处理一下每一个位置的数上一个出现的位置和在一个出现的位置
然后在分治内从两端同时向中间扫 $[tl:l\to mid,\;\;tr:r\to mid]$ ，去检查我们扫的 $tl,tr$ 是否有满足的，满足的直接去进行递归分治判断
这样每一次最坏的情况就是走 $\frac{r-l+1}{2}$ 次，时间复杂度 $O(nlogn)$

✅

const int N = 2e5 + 10;

int n;
int a[N];
int pre[N], nxt[N], id[N];

inline bool dfs_Div ( int l, int r ) {
        if ( l >= r ) return true;

        for ( int tl = l, tr = r; tl <= tr; tl ++, tr -- ) {
                if ( pre[tl] < l && r < nxt[tl] ) 
                        return dfs_Div(l, tl - 1) && dfs_Div(tl + 1, r);
                if ( pre[tr] < l && r < nxt[tr] ) 
                        return dfs_Div(l, tr - 1) && dfs_Div(tr + 1, r);
        }
        return false;
}

inline void Solve () {
        scanf("%d", &n); for ( int i = 0; i <= n; i ++ ) pre[i] = -1, nxt[i] = 0x3f3f3f3f;
        vector<int> nums;
        for ( int i = 1; i <= n; i ++ ) scanf("%d", &a[i]), nums.push_back(a[i]);
        sort ( nums.begin(), nums.end() );
        nums.erase(unique(nums.begin(), nums.end()), nums.end());
        for ( int i = 1; i <= n; i ++ ) a[i] = lower_bound(nums.begin(), nums.end(), a[i]) - nums.begin() + 1;

        for ( int i = 0; i <= n; i ++ ) id[i] = 0;
        for ( int i = 1; i <= n; i ++ ) {
                if ( id[a[i]] ) pre[i] = id[a[i]];
                id[a[i]] = i;
        }
        for ( int i = 0; i <= n; i ++ ) id[i] = 0;
        for ( int i = n; i >= 1; i -- ) {
                if ( id[a[i]] ) nxt[i] = id[a[i]];
                id[a[i]] = i;
        }

        puts(dfs_Div(1, n) ? "non-boring" : "boring");
}

---