计数DP

#

---

洛谷P1136_迎接仪式

🔗

💡

换与不换是一种决策，可以用 实现
换来换去太绕了，我们可以计算直接改变的 和 数量，最后计算这两个数量一样的 就行了

那么我们可以记录状态 表示在第 位之前，换来了 个 和 个 且这一位是 ，的最大价值

那么我们线性枚举，枚举第几位，枚举换出了多少个 和多少个
在第 位

如果这一位本身是 ，我们可以选择换还是不换
换： 产出了一个 ，上一个状态耗费的是 个换出 的方式，且可以因上一步最后为 的位数加价值，或者为 不改变，
不换： 本身是 也不会受到上一步影响，那么就简单汇聚一下，

如果这一位是
换： 变成了 ，与上一步无影响也耗费了一个 ，上个状态就是 ，汇聚一下，
不换： 本身可以和上一步的 产生影响，

最后遍历一下修改量 ，选择最大的

其中注意，初始是前面的都弄好了，且这一位不会产生影响，

✅

int N, K;
string s;

int dp[510][105][105][2];  

int main () {
        cin >> N >> K >> s; s = "0" + s;

        memset ( dp, -0x3f3f3f3f, sizeof dp );
        dp[0][0][0][1] = 0;

        for ( int i = 1; i <= N; i ++ ) {
                for ( int j = 0; j <= K; j ++ ) {
                        for ( int k = 0; k <= K; k ++ ) {
                                if ( s[i] == 'j' ) {
                                        dp[i][j][k][0] = max ( dp[i - 1][j][k][0], dp[i - 1][j][k][1] );
                                        if ( j ) dp[i][j][k][1] = max ( dp[i - 1][j - 1][k][0] + 1, dp[i - 1][j - 1][k][1] );
                                } else {
                                        dp[i][j][k][1] = max ( dp[i - 1][j][k][1], dp[i - 1][j][k][0] + 1 );
                                        if ( k ) dp[i][j][k][0] = max ( dp[i - 1][j][k - 1][0], dp[i - 1][j][k - 1][1] );
                                }
                        }
                }
        }

        int res = -0x3f3f3f3f;
        for ( int jk = 0; jk <= K; jk ++ ) {
                res = max ( res, max (dp[N][jk][jk][0], dp[N][jk][jk][1]) );
        }
        cout << res << endl;
}

---

洛谷P1357_花园

🔗

💡

首先看到 $m\le \min(n,5)$ ，可以意识到这是为了可以二进制枚举状态，也就是把上一步的状态压缩为一个二进制数
$100\%$ 的 $n$ 的数据范围我们可以用矩阵加速来求 $dp$ ，那么先考虑正常情况的 $dp$ 递推式

设前一位置包括自己的前 $m$ 个位置的状态为 $s$ （若 $idx=10,m=3$，那么 $s=[8,10]$的选用状态）
看一下转移情况 $abcd\to \_bcd$ （其中 $abcd$ 均表示每一个位置的状态
那么我们在这一位置对于前一位置的这个状态是会失去一位，那么即 $s\gg 1$
对于当前位置我们可以选择 $1$ 或者 $0$ ，第 $m-1$ 位空出来了可以在这个位上设置，那么就是 $s\gg 1\;|\;(1\ll (m-1))$ 或者 $s\gg 1$
但是这样转移我们要保证 $num1(s)\le k$ 与 $num1(ss\gg 1\;|\;(1\ll (m-1)))\le k$，做一个判断再决定是否进行计数转移

但是还有一个要考虑的问题是：这是一个环
环意味着首位呼应，$1\to n$ 成环就是 $1$ 与 $n$ 呼应，那么我们可以拎出来一个 $s_0$ 设置为 $[n-m+1,n]$ 的状态，最后统计的时候统计 $s_n=s_0$ 时的方案数即可

80分代码

const int N = 1e5 + 10;
const int mod = 1e9 + 7;

int n, m, k;
int64_t dp[N][1 << 5];

int main () {
        cin.tie(0)->sync_with_stdio(0);
        cin.exceptions(cin.failbit);

        cin >> n >> m >> k;

        int64_t res = 0;
        for (int s = 0; s < 1 << m; s ++) { // s_0 的状态
                if (__builtin_popcount(s) > k) continue;
                memset(dp, 0, sizeof dp);
                dp[0][s] = 1;
                for (int i = 1; i <= n; i ++) {
                        for (int t = 0; t < 1 << m; t ++) { // 枚举 s_{i-1} 的状态
                                if (__builtin_popcount(t) > k) continue;
                                (dp[i][t >> 1] += dp[i - 1][t]) %= mod;
                                if (__builtin_popcount(t >> 1 | (1 << (m - 1))) <= k) (dp[i][t >> 1 | (1 << (m - 1))] += dp[i - 1][t]) %= mod;
                        }
                }
                (res += dp[n][s]) %= mod;
        }
        cout << res << endl;
}

开始优化
由于之前已经想到这里 $n$ 太大可以用矩阵加速了，那么就是想矩阵
先看一波 $m=2,k=1$ 的转移关系
$u\;\to v$
$00\to 00\;(0\to 0)$
$00\to 10\;(0\to 2)$
$01\to 00\;(1\to 0)$
$01\to 10\;(1\to 2)$
$10\to 01\;(2\to 1)$

我们知道，每一个位置矩阵乘进制矩阵会变成下一个矩阵
在矩阵乘中是 左矩阵行 $\times$ 右矩阵列
右矩阵为进制矩阵，则如果产生了递推关系，应该是 $mat[v][u]=1$
在上面的例子即：
$\begin{matrix} &1&1&0&0\\ &0&0&1&0\\ &1&1&0&0\\ &0&0&0&0 \end{matrix}$

那么对进制矩阵求 $n$ 次幂，然后以乘单位矩阵的方式求对角线即可

✅

const int N = 1e5 + 10;
const int mod = 1e9 + 7;

int64_t n, m, k;
int full; // 1 << m

struct Matrix {
        int64_t mat[34][34];
        inline Matrix (int val) {
                for (int i = 0; i < full; i ++) 
                        for (int j = 0; j < full; j ++) 
                                mat[i][j] = (i == j) * val;
        }
};
inline Matrix mul_Matrix (Matrix a, Matrix b) {
        Matrix res(0);
        for (int i = 0; i < full; i ++) 
                for (int j = 0; j < full; j ++) 
                        for (int k = 0; k < full; k ++) 
                                (res.mat[i][j] += a.mat[i][k] * b.mat[k][j] % mod) %= mod;
        return res;
}
inline Matrix ksm_Matrix (Matrix a, int64_t b) {
        Matrix res(1);
        while (b) {
                if (b & 1) res = mul_Matrix(res, a);
                a = mul_Matrix(a, a);
                b >>= 1;
        }
        return res;
}

int main () {
        cin.tie(0)->sync_with_stdio(0);
        cin.exceptions(cin.failbit);

        cin >> n >> m >> k; full = 1 << m;

        Matrix base(0);
        for (int u = 0; u < full; u ++) {
                if (__builtin_popcount(u) > k) continue;
                int v1 = u >> 1, v2 = u >> 1 | (1 << (m - 1));
                if (__builtin_popcount(v1) <= k) base.mat[v1][u] = 1;
                if (__builtin_popcount(v2) <= k) base.mat[v2][u] = 1;
        }
        base = ksm_Matrix(base, n);

        int64_t res = 0;
        for (int i = 0; i < full; i ++) (res += base.mat[i][i]) %= mod;
        cout << res << endl;
}

---

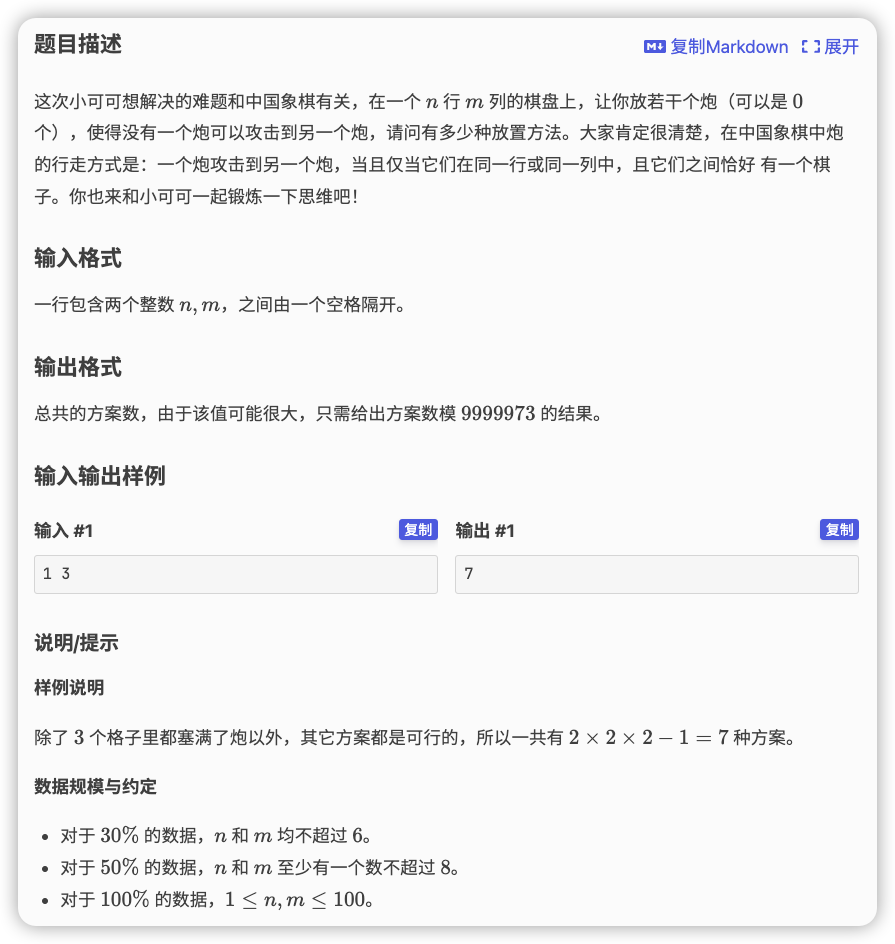
洛谷P2051_中国象棋

🔗

💡

一行一列不能有三个炮存在（az什么双重皇后问题）...
计数、矩阵，$dp$ 吧
如果某一列有一个棋，那么下一步如果选它会变成两个棋，所以在一行一列上，三种棋的状态是很重要且收到限制的
所以我们在状态内放置一个 $j$ 表示含一个棋子的列个数，$k$ 表示含两个棋子的列个数，第三维就不用开了，可以通过 $m-j-k$ 快速获得有几个列没有棋子
然后在行内向下走，注意一行只能选两个棋子
所以我们对于第 $i$ 行 $dp[i][j][k]$ ，枚举下一行在含一个棋子的列里面选 $a$ 列本来就含有一个棋子的，选 $b$ 列本来没有棋子的，那么下一个状态为 $dp[i+1][j-a+b][k+b]$ ，同时选择为组合数，累加转移时要乘上 $\binom{j}{a}\times \binom{m-k-j}{b}$ ，注意 $a+b\le 2$ 代表这一行不选超过两个棋子
最后累加一下 $dp[n][j][k]$ 即可

✅

const int mod = 9999973;
inline ll ksm (ll a, ll b) { ll res = 1; while (b) { if (b & 1) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv (ll x) { return ksm(x, mod - 2); }
const int N = 102;
ll f[N], ivf[N];
inline ll C (int n, int m) {
    return f[n] * ivf[m] % mod * ivf[n - m] % mod;
}

ll dp[N][N][N];

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    f[0] = 1;
    for (int i = 1; i < N; i ++) f[i] = (ll)f[i - 1] * i % mod;
    ivf[N - 1] = inv(f[N - 1]);
    for (int i = N - 2; i >= 0; i --) ivf[i] = (ll)ivf[i + 1] * (i + 1) % mod;

    memset(dp, -1, sizeof dp);
    int n, m; cin >> n >> m;

    dp[0][0][0] = 1;
    for (int i = 0; i < n; i ++) {
        for (int j = 0; j <= m; j ++) {
            for (int k = 0; m - k - j >= 0; k ++) {
                if (dp[i][j][k] == -1) continue;
                for (int a = 0; a <= j && a <= 2; a ++) {
                    for (int b = 0; b <= m - k - j && a + b <= 2; b ++) {
                        if (dp[i + 1][j - a + b][k + a] == -1) dp[i + 1][j - a + b][k + a] = 0;
                        (dp[i + 1][j - a + b][k + a] += C(j, a) * C(m - k - j, b) % mod * dp[i][j][k] % mod) %= mod;
                    }
                }
            }
        }
    }

    int res = 0;
    for (int j = 0; j <= m; j ++) {
        for (int k = 0; m - k - j >= 0; k ++) {
            if (~dp[n][j][k]) {
                (res += dp[n][j][k]) %= mod;
            }
        }
    }
    cout << res << endl;
}

---

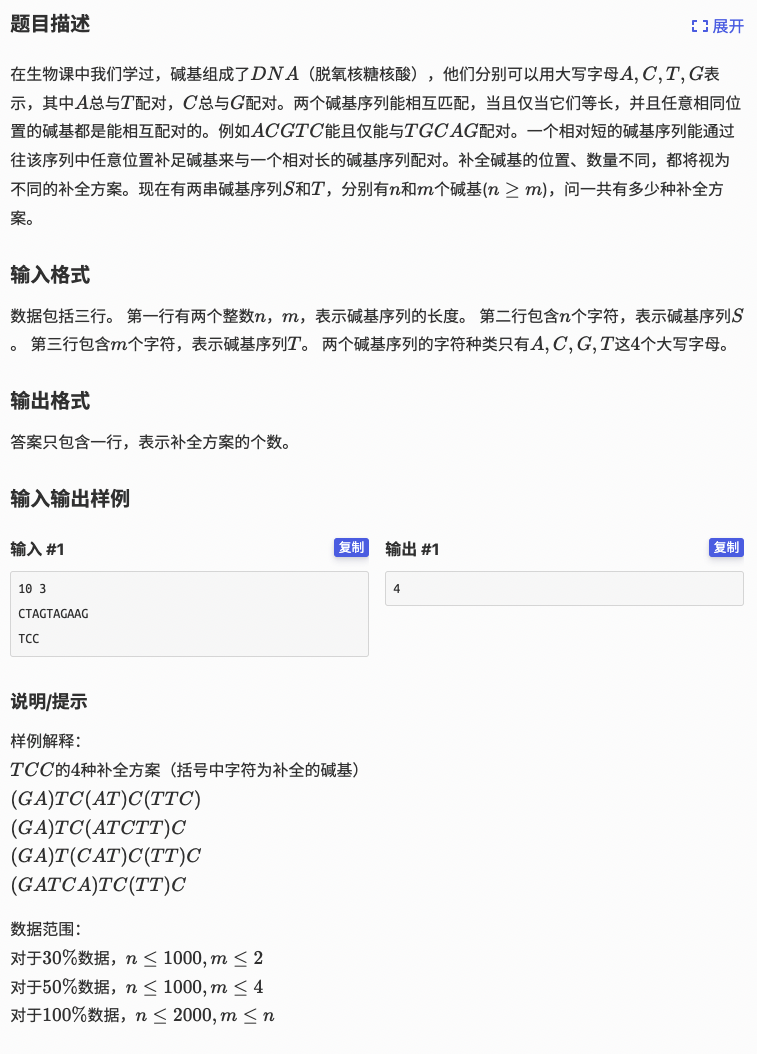
洛谷P5484_基因补全

🔗

💡

任务简化

要匹配的话我们按要求把字符串 转译一下
由于我们可以在字符串 中加入任何字符变成
反过来就是问我们在字符串 的子序列中能找到多少个

问题解法

这个问题就很简单了
我们枚举字符串 的下标 ， 能做出的贡献就是：
对于所有的 ，若 ，那么在字符串 的所有 字符全都接着 这个字符再往后走一步
如果 就是他自己要
那就是妥妥的 计数 了

伪代码设计

所以我们设置 表示外层枚举到 时，子序列结尾为 的方案数
那么转移方程为 ：

注意，这里倒着枚举 是防止同一步之前更新过的 加给

✅

数过大，普通的类型会溢出
这里只给出直观的普通类型 C++ 代码，改大数可以自行更改（我用的是 java

ll dp[2005];

int main () {
        ll n, m; cin >> n >> m;
        string s, t; cin >> s >> t;
        // 转义
        for ( int i = 0; i < n; i ++ ) {
                if ( s[i] == 'A' ) s[i] = 'T';
                else if ( s[i] == 'T' ) s[i] = 'A';
                else if ( s[i] == 'C' ) s[i] = 'G';
                else s[i] = 'C'; 
        } 
        // 计数
        for ( int i = 0; i < n; i ++ ) {
                for ( int j = m - 1; j >= 0; j -- ) {
                        if ( s[i] == t[j] ) {
                                if ( j ) dp[j] += dp[j - 1];
                                else dp[j] ++;
                        }
                }
        }
        cout << dp[m - 1] << endl;
}

---

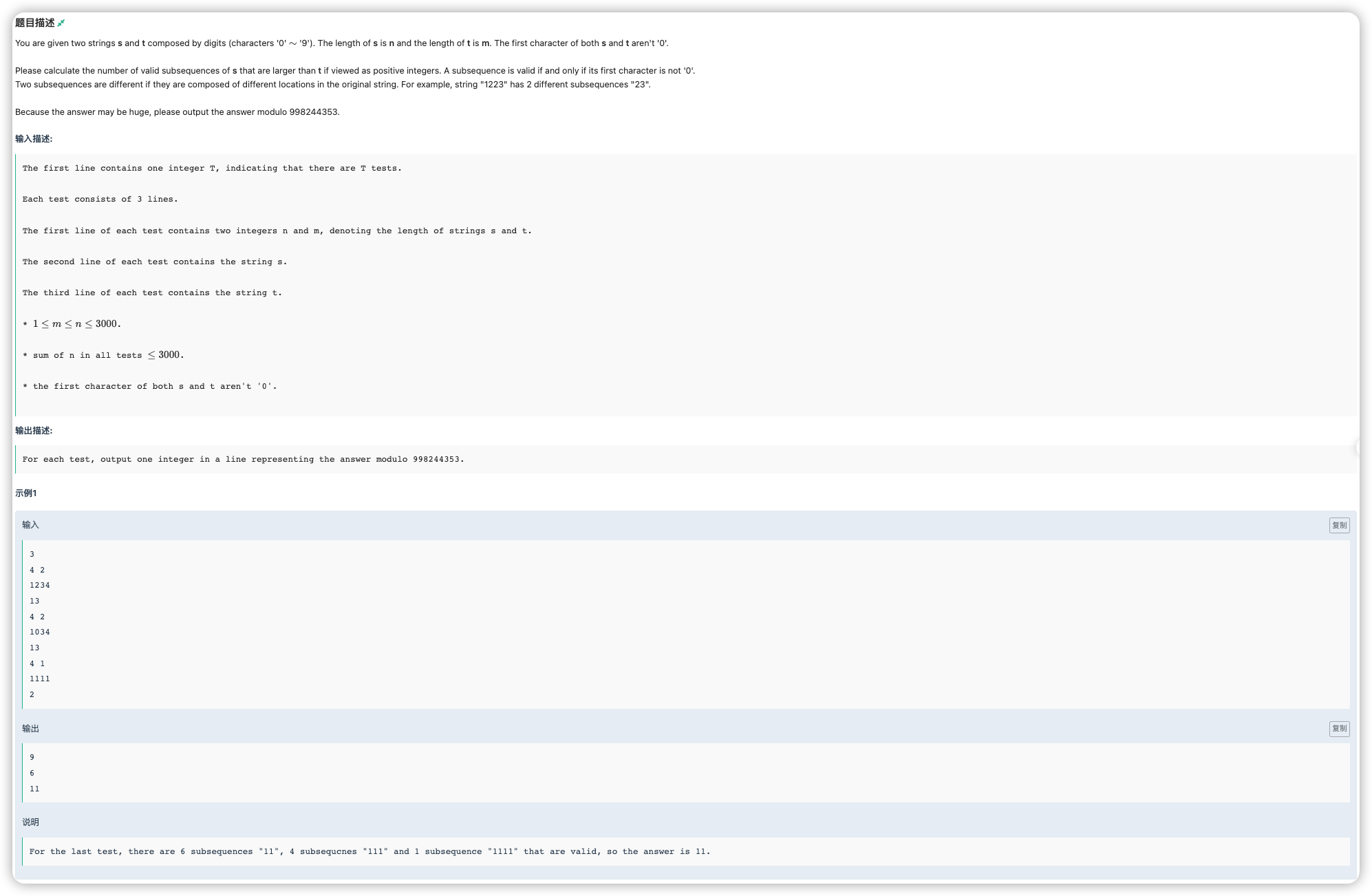
牛客2022国庆集训派对day3G_Subsequence1

🔗

💡

如果在 $s$ 中要获得和 $t$ 同长度的串，那么就是一个同长子序列的字典序偏序计数问题了
令 $s_s$ 表示 $s$ 的子序列，我们要看在哪一位让 $s_s>t$ ，这之后的是可以随便选的
如果 $s_i>t_j$ ，那么就需要计一个 $s$ 在 $i$ 前面能找到多少个与 $t[1,j-1]$ 可以匹配上的子序列
这个用一个 $dp$ 来实现，$dp[i][j]$ 表示 $s$ 在前 $i$ 位能匹配上 $t[1,j]$ 的子序列数量
$dp[i][]$ 用 $dp[i-1][]$ 来转移，枚举 $i-1$ 匹配了多少个，那么如果 $s_i=t_j$ ，$dp[i][j+1]$ 加上 $dp[i-1][j]$ ，然后正常继承关系为 $dp[i][j]+dp[i-1][j]$
处理好这个 $dp$ 后，看哪一位 $s_i>t_j$ ，找到后答案累加 $\binom{n-i}{m-j}\times dp[i-1][j-1]$ 即可，即表示前面都匹配上，后面随便选

当然最后也要加上长度超过 $m$ 的子序列数量，为 $\sum\limits_{i=m+1}n\binom{n-j}{i-1}$
由于不能有前导 $0$ ，就对于长度 $i$ 时，枚举一下 $s_j$ 是否为 $0$ ，如果为 $0$ ，说明以它开头的都不可以选，减去 $\binom{n-j}{i-1}$

✅

const int N = 3010;
const int mod = 998244353;
int f[N], ivf[N];
inline int C (int n, int m) {
    if (m > n) return 0;
    return (ll)f[n] * ivf[m] % mod * ivf[n - m] % mod;
}
inline int ksm (int a, int b) {
    int res = 1;
    while (b) {
        if (b & 1) res = 1ll * res * a % mod;
        a = 1ll * a * a % mod;
        b >>= 1;
    }
    return res;
}
inline int inv (int x) { return ksm(x, mod - 2); }

int n, m;
string s, t;
int dp[N][N];

inline void Solve () {
    int res = 0;
    cin >> n >> m >> s >> t;
    s = "0" + s;
    t = "0" + t;

    dp[0][0] = 1;
    
    for (int i = 1; i <= n; i ++) {
        for (int j = 0; j <= m; j ++) {
            if (j + 1 <= m && s[i] == t[j + 1]) {
                (dp[i][j + 1] += dp[i - 1][j]) %= mod;
            }
            (dp[i][j] += dp[i - 1][j]) %= mod;
        }
        for (int j = 1; j <= m; j ++) {
            if (s[i] > t[j]) {
                res += (ll)C(n - i, m - j) * dp[i - 1][j - 1] % mod;
                res %= mod;
            }
        }  
    }

    for (int i = 0; i <= n; i ++) for (int j = 0; j <= m; j ++) dp[i][j] = 0;

    for (int i = m + 1; i <= n; i ++) {
        (res += C(n, i)) %= mod;
        for (int j = 1; j <= n; j ++) {
            if (s[j] == '0') {
                res = ((res - C(n - j, i - 1)) % mod + mod) % mod;
            }
        }
    }
    cout << res << endl;
}

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    f[0] = 1;
    for (int i = 1; i < N; i ++) f[i] = (ll)f[i - 1] * i % mod;
    ivf[N - 1] = inv(f[N - 1]);
    for (int i = N - 2; i >= 0; i --) ivf[i] = (ll)ivf[i + 1] * (i + 1) % mod;

    int cass; cin >> cass; while ( cass -- ) {
        Solve ();
    }
}

---

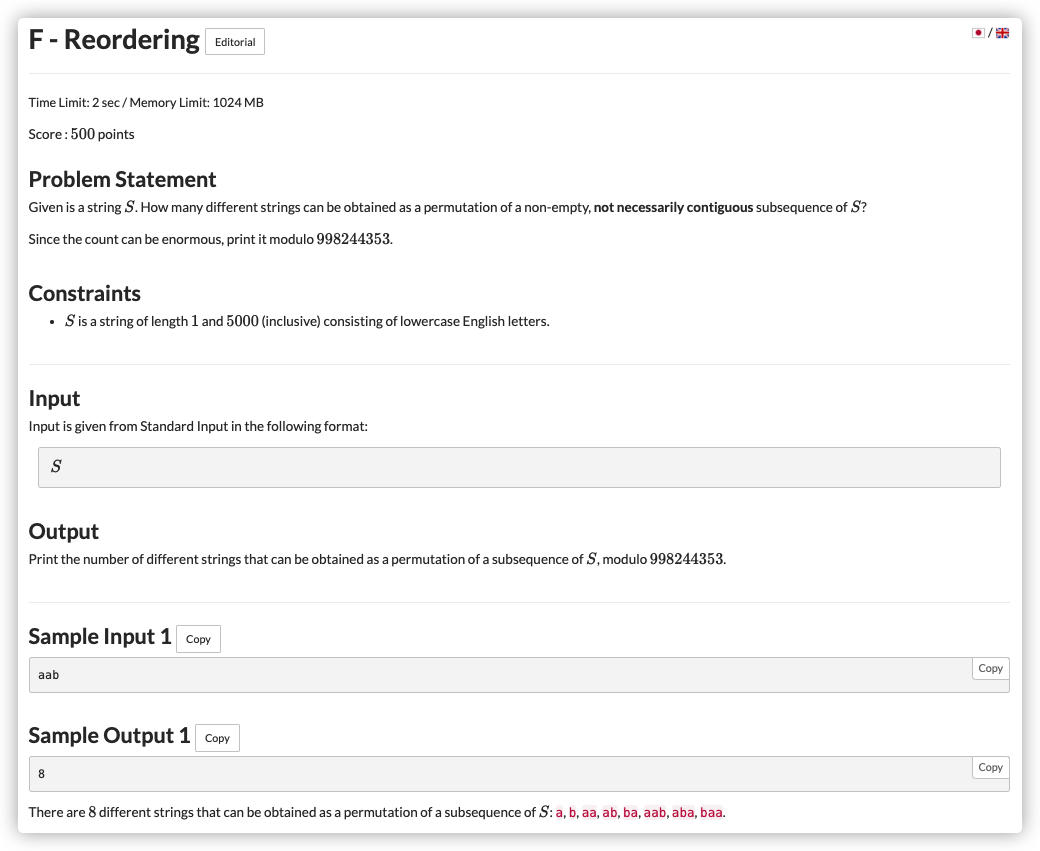
ABC234F_Reordering

🔗

💡

设 $'a'$ 有 $A$ 个， $'b'$ 有 $B$ 个 ...
那么答案即为

$$\sum\limits_{a=0}^A\sum\limits_{b=0}^B\sum\limits_{c=0}^C\dots\sum\limits_{z=0}^Z\frac{(a+b+c+\dots+z)!}{a!\times b!\times c!\times\dots\times z!}$$

观察分子分母性质
分母：计算下一个字符时枚举的个数可以直接乘阶乘
分子：同长度下分子相同

那么我们先不看分子，先去枚举字符枚举个数进行递推
令 $dp[i][j]$ 表示枚举到第 $i$ 个字符时 ，长度为 $j$ 时 个数$/j!$ 的结果
那么在枚举第 $i$ 个字符用了 $j$ 个，之前有了 $k$ 个字符时
$dp[i][j+k]=dp[i][j+k]+dp[i-1][k]\times \frac1{j!}$

然后最后统计答案将当前长度的阶乘乘上即可

✅

const int mod = 998244353;

ll dp[30][5010];
string s;
ll num[30];

inline ll ksm ( ll a, ll b ) { ll res = 1; while ( b ) { if ( b & 1 ) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv ( ll x ) { return ksm(x, mod - 2); }
ll ivf[5010], f[5010];
inline void get_F () {
	f[0] = ivf[0] = 1;
	for ( int i = 1; i < 5010; i ++ ) f[i] = f[i - 1] * i % mod, ivf[i] = ivf[i - 1] * inv(i) % mod;
}

int main () {
	get_F();

	cin >> s;
	for ( auto i : s ) num[i - 'a' + 1] ++;

	dp[0][0] = 1;
	for ( int i = 1; i <= 27; i ++ ) {
		for ( int j = 0; j <= s.size() - num[i]; j ++ ) {
			for ( int k = 0; k <= num[i]; k ++ ) {
				dp[i][j + k] = (dp[i][j + k] + dp[i - 1][j] * ivf[k] % mod) % mod;
			}
		}
	}
	ll res = 0;
	for ( int i = 1; i <= s.size(); i ++ ) res = (res + dp[27][i] * f[i] % mod) % mod;
	cout << res << endl;
}

---

ABC249E_RLE

🔗

💡

比赛的时候想的是用组合数学的插板法去分割，后来发现其实 $check()$ 的时候没法做到全面
计数问题组不出来就试着用 $dp$
注意到这个数据范围是想让用 $O(n^2)$ 的
那么我们可以开两个同级状态
$dp[i][j]$ 表示本来长度为 $i$ ，压缩为 $j$ 的方案数
由于长度不过四位数，那么我们可以得到下面的转移：
从 $[i-9,i-1]$ 到 $i$ ，令 $j$ 多了 $2$
从 $[i-99,i-10]$ 到 $i$ ，令 $j$ 多了 $3$
从 $[i-999,i-100]$ 到 $i$ ，令 $j$ 多了 $4$
从 $[i-9999,i-1000]$ 到 $i$ ，令 $j$ 多了 $5$
注意到若非第一次选择字符，后面的选择字符的方案只有 $25$ 个
即 $dp[i][j]=25\times(\sum\limits_{a=i-9}^{i-1}dp[a][j-2]+\sum\limits_{b=i-99}^{i-10}dp[b][j-3]+\sum\limits_{c=i-999}^{i=100}dp[c][j-4]+\sum\limits_{d=i-9999}^{i-1000}dp[d][j-5])$
要考虑一下第一次选择字符的情况，即 $j=to\_string(i).size()+1$ 时，此时我们要让 $dp[i][j]+1$

连加符号一个个算会很费时间，这里可以用 $dp$ 的前缀和得出区间和来进行计算，最后统计的时候用区间和得出第一个维度为 $n$ 的 $dp$ 即可

✅

const int N = 3003;
ll dp[N][N << 1]; // len:i->j
ll n, mod;

inline ll sum (int l, int r, int j) {
        if (l > r || r < 0 || j < 0) return 0;
        if (l <= 0) return dp[r][j];
        else return ((dp[r][j] - dp[l - 1][j]) % mod + mod) % mod;
}

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        cin >> n >> mod;

        dp[0][0] = 1;
        for (int i = 1; i <= n; i ++) {
                int len = to_string(i).size() + 1;
                for (int j = 0; j <= 2 * n; j ++) {
                        (dp[i][j] += 25 * sum(i - 9, i - 1, j - 2) % mod) %= mod;
                        (dp[i][j] += 25 * sum(i - 99, i - 10, j - 3) % mod) %= mod;
                        (dp[i][j] += 25 * sum(i - 999, i - 100, j - 4) % mod) %= mod;
                        (dp[i][j] += 25 * sum(i - 9999, i - 1000, j - 5) % mod) %= mod;
                        if (j == len) (dp[i][j] += 1) %= mod;
                        (dp[i][j] += dp[i - 1][j]) %= mod;
                }
        }

        ll res = 0;
        for (int i = 0; i < n; i ++) (res += ((dp[n][i] - dp[n - 1][i]) % mod + mod) % mod) %= mod;
        cout << res << endl;
}

---

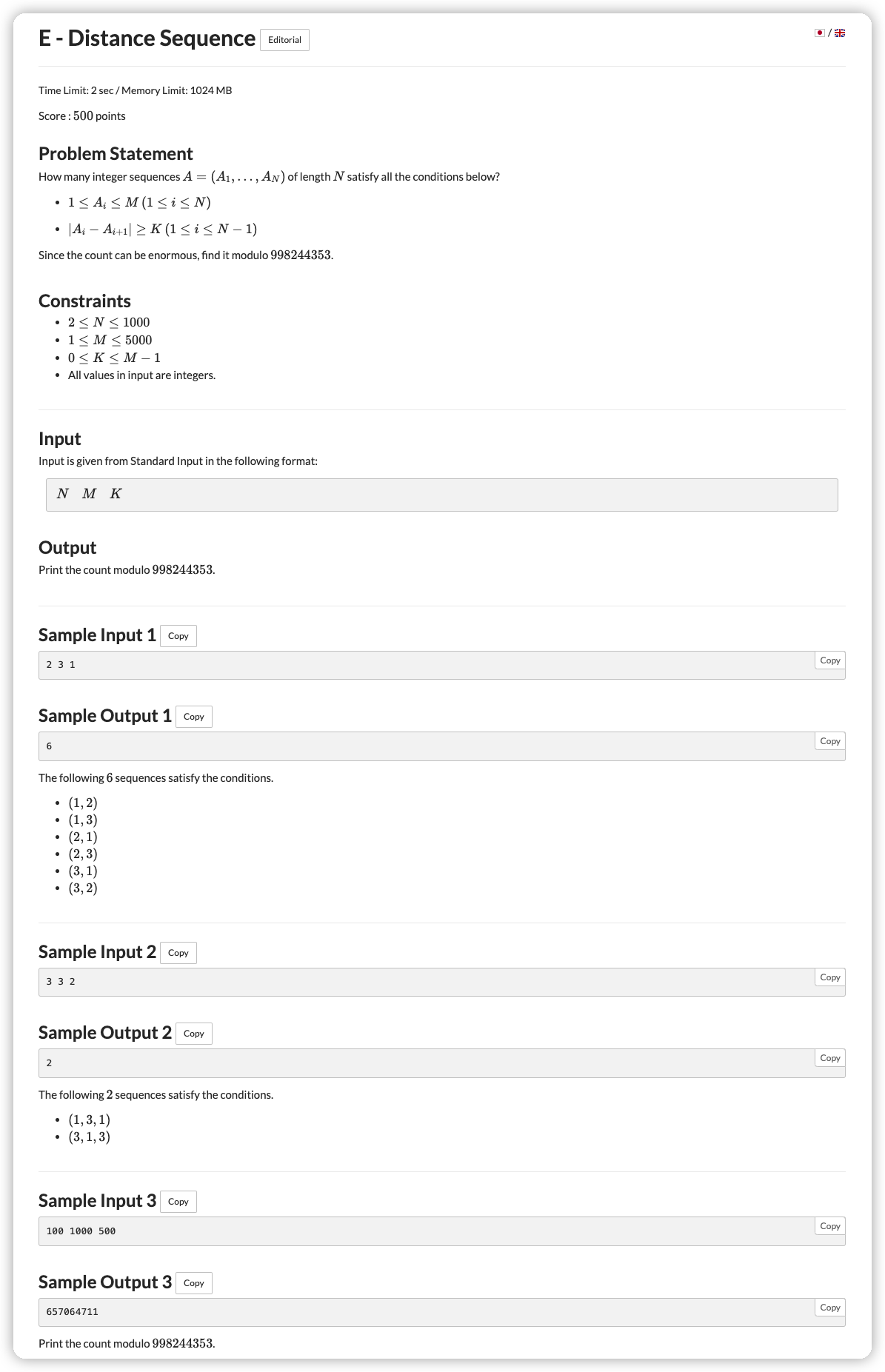
ABC253E_DistanceSequence

🔗

💡

这个一看数据量就是一个方案型 $dp$ ，枚举 $i$ 为 $a_i$ 的下标，枚举 $j$ 为 $a_i=j$ 时的方案数
如果 $j-k\ge 1$ 那么我们可以利用前面求得的 $\sum dp[i-1][1\rightarrow j-k]$
如果 $j+k\le m$ 那么我们可以利用前面求得的 $\sum dp[i-1][j+k\rightarrow m]$
由于是区间和，我们可以每一次预处理出来 $dp[i-1][]$ 的前缀和 ，然后求区间和直接用前缀相减即可
不过这里要注意 $k=0$ 时我们 $dp[i-1][j]$ 会被算两遍，要减去

✅

const int mod = 998244353;
const int N = 1003;
const int M = 5003;
 
ll dp[N][M], n, m, k;
ll sum[M];
 
inline ll add (ll a, ll b) {
        return (a + b) % mod;
}
inline ll sub (ll a, ll b) {
        return ((a - b) % mod + mod) % mod;
}
 
int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);
 
        cin >> n >> m >> k;
        for (int j = 1; j <= m; j ++) dp[1][j] = 1;
        for (int i = 2; i <= n; i ++) {
                for (int j = 1; j <= m; j ++) sum[j] = add(sum[j - 1], dp[i - 1][j]);
                for (int j = 1; j <= m; j ++) {
                        if (j - k >= 1) dp[i][j] = add(dp[i][j], sub(sum[j - k], sum[0]));
                        if (j + k <= m) dp[i][j] = add(dp[i][j], sub(sum[m], sum[j + k - 1]));
                        if (k == 0) dp[i][j] = sub(dp[i][j], sub(sum[j], sum[j - 1]));
                }
        }
 
        ll res = 0;
        for (int j = 1; j <= m; j ++) {
                res = add(res, dp[n][j]);
        }
        cout << res << endl;
}

---

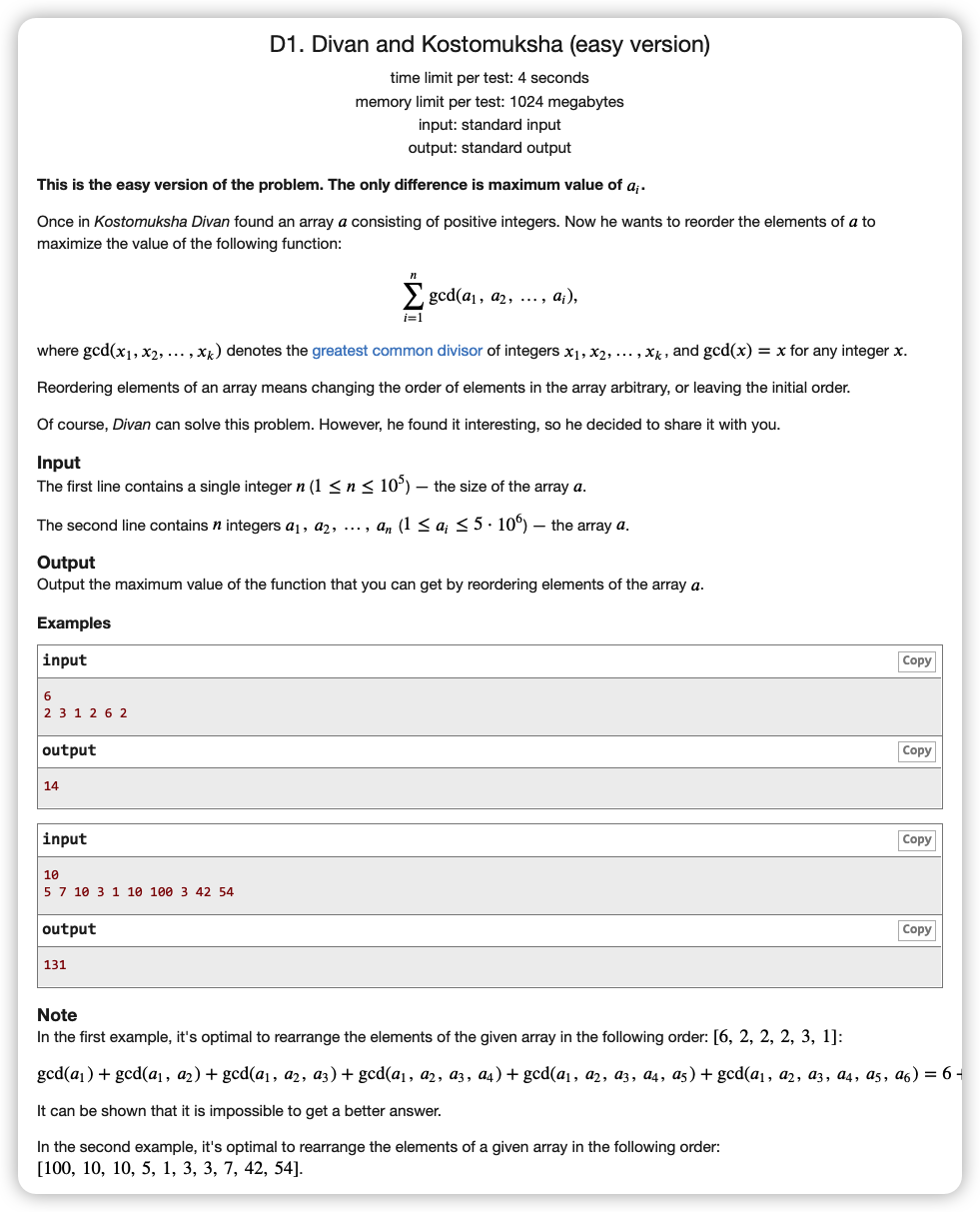
CodeForces1614D1Z_DivanAndKostomuksha（easy version）

🔗

💡

考虑前缀 $gcd$ 的特性，后者的因数集一定是前者因数集的子集，有了这个关系，我们用这个因数集做 $dp$
那么我们有一个递推关系就是用一个数去更新它的倍数
令 $dp[i]$ 表示 $i$ 与 $i$ 的因数所做出的贡献
其中 $i$ 一定是开始的 $gcd$ ，而 $i$ 的因数则是后面的数
即 $dp[1]=n$
对于递推，我们设置 $cnt[i]$ 表示为 $i$ 的倍数在 $[a]$ 中出现的次数
那么我们对于 $j$ 是 $i$ 的倍数
不难想到 $cnt[j]\le cnt[i]$
将 $i$ 转移到 $j$ 要更新的就是 $cnt[j]$ 的部分 ，在这一部分中将 $i$ 的贡献换为 $j$ ，那么 $dp[j]=max(dp[i]+(j-i)\times cnt[j])$

由于是倍数关系，则我们在求 $[cnt]$ 与 $[dp]$ 时均可以使用埃氏筛求解

✅

int main () {
        cin.tie(0)->sync_with_stdio(0);
        cin.exceptions(cin.failbit);

        int n; cin >> n;
        vector<int> a(n); for (int &i : a) cin >> i;

        int mx = *max_element(a.begin(), a.end());
        vector<int> cnt(mx + 1, 0); for (int i : a) cnt[i] ++;
        for (int i = 1; i <= mx; i ++) 
                for (int j = i + i; j <= mx; j += i) 
                        cnt[i] += cnt[j];
        
        vector<int64_t> dp(mx + 1, 0); dp[1] = n;
        int64_t res = 0;
        for (int i = 1; i <= mx; i ++) 
                for (int j = i + i; j <= mx; j += i)
                        dp[j] = max(dp[j], dp[i] + (int64_t)(j - i) * cnt[j]),
                        res = max(res, dp[j]);
        
        cout << res << endl;
}

---

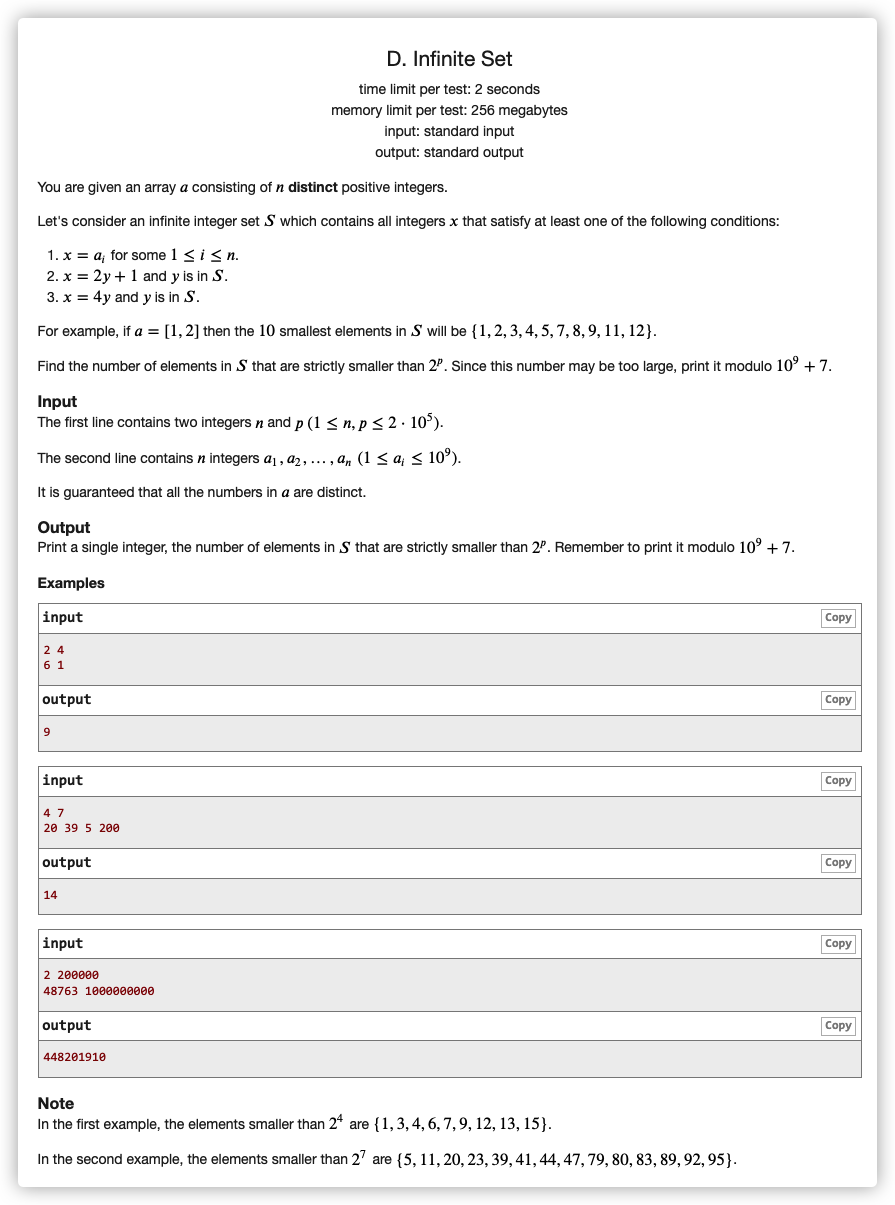
CodeForces1635D_InfiniteSet

🔗

💡

$2x+1$ 为奇，$4x$ 为偶
若 $a<b$，$a\in[a]$ 且 $b\in[a]$ 且 $a$ 可变为 $b$ ，删去 $b$ ，称为去重
去重操作从大到小，对数的奇偶性进行向下修正，直到为偶数且模 $4$ 不为 $0$ 停止，如果向下修正时当前数已经存在，那么需要删掉
去重后，剩下的所有在变化中将毫不相干

注意 $2^p$ 说明是一个二进制问题
考虑一下，对于

$$1_2\left\{\begin{aligned} &\stackrel{\times2+1}{\longrightarrow}11_2\\ &\stackrel{\times4}{\longrightarrow}100_2 \end{aligned}\right.$$

可以看出，一个 $x$ 位的数可以推到 $x+1$ 位与 $x+2$ 位
阶梯问题，所以是 $fibonacci$
那么对于一个有 $sz$ 位的数，可以变化出 $p$ 位以下的有 $p-sz+1$ 位
即 $fibonacci$ 前缀和 $sum[p-sz+1]$
对去重后的所有数累加即可

✅

const int N = 2e5 + 10;
const int mod = 1e9 + 7;
ll n, p;
set<ll> st;
vector<ll> a;

ll fibo[N];

int main () {
        ios::sync_with_stdio(false);
        fibo[1] = fibo[2] = 1;
        for ( int i = 3; i < N; i ++ ) fibo[i] = (fibo[i - 1] + fibo[i - 2]) % mod;
        for ( int i = 2; i < N; i ++ ) fibo[i] = (fibo[i] + fibo[i - 1]) % mod; // fibonacci 前缀和

        cin >> n >> p;
        for ( int i = 0; i < n; i ++ ) {
                ll x; cin >> x;
                st.insert(x);
                a.push_back(x);
        }
        // 去重
        sort ( a.begin(), a.end(), greater<ll>() );
        a.erase(unique(a.begin(), a.end()), a.end());
        for ( int i = 0; i < a.size(); i ++ ) {
                if ( *st.lower_bound(a[i]) != a[i] ) continue;

                ll cur = a[i];
                bool flag = false;
                while ( cur ) {
                        if ( cur & 1 ) cur = (cur - 1) / 2; // 反式 *2+1
                        else {
                                if ( cur % 4 ) break; // 化不下去了
                                else cur /= 4; // 反式 *4
                        }
                        if ( *st.lower_bound(cur) == cur ) { // [a]内存在
                                flag = true;
                                break;
                        }
                }
                if ( flag ) st.erase(a[i]);
        }
        // 逐个累加
        ll res = 0;
        for ( auto i : st ) {
                ll tmp = i;
                ll sz = 0; while ( tmp ) sz ++, tmp /= 2; 
                if ( p >= sz ) (res += fibo[p - sz + 1]) %= mod;
        }
        cout << res << endl;
}

---

ICPC2021台湾省赛G_GardenPark

🔗

💡

一个计数问题
而且每个权值小的边都可以将自己的方案数推给相邻权值大的边
就直接计数dp就完事了

由于我们是小边推给大边
这里要按边权从小打大开始遍历
并且发现这里走过一条边有不同的方向，所以我们设置一个 dp_up[i] 和一个 dp_down[i] 来表示终止于这条边上到下的方案数和从下到上的方案数

那么我们可以先从这条边深度大的点枚举它的相邻边，这样是累积 dp_up
如果相邻边小，我们要看这个相邻边是从深度小的推向深度大的还是深度大到深度小的
如果是小推大，那么就 dp_up[i] += dp_down[该邻边编号] 否则 dp_up[i] += do_up[该邻边编号]
选择深度小的点枚举相邻边同理

✅

ll n;
struct Edge {
        ll nxt, to, val;
        ll id; // 该边编号
} edge [400005];
ll head[200005], cnt;
inline void add_Edge ( ll from, ll to, ll val, ll id ) {
        edge [ ++ cnt ] = {head[from], to, val, id};
        head[from] = cnt;
}

struct Way {
        ll a, b, c;
} w[200005];

map<ll, vector<ll> > mp;
ll d[200005];

inline void dfs_Dep ( ll x, ll fa, ll dp ) {
        d[x] = dp;
        for ( ll i = head[x]; i; i = edge[i].nxt ) {
                if ( edge[i].to == fa ) continue;
                dfs_Dep(edge[i].to, x, dp + 1);
        }
}
ll dp_up[200005], dp_down[200005];

int main () {
        scanf("%lld", &n);
        for ( ll i = 0; i < n - 1; i ++ ) {
                scanf("%lld%lld%lld", &w[i].a, &w[i].b, &w[i].c);
                mp[w[i].c].push_back(i);
                add_Edge(w[i].a, w[i].b, w[i].c, i);
                add_Edge(w[i].b, w[i].a, w[i].c, i);
        }
        dfs_Dep(1, 1, 0);
        for ( auto m : mp ) {
                ll val = m.first;
                for ( ll ve = 0; ve < m.second.size(); ve ++ ) {
                        ll uppt = w[m.second[ve]].a;
                        ll dwpt = w[m.second[ve]].b;
                        ll lnvl = w[m.second[ve]].c;
                        if ( d[uppt] > d[dwpt] ) swap(uppt, dwpt);

                        dp_up[m.second[ve]] = dp_down[m.second[ve]] = 1;

                        // dp_dw
                        for ( ll i = head[uppt]; i; i = edge[i].nxt ) {
                                ll to = edge[i].to;
                                ll vl = edge[i].val;
                                ll id = edge[i].id;
                                if ( vl >= lnvl ) continue; // 严格小于
                                if ( d[to] > d[uppt] ) { // 这样看相邻边是向上推的
                                        dp_down[m.second[ve]] += dp_up[id];
                                } else { // 向下推的
                                        dp_down[m.second[ve]] += dp_down[id];
                                }
                        } 
                        // dp_up
                        for ( ll i = head[dwpt]; i; i = edge[i].nxt ) {
                                ll to = edge[i].to;
                                ll vl = edge[i].val;
                                ll id = edge[i].id;
                                if ( vl >= lnvl ) continue;
                                if ( d[to] > d[dwpt] ) {
                                        dp_up[m.second[ve]] += dp_up[id];
                                } else {
                                        dp_up[m.second[ve]] += dp_down[id];
                                }
                        }
                }
        }
        ll res = 0;
        for ( ll i = 0; i < n - 1; i ++ ) res += dp_up[i] + dp_down[i];
        cout << res << endl;
}

---

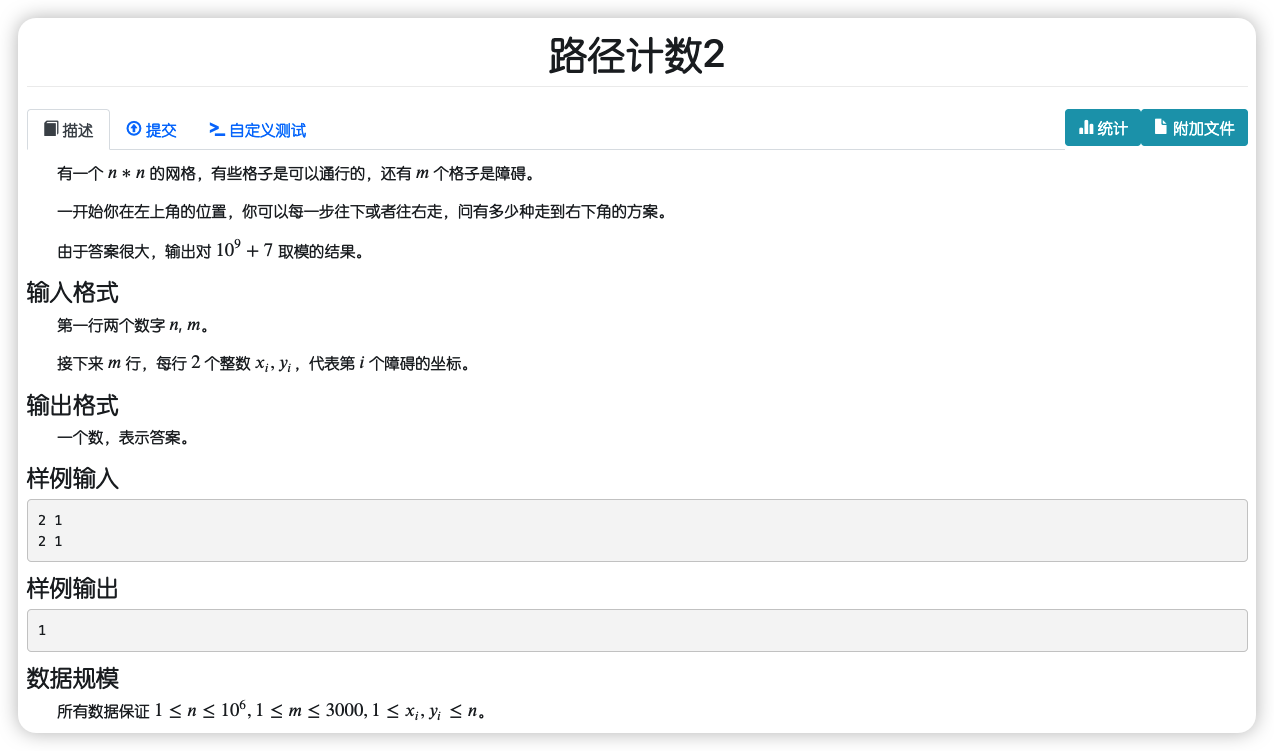
NamomoCamp2022春季div1每日一题_路径计数2

🔗

💡

直接从 $(1,1)$ 到 $(n,n)$ 很好求

令 $f[i][j]$ 表示从 $(x_i,y_i)\to(x_j,y_j)$ 会经过 $i$ 行 $j$ 列
观察矩阵 $f[i][j]=f[i][j-1]+f[i-1][j]\quad(i/j:0\to\infty)$ :

1	1	1	1
1	2	3	4
1	3	6	10
1	4	10	14

易知 $f[n][m]=\binom{n+m}{n}$

但是由于中间有障碍，要减去经过障碍到达 $(n,n)$ 的方案数

而前后障碍路径会相互嵌套，等于说如果有两个障碍 $(x_1,y_1),(x_2,y_2)$ ，减去 $(1,1)\to(x_1,y_1)\to(n,n)$ 与 $(1,1)\to(x_2,y_2)\to(n,n)$ 会多减一个 $(1,1)\to(x_1,y_1)\to(x_2,y_2)\to(n,n)$ ，要加上，那么即为容斥

由于在计算 $(1,1)$ 到 $i$ 个障碍物时，需要容斥掉前面的障碍物，所以我们需要一个状态去记录一下对于上述问题，前面障碍物的合法方案数
（前面是指满足 $x_j\le x_i,y_j\le y_i$ 的坐标）

令 $dp[i]$ 表示从 $(1,1)$ 到达 $(x_i,y_i)$ 在容斥掉 $1～(i-1)$ 这些障碍物的结果，也就是从 $(1,1)$ 不经过这些障碍物直接到达 $(x_i,y_i)$ 的方案数
我们用 $calc(\{x_1,y_1\},\{x_2,y_2\})$ 计算 $(x_1,y_1)\to(x_2,y_2)$ 的方案数
那么转移便是 $(1,1)\to(x_i,y_i)$ 的方案数容斥掉前面 $(x_j,y_j)\to(x_i,y_i)$ 的方案数乘上对应的 $dp[j]$
$dp[i]=calc(\{1,1\},\{x_i,y_i\})-\sum\limits_{j=1}^{i-1}calc(\{x_j,y_j\},\{x_i,y_i\})\times dp[j]$

我们将 $(n,n)$ 设为最后一个障碍物，答案便易得了

✅

const int N = 2e6 + 10;
const int M = 3e3 + 10;
int n, m;
vector<pair<int, int> > vec;

const int mod = 1e9 + 7;
inline ll ksm ( ll a, ll b ) { ll res = 1; while ( b ) { if ( b & 1 ) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv ( ll x ) { return ksm(x, mod - 2); }


ll ivf[N], f[N];
inline void get_F () { ivf[0] = f[0] = 1; for ( int i = 1; i < N; i ++ ) { ivf[i] = ivf[i - 1] * inv(i) % mod; f[i] = f[i - 1] * i % mod; } }
inline ll C ( int n, int m ) { return f[n] * ivf[m] % mod * ivf[n - m] % mod; }
inline ll calc ( pair<int, int> a, pair<int, int> b  ) { int curn = b.first - a.first + b.second - a.second; int curm = b.first - a.first; return C(curn, curm); }

ll dp[M];
int main () {
        get_F();
        scanf("%d%d", &n, &m);
        for ( int i = 0; i < m; i ++ ) {
                int x, y; scanf("%d%d", &x, &y);
                vec.push_back({x, y});
        }
        vec.push_back({n, n});
        sort ( vec.begin(), vec.end() );

        for ( int i = 0; i <= m; i ++ ) {
                dp[i] = calc({1, 1}, vec[i]);
                for ( int j = 0; j <= m; j ++ ) {
                        if ( i == j ) continue;
                        if ( vec[j].second <= vec[i].second && vec[j].first <= vec[i].first ) {
                                dp[i] -= dp[j] * calc(vec[j], vec[i]) % mod;
                                dp[i] = (dp[i] % mod + mod) % mod;
                        }
                }
        }
        printf("%lld\n", dp[m]);
}

---