树状数组

#

---

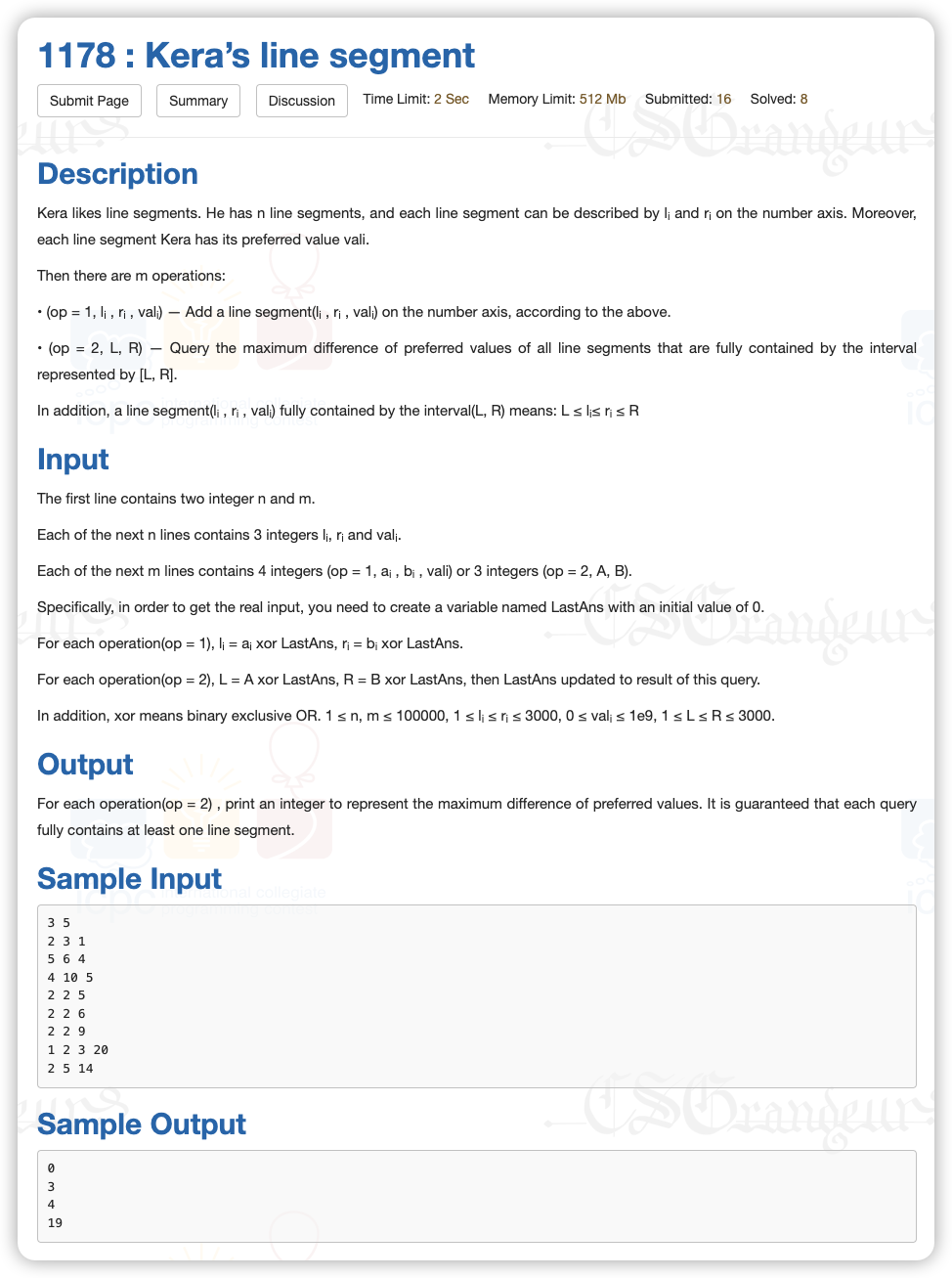
省赛2021广东K_Kera’sLineSegment

🔗

💡

双关键字的排序不好排，且这里 $1\le l\le r\le 3000$ ，这就是一个开 $n^2$ 空间和时间复杂度的数据量
如果是单纯开了二维数组然后暴力更新的话是特别慢的，但是有一种数据结构可以更新二维，就是二维树状数组
用二维树状数组的更新下，给定插入的 $[l,r]$ 里面 $l$ 向 $0$ 更新，$r$ 向 $n$ 更新，查询则是反过来，时间复杂度 $O(qlog^23000)$

✅

const int N  = 6010;
struct TrAry {
    int mn, mx;
} t[N][N];

inline int lowbit (int x) { return x & -x; }
inline void update (int id1, int id2, int c) {
    int x = id1;
    while (x) {
        int y = id2;
        while (y < N) t[x][y].mn = min(t[x][y].mn, c), t[x][y].mx = max(t[x][y].mx, c), y += lowbit(y);
        x -= lowbit(x);
    }
}
inline int query (int id1, int id2) {
    TrAry res = {0x3f3f3f3f, -1};
    int x = id1;
    while (x < N) {
        int y = id2;
        while (y) res.mn = min(res.mn, t[x][y].mn), res.mx = max(res.mx, t[x][y].mx), y -= lowbit(y);
        x += lowbit(x);
    }
    if (res.mn == 0x3f3f3f3f) return 0;
    return res.mx - res.mn;
}

int n, m;

int main () {
    for (int i = 0; i < N; i ++) for (int j = 0; j < N; j ++) t[i][j] = {0x3f3f3f3f, -1};

    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++) {
        int l, r, v; scanf("%d%d%d", &l, &r, &v);
        update(l, r, v);
    }
    int lasAns = 0;
    while (m --) {
        int op, l, r; scanf("%d%d%d", &op, &l, &r);
        l ^= lasAns;
        r ^= lasAns;
        if (op == 1) {
            int v; scanf("%d", &v);
            update(l, r, v);
        } else {
            lasAns = query(l, r);
            printf("%d\n", lasAns);
        }
    }
}

---

ABC221E_LEQ

🔗

💡

问题转化一下就是
从左向右，的贡献就是每个前面比它小的，在这个位置上的贡献为
由于区间长度总是参差不齐的
那么对于每个，我们都可以维护一个前缀贡献为
然后在的位置的时候的贡献容斥为即可，其中sum可以由树状数组的前缀得到
所以每次累加查询位置以前的总贡献，query(a[i]) * ksm(2, i)
然后在的位置上更新一下这个前缀贡献，update( a[i], ksm(ksm(2, i + 1), mod - 2) )

✅

#include <iostream>
#include <vector>
#include <algorithm>
#define ll long long
using namespace std;

const int N = 3e5 + 10;
const int mod = 998244353;
ll n, a[N];
vector<ll> nums;

inline ll ksm ( ll a, ll b ) {
	ll res = 1;
	while ( b ) {
		if ( b & 1 ) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}

namespace TreeArray {
	ll tr[N];
	inline ll lowbit ( ll x ) {
		return x & -x;
	}
	inline void update ( ll id, ll val ) {
		while ( id < N ) tr[id] = (tr[id] + val) % mod, id += lowbit(id);
	}
	inline ll query ( ll id ) {
		ll res = 0;
		while ( id > 0 ) res = (res + tr[id]) % mod, id -= lowbit(id);
		return res;
	}
} using namespace TreeArray;

int main() {
#ifndef ONLINE_JUDGE
	freopen("in.in", "r", stdin);
	freopen("out.out", "w", stdout);
#endif
	cin >> n;
	ll res = 0;
	for ( int i = 1; i <= n; i ++ ) 
		cin >> a[i],
		nums.push_back(a[i]);
	sort ( nums.begin(), nums.end() );
	nums.erase(unique(nums.begin(), nums.end()), nums.end());
	for ( int i = 1; i <= n; i ++ ) a[i] = lower_bound(nums.begin(), nums.end(), a[i]) - nums.begin() + 1;
	for ( int i = 1; i <= n; i ++ ) {
		res = (res + query(a[i]) * ksm(2, i) % mod) % mod;
		update (a[i], ksm(ksm(2, i + 1), mod - 2));	
	}
	cout << res << endl;
	return 0;
}

---

AcWing109_超快速排序

🔗

https://www.acwing.com/problem/content/109/

💡

对数据进行离散化操作，然后求逆序对即可

✅

/*
非最佳离散化写法，未完善
*/


#include <stack>
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <cstring>
#include <cstdio>
#include <map>
#include <queue>
#include <set>
#include <cmath>
#define rep1(i, a, n) for (int i = a; i <= n; i++)
#define rep2(i, a, n) for (int i = a; i >= n; i--)
#define mm(a, b) memset(a, b, sizeof(a))
#define elif else if
typedef long long ll;
void mc(int *aa, int *a, int len) { rep1(i, 1, len) * (aa + i) = *(a + i); }
const int INF = 0x7FFFFFFF;
const double G = 10;
const double eps = 1e-6;
const double PI = acos(-1.0);
const int mod = 1e9 + 7;
using namespace std;

int N;
int a[510000];
int flag[510000];
int C[510000];
int num[510000];

int lowbit(int x)
{
    return x & (-x);
}

int make_c(int x)
{
    int res = 0;
    int down_x = x + 1 - lowbit(x);
    rep2(i,x,down_x)
    {
        res += a[i];
    }
    return res;
}

int sum(int x)
{
    int res = 0;
    while(x>0)
        res += C[x], x -= lowbit(x);
    return res;
}

void update(int x,int val)
{
    while(x<=N)
        C[x] += val, x += lowbit(x);
}

int main()
{
    while(scanf("%d",&N)==1,N)
    {
        mm(C, 0);
        mm(a, 0);
        ll cnt = 0;
        rep1(i, 1, N) scanf("%d", &flag[i]), num[i] = flag[i];
        sort(num + 1, num + N + 1);
        rep1(i, 1, N)
        {
            flag[i] = lower_bound(num + 1, num + N + 1, flag[i]) - (num + 1) + 1;
            a[flag[i]] = 1;
            update(flag[i], 1);//a[flag[i]] + 1
            cnt += sum(N) - sum(flag[i]);
        }
        printf("%lld\n", cnt);
    }
}

---

POJ2352_Stars

🔗

http://poj.org/problem?id=2352

💡

因为y升序
所以我们不用管
每行插入之后看前面有多少个已经插入的就行了

✅

#pragma region
#pragma GCC optimize(3,"Ofast","inline")
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define eps 1e-6
#define PI acos(-1.0)
#define ll long long
#define INF 0x7FFFFFFF
#define Regal exit(0)
#define Chivas int main()
#define pb(x) push_back(x)
#define SP system("pause")
#define Max(a,b) ((a)>(b)?(a):(b))
#define Min(a,b) ((a)<(b)?(a):(b))
#define IOS ios::sync_with_stdio(false)
#define mm(a, b) memset(a, b, sizeof(a))
#define each_cass(cass) for (cin>>cass; cass; cass--)
#define test(a) cout << "---------" << a << "---------" << '\n'
 
using namespace std;
#pragma endregion

//全局变量
#pragma region
const int maxn = 40010;
int C[maxn];
int num[maxn] = {0};
int n;
#pragma endregion

//主体------------------------------------------

inline int Lowbit(int x){
    return x & (-x);
}

inline int Sum(int i){//前区间和
    int res = 0;
    while(i) res += C[i], i -= Lowbit(i);
    return res;
}

inline void UpDate(int i, int val){//后面的都冲上，万一有的放得更靠后呢？
    while(i <= maxn) C[i] += val, i += Lowbit(i);
}

Chivas{
    scanf("%d", &n);
    mm(C, 0);
    for(int i = 0, x, y; i < n; i ++){
        scanf("%d%d", &x, &y);
        x ++;
        UpDate(x, 1);//x位置更新完
        num[Sum(x)] ++;//统计
    }
    for(int i = 1; i <= n; i ++) printf("%d\n", num[i]);
    Regal;
}

---