树分治
Chivas-Regal
#
# 点分树
# AcWing2226_开店
# 🔗
# 💡
对于子树间的计算
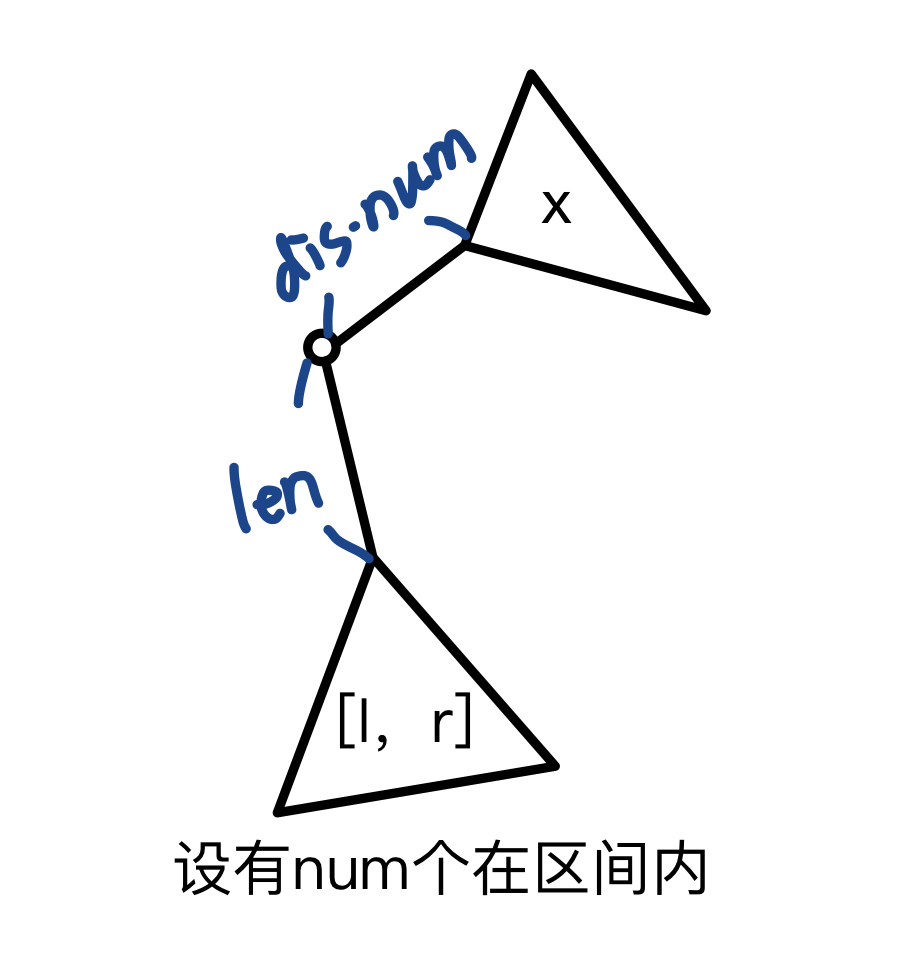
其中dis都可以很快求出
对于num和len
将子树内每个点信息存入重心排序,求dist前缀和
对于[L,R]对age二分出区间[a,b]
b - a + 1得出num
锁定出来的两个前缀和相减可以得到len
# ✅
const int N = 150010, M = N * 2;
int n, m, A;
struct Edge { int nxt, to, val; } edge [M]; int head[M], cnt;
int age[N];
bool st[N];
struct Father { int u, num; ll dist; };
vector<Father> f[N]; // f[i][j]表示节点i在j层的子树内的重心是谁,它是这层的第几个子树,离这个重心的距离
struct Son { int age; ll dist; friend bool operator < ( Son a, Son b ) { return a.age < b.age; } };
vector<Son> son[N][3]; // son[i][j]表示节点i的第j个子树内的所有节点
inline void add_Edge ( int from, int to, int val ) {
edge[ ++ cnt ] = { head[from], to, val };
head[from] = cnt;
}
inline int get_Sz ( int x, int fath ) {
if ( st[x] ) return 0;
int res = 1;
for ( int i = head[x]; ~i; i = edge[i].nxt ) {
int to = edge[i].to;
if ( to == fath ) continue;
res += get_Sz ( to, x );
}
return res;
}
inline int get_Wc ( int x, int fath, int tot, int &wc ) {
if ( st[x] ) return 0;
int sum = 1, mxSon = 0;
for ( int i = head[x]; ~i; i = edge[i].nxt ) {
int to = edge[i].to;
if ( to == fath ) continue;
int t = get_Wc ( to, x, tot, wc );
sum += t;
mxSon = max ( mxSon, t );
}
mxSon = max ( mxSon, tot - sum );
if ( mxSon <= tot / 2 ) wc = x;
return sum;
}
inline void get_Dis ( int x, int fath, ll dist, int wc, int k, vector<Son>& p ) {// wc的第k个子树内的节点
if ( st[x] ) return;
f[x].push_back({wc, k, dist}); // 自己这一层的重心,自己在第几个子树,离重心的距离
p.push_back({age[x], dist}); // 这个子节点的权值、距离
for ( int i = head[x]; ~i; i = edge[i].nxt ) {
int to = edge[i].to;
if ( to == fath ) continue;
get_Dis ( to, x, dist + edge[i].val, wc, k, p );
}
}
inline void get_Num ( int x ) {
if ( st[x] ) return ;
get_Wc ( x, -1, get_Sz ( x, -1 ), x );
st[x] = 1;
for ( int i = head[x], k = 0; ~i; i = edge[i].nxt, k ++ ) { // k: 在第k个子树
int to = edge[i].to;
if ( st[to] ) continue;
son[x][k].push_back({-1, 0}), son[x][k].push_back({A + 1, 0}); // 添加哨兵
get_Dis(to, -1, edge[i].val, x, k, son[x][k]); // 构建第k棵子树的所有点的信息
sort(son[x][k].begin(), son[x][k].end()); // 对这棵子树的点权排序
for ( int j = 1; j < son[x][k].size(); j ++ ) son[x][k][j].dist += son[x][k][j - 1].dist; // 让这颗子树按顺序的dist成为前缀和
}
for ( int i = head[x]; ~i; i = edge[i].nxt ) get_Num ( edge[i].to );
}
inline ll get_Qry ( int x, int l, int r ) {
ll res = 0;
for ( auto t : f[x] ) { // 一层一层枚举x所有父节点
if ( age[t.u] >= l && age[t.u] <= r ) res += t.dist;
for ( int i = 0; i < 3; i ++ ) {
if ( i == t.num || son[t.u][i].empty() ) continue;
int a = lower_bound ( son[t.u][i].begin(), son[t.u][i].end(), Son({l, -1}) ) - son[t.u][i].begin();
int b = lower_bound ( son[t.u][i].begin(), son[t.u][i].end(), Son({r + 1, -1}) ) - son[t.u][i].begin();
res += t.dist * (b - a) + son[t.u][i][b - 1].dist - son[t.u][i][a - 1].dist;
}
}
for ( int i = 0; i < 3; i ++ ) {
if ( son[x][i].empty() ) continue;
int a = lower_bound ( son[x][i].begin(), son[x][i].end(), Son({l, -1}) ) - son[x][i].begin();
int b = lower_bound ( son[x][i].begin(), son[x][i].end(), Son({r + 1, -1}) ) - son[x][i].begin();
res += son[x][i][b - 1].dist - son[x][i][a - 1].dist;
}
return res;
}
int main () {
#ifndef ONLINE_JUDGE
freopen("in.in", "r", stdin);
freopen("out.out", "w", stdout);
#endif
scanf("%d%d%d", &n, &m, &A);
for ( int i = 1; i <= n; i ++ ) scanf("%d", &age[i]);
memset ( head, -1, sizeof head );
for ( int i = 0, a, b, c; i < n - 1; i ++ ) {
scanf("%d%d%d", &a, &b, &c );
add_Edge ( a, b, c );
add_Edge ( b, a, c );
}
get_Num ( 1 );
ll res = 0;
while ( m -- ) {
int x, a, b; scanf("%d%d%d", &x, &a, &b);
int l = (a + res) % A, r = (b + res) % A;
if ( l > r ) swap ( l, r );
res = get_Qry ( x, l, r );
printf("%lld\n", res);
}
return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
# 点分治
# AcWing252_树
# 🔗
# 💡
路径分类:
1.两点都在一个子树内,那么递归处理子树即可
2.两点在不同子树内(路经重心),求所有子树内每一个点到重心的距离,两两匹配,如果和<=k,路径满足要求
但会有不应在本情况的对出现,即选中两个点在一个子树内,可以容斥地删掉不合法路径:减去两点都在一个子树地匹配情况
3.某个点是重心(边界情况),从重心开始向子树遍历,求每个点到重心的距离是不是k
如何求过重心的方案?
也就是给一堆数,任取两点总和<=k的方案数
排好序后对每个数向后二分最大是多少,也可以双指针取长度
容斥:
从当前点出发寻找重心,删去
求每个子树满足条件的值分别减去,将满足点加入大集合
最后加一下大集合的配对数量,递归子树继续解决
# ✅
const int N = 1e4 + 10, M = N * 2;
int n, m;
struct Edge { int nxt, to, val; } edge[M]; int head[M], cnt;
bool st[N];
int allSon[N], oneSon[N]; // 所有子树的点数、一个子树的点数
inline void Init () {
memset ( head, -1, sizeof head );
memset ( st, 0, sizeof st );
cnt = 0;
}
inline void add_Edge ( int from, int to, int val ) {
edge[ ++ cnt ] = { head[from], to, val };
head[from] = cnt;
}
inline int get_Sz ( int x, int fath ) { // 求子树大小
if ( st[x] ) return 0;
int res = 1;
for ( int i = head[x]; ~i; i = edge[i].nxt ) {
int to = edge[i].to;
if ( to == fath ) continue;
res += get_Sz ( to, x );
}
return res;
}
inline int get_Wc ( int x, int fath, int tot, int &wc ) { // 求重心,返回子树大小
if ( st[x] ) return 0;
int sum = 1, mxSon = 0; //子树大小、最大剩余块
for ( int i = head[x]; ~i; i = edge[i].nxt ) {
int to = edge[i].to;
if ( to == fath ) continue;
int t = get_Wc ( to, x, tot, wc );
sum += t;
mxSon = max ( mxSon, t );
}
mxSon = max ( mxSon, tot - sum ); // 与另一侧的块进行比较
if ( mxSon <= tot / 2 ) wc = x; // 如果最大剩余连通块小于总块的1/2,重心为它
return sum;
}
inline void get_Dis ( int x, int fath, int dist, int &tot ) { // 获取一棵子树的所有点到重心的距离
if ( st[x] ) return;
oneSon[tot ++] = dist;
for ( int i = head[x]; ~i; i = edge[i].nxt ) {
int to = edge[i].to;
if ( to == fath ) continue;
get_Dis ( to, x, dist + edge[i].val, tot );
}
}
inline int get_Num ( int a[], int k ) { // 双指针去查找满足加起来<=k的点数
sort ( a, a + k ); int res = 0;
for ( int i = k - 1, j = -1; i >= 0; i -- ) {
while ( j + 1 < i && a[j + 1] + a[i] <= m ) j ++;
j = min ( j, i - 1 );
res += j + 1;
}
return res;
}
inline int Solve ( int x ) {
if ( st[x] ) return 0;
get_Wc ( x, -1, get_Sz ( x, -1 ), x ); // 找重心
st[x] = 1; // 删重心
int res = 0, cnt_allSon = 0;
for ( int i = head[x]; ~i; i = edge[i].nxt ) {
int cnt_oneSon = 0, to = edge[i].to;
get_Dis ( to, -1, edge[i].val, cnt_oneSon ); // 记录一个子树的点
res -= get_Num ( oneSon, cnt_oneSon ); // 减去一个子树内满足条件的点对数
for ( int j = 0; j < cnt_oneSon; j ++ )
res += oneSon[j] <= m, // 与重心相连的路径
allSon[cnt_allSon ++] = oneSon[j]; // 这个子树点塞入总点中
}
res += get_Num ( allSon, cnt_allSon ); // 加上所有点满足条件的对
for ( int i = head[x]; ~i; i = edge[i].nxt ) res += Solve ( edge[i].to ); // 进行下一层
return res;
}
int main () {
#ifndef ONLINE_JUDGE
freopen("in.in", "r", stdin);
freopen("out.out", "w", stdout);
#endif
while ( scanf("%d%d", &n, &m) == 2, n || m ) {
Init();
for ( int i = 1, a, b, c; i < n; i ++ )
scanf("%d%d%d", &a, &b, &c),
add_Edge ( a, b, c ),
add_Edge ( b, a, c );
printf("%d\n", Solve(0));
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
# AcWing264_权值
# 🔗
# 💡
此时路径还是分成三类:
1.两点在一个子树内
2.两点在不同子树内
3.一点在子树重心上
重要还是处理第二种
我们可以设置一个哈希表或者说桶,去维护在距离重心为i的距离下,边数的最小值
那么我们在每次遍历一棵子树时,去查找当前子树的每个距离重心不大于m的点
对于每个点,如果距离=m说明是第三种,那么我们就可以直接拿res和这个点距离重心的边数进行比较
如果距离<m,我们去看在"m-距离"的桶中的值,然后用这个值+我们查找的点距离重心的边数与res进行对比
然后将这课子树的每个点记录进桶中,同时将我们塞入的每个点记录一下,再遍历下一个子树
最后将塞入过的点对应的桶重置,进入下一层递归
# ✅
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
#include <map>
#include <cstdio>
#define ll long long
#define x first
#define y second
#define pii pair<int, int>
#define INF 0x3f3f3f3f
using namespace std;
const int N = 2e5 + 10, M = 2 * N, S = 1e6 + 10;
struct Edge { int nxt, to, val; } edge [M]; int head[M], cnt;
int n, m;
bool st[N];
pii oneSon[N], allSon[N]; // first = 距离,second = 边数
int f[S]; // 维护在距离为i下,边数的最小值
int res = INF;
inline void Init () {
memset ( head, -1, sizeof head );
memset ( st, 0, sizeof st );
memset ( f, INF, sizeof f );
cnt = 0;
}
inline void Add_Edge ( int from, int to, int val ) {
edge [ ++ cnt ] = { head[from], to, val };
head[from] = cnt;
}
inline int get_Sz ( int x, int fath ) {
if ( st[x] ) return 0;
int res = 1;
for ( int i = head[x]; ~i; i = edge[i].nxt ) {
int to = edge[i].to;
if ( to == fath ) continue;
res += get_Sz ( to, x );
}
return res;
}
inline int get_Wc ( int x, int fath, int tot, int &wc ) {
if ( st[x] ) return 0;
int mxSon = 0, sum = 1;
for ( int i = head[x]; ~i; i = edge[i].nxt ) {
int to = edge[i].to;
if ( to == fath ) continue;
int t = get_Wc ( to, x, tot, wc );
mxSon = max ( mxSon, t );
sum += t;
}
mxSon = max ( mxSon, tot - sum );
if ( mxSon <= tot / 2 ) wc = x;
return sum;
}
inline void get_Dis ( int x, int fath, int dist, int cnt, int &tot ) {
if ( st[x] || dist > m ) return ;
oneSon[ tot ++ ] = { dist, cnt };
for ( int i = head[x]; ~i; i = edge[i].nxt ) {
int to = edge[i].to;
if ( to == fath ) continue;
get_Dis ( to, x, dist + edge[i].val, cnt + 1, tot );
}
}
inline void Solve ( int x ) {
if ( st[x] ) return ;
get_Wc ( x, -1, get_Sz ( x, -1 ), x );
st[x] = true;
int cnt_allSon = 0;
for ( int i = head[x]; ~i; i = edge[i].nxt ) {
int to = edge[i].to, cnt_oneSon = 0;
get_Dis ( to, x, edge[i].val, 1, cnt_oneSon );
for ( int j = 0; j < cnt_oneSon; j ++ ) {
auto t = oneSon[j];
if ( t.x == m ) res = min ( res, t.y ); // 可以直接根据这个节点建立[重心,节点]的路径判断一下个数最小值
else res = min ( res, f[m - t.x] + t.y ); // 根据之前维护出来的哈希表内的判断一下个数最小值
}
for ( int j = 0; j < cnt_oneSon; j ++ ) {
auto t = oneSon[j];
f[t.x] = min ( f[t.x], t.y ); // 将当前子树的加入哈希表
allSon[ cnt_allSon ++ ] = t;
}
}
for ( int i = 0; i < cnt_allSon; i ++ ) { // 把这一个大连通块的重置为INF
auto t = allSon[i];
f[t.x] = INF;
}
for ( int i = head[x]; ~i; i = edge[i].nxt ) {
Solve(edge[i].to);
}
}
int main () {
#ifndef ONLINE_JUDGE
freopen("in.in", "r", stdin);
freopen("out.out", "w", stdout);
#endif
Init ();
scanf("%d%d", &n, &m);
for ( int i = 0, a, b, c; i < n; i ++ ) {
scanf("%d%d%d", &a, &b, &c);
Add_Edge ( a, b, c );
Add_Edge ( b, a, c );
}
Solve(0);
if ( res == INF ) res = -1;
printf("%d\n", res);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111



