区间DP

#

---

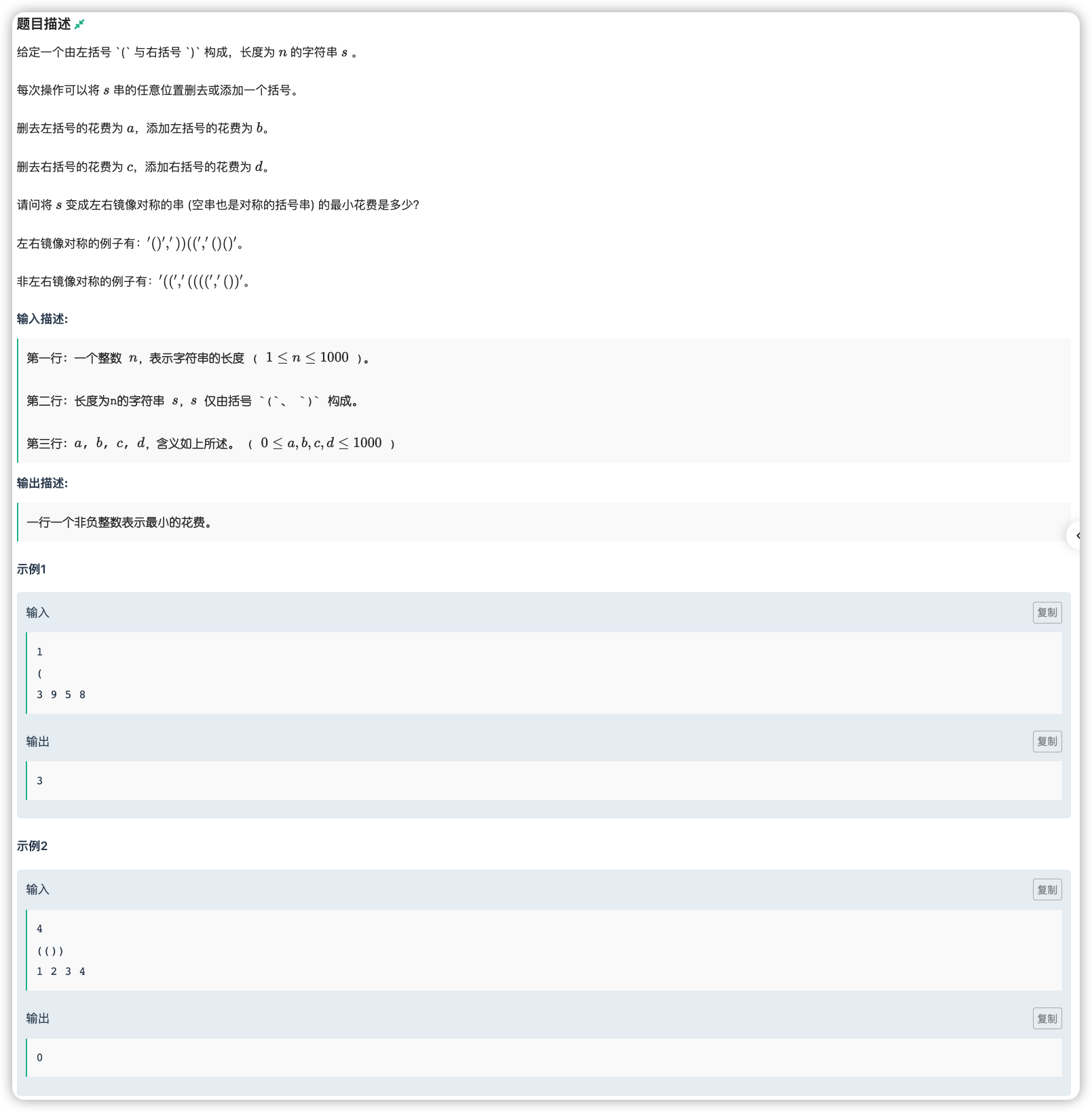
河南萌新联赛2022（6）J_对称括号串

🔗

💡

全局对称，只有局部对称才有可能让全局对称，且看到 $n\le 1000$ ，明显区间 $dp$
令 $dp[l][r]$ 表示区间 $[l,r]$ 对称的最小花费
那么首先是一个不计任何情况的转移
区间长度从小到大，既然 $[l+1,r]$ 已经对称了，那么消除掉 $s[l]$ 的不对称即可，即 $dp[l][r]=min(dp[l][r],dp[l+1][r]+s[l]='('?min(a,d):min(b,c)))$
同理 $[l,r-1]$ 已经对称，消掉 $s[r]$ 的不对称 $dp[l][r]=min(dp[l][r],dp[l][r-1]+s[r]='('?min(a,d):min(b,c)))$
但是有可能我们不消掉任何的东西就可以对称，即 $s[l]\neq s[r]$ 的时候， $dp[l][r]$ 可以通过不花费任何的价钱从 $dp[l+1][r-1]$ 转移过来
转移结束，码就完了

✅

int n, a, b, c, d;
string s;
int dp[1010][1010];

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n;
    cin >> s; s = " " + s;
    cin >> a >> b >> c >> d;

    memset(dp, 0x3f, sizeof dp);
    for (int i = 1; i <= n; i ++) dp[i + 1][i] = 0;

    for (int len = 1; len <= n; len ++) {
        for (int i = 1; i + len - 1 <= n; i ++) {
            int j = i + len - 1;
            dp[i][j] = min(dp[i][j], dp[i + 1][j] + (s[i] == '(' ? min(a, d) : min(b, c)));
            dp[i][j] = min(dp[i][j], dp[i][j - 1] + (s[j] == '(' ? min(a, d) : min(b, c)));
            if (s[i] != s[j]) dp[i][j] = min(dp[i][j], dp[i + 1][j - 1]);
        }
    }

    cout << dp[1][n] << endl;
}

---

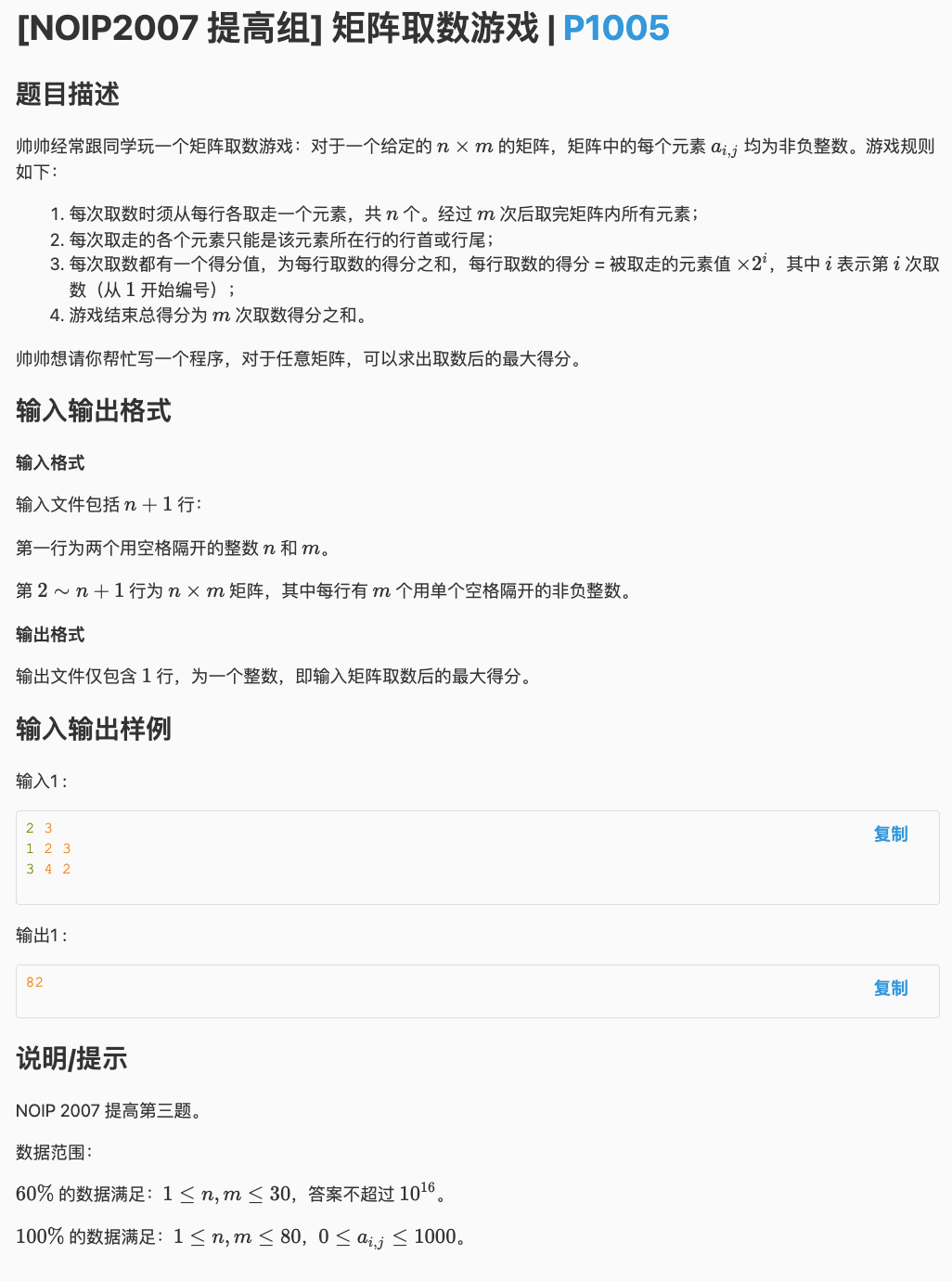
洛谷P1005_矩阵取数游戏

🔗

💡

由于每一行互不影响，所以我们一行一行分开处理 每行两个端点左右可以选左也可以选右 且每一个都有自己的权值，要求从选左选右序列中找到一个价值最大的 那么一看就有区间dp那味儿了 如果dp数组两个下标 维护的是选到 时的最大值 那么这个是可以通过转移的，即 表示已经选过的个数

✅

const LL N = 100;
LL a[N];
ll n, m;
LL res = 0;
LL dp[N][N];

inline LL ksm ( LL a, LL b ) {
        LL res = 1;
        while ( b ) {
                if ( b % 2 ) res = res * a;
                a = a * a;
                b /= 2;
        }
        return res;
}

inline LL Solve () {
        memset ( dp, 0, sizeof dp );
        LL ans = 0;
        for ( int i = 1; i <= m; i ++ ) { ll x; cin >> x; a[i] = x; }
        for ( int i = 1; i <= m; i ++ ) {
                for ( int j = m; j >= i; j -- )
                        dp[i][j] = max (
                                dp[i - 1][j] + a[i - 1] * ksm ( 2, m - j + i - 1 ), 
                                dp[i][j + 1] + a[j + 1] * ksm ( 2, m - j + i - 1 )
                        );
        }
        for ( int i = 1; i <= m; i ++ ) ans = max ( ans, dp[i][i] + ksm ( 2, m ) * a[i] );
        return ans;
}

inline void Print_128 ( LL x ) {
        if ( x == 0 ) { cout << 0 << endl; return; }
        string res;
        while ( x ) res += x % 10 + '0', x /= 10;
        reverse ( res.begin(), res.end() );
        cout << res << endl;
}

int main () {
        cin >> n >> m;
        for ( int i = 1; i <= n; i ++ ) res += Solve ();
        Print_128(res);
}

---

洛谷P1220_关路灯

🔗

💡

这种左右端点决策扩展的问题，应想到用区间DP

人是一步步走的，那么这里就出现了四种转移方式 从的 走向 从的 走向 从的 走向 从的 走向 那么也对应了不同的影响 从 走向 这一段产生的影响为 "未关掉的灯泡数量的功率和 的路程"

功率和我们可以记录功率前缀和，然后总和减去关掉过的区间灯泡功率和

inline int Work ( int i, int j ) {
        return a[i - 1].y + a[n].y - a[j].y;
}

路程直接就距离相减即可

inline int WalkTime ( int i, int j ) {
        return abs(a[j].x - a[i].x);
}

状态就记录区间，然后再记录一下当前在区间 的左侧 还是右侧 那么转移方程为

✅

# include <iostream>
# include <algorithm>
# include <cstring>
# include <vector>
# include <map>

# define ll long long

using namespace std;

const int N = 55;
int dp[N][N][2];

# define pii pair<int, int>
# define x first
# define y second

int n, c;
pii a[N];

inline int Work ( int i, int j )     { return a[i - 1].y + a[n].y - a[j].y; }
inline int WalkTime ( int i, int j ) { return abs(a[j].x - a[i].x); }

int main () {
        ios::sync_with_stdio(false);

        cin >> n >> c;
        for ( int i = 1; i <= n; i ++ ) cin >> a[i].x >> a[i].y;
        for ( int i = 1; i <= n; i ++ ) a[i].y += a[i - 1].y;
  
        memset ( dp, 0x3f3f3f3f, sizeof dp );
        dp[c][c][0] = dp[c][c][1] = 0;

        for ( int i = c; i >= 1; i -- ) {
                for ( int j = c; j <= n; j ++ ) {
                        dp[i - 1][j][0] = min ( dp[i - 1][j][0], dp[i][j][1] + WalkTime ( i - 1, j ) * Work ( i, j ) );
                        dp[i - 1][j][0] = min ( dp[i - 1][j][0], dp[i][j][0] + WalkTime ( i - 1, i ) * Work ( i, j ) );
                        dp[i][j + 1][1] = min ( dp[i][j + 1][1], dp[i][j][1] + WalkTime ( j, j + 1 ) * Work ( i, j ) );
                        dp[i][j + 1][1] = min ( dp[i][j + 1][1], dp[i][j][0] + WalkTime ( i, j + 1 ) * Work ( i, j ) );
                }
        }

        cout << min ( dp[1][n][0], dp[1][n][1] ) << endl;
  
}

---

CodeForces1132F_ClearTheString

🔗

💡

一眼区间 $dp$ ，但是有地方没考虑清楚 $wa$ 半天 ... 首先一个正常扩张就是，如果 $l=r$ ，那么 $l$ 可以和 $r$ 一起从 $[l+1,r]$ 向外扩，或者 $r$ 与 $l$ 一起从 $[l,r-1]$ 向外扩，这一步是不费次数的
所以 $if\;(s_l=s_r):\quad dp_{l,r}=\min(dp_{l,r},dp_{l+1,r},dp_{l,r-1})$
如果 $l\neq r$ 那么就需要多加一次操作了，原理和上面一样
所以 $else:\quad dp_{l,r}=\min(dp_{l,r},dp_{l+1,r}+1,dp_{l,r-1}+1)$

当然用 $l=r$ 去判断是不全面的，因为有可能会出现分区域的可能性，即有很多个部分，每个部分都是从其中一个点开始向外扩散
比如 $abaccdc$
这样就要取一个区间被划分为两个部分的 $\min$ ，也就是枚举这个区间的断点 $k$ ，维护 $dp_{l,r}=\min(dp_{l,r},dp_{l,k}+dp_{k,r}-1)$
之所以不是取 $dp_{l,k}+dp_{k+1,r}$ ，是因为有可能 $l,k,r$ 是一起删掉的，所以重复算 $k$ 不管是不是一起都稳定 $+1$ ，就 $dp_{l,k}+dp_{k,r}$ 减掉一个 $1$ 即可

✅

int n; 
char s[510];
int dp[510][510];

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        cin >> n >> (s + 1);
        memset(dp, 0x3f, sizeof dp);
        for (int i = 1; i <= n; i ++) dp[i][i] = 1;
        for (int len = 2; len <= n; len ++) {
                for (int l = 1; l + len - 1 <= n; l ++) {
                        int r = l + len - 1;
                        if (s[l] == s[r]) dp[l][r] = min({dp[l][r], dp[l + 1][r], dp[l][r - 1]});
                        else dp[l][r] = min({dp[l][r], dp[l + 1][r] + 1, dp[l][r - 1] + 1});
                        for (int i = l; i <= r; i ++) {
                                dp[l][r] = min(dp[l][r], dp[l][i] + dp[i][r] - 1);
                        }
                }
        }
        cout << dp[1][n] << endl;
}

---

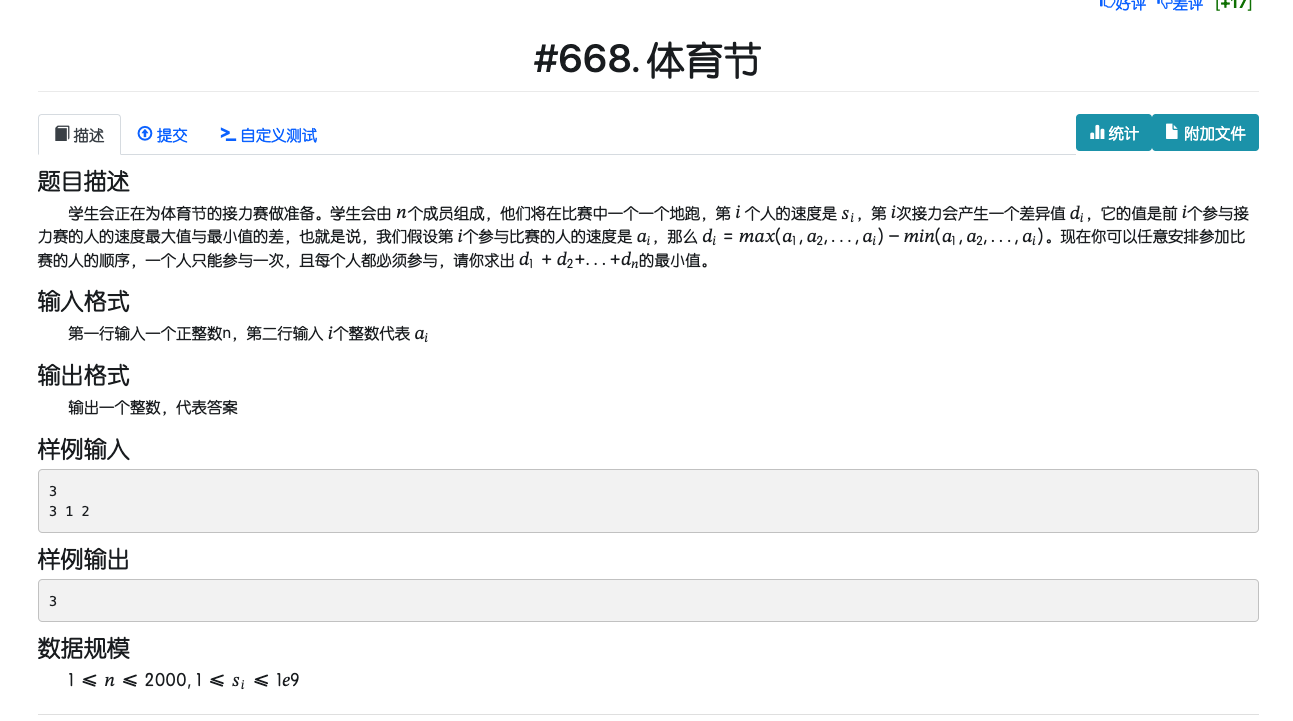
DaimayuanOnlineJudge_体育节

🔗

💡

建个模型，其实每次肯定想选择离最大值最小值比较近的点，且这个范围只会扩张，也就是说，不会选择在最大值最小值区间内的点，因为这个点现在选也不如早点选
既然它范围只会扩张，故如果排序后，那么每次选择的必定是一段连续的区间
这样来看可以利用区间 $dp$ 枚举 $l,r$ ，求一下这一步是扩张了 $l$ 还是 $r$
维护 $dp[l][r]$ 的最小值，即 $dp[l][r]=min(dp[l+1][r],dp[l][r-1])+a[r]-a[l]$
最后算 $dp[1][m]$ 即可

✅

const int N = 2010;
int a[N], n;
ll dp[N][N];

int main () {
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);
    sort(a + 1, a + 1 + n);
    for (int i = 1; i <= n; i ++) for (int j = 1; j <= n; j ++) dp[i][j] = 2e18;
    for (int i = 1; i <= n; i ++) dp[i][i] = 0;
    for (int len = 2; len <= n; len ++) {
        for (int i = 1; i + len - 1 <= n; i ++) {
            int j = i + len - 1;
            dp[i][j] = min(dp[i + 1][j], dp[i][j - 1]) + a[j] - a[i];
        }
    }
    printf("%lld\n", dp[1][n]);
}

---

ICPC2014CERCL_OuterSpaceInvaders

🔗

💡

有几个位置信息，画一个坐标轴好看一些

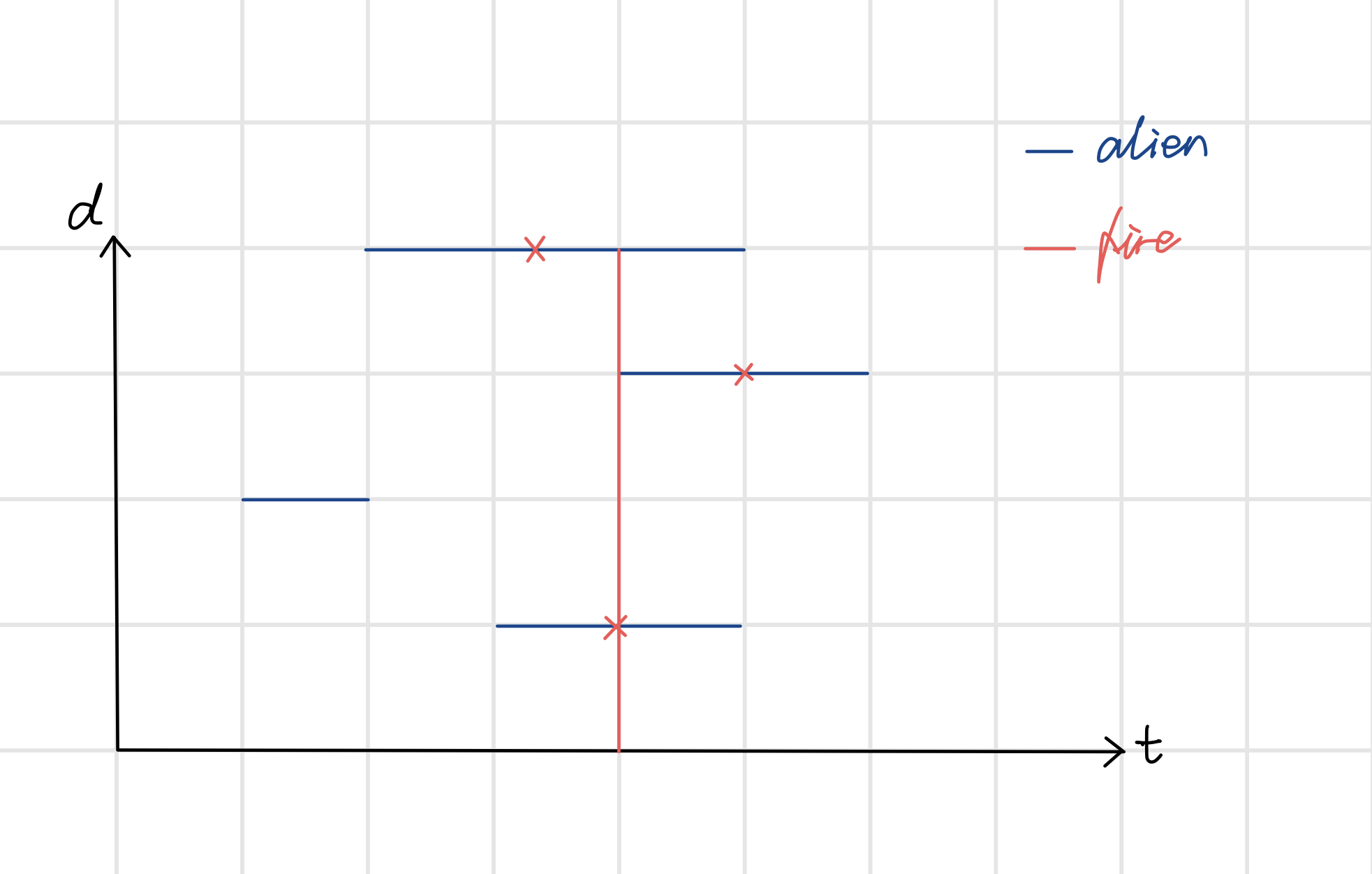
我们必须做的事情是把 $d$ 最大的那个外星人给干碎
那么下面的有可能会一起被干碎
这里我们无法确定我们在哪攻击能使结果最小，考虑 $dp$
$dp[l][r]$ 为将完整存在于 $[l,r]$ 的外星人全部干碎的最小花费
那么可以 $DFS(l,r)$ 分治 $+$ 记忆化
每次去找 $[l,r]$ 内的最大 $d$ 的外星人 $x$，枚举在 $[x.l,x.r]$ 内的 $m$ 位置建立 $fire$ ，花费 $x.d$，那么剩余的外星人则在 $[l,m-1],[m+1,r]$
递归去查即可

我们不可能每一次 $DFS$ 都暴力 $[1,n]$ 维护一遍完整在 $[l,r]$ 内的 $d$ 最大的外星人信息
可以提前预处理好 $mx[l][r],id[l][r]$ 作为最大 $d$ 和最大 $d$ 的外星人编号
虽然 $1\le l\lt r\le 10000$，但是可以想到这里 $[l,r]$ 离散化后并不会影响结果，该交叉交叉，该包含包含，该分离分离
所以将 $[l,r]$ 离散化后最大为 $600$
用离散化后的 $[l,r]$ 去更新这两个记录值即可

那么我们 $DFS$ 内就很好求了，只用一重循环在 $[id[l][r].l,id[l][r].r]$ 跑该区间内 $fire$ 的位置即可

✅

记忆化分治DFS写法

# define tpliii tuple<int, int, int>
const int N = 305;
int n;
tpliii alien[N];
vector<int> nums;
 
int mx[N << 1][N << 1];
int id[N << 1][N << 1];
int dp[N << 1][N << 1];
 
inline int DFS ( int l, int r ) {
        if ( l == r ) return 0;
        if ( dp[l][r] ) return dp[l][r];
 
        int mxd = mx[l][r], mxid = id[l][r];
        int res = 0x3f3f3f3f;
        for ( int i = get<0>(alien[mxid]); i <= get<1>(alien[mxid]); i ++ ) {
                int cur = 0;
                if ( l < i - 1 && ~id[l][i - 1] ) cur += DFS(l, i - 1);
                if ( i + 1 < r && ~id[i + 1][r] ) cur += DFS(i + 1, r);
                res = min(res, cur);
        }
        res += mxd;
        return dp[l][r] = res;
}
 
 
inline void Solve () {
        nums.clear();
        memset(mx, 0, sizeof mx);
        memset(id, -1, sizeof id);
        memset(dp, 0, sizeof dp);
 
        scanf("%d", &n);
        for ( int i = 0; i < n; i ++ ) {
                int a, b, c; scanf("%d%d%d", &a, &b, &c);
                alien[i] = {a, b, c};
                nums.push_back(a); nums.push_back(b);
        }
 
        sort ( nums.begin(), nums.end() );
        nums.erase(unique(nums.begin(), nums.end()), nums.end());
        auto get_Id = [&]( int x ) { return lower_bound(nums.begin(), nums.end(), x) - nums.begin(); };
        int L = 0x3f3f3f3f, R = 0;
        for ( int i = 0; i < n; i ++ ) {
                alien[i] = {get_Id(get<0>(alien[i])), get_Id(get<1>(alien[i])), get<2>(alien[i])};
                L = min(L, get<0>(alien[i]));
                R = max(R, get<1>(alien[i]));
        }
        for ( int l = L; l <= R; l ++ ) {
                for ( int r = l; r <= R; r ++ ) {
                        for ( int i = 0; i < n; i ++ ) {
                                int al = get<0>(alien[i]), ar = get<1>(alien[i]), d = get<2>(alien[i]);
                                if ( l <= al && ar <= r ) {
                                        if ( mx[l][r] < d ) {
                                                mx[l][r] = d;
                                                id[l][r] = i;
                                        }
                                }
                        }
                }
        }
        printf("%d\n", DFS(L, R));
}

区间DP递推写法

# define tpliii tuple<int, int, int>
const int N = 305;
int n;
tpliii alien[N];
vector<int> nums;
int mx[N << 1][N << 1];
int id[N << 1][N << 1];
 
int dp[N << 1][N << 1];
 
inline void Solve () {
        mp.clear();
        nums.clear();
        memset(mx, 0, sizeof mx);
        memset(id, -1, sizeof id);
        memset(dp, 0x3f3f3f3f, sizeof dp);
 
        scanf("%d", &n);
        for ( int i = 0; i < n; i ++ ) {
                int a, b, c; scanf("%d%d%d", &a, &b, &c);
                alien[i] = {a, b, c};
                nums.push_back(a); nums.push_back(b);
        }
 
        sort ( nums.begin(), nums.end() );
        nums.erase(unique(nums.begin(), nums.end()), nums.end());
        auto get_Id = [&]( int x ) { return lower_bound(nums.begin(), nums.end(), x) - nums.begin(); };
        int L = 0x3f3f3f3f, R = 0;
        for ( int i = 0; i < n; i ++ ) {
                alien[i] = {get_Id(get<0>(alien[i])), get_Id(get<1>(alien[i])), get<2>(alien[i])};
                L = min(L, get<0>(alien[i]));
                R = max(R, get<1>(alien[i]));
        }
        for ( int l = L; l <= R; l ++ ) {
                for ( int r = l; r <= R; r ++ ) {
                        for ( int i = 0; i < n; i ++ ) {
                                int al = get<0>(alien[i]), ar = get<1>(alien[i]), d = get<2>(alien[i]);
                                if ( l <= al && ar <= r ) {
                                        if ( mx[l][r] < d ) {
                                                mx[l][r] = d;
                                                id[l][r] = i;
                                        }
                                }
                        }
                }
        }
        for ( int i = L; i <= R; i ++ ) dp[i][i] = 0;
        for ( int len = 1; len <= R - L + 1; len ++ ) {
                for ( int l = L; l <= R; l ++ ) {
                        int r = l + len - 1;
                        if ( r > R ) continue;
                        for ( int m = get<0>(alien[id[l][r]]); m <= get<1>(alien[id[l][r]]); m ++ ) {
                                int cur = 0;
                                if ( l < m - 1 && ~id[l][m - 1] ) cur += dp[l][m - 1];
                                if ( m + 1 < r && ~id[m + 1][r] ) cur += dp[m + 1][r];
                                dp[l][r] = min(dp[l][r], cur + mx[l][r]);
                        }
                }
        }
        printf("%d\n", dp[L][R]);
}

---

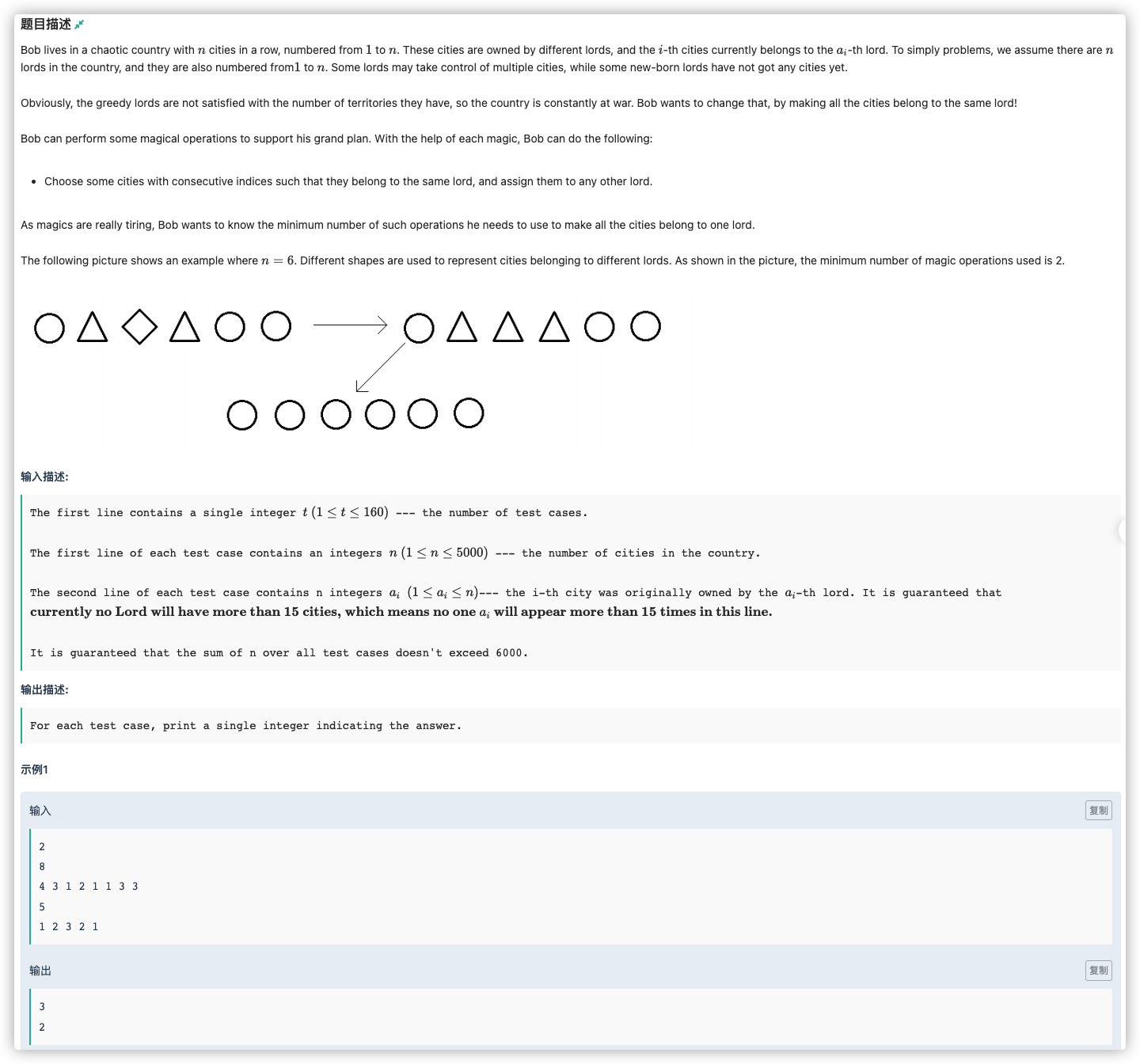
ICPC2020南京站C_Cities

🔗

💡

考虑这样一个最普遍的数列 $[1,2,3,4,5]$ ，它想变成同一个数一定要从左往右一次次变 $n-1$ 次
那么再看这样一个可以优化的数列 $[1,2,3,2,5]$ ，它想变成同一个数可以让两个 $2$ 中间的数向外扩展从而白嫖一次操作，也就是说每出现一次 $[x,\dots,x]$ 我们就可以完成一次匹配从而白嫖一次操作

注意这些匹配不可交叉，也就是说对于 $x\lt l,y\in [l,r]$ 我们又匹配 $[x,y]$

那么这就是一个区间问题，看一下数据范围 $1\le n\le 5000$ 那么就直接开区间 $dp$ 就行
我们令 $dp[l][r]$ 表示 $[l,r]$ 内的最大匹配数

• $l$ 可以不配对，$dp[l][r]=max(dp[l+1][r])$
• $l$ 可以配对，对于 $[l+1,r]$ 的每一个和 $a[l]$ 相等的元素 $a[m]$ ，我们都可以让它和 $a[l]$ 配对，由于不交叉性，$dp[l][r]=max(dp[l+1][m-1]+dp[m][r]+1)$

那么最后就最大可以白嫖 $dp[1][n]$ 次，结果便是 $n-1-dp[1][n]$

✅

const int N = 5e3 + 10;
vector<int> pos[N];
int n;
int a[N];
int dp[N][N];


inline void Solve () {
        cin >> n;
        memset(dp, 0, sizeof dp);
        for ( int i = 1; i <= n; i ++ ) pos[i].clear();
        for ( int i = 1; i <= n; i ++ ) {
                cin >> a[i];
                pos[a[i]].push_back(i);
        }

        for ( int len = 1; len <= n; len ++ ) {
                for ( int l = 1; l <= n; l ++  ) {
                        int r = l + len - 1; if ( r > n ) continue;

                        dp[l][r] = max(dp[l + 1][r], dp[l][r]);

                        auto beg = upper_bound(pos[a[l]].begin(), pos[a[l]].end(), l);

                        for ( auto m = beg; m != pos[a[l]].end() && *m <= r; m ++ ) {
                                dp[l][r] = max(dp[l][r], dp[l + 1][*m - 1] + dp[*m][r] + 1);
                        }
                }
        }
        cout << n - 1 - dp[1][n] << endl;
}

---

NamomoCamp2022春季div1每日一题_NoCrossing

🔗

💡

在图上画一画可行的走法便可得到这个题要考虑好我们走的点在坐标上一定要是让 $[l,r]$ 不断下压的这非常有区间 $dp$ 的味道那么我们维护 $dp[s][l][r][to]$

• $s$ 为滚动下标
• $l,r$ 为我们维护的区间
• $to$ 指方向，也意味着在 $[l,r]$ 区间内我们最终会停在 $0/1:l/r$ 那么状态转移即为

$[l,mid]$ 一定是停在 $mid$ ，毕竟 $mid\to l$ 没有可转移的状态 $[mid,r]$ 同理也是停在 $mid$ $[l,mid],[mid,r]$ 都可以由 $l\to r\to mid$ 和 $r\to l\to mid$ 可以固定出来 所以 $dp[l,mid],dp[mid,r]$ 都由 $dp[l,r][1]+g[r][mid]$ 和 $dp[l,r][0]+g[l][mid]$ 维护最小值

更新 $k$ 次后我们即可得到我们想要的

✅

const int M = 2010,
          N = 110;

int g[N][N];
int n, m, k;
int dp[2][N][N][2]; // s, l, r, to{{0,left},{1,right}}


int main () {
        scanf("%d%d%d", &n, &k, &m);
        memset(g, 0x3f3f3f, sizeof g);
        for ( int i = 0; i < m; i ++ ) {
                int a, b, c; scanf("%d%d%d", &a, &b, &c);
                g[a][b] = min(g[a][b], c);
        }
        memset(dp[0], 0x3f3f3f3f, sizeof dp[0]);
        for ( int i = 1; i <= n; i ++ ) dp[0][0][i][1] = dp[0][i][n + 1][0] = 0;
        for ( int S = 1; S <= k - 1; S ++ ) {
                int s = S & 1;
                memset(dp[s], 0x3f3f3f3f, sizeof dp[s]);
                for ( int l = 0; l <= n + 1; l ++ ) {
                        for ( int r = l + 2; r <= n + 1; r ++ ) {
                                for ( int mid = l + 1; mid < r; mid ++ ) {
                                        int tmp = min(dp[!s][l][r][1] + g[r][mid], dp[!s][l][r][0] + g[l][mid]);
                                        dp[s][l][mid][1] = min(dp[s][l][mid][1], tmp);
                                        dp[s][mid][r][0] = min(dp[s][mid][r][0], tmp);
                                }
                        }
                }
        }
        int res = 0x3f3f3f3f;
        for ( int l = 0; l <= n + 1; l ++ ) {
                for ( int r = l + 1; r <= n + 1; r ++ ) {
                        res = min({res, dp[k - 1 & 1][l][r][0], dp[k - 1 & 1][l][r][1]});
                }
        }
        cout << (res == 0x3f3f3f3f ? -1 : res) << endl;
}

---