线性DP

Chivas-Regal

#

# 洛谷P1108_低价购买

# 🔗

# 💡

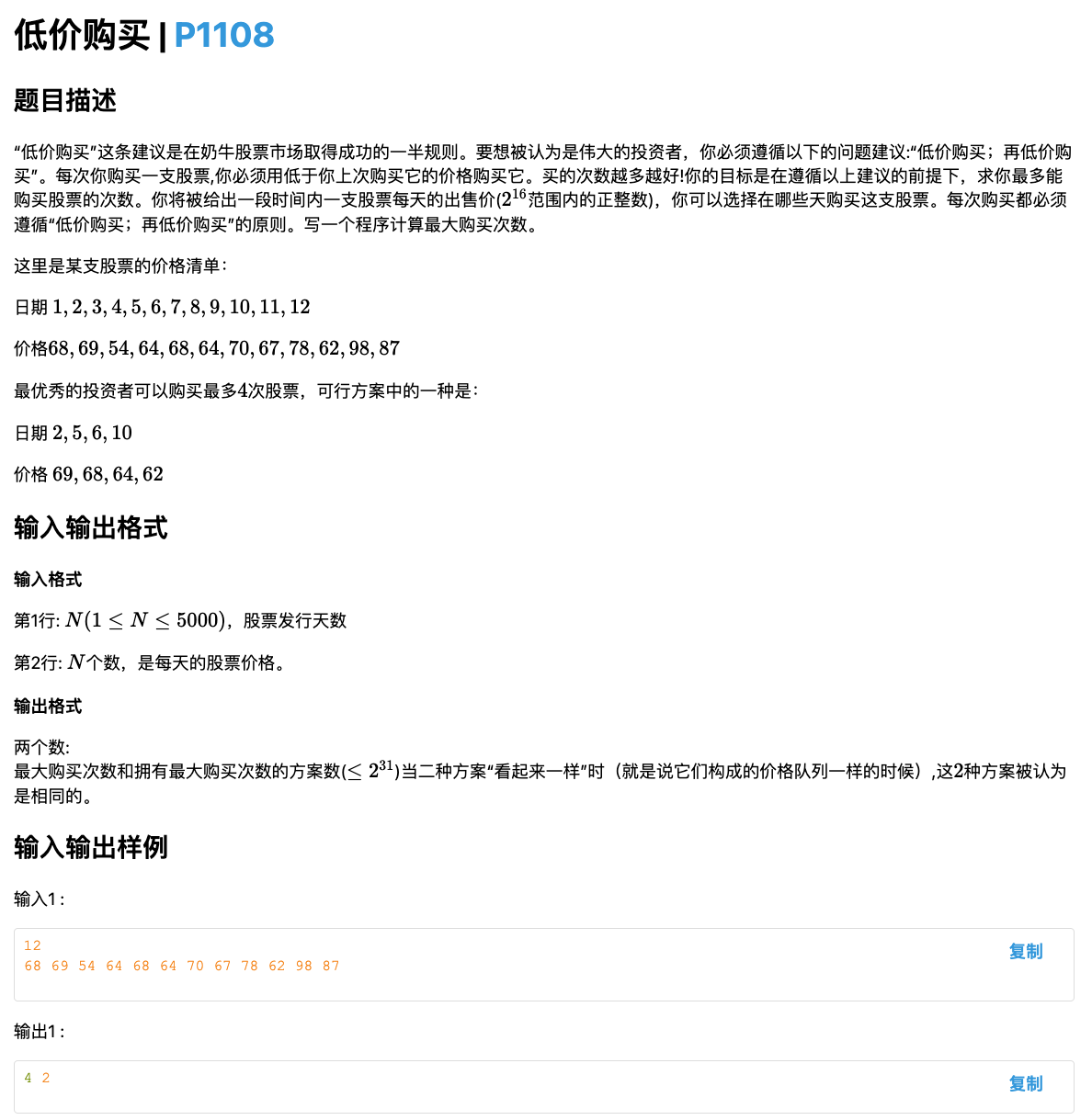
第一问仔细一分析就知道是个最长下降子序列
那么关键就是第二问：求最长下降子序列的个数
是这道题 (opens new window) 的深化版，就是多了一份同样的数列去重
去重是最难想的，因为没有去重的话我们每次就以 $\inline j$ 更新 $\inline i$ 的时候都递加一下这个长度的数量即可

求最长下降子序列的时候是前缀一个个递推的
我们在这里可以接着递推的时候求
设置 $\inline \{dp2\}$ 为方案数 $\inline \{dp\}$ 数组， $\inline \{dp1\}$ 是前缀最长下降子序列数组

如果 $\inline a_i=a_j$ 且 $\inline dp_i=dp_j$ 说明转移给 $\inline a_j$ 的也可以以同样的方式转移给 $\inline a_i$ ，那么此时我们就不需要 $\inline dp2_j$ 了，直接用 $\inline dp2_i$ 就可以表示
如果 $\inline a_j>a_i$ 且 $\inline dp1_j+1=dp1_i$ ，则说明这里有 $\inline dp1_i$ 通过 $\inline dp1_j$ 转移来
所以我们在方案数 $\inline dp2_i$ 可以继承 $\inline dp2_j$ 即 $\inline dp2_i+=dp2_i$

我们可以顺求 $\inline max\{dp1\}=res1$ 处理完之后累加一下每一个 $\inline dp1=res$ 的 $\inline dp2$

# ✅

#include <iostream>

#define ll long long

using namespace std;

const int N = 1e4;
int n, a[N];
ll dp1[N], dp2[N];
ll res1, res2;

int main () {
        cin >> n;
        for ( int i = 0; i < n; i ++ ) {
                cin >> a[i]; 
                dp1[i] = 1;
                for ( int j = 0; j < i; j ++ ) if ( a[j] > a[i] ) dp1[i] = max ( dp1[i], dp1[j] + 1 );
                for ( int j = 0; j < i; j ++ ) {
                        if ( a[i] == a[j] && dp1[i] == dp1[j] ) dp2[j] = 0;
                        else if ( a[j] > a[i] && dp1[j] + 1 == dp1[i] ) dp2[i] += dp2[j];
                }
                if ( !dp2[i] ) dp2[i] = 1;
                res1 = max ( res1, dp1[i] );
        }
        for ( int i = 0; i < n; i ++ ) if ( dp1[i] == res1 ) res2 += dp2[i];
        cout << res1 << " " << res2 << endl; 
        return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# 洛谷P1156_垃圾陷阱

# 🔗

# 💡

这道题，每个地方吃垃圾和踩垃圾，两种中决策出来一个
受到饱腹感的限制

这不就 $\inline DP$ 吗
我们想要进行取最优的是高度，所以我们状态表示的是高度
而那两个限制就放在维度中
令 $\inline dp[i][j]$ 表示第 $\inline i$ 个垃圾，有 $\inline j$ 饱腹感的最高高度

那么我们在枚举到 $\inline i$ 的时候，有吃和踩两种
踩无法让饱腹感更高但是可以贡献高度： $\inline dp[i][j]=max(dp[i-1][j],dp[i-1][j+gbgs[i].t-gbgs[i-1].t]+gbgs[i].h)$
吃无法让高度更高但是要更新更高的饱腹感： $\inline dp[i][j+gbgs[i].f]=max(dp[i][j+gbgs[i].f],dp[i-1][j+gbgs[i].t-gbgs$

设计一个饱腹感变量让它每次都吃
也就是最高的饱腹感
不仅用作遍历，还用作判断，如果中间断时间过大，那么一定是走不上去就被饿死了，所以中间判断一下够不够减这个时间，不够的话就根据上一次时间和饱腹感输出时间
如果中间 $\inline dp$ 比 $\inline D$ 更高了，那么就直接输出这个时间，能走上去

最后还是没走上去的话，就每次都吃统计一下总饱腹感，然后输出这个饱腹感就是坚持的时间

# ✅

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>

#define ll long long

using namespace std;

int D, G;
struct Gbg {
        int t, f, h;
};
vector<Gbg> gbgs;

int no_hungry = 10;
int dp[110][4010]; // dp[i][j]：第i个垃圾，有j饱腹感，表示最高高度

int main () {
        memset(dp, -1, sizeof dp );

        cin >> D >> G;
        for ( int i = 0; i < G; i ++ ) {
                int t, f, h; cin >> t >> f >> h;
                gbgs.push_back({t, f, h});
        }
        gbgs.push_back({0, 0, 0});
        sort ( gbgs.begin(), gbgs.end(), [&]( Gbg a, Gbg b ) { return a.t < b.t; });

        dp[0][10] = 0;

        for ( int i = 1; i <= G; i ++ ) {
                if ( no_hungry - gbgs[i].t + gbgs[i - 1].t < 0 ) {
                        cout << gbgs[i - 1].t + no_hungry << endl;
                        return 0;
                }
                no_hungry -= gbgs[i].t - gbgs[i - 1].t;
                for ( int j = 0; j <= no_hungry; j ++ ) {
                        if ( dp[i - 1][j + gbgs[i].t - gbgs[i - 1].t] != -1 ) {
                                dp[i][j] = max ( dp[i][j], dp[i - 1][j + gbgs[i].t - gbgs[i - 1].t] + gbgs[i].h ),
                                dp[i][j + gbgs[i].f] = max ( dp[i][j + gbgs[i].f],  dp[i - 1][j + gbgs[i].t - gbgs[i - 1].t] );
                                if ( dp[i][j] >= D || dp[i][j + gbgs[i].f] >= D ) { cout << gbgs[i].t << endl; return 0; }
                        }
                }
                no_hungry += gbgs[i].f;
        }

        no_hungry = 10;
        for ( Gbg gbg : gbgs ) no_hungry += gbg.f;
        cout << no_hungry << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

# 洛谷P1174_打砖块

# 🔗

# 💡

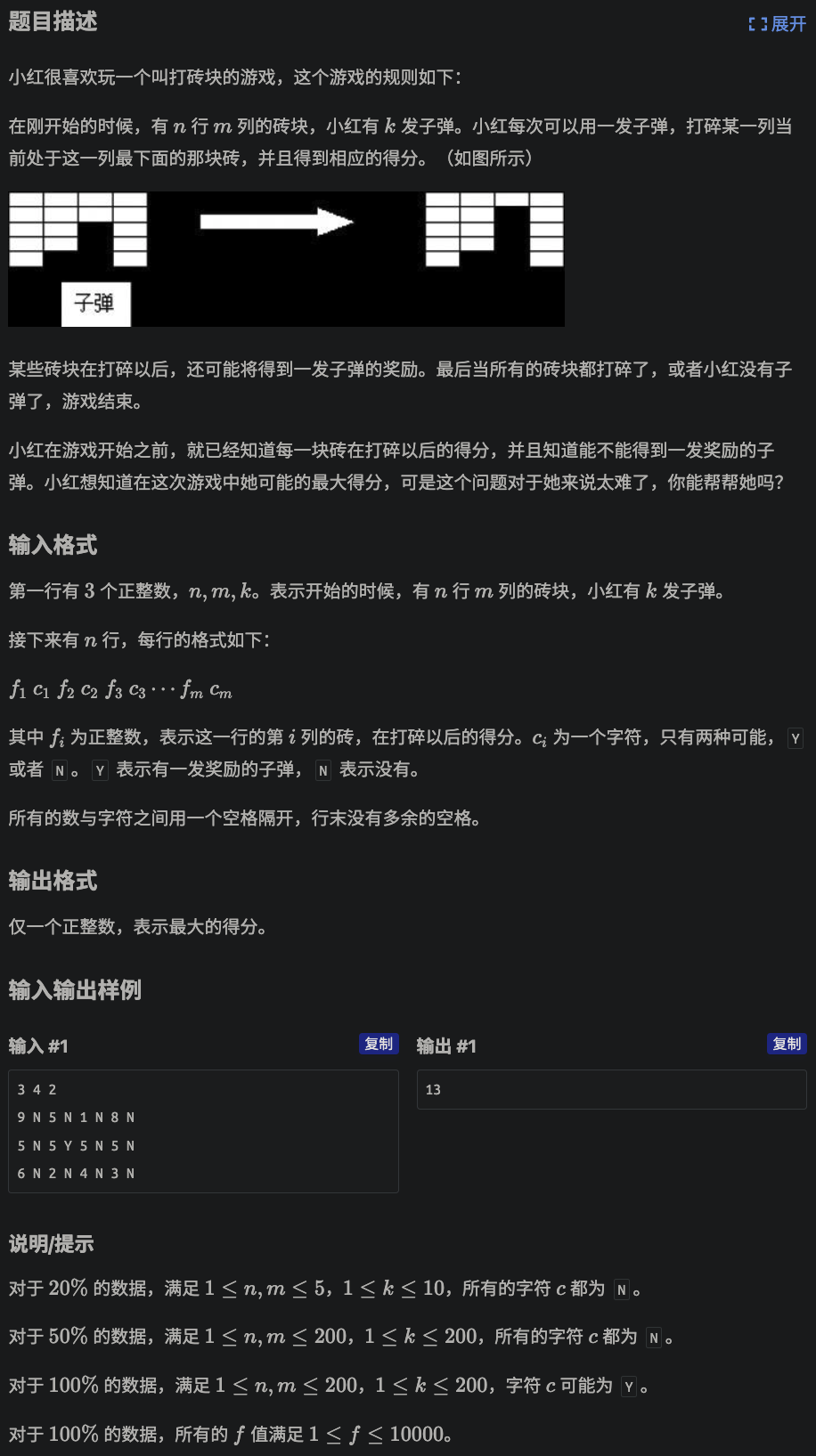
很麻烦的一道 $\inline dp$ 加贪心
首先每一次要选哪个点进行射击时决策，所以我们想到 $\inline dp$

由于在不同的行花费不同的子弹能得到不同的价值，而我们有这个子弹数
所以预处理出

int dn[210][210];  // 每一列往上打的最后落脚点是 'N'
int dy[210][210];  // 每一列往上打的最后落脚点是 'Y'

inline void pre_D ( int j ) {
        int cnt = N, k = 0;
        while ( cnt >= 1 ) {
                while ( cnt >= 1 && c[cnt][j] == 'Y' ) 
                        dy[j][k] += a[cnt][j],
                        cnt --;
                while ( cnt >= 1 && c[cnt][j] == 'N' )
                        k ++,
                        dn[j][k] = dy[j][k - 1] + a[cnt][j],
                        dy[j][k] = dn[j][k],
                        cnt --;
        }
}

for ( int j = 1; j <= M; j ++ ) pre_D ( j );

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

其次是 $\inline dp$
由于限制为子弹数量和列数
所以我们设置 $\inline dp[i][j]$ 表示在第 $\inline i$ 列用了 $\inline j$ 颗子弹的最大价值
但是 $\inline 'N'$ 和 $\inline 'Y'$ 不一样，他们会影响你是否用光你的子弹

所以加一维
$\inline dp1[i][j]$ ：前 $\inline i$ 列刚好打到 $\inline j$ 颗子弹就可以停下
$\inline dp2[i][j]$ ：前 $\inline i$ 列没打完 $\inline j$ 颗子弹就要停下了

枚举:
$\inline i$ 列
$\inline k$ 有的的子弹数量
$\inline x$ 用了的子弹数量

那么有三种情况
$\inline 1.$ 没用完，对于 $\inline dp1$ : $\inline =max($

$\inline 2.$ 用完了，但是之前没有用完
$\inline dp1[j][k]=max(dp1[j-1]k-x]+dy[j][x])$
即前几步打完了，你这里就使劲走也不一定走到 $\inline 'N'$ 这个你满意的极限位置

$\inline 3.$ 用完了，且之前也用完了
$\inline dp1[i][j]=max($
即前几部没打完，你这里使劲走走到最后一步一定是 $\inline 'n'$

由于子弹肯定打完最好，所以最后一步一定是 $\inline dp1[m][k]$

# ✅

#include <iostream>

#define ll long long

using namespace std;

int N, M, K;
int a[210][210]; char c[210][210];
int dn[210][210];  // 每一列往上打的最后落脚点是 'N'
int dy[210][210];  // 每一列往上打的最后落脚点是 'Y'
int dp1[210][210]; // dp1[i][j]: 前 i 列刚好打到第 j 颗子弹就可以停
int dp2[210][210]; // dp2[i][j]: 前 i 列没打完第 j 颗子弹

inline void pre_D ( int j ) {
        int cnt = N, k = 0;
        while ( cnt >= 1 ) {
                while ( cnt >= 1 && c[cnt][j] == 'Y' ) 
                        dy[j][k] += a[cnt][j],
                        cnt --;
                while ( cnt >= 1 && c[cnt][j] == 'N' )
                        k ++,
                        dn[j][k] = dy[j][k - 1] + a[cnt][j],
                        dy[j][k] = dn[j][k],
                        cnt --;
        }
}

int main () {
        cin >> N >> M >> K;
        for ( int i = 1; i <= N; i ++ ) for ( int j = 1; j <= M; j ++ ) cin >> a[i][j] >> c[i][j];
        for ( int j = 1; j <= M; j ++ ) pre_D ( j );

        for ( int j = 1; j <= M; j ++ ) {                 // 枚举每一列
                for ( int k = 0; k <= K; k ++ ) {         // 枚举有 k 发子弹
                        for ( int x = 0; x <= k; x ++ ) { // 枚举用了 x 发子弹
                                dp2[j][k] = max ( dp2[j][k], max(dp2[j - 1][k - x], dp1[j - 1][k - x]) + dy[j][x] ); // 没打完，你不一定走到 'N' 这个你满意的极限位置
                                if ( x < k ) dp1[j][k] = max ( dp1[j][k], dp1[j - 1][k - x] + dy[j][x] ); // 前几步打完了，你这里就eng走也不一定走到 'N' 这个你满意的极限位置
                                if ( x > 0 ) dp1[j][k] = max ( dp1[j][k], dp2[j - 1][k - x] + dn[j][x] ); // 前几步没打完，你这里就eng走单必须要走到 'N' 这个你满意的极限位置
                        }
                }
        }
        cout << dp1[M][K] << endl; // 打 'Y' 上会得到反馈（再送你一颗继续打，所以最后一发一定要打在 'N' 上
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

# 洛谷P1437_敲砖块

# 🔗

# 💡

首先想到对于每一个点，去枚举上一次敲掉的点
发现有很多点不可选，且对于枚举过的点的状态因为转移方式不同，很有可能让这个点失去了之前递推的意义，即产生后效性，这个思路或许行不通
那么我们根据这种打断线索的朴素情况画图

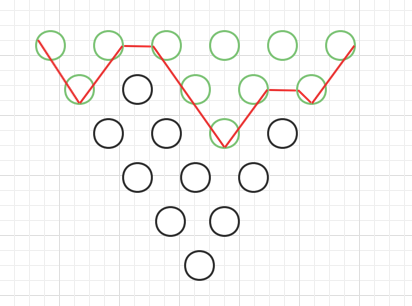
20220406235423
其中绿色的为敲掉的砖，红色的是敲掉的砖形成的下界轮廓线
结合矩阵表示下： $a_{i-1,j}$ 与 $a_{i-1,j+1}$ 敲掉后，才可以敲 $a_{i,j}$ 得出：
轮廓线从左到右的走向中：前一列的 $[0,i+1]$ 可以推出该列的 $i$
那么对轮廓线走向做 $dp$

令

dp_{i,j,k}

表示第 $j$ 列轮廓线下界在第 $i$ 行，已经敲掉了 $k$ 块砖的最大价值
那么根据上面我们推的
枚举上一列的轮廓线下界为

t:[0,j+1]

枚举本列下界的花费为

k:[i,m]

注意由于我们这一列下界选 $i$ 那么必定要花费 $i$ 个，如果 $k<i$ 则无法得出上一列状态
则转移方程便是：

dp[i][j][k]=max(dp[t][j-1][k-i]+sum[i][j])

其中 $sum[i][j]$ 表示我们第 $i$ 列从上到下选 $j$ 个的价值，可以预处理出来，不预处理的话要多开一重循环增大复杂度
总复杂度： $O(n^3m)$

# ✅

const int N = 51;
int n, m, a[N][N];
int dp[N][N][N * N];
int sum[N][N];

int main () {
        cin.tie(0)->sync_with_stdio(0);
        cin.exceptions(cin.failbit);
        
        cin >> n >> m;
        for (int i = 1; i <= n; i ++) 
                for (int j = 1; j <= n - i + 1; j ++) 
                        cin >> a[i][j], 
                        sum[i][j] = sum[i - 1][j] + a[i][j];
                        
        for (int j = 1; j <= n; j ++) 
                for (int i = 0; i <= n - j + 1; i ++)
                        for (int k = i; k <= m; k ++) 
                                for (int t = 0; t <= i + 1; t ++) 
                                        dp[i][j][k] = max(dp[i][j][k], dp[t][j - 1][k - i] + sum[i][j]);

        cout << max(dp[0][n][m], dp[1][n][m]) << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 洛谷P2331_最大子矩阵

# 🔗

# 💡

注意 $m$ 要么是 $1$ 要么是 $2$ ，可以以这个作为突破口

$m=1$ ：
这就是一个 $K$ 个连续不想交子段和问题
多了一维而已
令 $dp[i][k]$ 表示到第 $i$ 个，选了 $k$ 个子段的最大值
$dp[i][k]=\max\limits_{j\in[0,i-1]}dp[j][k-1]+sum[i]-sum[j]$
当然还要维护一下不选的最大值 $dp[i][k]=\max(dp[i][k],dp[i-1][k])$

$m=2$ ：
比上一个情况多一行，那么就设 $dp[i][j][k]$ 表示第一行到第 $i$ 个，第二行到第 $j$ 个，选了 $k$ 个子矩阵的最大值
那么我们分开看这两行
$dp[i][j][k]=\max\limits_{l\in[0,i-1]}dp[l][j][k-1]+sum1[i]-sum1[l]$
$dp[i][j][k]=\max\limits_{l\in[0,j-1]}dp[i][l][k-1]+sum2[j]-sum2[l]$
当然如果 $i=j$ 时，我们可以用一个高为 $2$ 的子矩阵填满
$dp[i][j][k]=\max\limits_{l\in[0,i-1]}dp[l][l][k-1]+sum1[i]+sum2[j]-sum1[l]-sum2[l]$
还要维护一下不选的最大值 $dp[i][j][k]=\max(dp[i][j][k],dp[i-1][j][k],dp[i][j-1][k])$

最后看位置维为 $n$ ，个数维为 $K$ 时的值即可

# ✅

int dp1[102][11];
int dp2[102][102][11];

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        int n, m, K; cin >> n >> m >> K;
        if (m == 1) {
                vector<int> a(n + 1); for (int i = 1; i <= n; i ++) cin >> a[i];
                vector<int> sum(n + 1, 0); for (int i = 1; i <= n; i ++) sum[i] = sum[i - 1] + a[i];
                for (int i = 1; i <= n; i ++) {
                        for (int j = 0; j < i; j ++) {
                                for (int k = 1; k <= K; k ++) {
                                        dp1[i][k] = max(dp1[i][k], dp1[i - 1][k]);
                                        dp1[i][k] = max(dp1[i][k], dp1[j][k - 1] + sum[i] - sum[j]);
                                }
                        }
                }
                cout << dp1[n][K] << endl;          
        } else {
                vector<int> a1(n + 1), a2(n + 1); for (int i = 1; i <= n; i ++) cin >> a1[i] >> a2[i];
                vector<int> sum1(n + 1, 0), sum2(n + 1, 0); for (int i = 1; i <= n; i ++) sum1[i] = sum1[i - 1] + a1[i], sum2[i] = sum2[i - 1] + a2[i];
                for (int i = 1; i <= n; i ++) {
                        for (int j = 1; j <= n; j ++) {
                                for (int k = 1; k <= K; k ++) {
                                        dp2[i][j][k] = max(dp2[i - 1][j][k], dp2[i][j - 1][k]);
                                        for (int l = 0; l < i; l ++) 
                                                dp2[i][j][k] = max(dp2[i][j][k], dp2[l][j][k - 1] + sum1[i] - sum1[l]);
                                        for (int l = 0; l < j; l ++) 
                                                dp2[i][j][k] = max(dp2[i][j][k], dp2[i][l][k - 1] + sum2[j] - sum2[l]);
                                        if (i == j) 
                                                for (int l = 0; l < i; l ++) 
                                                        dp2[i][j][k] = max(dp2[i][j][k], dp2[l][l][k - 1] + sum1[i] + sum2[j] - sum1[l] - sum2[l]);
                                }
                        }
                }
                cout << dp2[n][n][K] << endl;
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

# 洛谷P2498_SkiLessonsG

# 🔗

# 💡

成员变量

class[i] {beg, lst, can} 第 $i$ 节课开始时间，持续时间，能力值

我们贪心地让在 $j$ 能力下，选择滑雪时间最短的场滑雪用时
即设置 mntim[j]
我们设置 $dp[i][j]$ 表示第 $i$ 时刻，能力值为 $j$ ，滑过雪的最大次数
那么一次有三种选择

学习：若此时是第 $k$ 门课的开始时间且 $class[k].can>j$ ， $dp[i+class[k].lst][class[k].can]=max(this,dp[i][j])$
滑雪：若 $i+mntim[j]\le t$ ， $dp[i+mntim[j]][j]=max(this,dp[i][j]+1)$
摸鱼： $dp[i+1][j]=max(this,dp[i][j])$

# ✅

const int N = 3e4 + 10;
int t, s, n;
struct cls {
        int beg, lst, can;
} cls[N];
struct path {
        int tim, ned;
} pth[N];
int mntim[110];
int dp[N][110]; 
int maxcan = 1;

int main () {
        ios::sync_with_stdio(false);

        cin >> t >> s >> n;
        for ( int i = 1; i <= s; i ++ ) 
                cin >> cls[i].beg >> cls[i].lst >> cls[i].can,
                maxcan = max(maxcan, cls[i].can);

        memset(mntim, 0x3f3f3f3f, sizeof mntim);
        for ( int i = 1; i <= n; i ++ ) 
                cin >> pth[i].ned >> pth[i].tim,
                mntim[pth[i].ned] = min(mntim[pth[i].ned], pth[i].tim);
        for ( int i = 1; i <= 101; i ++ )  
                mntim[i] = min(mntim[i], mntim[i - 1]);

        memset(dp, -0x3f3f3f3f, sizeof dp);
        dp[0][1] = 0;
        for ( int i = 0; i <= t; i ++ ) {
                for ( int j = 1; j <= maxcan; j ++ ) {
                        if ( dp[i][j] < 0 ) continue; // 无法转移
                        for ( int k = 1; k <= s; k ++ ) {
                                if ( cls[k].beg != i || cls[k].can <= j || i + cls[k].lst > t ) continue;
                                dp[i + cls[k].lst][cls[k].can] = max(dp[i + cls[k].lst][cls[k].can], dp[i][j]); // 学习
                        }
                        dp[i + 1][j] = max(dp[i + 1][j], dp[i][j]); // 什么也不干
                        if ( i + mntim[j] <= t ) 
                                dp[i + mntim[j]][j] = max(dp[i + mntim[j]][j], dp[i][j] + 1); // 滑雪
                }
        }

        int res = -0x3f3f3f3f;
        for ( int i = 0; i <= t; i ++ ) {
                for ( int j = 1; j <= maxcan; j ++ ) {
                        res = max(res, dp[i][j]);
                }
        }
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

# 洛谷P2606_排列计数

# 🔗

# 💡

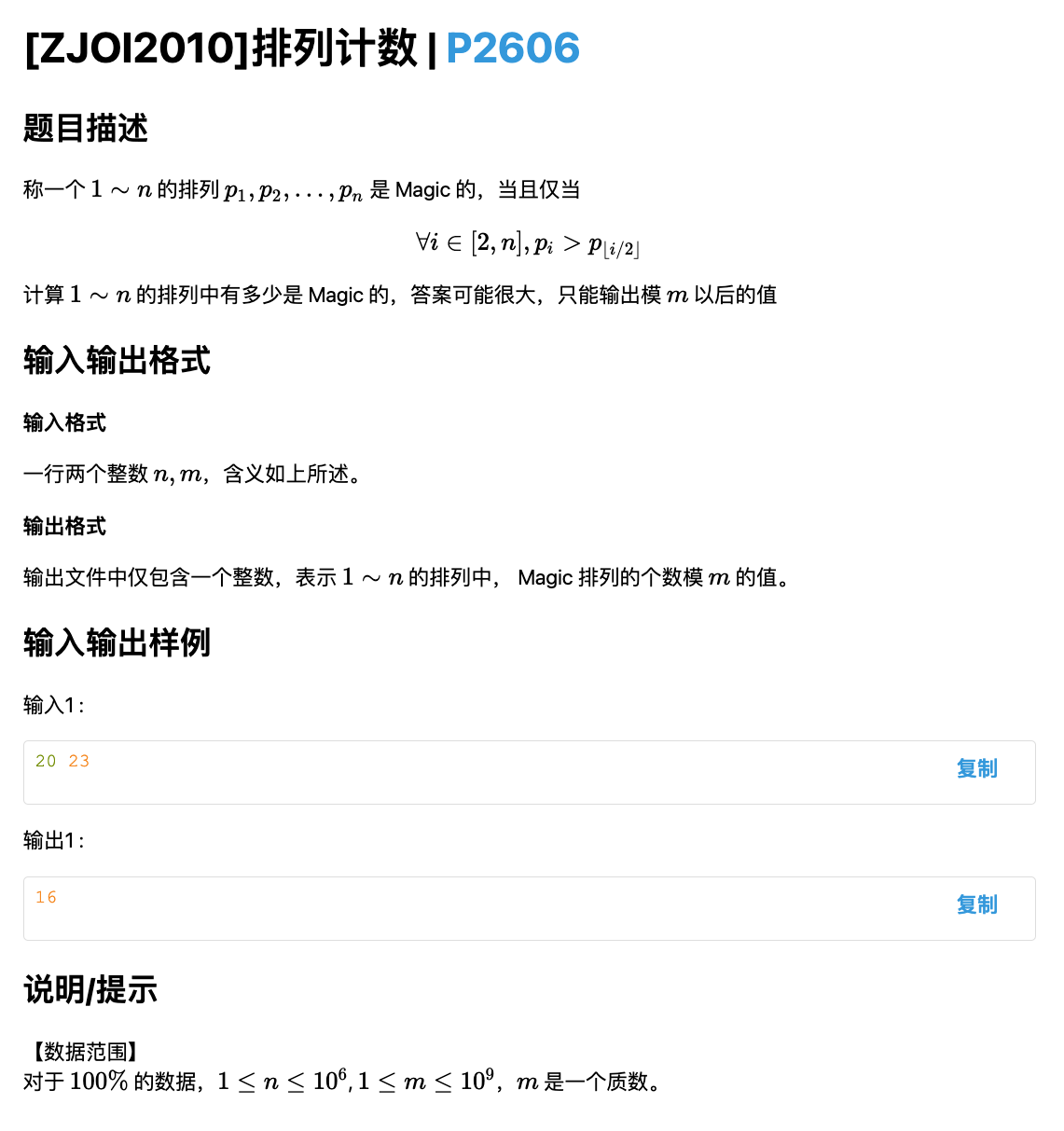
看到这个约束条件 $\inline 1\rightarrow2\And3,2\rightarrow4\And5,...$
我们可以构建出一棵二叉树
从 $\inline 1$ 开始，我们有 $\inline Sz_1$ 个节点，可以选择 $\inline \binom{Sz_1-1}{Sz_2}$ 放入二号子树，其余放入三号子树
通俗地说，就是 $\inline$ 放入左子树，其余放入右子树
这样就是 $\inline C(S$

注意模数可能很小，所以我们需要用 $\inline Lucas$ 定理

# ✅

const int N = 3e6 + 10;

int n, mod;

inline ll ksm ( ll a, ll b ) { ll res = 1; while ( b ) { if ( b & 1 ) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv ( ll x ) { return ksm(x, mod - 2); }
ll fac[N]; inline void get_Fac () { fac[0] = 1; for ( int i = 1; i < N; i ++ ) fac[i] = fac[i - 1] * i % mod; }
inline ll C ( ll n, ll m ) { 
        if ( n < m )   return 0;
        if ( n < mod ) return fac[n] * inv(fac[n - m]) % mod * inv(fac[m]) % mod; 
        return C ( n / mod, m / mod ) * C ( n % mod, m % mod ) % mod;
}

namespace Tree {
        ll sz[N];
        inline void get_Sz ( ll x ) {
                sz[x] = 1;
                if ( x * 2 <= n )     get_Sz ( x * 2 ),     sz[x] += sz[x * 2];
                if ( x * 2 + 1 <= n ) get_Sz ( x * 2 + 1 ), sz[x] += sz[x * 2 + 1];
        }
        inline ll dfs ( ll x ) {
                if ( x > n ) return 1; 
                return C ( sz[x] - 1, sz[2 * x] ) * dfs ( 2 * x ) % mod * dfs ( 2 * x + 1 ) % mod;
        }
} using namespace Tree;

int main () { 
        cin >> n >> mod;
        get_Fac (); get_Sz ( 1 );
        cout << dfs ( 1 ) << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# 洛谷P4059_找爸爸

# 🔗

# 💡

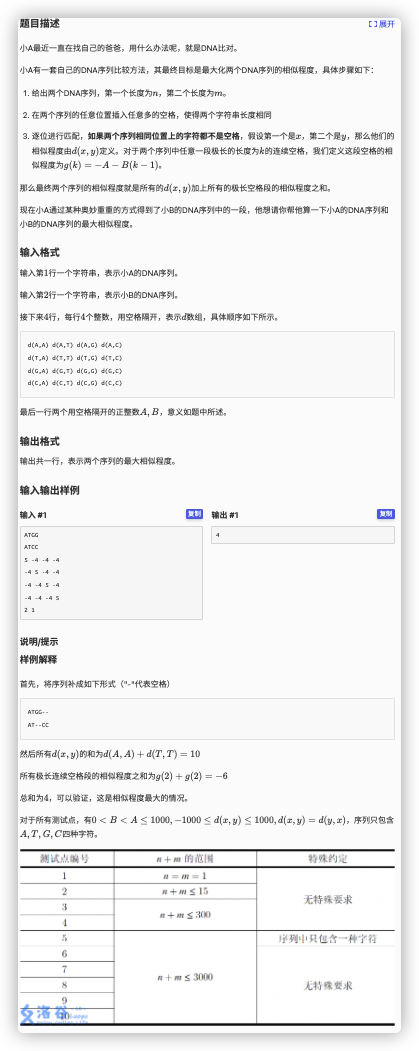
限制：字符串位置匹配、空格分布情况
状态： $dp[i][j][k]$ 表示 $a$ 串用了 $i$ 个， $b$ 串用了 $j$ 个， $k=0/1/2\;\to\;$ 两串结尾无空格 $/$ 空格在 $a$ 串 $/$ 空格在 $b$ 串

对于连续空格我们可以将 $g(k)=-A-B(k-1)$ 这个公式看作在连续的空格中，我们只有第一个空格的贡献为 $-A$ ，其余均为 $-B$
建立三种转移：
此刻任意一个都不用空格，那便是都用了字母
$dp[i][j][0]=max(dp[i-1][j-1][])+d(a[i],b[i])$
$a$ 用空格，那便是之前还是 $a$ 最后的可以续上一个 $-B$ ，其他的都只能续 $-A$
$dp[i][j][1]=max(dp[i-1][j][0]-A,dp[i][j-1][1]-B,dp[i][j-1][2]-A)$
$b$ 用空格同理
$dp[i][j][2]=max(dp[i-1][j][0]-A,dp[i-1][j][1]-A,dp[i-1][j][2]-B)$

最后统计用完字符的状态即 $max(dp[n][m][])$

# ✅

int g[300][300];
int dp[3005][3005][3];
int A, B;
string a, b;
int n, m;

int main () {
        cin >> a >> b;

        vector<char> DNA = {'A', 'T', 'G', 'C'};
        for ( int i = 0; i < 4; i ++ ) {
                for ( int j = 0; j < 4; j ++ ) {
                        cin >> g[DNA[i]][DNA[j]];
                }
        }
        cin >> A >> B;
        n = a.size(), m = b.size();
        a = " " + a, b = " " + b;
        for ( int i = 1; i <= max(n, m); i ++ ) {
                dp[0][i][0] = dp[i][0][0] = dp[0][i][2] = dp[i][0][1] = -0x3f3f3f3f;
                dp[0][i][1] = dp[i][0][2] = - A - B * (i - 1);
        }
        dp[0][0][1] = dp[0][0][2] = -0x3f3f3f3f;
        for ( int i = 1; i <= n; i ++ ) {
                for ( int j = 1; j <= m; j ++ ) {
                        dp[i][j][0] = max({dp[i - 1][j - 1][0], dp[i - 1][j - 1][1], dp[i - 1][j - 1][2]}) + g[a[i]][b[j]];
                        dp[i][j][1] = max({dp[i][j - 1][0] - A, dp[i][j - 1][1] - B, dp[i][j - 1][2] - A});
                        dp[i][j][2] = max({dp[i - 1][j][0] - A, dp[i - 1][j][1] - A, dp[i - 1][j][2] - B});
                }
        }
        cout << max({dp[n][m][0], dp[n][m][1], dp[n][m][2]}) << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

# 洛谷P3694_邦邦的大合唱站队

# 🔗

# 💡

这也就是哪个匹配不上哪个走的问题，且所有的既然都在一起那么这就被分为了 $m\le 20$ 块
开始想全排列但是肯定会超，实现全排列操作的最值问题开始状压
令 $dp[s]$ 表示在已有乐团状态为 $s$ 的情况下，匹配不上的最大值

区间匹配也就是看区间有几个数 $x$ ，这就是一个前缀和作差卡区间和的问题
那么要匹配下一位的起始为 $\sum\limits_{i=1}^{20}[s_i=1]sum[n][s_i]$ ，若要填入一个没有的 $j$ 终点为起始加上 $sum[n][s_{j}]$
不匹配数为 $(r-l)-(sum[r][j]-sum[l][j])$

# ✅

const int N = 1e5 + 10;
const int M = 30;

int n, m;
int sum[N][M];
int a[N];

int dp[2000006];

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n >> m;
    for (int i = 1; i <= n; i ++) cin >> a[i];
    for (int i = 1; i <= n; i ++) {
        for (int j = 1; j <= m; j ++) {
            sum[i][j] = sum[i - 1][j] + (a[i] == j);
        }
    }

    memset(dp, 0x3f, sizeof dp);
    dp[0] = 0;
    for (int s = 0; s < (1 << m); s ++) {
        int num = 0;
        for (int i = 0; i < m; i ++) if (s >> i & 1) num += sum[n][i + 1];
        for (int i = 0; i < m; i ++) {  
            if (s >> i & 1) continue;
            int l = num, r = l + sum[n][i + 1];
            dp[s | (1 << i)] = min(dp[s | (1 << i)], dp[s] + (r - l) - (sum[r][i + 1] - sum[l][i + 1]));
        }
    }
    cout << dp[(1 << m) - 1];
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

# 牛客2021多校（5）D_DoubleStrings

# 🔗

# 💡

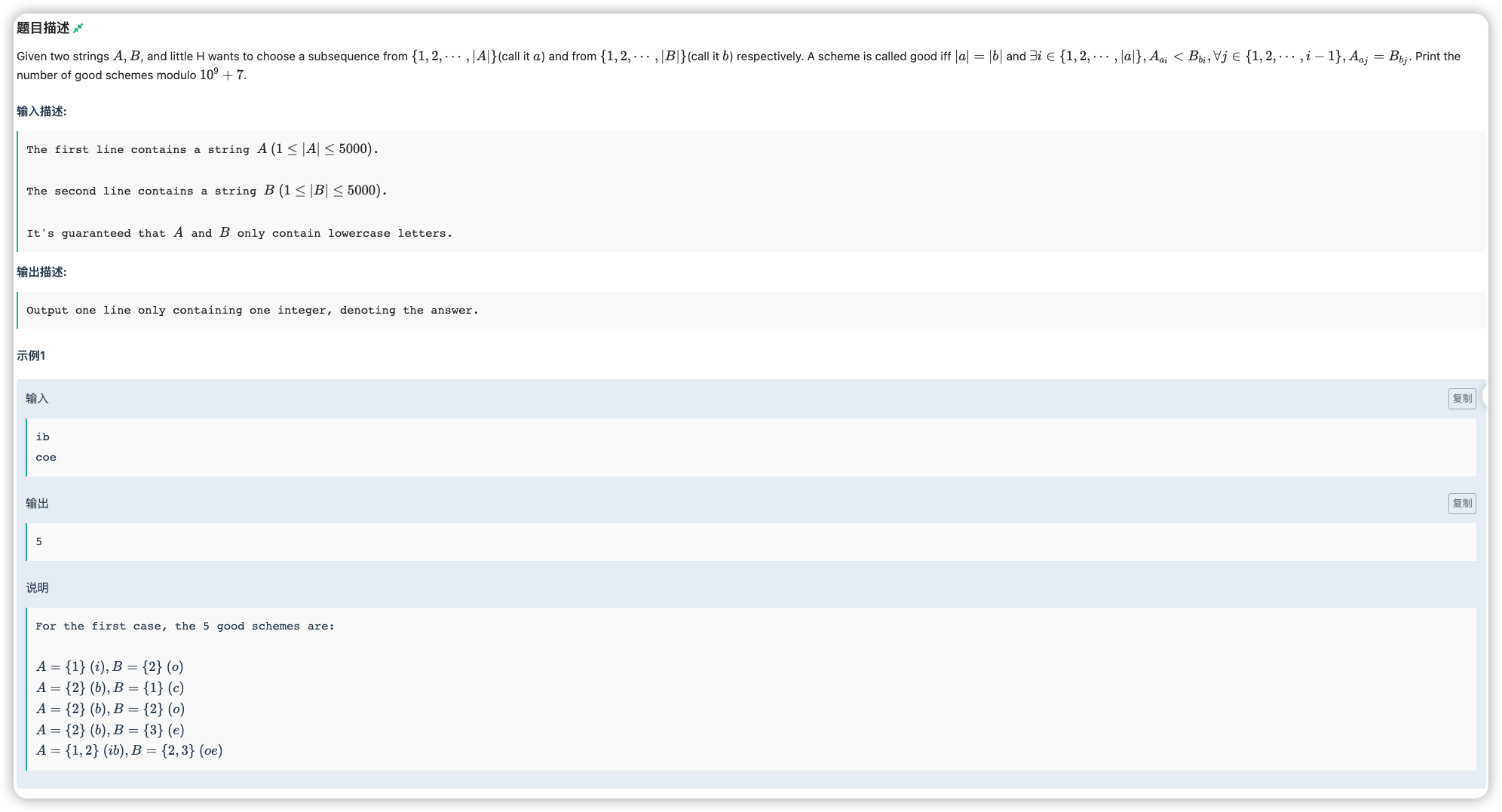
题面好乱...，翻译一下就是找到字符串 $A$ 中和字符串 $B$ 中挑同样长度的子序列 $a,b$ 使得 $a<b$ ，问有多少种挑法
满足一个字符串小于的首先是要求前面有长度为任意的相同前缀，然后第一个不同的满足 $a_i< b_i$ ，所以用 $dp[i][j]$ 维护 $A$ 的前 $i$ 个位置和 $B$ 的前 $j$ 个位置有多少个相同的子序列
转移使用容斥的思想，在 $A[i]\neq B[j]$ 时 $dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]$
当然如果相等就可以接着 $dp[i-1][j-1]$ 了
然后如果 $A[i]<B[j]$ 说明这一个位置可以作为两子序列第一个不同的位置，令答案加上 $dp[i-1][j-1]$ 乘上后面任意选的方案数
假设 $A$ 后面还剩 $n$ 个， $B$ 后面还剩 $m$ 个，则后面任意选的方案数为
$\sum\limits_{i=1}^{min(n,m)}C_n^{i}C_m^{i}=\sum\limits_{i=1}^{min(n,m)}C_n^{n-i}C_m^i=C_{n+m}^n$
所以当 $A[i]<B[j]$ 时，累加 $dp[i-1][j-1]\times C_{n-i+m-i}^{n-i}$ 即可

# ✅

const int N = 5010;
const int mod = 1e9 + 7;
int n, m;
ll dp[N][N];

ll f[N << 1], ivf[N << 1];
inline ll ksm (ll a, int b) { ll res = 1; while (b) { if (b & 1) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv (ll x) { return ksm(x, mod - 2); }
inline ll C (int n, int m) { return f[n] * ivf[m] % mod * ivf[n - m] % mod; }


int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    f[0] = 1;
    for (int i = 1; i < N * 2; i ++) f[i] = f[i - 1] * i % mod;
    ivf[N * 2 - 1] = inv(f[N * 2 - 1]);
    for (int i = N * 2 - 2; i >= 0; i --) ivf[i] = ivf[i + 1] * (i + 1) % mod;

    string a, b; cin >> a >> b;
    n = a.size(); m = b.size();
    a = " " + a;
    b = " " + b;

    ll res = 0;
    dp[0][0] = 1;
    for (int i = 1; i <= n; i ++) dp[i][0] = 1;
    for (int j = 1; j <= m; j ++) dp[0][j] = 1;
    for (int i = 1; i <= n; i ++) {
        for (int j = 1; j <= m; j ++) {
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1];
            if (a[i] == b[j]) dp[i][j] += dp[i - 1][j - 1];
            if (a[i] < b[j])  res += dp[i - 1][j - 1] * C(n - i + m - j, n - i) % mod;
            dp[i][j] = (dp[i][j] % mod + mod) % mod;
            res %= mod;
        }
    }
    cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

# 牛客2022多校（7）J_MelborpElcissalc

# 🔗

# 💡

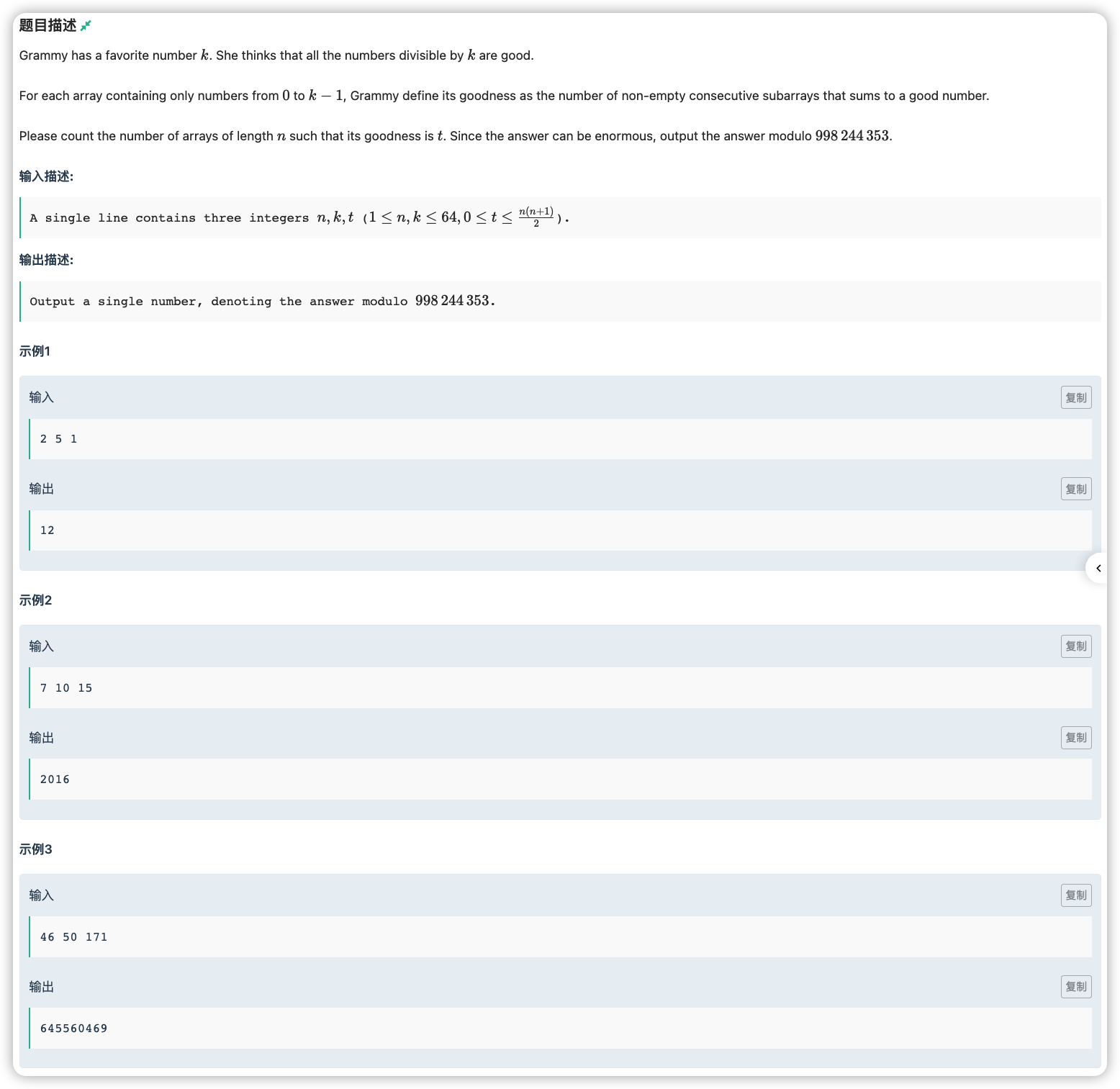
直接考虑状态情况很难处理，先简化一下问题：对于一个给定的数组 $[a]$ ，计算有多少个好子段。
好数要求是 $k$ 的倍数经典套路就是模 $k$ 为 $0$
子段和为 $sum[r]-sum[l-1]$ ，这就需要模 $k$ 意义下 $sum[r]\equiv sum[l]$
如果模 $k$ 等于 $d$ 的前缀和数量我们设置为 $x_d$ 个，那么显然有 $\sum\limits_{i=0}^{k-1}\frac{x_i(x_i-1)}{2}$ 个好子段
则题目问的就是让构造出 $[x]$ 满足 $\sum\limits_{i=0}^{k-1}\frac{x_i(x_i-1)}{2}=t$ 注意这里只有一组变量 $[x]$ ，这随便就可以进行 $dp$ 了，要考虑好限制条件
由于 $sum[0]$ 也要统计，所以 $\sum\limits_{i=0}^{k-1}\frac{x_i(x_i-1)}{2}=t$ 且 $\sum\limits_{i=0}^{k-1}x_i=n+1$
两个限制一个顺序，开三维 $dp[a][b][c]$ 表示前 $a$ 个数， $\sum\limits_{i=0}^a\frac{x_i(x_i-1)}{2}=c$ ， $\sum\limits_{i=0}^a x_i=b$
第一重枚举 $a$ ，第二重枚举 $b$ ，第三重枚举 $c$ ，第四重枚举 $x_{a+1}$ 是多少，状态增值就是上面的限制，直接转移。
但是注意到 $[x]$ 的大小是可以参差不齐的，说明这 $b1$ 个数是可以插进前面 $b$ 个数的空中的， $0$ 是卡在 $[sum]$ 前的，所以有 $b$ 个空，它们是不同的，而且 $b1$ 个数是相同的，经典球盒模型在 $b$ 不为 $0$ 时带上 $\binom{b1+b-1}{b-1}$ 乘起来转移
最后求一下 $dp[k][n+1][t]$ 就好了

# ✅

const int mod = 998244353;
inline ll ksm (ll a, ll b) {
        ll res = 1;
        while (b) {
                if (b & 1) res = res * a % mod;
                a = a * a % mod;
                b >>= 1;
        }
        return res;
}
inline ll inv (ll x) {return ksm(x, mod - 2);}
 
ll dp[80][80][10000];
ll f[1000], ivf[1000];
inline ll C (ll n, ll m) {
        return f[n] * ivf[m] % mod * ivf[n - m] % mod;
}
 
int n, k, t;
 
int main () {
        f[0] = 1;
        for (int i=1; i < 1000; i ++) f[i] = f[i - 1] * i % mod;
        ivf[999] = inv(f[999]);
        for (ll i = 998; i >= 0; i --) ivf[i] = ivf[i + 1] * (i + 1) % mod;
        
        scanf("%d%d%d", &n, &k, &t);
        
        dp[0][0][0] = 1;
        for (int a = 0; a < k; a ++) {
                for (int b = 0; b <= n + 1; b ++) {
                        for (int c = 0; c <= t; c ++) {
                                if (!dp[a][b][c]) continue; // *剪枝，为 0 的情况挺多的，可以把 5s 优化为 1s
                                for (int b1 = (a == 0 ? 1 : 0); b1 + b <= n + 1 && c + (b1 - 1) * b1 / 2 <= t; b1 ++) {
                                        if (a && b) dp[a + 1][b + b1][c + (b1 - 1) * b1 / 2] += dp[a][b][c] * C(b1 + b - 1, b - 1) % mod;
                                        else dp[a + 1][b + b1][c + (b1 - 1) * b1 / 2] += dp[a][b][c] % mod;
                                        dp[a + 1][b + b1][c + (b1 - 1) * b1 / 2] %= mod;
                                }
                        }
                }
        }
        printf("%lld\n", dp[k][n + 1][t]);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

# 省赛2021上海B_小A的卡牌游戏

# 🔗

# 💡

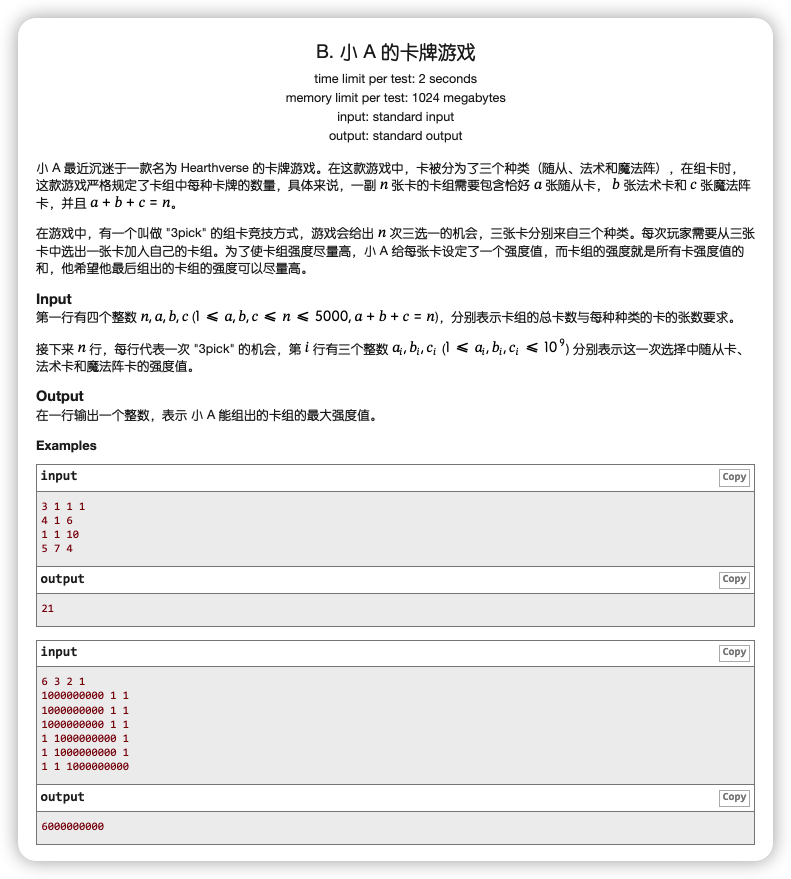
这是一个三元组，问题化简到二元组去思考
即如果只有 $AB$ 的话，可以让 $B$ 先选，但要求是不能过度影响 $A$ 的选择
一个基础的想法是让 $B$ 选第二列最大的几个，但是这样可能会导致出现类似于 $(1,5),(5,7)$ 这样的两个二元组，如果 $B$ 先选了第二个二元组的 $7$ ，然后 $A$ 只能选 $1$ ，是比较亏的
所以我们肯定是希望 $B$ 选的二元组中，在不选 $a$ 选 $b$ 的情况下，赚得多或者亏得少，转化过来就是 $b-a$ 尽可能大
所以按 $b-a$ 从大到小排序，然后顺次选择即可
回归到三元组上，多了一个 $C$ ， $C$ 是一个分配问题，而且在排序完之后就是一个二维的，怎么写都行，这里开一个 $dp[i][j]$ 表示第 $i$ 个之前， $C$ 选了 $j$ 个
那么在转移的时候，如果 $j>0$ ，这一个可以选 $j$ ， $dp[i][j]=max(dp[i][j],dp[i-1][j-1]+c_i)$
如果不选 $c$ ，看看到这一步为止有多少个不选 $c$ 的，即 $i-j$ ，如果不够 $B$ 个，那么优先选 $b$ ，否则选 $a$

# ✅

struct Pick {
    int a, b, c;
    inline friend bool operator < (Pick A, Pick B) {
        return A.b - A.a > B.b - B.a;
    }
};

ll dp[5100][5100];
int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n; cin >> n;
    int A, B, C; cin >> A >> B >> C;

    vector<Pick> v(n + 1);
    for (int i = 1; i <= n; i ++) {
        cin >> v[i].a >> v[i].b >> v[i].c;
    } sort(v.begin() + 1, v.end());

    memset(dp, -0x3f, sizeof dp);
    for (int i = 0; i < 5100; i ++) dp[i][0] = 0;
    for (int i = 1; i <= n; i ++) {
        for (int j = 0; j <= i && j <= C; j ++) {
            if (j) dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + v[i].c);
            if (i - j <= B) dp[i][j] = max(dp[i][j], dp[i - 1][j] + v[i].b);
            else dp[i][j] = max(dp[i][j], dp[i - 1][j] + v[i].a);
        }   
    }
    cout << dp[n][C] << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# ABC189D_LogicalExpression

# 🔗

https://vjudge.net/problem/AtCoder-abc189_d

# 💡

可以看出这是一道两套子问题互相来回交汇的方案数问题
由于中途中选TF是比较随意的，所以我们先列出TF的关系式：

$\begin{matrix}&F\;&\And\;&F\;&=\;&F\\&F\;&\And\;&T\;&=\;&F\\&T\;&\And\;&F\;&=\;&F\\&T\;&\And\;&T\;&=\;&T\\\\&F\;&|\;&T\;&=\;&T\\&T\;&|\;&T\;&=\;&T\\&T\;&|\;&F\;&=\;&T\\&F\;&|\;&F\;&=\;&F \end{matrix}$

这两套方案即是这一位为T或F的两种状态
那么我们设置dpT, dpF为状态表示
然后就是利用上面的式子

在 "or" 中，T可以由两个T和一个F转移来，F可以由一个F转移来
在 "and" 中，F可以由两个F和一个T转移来，T可以由一个T转移来
得到转移方程式，开始写程序

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/

//#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << endl

#define CHIVAS_ int main()
#define _REGAL exit(0)
#define SP system("pause")
#define IOS ios::sync_with_stdio(false)

//#define map unordered_map

#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cass = inputInt(); cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;


template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal <vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i])MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal <vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i])MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
template<typename T> vector<T>& operator-- (vector<T> &v){for (auto& i : v) --i; return v;}
template<typename T> vector<T>& operator++ (vector<T> &v){for (auto& i : v) ++i; return v;}
template<typename T> istream& operator>>(istream& is, vector<T> &v){for (auto& i : v) is >> i; return is;}
template<typename T> ostream& operator<<(ostream& os, vector<T> v){for (auto& i : v) os << i << ' '; return os;}
inline int inputInt(){int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);}
inline void outInt(int X){if(X<0) {putchar('-'); X=~(X-1);}int s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline ll inputLL(){ll X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1); }
inline void outLL(ll X){if(X<0) {putchar('-'); X=~(X-1);}ll s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}

const int N = 100;
string s[N];
ll n, dpT[N], dpF[N];

CHIVAS_{
        n = inputInt();
        for ( int i = 1; i <= n; i ++ ) cin >> s[i];

        dpT[0] = dpF[0] = 1; // 初始选谁就是谁，也就只有一种方式去求解
        for ( int i = 1; i <= n; i ++ ) {
                if ( s[i] == "OR" ) dpT[i] = dpT[i - 1] * 2 + dpF[i - 1], dpF[i] = dpF[i - 1];
                else                dpF[i] = dpF[i - 1] * 2 + dpT[i - 1], dpT[i] = dpT[i - 1];
        }

        outLL(dpT[n]);
        _REGAL;
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96

# ABC237F_|LIS|=3

# 🔗

# 💡

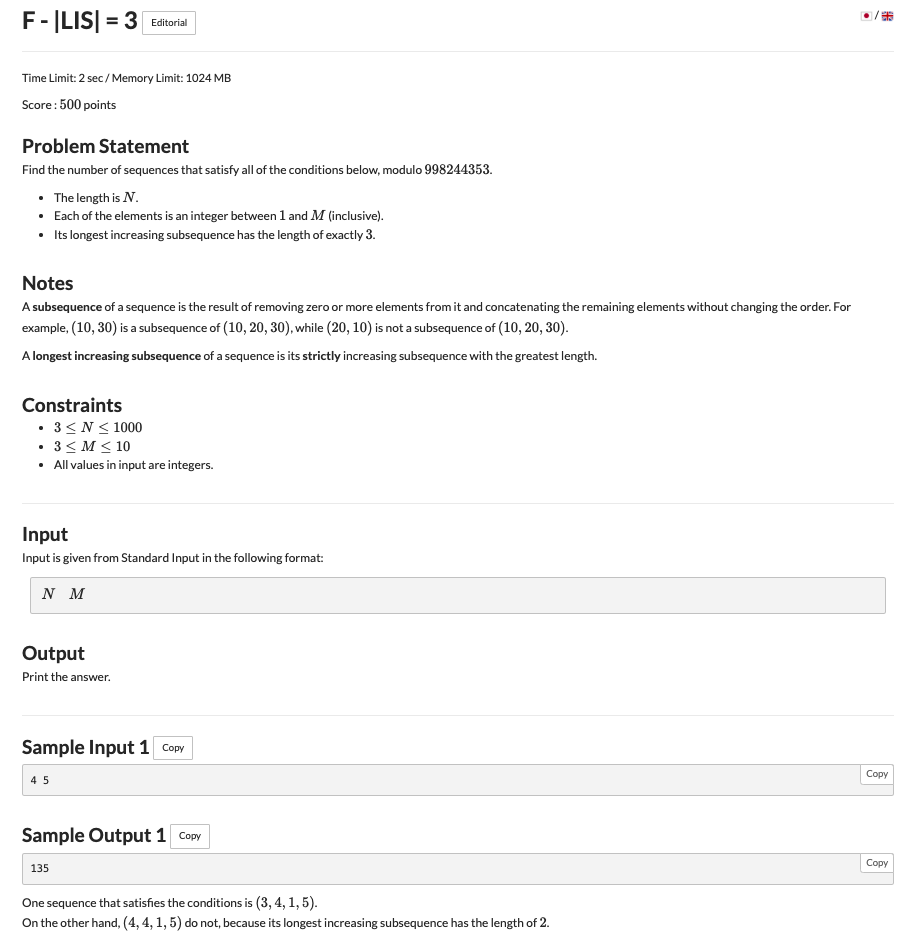
由于个数限定为 $3$ ，这是一个手动枚举的突破口
我们令 $dp(i,a_1,a_2,a_3)$ 表示在第 $i$ 位，上升子序列最后一位最小是 $a_j$ 时的方案数
枚举顺序便是 $i,a_1,a_2,a_3,x$ ， $x$ 表示第 $i$ 为接 $x$ 时的方案数
最后求一下这三个上升子序列在最后一位递增时的方案数总和（即长序列包含小序列

# ✅

ll n, m;
ll dp[1005][15][15][15];
const int mod = 998244353;

int main () {
        ios::sync_with_stdio(false);

        cin >> n >> m;
        dp[0][m + 1][m + 1][m + 1] = 1;
        for ( int i = 1; i <= n; i ++ ) {
                for ( int a1 = 1; a1 <= m + 1; a1 ++ ) {
                        for ( int a2 = 1; a2 <= m + 1; a2 ++ ) {
                                for ( int a3 = 1; a3 <= m + 1; a3 ++ ) {
                                        for ( int x = 1; x <= m; x ++ ) {
                                                if ( x <= a1 )      (dp[i][x][a2][a3] += dp[i - 1][a1][a2][a3]) %= mod;
                                                else if ( x <= a2 ) (dp[i][a1][x][a3] += dp[i - 1][a1][a2][a3]) %= mod;
                                                else if ( x <= a3 ) (dp[i][a1][a2][x] += dp[i - 1][a1][a2][a3]) %= mod;
                                        }
                                }
                        }
                }
        }
        ll res = 0;
        for ( int a1 = 1; a1 <= m; a1 ++ ) 
                for ( int a2 = a1 + 1; a2 <= m; a2 ++ ) 
                        for ( int a3 = a2 + 1; a3 <= m; a3 ++ ) 
                                res += dp[n][a1][a2][a3],
                                res %= mod;
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

# ABC243G_Sqrt

# 🔗

# 💡

首先在 $O(n^{\frac 12})$ 一个很容易思考到的方式
用 $dp[x]$ 记录 $x$ 的答案
转移方程为 $dp[x]=\sum\limits_{i=1}^{\left\lfloor\sqrt x\right\rfloor}dp[i]$
但这个时间还是过长，考虑 $O(n^{\frac 14})$
思考对于每个 $x$ 第二层 $i$ 出现的次数
对于第二层的 $dp[i]$ ，在 $i*i\to \sqrt x$ 均会出现
那么 $dp[x]=\sum\limits_{i=1}^{\left\lfloor\sqrt{\sqrt{x}}\right\rfloor}dp[i]\times (\sqrt{x}-i\times i+1)$

# ✅

ll dp[55000];

inline void Solve () {
        ll x; cin >> x;
        ll sq = sqrt((long double)x);
        ll res = 0;
        for ( ll i = 1; i * i <= sq; i ++ ) {
                res += dp[i] * (sq - i * i + 1);
        }
        cout << res << endl;
}

int main () {
        cin.tie(0)->sync_with_stdio(0);
        cin.exceptions(cin.failbit);

        dp[1] = 1;
        for ( int i = 2; i < 55000; i ++ ) {
                for ( int j = 1; j * j <= i; j ++ ) {
                        dp[i] += dp[j];
                }
        }

        int cass; cin >> cass; while ( cass -- ) {
                Solve ();
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# ABC251E_TakahashiAndAnimals

# 🔗

# 💡

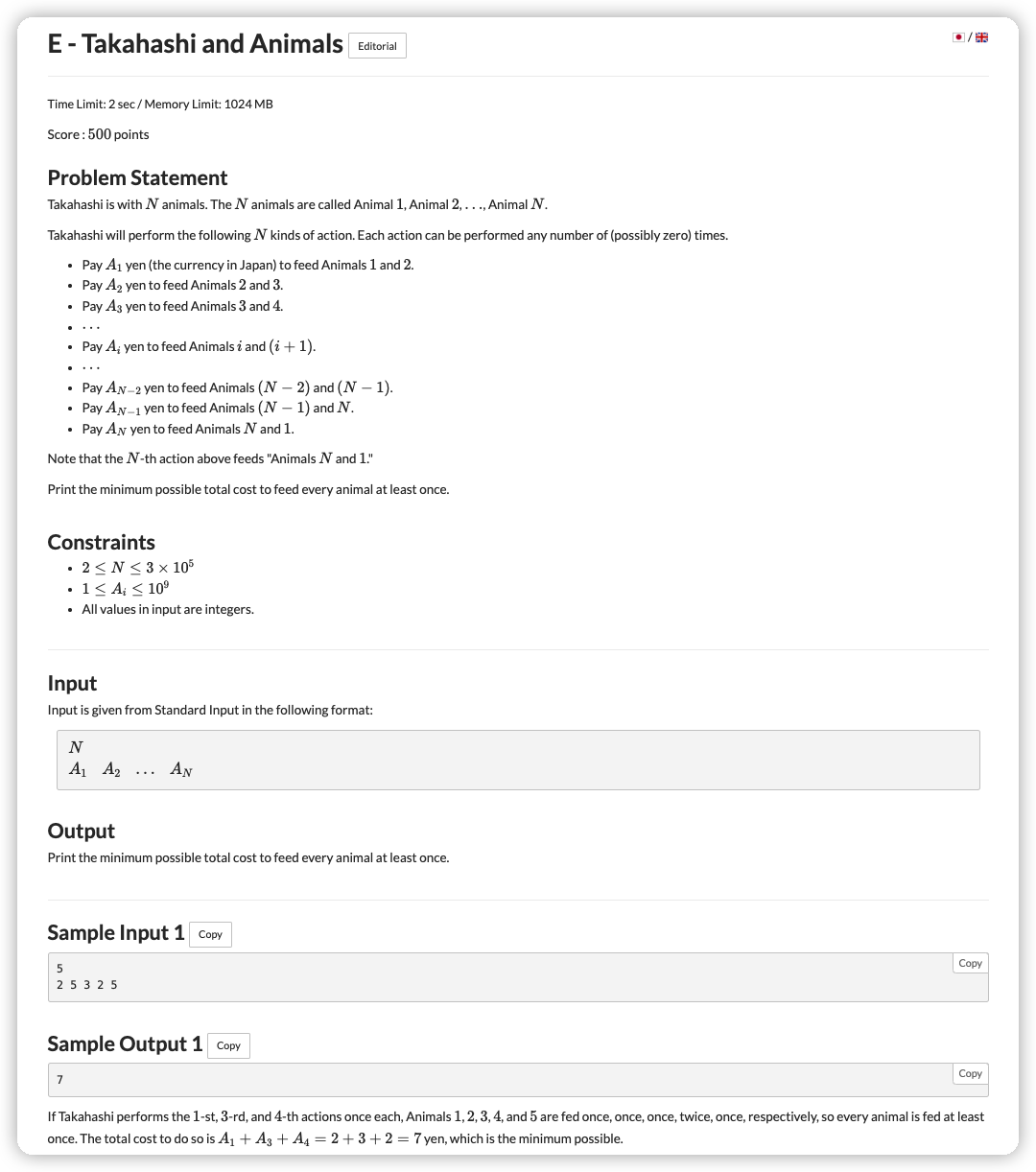
这个就是相邻两位不能都不选的一个问题，经典了，直接上 $dp$
$dp[i][0/1]$ 分别表示在第 $i$ 位上，不选和选的情况
那么 $dp[i][0]=min(dp[i-1][1])$
$dp[i][1]=min(dp[i][1],min(dp[i-1][0],dp[i-1][1])+a[i])$
但是这里多了一个要求就是一个环，第 $0$ 位和第 $n$ 位选取状态必须相同

可以 $dp$ 两次，一次初始值设置为 $dp[0][0]=0$ ，一次 $dp[0][1]=a[0]$
然后 $dp$ 从 $0$ 到 $n$ ，求一下 $n$ 第一种情况的 $dp[n][0]$ 和第二种情况的 $dp[n][1]$ 的最小值即可

# ✅

const int N = 3e5 + 10;
int n; ll a[N];
ll dp[N][2];
ll res = 1e18;

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        cin >> n;
        for (int i = 0; i < n; i ++) cin >> a[i]; a[n] = 0;

        for (int i = 0; i < N; i ++) dp[i][0] = dp[i][1] = 1e18;
        dp[0][1] = a[0];
        for (int i = 1; i <= n; i ++) {
                dp[i][1] = min(dp[i][1], min(dp[i - 1][0], dp[i - 1][1]) + a[i]);
                dp[i][0] = min(dp[i][0], dp[i - 1][1]);
        }
        res = min(res, dp[n][1]);

        for (int i = 0; i < N; i ++) dp[i][0] = dp[i][1] = 1e18;
        dp[0][0] = 0;
        for (int i = 1; i <= n; i ++) {
                dp[i][1] = min(dp[i][1], min(dp[i - 1][0], dp[i - 1][1]) + a[i]);
                dp[i][0] = min(dp[i][0], dp[i - 1][1]);
        }
        res = min(res, dp[n][0]);

        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

# ABC252G_Pre-Order

# 🔗

# 💡

首先获取一个冷知识：对于给定的一个先序遍历序列，有卡特兰数 $n$ 个树（虽然对这题没什么用处
对于这个题，其实很容易想到是dp，因为对于根为 $A_x$ ，形成 $A_{[x,y]}$ 的子树如果已知的话，可以直接接在右链任何一个节点的右侧
但是比赛的时候转移方程推不出来

这里默认 $0$ 为根，设置 $dp[l][r]$ 为 $0,A_l,A_{l+1},\dots,A_{r-1}$ 即 $r-l+1$ 个节点形成的树的方案数
其中 $0$ 和 $1$ 为根是一样的，那么我们省去 $1$ 这个点，对于输入 $A_{[0,n-1]}$ 求的是 $dp[1][n]$
转移是：

$A_l$ 是 $0$ 唯一的子节点，则有 $dp[l+1][r]$ 种
$0$ $0$ 有别的后代 $A_k$ $A_{k}$ ，那么 $A_l<A_k$ $A_{l} < A_{k}$ ，这种情况为
- $l$ 的子树有 $dp[l+1][k]$ 种
- $k$ 的子树有 $dp[k][r]$ 种即一共 $dp[l+1][k]\times dp[k][r]$ 种

所以转移方程为 $dp[l][r]=dp[l+1][r]+\sum\limits_{k>l,a[l]<a[k]}dp[l+1][k]\times dp[k][r]$

初始化为 $dp[l][l]=1$

# ✅

# include "bits/stdc++.h"

using namespace std;
using ll = long long;

const int mod = 998244353;
const int N = 510;

int n, a[N];
ll dp[N][N];


int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        cin >> n;
        for (int i = 0; i < n; i ++) cin >> a[i];

        for (int l = n; l >= 1; l --) {
                dp[l][l] = 1;
                for (int r = l + 1; r <= n; r ++) {
                        dp[l][r] = dp[l + 1][r];
                        for (int k = l + 1; k < r; k ++) {
                                if (a[l] < a[k])
                                        (dp[l][r] += dp[l + 1][k] * dp[k][r] % mod) %= mod;
                        }
                }
        }

        cout << dp[1][n] << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

# AcWing895_最长上升子序列

# 🔗

# 💡

数据量1000，可以用n^2的复杂度去解
在上升子序列中，考虑每一位都必须比前面那一位要大
我们设置dp[i]表示从第1位到第i位的最长上升子序列
所以我们在枚举每一位(设为a[i])的时候
都利用前面的dp最优解去查一下
如果有一位(设为a[j])的值小于a[i]
那么我们完全可以把 $a[i]$ 放到a[j]后面，得到的这一种子序列dp[i]=dp[j]+1
时间复杂度：O(n^2)

# ✅

const int N = 1005;

int a[N];
int dp[N];
int res;

int main(){
    int n; read(n);
    for(int i = 1, x; i <= n; i ++)  read(a[i]);
    for(int i = 1; i <= n; i ++){ dp[i] = 1;//初始化为1，因为自己本身一个数就是一个LIS
        for(int j = 1; j < i; j ++) if(a[j] < a[i]) dp[i] = MAX(dp[j] + 1, dp[i]);//如果前面的某一位小于当前的这一位，完全可以把这一位接到前面那一位后面
        res = MAX(res, dp[i]);//维护一下最大答案
    }write(res);
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# AcWing3499_序列最大收益

# 🔗

# 💡

是一个决策某个位置删不删的问题，所以DP可解
我第一反应是区间DP，但是我们需要一维去记录删掉多少个元素
所以我们用一维表示枚举的位数，一维表示删除多少个元素
就变成了一道线性DP

发现这个几乎可以用LIS问题的方法 (opens new window)写，相比较于LIS问题
少了个大小的限制，但多了个对删除多少个元素的限制
同时把a[i]接到a[j]后面的收益从1变成了w[a[i]][a[j]]
数据量200，明显是让我们加一重循环去维护第二维的

所以问题就转化成了一个带一点变动的LIS问题

# ✅

const int N = 210;
int w[N][N], a[N];
int dp[N][N];//dp[i][j]表示到第i位删去了j个元素后的最优解
int n, k, m;
int res;

int main(){
    read(n); read(k); read(m);
    for(int i = 1; i <= m; i ++) read(a[i]);
    for(int i = 1; i <= n; i ++) for(int j = 1; j <= n; j ++) read(w[i][j]);
    
    for(int i = 1; i <= m; i ++){			//推到了第几位
        for(int j = 0; j <= k; j ++){		//枚举到第i位删去多少个
            for(int o = 1; o < i; o ++){	//枚举第i位以前的o位，并代表 (i, o) 的元素是我们跳过的
                if(j >= i - o - 1)			//检查一下第i位要删去的这j个元素够不够跳跃 (i, o) 这么多个元素
                 	//第i位删了 o 个，所以第o个位置的状态是删去 j-(i-o+1) 个，拼到后面得到w[a[o]][a[i]]
                    dp[i][j] = MAX(dp[i][j], dp[o][j - (i - o - 1)] + w[a[o]][a[i]]),
                    res = MAX(dp[i][j], res);//维护最大值
            }
        }
    }write(dp[m][k]);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

# CodeForces376D_MaximumSubmatrix2

# 🔗

https://codeforces.com/contest/376/problem/D

# 💡

本题使用了DP悬线法
即：我们求出每个点的向上最长延伸距离 x 、向左最长延伸距离 y ，从上向下缩个 y ，然后枚举点维护 x * y 的最大值即可求得最大条件矩阵面积
我们缩 y 的目的是：我们可能在最长向上延伸距离中，上面有的点的左延伸距离比下面的短，导致我们用下面的点的 x * y 形成的子矩阵是个不符合条件的子矩阵，所以我们要缩边

但是本题有个约定是：我们可以改变行的顺序
那么这样我们就可以对每一列的最长向左延伸距离做个降序排序，从而使得我们不需要再缩边
而我们每个最长向左延伸距离在有数的时候，我们的矩阵点都是1，所以我们排过序后，最长向上延伸距离就是这个点的行号
最后同理，扫一遍维护一下即可

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/

//#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << endl

#define CHIVAS_ int main()
#define _REGAL exit(0)
#define SP system("pause")
#define IOS ios::sync_with_stdio(false)

//#define map unordered_map

#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cass = inputInt(); cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;


template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal <vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i])MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal <vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i])MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
template<typename T> vector<T>& operator-- (vector<T> &v){for (auto& i : v) --i; return v;}
template<typename T> vector<T>& operator++ (vector<T> &v){for (auto& i : v) ++i; return v;}
template<typename T> istream& operator>>(istream& is, vector<T> &v){for (auto& i : v) is >> i; return is;}
template<typename T> ostream& operator<<(ostream& os, vector<T> v){for (auto& i : v) os << i << ' '; return os;}
inline int inputInt(){int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);}
inline void outInt(int X){if(X<0) {putchar('-'); X=~(X-1);}int s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline ll inputLL(){ll X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1); }
inline void outLL(ll X){if(X<0) {putchar('-'); X=~(X-1);}ll s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}

const int N = 5e3 + 10;
int n, m;
char Map[N][N];
int dp[N][N]; //优化版的悬线法： dp[j][i] 表示 在第j列第i行的左1边界与当前位置的距离

inline void solve () {
        n = inputInt(), m = inputInt();
        for ( int i = 1; i <= n; i ++ ) {
                scanf("%s", Map[i] + 1);
                for ( int j = 1; j <= m; j ++ ) {
                        dp[j][i] = Map[i][j] == '1' ? dp[j - 1][i] + 1 : 0; // 同列中递推一下
                }
        }

        int res = 0;
        for ( int j = 1; j <= m; j ++ ) {
                sort ( dp[j] + 1, dp[j] + 1 + n, greater<int>() ); // 每一列中每个点的左延伸进行降序排序
                for ( int i = 1; i <= n && dp[j][i]; i ++ ) res = MAX(res, dp[j][i] * i); // 维护最大条件子矩阵
        }
        outInt(res); puts("");
}

CHIVAS_{
        solve();
        _REGAL;
};

# CodeForces999F_CardsAndJoy

# 🔗

# 💡

就是这么多的牌每个牌都分给一个人，每个人分到的不超过 $k$ 个
那么问题就是每个牌分给谁
注意对于第 $i$ 个人，只有牌为 $f(i)$ 的才有贡献，别的牌都是充数的，那么将第一个样例的分配方法在每个人去掉不是 $f(i)$ 的牌后，其实就是一个对于相同 $f$ 的人，每个人分配到的 $f$ 的数量问题
如果此时有 $m$ 个牌面为 $x$ 的牌，有 $n$ 个喜欢这个牌面的人，那么问题就是把这 $m$ 张牌分给 $n$ 个人，求最大价值
这就是一个很明显的三重循环 $dp$ 了， $dp[i][j]$ 表示前 $i$ 个人有 $j$ 个牌的最大价值，然后第三维去枚举第 $i$ 个人获得多少张牌即可

# ✅

const int N = 510;
int dp[N][N * 10];

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        int n, K; cin >> n >> K;
        map<int, int> card; for (int i = 0; i < n * K; i ++) {
                int x; cin >> x;
                card[x] ++;
        }
        map<int, int> favo; for (int i = 0; i < n; i ++) {
                int x; cin >> x;
                favo[x] ++;
        }
        vector<int> h(K + 1); for (int i = 1; i <= K; i ++) cin >> h[i]; h[0] = 0;

        int res = 0;
        for (auto i : card) {
                int y = favo[i.first];
                int x = i.second;
                if (!y) continue;
                x = min(x, K * y);

                for (int i = 0; i <= y; i ++) for (int j = 0; j <= x && j <= i * K; j ++) dp[i][j] = -1;
                dp[0][0] = 0;

                for (int i = 1; i <= y; i ++) {
                        for (int j = 0; j <= x && j <= i * K; j ++) {
                                for (int k = min(j, K); k >= 0; k --) {
                                        if (dp[i - 1][j - k] == -1) continue;
                                        dp[i][j] = max(dp[i][j], dp[i - 1][j - k] + h[k]);
                                }
                        }
                }
                res += dp[y][x];
        }
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

# CodeForces1427C_TheHardWorkOfPaparazzi

# 🔗

# 💡

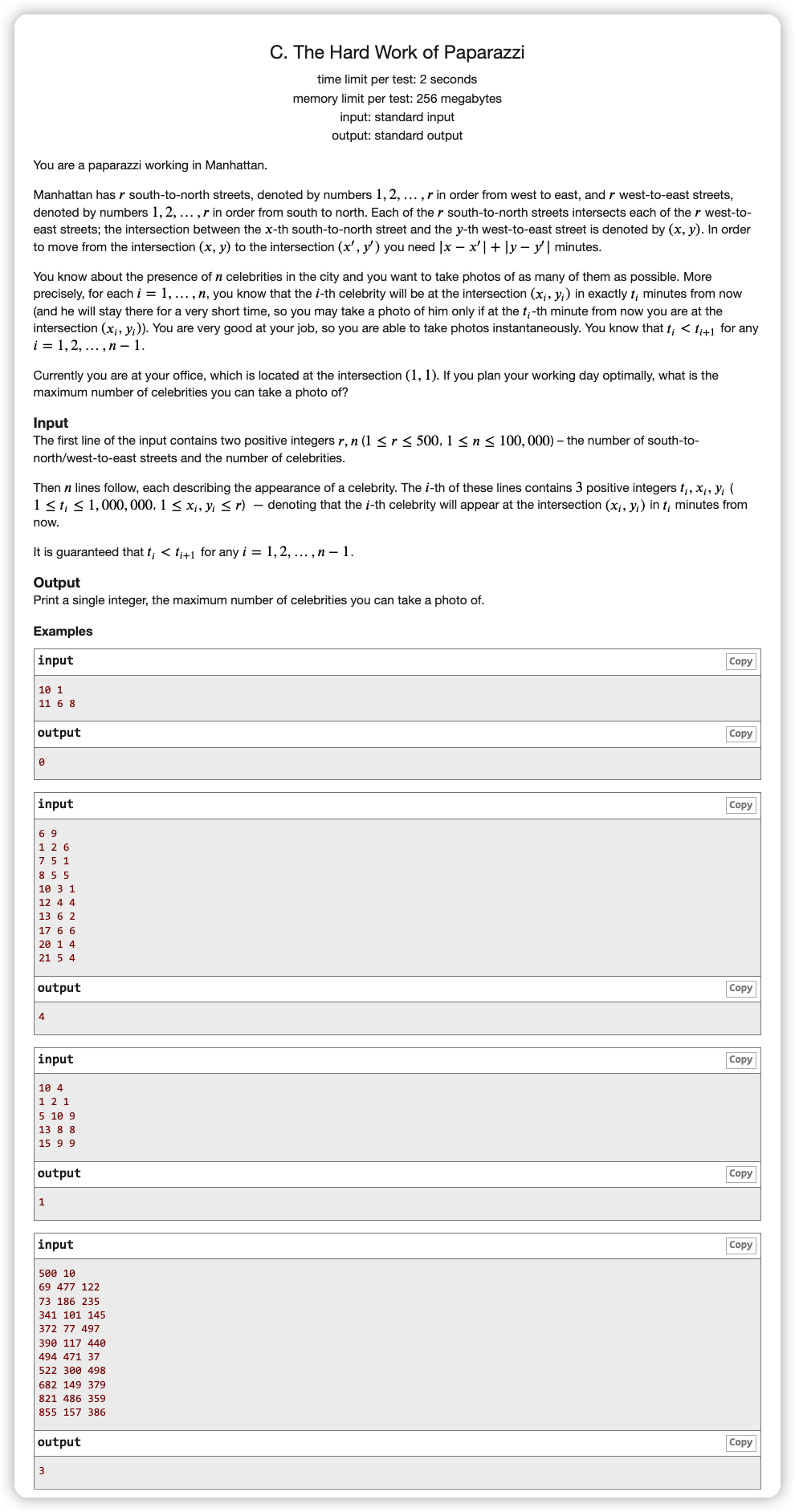
首先一个 $O(n^2)$ 的算法是很好想的，即枚举 $i$ ，枚举 $j$ 为 $[0,i-1]$ ，如果满足 $dis(a_i,a_j)\le t_i-t_j$ 的话就代表可以转移，就维护一下最大值即可
但是这是一个 $O(n^2)$ ，这样 $r$ 并没有用上，考虑 $r$ 有什么用
其实应该有条件反射 $n\times m$ 的矩阵最大曼哈顿距离为 $n+m-2$ ，这里最大就是 $r*2-2$ ，就意味着两个时间差如果超过 $r*2$ 的话那么一定是可以转移的
所以其实需要去检查来转移的只有 $[i-2r,i-1]$ ，更靠前的可以直接维护一个变量表示他们的最大值，然后维护 $dp[i]$ 统计能转移的最大值 $+1$

# ✅

struct node { int t, x, y; };
inline int dis (node a, node b) {
        return abs(a.x - b.x) + abs(a.y - b.y);
}

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        int r, n; cin >> r >> n;
        vector<node> a(n + 1); for (int i = 1; i <= n; i ++) cin >> a[i].t >> a[i].x >> a[i].y;
        a[0] = {0, 1, 1};

        vector<int> dp(n + 1, -1); dp[0] = 0;
        int pre = -2;
        for (int i = 1; i <= n; i ++) {
                for (int j = max(0, i - 2 * r); j < i; j ++) {
                        if (dp[j] == -1) continue;
                        if (a[i].t - a[j].t >= dis(a[i], a[j])) 
                                dp[i] = max(dp[i], dp[j] + 1);
                }
                dp[i] = max(dp[i], pre + 1);
                if (i - 2 * r >= 0) pre = max(pre, dp[i - 2 * r]);
        }

        int res = 0;
        for (int i = 1; i <= n; i ++) res = max(res, dp[i]); 
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

# CodeForces1475G_StrangeBeauty

# 🔗

# 💡

就是说我们剩下的数组中，任意一对都必须一个是另一个倍数
如果 $a$ 是 $b$ 的倍数，那么 $a\ge b$
那么我们如果对其排一个序的话，就可以确定一个位置可以连后面的是它的倍数的位置
而删除的最少就是保留的最多，也就是求一个这里面的最长路
这里连边过多，我们肯定不能一一枚举，但是枚举倍数，也就是一个埃氏筛的套路复杂度
我们从小往大去枚举一条边的起点，然后用枚举倍数的方式去枚举它的终点（注意有的起点或终点可能不存在，所以不要更新）
对于起点 $u$ 和终点 $v$ ，已知相同的的也可以互成倍数，那么我们记录 $v$ 是否存在的时候可以直接记录它的出现次数 $num$ ，然后最长路的转移就直接 $dp[v]=max(dp[v],dp[u]+num[v])$

# ✅

const int N = 2e5 + 10;
int a[N], num[N], n, dp[N];

inline void Solve () {

        memset(num, 0, sizeof num);
        memset(dp, 0, sizeof dp);

        cin >> n;
        for (int i = 1; i <= n; i ++) cin >> a[i], num[a[i]] ++, dp[a[i]] ++;

        for (int i = 1; i < N; i ++) {
                if (!num[i]) continue;
                for (int j = i + i; j < N; j += i) {
                        if (num[j]) dp[j] = max(dp[j], dp[i] + num[j]);
                }
        }

        int res = 0;
        for (int i = 1; i < N; i ++) res = max(res, dp[i]);
        cout << n - res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

# CodeForces1512F_Education

# 🔗

# 💡

可以感性考虑一波，要攒钱肯定是选择一个位置好好攒钱，那么在这道题中，就是我们肯定是走到某个位置了，然后停下专心致志攒钱一直攒到 $c$
同时也要注意前面也有一个贪心的方式，我没必要在每一关攒到刚好能突破的钱数后直接突破到下一关，而是可以选择一个攒钱较为快的位置，一直攒攒到能直接突破中间的所有关卡走到我们想走的位置
这是一个链性的，就比如说我如果要走到 $a$ ，我在 $b$ 处攒钱更快能过去，而我想要在 $b$ 处攒钱，我就选择一个 $c$ 处攒钱更快
而攒钱更快，就是对应的 $a$ 更大，那么我们对于每一个 $i$ ，记录一个前缀中 $a_{1,i-1}$ 最大的位置，形成数组 $id\_pre\_max[]$ ，然后转移的时候，就从记录的这个位置中进行转移，到这里就可以开始使用 $dp$ 了
我们 $dp$ 记录双关键字，第一个表示我们花费的天数，第二个表示剩余的钱数
对于 $i$ 的天数，则是我在 $id\_pre\_max[i]$ 中剩余的钱数的基础上，要攒到超过 $\sum\limits_{j=id\_pre\_max[i]}^{i-1}b_j$ 以供突破连续关卡需要的天数，这个直接向上取整就行，同时要加上我这一段突破的次数，因为每次突破需要一天
对于 $i$ 的钱数，是我们突破需要的天数乘上之前那个最大的 $a$ 的值带上之前剩余的钱数，是我们赚的。而突破这一连续的关卡是我们亏的，赚的减去亏的即可。

有一个细节点，如果我们在 $id\_pre\_max[i]$ 这个位置上剩余的钱数不低于我们突破到我们想到的位置的话，我们在前缀最大位置上攒钱的天数应该为 $0$

# ✅

struct node {
        ll d, m;
        inline friend bool operator < (node a, node b) {
                if (a.d != b.d) return a.d > b.d;
                return a.m < b.m;
        }
};
 
const int N = 2e5 + 10;
ll a[N], b[N];
ll n, c;
node dp[N];
ll mxi, mxv;
int id_pre_max[N];
ll pre_b[N];
 
inline void Solve () {
        cin >> n >> c;
        for (int i = 1; i <= n; i ++) cin >> a[i];
        for (int i = 1; i < n; i ++)  cin >> b[i], pre_b[i] = pre_b[i - 1] + b[i];
 
        mxv = mxi = 0;
        for (int i = 1; i <= n; i ++) {
                id_pre_max[i] = mxi;
                if (a[i] >= mxv) mxv = a[i], mxi = i;
        }
 
        dp[1] = {0, 0};
        for (int i = 2; i <= n; i ++) {
                ll up = pre_b[i - 1] - pre_b[id_pre_max[i] - 1] - dp[id_pre_max[i]].m; // 我们要攒多少钱
                ll work_day = up / a[id_pre_max[i]] + (up % a[id_pre_max[i]] != 0); if (up <= 0) work_day = 0; // 需要工作的天数
                ll d = dp[id_pre_max[i]].d + work_day + (i - id_pre_max[i]); // 转移过程的天数
                ll m = dp[id_pre_max[i]].m + work_day * a[id_pre_max[i]] - (pre_b[i - 1] - pre_b[id_pre_max[i] - 1]); // 
                dp[i] = {d, m};
        }
        ll res = 1e18;
        for (int i = 1; i <= n; i ++) {
                res = min(res, dp[i].d + (c - dp[i].m) / a[i] + ((c - dp[i].m) % a[i] != 0));
        }
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

# CodeForces1583C_OmkarAndDetermination

# 🔗

# 💡

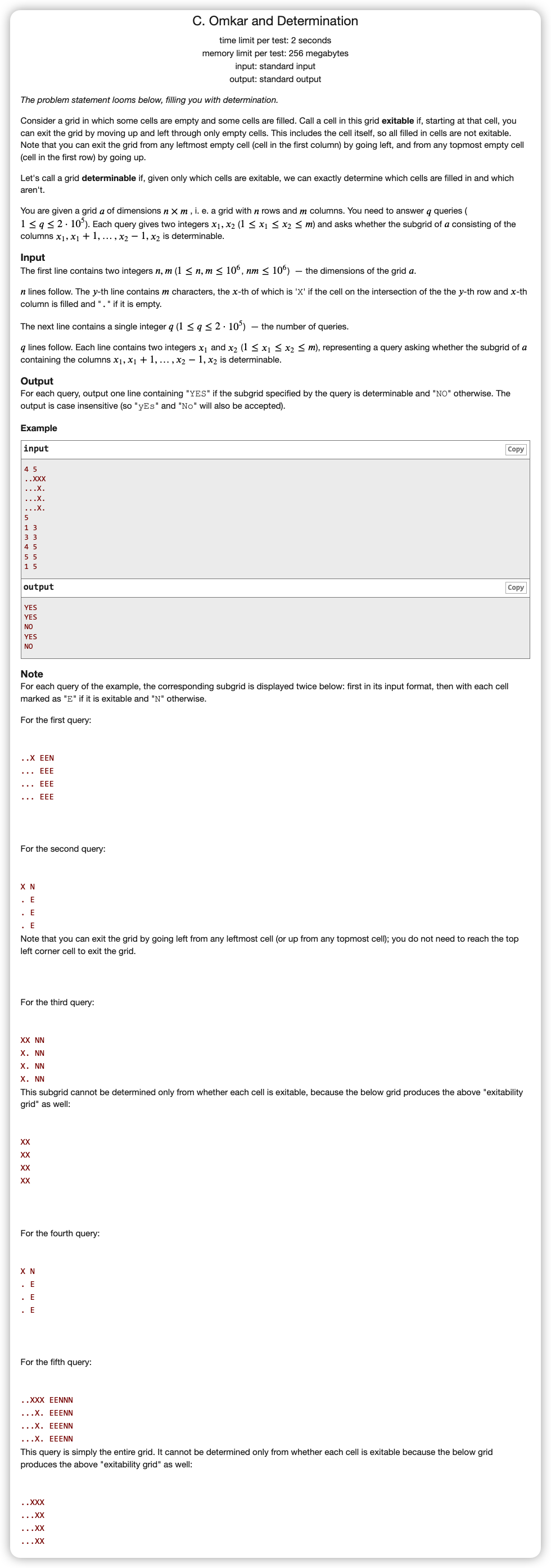
由于我们每次是截取中间一部分子矩阵，则不需要某个位置继承左侧和上侧的可走情况
那么在不继承下，其实就归根于每个“不可走链”的最原始的点，那么就是左侧和右侧都为 $'X'$ 的点
这样我们可以对这样的点的贡献设置为 $1$
如果某列中存在这样的点，就将这一列的 $flag$ ，令 $sum[j]$ 为第 $j$ 列的 $flag$ 前缀和

对与查询 $[l,r]$ ， $l$ 列是一定不存在不确定的点的，那么就查 $[l+1,r]$ 的区间和是否不为 $0$ ，如果是的话就说明这个矩阵内存在不确定的点，就输出 NO 即可

# ✅

int main () {
        cin.tie(0)->sync_with_stdio(0);
        cin.exceptions(cin.failbit);

        int n, m; cin >> n >> m;
        vector<string> a(n + 1); a[0] = string(m + 1, '.');
        for (int i = 1; i <= n; i ++) {
                string s; cin >> s;
                a[i] = "." + s;
        }


        vector<int> sum(m + 1, 0);
        for (int j = 1; j <= m; j ++) {
                for (int i = 1; i <= n; i ++) {
                        sum[j] |= a[i - 1][j] == 'X' && a[i][j - 1] == 'X';
                }
                sum[j] += sum[j - 1];
        }

        int q; cin >> q;
        while ( q -- ) {
                int l, r; cin >> l >> r;
                if (sum[r] - sum[l]) cout << "NO\n";
                else cout << "YES\n";
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# CodeForces1601B_FrogTraveler

# 🔗

# 💡

分析这个问题
首先这个问题是一个类似于最短路的问题，我们要跳最少的次数到达目的地，需要更新
同时这个问题也要维护路径，需要记录最短路前驱

如果把它按最短路单纯地连边的话，边数可能会到达 $\frac{n^2}{2}$ ，非常大，时间空间都过不去
注意到一个点可以跑的点是它后面连续的一段点，考虑到其实 $dijkstra$ 就是一个 $dp$ 的转移，那么用线段树区间修改进行这个 $dp$ 的转移操作

但是注意到有一个下滑的过程，由于我们要使用这个连续的下标，我们就要在用 $a_i$ 时，用 $i$ 这个点的最短距离 $+1$ 更新 $[i+b_i-a_{i+b_i},i+b_i-1]$
因为我们路径记录的都是下滑之前的路径点，所以标记这次更新是用 $i$ 更新的即可
所以我们要有一个双关键字的懒标记，一个关键字是更新的距离，另一个则是更新出第一个关键字的出发点
线段树懒标记往下推的时候，需要考虑需不需要更改这两个关键字，而当子树的 $l=r$ 了话，就代表我们推到底了，如果将距离更新为更短了，就要直接修改 $pre[l]$

# ✅

const int N = 3e5 + 10;
const int inf = 0x3f3f3f3f;
 
int pre[N]; // 最短路的前驱
struct node {
        int val;
        pair<int, int> lazy;
} t[N << 2];
inline void pushUp (int rt) {
        t[rt].val = max(t[rt << 1].val, t[rt << 1 | 1].val);
}
inline void pushDown (int l, int r, int rt) {
        if (t[rt].lazy.first == inf) return;
        node &fa = t[rt], &ls = t[rt << 1], &rs = t[rt << 1 | 1];
        // 更短的话，更新的原因点也要修改
        if (ls.lazy.first > fa.lazy.first) ls.lazy = fa.lazy;
        if (rs.lazy.first > fa.lazy.first) rs.lazy = fa.lazy;
        int mid = (l + r) >> 1;
        // 叶子节点，如果需要更新的话就把 pre 更新了
        if (mid - l + 1 == 1) { 
                if (ls.val > fa.lazy.first) {
                        pre[l] = fa.lazy.second;
                        ls.val = fa.lazy.first;
                }
        } else {       
                ls.val = min(ls.val, fa.lazy.first);
        }
        if (r - mid == 1) {
                if (rs.val > fa.lazy.first) {
                        pre[r] = fa.lazy.second;
                        rs.val = fa.lazy.first;
                }
        } else {
                rs.val = min(rs.val, fa.lazy.first);
        }
        fa.lazy = {inf, -1};
}
inline void Build (int l, int r, int rt) {
        t[rt] = {inf, {inf, -1}};
        if (l == r) return;
        int mid = (l + r) >> 1;
        Build(l, mid, rt << 1);
        Build(mid + 1, r, rt << 1 | 1);
}
inline void Update (int a, int b, int c, int id, int l, int r, int rt) {
        if (a <= l && r <= b) {
                if (t[rt].lazy.first > c) t[rt].lazy = {c, id};
                // 同理，叶子结点要看情况直接更新 pre
                if (l == r) {
                        if (t[rt].val > c) {
                                t[rt].val = c;
                                pre[l] = id;
                        }
                } else {
                        t[rt].val = min(t[rt].val, c);
                }
                return;
        }
        pushDown(l, r, rt);
        int mid = (l + r) >> 1;
        if (a <= mid) Update(a, b, c, id, l, mid, rt << 1);
        if (b > mid) Update(a, b, c, id, mid + 1, r, rt << 1 | 1);
        pushUp(rt);
}
inline int Query (int id, int l, int r, int rt) {
        if (l == r) return t[rt].val;
        pushDown(l, r, rt);
        int mid = (l + r) >> 1;
        if (id <= mid) return Query(id, l, mid, rt << 1);
        else return Query(id, mid + 1, r, rt << 1 | 1);
}
 
 
int a[N], b[N], n;
int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);
 
        cin >> n;
        for (int i = 1; i <= n; i ++) cin >> a[i];
        for (int i = 1; i <= n; i ++) cin >> b[i];
 
        Build(0, n, 1);
        Update(n, n, 0, n + 1, 0, n, 1);
 
        for (int i = n; i >= 1; i --) {
                int ti = i + b[i];
                // 用当前所在点的最短路 去 更新下滑过后的点所能跑到的区间，并记录这次更新是当前所在点更新的
                if (a[ti]) Update(ti - a[ti], ti - 1, Query(i, 0, n, 1) + 1, i, 0, n, 1);
        }
        for (int i = 0; i <= n; i ++) Query(i, 0, n, 1); // 懒标记全推下去
 
        if (t[1].val == inf) {
                cout << "-1\n";
                return 0;
        }
        cout << t[1].val << endl;
        vector<int> res;
        int cur = 0;
        while (pre[cur] != n + 1) {
                res.push_back(cur);
                cur = pre[cur];
        }
        reverse(res.begin(), res.end());
        for (auto i : res) cout << i << " ";
}

# CodeForces1625C_RoadOptimization

# 🔗

# 💡

开始两发贪心上去，想着每次删去一个删掉后最省时的点，结果wa了，后来一想删掉当前阶段最省时的不一定能保证这个操作对于最后阶段最优
观测一下数据量 $\inline n\le500$ ，三重循环能破，跑 $\inline dp$ 吧
限制为终止哪个点，最多删 $\inline k$ 个点
于是我们设置 $\inline dp[i][j]$ 表示到第 $\inline i$ 个点删去了 $\inline j$ 个点，可以跑出来的最短时间
由于如果删掉一个点后，我们的速度是继承该点之前没有删掉的点
所以我们三重循环，一重 $\inline i$ 枚举到哪个点了，一重枚举删了 $\inline j$ 个点，一重枚举上一个点是 $\inline k$
如果第 $\inline i$ 个点要删掉了， $\inline dp[i][j + 1] = min(dp[i][j + 1], dp[o][j - (i - o - 1)] + time(o, i))$
如果不删的话 $\inline dp[i][j] = min(dp[i][j], dp[o][j - (i - o - 1)] + time(o, i))$ ，即然是从 $\inline o$ 跳过来的，那么中间的也必然被删掉了，所以 $\inline o$ 的时候是删去了 $\inline j-(i-o-1)$ 次

# ✅

ll n, l, k;
ll d[510], a[510];
 
ll dp[510][510];
 
inline ll tm ( int x, int y ) { // x -> y
        return (d[y] - d[x]) * a[x];
}
 
int main () {
        ios::sync_with_stdio(false);
        cin >> n >> l >> k;
        for ( ll i = 0; i < n; i ++ ) cin >> d[i];
        for ( ll i = 0; i < n; i ++ ) cin >> a[i];
        d[n] = l, a[n] = 0;
 
        memset(dp, 0x3f3f3f3f, sizeof dp);
        dp[0][0] = 0;
        for ( int i = 1; i <= n; i ++ ) {
                for ( int j = 0; j < min((ll)i, k + 1); j ++ ) {
                        for ( int o = i - j - 1; o < i; o ++ ) {
                                dp[i][j + 1] = min(dp[i][j + 1], dp[o][j - (i - o - 1)] + tm(o, i));
                                dp[i][j] = min(dp[i][j], dp[o][j - (i - o - 1)] + tm(o, i));
                        }
                }
        }
        ll res = 0x3f3f3f3f;
        for ( int j = 0; j <= k; j ++ ) res = min(res, dp[n][j]);
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

# CodeForces1650G_CountingShortcuts

# 🔗

# 💡

题目问的是很简单，就是问最短路和次短路(如果 $dis1[t]=dis0[t]+1$ )的个数和
由于边长均为一，所以没有什么必要去专门用最短路计数和次短路计数
我们可以采用一种递推的方式求解

令 $dp[u][1]$ 为 $s\to u$ 的次短路计数， $dp[u][0]$ 则为最短路计数
若 $dis[u]=dis[v]$ 则说明将会出现一条 $v\to u$ 的次短路，（因为最短路从 $v\to u$ 加一了）， $dp[u][1]=dp[u][1]+dp[v][0]$
若 $dis[u]>dis[v]$ 则说明 $v\to u$ 顺延下去即可， $dp[u][1]=dp[u][1]+dp[v][1]$
至于最短路计数，我们就可以和上一条一样， $dp[v][0]=dp[v][0]+dp[u][0]$
这里的递推顺序需要一点感性思考，现将一个点汇聚完再开下一个点，这样也就是用 $BFS$ 会更好实现
至于求 $dis$ 、 $dp0$ 、 $dp1$ 可以开做三个 $BFS$ 处理会更清晰

# ✅

const int N = 2e5 + 10;
const int M = 4e5 + 10;
const int mod = 1e9 + 7;

struct Edge {
        int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge ( int from, int to ) {
        edge[++cnt] = { head[from], to };
        head[from] = cnt;
}

int n, m;
ll dp[N][2];
int vis[N];
int dis[N];

inline void BFS1 ( int s ) { // 求 dis
        memset(vis, 0, sizeof vis);
        queue<pair<int, int> > que;
        que.push({s, 0});
        while ( que.size() ) {
                pair<int, int> pu = que.front(); que.pop();
                int u = pu.first, dep = pu.second;
                if ( vis[u] ) continue; vis[u] = 1;
                dis[u] = dep;
                for ( int i = head[u]; i; i = edge[i].nxt ) {
                        int v = edge[i].to;
                        if ( vis[v] ) continue;
                        que.push({v, dep + 1});
                }
        }
}
inline void BFS2 ( int s ) { // 求 dp0
        queue<int > que;
        memset(vis, 0, sizeof vis);
        que.push(s);
        dp[s][0] = 1;
        while ( que.size() ) {
                int u = que.front(); que.pop();
                if ( vis[u] ) continue; vis[u] = 1;
                for ( int i = head[u]; i; i = edge[i].nxt ) {
                        int v = edge[i].to;
                        if ( dis[v] > dis[u] ) (dp[v][0] += dp[u][0]) %= mod, que.push(v);
                }
        }
}
inline void BFS3 ( int s ) { // 求 dp1
        memset(vis, 0, sizeof vis);
        queue<int> que;
        que.push(s);
        while ( que.size() ) {
                int u = que.front(); que.pop();
                if ( vis[u] ) continue; vis[u] = 1;
                for ( int i = head[u]; i; i = edge[i].nxt ) {
                        int v = edge[i].to;
                        if ( !vis[v] ) que.push(v);
                        if ( dis[u] == dis[v] ) (dp[u][1] += dp[v][0]) %= mod;
                        if ( dis[u] > dis[v] )  (dp[u][1] += dp[v][1]) %= mod;
                }
        }
}

inline void Solve () {
        cnt = 0;    
        scanf("%d%d", &n, &m);
        for ( int i = 0; i <= n; i ++ ) head[i] = dp[i][0] = dp[i][1] = 0;
        int s, t; scanf("%d%d", &s, &t); 
        for ( int i = 0; i < m; i ++ ) {
                int u, v; scanf("%d%d", &u, &v);
                add_Edge(u, v);
                add_Edge(v, u);
        }
        BFS1(s);
        BFS2(s);
        BFS3(s);
        printf("%lld\n", (dp[t][0] + dp[t][1]) % mod);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

# CodeForces1699D_AlmostTripleDeletions

# 🔗

# 💡

注意到 $\sum n\le 10000$ 这是一个二重循环
如果我们想保留 $x$ ，而数列是这样的 $...x\;y\;y\;z\;x...$ 那么我们想将中间的 $y\;y\;z$ 删干净
但是注意到最后会留下来一个，只能和 $x$ 对删
而如果中间是 $y\;y\;y$ 那么意味着我们要删掉 $3$ 个 $x$

计算最后中间留下来几个的方法是取出现最多的数个数 $most$ ，和中间所有的个数 $all$ ，如果 $all$ 是偶数且 $2most\le all$ 则意味着一个都不剩，否则如果 $2most>all$ 要剩 $2most-all$ 个，再不是就 $all$ 奇数的话剩下 $1$ 个

这样考虑数值很麻烦，因为有一种贪心方式是 $...x\;y\;y\;x\;z\;z\;z\;x...$ ，这种我们可以将中间的 $x$ 也算作我们想删干净的元素，这样中间全部都能删掉
但是可以发现我们最后剩的是 $...xx...$ ，这两个 $x$ 是前后拼接成的，再考虑上面的第一条也就是能删完的条件，可以联想到二维 $dp$ 中的最长上升子序列的复杂度
即对于 $i,j$ 如果中间和 $ij$ 满足某种条件就可以将 $i$ 拼在 $j$ 后面，条件已经有了，即 $a[i]=a[j]$ 且 $all\in\{even\}$ 且 $2most\le all$
（这里 $most$ 和 $all$ 可以让 $j$ 从后往前扫动态维护一轮即可）

要注意我们可能维护的数值后面也可以删干净，所以最后再扫一轮判断后面可以不可以删干净，如果可以的话就直接将这个 $dp[i]$ 也维护进去

# ✅

inline void Solve () {
        int n; cin >> n;
        vector<int> a(n + 1); for (int i = 1; i <= n; i ++) cin >> a[i];
 
        vector<int> dp(n + 1, -0x3f3f3f3f);
        vector<int> num(n + 1, 0);
        dp[0] = 0;
        for (int i = 1; i <= n; i ++) {
                int most = 0;
                for (int j = i - 1; j >= 0; j --) {
                        // all 就是 i-j-1
                        if ((i - j - 1) % 2 == 0 && (i - j - 1) / 2 >= most && (a[j] == a[i] || j == 0)) { // 注意 i 也可以拼在 0 后面
                                dp[i] = max(dp[i], dp[j] + 1);
                        }
                        most = max(most, ++num[a[j]]);
                }
                for (int j = 0; j < i; j ++) num[a[j]] --;
        }
        
        int res = 0;
        int most = 0;
        for (int i = n; i >= 1; i --) {
                if ((n - i) % 2 == 0 && (n - i) / 2 >= most) res = max(res, dp[i]);
                most = max(most, ++num[a[i]]);
        }
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# DaimayuanOnlineJudge665_数组划分

# 🔗

# 💡

按位了话，肯定最高位更希望是 $1$
所以我们按位从高到低枚举，看看当前答案将这一位设为 $1$ 能否成功分出来 $k$ 段
如果能分成的话就设为 $1$ ，不管这一位会不会对下一位带影响，因为就算下面所有位都是 $1$ 也没法补齐这一位的缺失
在检查 $res$ 能否分成 $k$ 段的时候，可以使用 $dp$
令 $dp[i][kk]$ 表示第 $i$ 个数以前有 $kk$ 段能否成立，那么对于第 $j$ 个数转移到第 $i$ 个数，也就是从 $j+1$ 到 $i$ 为一段，要满足这一段区间和中的 $1$ 是 $res$ 的超集，即 $(sum[i]-sum[j])\& x=x$
在满足这个的时候转移，这样就是一个 $n^3$ 的过程了，最后看看 $dp[n][k]$ 是不是 $true$ 就行了

# ✅

const int N = 110;

int n, K;
ll a[N], sum[N];
bool dp[N][N];

inline bool check (ll x) {
    memset(dp, 0, sizeof dp);
    dp[0][0] = true;
    for (int i = 1; i <= n; i ++) {
        for (int j = 1; j <= i; j ++) {
            if (((sum[i] - sum[j - 1]) & x) != x) continue;
            for (int k = 1; k <= K; k ++) {
                dp[i][k] |= dp[j - 1][k - 1];
            }
        }
    }
    return dp[n][K];
}

int main () {
    scanf("%d%d", &n, &K);
    for (int i = 1; i <= n; i ++)
        scanf("%lld", &a[i]),
        sum[i] = sum[i - 1] + a[i];

    ll res = 0;
    for (int i = 55; i >= 0; i --) {
        if (check(res | (1ll << i))) res |= 1ll << i;
    }
    printf("%lld\n", res);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

# DaimayuanOnlineJudge699_并行排序

# 🔗

# 💡

前面的大的可以连接后面的小的
同边染异色，在图上就是最大完全子图，对应这里就是最长下降子序列，也就是反过来的最长上升子序列
反一下求一下 $LIS$ 的长度即可

# ✅

int a[1000006];

inline void Solve () {
    int n; cin >> n;
    for (int i = 1; i <= n; i ++) {
        cin >> a[i];
    }
    reverse(a + 1, a + 1 + n);
    vector<int> v;
    for (int i = 1; i <= n; i ++) {
        if (v.empty() || v.back() < a[i]) v.push_back(a[i]);
        else v[lower_bound(v.begin(), v.end(), a[i]) - v.begin()] = a[i];
    }
    cout << (int)v.size() << endl;
}

int main () {
    ios::sync_with_stdio(false);
    cin.tie(0);

    int cass; cin >> cass; while (cass --) {
        Solve ();
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# HDUOJ1176_免费馅饼

# 🔗

https://acm.hdu.edu.cn/showproblem.php?pid=1176

# 💡

可以看作是一个倒着的数塔，每个点连接三条边
其中高度就是它给的时间，毕竟时间越长离地面越远
然后我们记录一下出现过的最高高度，就当作塔底遍历起点
每一个单位时间可以移动左一格、右一格、不动。
所以得到三条边的递推式为：dp[i][j] += MAX(dp[i + 1][j], MAX(dp[i + 1][j + 1], dp[i + 1][j - 1]));

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/

//#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << endl

#define CHIVAS_ int main()
#define _REGAL exit(0)
#define SP system("pause")
#define IOS ios::sync_with_stdio(false)

//#define map unordered_map

#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cass = inputInt(); cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;


template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal <vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i])MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal <vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i])MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
template<typename T> vector<T>& operator-- (vector<T> &v){for (auto& i : v) --i; return v;}
template<typename T> vector<T>& operator++ (vector<T> &v){for (auto& i : v) ++i; return v;}
template<typename T> istream& operator>>(istream& is, vector<T> &v){for (auto& i : v) is >> i; return is;}
template<typename T> ostream& operator<<(ostream& os, vector<T> v){for (auto& i : v) os << i << ' '; return os;}
inline int inputInt(){int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);}
inline void outInt(int X){if(X<0) {putchar('-'); X=~(X-1);}int s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline ll inputLL(){ll X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1); }
inline void outLL(ll X){if(X<0) {putchar('-'); X=~(X-1);}ll s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}

const int N = 2e5 + 5;
int dp[N][15];

CHIVAS_{
        int n;
        while ( scanf("%d", &n) == 1 ,n) {
                int h = 0;
                MEM(dp, 0);
                for ( int i = 0; i < n; i ++ ) {
                        int x = inputInt(), t = inputInt();
                        dp[t][x] ++; // 初始值
                        h = MAX(h, t); // 记录塔高
                }
                for ( int i = h; i >= 0; i -- ) {
                        for ( int j = 0; j <= 10; j ++ ) {
                                dp[i][j] += MAX(dp[i + 1][j], MAX(dp[i + 1][j + 1], dp[i + 1][j - 1]));
                        }
                }
                outInt(dp[0][5]); puts("");
        }
        _REGAL;
};

# HDUOJ2041_超级楼梯

# 🔗

http://acm.hdu.edu.cn/showproblem.php?pid=2041

# 💡

递推的思想
每一个台阶都可以由前一个与前两个得来
所以sum[i] = sum[i - 1] + sum[i - 2]

# ✅

#pragma region
#pragma GCC optimize(3,"Ofast","inline")
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define eps 1e-6
#define PI acos(-1.0)
#define ll long long
#define INF 0x7FFFFFFF
#define Regal exit(0)
#define Chivas int main()
#define pb(x) push_back(x)
#define SP system("pause")
#define Max(a,b) ((a)>(b)?(a):(b))
#define Min(a,b) ((a)<(b)?(a):(b))
#define IOS ios::sync_with_stdio(false)
#define mm(a, b) memset(a, b, sizeof(a))
#define each_cass(cass) for (cin>>cass; cass; cass--)
#define test(a) cout << "---------" << a << "---------" << '\n'
 
using namespace std;
#pragma endregion

//全局变量
#pragma region

#pragma endregion

//主体------------------------------------------

inline void solve(){
    ll n; cin >> n;
    vector<ll> vec;
    vec.push_back(0);
    vec.push_back(1);
    vec.push_back(1);
    for(int i = 3; i <= n ; i++) vec.push_back(vec.back() + vec[vec.size() - 2]);
    cout << vec[n] << endl;
}

Chivas{
    int cass;
    each_cass(cass){
        solve();
    }
    Regal;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

# HDUOJ2084_数塔

# 🔗

http://acm.hdu.edu.cn/showproblem.php?pid=2084

# 💡

重在决策处理与遍历顺序
因为我们要收集最高点的最大值
只能通过下面的子节点给予贡献
所以从下向上，层层决策累加求得
dp[x][y] += MAX(dp[x + 1][y], dp[x + 1][y + 1]) 选取左右节点最大值

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'

#define CHIVAS_ int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
//#define map unordered_map

#define _int(a) int a; cin >> a
#define  _ll(a) ll a; cin >> a
#define _char(a) char a; cin >> a
#define _string(a) string a; cin >> a
#define _vectorInt(a, n) vector<int>a(n); cin >> a
#define _vectorLL(a, b) vector<ll>a(n); cin >> a

#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cass = inputInt(); cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
template<typename T>             vector<T>& operator--            (vector<T> &v){for (auto& i : v) --i;            return  v;}
template<typename T>             vector<T>& operator++            (vector<T> &v){for (auto& i : v) ++i;            return  v;}
template<typename T>             istream& operator>>(istream& is,  vector<T> &v){for (auto& i : v) is >> i;        return is;}
template<typename T>             ostream& operator<<(ostream& os,  vector<T>  v){for (auto& i : v) os << i << ' '; return os;}
inline int inputInt(){int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);}
inline void outInt(int X){if(X<0) {putchar('-'); X=~(X-1);}int s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline ll inputLL(){ll X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1); }
inline void outLL(ll X){if(X<0) {putchar('-'); X=~(X-1);}ll s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}


const int N = 110;
int dp[N][N];
int n;

CHIVAS_{
        int cass;
        EACH_CASE ( cass ) {
                n = inputInt();
                for ( int i = 1; i <= n; i ++ )
                        for ( int j = 1; j <= i; j ++ )
                                dp[i][j] = inputInt();
                for ( int i = n - 1; i >= 1; i -- )
                        for ( int j = 1; j <= i; j ++ )
                                dp[i][j] += MAX(dp[i + 1][j], dp[i + 1][j + 1]);
                outInt(dp[1][1]); puts("");
        }
        _REGAL;
};

# HDU2021多校(3)I_RiseInPrice

# 🔗

# 💡

首先映入眼帘是一个 $n\le 100$ ，结合 $T\le 10$ 这明显是想让我们 $n^3$ 到 $n^4$ 的复杂度，而题目只是想让跑一个普通的矩阵 $dp$ ，随便 $n^2$ 就够用了吧
写着写着发现不对劲，状态的最大结果无法通过单纯地 $\sum a$ 和 $\sum b$ 决定，有可能 $3,3$ 比 $2,5$ 到后面更大
思考如何利用再开一个 $100$ ，发现还有一个关键信息也是题目中提醒我们的，就是总路线长度为 $2n-2$ ，并且我们要明确我们麻烦的地方是 " $dp$ 获取不到最大值" ，于是我们可以用 $dp$ 获得 $100$ 个较大的值，然后转移用这些值进行转移即可
故我们依旧是按 $sum1\times sum2$ 定谁大谁小，每次转移提出来最大的 $100$ 个进行转移，最后算一下 $dp[n][n]$ 最大位置的 $sum1\times sum2$ 即可

# ✅

const int N = 105;
struct node {
    ll v1, v2;
    inline friend bool operator < (node a, node b) {
        return a.v1 * a.v2 > b.v1 * b.v2;
    }
};
vector<node> dp[N][N];
int n;
ll a[N][N], b[N][N];

inline void Solve () {
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++) for (int j = 1; j <= n; j ++) scanf("%lld", &a[i][j]);
    for (int i = 1; i <= n; i ++) for (int j = 1; j <= n; j ++) scanf("%lld", &b[i][j]);
    for (int i = 1; i <= n; i ++) for (int j = 1; j <= n; j ++) dp[i][j].clear();


    dp[1][1].push_back({a[1][1], b[1][1]});
    for (int i = 2; i <= n; i ++) {
        for (int k = 0; k < 50 && k < dp[i - 1][1].size(); k ++) {
            dp[i][1].push_back({dp[i - 1][1][k].v1 + a[i][1], dp[i - 1][1][k].v2 + b[i][1]});
        }
        sort(dp[i][1].begin(), dp[i][1].end());
    }
    for (int j = 2; j <= n; j ++) {
        for (int k = 0; k < 50 && k < dp[1][j - 1].size(); k ++) {
            dp[1][j].push_back({dp[1][j - 1][k].v1 + a[1][j], dp[1][j - 1][k].v2 + b[1][j]});
        }
        sort(dp[1][j].begin(), dp[1][j].end());
    }

    for (int i = 2; i <= n; i ++) {
        for (int j = 2; j <= n; j ++) {
            for (int k = 0; k < 50 && k < dp[i - 1][j].size(); k ++) {
                dp[i][j].push_back({dp[i - 1][j][k].v1 + a[i][j], dp[i - 1][j][k].v2 + b[i][j]});
            }
            for (int k = 0; k < 50 && k < dp[i][j - 1].size(); k ++) {
                dp[i][j].push_back({dp[i][j - 1][k].v1 + a[i][j], dp[i][j - 1][k].v2 + b[i][j]});
            }
            sort(dp[i][j].begin(), dp[i][j].end());
        }
    }

    printf("%lld\n", dp[n][n][0].v1 * dp[n][n][0].v2);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

# ICPC2020吉林站C_StringGame

# 🔗

# 💡

~~依稀记得好像做过类似的题来着~~
我们每次遇到一个字母 $\inline c$
在所给序列 $\inline c$ 出现的位置假设为 $\inline i$
因为当这个字母出现之后，比它小一位也就是 $\inline i-1$ 位多了一个渠道推向第 $\inline i$ 位，那么：
如果 $\inline i\neq1$ 那么 $\inline dp[i]+=dp[i-1]$
而当 $\inline i=1$ 时，我们只是做到让推的源头 $\inline +1$ 而已，那么：
如果 $\inline i=1$ 那么 $\inline dp[i]++$

# ✅

const int N = 1e3 + 10;
const int mod = 1e9 + 7;
ll dp[N];
int main () {
        ios::sync_with_stdio(false);
        string s1, s2;
        while ( cin >> s1 >> s2 ) {
                memset ( dp, 0, sizeof dp );
                for ( int i = 0; i < s1.size(); i ++ ) {
                        for ( int j = s2.size() - 1; j >= 0; j -- ) {
                                if ( s1[i] == s2[j] ) {
                                        if ( j ) dp[j] = (dp[j] + dp[j - 1]) % mod;
                                        else     dp[j] = (dp[j] + 1) % mod;
                                }
                        }
                }
                cout << dp[s2.size() - 1] << endl;
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# ICPC2021南京站J_Xingqiu'sJoke

# 🔗

# 💡

第二个样例 9 8 提供的已经很接近了
假设 $a<b$ , 设置 $d=b-a$ ，如果 $d=1$ ，那么步数即为 $a-1$
对于操作一二，我们不会让 $d$ 产生变化，但有可能让 $a$ 变成 $1$
由于操作三提供的效应是很明显的，那么我们可以让 $a,b$ 去上升或者下降到可除一个质数 $p$
由于 $a\equiv b(mod\;p)\Leftrightarrow d\equiv b-a\equiv0(mod\;p)$
也就是说这个 $p$ 一定是 $d$ 的质因数，而我们在除时也会让 $d$ 越来越靠近 $1$
所以对于 $f(a,d)$ 我们可以枚举 $d$ 的质因数 $g$ ，每一步让 $a$ 去选择

min(a-1,\{f(\left\lfloor\frac ag\right\rfloor,\frac dg)+\stackrel{a}{\underset{g}{\downarrow}}+1,f(\left\lceil\frac ag\right\rceil,\frac dg)+\stackrel{g}{\underset{a}{\uparrow}}+1\})

对于 $f(a,d)$ 我们可以采用记忆化搜索的方式
出口便是 $a=1$ 或者 $d=1$ 或者 $dp.count(\{a,d\})$

# ✅

const int N = 1e5 + 10;
vector<ll> prime;
int ntp[N];
 
inline void Sieve () {
        ntp[0] = ntp[1] = true;
        for ( int i = 2; i < N; i ++ ) {
                if ( !ntp[i] ) prime.push_back(i);
                for ( int j = 0; j < prime.size() && i * prime[j] < N; j ++ ) {
                        ntp[i * prime[j]] = true;
                        if ( i % prime[j] == 0 ) break;
                }
        }
}
 
vector<int> divid;
 
map<pair<int, int>, int> dp;
 
inline int DFS ( int a, int d ) {
        if ( a == 1 ) return 0;
        if ( d == 1 ) return a - 1;
        if ( dp.count({a, d}) ) return dp[{a, d}];
        
        int res = a - 1;
        for ( auto x : divid ) {
                if ( x > d ) break;
                if ( d % x ) continue;
                res = min({res, DFS(a / x, d / x) + a % x + 1, DFS(a / x + 1, d / x) + x - a % x + 1});
        }
        return dp[{a, d}] = res;
}
 
inline void Solve () {
        int a, b; scanf("%d%d", &a, &b);
        if ( b < a ) swap(a, b);
        int d = b - a;
        if ( a == 1 ) {
                puts("0");
                return;
        }
        divid.clear();
        dp.clear(); // T点2，本来记忆化就没事，数据毒瘤会存非常多然后还大部分无关每次都要查询半天  
        for ( int i = 0; i < prime.size() && prime[i] * prime[i] <= d; i ++ ) {
                if ( d % prime[i] == 0 ) divid.push_back(prime[i]); // T点1，只存一个
                while ( d % prime[i] == 0 ) 
                        d /= prime[i];
        }
        if ( d > 1 ) divid.push_back(d);
        printf("%d\n", DFS(a, b - a));
}
 
int main () {
        Sieve();
        int cass; scanf("%d", &cass); while ( cass -- ) {
                Solve ();
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

# NCD2019C_HasanAndHisLazyStudents

# 🔗

# 💡

求最长上升子序列的长度以及它的个数
可以看做是这道题 (opens new window)的简化版，因为这里是按下标看的
并不需要涉及一样的数列去重

在这个地方就省去很多处理的步骤
还是一个 $\inline dp1[i]$ 表示结尾是 $\inline i$ 的最长上升子序列长度，一个 $\inline dp2[i]$ 表示结尾是 $\inline i$ 的最长上升子序列的数量
$\inline 100$ 的数据量，那么我们求它的时候就是正常的前面的进行

在求 $\inline dp2[i]$ 时，我们一样枚举 $\inline i$ 前面的 $\inline j$ ，如果 $\inline a[j]<a[i]$ 并且 $\inline dp1[i]=dp1[j]+1$ ，就说明这个 $\inline dp[i]$ 有一部分方案是由 $\inline dp1[j]$ 转移过来的
那么我们汇聚一下方案数也就是 $\inline dp2[i]+=dp2[j]$ 就可以了（记得在 $\inline dp1[i]=1$ 的情况下说明 $\inline i$ 没有别的推过来，它自己是唯一一种方案，要设置为 $\inline 1$

# ✅

ll dp1[1005], dp2[1005];
ll a[1005];

inline void Solve () {
        memset(dp1, 0, sizeof dp1);
        memset(dp2, 0, sizeof dp2);
        ll n; cin >> n;
        ll res1 = 1, res2 = 1;

        for ( ll i = 1; i <= n; i ++ ) cin >> a[i];
        for ( ll i = 1; i <= n; i ++ ) {
                dp1[i] = 1;
                for ( ll j = 1; j < i; j ++ ) {
                        if ( a[j] < a[i] ) dp1[i] = max(dp1[j] + 1, dp1[i]);
                }        
        }
        for ( ll i = 1; i <= n; i ++ ) {
                if ( dp1[i] == 1 ) {
                        dp2[i] = 1;
                        continue;
                }
                for ( ll j = 0; j < i; j ++ ) {
                        if ( a[j] < a[i] && dp1[j] + 1 == dp1[i] ) {
                                dp2[i] += dp2[j];
                                dp2[i] %= mod;
                        }
                }
        }

        ll res = 0;
        ll longest = 0;
        for ( ll i = 1; i <= n; i ++ ) {
                longest = max(longest, dp1[i]);
        }
        for ( ll i = 1; i <= n; i ++ ) {
                if ( dp1[i] == longest ) res += dp2[i], res %= mod;
        }
        cout << longest << " " << res << endl;
}

int main () {
        ios::sync_with_stdio(false);
        ll cass; cin >> cass; while ( cass -- ) {
                Solve ();
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

# UVA10590_BoxesOfChocolatesAgain

# 🔗

https://vjudge.net/problem/UVA-10590

# 💡

本题是一道经典的DP题目
我们可以用dp[i][j] 表示在最大的数不超过 j 的前提下，形成了和为 i 的方案数目
那么构建出 dp[i][j] ，我们可以通过两种情况获得：
1.最后一个数不超过j-1，即dp[i][j - 1]
2.最后一个数等于j，即dp[i - j][j]
那么得到状态转移方程：dp[i][j] = dp[i][j - 1] + dp[i - j][j]
由于我们是以前面那一维实现的，所以构造出滚动数组剪掉后面一维从而压缩空间即可

PS：数据过大，使用高精或者java、python大数库（逃

# ✅

import java.math.BigInteger;
import java.util.*;

public class Main {
        public static void main(String[] args) {
                int N = 5005;
                Scanner input = new Scanner(System.in);
                BigInteger[] dp = new BigInteger[N];

                dp[0] = BigInteger.ONE;
                for ( int i = 1; i < N; i ++ ) dp[i] = BigInteger.ZERO;
                for ( int j = 1; j < N; j ++ ) {
                        for ( int i = j; i < N; i ++ ) dp[i] = dp[i].add(dp[i - j]);
                }

                while( input.hasNext() ) System.out.println(dp[input.nextInt()]);
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

计数DP 区间DP