Chivas-Regal

前缀-差分

#

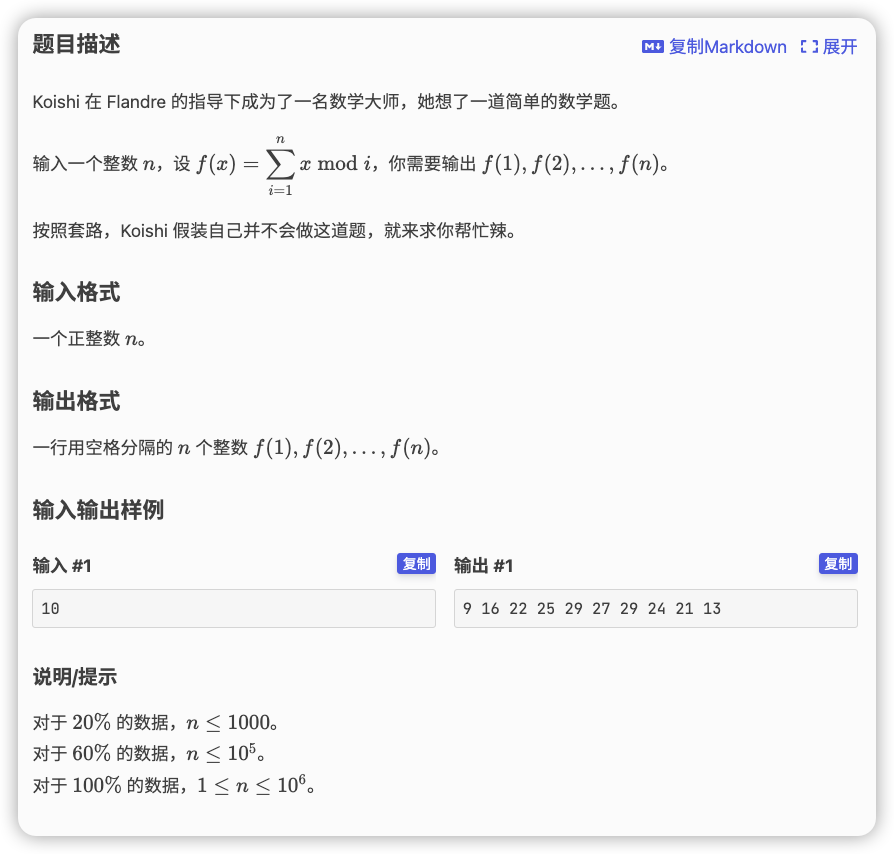
# 洛谷P3708_koishi的数学题

# 🔗

20221009152605

# 💡

for (int i = 2; i <= n; i ++) {
    int l = 1;
    for (int j = i; j <= n; j += i) {
        int r = j - 1;
        update(l, r, 1, 1, n, 1);
        update(j, j, -i + 1, 1, n, 1);
        l = j + 1;
    }
    if (l != n + 1) {
        update(l, n, 1, 1, n, 1);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
for (int i = 2; i <= n; i ++) {
    int l = 1;
    for (int j = i; j <= n; j += i) {
        int r = j - 1;
        update(l, r, 1, 1, n, 1);
        update(j, j, -i + 1, 1, n, 1);
        l = j + 1;
    }
    if (l != n + 1) {
        update(l, n, 1, 1, n, 1);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

看一个数 xx
对于 i∈[⌊x2⌋+1,x−1]i\in[\left\lfloor\frac x2\right\rfloor+1,x-1] 贡献为 x−ix-i
对于 i∈[⌊x3⌋+1,⌈x2⌉−1]i\in[\left\lfloor\frac x3\right\rfloor+1,\left\lceil\frac x2\right\rceil-1] 贡献为 x−2ix-2i
...
对于 i∈[⌊xa⌋+1,⌊xa−1⌋−1]i\in[\left\lfloor\frac xa\right\rfloor+1,\left\lfloor\frac x{a-1}\right\rfloor-1] 是 x−(a−1)ix-(a-1)i
这个还要去 n2n^2 枚举找，不太可行
那么看一个模 ii
对于 x∈[1,n]x\in[1,n] 的贡献分别是 1,2,...,i−1,0,1,2,...,i−1,...1,2,...,i-1,0,1,2,...,i-1,...
这就是好几段长度为 ii 的等差数列加啊，用线段树维护差分数组然后对于每段 [l,r][l,r] ，使 [l,r−1]+1,[r]−i+1[l,r-1]+1,[r]-i+1
好了线段树码上去 O(nlognlogn)O(nlognlogn) 6060 分 ，考虑怎么把这个 loglog 划掉，众所周知 O(1)O(1) 区间加减是直接用差分数组，但是这里怎么用呢
看一下 6060 分的线段树代码的更新部分

for (int i = 2; i <= n; i ++) {
    int l = 1;
    for (int j = i; j <= n; j += i) {
        int r = j - 1;
        update(l, r, 1, 1, n, 1);
        update(j, j, -i + 1, 1, n, 1);
        l = j + 1;
    }
    if (l != n + 1) {
        update(l, n, 1, 1, n, 1);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

啊这，好像大部分都是加 11 然后单点减每个 jj 的倍数点就好了啊
每一个位置加了 n−1n-1 次 11
然后枚举 ii 时的第 jj 个位置减去 ii 就好了
最后输出差分数组的前缀和
嗯 100100 分了

# ✅

ll dir[1000010];

int main () {
    int n; scanf("%d", &n);
    for (int i = 1; i <= n; i ++) dir[i] += n - 1;
    for (int i = 2; i <= n; i ++) {
        for (int j = i; j <= n; j += i) {
            dir[j] -= i;
        }
    }

    for (int i = 1; i <= n; i ++) {
        printf("%lld ", dir[i] += dir[i - 1]);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 洛谷T214799_夏摩山谷II

# 🔗

# 💡

本题在 T214551T214551 《夏摩山谷》 (opens new window) 中本身是一个推公式题，后来被 There,hello 大大 (opens new window) 发现了新的思考方式，我在此思考方式上进行深化拓展，便诞生了 HardversionHard\;version

我们先看一个二重传递

∑i=1n∑j=1ij=∑i=1n∑j=1i∑k=1j1\begin{aligned} &\sum\limits_{i=1}^n\sum\limits_{j=1}^ij\\=&\sum\limits_{i=1}^n\sum\limits_{j=1}^i\sum\limits_{k=1}^j1 \end{aligned}

将其化为了三重传递

我们发现在这里 jj 是 11 的第 jj 个前缀和， jj 是其上界
所以对于最内重，其值为 S1{}S_1\{\}
我们令 1=S01=S_0 ，则 S1j=∑k=1jS0kS_{1_j}=\sum\limits_{k=1}^jS_{0_k}

而对于第二重，它的值是 ...∑j=1iS1j...\sum\limits_{j=1}^iS_{1_j}
有了上面的基础，我们不难看出这是一个关于 S1{}S_1\{\} 的第 ii 个前缀和，ii 是上界
所以对于第二重，其值为 S2{}S_2\{\}
S2i=∑j=1iS1jS_{2_i}=\sum\limits_{j=1}^iS_{1_j}

对于第三重，同理，这是一个关于 S2{}S_2\{\} 的第 nn 个前缀和， nn 是上界

模型建立
我们思考一下什么时候会产生这种前缀和关系且第一重是 11 的
对于上述的前缀和公式 S[i][j]=s[i][j−1]+s[i−1][j−1]S[i][j]=s[i][j-1]+s[i-1][j-1]
可以想到这个东西是杨辉三角的转置矩阵的递推式

那么对于一个 kk 重，其上界为 nn 的宁静公式
可以变成一个 k+1k+1 重从 ∑ak+1=1ak1\sum\limits_{a_{k+1}=1}^{a_k}1 开始的式子

对于这样的式子，我们更是对 kk 进行了 +1+1 的延伸，而对于 ∑a1=1n\sum\limits_{a_1=1}^n 是又向外扩展了一层才是解
所以其值在杨辉三角的第 k+2k+2 列
因 nn 为每一个正整数都是成立且具备值的，所以应从第 k+2k+2 列的从上往下第一个 11 开始走 nn 个行，即为 k+2+n−1=k+n+1k+2+n-1=k+n+1 行

note

杨辉三角的第一行第一列都是从 00 开始

那么便有了答案：Ck+nk+1%modC_{k+n}^{k+1}\%mod

而 nn 和 kk 都很大，而模数很小，这是一个突破口，所以应用 LucasLucas 定理求组合数

# ✅

ll n, mod, k;

inline ll ksm ( ll a, ll b ) { ll res = 1; while ( b ) { if ( b & 1 ) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv ( ll x ) { return ksm(x, mod - 2); }

inline ll C(ll n, ll m) {
        ll up = 1, down = 1;
        for ( ll i = 0; i < m; i ++ ) {
                up = up * (n - i) % mod;
                down = down * (i + 1) % mod;
        }
        return up * inv(down) % mod;
}
inline ll Lucas ( ll n, ll m ) {
        if ( !m ) return 1ll;
        return C(n % mod, m % mod) * Lucas(n / mod, m / mod) % mod;
}

int main () {
        ios::sync_with_stdio(false);
        cin >> n >> mod >> k;
        cout << Lucas(n + k, k + 1) << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

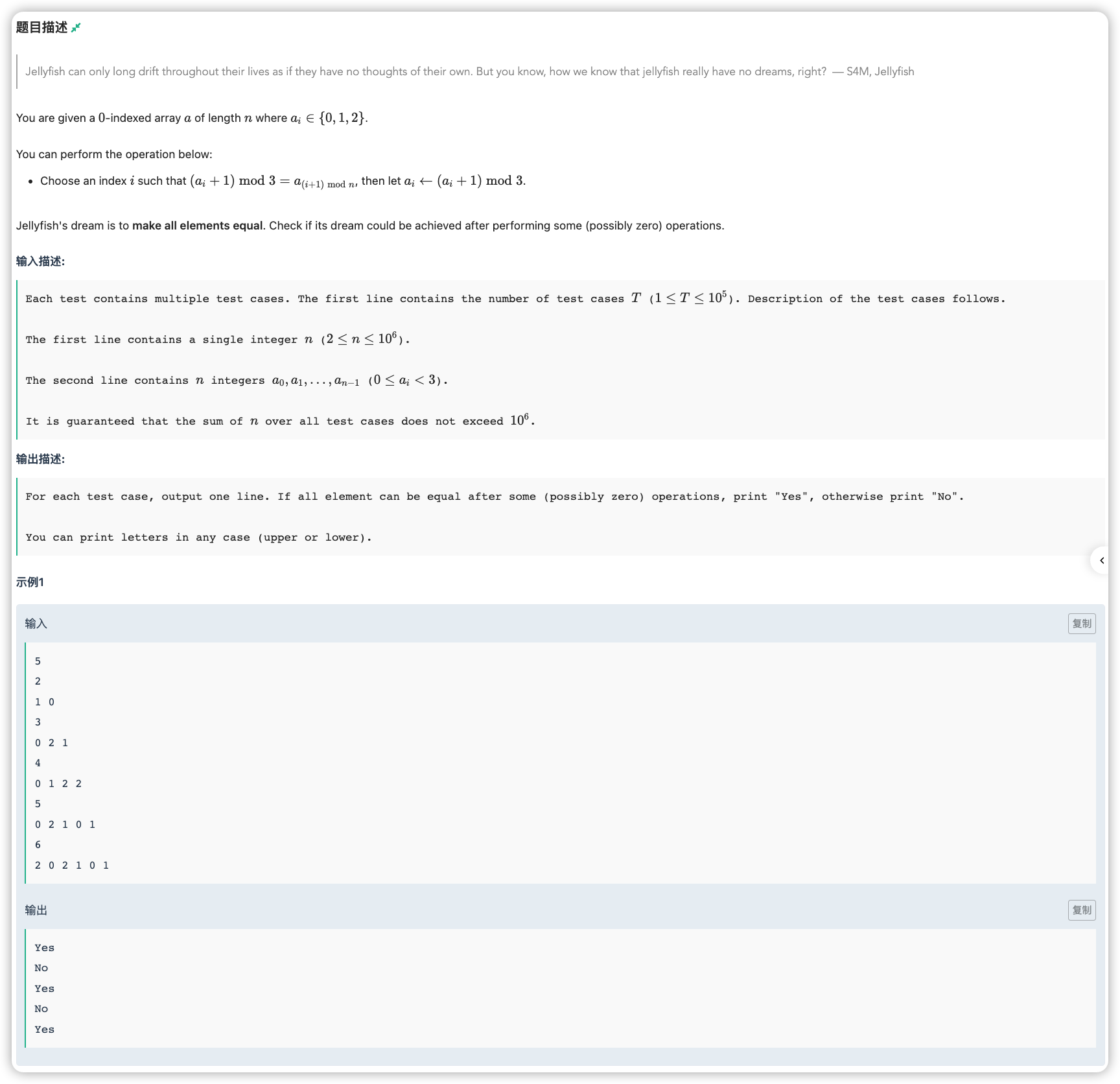
# 牛客2022多校（加赛）J_JellyfishAndItsDream

# 🔗

20220817214747

# 💡

环上修改，看看整体能不能修改到一样，这是一个差分的套路
修改到一样意味着差分数组为零，对于一次修改，它只能加一后等于下一个。
而修改不了的位置可以视作差分减值的垃圾箱，可以将前面任意位置的加值结尾为这个垃圾箱，那么只要保证加法不少于垃圾箱的个数即可，如果加法少于垃圾箱，则意味着垃圾箱喂不满，即为 NoNo
否则为 YesYes

# ✅

inline void Solve () {
    int n; cin >> n;
    vector<int> a(n); for (int &i : a) cin >> i;

    int add = 0, del = 0;
    for (int i = 0; i < n; i ++) {
        if (a[(i + 1) % n] == (a[i] + 1) % 3) add ++;
        if (a[(i + 1) % n] == (a[i] + 2) % 3) del ++;
    }
    if (add >= del) cout << "Yes\n";
    else cout << "No\n";
}
1
2
3
4
5
6
7
8
9
10
11
12

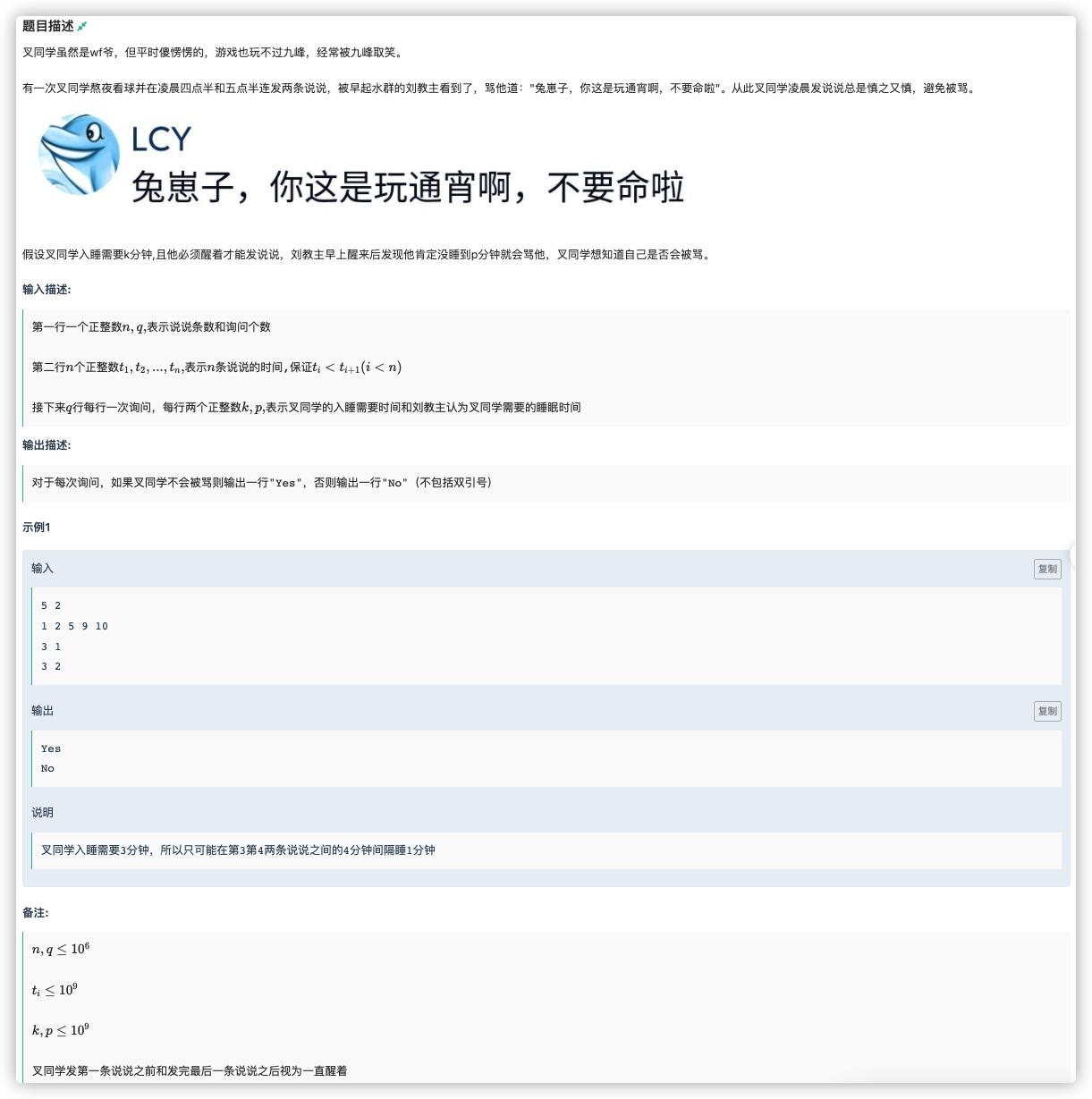
# 牛客2022寒假算法基础集训营5I_兔崽小孩

# 🔗

# 💡

抽象问题：
给出一个数列，抽出其中差值，每次询问 kk ，让每个差值减去 kk ，最小减到 00 ，问最后的剩余值是否大于等于 pp

可以知道比 kk 小的均是无贡献的
那么有了大小关系我们升序排序
计算出在减去 00 时的后缀和
然后每次询问用 upper_bound 求出有多少个差值 >k>k ，个数为 numnum，是从第 idid 个开始
那么剩余值便是 sum[id]−num×ksum[id]-num\times k

# ✅

vector<ll> t;
int n, Q;
ll sum[1000005];

int main () {

        read(n); read(Q);
        for ( int i = 0; i < n; i ++ ) {
                ll x; read(x);
                t.push_back(x);
        }
        vector<ll> vec; for ( int i = 1; i < n; i ++ ) vec.push_back(t[i] - t[i - 1]);
        sort ( vec.begin(), vec.end() );
        for ( int i = vec.size() - 1; i >= 0; i -- ) sum[i] = sum[i + 1] + vec[i];
        for ( int i = 0; i < Q; i ++ ) { 
                ll k, p; read(k); read(p); 
                ll id = upper_bound(vec.begin(), vec.end(), k) - vec.begin(); 
                ll num = (int)vec.size() - id;
                ll rel = sum[id] - num * k; 
                if ( rel >= p ) puts("Yes");
                else puts("No");
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# ABC233F_ParenthesisChecking

# 🔗

# 💡

括号匹配的本质是两两相消。
对于每一个位置的点重定义一下它的权值：'(' = 1，')' = -1
在累加过程中，可以和相消为，所以计算总贡献

那么可以记录一个权值前缀和
那么对于每一个区间，如果其中的最小值小于 的前缀和的话，那么就一定是不匹配的（最小值的位置前右括号太多了
当然如果本身 的前缀和不等于 的前缀和就也是不匹配的
这里的最小值可以使用线段树进行维护，修改便直接在线段树上修改如果本身是'('，修改后区间-2，否则+2

# ✅

#include <iostream>
#include <vector>
#include <algorithm>
#include <set>
#include <map>
#include <deque>

using namespace std;

#define ll long long

const int N = 2e5 + 10;
char s[N];
int a[N], n, q;

namespace SegmentTree {
        struct Sgtr { int val, lazy; } sgtr[N << 2];
        inline void push_Up ( int rt ) {
                sgtr[rt].val = min ( sgtr[rt << 1].val, sgtr[rt << 1 | 1].val );
        }
        inline void push_Down ( int l, int r, int rt ) {
                if ( !sgtr[rt].lazy ) return;
                sgtr[rt << 1].val += sgtr[rt].lazy;
                sgtr[rt << 1 | 1].val += sgtr[rt].lazy;
                sgtr[rt << 1].lazy += sgtr[rt].lazy;
                sgtr[rt << 1 | 1].lazy += sgtr[rt].lazy;
                sgtr[rt].lazy = 0;
        }
        inline void Build ( int l, int r, int rt ) {
                if ( l == r ) { sgtr[rt].val = a[l]; return; }
                int mid = (l + r) >> 1;
                Build ( l, mid, rt << 1 );
                Build ( mid + 1, r, rt << 1 | 1 );
                push_Up ( rt ); 
        }
        inline void Update ( int a, int b, int c, int l, int r, int rt ) {
                if ( a <= l && r <= b ) { sgtr[rt].lazy += c, sgtr[rt].val += c; return; }
                if ( a > r || b < l ) return;
                int mid = (l + r) >> 1;
                push_Down ( l, r, rt );
                Update ( a, b, c, l, mid, rt << 1 );
                Update ( a, b, c, mid + 1, r, rt << 1 | 1 );
                push_Up ( rt );
        }
        inline int Query ( int a, int b, int l, int r, int rt ) {
                if ( a <= l && r <= b ) return sgtr[rt].val;
                if ( a > r || b < l )   return N;
                int mid = (l + r) >> 1;
                push_Down ( l, r, rt );
                return min ( Query ( a, b, l, mid, rt << 1 ), Query ( a, b, mid + 1, r, rt << 1 | 1) ); 
        }
} using namespace SegmentTree;

int main () {
        ios::sync_with_stdio(false);
        cin >> n >> q >> (s + 1);
        for ( int i = 1; i <= n; i ++ ) 
                if ( s[i] == '(' ) a[i] = a[i - 1] + 1;
                else               a[i] = a[i - 1] - 1;
        Build ( 1, n, 1 );
        while ( q -- ) {
                int op, l, r; cin >> op >> l >> r;
                if ( op == 1 ) {
                        if ( s[l] == s[r] ) continue;
                        if ( s[l] == '(' ) Update ( l, r - 1, -2, 1, n, 1 );
                        else               Update ( l, r - 1,  2, 1, n, 1 );
                        swap ( s[l], s[r] );
                } else {
                        int L = l == 1 ? 0 : Query ( l - 1, l - 1, 1, n, 1 ), R = Query ( r, r, 1, n, 1 );
                        if ( L != R ) { cout << "No" << endl; continue; }
                        if ( Query ( l, r, 1, n, 1 ) < L ) { cout << "No" << endl; continue; }
                        cout << "Yes" << endl;
                }
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

# AcWing3494_最大的和

# 🔗

# 💡

我们想获取区间内选了之后的sum变化，即选取能让答案增加最多的区间
因此我们就需要两个数值来对比

可以使用两个前缀和
一个是只记录选了1的数的前缀和，一个是记录全选的前缀和
两个前缀和在k的区间内的差值，就是这k个数从只选1到全选之后所能做出的贡献
记录贡献最大值，然后加上第一个前缀和[n]

# ✅

const int N = 1e5 + 10;

ll n, k;
ll a[N], b[N], sum1[N], sum2[N];
ll res;

int main(){
    read(n); read(k);
    for(int i = 1; i <= n; i ++) read(a[i]);
    for(int i = 1; i <= n; i ++) read(b[i]), 
    	sum1[i] = sum1[i - 1] + a[i] * b[i], 
    	sum2[i] = sum2[i - 1] + a[i];

    for(int i = k; i <= n; i ++) 
    	res = MAX(res, (sum2[i] - sum2[i - k]) - (sum1[i] - sum1[i - k]));
    res += sum1[n];
    
    write(res);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# ABC250E_PrefixEquality

# 🔗

# 💡

由于查询的时候都是前缀，那么我们肯定希望 aa 中的每一个数在 bb 中出现的越早越好
那么就存一个对于每一个 ii ， aia_i 在 bb 中出现的最小下标
对于一次查询 X,YX,Y
我们只要保证在 XX 以前的 ii 的 aia_i 出现的最小下标均小于 YY 即可
那么我们现在只需要知道对于每一个 aa 的前缀，最后出现的最小下标在哪，这个前缀设置为 mxamxa
这样对于上面的问题转换就是 mxa[X]≤Ymxa[X]\le Y 即可
对于 bb 同理

# ✅

const int N = 2e5 + 10;
int a[N], b[N];
int n;
int q;
 
map<int, int> ainb, bina;
int mxa[N], mxb[N];
 
int main () {
        scanf("%d", &n);
        for (int i = 1; i <= n; i ++) {
                scanf("%d", &a[i]);
                if (!bina.count(a[i])) bina[a[i]] = i;
        }
        for (int i = 1; i <= n; i ++) {
                scanf("%d", &b[i]);
                if (!ainb.count(b[i])) ainb[b[i]] = i;
        }
 
        for (int i = 1; i <= n; i ++) {
                if (i == 1) {
                        mxa[i] = ainb.count(a[i]) ? ainb[a[i]] : 0x3f3f3f3f;
                        mxb[i] = bina.count(b[i]) ? bina[b[i]] : 0x3f3f3f3f;
                } else {
                        mxa[i] = max(mxa[i - 1], ainb.count(a[i]) ? ainb[a[i]] : 0x3f3f3f3f);
                        mxb[i] = max(mxb[i - 1], bina.count(b[i]) ? bina[b[i]] : 0x3f3f3f3f);
                }
        }
 
        scanf("%d", &q);
        while (q --) {
                int x, y; scanf("%d%d", &x, &y);
                if (mxa[x] > y || mxb[y] > x) puts("No");
                else puts("Yes");
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

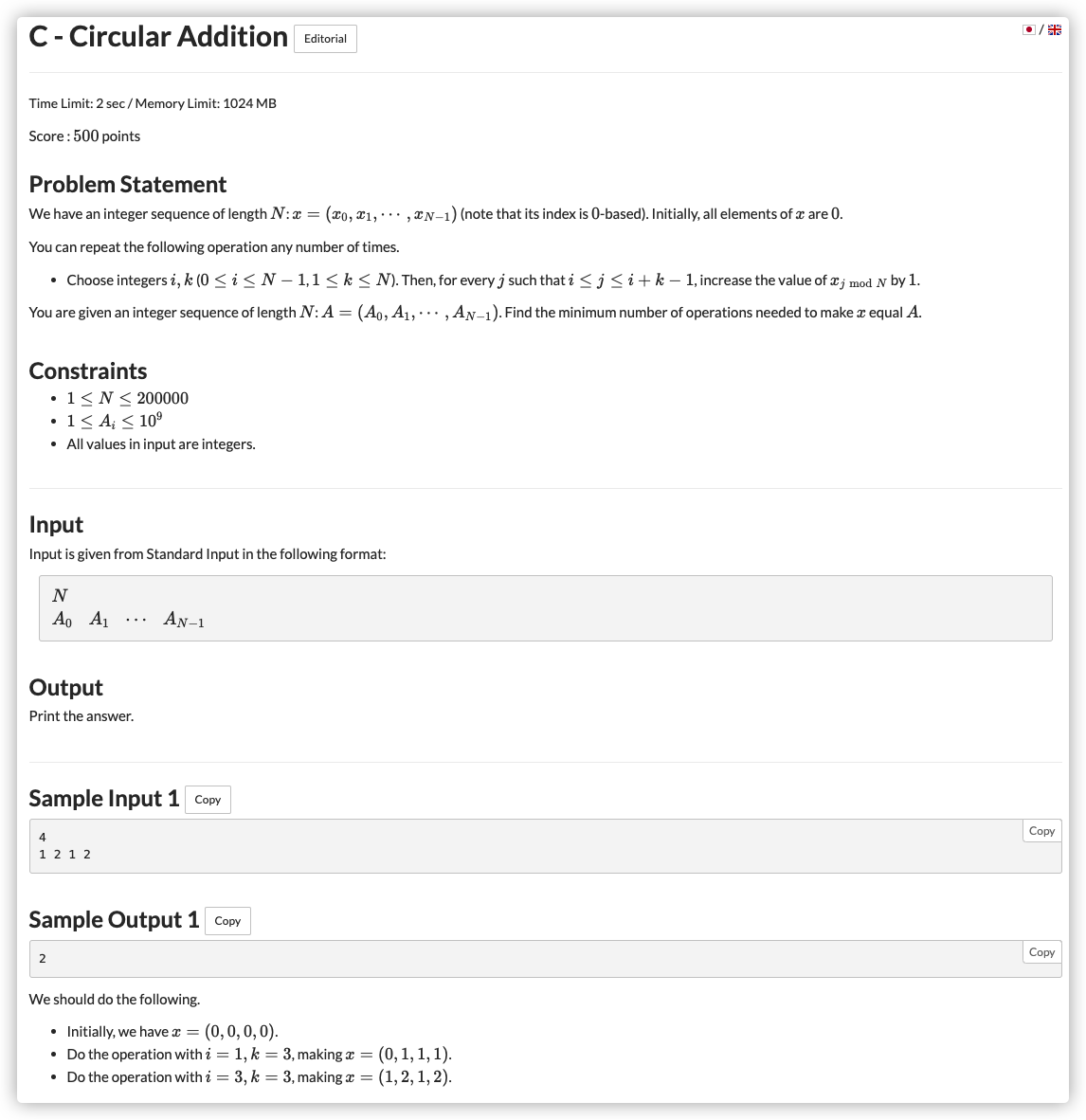
# ARC136C_CircularAddition

# 🔗

20220303012838

# 💡

这种区间加到目标数组经典问题，作为 [a][a] 差分出来数组 [b][b] 来看，每个数上升都可选择一个位置下降
设全 00 数组为 [c][c]
在本问题中由于前后相连，所以差分数组中 ∑[b>0]=−∑[b<0]\sum[b>0]=-\sum[b<0]
利用原式只算 ∑[b>0]\sum[b>0] 即可将所有的 [c][c] 提升至与 [a][a] 坡度相同

但是由于数值可能偏高，即坡度上去但是整体不够，这就考虑最大数值即可，这种问题会出现在 max[a]>∑[b>0]max[a]>\sum[b>0] ，易证此时 min[a]>0min[a]>0 ，那么先让整体减到 max[a]=∑[b>0]max[a]=\sum[b>0] 即可
结果即 max(max[a],∑[b>0])max(max[a],\sum[b>0])

数值不可能出现低于提升后的 [c][c] 的情况，因为我们提升坡度没有必要整体上升

# ✅

const int N = 2e5 + 10;
int n;
ll a[N];

int main () {
	ios::sync_with_stdio(false);
	cin >> n;
	for ( int i = 0; i < n; i ++ ) cin >> a[i];

	ll res = 0;
	for ( int i = 0; i < n; i ++ ) {
		res += max(a[(i + 1) % n] - a[i], 0ll);
	}
	cout << max(res, *max_element(a, a + n)) << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

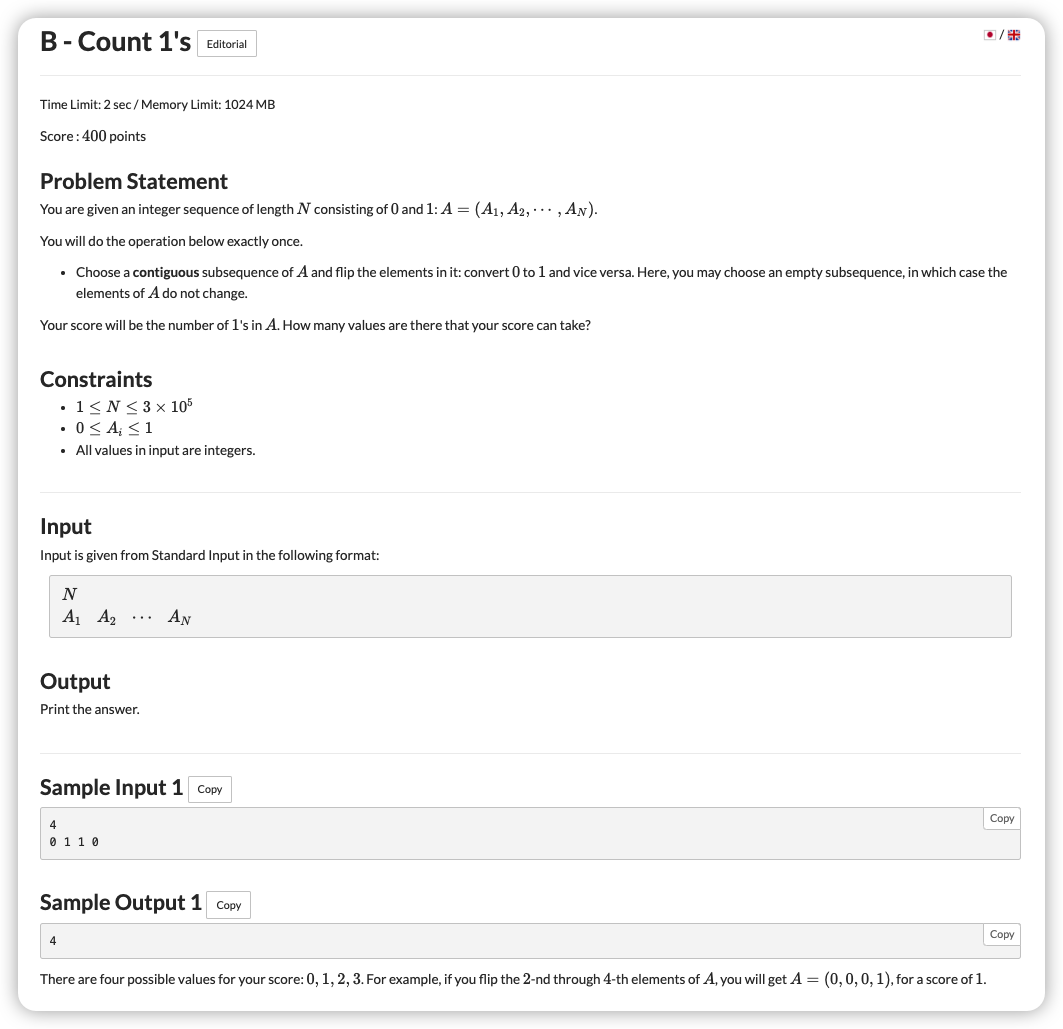
# ARC137B_Count1's

# 🔗

20220320184422

# 💡

考虑到 11 反转会让总和 −1-1 ，00 则会 +1+1
那么我们要得到总和可以形成的区间即可
对 aia_i 重新赋值后，我们统计最大子段和即为可以上升的量，最小子段和即为可以下降的量
那么答案所在的区间即为 [sum−minsum,sum+maxsum][sum-min_sum,sum+max_sum]
用前缀和统计一下 minsum,maxsummin_sum,max_sum 即可

# ✅

# include "bits/stdc++.h"

using namespace std;
using ll = long long;

inline ll gcd ( ll a, ll b ) { return b ? gcd(b, a % b) : a; }

int main () {
        cin.tie(0)->sync_with_stdio(0);
        cin.exceptions(cin.failbit);

        int num = 0;

        int n; cin >> n;
        vector<int> a(n); for ( auto &i : a ) cin >> i;
        vector<int> sum(n + 1);
        for ( int i = 1; i <= n; i ++ ) {
                sum[i] = sum[i - 1] + (a[i - 1] == 0 ? 1 : -1);
        }

        int mxsum = sum[0];
        int mnres = 0x3f3f3f3f;
        for ( int i = 1; i <= n; i ++ ) {
                mxsum = max(mxsum, sum[i]);
                mnres = min(mnres, sum[i] - mxsum);
        }
        int mnsum = sum[0];
        int mxres = 0;
        for ( int i = 1; i <= n; i ++ ) {
                mnsum = min(mnsum, sum[i]);
                mxres = max(mxres, sum[i] - mnsum);
        }

        cout << mxres - mnres + 1 << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

# CodeForces1629C_MeximumArray

# 🔗

# 💡

要理解字典序在这一道题的意义
即如果后面有能让它 MexMex 上升的数字，它都要坚持往后走
所以我们设置一个 wana 来表示我们想要什么数字

如果后面的东西要去一个个遍历来 check 的话，必然是一个 O(n2)O(n^2) 复杂度的代码，显然是过不去的

那么我们可以用后缀的思想，设置一个 map: mp 来表示后面对应的数字有多少个
这个可以先存一边预处理，然后在遍历的时候一个个删掉就行了

wana 开始设置为 -1 ，如果后面有 wana+1 即 mp[wana + 1] != 0 ，那么我们就继续往后走
但是要考虑到的是，这个数组不一定是严格升序的，也就是说它有可能在遍历的途中凑到的数，可以在走到 wana+1 的过程中让最后的 wana 进一步提升
这个我们就可以设立一个遍历中的 map: cur 来表示当前过程内每一个数字都走过了多少次

在找到 wana+1 之后，我们去检查 cur 中有没有下一个 wana+1 来对它进一步提升，来获取我们当前真正想要的 wana+1 是多少，然后继续判断和走就行了

如果后面没有 wana+1 的话，我们就要塞入答案并且对 wana 重新初始化与 cur 的清空

时间复杂度: O(2n)O(2n)

# ✅

int a[200005];
 
inline void Solve () {
        int n; cin >> n;
        map<int, int> mp;
        for ( int i = 0; i < n; i ++ ) cin >> a[i], mp[a[i]] ++;
        vector<int> b;
        int wana = -1;
        map<int, int> cur;
        for ( int i = 0; i < n; i ++ ) {
                mp[a[i]] --;
                cur[a[i]] ++;
                if ( a[i] == wana + 1 ) {
                        while ( cur[wana + 1] ) wana ++;
                }
 
                if ( mp[wana + 1] == 0 ) {
                        b.push_back(wana + 1);
                        wana = -1;
                        cur.clear();
                }
        }
        cout << b.size() << endl;
        for ( int i = 0; i < b.size(); i ++ ) cout << b[i] << " ";
        cout << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

# CodeForces608B_HammingDistanceSum

# 🔗

# 💡

求一位一位匹配下的不相似度和
那么考虑一下可以计算一下a串每个位置的元素对这个匹配度的贡献值
锁定一下这个位置都能和b串的哪个区间的字符匹配
计算可得是[i,b.size()-a.size()+i]的区间匹配

如果当前a[i]是'1'，那么我们统计一下这个区间内的'0'的个数
如果当前a[i]是'0'，那么我们统计一下这个区间内的'1'的个数

预处理一下前缀和，然后对于枚举每个b[i]求一下对应的区间和累加即可

# ✅

#include <iostream>
#define ll long long

using namespace std;

const int N = 2e5 + 10;
ll sum[2][N], res;
// sum[i][j]表示j以前i出现的个数

int main () {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif
        string a, b; cin >> a >> b;
        a = "0" + a,   b = "0" + b;

        for ( int i = 1; i < b.size(); i ++ ) 
                sum[1][i] = sum[1][i - 1] + (b[i] == '1'),
                sum[0][i] = sum[0][i - 1] + (b[i] == '0');

        for ( int i = 1; i <= a.size(); i ++ ) {
                if ( a[i] == '1' ) res = res + sum[0][b.size() - a.size() + i] - sum[0][i - 1];
                else               res = res + sum[1][b.size() - a.size() + i] - sum[1][i - 1];
        }
        cout << res << endl;
        return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# CodeForces611C_NewYearAndDomino

# 🔗

# 💡

因为行和列地位一样，接下来说行的性质也就是列的性质

对于每个区间[l,r]我们查询的时候对于[l,l+1]和[l+1,l]的摆放方式其实是一样的，所以我们可以默认这个牌向左（上）摆放
而摆放方式只有两种：左和上
那么我们可以做两套前缀和
sumrow[i][j]表示第i行的前j个格子可以横着放多少个牌
sumcol[i][j]表示第j列第前i个格子可以竖着放多少个牌
那么对于初始化的时候，如果当前格子和上一个格子有一个是"#"那么都不能累加，因为都没法放

然后查询的时候，直接查sum[][r]-sum[][l]或sum[r][]-sum[l][]即可
因为我们不需要第l个，它没法贡献
每一行和每一列都遍历一次累加计算一下

# ✅

#include <iostream>
#include <algorithm>
#include <map>
#include <cmath>
#include <vector>
#include <list>
using namespace std;
#define ll long long
#define eps 1e-12

const ll N = 510;
ll sumcol[N][N], sumrow[N][N];

int main () {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif
        ll n, m; cin >> n >> m;
        string Map[N];
        for ( ll i = 0; i < n; i ++ ) cin >> Map[i];
        for ( ll i = 0; i < n; i ++ ) {
                for ( ll j = 1; j < m; j ++ ) {
                        if ( Map[i][j - 1] == '.' && Map[i][j] == '.' ) sumrow[i][j] = sumrow[i][j - 1] +  1;
                        else sumrow[i][j] = sumrow[i][j - 1];  
                }
        }
        for ( ll j = 0; j < m; j ++ ) {
                for ( ll i = 1; i < n; i ++ ) {
                        if ( Map[i - 1][j] == '.' && Map[i][j] == '.' ) sumcol[i][j] = sumcol[i - 1][j] +  1;
                        else sumcol[i][j] = sumcol[i - 1][j];  
                }
        }
        ll q; cin >> q;
        while ( q -- ) {
                ll res =  0;
                ll x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
                x1 --, y1 --, x2 --, y2 --;
                for ( ll i = x1; i <= x2; i ++ ) res += sumrow[i][y2] - sumrow[i][y1];
                for ( ll i = y1; i <= y2; i ++ ) res += sumcol[x2][i] - sumcol[x1][i];
                cout << res << endl;
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

# CodeForces612D_TheUnionOfK-Segments

# 🔗

# 💡

这道题可以看作一个个[l,r]铺布，看最好多少
能很快想到可以用数组去模拟高度
范围这么大就告辞
那么就可以使用差分数组的思想：只改两个点打到区间修改的目的
由于全放在一个完整图的数组里面我们遍历的时候不好遍历，所以数组内只放置l和r的位置

对l和r都存在的数组进行升序排序，并设一个记录高度的值 对于一个l，如果在这个位置+1之后是k，说明是一个满足题意的区间的开始，塞入答案
对于一个r，如果在这个位置-1之前是k，说明是一个满足题意的区间的结束，塞入答案
但要考虑两相邻区间贴着的情况，也就是同一个点存在一个l也存在一个r，那么此时我们可以先去使用l进行高度+1再用r进行高度-1，这样就安全了

输出的时候一次输出两个就行了

# ✅

#include <iostream>
#include <algorithm>
#include <map>
#include <cmath>
#include <vector>
#include <cstring>
#include <list>
using namespace std;
#define ll long long
const ll mod = 998244353;
const double PI = acos(-1.0);
const double eps = 1e-9;

int main () {
        ios::sync_with_stdio(false);
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif
        int k, n; cin >> n >> k;
        vector<pair<int, int> > vec;
        for ( int i = 0; i < n; i ++ ) {
                int x, y; cin >> x >> y;
                vec.push_back({x, 1});
                vec.push_back({y, -1});
        }
        sort ( vec.begin(), vec.end(), [] ( pair<int, int> a, pair<int, int> b) {
                if ( a.first != b.first ) return a.first < b.first;
                return a.second > b.second;
        });

        vector<int> res;
        int lvl = 0; // 高度
        for ( int i = 0; i < vec.size(); i ++ ) {
                if ( vec[i].second == 1 ) {
                        lvl ++;
                        if ( lvl == k ) res.push_back(vec[i].first);
                } else {
                        if ( lvl == k ) res.push_back(vec[i].first);
                        lvl --;
                }
        }
        cout << res.size() / 2 << endl;
        for ( int i = 0; i < res.size(); i += 2 ) {
                cout << res[i] << " " << res[i + 1] << endl;
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

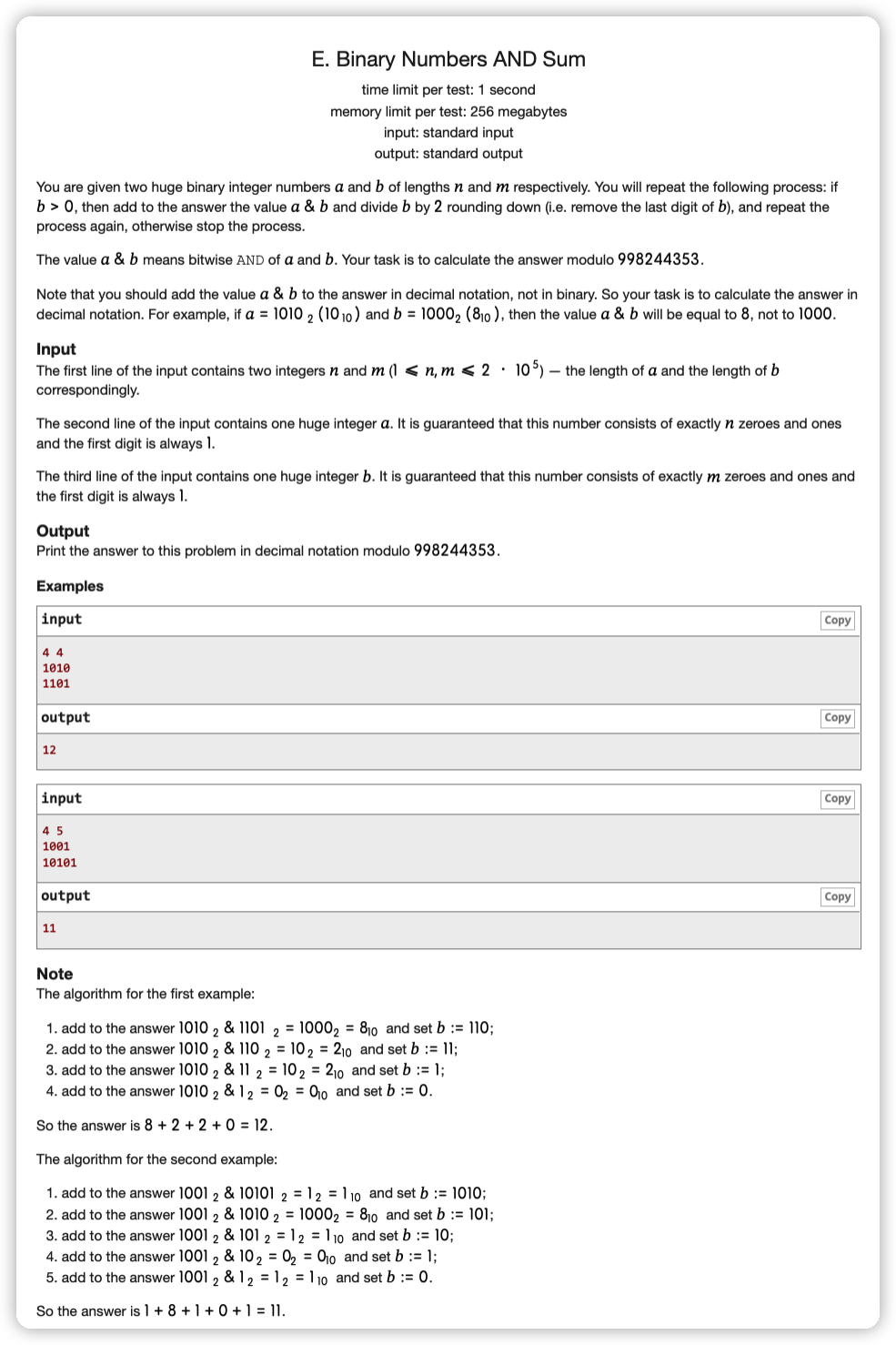
# CodeForces1066E_BinaryNumbersANDSum

# 🔗

20220707170624

# 💡

由于 bb 是不断往后移动的，并且对于 bb 的每一个 11 ，碰到 aa 的 11 时会产生贡献，那么就考虑位 11 上的贡献和
让 abab 位对应，先翻转一下
对于 bb 的每一个 11 的位置 ii ，左移过程中碰到的 11 一定都在 ii 前面，设 ii 前 aa 的 11 位为 jj ，那么产生的贡献为 2i2^i
这是一个前缀和的问题
就预处理出来 aa 每一位的前缀和，然后扫描 bb ，在遇到 11 时对其累加即可

# ✅

const int N = 2e5 + 10;
const int mod = 998244353;
int n, m;
ll pre[N];
string a, b;
 
int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);
 
        cin >> n >> m;
        cin >> a >> b;
 
        reverse(a.begin(), a.end());
        reverse(b.begin(), b.end());
        ll pw2 = 2;
        for (int i = 0; i < n; i ++) {
                if (i == 0) {
                        pre[i] = a[i] == '1';
                        continue;
                }
                if (a[i] == '1') {
                        pre[i] = (pre[i - 1] + pw2) % mod;
                } else {
                        pre[i] = pre[i - 1];
                }
                pw2 = pw2 * 2 % mod;
        }
        for (int i = n; i <= m; i ++) pre[i] = pre[i - 1];
        ll res = 0;
        for (int i = 0; i < m; i ++) {
                if (b[i] == '1') res += pre[i], res %= mod;
        }
        cout << res << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

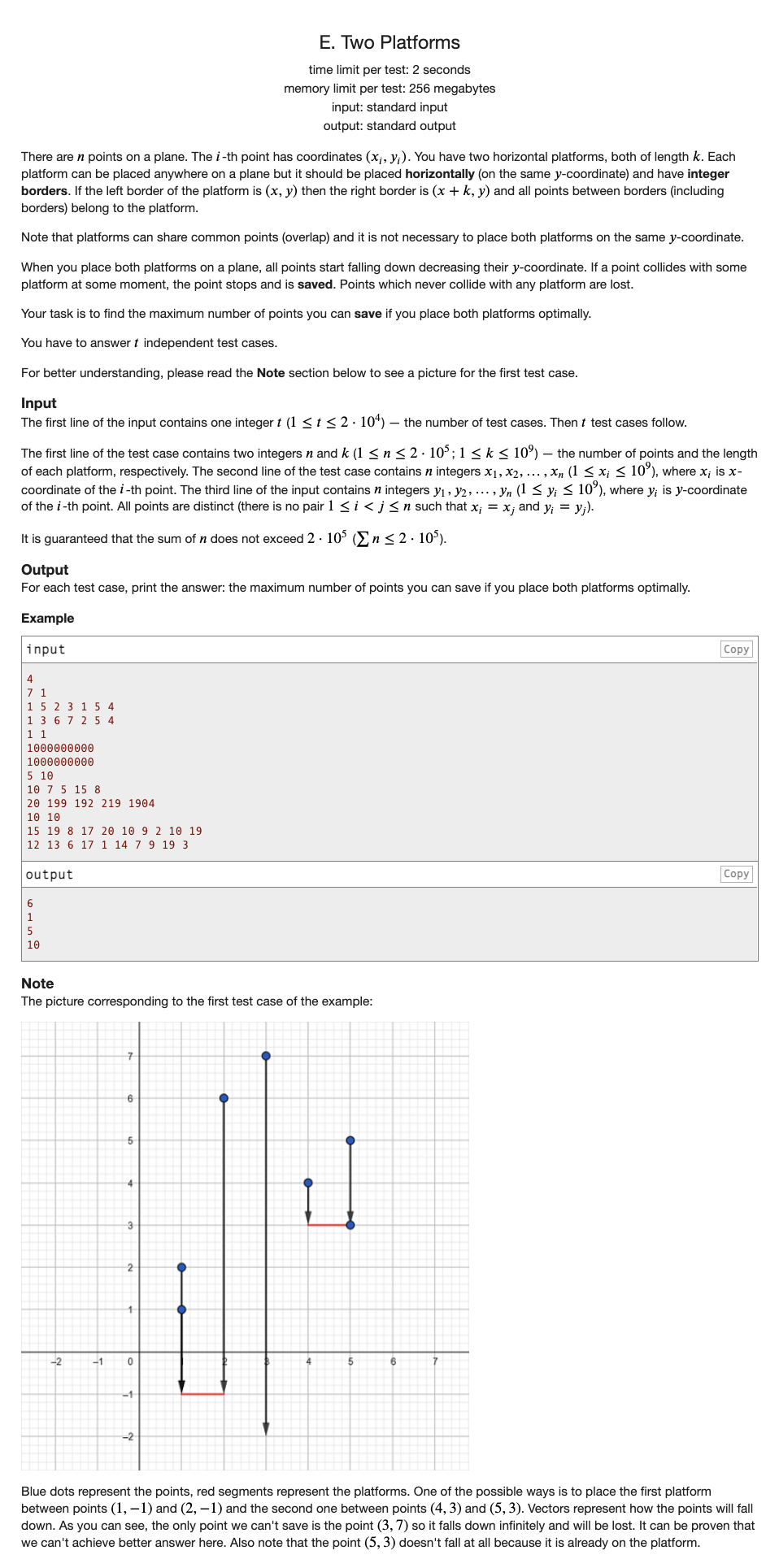
# CodeForces1409E_TwoPlatforms

# 🔗

# 💡

首先分析这是两块板子，必然是一前一后
那么我们可以设置一个前缀最大覆盖，一个后缀最大覆盖
每次对当前的球二分出最多能覆盖多少个点，并将当前的前缀或者后缀赋值为max(之前的覆盖最大值，这一次点覆盖最大值)
然后枚举断点，扫一遍维护一下max(res, pre[i] + nxt[i + 1])

# ✅

#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
#define ll long long
 
using namespace std;

const int N = 2e5 + 10;
ll n, k;
ll a[N];
ll pre[N], nxt[N]; // 前缀挡球最大个数，后缀挡球最大个数  
 
int main () {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif
        ll cass; scanf("%lld", &cass); while ( cass -- ) {
                scanf("%lld%lld", &n, &k);
                a[0] = a[n + 1] = 1e18;
                pre[0] = nxt[n + 1] = 0;

                for ( int i = 1; i <= n; i ++ ) scanf("%lld", &a[i]);
                for ( int i = 1, x; i <= n; i ++ ) scanf("%d", &x); // 高度没啥用
                sort ( a + 1, a + n + 1 );

                for ( int i = 1; i <= n; i ++ ) 
                        pre[i] = max ( pre[i - 1], (ll)i - (lower_bound(a + 1, a + i + 1, a[i] - k) - a) + 1); // 向前二分
                for ( int i = n; i >= 1; i -- ) 
                        nxt[i] = max ( nxt[i + 1], ((ll)(upper_bound(a + i, a + n + 1, a[i] + k) - a) - 1) - i + 1); // 向后二分
                ll res = 0;
                for ( int i = 0; i <= n; i ++ ) res = max ( res, pre[i] + nxt[i + 1] );
                printf("%lld\n", res);
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

# CodeForces1634F_FibonacciAdditions

# 🔗

20220420202813

# 💡

让两数相同也就是差为 00 ，那么令 ci=ai−bic_i=a_i-b_i

只要让所有的 cic_i 都满足 ci=0c_i=0 即可
区间加可以联想到线段树 O(logn)O(logn) 或者差分数值的 O(1)O(1) 的修改方式
考虑如果不是区间加 fibonaccifibonacci ，而是区间加一个固定的数，那么只要让 cic_i 的差分数组都为 00 就行

朴素差分下 di=ci−ci−1d_i=c_i-c_{i-1}
而由于这个区间加的是 fibonaccifibonacci 如果还按朴素的差分了话，我们每一个位置都要修改（那恭喜你白差分了！）
所以要考虑一种更为方便的差分形式
关注一波 fibonaccifibonacci 的公式：fiboi=fiboi−1+fiboi−2fibo_i=fibo_{i-1}+fibo_{i-2}
需要一种方式，在区间修改后，区间内部的 dd 是不变的
那么让 di=ci−ci−1−ci−2d_i=c_i-c_{i-1}-c_{i-2}

考虑这样的差分下，如何去区间修改
先看令 aa 数组修改区间 [l,r][l,r]
发现 clc_l 依旧是 +1+1 这样就让 dl+1d_l+1 即可
由于 cr−1+fibor−l,cr+fibor−l+1c_{r-1}+fibo_{r-l},\;c_{r}+fibo_{r-l+1}
则 dr+1−fibor−l−fibor−l+1=dr+1−fibor−l+2d_{r+1}-fibo_{r-l}-fibo_{r-l+1}=d_{r+1}-fibo_{r-l+2}
则 dr+2−fibor−l+1d_{r+2}-fibo_{r-l+1}
这样修改即可
而对 bb 数组的修改就反过来即可

一边修改一边统计修改后对 00 个数的贡献
每次当 00 的个数为 nn 时即 Yes
否则是 No

# ✅

int main () {
        std::ios::sync_with_stdio(false);
        std::cin.tie(nullptr);

        int n, q, mod; std::cin >> n >> q >> mod;

        std::vector<int> fibo(n + 10, 0);
        fibo[1] = fibo[2] = 1;
        for (int i = 3; i <= n; i ++) fibo[i] = (1ll * fibo[i - 2] + fibo[i - 1]) % mod;

        std::vector<int> a(n), b(n), c(n), d(n);
        int num_zero = 0;

        std::function <void(int, int)> Update = [&](int i, int val) {
                num_zero -= d[i] == 0;
                d[i] = (1ll * d[i] + val + mod) % mod;
                num_zero += d[i] == 0;
        };

        for (int &i : a) std::cin >> i, i %= mod;
        for (int &i : b) std::cin >> i, i %= mod;
        for (int i = 0; i < n; i ++) c[i] = (1ll * a[i] - b[i] + mod) % mod;
        for (int i = 0; i < n; i ++) {
                if (i == 0) d[i] = c[i];
                else if (i == 1) d[i] = (1ll * c[i] - c[i - 1] + mod) % mod;
                else d[i] = (1ll * c[i] - c[i - 1] - c[i - 2] + 2 * mod) % mod;
        }

        for (int i = 0; i < n; i ++) num_zero += d[i] == 0;

        for (int i = 0; i < q; i ++) {
                char op; std::cin >> op;
                int l, r; std::cin >> l >> r;
                l --, r --;
                
                if (op == 'A') {
                        Update(l, fibo[1]);
                        if (r + 1 < n) Update(r + 1, -fibo[r - l + 2]);
                        if (r + 2 < n) Update(r + 2, -fibo[r - l + 1]);
                } else {
                        Update(l, -fibo[1]);
                        if (r + 1 < n) Update(r + 1, fibo[r - l + 2]);
                        if (r + 2 < n) Update(r + 2, fibo[r - l + 1]);
                }

                if (num_zero == n) std::cout << "Yes\n";
                else std::cout << "No\n";
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

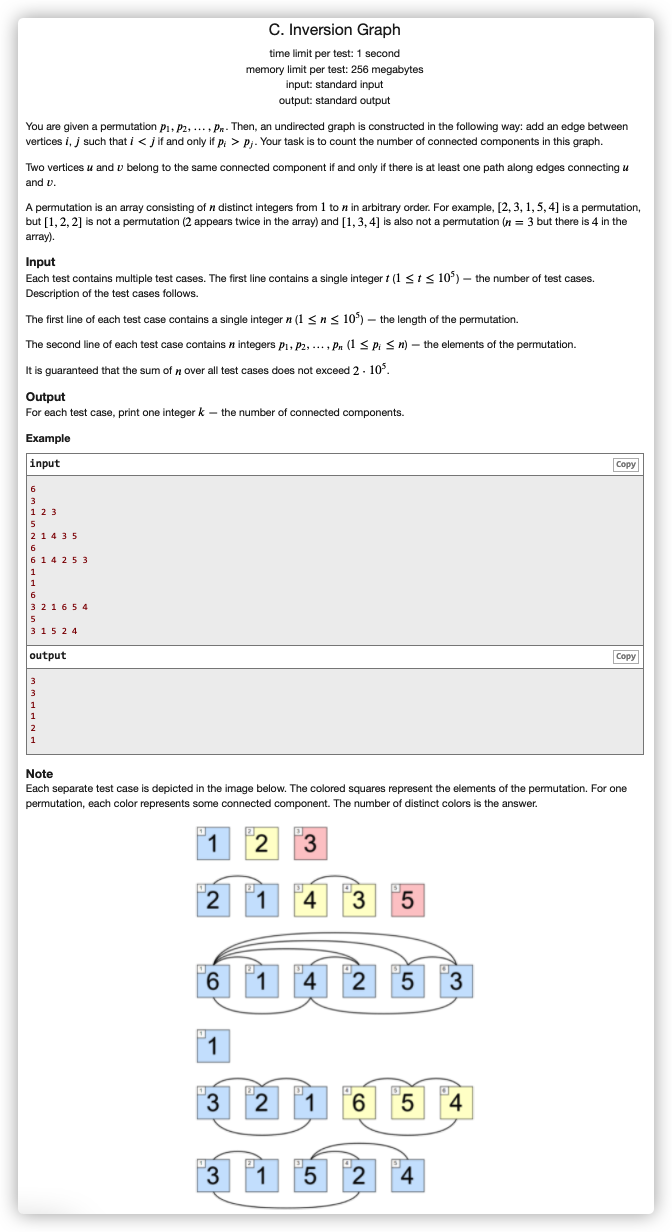
# CodeForces1638C_InversionGraph

# 🔗

# 💡

分析一下
如果一个数 aka_k ，前面有 ai>aka_i>a_k ，那么这个数可以被归入 aia_i 下
如果一个数 aja_j 过小，那么前面都会是比它大的都可以和它相连，直到前面没有比它大的了
这样下来就是一个考虑前缀最大值的问题了
我们从后往前维护最小值，如果这个位置前面没有比当前最小值更大的数了，就重启最小值并使答案 +1+1

# ✅

const int N = 1e5 + 10;
int mx[N];
int a[N];

inline void Solve () {
        int n; cin >> n;
        for ( int i = 1; i <= n; i ++ ) {
                cin >> a[i];
                mx[i] = max(mx[i - 1], a[i]);
        }
        int res = 0;
        int mn = 0x3f3f3f3f;
        for ( int i = n; i >= 1; i -- ) {
                mn = min(mn, a[i]);
                if ( mx[i - 1] < mn ) {
                        res ++;
                        mn = 0x3f3f3f3f;
                }
        }
        cout << res << endl;
}

int main () {
        ios::sync_with_stdio(false);
        int cass; cin >> cass; while ( cass -- ) {
                Solve ();
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# CodeForces1644C_IncreaseSubarraySums

# 🔗

# 💡

如果两个位置加得太远，那么和就加一个没什么区别
所以应该考虑到，应该是加连续的位置来获得更大的收益
每次加完后取长度不小于 kk 的最长连续子区间，因为如果说 <k<k 可以得到更大的结果，这个通过维护当前 f[k]f[k] 与 f[k−1]f[k-1] 的 maxmax 即可考虑在内
对于长度不小于 kk 的连续子区间，我们维护一个前缀和，再维护一个前缀和的前缀最小值
那么以 ii 结尾的长度不小于 kk 的连续最小子区间即可通过 sum[i]−mnsum[i−k]sum[i]-mnsum[i-k] 得到
每次先行扫描一遍维护一下当前最大值，然后 f[k]=max(mx,f[k−1])f[k]=max(mx,f[k-1]) 即可

# ✅

const ll N = 5010;
ll a[N];
ll sum[N];
ll mnsum[N];
ll f[N];

inline void Solve () {
        f[0] = 0;
        ll n, x; cin >> n >> x;
        for ( ll i = 1; i <= n; i ++ ) cin >> a[i], sum[i] = sum[i - 1] + a[i];
        for ( ll i = 1; i <= n; i ++ ) mnsum[i] = min(mnsum[i - 1], sum[i]);
        for ( ll k = 1; k <= n; k ++ ) {
                ll mx = 0;
                for ( ll i = k; i <= n; i ++ ) {
                        ll j = i - k + 1;
                        mx = max(mx, sum[i] - mnsum[j - 1] + k * x);
                }
                f[k] = max(f[k - 1], mx);
        }
        for ( ll i = 0; i <= n; i ++ ) cout << f[i] << " "; cout << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

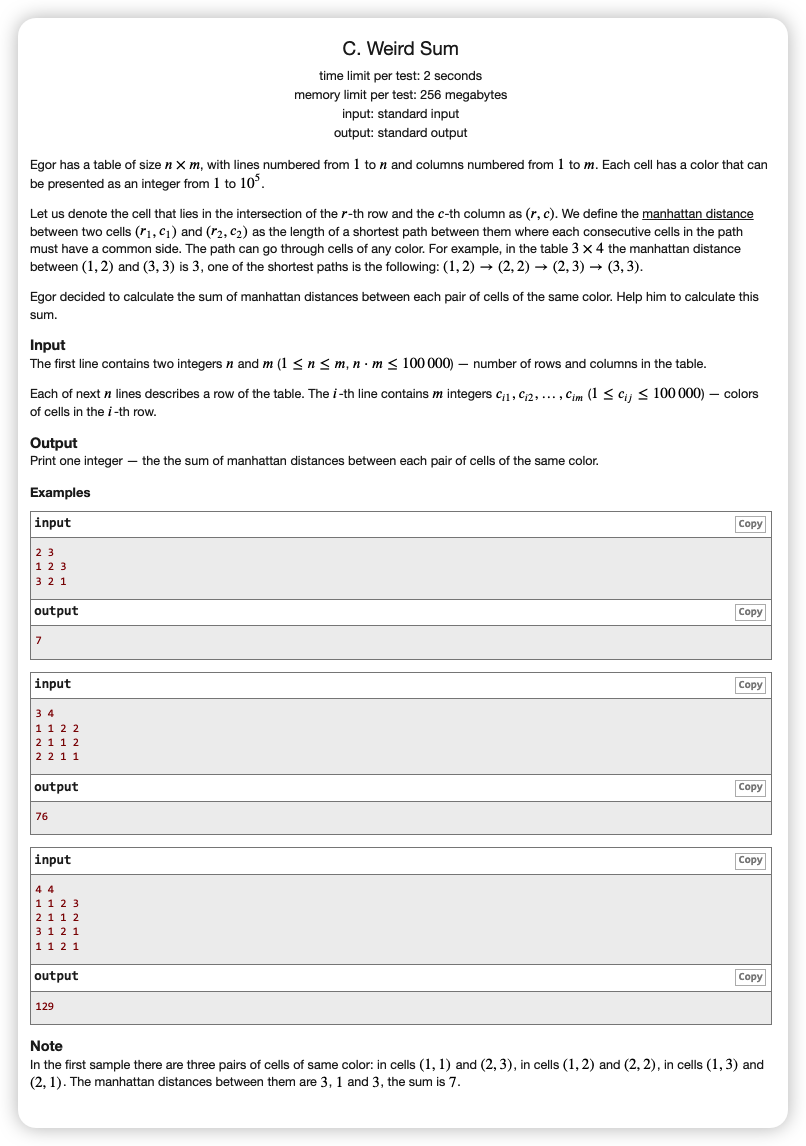
# CodeForces1649C_WeirdSum

# 🔗

20220308091913

# 💡

对于这种没对产生一次贡献的，我们思考对于一个元素，它和前面配对的贡献
按这个顺序来
即如果有 (a,b),(c,d),(e,f)(a,b),(c,d),(e,f)
价值为 ∣c−a∣+∣d−b∣+∣e−a∣+∣e−c∣+∣f−b∣+∣f−d∣=(∣c−a∣+∣e−a∣+∣e−c∣)+(∣d−b∣+∣f−b∣+∣f−d∣)|c-a|+|d-b|+|e-a|+|e-c|+|f-b|+|f-d|=(|c-a|+|e-a|+|e-c|)+(|d-b|+|f-b|+|f-d|)
可以发现我们完全可以将横纵坐标分开各自考虑
排一下序即可解除绝对值
那么对于 i:1→m(xi,yi)i:1\to m (x_i,y_i) ，答案即为

∑i=1m(i−1)xi−∑j=1i−1xj\sum\limits_{i=1}^m(i-1)x_i-\sum\limits_{j=1}^{i-1}x_j

对于 yy 同理
那么后面的那个 ∑j=1i−1xj\sum\limits_{j=1}^{i-1}x_j 我们完全可以利用前缀和去记录

# ✅

vector<ll> vec[100005][2];
set<int> clr;
 
inline void Solve () {
        int n, m; scanf("%d%d", &n, &m);
        for ( int i = 0; i < n; i ++ ) {
                for ( int j = 0; j < m; j ++ ) {
                        int x; scanf("%d", &x);
                        vec[x][0].push_back(i);
                        vec[x][1].push_back(j);
                        clr.insert(x);
                }
        }
 
 
        for ( auto i : clr ) sort ( vec[i][0].begin(), vec[i][0].end() ), sort ( vec[i][1].begin(), vec[i][1].end() );
 
        ll res = 0;
        for ( auto c : clr ) {
                ll sum = vec[c][0][0];
                for ( int i = 1; i < vec[c][0].size(); i ++ ) {
                        res += vec[c][0][i] * i - sum;
                        sum += vec[c][0][i];
                }
                sum = vec[c][1][0];
                for ( int i = 1; i < vec[c][1].size(); i ++ ) {
                        res += vec[c][1][i] * i - sum;
                        sum += vec[c][1][i];
                }
        }
 
        printf("%lld\n", res);
 
 
 
        for ( auto i : clr ) vec[i][0].clear(), vec[i][1].clear();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

# CodeForces1691D_MaxGEQSum

# 🔗

20220602003452

# 💡

首先看到这个区间最大值要大于某个条件，那么就可以通过单调栈先预处理出来每一个 aia_i 作为最大值所能覆盖的区间 [li,ri][l_i,r_i]
我们变一下题目中要求的式子，让两侧同时减去 maxmax
即: ∑j=liriaj−ai≤0\sum\limits_{j=l_i}^{r_i}a_j-a_i\le 0
这是一个很像前缀和相减的式子
分析一下 li,i,ril_i,i,r_i 这个段，从 ii 走到 lil_i 并不断累加路上的值，每一个位置都不能大于 aia_i 。从 ii 走到 rir_i 累加，每一个位置也不能大于 aia_i
那么我们维护一个前缀和 sum1sum_1 一个后缀和 sum2sum_2 ，这也就是说前缀和的 max⁡(sum1[i,ri])\max(sum1[i,r_i]) 绝对不能超过 sum1isum1_i ，同时后缀和的 max⁡(sum2[li,i])\max(sum2[l_i,i]) 也绝对不能超过 sum2isum2_i
这又要加一个区间最大值的工具，由于只有查询，可以开两个 stst 表分别维护前缀和的区间最大值和后缀和的区间最大值
然后每次按上面推出来的查一下就行

# ✅

const int N = 2e5 + 10;
ll sum1[N], sum2[N], n, a[N];
ll st1[N][30], st2[N][30];
int l[N], r[N];
stack<ll> stk;
 
inline void Build () {
        for (int i = 1; i <= n; i ++) st1[i][0] = sum1[i], st2[i][0] = sum2[i];
        int k = 32 - __builtin_clz(n) - 1;
        for ( int j = 1; j <= k; j ++ ) {
                for ( int i = 1; i + (1 << j) - 1 <= n; i ++ ) {
                        st1[i][j] = max(st1[i][j - 1],st1[i + (1 << (j - 1))][j - 1]);
                        st2[i][j] = max(st2[i][j - 1],st2[i + (1 << (j - 1))][j - 1]);
                }
        }
}
inline ll Query1 ( int l, int r ) {
        int k = 32 - __builtin_clz(r - l + 1) - 1;
        return max(st1[l][k], st1[r - (1 << k) + 1][k]);
}
inline ll Query2 ( int l, int r ) {
        int k = 32 - __builtin_clz(r - l + 1) - 1;
        return max(st2[l][k], st2[r - (1 << k) + 1][k]);
}
 
inline void Solve () {
        cin >> n;
        for (int i = 1; i <= n; i ++) cin >> a[i], sum1[i] = sum1[i - 1] + a[i];
        sum2[n + 1] = 0;
        for (int i = n; i >= 1; i --) sum2[i] = sum2[i + 1] + a[i];
 
        Build();
 
        // 单调栈求 l[i],r[i]
        stk = stack<ll>();
        for (ll i = 1; i <= n; i ++) {
                while ( stk.size() && a[i] >= a[stk.top()] ) stk.pop();
                l[i] = (stk.size() ? stk.top() + 1 : 1);
                stk.push(i);
        }
        stk = stack<ll>();
        for (ll i = n; i >= 1; i --) {
                while ( stk.size() && a[i] >= a[stk.top()] ) stk.pop();
                r[i] = (stk.size() ? stk.top() - 1 : n);
                stk.push(i);
        }
 
        for (int i = 1; i <= n; i ++) {
                if (Query2(l[i], i) - sum2[i] > 0) {
                        cout << "NO\n";
                        return;
                }
                if (Query1(i, r[i]) - sum1[i] > 0) {
                        cout << "NO\n";
                        return;
                }
        }
 
        cout << "YES\n";
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

# HDU2021多校(1)5_Minimumspanningtree

# 🔗

https://acm.hdu.edu.cn/showproblem.php?pid=6954

# 💡

在模拟中得到每个数连边后做出的贡献值是一定的
这个贡献值对后面的所有数都有贡献
所以我们使用差分记录这个贡献值
然后在处理完差分之后前缀累加一下得到每个输入的输出

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
//#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <ctime>
#include <cmath>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '<br>'

#define CHIVAS_ int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
#define beginTime clock_t startTime, toTime;startTime=clock();
#define endTime toTime=clock();cout << "The run time is:" << (double)(toTime - startTime)/CLOCKS_PER_SEC<<"s"<<endl;

//#define map unordered_map

#define _int(a) int a; cin >> a
#define  _ll(a) ll a; cin >> a
#define _char(a) char a; cin >> a
#define _string(a) string a; cin >> a
#define _vectorInt(a, n) vector<int>a(n); cin >> a
#define _vectorLL(a, b) vector<ll>a(n); cin >> a

#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cass = inputInt(); cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;


template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
template<typename T>             vector<T>& operator--            (vector<T> &v){for (auto& i : v) --i;            return  v;}
template<typename T>             vector<T>& operator++            (vector<T> &v){for (auto& i : v) ++i;            return  v;}
template<typename T>             istream& operator>>(istream& is,  vector<T> &v){for (auto& i : v) is >> i;        return is;}
template<typename T>             ostream& operator<<(ostream& os,  vector<T>  v){for (auto& i : v) os << i << ' '; return os;}
inline int inputInt(){int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);}
inline void outInt(int X){if(X<0) {putchar('-'); X=~(X-1);}int s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline ll inputLL(){ll X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1); }
inline void outLL(ll X){if(X<0) {putchar('-'); X=~(X-1);}ll s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}

const int N = 1e7 + 10;
vector<ll> prime;
bool isprime[N];
ll dir[N], a[N]; // 差分数组，答案数组
int cass;

inline void Get_euler() {
        isprime[0] = isprime[1] = 1;
        for ( ll i = 2; i < N; i ++ ) {
                if( !isprime[i] ) { prime.push_back(i), dir[i] = (i == 2 ? 0 : 2 * i); } // 除了2以外的质数都要和2连一般
                for ( ll j = 0; j < prime.size() && prime[j] * i < N; j ++ ) {
                        isprime[i * prime[j]] = 1;
                        dir[i * prime[j]] = i * prime[j]; // 不是质数，差分等于它自己
                        if ( i % prime[j] == 0 ) break;
                }
        }

        for ( ll i = 1; i <= N; i ++ ) a[i] = a[i - 1] + dir[i];
}



CHIVAS_{beginTime

        Get_euler();
        EACH_CASE ( cass ) {
                outLL(a[inputLL()]); puts("");
        }

        endTime _REGAL;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122

# HDU2021多校(5)9_Array

# 🔗

# 💡

与LuoguP4062 Yazid 的新生舞会 (opens new window)一样，是求含有绝对众数的区间个数，但是数据量是1e6所以最多只能有一个log，但是如果一个 log就很难做到很多分治类做法

对于一个数x，对于第i个位置，如果当前位置是x那么就可以设置为1，否则是-1
那么对这个值求一下前缀和sum，如果对于一个位置sum[i]-sum[j]>0，说明这段区间内这个数出现个数比别的所有数出现个数要多
那么问题就转化为，对于每个数x，建立完sum数组之后，求每一个位置前面sum[j] < sum[i]的个数

可以维护一个f1数组用来维护每一个sum的个数，f2数组是用来对f1进行区间修改的差分数组
在当前这一段一直出现x或者未到最小值，可以直接线性求解，SUM不断累加sum[个数]
如果到了最小值并且还是没有出现x，意味着一直下减，前面一定不会出现解
那么就可以跳过这一段，里面的要改的数可以通过区间修改一起改了，同时SUM重置为0

# ✅

#include <iostream>
#include <map>
#include <vector>
#include <cstring>
#include <algorithm>
#include <unordered_map>

#define ll long long
using namespace std;


const int N = 2e6 + 10;

map<int, vector<int> > g;

int n, cass, a[N]; 
ll res = 0;

inline void Solve ( int x ) {
        g[x].push_back(n + 1);
        unordered_map<ll, ll> f1, f2;
        f1[0] = 1; ll sum = 0/*前面多少个比当前前缀和小的*/, tmp = 0/*当前前缀和*/, minn = 0/*前面出现过的最小前缀和*/;
        for ( int i = 1, j = 0; i <= n; i ++ ) {
                if ( i > g[x][j] ) j ++; // 保持g[x][j]一直 >= i
                if ( a[i] == x ) {
                        tmp ++; 
                        f1[tmp] += f2[tmp] + 1; // 利用差分的f2让f1往前走一步
                        f2[tmp + 1] += f2[tmp]; f2[tmp] = 0;
                        sum += f1[tmp - 1]; // 又多了一个比tmp小的
                        res += sum;
                } else if ( tmp - 1 <= minn ) { // 这个区间跳过
                        int len = g[x][j] - i; // 跳过区间的每个sum的个数 ++
                        ++ f2[tmp - len + 1]; -- f2[tmp]; // 区间修改
                        ++ f1[tmp - len];
                        tmp -= len;
                        i = g[x][j] - 1;
                        sum = 0; // 最小的，前面没有更小的了，所以sum清0
                } else {
                        sum -= f1[-- tmp]; // 就是光减而已，也没多什么，就利用已有的f1计算即可
                        res += sum;
                        ++ f1[tmp];
                }
                if ( tmp < minn ) minn = tmp; // 最小值维护一下
        }
}

int main () {
        ios::sync_with_stdio(false);
        for ( cin >> cass; cass; cass -- ) {
                cin >> n;
                for ( int i = 1; i <= n; i ++ ) {
                        cin >> a[i];
                        g[a[i]].push_back(i); // 对每个存一下位置
                }
                res = 0;
                for ( auto v : g ) { // 分开解决
                        Solve(v.first);
                        g[v.first].clear(); // 在求完就可以删掉了
                }
                cout << res << endl;
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

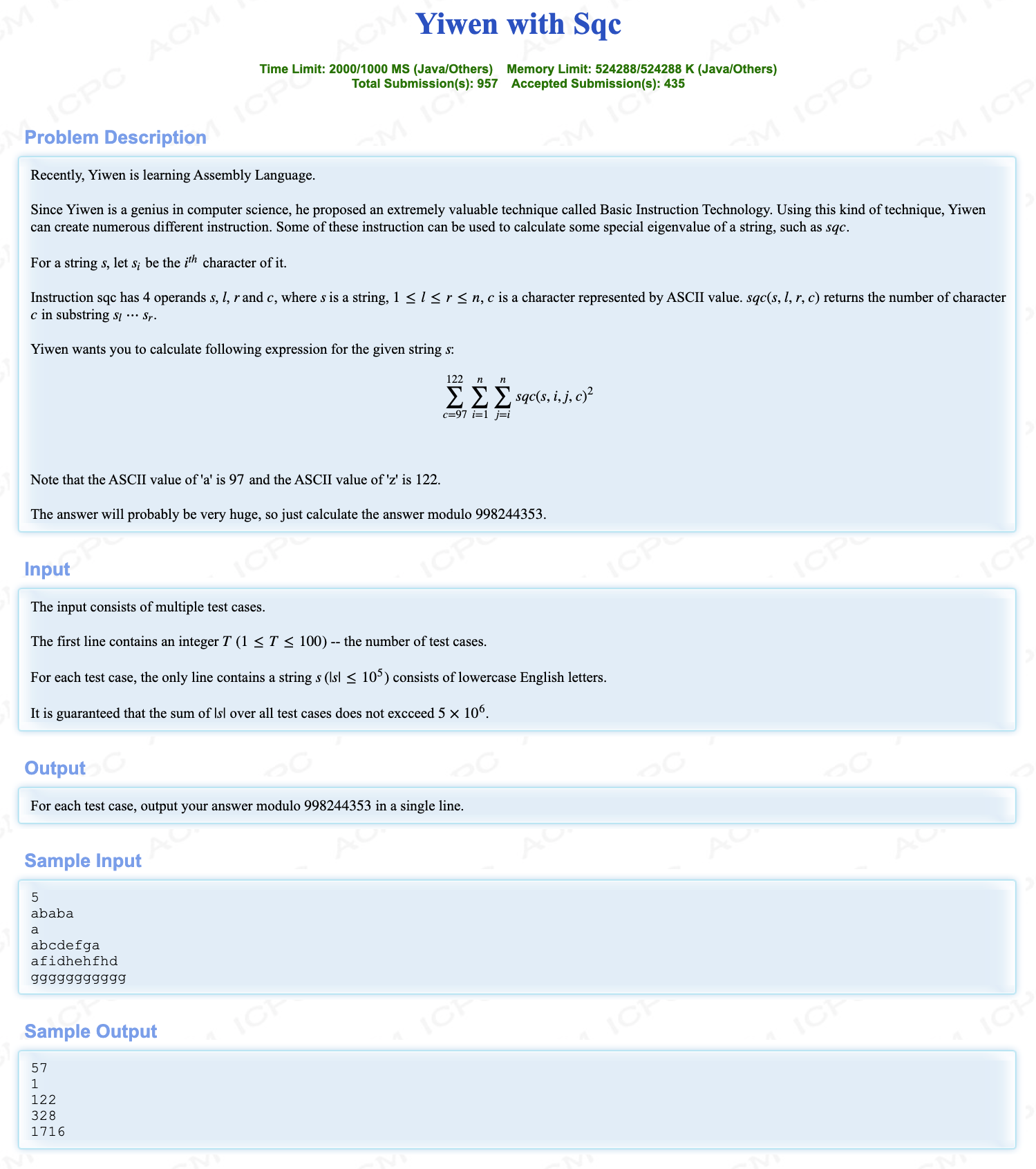
# HDU2021多校(7)12_YiwenwithSqc

# 🔗

# 💡

对于这种，我们分开考虑贡献
对于一个字符出现的位置进行记录
并可以得出一个个这个字符没有出现的连续段落，大小设置为sz

相差i个的段落的位置个数的相乘每一个贡献是i^2
那么对于每个字符贡献就是

看到这个式子应很快反应到，对于j:[2->sz]，每次累加的都是(j-1)的三个前缀和

所以设三个前缀和
sum1[i] 表示 a[i] * i * i 的前缀和
sum2[i] 表示 a[i] * i 的前缀和
sum3[i] 表示 a[i] 的前缀和
然后j从2往n遍历，每次加上a[j] * j * j * sum3[j-1]再减去a[j] * j * 2 * sum2[j - 1]再加上a[j] * sum1[j - 1]

把每个字符求得的贡献累加一下即可

# ✅

const ll mod = 998244353;

const ll N = 1e5 + 10;
ll sum1[N], sum2[N], sum3[N];

inline void Solve() {
        map<char, vector<ll> > los, mp;
        string s; cin >> s;
        for ( ll i = 0; i < s.size(); i ++ ) {
                mp[s[i]].push_back(i);
        }
        for ( auto i : mp ) {
                los[i.first].push_back(0); // 整体向后移，方便前缀和记录
                los[i.first].push_back(i.second[0] + 1);// 初始的区间
                for ( ll j = 1; j < i.second.size(); j ++ ) los[i.first].push_back(i.second[j] - i.second[j - 1]); // 两两区间
                los[i.first].push_back(s.size() - i.second.back()); // 最后的区间
        }
        ll res = 0;
        for ( auto i : los ) {
                for ( ll j = 1; j < i.second.size(); j ++ ) {
                        sum1[j] = (sum1[j - 1] + i.second[j] * j % mod * j % mod ) % mod;
                        sum2[j] = (sum2[j - 1] + i.second[j] * j % mod) % mod;
                        sum3[j] = (sum3[j - 1] + i.second[j]) % mod;
                }
                for ( ll j = 2; j < i.second.size(); j ++ ) {
                        res = ( res + i.second[j] * j % mod * j % mod * sum3[j - 1] % mod) % mod;
                        res = ((res - i.second[j] * j % mod * 2 % mod * sum2[j - 1] % mod) % mod + mod) % mod;
                        res = ( res + i.second[j] * sum1[j - 1] % mod) % mod;
                }
        }
        cout << res << endl;
}

int main () {
        ios::sync_with_stdio(false);
        ll cass; cin >> cass; while ( cass -- ) {
                Solve();
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

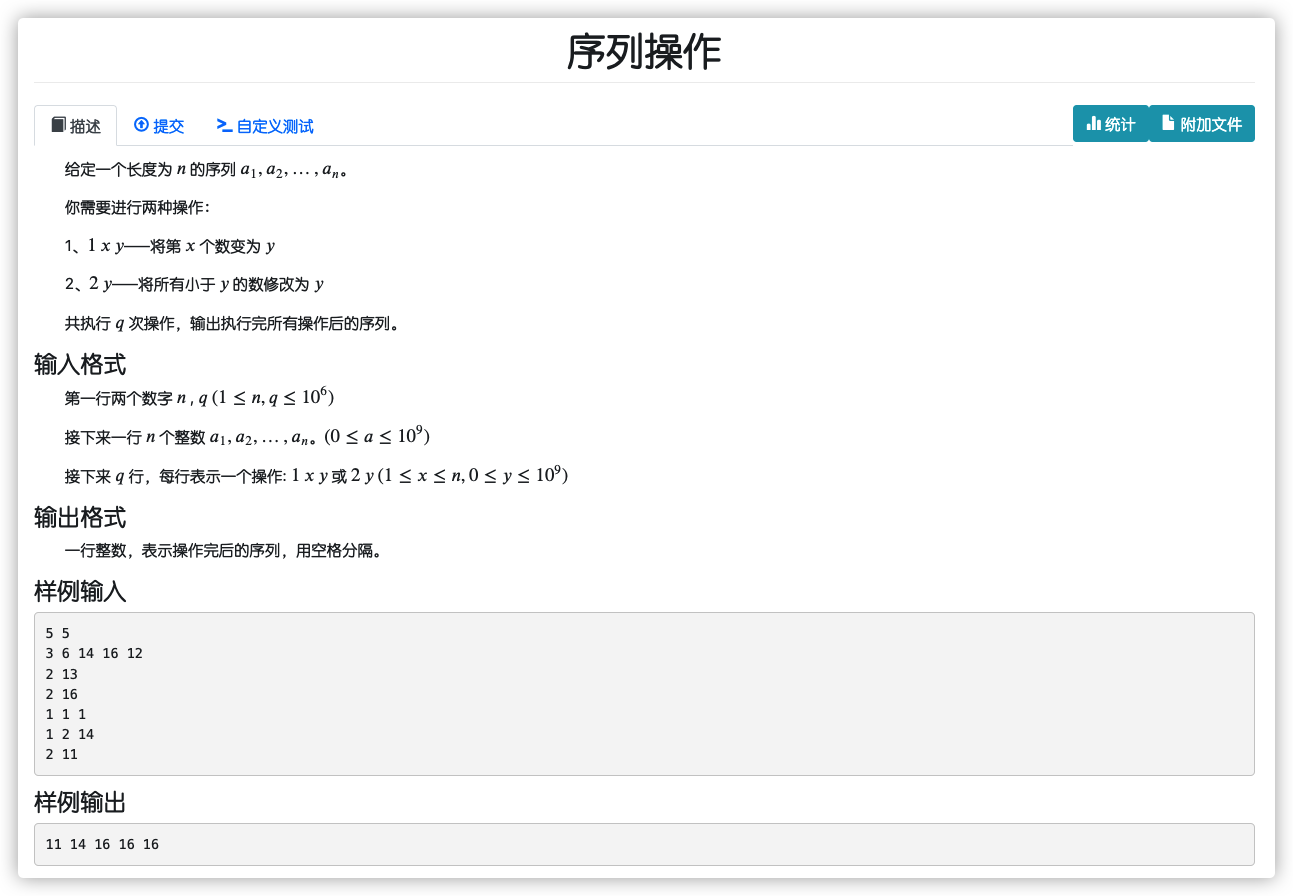
# NamomoCamp2022春季div1每日一题_序列操作

# 🔗

20220302120657

# 💡

关注一下操作一，如果修改之后存在比这次操作一的那个数更大的操作二
那么就一定会被变成后面操作的最大的操作二
而操作二后面如果存在操作一，不影响操作一，所以看操作一的最后一个数
那么就对时间建立后缀操作二最大值
对每次操作一取 maxmax 这次操作一的值和后面操作二的最大值
为了方便可以将默认序列添加时间戳为 −1-1 修改值为 aia_i 的操作一

# ✅

const int N = 1e6 + 10;
int n, m, a[N];
pair<int, int> ope1[N]; // first: time, second: val
int suf[N];


int main () {
	ios::sync_with_stdio(false);
	cin >> n >> m;
	for ( int i = 1; i <= n; i ++ ) cin >> a[i], ope1[i] = {-1, a[i]};
	for ( int i = 0; i < m; i ++ ) {
		int op; cin >> op;
		if ( op == 1 ) {
			int x, y; cin >> x >> y;
			ope1[x] = {i, y};
		} else {
			int y; cin >> y;
			suf[i] = y;
		}
	}

	for ( int i = m - 1; i >= 0; i -- ) suf[i] = max(suf[i + 1], suf[i]);

	for ( int i = 1; i <= n; i ++ ) {
		cout << max(ope1[i].second, suf[ope1[i].first + 1]) << " ";
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

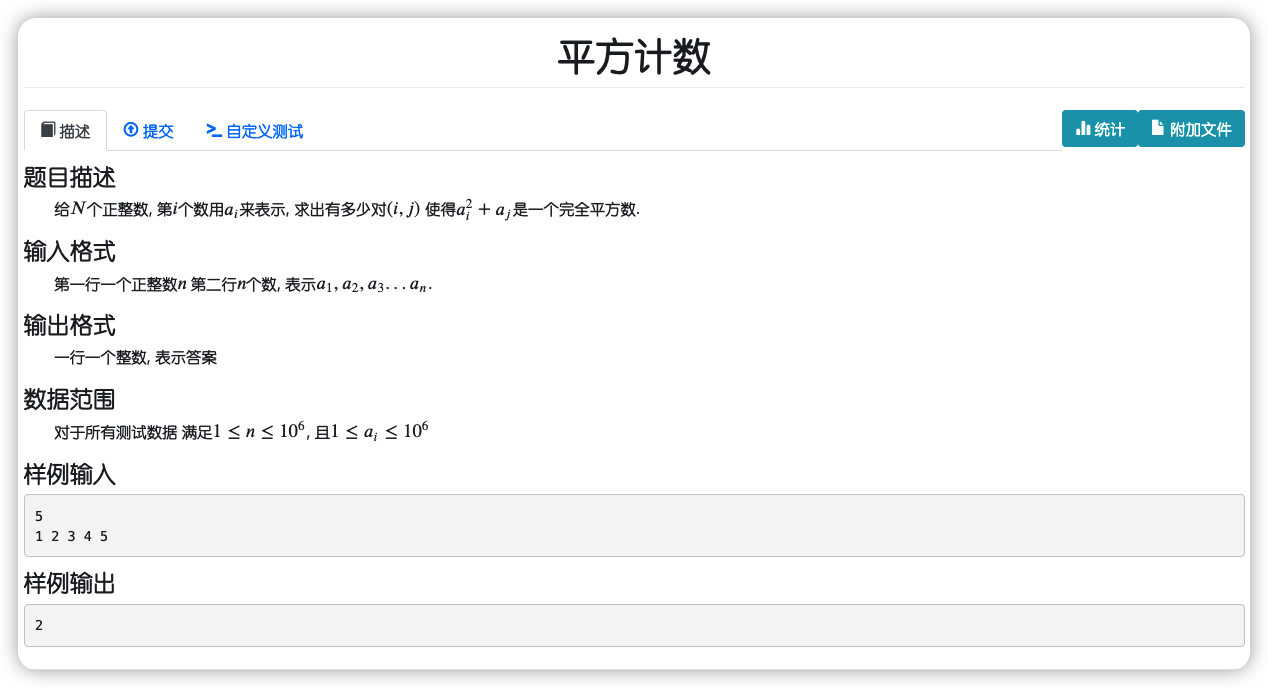
# NamomoCamp2022春季div1每日一题_平方计数

# 🔗

20220322102549

# 💡

看到这种对数的就应该去想前缀计数找满足的对数
一个平方数加一个数仍然是平方数
有了这两个特征就考虑这个公式：

x2+(2x+1)=(x+1)2x2+(4x+4)=(x+2)2x2+(6x+9)=(x+3)2x^2+(2x+1)=(x+1)^2\\x^2+(4x+4)=(x+2)^2\\x^2+(6x+9)=(x+3)^2

看到后面的是倍数关系，可以通过对于每一个 aia_i 枚举后面括号的内容做一个 O(nlogn)O(nlogn) 的算法
后面的一定是比 xx 要大的，那么就从大到小扫 aia_i 然后扫完统计完就插入 num[ai]+1num[a_i]+1

# ✅

const int N = 1e6 + 10;
int num[N];
int a[N];

int main () {
        int n; scanf("%d", &n);
        for ( int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
        sort ( a, a + n, greater<ll>() );

        int res = 0;
        for ( int i = 0; i < n; i ++ ) {
                for ( int j = 1; 2 * j * a[i] + j * j <= a[0]; j ++ ) {
                        res +=  num[2 * j * a[i] + j * j];
                }
                num[a[i]] ++;
        }
        printf("%d\n", res);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Last Updated: 10/14/2023, 7:51:49 PM

双指针