平衡树

#

---

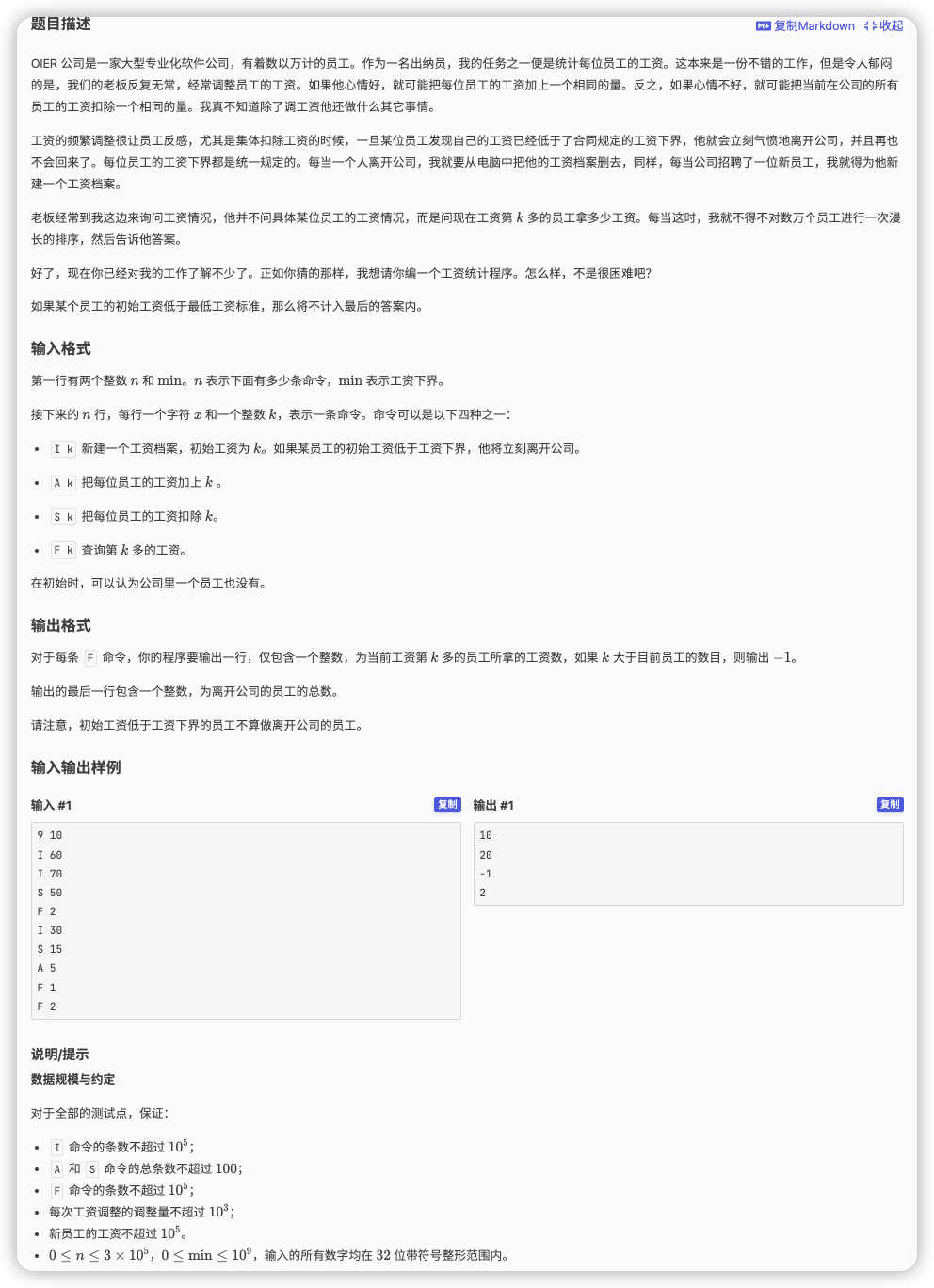
洛谷P1486_郁闷的出纳员

🔗

💡

新来员工、离开员工
这就是一个加点和删点的问题
然后看见数值加、数值减、查询全局第 $k$ 大，秒用平衡树
全局的数值加减用一个懒标记实时 pushdown 即可
小的要退出，就每次操作结束后找到最左边的数，判断一下是不是小于下界，小的话删掉
查询全局第 $k$ 大就用记录的子树大小 size 在树上走就行了

✅

const int N = 3e5 + 10;
struct node {
    int l, r;
    int key, val;
    int lazy, size;
} t[N];
int cnt, root;
mt19937 rnd(233);

inline int newnode (int val) {
    t[++cnt] = {0, 0, (int)rnd(), val, 0, 1};
    return cnt;
}
inline void pushup (int now) {
    t[now].size = t[t[now].l].size + t[t[now].r].size + 1;
}
inline void pushdown (int now) {
    if (!t[now].lazy) return;
    t[now].val += t[now].lazy;
    if (t[now].l) t[t[now].l].lazy += t[now].lazy;
    if (t[now].r) t[t[now].r].lazy += t[now].lazy;
    t[now].lazy = 0;
}
inline void Split (int now, int val, int &x, int &y) {
    if (!now) {
        x = y = 0;
    } else {
        pushdown(now);
        if (val < t[now].val) {
            y = now;
            Split(t[now].l, val, x, t[now].l);
        } else {
            x = now;
            Split(t[now].r, val, t[now].r, y);
        }
        pushup(now);
    }
}
inline int Merge (int x, int y) {
    if (!x || !y) return x + y;
    if (t[x].key >= t[y].key) {
        pushdown(x);
        t[x].r = Merge(t[x].r, y);
        pushup(x);
        return x;
    } else {
        pushdown(y);
        t[y].l = Merge(x, t[y].l);
        pushup(y);
        return y;
    }
}
inline void Insert (int val) {
    int x, y;
    Split(root, val, x, y);
    root = Merge(Merge(x, newnode(val)), y);
}
inline void Delete (int val) {
    int x, y, z; 
    Split(root, val, x, z);
    Split(x, val - 1, x, y);
    y = Merge(t[y].l, t[y].r);
    root = Merge(Merge(x, y), z);
}
inline int Min (int now) {
    pushdown(now);
    while (t[now].l) now = t[now].l, pushdown(now);
    return t[now].val;
}
inline int Num (int rnk) {
    int now = root;
    while (now) {
        pushdown(now);
        if (rnk == t[t[now].l].size + 1) break;
        if (rnk <= t[t[now].l].size) now = t[now].l;
        else rnk -= t[t[now].l].size + 1, now = t[now].r;
    }
    return t[now].val;
}

int SIZE, LEAVE;
int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, down; cin >> n >> down;

    while (n --) {
        char op; cin >> op;
        int k; cin >> k;
        switch (op) {
            case 'I':
                if (k >= down) 
                    Insert(k), 
                    SIZE ++;
                break;
            case 'A':
                t[root].lazy += k;
                break;
            case 'S':
                t[root].lazy -= k;
                break;
            default:
                if (k > SIZE) cout << "-1\n";
                else cout << Num(SIZE - k + 1) << endl;
                break;
        }

        while (SIZE > 0) {
            int mn = Min(root);
            if (mn < down) Delete(mn), SIZE --, LEAVE ++;
            else break;
        }
    }
    cout << LEAVE << endl;
}

---

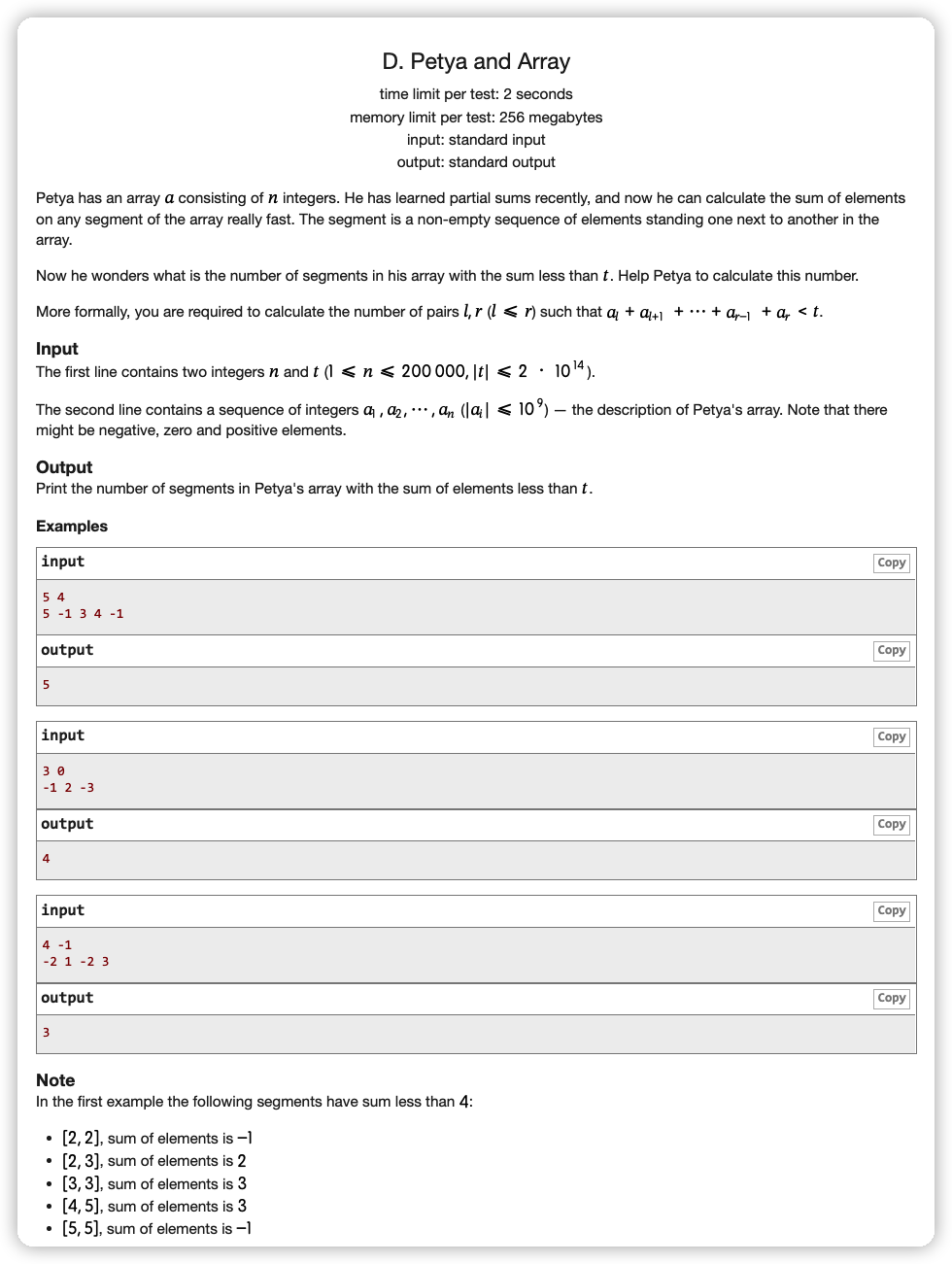
CodeForces1042D_PetyaAndArray

🔗

💡

（设前缀和为 $[pre]$ ）
问题就是累加 对于每一个 $i$ ，它前面的 $j$ 有多少个满足 $pre_i-pre_j<k$
本来想二分或者双指针直接莽，突然发现它的前缀和不存在单调性，没法移动
式子可以变成 $pre_j+k>pre_i$ 那这个问题就只能用数据结构边计算边更新，每次累加查询数据结构里面插入过的大于 $pre_i$ 的数量，然后塞入 $pre+k$
用权值线段树了话发现这些数都特别大，并且查询范围时存在加减关系，离散化有一点麻烦
而只有大小关系，可以直接平衡树实现：将 $fhq-treap$ 按 $val$ 分裂后右树的大小就是查询结果

✅

const int N = 2e5 + 10;
struct node {
        int l, r;
        ll val; int key;
        int size;
} t[N];
int root, cnt;
mt19937 rnd(233);
inline int newnode (ll val) {
        t[++cnt] = {0, 0, val, (int)rnd(), 1};
        return cnt;
}
inline void pushup (int now) {
        t[now].size = t[t[now].l].size + t[t[now].r].size + 1;
}
inline void Split (int now, ll val, int &x, int &y) {
        if (!now) {
                x = y = 0;
        } else {
                if (val < t[now].val) {
                        y = now;
                        Split(t[now].l, val, x, t[y].l);
                        pushup(y);
                } else {
                        x = now;
                        Split(t[now].r, val, t[now].r, y);
                        pushup(x);
                }
        }
}
inline int Merge (int x, int y) {
        if (!x || !y) return x + y;
        if (t[x].key >= t[y].key) {
                t[x].r = Merge(t[x].r, y);
                pushup(x);
                return x;
        } else {
                t[y].l = Merge(x, t[y].l);
                pushup(y);
                return y;
        }
}
inline void Insert (ll val) {
        int x, y;
        Split(root, val, x, y);
        root = Merge(Merge(x, newnode(val)), y);
}
inline int get_BiggerSize (ll val) {
        int x, y;
        Split(root, val, x, y);
        int res = t[y].size;
        root = Merge(x, y);
        return res;
}

int n; 
ll k;
int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        cin >> n >> k;
        ll sum = 0;
        ll res = 0;    
        Insert(k);
        for (int i = 0; i < n; i ++) {
                ll x; cin >> x;
                sum = sum + x;
                res = res + get_BiggerSize(sum);
                Insert(sum + k);
        } 
        cout << res << endl;
}

---