二分图染色

#

---

洛谷P6268_舞会

🔗

💡

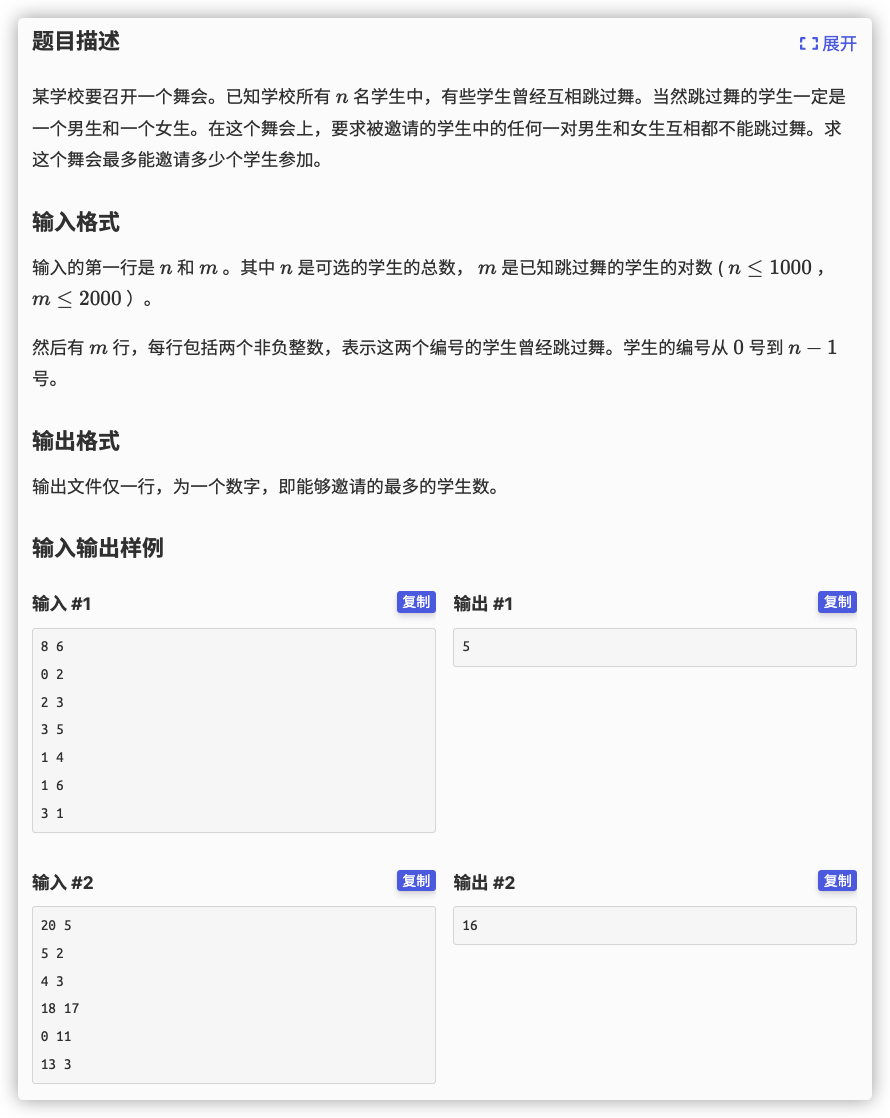
两两不配对，求最多配对点
求最大独立集即可
求之前先要男女染色

✅

const int N = 1005;
const int M = 4010;

struct Edge {
        int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge ( int from, int to ) {
        edge[++cnt] = { head[from], to };
        head[from] = cnt;
}

int e[N][N];
int n, m;
vector<int> b, g;
bool col[N];

int match[N];
bool st[N];

inline void Color ( int x, int dep ) {
        dep == 1 ? g.push_back(x) : b.push_back(x); 
        col[x] = true;
        for ( int i = 1; i <= n; i ++ ) 
                if ( e[x][i] && !col[i] ) 
                        Color(i, 3 - dep);
}

inline bool Find ( int x ) {
        for ( int i = head[x]; i; i = edge[i].nxt ) {
                int y = edge[i].to;
                if ( !st[y] ) {
                        st[y] = true;
                        if ( !match[y] || Find(match[y]) ) {
                                match[y] = x;
                                return true;
                        }
                }
        }
        return false;
}

int main () {
        ios::sync_with_stdio(false);
        cin >> n >> m;
        for ( int i = 0; i < m; i ++ ) {
                int a, b; cin >> a >> b;
                a ++, b ++;
                e[a][b] = e[b][a] = 1;
                add_Edge(a, b);
                add_Edge(b, a);
        }
        for ( int i = 1; i <= n; i ++ ) if ( !col[i] ) Color(i, 1);
        
        int res = 0;
        for ( int i = 0; i < b.size(); i ++ ) {
                for ( int j = 0; j < g.size(); j ++ ) st[g[j]] = false;
                if ( Find(b[i]) ) res ++;
        }
        cout << n - res << endl;
}

---

省赛2021江苏J_Anti-merge

🔗

💡

相同的会删去，我们要加标签来防止有数被删去
可以将相邻的一样的数看作连通块，我们要想让这个联通块两两隔开，其实就加一个编号就行了
那么这道题答案的第一个数只有 和 两种可能
而对于连通块，我们从一个点 开始 出这个连通块，看看是离 距离为奇数加标签用的多还是偶数加标签用的多，我们选用最少的标签加法

✅

const int N = 510;
int g[N][N], vis[N][N];
int n, m;
int chos_which[N][N];

int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};

struct node { int a, b, c; };
int res1;
vector<node> res2;

int n1, n0;
inline void DFS ( int x, int y, int flag, int num, int op ) { // flag：0计数，12加标签
        if ( vis[x][y] ) return; vis[x][y] = 1;
        if ( flag ) n1 ++; // 距离为奇数要加标签的数量
        else n0 ++; // 距离为偶数要加标签的数量
        if ( op == 1 ) { // 距离为奇数且要加标签
                if ( flag ) res2.push_back({x, y, 1});
        } else if ( op == 2 ) { // 距离为偶数且要加加标签
                if ( !flag ) res2.push_back({x, y, 1});
        }

        for ( int i = 0; i < 4; i ++ ) {
                int nx = x + dx[i], ny = y + dy[i];
                if ( nx <= 0 || nx > n || ny <= 0 || ny > m ) continue;
                if ( g[nx][ny] != num ) continue;
                DFS(nx, ny, flag ^ 1, num, op);
        }
}

int main () {
        ios::sync_with_stdio(false);
        cin >> n >> m;
        for ( int i = 1; i <= n; i ++ ) {
                for ( int j = 1; j <= m; j ++ ) {
                        cin >> g[i][j];
                }
        }
        vector<pair<int, int> > nod_fath; // 一个连通块的根
        for ( int i = 1; i <= n; i ++ ) {
                for ( int j = 1; j <= m; j ++ ) {
                        if ( vis[i][j] ) continue;
                        n1 = n0 = 0;
                        DFS(i, j, 0, g[i][j], 0);
                        if ( n1 >= n0 ) chos_which[i][j] = 2;
                        else chos_which[i][j] = 1;
                        if ( n1 ) res1 = 1;
                        nod_fath.push_back({i, j});
                }
        }
        if ( !res1 ) cout << "0 0" << endl; // 不需要加标签
        else {
                memset(vis, 0, sizeof vis );
                for ( auto i : nod_fath ) {
                        DFS(i.first, i.second, 0, g[i.first][i.second], chos_which[i.first][i.second]);
                }
                cout << res1 << " " << res2.size() << endl;
                for ( int i = 0; i < res2.size(); i ++ ) {
                        cout << res2[i].a << " " << res2[i].b << " " << res2[i].c << endl;
                }

        }
}

---

CodeForces1605D_Treelabeling

🔗

💡

由于Eikooc只决定这个点放哪，但是先走的是Sushi
我们可以想一种方法让断开的点尽量多，这样Eikooc放到很多个位置Sushi都走不动

思考一下断边的条件：
这样的话只要邻边的二进制位数不同就一定可以
由于二进制位数相同的是一个集合
我们确保邻点不在同一集合即可

由于二进制可以合并成任意我们想要的数且二进制位数相同的数本身就是一个二的幂次
对点二分染色一下
让染色相同的点必须包含完整的二进制集合，不能有染色不同的点二进制位数相同的情况

那么我们就对 分二进制块之后每次一个完整的二进制块分给当前颜色数量最多的点集，给他们赋一下编号然后从该集合中删去

✅

const int N = 4e5 + 10;
int res[N];
struct Edge {
        int nxt, to;
} edge[N];
int head[N], cnt;
int n; 
vector<int> vec[2];

inline void add_Edge ( int from, int to ) {
        edge[ ++ cnt ] = { head[from], to };
        head[from] = cnt;
}
inline void DFS ( int x, int fath, int dep ) {
        vec[dep].push_back(x);
        for ( int i = head[x]; ~i; i = edge[i].nxt ) {
                int to = edge[i].to;
                if ( to == fath ) continue;
                DFS ( to, x, dep^1 );
        }
}

inline void Solve () {
        scanf("%d", &n);

        int stt = 0; while ( (1 << stt) <= n ) stt ++; stt --; // 有多少个二进制块
        for ( int i = 0; i <= n * 2 + 5; i ++ ) head[i] = res[i] = -1, cnt = 0;
        vec[0].clear(); vec[1].clear();

        for ( int i = 0; i < n - 1; i ++ ) {
                int a, b; scanf("%d%d", &a, &b);
                add_Edge ( a, b );
                add_Edge ( b, a );
        }
        DFS ( 1, 1, 0 ); // 染色
        for ( ; stt >= 0; stt -- ) {
                int to; // 选择点数量最多的色块
                if ( max(vec[0].size(), vec[1].size()) == vec[0].size() ) to = 0; 
                else                                                      to = 1;
                for ( int i = min(n, (1 << (stt + 1)) - 1); i >= (1 << stt); i -- ) { // 一个完整的二进制块
                        res[vec[to].back()] = i;
                        vec[to].pop_back();
                }
        }
        for ( int i = 1; i <= n; i ++ ) printf("%d ", res[i]);
        printf("\n");
}

int main () {
        int cass; scanf("%d", &cass); while ( cass -- ) {
                Solve ();
        }
}

---