后缀数组

#

---

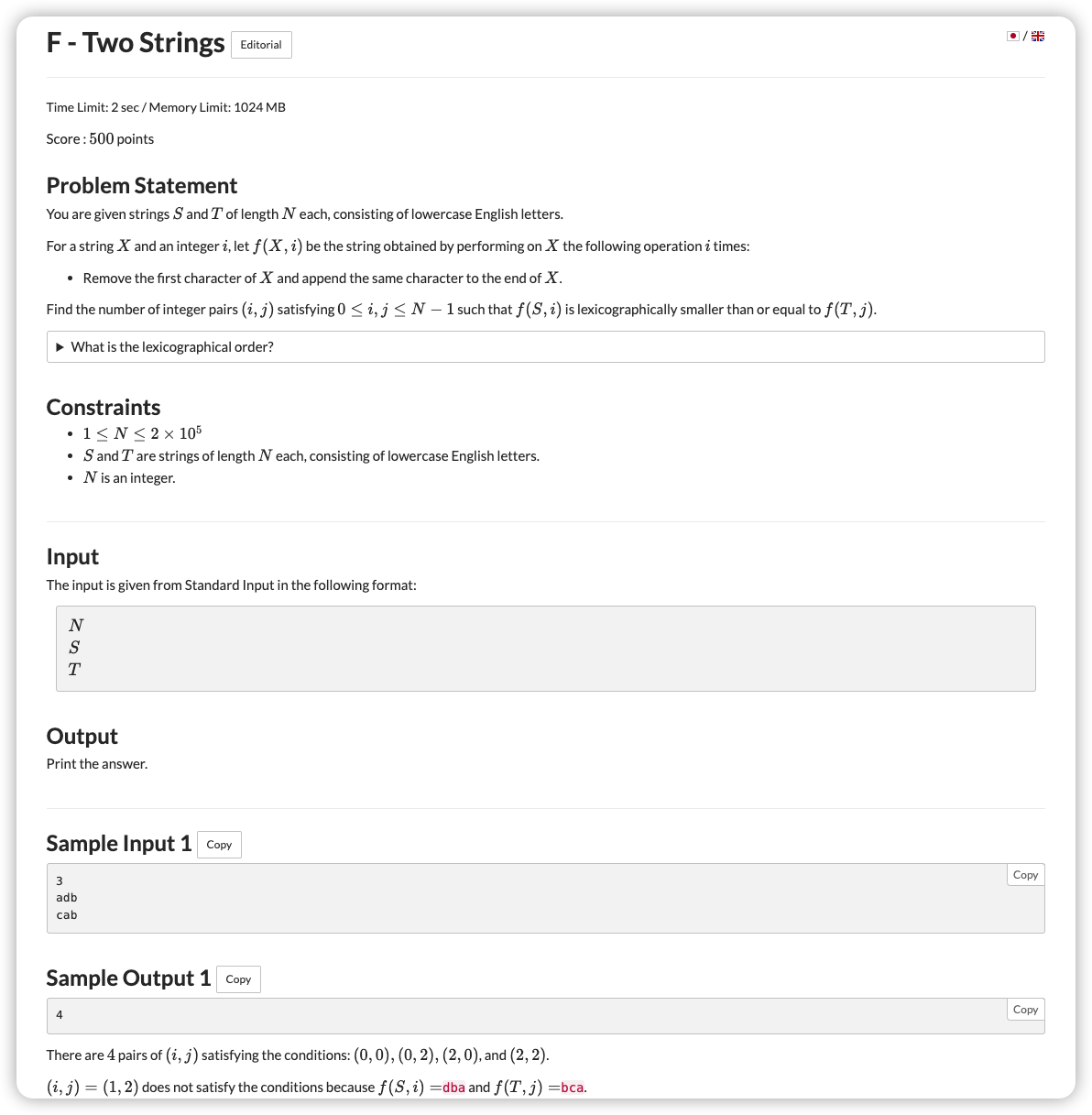
ABC272F_TwoStrings

🔗

💡

这相当于就是一个全部环形字符串的大小顺序问题
开始肯定想全 sort 一遍，但是肯定超
环形已知就是把两个字符串复制在一起，那后缀的前缀序进行排序就是后缀数组啦
处理起来 $sstt$ 形成的字符串的 $sa$ ，然后一个 $cnt$ 维护向后走的时候遇到的属于第一个 $s$ 的个数，当遇到属于第一个 $t$ 的时候，让答案累加上 $cnt$
注意 $ss$ 的末尾要严格小于 $a\to z$ 的任何一个字符，$tt$ 的末尾要严格大于，才能保证求到的是 $s'\le t'$ 的数量

✅

const int N = 2e6 + 10;

class Suffix_Array {
public:
    int n;
    char s[N];
    int sa[N], rk[N], rk2[N], ht[N];

    Suffix_Array () {}
    Suffix_Array (int _n, char *_s) {
        n = _n;
        for (int i = 1; i <= n; i ++) s[i] = _s[i];
    }
    inline void get_Sa () {
        for (int i = 1; i <= n; i ++) {
            sa[i] = i;
            rk[i] = s[i];
        }
        for (int k = 1; k <= n; k <<= 1) {
            auto cmp = [&](int i, int j) {
                if (rk[i] != rk[j]) return rk[i] < rk[j];
                int ri = (i + k <= n ? rk[i + k] : -1);
                int rj = (j + k <= n ? rk[j + k] : -1);
                return ri < rj;
            };
            sort(sa + 1, sa + 1 + n, cmp);
            for (int i = 1; i <= n; i ++) rk2[sa[i]] = rk2[sa[i - 1]] + cmp(sa[i - 1], sa[i]);
            for (int i = 1; i <= n; i ++) rk[i] = rk2[i];
        }
    }
    inline void get_Ht () {
        for (int i = 1; i <= n; i ++) rk[sa[i]] = i;
        ht[1] = 0;
        for (int i = 1, h = 0; i <= n; i ++) {
            int j = sa[rk[i] - 1];
            if (h > 0) h --;
            for (; j + h <= n && i + h <= n; h ++) if (s[j + h] != s[i + h]) break;
            ht[rk[i]] = h;
        }
    }
};

char s[N];
char t[N];

Suffix_Array sa;

ll cnt = 0;

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n; cin >> n;
    cin >> (s + 1);
    cin >> (t + 1);
    for (int i = 1; i <= n; i ++) sa.s[i] = s[i];
    for (int i = 1; i <= n; i ++) sa.s[i + n] = s[i];
    for (int i = 1; i <= n; i ++) sa.s[i + 2 * n + 1] = t[i];
    for (int i = 1; i <= n; i ++) sa.s[i + 3 * n + 1] = t[i];
    sa.s[n * 2 + 1] = '#';
    sa.s[n * 4 + 2] = '|';

    sa.n = n * 4 + 2;
    sa.get_Sa();
    sa.get_Ht();

    ll res = 0;
    for (int i = 1; i <= 4 * n + 1; i ++) {
        if (sa.sa[i] > n * 2 + 1 && sa.sa[i] <= n * 3 + 1) {
            res += cnt;
        } else if (sa.sa[i] > 0 && sa.sa[i] <= n) {
            cnt ++;
        }
    }
    cout << res << endl;
}

---

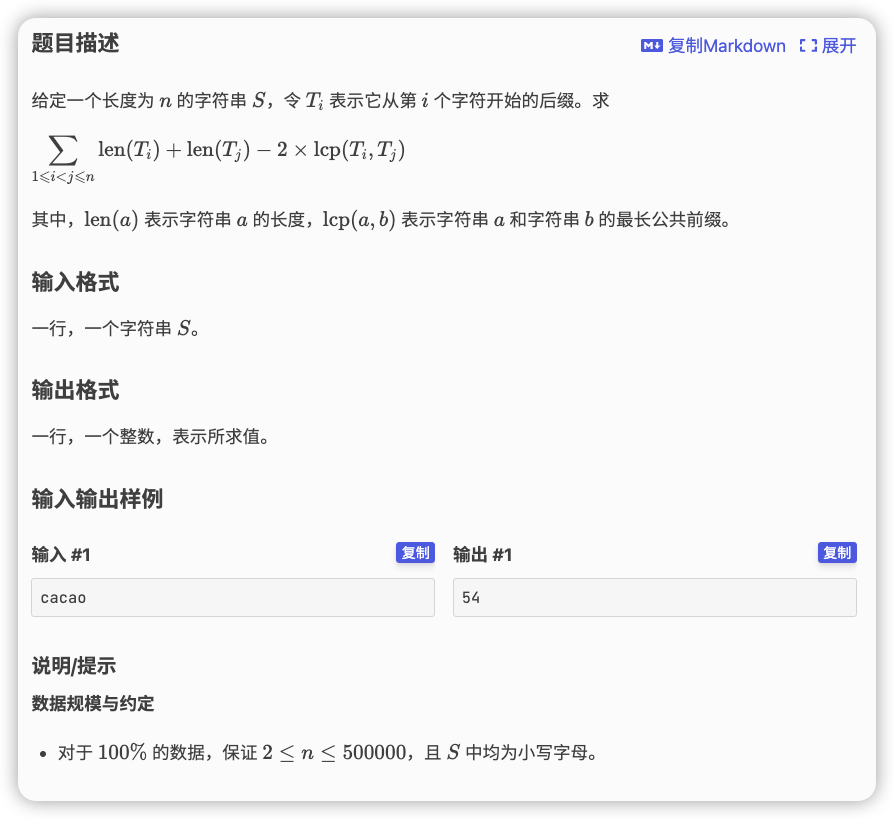
洛谷P4248_差异

🔗

💡

这个式子一看就能拆，因为 $T_i$ 和 $T_j$ 有关系的时候就只有后面的 $lcp$
三项提开，前两项再合并 $\frac{(n-1)n(n+1)}{2}-\sum\limits_{1\le i<j\le n}lcp(T_i,T_j)$
想一下 $lcp$ 在什么地方能求，就是 $lcp(sa[i],sa[j])=\min\limits_{k=i+1}^jht[k]$
既然是两两都有，那么下标可以转换为排名，也就是求所有排名区间最小 $ht$ 的和
这就是一个处理一个位置作为最小值覆盖的 $l,r$ 的问题，求完 $lr$ 后，累计一下以 $i$ 为最小值的区间数和 $ht$ 的乘积也就是 $2\times(i-l_i+1)(r_i-i+1)\times ht[i]$ 即可

✅

const int N = 5e5 + 10;
int n;
char s[N];
int rk[N], rk2[N], sa[N], ht[N];

inline void get_Sa () {
    for (int i = 1; i <= n; i ++) {
        rk[i] = s[i];
        sa[i] = i;
    }
    for (int k = 1; k <= n; k <<= 1) {
        auto cmp = [&](int i, int j) {
            if (rk[i] != rk[j]) return rk[i] < rk[j];
            int ri = (i + k <= n ? rk[i + k] : -1);
            int rj = (j + k <= n ? rk[j + k] : -1);
            return ri < rj;
        };
        sort(sa + 1, sa + 1 + n, cmp);
        for (int i = 1; i <= n; i ++) rk2[sa[i]] = rk2[sa[i - 1]] + cmp(sa[i - 1], sa[i]);
        for (int i = 1; i <= n; i ++) rk[i] = rk2[i];
    }
}
inline void get_Ht () {
    for (int i = 1; i <= n; i ++) rk[sa[i]] = i;
    ht[1] = 0;
    for (int i = 1, h = 0; i <= n; i ++) {
        int j = sa[rk[i] - 1];
        if (h > 0) h --;
        for (; j + h <= n && i + h <= n; h ++) if (s[i + h] != s[j + h]) break;
        ht[rk[i]] = h;
    }
}

int l[N], r[N];
stack<int> stk;
int main () {
    scanf("%s", s + 1);
    n = strlen(s + 1);

    get_Sa(); get_Ht();

    ll res = (ll)(n - 1) * n * (n + 1) / 2;

    stk = stack<int>();
    for (int i = 2; i <= n; i ++) {
        while (!stk.empty() && ht[stk.top()] > ht[i]) r[stk.top()] = i - 1, stk.pop();
        if (stk.empty()) l[i] = 2;
        else l[i] = stk.top() + 1;
        stk.push(i);
    } while (stk.size()) r[stk.top()] = n, stk.pop();

    for (int i = 2; i <= n; i ++) {
        res -= 2ll * (i - l[i] + 1) * (r[i] - i + 1) * ht[i];
    }
    printf("%lld\n", res);
}

---

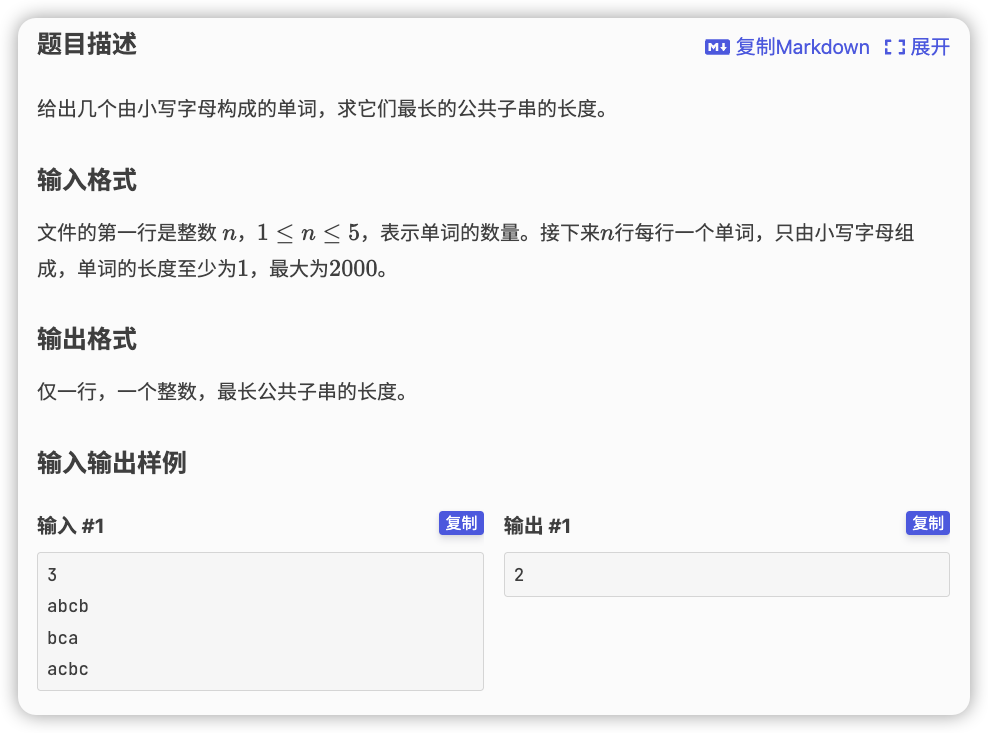
洛谷P5546_公共串

🔗

💡

子串可以用后缀的前缀截出来，公共子串则是几个串某个后缀的 $lcp$
将他们放在一起求出 $height$ 数组，即将其拼接，通过不在限定字符范围内的字符连接
在这个 $height$ 数组内，找出连续的段 $[l,r]$ 保证 $|set_{i=l}^rsa_i|=n$ 即这些 $rank$ 的 $sa$ 值包含了所有的串，说明这一段的 $ht$ 最小值即为一个公共子串的长度
由于固定右端点后，区间越短其 $min$ 越大，所以使用双指针动态缩 $l$ ，对于每一个满足上述要求的区间，求其 $\min\limits_{i=l+1}^rht_i$ ，维护这个最大值即可
最小值的求法可以通过 $ST$ 表、线段树、单调队列....

✅

const int N = 1e6 + 10;
int sa[N], rk[N], rk2[N], ht[N];

int n;
int len[10];
char s[10][N];
int len_str;
char str[N];

int k; inline bool cmp (int i, int j) {
    if (rk[i] != rk[j]) return rk[i] < rk[j];
    int ri = (i + k <= len_str ? rk[i + k] : -1);
    int rj = (j + k <= len_str ? rk[j + k] : -1);
    return ri < rj;
}
inline void get_Sa () {
    for (int i = 1; i <= len_str; i ++) {
        sa[i] = i;
        rk[i] = str[i];
    }
    for (k = 1; k <= len_str; k <<= 1) {
        sort(sa + 1, sa + 1 + len_str, cmp);
        for (int i = 1; i <= len_str; i ++) rk2[sa[i]] = rk2[sa[i - 1]] + cmp(sa[i - 1], sa[i]);
        for (int i = 1; i <= len_str; i ++) rk[i] = rk2[i];
    }
}
inline void get_Ht () {
    for (int i = 1; i <= len_str; i ++) rk[sa[i]] = i;
    ht[1] = 0;
    for (int i = 1, h = 0; i <= len_str; i ++) {
        int j = sa[rk[i] - 1];
        if (h > 0) h --;
        for (; j + h <= len_str && i + h <= len_str; h ++) if (str[j + h] != str[i + h]) break;
        ht[rk[i]] = h;
    }
}

int main () {
    vector<int> v;
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++) { 
        scanf("%s", s[i] + 1);
        len[i] = strlen(s[i] + 1);
    }

    for (int i = 1; i <= n; i ++) {
        for (int j = 1; j <= len[i]; j ++) str[++len_str] = s[i][j];
        if (i < n) str[++len_str] = '0' + i;
        v.push_back(len_str);
    }
    get_Sa(); get_Ht();

    deque<pair<int, int> > dqe;
    int res = 0, sum = 0;
    int cnt[6] = {0};
    int l = 1, lid = lower_bound(v.begin(), v.end(), sa[1]) - v.begin() + 1;
    for (int i = 1; i <= len_str; i ++) {
        int iid = lower_bound(v.begin(), v.end(), sa[i]) - v.begin() + 1;
        sum += !cnt[iid]; cnt[iid] ++;
        while (cnt[lid] > 1) {
            cnt[lid] --;
            l ++;
            lid = lower_bound(v.begin(), v.end(), sa[l]) - v.begin() + 1;
        }
        while (dqe.size() && dqe.front().first <= l) dqe.pop_front();
        while (dqe.size() && dqe.back().second >= ht[i]) dqe.pop_back();
        dqe.push_back({i, ht[i]});
        if (sum == n) res = max(res, dqe.empty() ? 0 : dqe.front().second);
    }
    cout << res << endl;
}

---

EC-Final2021B_BeautifulString

🔗

💡

一个划分其实主要来讲可以看做三部分：$"s_1","s_{23}","s_{56}"$ ，其中 $s_1$ 相等的串有三个，所以可以通过枚举 $s_1,s_{23}$ 开始的位置来求这个一个长度的 $s_1$ 是否可行
由于 $s_{23}$ 是中间的串，所以先枚举 $s_{23}$ 的开始位置，然后枚举 $|s_1|$ ，如果满足 $lcp(s_{23},s_1)\ge |s_1|$ ，则代表这个长度可行，记录一个 $sum[|s_1|]=1$
获取到所有的可行状态后求两次前缀和来得到 ”所有子串“ 的 ”所有分割“ 方案
然后枚举 $s_{56}$ 的开始位置，求 $lcp(s_{23},s_{56})$ 也就是对应这两个串下可行的 $s_{23}$ 最长长度，保证不超过 $s_{23}$ 的长度，然后将其减一后得到 $s_1$ 的最长长度 $l$ ，将 $sum[l]$ 加入答案即可

✅

const int N = 5e3 + 10;

int sa[N], rk[N], rk2[N], ht[N];
inline void get_Sa (const char *s, const int n) {
    for (int i = 1; i <= n; i ++) {
        sa[i] = i;
        rk[i] = s[i];
    }
    for (int k = 1; k <= n; k <<= 1) {
        auto cmp = [&](int i, int j) {
            if (rk[i] != rk[j]) return rk[i] < rk[j];
            int ri = (i + k <= n ? rk[i + k] : -1);
            int rj = (j + k <= n ? rk[j + k] : -1);
            return ri < rj;
        };
        sort(sa + 1, sa + 1 + n, cmp);
        for (int i = 1; i <= n; i ++) rk2[sa[i]] = rk2[sa[i - 1]] + cmp(sa[i - 1], sa[i]);
        for (int i = 1; i <= n; i ++) rk[i] = rk2[i];
    }
}
int st[N][30];
inline void get_Ht (const char *s, const int n) {
    for (int i = 1; i <= n; i ++) rk[sa[i]] = i;
    for (int i = 1, h = 0; i <= n; i ++) {
        if (h > 0) h --;
        int j = sa[rk[i] - 1];
        for (; i + h <= n && j + h <= n; h ++) if (s[i + h] != s[j + h]) break;
        ht[rk[i]] = h;
    }
    int k = 32 - __builtin_clz(n) - 1;
    for (int i = 1; i <= n; i ++) st[i][0] = ht[i];
    for (int j = 1; j <= k; j ++) {
        for (int i = 1; i + (1 << j) - 1 <= n; i ++) {
            st[i][j] = min(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
        }
    }
}
inline int Lcp (int i, int j) {
    if (rk[i] + 1 > rk[j]) swap(i, j);
    int l = rk[i] + 1, r = rk[j];
    int k = 32 - __builtin_clz(r - l + 1) - 1;
    return min(st[l][k], st[r - (1 << k) + 1][k]);
}

int n;
char s[N];

int sum[N];
inline void Solve () {
    scanf("%s", s + 1);
    n = strlen(s + 1);
    
    for (int i = 1; i <= n; i ++) sa[i] = rk[i] = rk2[i] = ht[i] = 0;
    get_Sa(s, n);
    get_Ht(s, n);

    ll res = 0;
    for (int s2 = 2; s2 + 3 <= n; s2 ++) {
        for (int i = 1; i <= n; i ++) sum[i] = 0;
        for (int len = 1; len < s2; len ++) {
            if (Lcp(s2 - len, s2) >= len) sum[len] = 1;
        }
        for (int i = 1; i <= n; i ++) sum[i] += sum[i - 1];
        for (int i = 1; i <= n; i ++) sum[i] += sum[i - 1];
        for (int s5 = s2 + 3; s5 <= n; s5 ++) {
            res += sum[max(0, min(s5 - s2 - 1, Lcp(s5, s2)) - 1)];
        }
    }
    printf("%lld\n", res);
}

---