#

---

洛谷P1390_公约数的和

🔗

💡

看见 $gcd$ 首先把式子变成我们常用的莫反套路

$$\begin{aligned} &\sum\limits_{i=1}^n\sum\limits_{j=i+1}^ngcd(i,j)\\ =&\sum\limits_{k=1}^n\sum\limits_{i=1}^n\sum\limits_{j=i+1}^n[gcd(i,j)=k]*k\\ =&\sum\limits_{k=1}^nk\frac{\sum\limits_{i=1}^n\sum\limits_{j=1}^n[gcd(i,j)=k]-1}2\\ =&\sum\limits_{k=1}^nk\frac{\sum\limits_{i=1}^{\left\lfloor\frac{n}{k}\right\rfloor}\sum\limits_{j=1}^{\left\lfloor\frac{n}{k}\right\rfloor}[gcd(i,j)=1]-1}2 \end{aligned}$$

减 $1$ 是为了减去 $i=j=1$ 的情况，除 $2$ 是为了消除重复枚举一对的情况

那么对于里面的
$\sum\limits_{i=1}^{\left\lfloor\frac{n}{k}\right\rfloor}\sum\limits_{j=1}^{\left\lfloor\frac{n}{k}\right\rfloor}[gcd(i,j)=1]$
我们让
$n'=\left\lfloor\frac{n}{k}\right\rfloor$
可以感性地利用莫比乌斯反演化简为
$\sum\limits_{d=1}^{n'}\mu(d)\left \lfloor \frac {n'}d \right \rfloor \left \lfloor \frac {n'}d \right \rfloor$
(具体操作看这里)

由于 $n'k=n$ 是一个曲线函数，则总时间复杂度不会太高
我们对上面化简后的式子写成一个函数 $Solve()$
则
$res = \sum\limits_{k=1}^nk\frac{Solve()-1}{2}$
$Solve()$ 里面随便杜教筛一下随便数论分块一下

✅

const ll N = 2e6 + 10;
namespace Number {
        ll mu[N], sum[N];
        bool notprime[N];
        vector<ll> prime;
        inline void Sieve () {
                mu[1] = notprime[1] = notprime[0] = 1;
                for ( ll i = 2; i < N; i ++ ) {
                        if ( !notprime[i] ) 
                                prime.push_back(i),
                                mu[i] = -1;
                        for ( ll j = 0; j < prime.size() && i * prime[j] < N; j ++ ) {
                                notprime[i * prime[j]] = 1;
                                if ( i % prime[j] == 0 ) break;
                                mu[i * prime[j]] = -mu[i];
                        }
                }
                for ( ll i = 1; i < N; i ++ ) sum[i] = sum[i - 1] + mu[i]; 
        }
        inline ll g ( ll k, ll x ) { return k / (k / x); }

        map<ll, ll> S;
        inline ll SUM ( ll x ) {
                if ( x < N ) return sum[x];
                if ( S[x] ) return S[x];
                ll res = 1;
                for ( ll L = 2, R; L <= x; L = R + 1 ) {
                        R = min ( x, g(x, L) );
                        res -= (R - L + 1) * SUM(x / L);
                } return S[x] = res;
        }
} using namespace Number;

inline ll Solve ( ll n, ll k ) {
        ll res = 0; n /= k;
        for ( ll l = 1, r; l <= n; l = r + 1 ) {
                r = min(n, g(n, l));
                res += (SUM(r) - SUM(l - 1)) * (n / l) * (n / l);
        }
        return res;
}

int main () {
        ios::sync_with_stdio(false); Sieve ();
        ll n; cin >> n;
        ll res = 0;
        for ( ll k = 1; k <= n; k ++ ) {
                res += k * (Solve(n, k) - 1) / 2;
        }
        cout << res << endl;
}

---

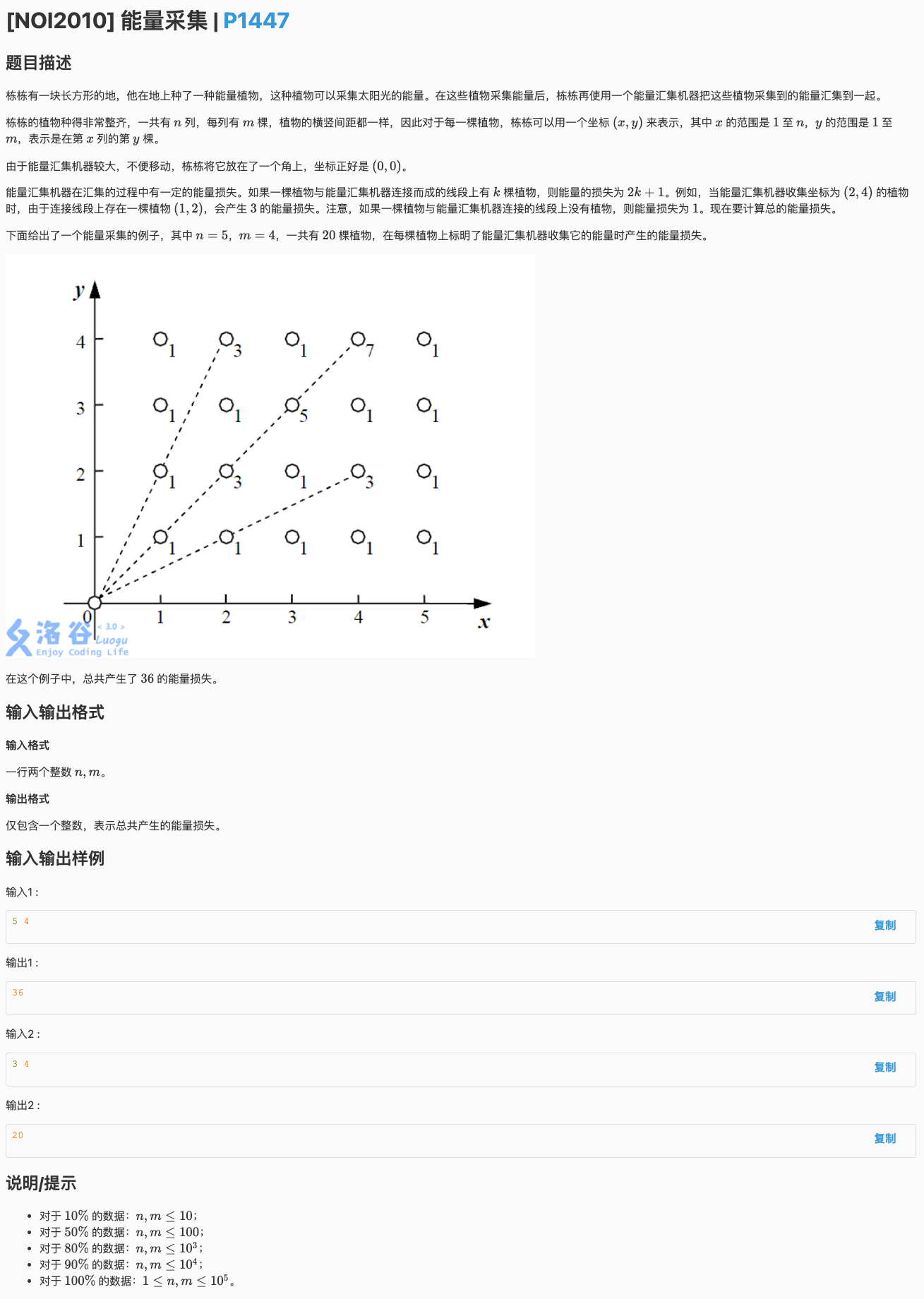
洛谷P1447_能量采集

🔗

💡

这个和仪仗队那个很像啊
$(i,j)$ 位置上的点它前面挡住的人数就是 $gcd(i,j)$
所以我们把柿子抽象出来
$\begin{aligned}main(n,m)=&\sum\limits_{i=1}^n\sum\limits_{j=1}^m(2*(i,j)-1)\\=&2\sum\limits_{i=1}^n\sum\limits_{j=1}^m(i,j)-nm\end{aligned}$
对于 $solve(n,m)=\sum\limits_{i=1}^n\sum\limits_{j=1}^m(i,j)=\sum\limits_{k=1}^{mn}k\sum\limits_{i=1}^n\sum\limits_{j=1}^m[(i,j)=k]$
感性地莫反一下
$f(k)=\sum\limits_{i=1}^n\sum\limits_{j=1}^m[(i,j)=k]$
$F(k)=\sum\limits_{i=1}^n\sum\limits_{j=1}^m[k|(i,j)]=\frac nk\frac mk$
$f(k)=\sum\limits_{d=1}^{\frac{mn}k}\mu(d)\frac n{dk}\frac m{dk}$

$\begin{aligned}&solve(n,m)\\=&\sum\limits_{k=1}^{mn}k\sum\limits_{d=1}^{\frac nk}\mu(d)\frac n{dk}\frac m{dk}\quad\quad&(T=dk)\\=&\sum\limits_{k=1}^{mn}k\sum\limits_{\frac Tk}^{\frac {mn}k}\mu(\frac Tk)\frac nT\frac mT\\=&\sum\limits_{T=1}^{mn}\frac nT\frac mT\sum\limits_{k|T}k\mu(\frac Tk)\end{aligned}$
$\sum\limits_{k|T}k\mu(\frac Tk)$ 感性地狄利克雷卷积一下 $=(\mu*Id)(T)=\phi(T)$
$=\sum\limits_{T=1}^{mn}\frac nT\frac mT\phi(T)$

数不大直接暴力跑就行

✅

namespace Number {
        const int N = 1e5 + 10;
        int phi[N];
        bool not_prime[N];
        vector<int> prime;

        inline void Sieve () {
                not_prime[0] = not_prime[1] = phi[1] = 1;
                for ( int i = 2; i < N; i ++ ) {
                        if ( !not_prime[i] ) 
                                prime.push_back(i),
                                phi[i] = i - 1;
                        for ( int j = 0; j < prime.size() && i * prime[j] < N; j ++ ) {
                                not_prime[i * prime[j]] = 1;
                                if ( i % prime[j] == 0 ) {
                                        phi[i * prime[j]] = phi[i] * prime[j];
                                        break;
                                } else phi[i * prime[j]] = phi[i] * (prime[j] - 1);
                        }
                }
        }
} using namespace Number;

int main () {
        Sieve ();
        int n, m; cin >> n >> m;
        ll res = 0;
        for ( int i = 1; i <= min (m, n); i ++ ) {
                res += (ll)(m / i) * (n / i) * phi[i];
        }
        cout << res * 2 - (ll)n * m << endl;
}

---

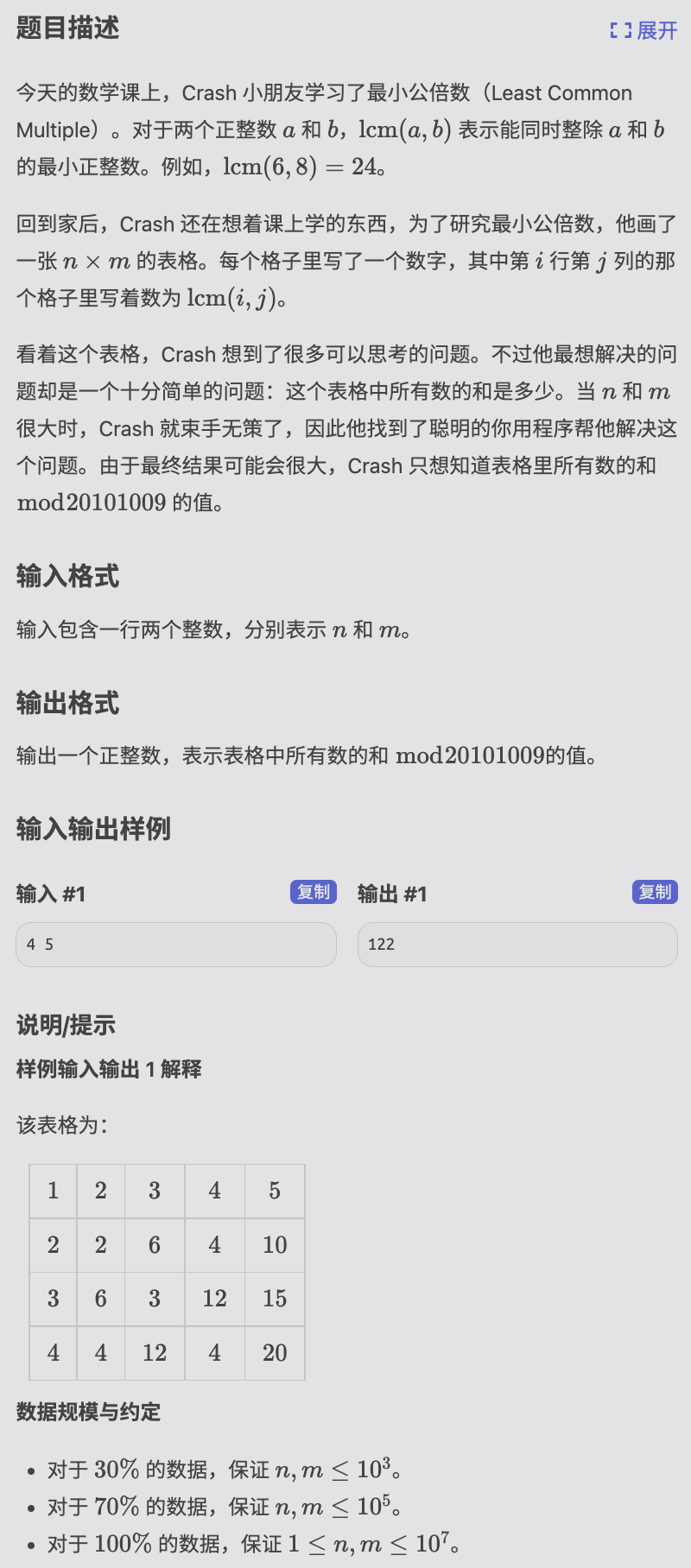
洛谷P1829_Crash的数字表格

🔗

💡

$(1)\\\begin{aligned}mian(n,m)=&\sum\limits_{i=1}^n\sum\limits_{j=1}^mlcm(i,j)\\=&\sum\limits_{k=1}^{mn}\sum\limits_{i=1}^n\sum\limits_{j=1}^m\frac {i\times j\times[(i,j)=k]}k\end{aligned}$

$i'=\frac ik,\;j'=\frac jk$

${\color{red}main(n,m)}=\sum\limits_{k=1}^{mn}k\sum\limits_{i'=1}^{\left\lfloor\frac nk\right\rfloor}\sum\limits_{j'=1}^{\left\lfloor\frac mk\right\rfloor}i'\times j'\times [(i',j')=1]{\color{red}=\sum\limits_{k=1}^{mn}ksolve(\left\lfloor\frac nk\right\rfloor,\left\lfloor\frac mk\right\rfloor)}$

$(2)\\solve(n,m)=\sum\limits_{i=1}^n\sum\limits_{j=1}^mi\times j\times [gcd(i,j)=1]$

$f(k)=\sum\limits_{i=1}^n\sum\limits_{j=1}^m[(i,j)=k]ij$

$F(k)=\sum\limits_{i=1}^n\sum\limits_{j=1}^m[k\mid(i,j)]ij$

$i',j'$ 枚举 $k$ 倍数， $n'=\left\lfloor\frac nk\right\rfloor,\;m'=\left\lfloor\frac mk\right\rfloor,\;i'=\frac ik,\;j'=\frac jk,\;i=i'k,\;j=j'k$

$F(k)=\sum\limits_{i'=1}^{n'}\sum\limits_{j'=1}^{m'}i'kj'k=k^2\frac{n'(1+n')}2\frac{m'(1+m')}2=\frac{k^2n'(1+n')m'(1+m')}4$

$f(k)=\sum\limits_{k\mid d}\mu(\frac dk)F(d)$

${\color{red}solve(n,m)}=f(1)=\sum\limits_{d=1}^{mn}\mu(d)F(d)=\sum\limits_{d=1}^{mn}\mu(d)\frac{d^2\left\lfloor\frac nd\right\rfloor(1+\left\lfloor\frac nd\right\rfloor)\left\lfloor\frac md\right\rfloor(1+\left\lfloor\frac md\right\rfloor)}4{\color{red}=\sum\limits_{d=1}^{mn}\mu(d)d^2calc(\left\lfloor\frac nd\right\rfloor,\left\lfloor\frac md\right\rfloor)}$

$(3)\\calc(n,m)=\frac{n(1+n)m(1+m)}4$

综上所述

$\left\{\begin{aligned}&main(n,m)=\sum\limits_{k=1}^{mn}ksolve(\left\lfloor\frac nk\right\rfloor,\left\lfloor\frac mk\right\rfloor)\\&solve(n,m)=\sum\limits_{d=1}^{mn}\mu(d)d^2calc(\left\lfloor\frac nd\right\rfloor,\left\lfloor\frac md\right\rfloor)\end{aligned}\right.$

$\left\{\begin{aligned}&(1)\quad mian(n,m)=\sum\limits_{i=1}^n\sum\limits_{j=1}^mlcm(i,j)\\&(2)\quad solve(n,m)=\sum\limits_{i=1}^n\sum\limits_{j=1}^mi\times j\times [gcd(i,j)=1]\\&(3)\quad calc(n,m)=\frac {n(1+n)m(1+m)}4\end{aligned}\right.$

剩下的就是利用这个公式进行两重数论分块写了

✅

namespace Number {
        const ll N = 1e7 + 10;
        const ll mod = 20101009;
        ll mu[N], sum[N];
        bool notprime[N];
        vector<ll> prime;
        inline ll ksm ( ll a, ll b ) {
                ll res = 1;
                while ( b ) {
                        if ( b & 1 ) res = res * a % mod;
                        a = a * a % mod;
                        b >>= 1;
                }
                return res;
        }
        inline void Sieve () {
                notprime[0] = notprime[1] = mu[1] = 1;
                for ( ll i = 2; i < N; i ++ ) {
                        if ( !notprime[i] ) 
                                prime.push_back(i),
                                mu[i] = -1;
                        for ( ll j = 0; j < prime.size() && prime[j] * i < N; j ++ ) {
                                notprime[i * prime[j]] = 1;
                                if ( i % prime[j] == 0 ) break;
                                mu[i * prime[j]] = -mu[i];
                        }
                }
                for ( int i = 1; i < N; i ++ ) sum[i] = (sum[i - 1] + (mu[i] + mod) * i % mod * i % mod) % mod;
        }
        inline ll g ( ll n, ll k ) { return n / (n / k); }
        inline ll inv ( ll x ) { return ksm(x, mod - 2); }
} using namespace Number;

inline ll Calc ( ll x, ll y ) {
        return (1 + x) * x % mod * (1 + y) % mod * y % mod * inv(4) % mod;
}

inline ll Solve (ll n, ll m, ll k) {
        n /= k, m /= k;
        ll mn = min ( m, n );
        ll res = 0;
        for ( ll l = 1, r; l <= mn; l = r + 1 ) {
                r = min(g(n, l), g(m, l));
                res = (res + (sum[r] - sum[l - 1] + mod) % mod * Calc(n / l, m / l) % mod) % mod;
        }
        return res;
}

int main () {
        ios::sync_with_stdio(false); Sieve ();
        ll n, m; cin >> n >> m;
        ll mn = min ( m, n );
        ll res = 0;
        for ( ll l = 1, r; l <= mn; l = r + 1 ) {    
                r = min(g(n, l), g(m, l));
                res = (res + ( l + r ) * ( r - l + 1 ) % mod * inv(2) % mod * Solve ( n, m, l ) % mod) % mod;
        }
        cout << res << endl;
}

---

洛谷P2158_仪仗队

🔗

https://www.luogu.com.cn/problem/P2158

💡

我们要求得：
$\sum\limits_{i = 1}^n\sum\limits_{j=1}^n[gcd(i, j) = 1]$

所以设：
$f(x) =\sum\limits_{i=1}^n\sum\limits_{j=1}^n[gcd(i,j)=x]$

为使：
$F(x) = \sum\limits_{x|d}f(d)$

设：
$F(x)=\sum\limits_{i=1}^n\sum\limits_{j=1}^n[x|gcd(i,j)]$

根据莫比乌斯阿反演定理得
$f(x)=\sum\limits_{x|d}\mu(\frac dx)F(d)$

可以发现：
$F(d)=\sum\limits_{i=1}^n[d|i] * \sum\limits_{j=1}^n[d|j] = \left \lfloor \frac nd \right \rfloor * \left \lfloor \frac nd \right \rfloor$

所以化简为：
$f(x)=\sum\limits_{x|d}\mu(\frac dx)\left \lfloor \frac nd \right \rfloor \left \lfloor \frac nd \right \rfloor$

我们要求的是$f(1)$

所以：
$f(1)=\sum\limits_{d=1}^{n}\mu(d)\left \lfloor \frac nd \right \rfloor \left \lfloor \frac nd \right \rfloor$

✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'

#define CHIVAS_ int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
//#define map unordered_map

#define _int(a) int a; cin >> a
#define  _ll(a) ll a; cin >> a
#define _char(a) char a; cin >> a
#define _string(a) string a; cin >> a
#define _vectorInt(a, n) vector<int>a(n); cin >> a
#define _vectorLL(a, b) vector<ll>a(n); cin >> a

#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cin >> cass; cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

template<typename T> inline void Read(T &x){T f = 1; x = 0;char s = getchar();while(s < '0' || s > '9'){if(s == '-') f = -1; s = getchar();}while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}x*=f;}
template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
template<typename T>             vector<T>& operator--            (vector<T> &v){for (auto& i : v) --i;            return  v;}
template<typename T>             vector<T>& operator++            (vector<T> &v){for (auto& i : v) ++i;            return  v;}
template<typename T>             istream& operator>>(istream& is,  vector<T> &v){for (auto& i : v) is >> i;        return is;}
template<typename T>             ostream& operator<<(ostream& os,  vector<T>  v){for (auto& i : v) os << i << ' '; return os;}


//欧拉函数-------------------------------------------------------------------------------------------------------------------------

const int maxn = 40010;
bool isprime[maxn];
vector<int> prime;
int phi[maxn];

inline void GET_PHI(){
        phi[1] = 1;
        isprime[0] = isprime[1] = 1;
        for(int i = 2; i <= maxn; i ++){
                if(!isprime[i]) prime.push_back(i), phi[i] = i - 1;//质数的欧拉值为本身-1
                for(int j = 0; j < prime.size() && i * prime[j] <= maxn; j ++){
                        isprime[i * prime[j]] = true;
                        if(i % prime[j] == 0){
                                phi[i * prime[j]] = phi[i] * prime[j];//积性函数性质
                                break;
                        }else phi[i * prime[j]] = phi[i] * (prime[j] - 1);
                }
        }
}

inline void solve1(){GET_PHI();
        int n; cin >> n;
        int res = 0;
        for(int i = 1; i < n; i ++) res += phi[i];//欧拉值累加
        cout << (n == 1? 0 : (res << 1 | 1)) << endl;
}

//--------------------------------------------------------------------------------------------------------------------------------


//莫比乌斯反演----------------------------------------------------------------------------------------------------------------------

const int maxn = 40010;

bool isprime[maxn];
ll mu[maxn], sum[maxn];//Mobius函数表
ll n;
vector<ll> prime;

inline void Mobius(){//线性筛
        isprime[0] = isprime[1] = 1;
        mu[1] = 1;//特判mu[i] = 1
        for(ll i = 2; i <= maxn; i ++){
                if( !isprime[i] ) mu[i] = -1, prime.push_back(i);//质数的质因子只有自己，所以为-1
                for(ll j = 0; j < prime.size() && i * prime[j] <= maxn; j ++){
                        isprime[i * prime[j]] = 1;
                        if(i % prime[j] == 0) break;
                        mu[i * prime[j]] = -mu[i];//积性函数性质： (i * prime[j])多出来一个质数因数(prime[j])，修正为 (-1) * mu[i]
                }
        }
        //剩余的没筛到的是其他情况，为0

        for(int i = 1; i < maxn; i ++) sum[i] = sum[i - 1] + mu[i];//记录前缀和，为了整除分块
}

inline ll g(ll k, ll x){ return k / (k / x); }//整除分块的r值

inline void solve2(){Mobius();
        cin >> n; n --;
        if(n == 0){
                cout << 0 << endl;
                return;
        }
        ll res = 0;
        for(ll l = 1, r; l <= n; l = r + 1){//整出分块累加
                r = MIN(n, g(n, l));
                res += (ll)(sum[r] - sum[l - 1]) * (n / l) * (n / l);//公式
        }
        cout << res + 2 << endl;//+两个坐标轴的贡献

}

//--------------------------------------------------------------------------------------------------------------------------------

CHIVAS_{
        solve1();
        _REGAL;
}

---

洛谷P2522_Problemb

🔗

💡

题意让求:
$f(k)=\sum_{x=A}^B\sum_{y=C}^D[gcd(x,y)=k]$

为了满足：
$F(k)=\sum_{n|d}f(d)$

设：
$F(k)=\sum_{x=A}^B\sum_{x=C}^D[k|gcd(x,y)]$

为使枚举的$x,y$均为$k$的倍数
令$x' = \frac xk,\quad y' = \frac yk$，我们枚举倍数
则$F(k)=\sum_{x'=\frac{A - 1}{k}}^{\frac Bk}\sum_{y'=\frac{C-1}{k}}^{\frac Dk}=(\left \lfloor \frac Bk \right \rfloor-\left \lfloor \frac{A-1}k \right \rfloor)*(\left \lfloor \frac Dk\right \rfloor -\left \lfloor \frac{C-1}k \right \rfloor)$

根据莫比乌斯反演定理得：
$f(k)=\sum_{k|d}\mu(\frac dk)F(d)$
为了使枚举到的d均为k的倍数
我们设$d' = \frac dk\quad H'=\frac Hk$，此时$d=d'k$

则$f(k)=\sum_{d'=1}^{min(\frac Bk,\frac Dk)}\mu(d')F(d'k)$

$\because F(d'k)=(\left \lfloor \frac B{d'k} \right \rfloor-\left \lfloor \frac{A-1}{d'k} \right \rfloor)*(\left \lfloor \frac D{d'k}\right \rfloor -\left \lfloor \frac{C-1}{d'k} \right \rfloor$

令$A'=\frac{A-1}k,\quad B'=\frac Bk,\quad C'=\frac{C-1}k,\quad D'=\frac Dk$

$\therefore f(k)=\sum_{d'=1}^{min(B',D')}\mu(d')(\left \lfloor \frac {B'}{d'} \right \rfloor-\left \lfloor \frac{A'}{d'} \right \rfloor)(\left \lfloor \frac {D'}{d'}\right \rfloor -\left \lfloor \frac{C'}{d'} \right \rfloor$

✅

const ll maxn = 2e6 + 10;//杜教筛的安全maxn

ll mu[maxn];//Mobius函数表
vector<ll> prime;
ll isprime[maxn];
ll sum[maxn];//mu的前缀和

inline void Mobius(){//线性筛
        mu[1] = 1;//特判mu[i] = 1
        isprime[0] = isprime[1] = 1;
        for(ll i = 2; i < maxn; i ++){
                if(!isprime[i]) mu[i] = -1, prime.push_back(i);//质数的质因子只有自己，所以为-1
                for(ll j = 0; j < prime.size() && i * prime[j] < maxn; j ++){
                        isprime[i * prime[j]] = 1;
                        if(i % prime[j] == 0) break;
                        mu[i * prime[j]] = - mu[i];//积性函数性质： (i * prime[j])多出来一个质数因数(prime[j])，修正为 (-1) * mu[i]
                }
        }
        //剩余的没筛到的是其他情况，为0
        for(ll i = 1; i < maxn; i ++) sum[i] = sum[i - 1] + mu[i];//记录前缀和，为了整除分块
}

inline ll g(ll k, ll x){ return k / (k / x); }//整除分块的r值


map<ll, ll> S;//杜教筛处理出的前缀和


inline ll SUM(ll x){//杜教筛
        if(x < maxn) return sum[x];
        if(S[x]) return S[x];
        ll res = 1;
        for(ll L = 2, R; L <= x; L = R + 1){
                R = MIN(x, g(x, L));
                res -= (R - L + 1) * SUM(x / L);//模数相减会出负数，所以加上一个mod
        }return S[x] = res;
}

inline void solve(){
        ll A, B, C, D, K; cin >> A >> B >> C >> D >> K;
        A = (A - 1) / K, B = B / K, C = (C - 1) / K, D = D / K;
        ll n = MIN(B, D);
        ll res = 0;
        for(ll l = 1, r; l <= n; l = r + 1){
                ll cmp1 = (A / l)? MIN(g(A, l), g(B, l)) : g(B, l);//防止除0
                ll cmp2 = (C / l)? MIN(g(C, l), g(D, l)) : g(D, l); //防止除0
                r = MIN(cmp1, cmp2);//确定块右端点

                res += (sum[r] - sum[l - 1]) * (B / l - A / l) * (D / l - C / l);//公式
        }cout << res << endl;
}

CHIVAS_{Mobius();
        ll cass;
        EACH_CASE(cass){
                solve();
        }
        _REGAL;
}

---

洛谷P2568_GCD

🔗

💡

$\begin{aligned}&\sum\limits_{i=1}^n\sum\limits_{j=1}^n[gcd(i,j)\in\{prime\}]\\=&\sum\limits_{p\in \{prime\}}^{\le n}\sum\limits_{i=1}^n\sum\limits_{j=1}^n[gcd(i,j)=p]\\=&\sum\limits_{p\in\{prime\}}^{\le n}\sum\limits_{i=1}^{\left\lfloor\frac np\right\rfloor}\sum\limits_{j=1}^{\left\lfloor\frac np\right\rfloor}[gcd(i,j)=1]\end{aligned}$
对于$\sum\limits_{i=1}^{\left\lfloor\frac np\right\rfloor}\sum\limits_{j=1}^{\left\lfloor\frac np\right\rfloor}[gcd(i,j)=1]$
我们可以使用莫反变成$\mu(d)\left\lfloor\frac nd\right\rfloor^2$
（具体操作请看这里） 那么就是让求
$\sum\limits_{p\in\{prime\}}^{\le n}\sum\limits_{d=1}^{\left\lfloor\frac np\right\rfloor}\mu(d)\left\lfloor\frac nd\right\rfloor^2$
素数表直接用莫比乌斯函数打表得到的即可

✅

namespace Number {
        const ll N = 1e7 + 10;
        bool notprime[N];
        ll mu[N];
        vector<ll> prime;
        ll sum[N];

        inline void Sieve () {
                notprime[1] = notprime[0] = mu[1] = 1;
                for ( ll i = 2; i < N; i ++ ) {
                        if ( !notprime[i] ) 
                                prime.push_back(i),
                                mu[i] = -1;
                        for ( ll j = 0; j < prime.size() && i * prime[j] < N; j ++ ) {
                                notprime[i * prime[j]] = 1;
                                if ( i % prime[j] == 0 ) continue;
                                mu[i * prime[j]] = -mu[i];
                        }
                }
                for ( ll i = 1; i < N; i ++ ) sum[i] = sum[i - 1] + mu[i];
        }

        inline ll g ( ll k, ll x ) { return k / (k / x); }

        map<ll, ll> S;
        inline ll SUM ( ll x ) {
                if ( x < N ) return sum[x];
                if ( S[x] ) return S[x];
                ll res = 1;
                for ( ll L = 2, R; L <= x; L = R + 1 ) {
                        R = min ( x, g(x, L) );
                        res -= (R - L + 1) * SUM(x / L);
                } return S[x] = res;
        }
} using namespace Number;

inline ll Solve ( ll n, ll k ) {
        n /= k;
        ll res = 0;
        for ( ll l = 1, r; l <= n; l = r + 1 ) {
                r = g(n, l);
                res += (SUM(r) - SUM(l - 1)) * (n / l) * (n / l);
        }
        return res;
}

int main () {
        ios::sync_with_stdio(false); Sieve ();
        int n; cin >> n;
        ll res = 0;
        for ( int i = 0; i < prime.size() && prime[i] <= n; i ++ ) res += Solve (n, prime[i]);
        cout << res << endl;
}

---

洛谷P3172_选数

🔗

https://www.luogu.com.cn/problem/P3172

💡

题目让求
$\sum\limits_{i_1=L}^H\sum\limits_{i_2=L}^H....\sum\limits_{i_n=L}^H[gcd=k]$

所以我们令:
$f(k)=\sum\limits_{i_1=L}^H\sum\limits_{i_2=L}^H....\sum\limits_{i_n=L}^H[gcd=k]$

为满足:
$F(k)=\sum\limits_{k|d}f(d)$

令：
$F(k) = \sum\limits_{i_1=L}^H\sum\limits_{i_2=L}^H....\sum\limits_{i_n=L}^H[k|gcd]$

为了使每个i都是k的倍数保证每次枚举都是可以使得$[k|gcd]=1$
我们设$i'=\frac ik$，枚举$i'$，也就是k的倍数
得到：
$F(k) = \sum\limits_{i_1'=\frac{L-1}{k}}^\frac Hk\sum\limits_{i_2'=\frac{L-1}{k}}^\frac Hk....\sum\limits_{i_n'=\frac{L-1}{k}}^\frac Hk1$

可以化简为：
$F(k)=(\left \lfloor \frac{H}{k} \right \rfloor - \left \lfloor \frac{L-1}{k} \right \rfloor )^n$

由莫反定理得：
$f(k)=\sum\limits_{k|d}\mu(\frac dk)F(d)$
为了使枚举到的d均为k的倍数
我们设$d' = \frac dk\quad H'=\frac Hk\quad L'=\frac{L-1}{k}$，此时$d=d'k$

则：
$f(k)=\sum\limits_{d'=1}^{H'}\mu(d')F(d'k)$

此时$F(d'k)=(\left \lfloor \frac{H}{d'k} \right \rfloor - \left \lfloor \frac{L-1}{d'k} \right \rfloor )^n$

所以：
$f(k)=\sum_{d'=1}^{H'}\mu(d')(\left \lfloor \frac{H'}{d'} \right \rfloor - \left \lfloor \frac{L'}{d'} \right \rfloor )^n$

因为$H'$可能会很大，所以我们整除分块
同时需要前缀和以便得到很大的数的莫比乌斯函数
这里用杜教筛计算前缀和即可

✅

#include <iostream>
#include <vector>
#include <map>
#define ll long long

using namespace std;

const ll maxn = 2e6 + 10;//杜教筛的安全maxn
const ll mod = 1e9 + 7;

ll mu[maxn];//Mobius函数表
vector<ll> prime;
ll isprime[maxn];
ll sum[maxn];//mu的前缀和

inline void Mobius(){//线性筛
        mu[1] = 1;//特判mu[i] = 1
        isprime[0] = isprime[1] = 1;
        for ( ll i = 2; i < maxn; i ++ ) {
                if ( !isprime[i] ) mu[i] = -1, prime.push_back(i);//质数的质因子只有自己，所以为-1
                for ( ll j = 0; j < prime.size() && i * prime[j] < maxn; j ++ ) {
                        isprime[i * prime[j]] = 1;
                        if ( i % prime[j] == 0 ) break;
                        mu[i * prime[j]] = - mu[i];//积性函数性质： (i * prime[j])多出来一个质数因数(prime[j])，修正为 (-1) * mu[i]
                }
        }
        //剩余的没筛到的是其他情况，为0
        for ( ll i = 1; i < maxn; i ++ ) sum[i] = sum[i - 1] + mu[i];//记录前缀和，为了整除分块
}

map<ll, ll> S;//杜教筛处理出的前缀和

inline ll g ( ll k, ll x ) { return k / (k / x); }//整除分块的r值

inline ll SUM ( ll x ) {//杜教筛
        if ( x < maxn ) return sum[x];
        if ( S[x]) return S[x];
        ll res = 1;
        for ( ll L = 2, R; L <= x; L = R + 1 ) {
                R = min ( x, g ( x, L ) );
                res = ( res - (R - L + 1) * SUM(x / L) % mod + mod ) % mod;//模数相减会出负数，所以加上一个mod
        }return S[x] = res;
}

inline ll ksm ( ll a, ll b ) {//计算那个n次方
        ll res = 1;
        while ( b ) {
                if ( b & 1 ) res = res * a % mod;
                a = a * a % mod;
                b >>= 1;
        } return res;
}

int main () { Mobius();
        ll n, k, L, H; cin >> n >> k >> L >> H; L = (L - 1) / k, H /= k;//L直接处理为L'，H直接处理为H'
        ll res = 0;
        for ( ll l = 1, r; l <= H; l = r + 1 ) {

                if ( L / l) r = min(g(L, l), g(H, l));//防止出现除0的情况
                else r =  g ( H, l );

                res = ( res + ( SUM ( r ) - SUM ( l - 1 ) + mod ) * ksm ( H / l - L / l, n ) % mod ) % mod;//公式，但模数相减会出负数，所以加上一个mod
        } cout << res << endl;
}

---

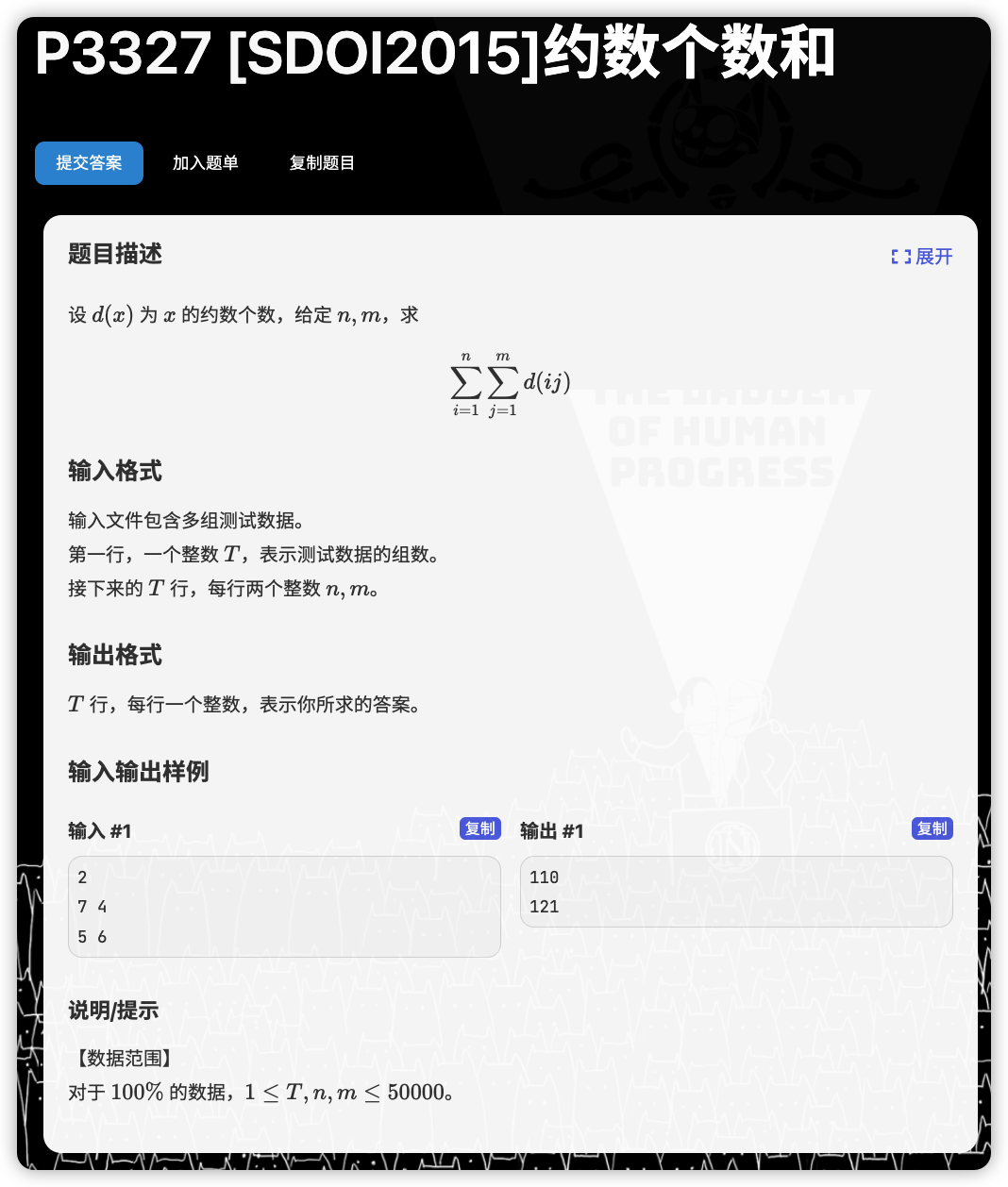
洛谷P3327_约数个数和

🔗

💡

$\begin{aligned} &\sum\limits_{i=1}^n\sum\limits_{j=1}^md(ij)\\ =&\sum\limits_{i=1}^n\sum\limits_{j=1}^m\sum\limits_{a|i}\sum\limits_{b|j}[(a,b)=1]\qquad&(d(ij)=\sum\limits_{a|i}\sum\limits_{b|j}[(a,b)=1])\\ =&\sum\limits_{i=1}^n\sum\limits_{j=1}^m\sum\limits_{a|i}\sum\limits_{b|j}\sum\limits_{x|(a,b)}\mu(x)&(\sum\limits_{y|x}\mu(y)=[x=1])\end{aligned}$
将 $x$ 提前，$i,j$ 枚举 $x$ 倍数
中间跳过了 $a,b$ 所以对于 $i$ 是要出现 $d(\frac ix)$ 次，对于 $j$ 是要出现 $d(\frac jx)$ 次
则原式
$=\sum\limits_{i=1}^n\sum\limits_{j=1}^m\sum\limits_{x|i,x|j}\mu(x)d(\frac ix)d(\frac jx)$
$=\sum\limits_{x=1}^{min(n,m)}\mu(x)\sum\limits_{x|i}d(\frac xi)\sum\limits_{x|j}d(\frac xj)$
令 $i=\frac ix,j=\frac jx$ 则原式
$=\sum\limits_{x=1}^{min(n,m)}\mu(x)\sum\limits_{i=1}^{\left\lfloor\frac nx\right\rfloor}d(i)\sum\limits_{j=1}^{\left\lfloor\frac mx\right\rfloor}d(j)$
令 $sumd(x)=\sum\limits_{i=1}^xd(i)$
则原式
$=\sum\limits_{x=1}^{min(n,m)}\mu(x)sumd(\left\lfloor\frac nx\right\rfloor)sumd(\left\lfloor\frac mx\right\rfloor)$

我们求 $d(i)$ 可以使用唯一分解定理 $i=p_1^{a_1}p_2^{a_2}...p_k^{a_k}\rightarrow d(i)=\sum\limits_{i=1}^k(a_i+1)$ 进行预处理，$sumd(i)$ 即为前缀和
这样我们就可以对这个最终式子进行数论分块了

✅

const int N = 5e4 + 10;

namespace Number {
        bool ntp[N];
        vector<int> prime;
        int mu[N];
        ll d[N];
        map<int, int> cntp[N];
        inline void Sieve () {
                ntp[0] = ntp[1] = true;
                mu[1] = 1;
                for (int i = 2; i < N; i ++) {
                        if (!ntp[i]) prime.push_back(i), mu[i] = -1;
                        for (int j = 0; j < prime.size() && i * prime[j] < N; j ++) {
                                ntp[i * prime[j]] = 1;
                                if (i % prime[j] == 0) break;
                                mu[i * prime[j]] = -mu[i];
                        }
                }
                for (int i = 1; i < N; i ++) d[i] = 1;
                for (int p : prime) {
                        for (int j = p; j < N; j += p) {
                                int tmp = j;
                                while (tmp % p == 0) tmp /= p, cntp[j][p] ++;
                        }
                }
                for (int i = 1; i < N; i ++) {
                        for (auto j : cntp[i]) {
                                d[i] *= 1ll * j.second + 1;
                        }
                }
                for (int i = 1; i < N; i ++) mu[i] += mu[i - 1], d[i] += d[i - 1];
        }
} using namespace Number;

inline int g (int k, int x) {return k / (k / x);}

inline void Solve () {
        int n, m; cin >> n >> m;
        ll res = 0; int mn = min(n, m);
        for (int l = 1, r; l <= mn; l = r + 1) {
                r = min(g(n, l), g(m, l));
                res += 1ll * (mu[r] - mu[l - 1]) * d[n / l] * d[m / l];
        }
        cout << res << endl;
}

int main () {
        cin.tie(0)->sync_with_stdio(0);
        cin.exceptions(cin.failbit);

        Sieve();

        int cass; cin >> cass; while (cass --) {
                Solve();
        }
}

---

洛谷P3455_ZAP-Queries

🔗

💡

题意让求:
$\sum\limits_{x=1}^a\sum\limits_{y=1}^b[gcd(x, y)=k]$

我们只需要设置：
$f(k)=\sum\limits_{x=1}^a\sum\limits_{y=1}^b[gcd(x, y)=k]$

为使$F(n)=\sum\limits_{n|d}f(d)$成立

我们设置
$F(k)=\sum\limits_{x=1}^a\sum\limits_{y=1}^b[k|gcd(x, y)]$

为了准确计算所有$[k|gcd(x,y)]=1$的情况
我们用$x'=\frac xk,\quad y'=\frac yk$来表示我们枚举的都是k的倍数

则此时$F(k)=\sum\limits_{x'=1}^{\frac ak}\sum\limits_{y'=1}^{\frac bk}1 = \left \lfloor \frac ak \right \rfloor * \left \lfloor\frac bk \right \rfloor$

根据莫比乌斯反演定理得
$f(k)=\sum\limits_{k|d}\mu(\frac dk)F(d)$

我们枚举k的倍数，所以设$d'=\frac dk,\quad d=d'k$，枚举$d'$
并设$a'=\left \lfloor \frac ak\right \rfloor,b'=\left \lfloor \frac bk\right \rfloor$

则$f(k)=\sum\limits_{d'=1}^{min(a',b')}\mu(d')F(d'k)$

$\because F(d'k)= \left \lfloor \frac a{d'k} \right \rfloor * \left \lfloor\frac b{d'k} \right \rfloor$

则$F(d'k)=\left \lfloor \frac {a'}{d'} \right \rfloor * \left \lfloor\frac {b'}{d'} \right \rfloor$

$f(k)=\sum\limits_{d'=1}^{min(a',b')}\mu(d')\left \lfloor \frac {a'}{d'}\right \rfloor\left \lfloor \frac{b'}{d'}\right \rfloor$

✅

const ll maxn = 5e4 + 10;

ll mu[maxn];//Mobius函数表
vector<ll> prime;
ll isprime[maxn];
ll sum[maxn];//mu的前缀和

inline void Mobius(){//线性筛
        mu[1] = 1;//特判mu[i] = 1
        isprime[0] = isprime[1] = 1;
        for(ll i = 2; i < maxn; i ++){
                if(!isprime[i]) mu[i] = -1, prime.push_back(i);//质数的质因子只有自己，所以为-1
                for(ll j = 0; j < prime.size() && i * prime[j] < maxn; j ++){
                        isprime[i * prime[j]] = 1;
                        if(i % prime[j] == 0) break;
                        mu[i * prime[j]] = - mu[i];//积性函数性质： (i * prime[j])多出来一个质数因数(prime[j])，修正为 (-1) * mu[i]
                }
        }
        //剩余的没筛到的是其他情况，为0
        for(ll i = 1; i < maxn; i ++) sum[i] = sum[i - 1] + mu[i];//记录前缀和，为了整除分块
}

inline ll g(ll k, ll x){ return k / (k / x); }//整除分块的r值

inline void solve(){
        ll a, b, d; scanf("%lld%lld%lld", &a, &b, &d); a /= d, b /= d;
        ll res = 0;
        ll n = MIN(a, b);//求最小边界
        for(ll l = 1, r; l <= n; l = r + 1){
                r = MIN(n, MIN(g(a, l), g(b, l)));//解块
                res += (sum[r] - sum[l - 1]) * (a / l) * (b / l);//套公式
        }printf("%lld\n", res);
}

CHIVAS_{Mobius();
        int cass;
        scanf("%d", &cass);
        while(cass --){
                solve();
        }
        _REGAL;
}

---

洛谷P3704_数字表格

🔗

💡

$\begin{aligned}&main(n,m)\\=&\prod\limits_{i=1}^n\prod\limits_{j=1}^mf_{(i,j)}\\=&\prod_{k=1}^{mn}f_k^{\sum\limits_{i=1}^n\sum\limits_{j=1}^m[(i,j)=k]}\\=&\prod\limits_{k=1}^{mn}f_k^{\sum\limits_{d=1}^{\left\lfloor\frac {mn}k\right\rfloor}\mu(d)\left\lfloor\frac {n}{dk}\right\rfloor\left\lfloor\frac {m}{dk}\right\rfloor}\end{aligned}$

两个变量换成一个 $T=dk,\;k=\frac Td,\;d=\frac Tk$

$=\prod\limits_{k=1}^{mn}f_k^{\sum\limits_{\frac Tk=1}^{mn}\mu(\frac Tk)\left\lfloor\frac mT\right\rfloor\left\lfloor\frac nT\right\rfloor}$

指数可以看做 $T$ 枚举 $k$ 倍数

$=\prod\limits_{T=1}^{mn}\prod\limits_{k\mid T}f_k^{\mu(\frac Tk)\left\lfloor\frac mT\right\rfloor\left\lfloor\frac nT\right\rfloor}$

令 $g(T)=\prod\limits_{k\mid T}f_k^{\mu(\frac Tk)}$

$=\prod\limits_{T=1}^{mn}g(T)^{\left\lfloor\frac mT\right\rfloor\left\lfloor\frac nT\right\rfloor}$

$g(T)$ 可以预处理，外层数论分块

✅

namespace Number {
        const ll N = 1e6 + 10;
        const ll mod = 1e9 + 7;
        ll mu[N], sum[N], g[N], f[N];
        bool notprime[N];
        vector<ll> prime;
        inline ll ksm ( ll a, ll b ) {
                ll res = 1;
                while ( b ) {
                        if ( b & 1 ) res = res * a % mod;
                        a = a * a % mod;
                        b >>= 1;
                }
                return res;
        }
        inline void Sieve () {
                notprime[0] = notprime[1] = mu[1] = f[1] = g[0] = g[1] = 1; f[0] = 0;
                for ( ll i = 2; i < N; i ++ ) {
                        f[i] = (f[i - 1] + f[i - 2]) % mod, g[i] = 1;
                        if ( !notprime[i] ) 
                                prime.push_back(i),
                                mu[i] = -1;
                        for ( ll j = 0; j < prime.size() && prime[j] * i < N; j ++ ) {
                                notprime[i * prime[j]] = 1;
                                if ( i % prime[j] == 0 ) break;
                                mu[i * prime[j]] = -mu[i];
                        }
                }
        }
        inline ll Inv ( ll x ) { return ksm(x, mod - 2); }
        inline ll Get ( ll n, ll k ) { return n / (n / k); }
        inline void Pre () {
                for ( ll i = 0; i < N; i ++ ) sum[i] = (sum[i - 1] + mu[i]) % mod;
                for ( ll k = 1; k < N; k ++ ) {
                        for ( ll T = k; T < N; T += k ) {
                                if ( mu[T / k] == 1 )        g[T] = g[T] * f[k] % mod; 
                                else if ( mu[T / k] == -1 )  g[T] = g[T] * Inv(f[k]) % mod;
                        }
                }
                for ( ll i = 1; i < N; i ++ ) g[i] = g[i - 1] * g[i] % mod;
        }
} using namespace Number;

inline void Solve () {
        ll n, m; cin >> n >> m; ll mn = min ( m, n );
        ll res = 1;
        for ( ll l = 1, r; l <= mn; l = r + 1 ) {
                r = min ( Get(n, l), Get(m, l) );
                res = res * ksm( g[r] * Inv(g[l - 1]) % mod, (m / l) * (n / l) % (mod - 1) ) % mod;
        }
        cout << res << endl;
}

int main () {
        ios::sync_with_stdio(false); Sieve (); Pre ();
        ll cass; cin >> cass; while ( cass -- ) Solve ();
}

---

洛谷P3768_简单的数学题

🔗

💡

$\begin{aligned}main(n)=&\sum\limits_{i=1}^n\sum\limits_{j=1}^nij(i,j)\\=&\sum\limits_{k=1}^nk\sum\limits_{i=1}^ni\sum\limits_{j=1}^nj[(i,j)=k]\\=&\sum\limits_{k=1}^nk{\color{red}f(k)}\end{aligned}$

莫比乌斯反演一下
$f(k)=\sum\limits_{i=1}^n\sum\limits_{j=1}^n[(i,j)=k]$ $\begin{aligned}F(k)=&\sum\limits_{i=1}^n\sum\limits_{j=1}^n[k\mid(i,j)]\\=&\sum\limits_{i=1}^{\frac nk}ik\sum\limits_{j=1}^{\frac nk}jk\\=&k^2(\frac{(1+\frac nk)\frac nk}2)^2\end{aligned}$
$\begin{aligned}\therefore f(k)=&\sum\limits_{d=1}^n\mu(\frac dk)F(d)\\=&\sum\limits_{d=1}^{\frac nk}\mu(d)F(dk)\\=&\sum\limits_{d=1}^{\frac nk}\mu(d)(dk)^2(\frac{(1+\frac n{dk})\frac n{dk}}2)^2\\=&\sum\limits_{d=1}^{\frac nk}\mu(d)(dk)^2{\color{red}sum(\frac n{dk})}^2\end{aligned}$
$main(n)=\sum\limits_{k=1}^nk\sum\limits_{d=1}^{\frac nk}\mu(d)(dk)^2sum(\frac n{dk})^2$
令 $T=dk$
$\begin{aligned}main(n)=&\sum\limits_{k=1}^nk\sum\limits_{\frac Tk=1}^{\frac nk}\mu(\frac Tk)T^2sum(\frac nT)^2\\=&\sum\limits_{T=1}^nT^2sum(\frac nT)\sum\limits_{k|T}k\mu(\frac Tk)\end{aligned}$

对于 $\sum\limits_{k|T}k\mu(\frac Tk)$ 这部分，应该很感性地认识到这是狄利克雷卷积里的性质
那么直接 $\begin{aligned}&\sum\limits_{k|T}k\mu(\frac Tk)\\=&(\mu*Id)(T)\\=&\phi(T)\end{aligned}$ $\therefore main(n)=\sum\limits_{T=1}^nT^2sum(\frac nT)\phi(T)$

注意到 $T^2$ 不可数论分块相等
所以我们考虑与 $\phi(T)$ 放在一起进行杜教筛

#

ll n, mod, res;

namespace Number {
       const int N = 1e7;
       ll phi[N], sum[N];
       bool not_prime[N];
       vector<int> prime;
       
       inline void Sieve () {
               not_prime[1] = not_prime[0] = phi[1] = 1;
               for ( int i = 2; i < N; i ++ ) {
                       if ( !not_prime[i] ) 
                               prime.push_back(i),
                               phi[i] = i - 1;
                       for ( int j = 0; j < prime.size() && (ll)i * prime[j] < N; j ++ ) {
                               not_prime[i * prime[j]] = 1;
                               if ( i % prime[j] == 0 ) { 
                                       phi[i * prime[j]] = phi[i] * prime[j];
                                       break;
                               } else phi[i * prime[j]] = phi[i] * ( prime[j] - 1 );
                       }
               }
               for ( ll i = 1; i < N; i ++ ) sum[i] = (sum[i - 1] + i * i % mod * phi[i] % mod) % mod;
       }

       inline ll g( ll k, ll x ) { return k / (k / x); }
       inline ll ksm ( ll a, ll b ) { ll res = 1; while ( b ) { if ( b & 1 ) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
       inline ll inv ( ll x ) { return ksm(x, mod - 2); }
       ll inv2; inline ll sigma_1_to_n ( ll n ) { n %= mod; return n * (n + 1) % mod * inv2 % mod; }
       ll inv6; inline ll sigma_1mi_to_nmi ( ll n ) { n %= mod; return n * (n + 1) % mod * (n + n + 1) % mod * inv6 % mod; }

       map<ll, ll> S;
       inline ll SUM ( ll x ) {
               if(x < N) return sum[x];
               if(S[x]) return S[x];
               ll res = sigma_1_to_n(x) * sigma_1_to_n(x) % mod;
               for(ll L = 2, R; L <= x; L = R + 1){
                       R = min(x, g(x, L));
                       res = (res - (sigma_1mi_to_nmi(R) - sigma_1mi_to_nmi(L - 1) + mod) % mod * SUM(x / L) % mod + mod) % mod;
               }return S[x] = res;
       }
} using namespace Number;


int main () {
       cin >> mod >> n; 
       Sieve (); inv2 = inv(2); inv6 = inv(6);
       for ( ll l = 1, r; l <= n; l = r + 1 ) {
               r = g(n, l);
               ll add = (SUM(r) - SUM(l - 1) + mod) % mod * sigma_1_to_n( n / l ) % mod * sigma_1_to_n( n / l ) % mod;
               res = (res + add) % mod;
       }
       cout << res << endl;
}

---

洛谷P3911_最小公倍数之和

🔗

💡

先变一下柿子
$\begin{aligned}&\sum\limits_{i=1}^n\sum\limits_{j=1}^nlcm(a_i,a_j)\\=&\sum\limits_{i=1}^n\sum\limits_{j=1}^na_ia_j\frac1{(a_i,a_j)}\\=&\sum\limits_{k=1}^{mx}\frac 1k\sum\limits_{i=1}^n\sum\limits_{j=1}^na_ia_j[(a_i,a_j)=k]\\=&\sum\limits_{k=1}^{mx}\frac 1kf(k)\end{aligned}$
接下来就是感性的莫反
$F(k)=\sum\limits_{i=1}^n\sum\limits_{j=1}^na_ia_j[k|(a_i,a_j)]$
可以发现这个 $F(k)$ 是可以通过埃氏筛预处理出来的
那么就直接
$f(k)=\sum\limits_{d=1}^{\frac Nk}\mu(d)F(dk)$
则原柿就是
$\sum\limits_{k=1}^N\frac 1k\sum\limits_{d=1}^{\frac Nk}\mu(d)F(dk)$

发现线性增长的 $k$ 对应的 $T$ 的范围递减得很快
所以直接暴力就行了

✅

const int N =  1e5 + 10;
int a[N], n;
ll F[N];

namespace Number {
        int mu[N];
        bool not_prime[N];
        vector<int> prime;
        inline void Sieve () {
                not_prime[0] = not_prime[1] = mu[1] = 1;
                for ( int i = 2; i < N; i ++ ) {
                        if ( !not_prime[i] ) 
                                prime.push_back(i),
                                mu[i] = -1;
                        for ( int j = 0; j < prime.size() && i * prime[j] < N; j ++ ) {
                                not_prime[i * prime[j]] = true;
                                if ( i % prime[j] == 0 ) break; 
                                mu[i * prime[j]] = -mu[i];
                        }
                }
        }

        ll mark[N];
        inline void Pre () {
                for ( int i = 0; i < n; i ++ ) mark[a[i]] += a[i];
                for ( int d = 1; d < N; d ++ ) {
                        for ( int i = d; i < N; i += d ) {
                                F[d] += mark[i];
                        }
                        F[d] *= F[d];
                }
        }
} using namespace Number;

int main () {
        cin >> n; for ( int i = 0; i < n; i ++ ) cin >> a[i];
        Pre (); Sieve ();
        ll res = 0;
        for ( int k = 1; k < N; k ++ ) {
                ll cur = 0;
                for ( int d = 1; d < N / k; d ++ ) cur += mu[d] * F[d * k];
                res += cur / k;
        }
        cout << res << endl;
}

---

洛谷P4619_旧试题

🔗

💡

拆法与 洛谷P3327_约数个数和 类似
$\begin{aligned} &\sum\limits_{i=1}^A\sum\limits_{j=1}^B\sum\limits_{k=1}^Cd(ijk)\\ =&\sum\limits_{i=1}^A\sum\limits_{j=1}^B\sum\limits_{k=1}^C\sum\limits_{a|i}\sum\limits_{b|j}\sum\limits_{c|k}[(a,b)=1][(a,c)=1][(b,c)=1]\\ =&\sum\limits_{a=1}^A\left\lfloor\frac Aa\right\rfloor\sum\limits_{b=1}^B\left\lfloor\frac Bb\right\rfloor\sum\limits_{c=1}^C\left\lfloor\frac Cc\right\rfloor[(a,b)=1][(a,c)=1][(b,c)=1]\\ =&\sum\limits_{a=1}^A\left\lfloor\frac Aa\right\rfloor\sum\limits_{b=1}^B\left\lfloor\frac Bb\right\rfloor\sum\limits_{c=1}^C\left\lfloor\frac Cc\right\rfloor\sum\limits_{x|(a,b)}\mu(x)\sum\limits_{y|(a,c)}\mu(y)\sum\limits_{z|(b,c)}\mu(z)\\ =&\sum\limits_{x=1}^{min(A,B)}\mu(x)\sum\limits_{y=1}^{min(A,C)}\mu(y)\sum\limits_{z=1}^{min(B,C)}\mu(z)\sum\limits_{[x,y]|a}\left\lfloor\frac Aa\right\rfloor\sum\limits_{[x,z]|b}\left\lfloor\frac Bb\right\rfloor\sum\limits_{[y,z]|c}\left\lfloor\frac Cc\right\rfloor \end{aligned}$
后面的 $\sum\limits_{[x,y]|a}\left\lfloor\frac Aa\right\rfloor$ 可以通过 $O(nlogn)$ 预处理出来
令
$f_a[x]=\sum\limits_{x|i}\left\lfloor\frac Ax\right\rfloor$
$f_b[x]=\sum\limits_{x|i}\left\lfloor\frac Bx\right\rfloor$
$f_c[x]=\sum\limits_{x|i}\left\lfloor\frac Cx\right\rfloor$
则原式
$=\sum\limits_{x=1}^{min(A,B)}\mu(x)\sum\limits_{y=1}^{min(A,C)}\mu(y)\sum\limits_{z=1}^{min(B,C)}\mu(z)f_a([x,y])f_b([x,z])f_c([y,z])$

这样的话硬枚举依旧是 $O(n^3)$
但是硬枚举的话也能想到用 $mu[x]\neq 0$ 以及 $[x,y]\le A$ 这样去剪枝
那么可以开一波 三元环 优化
在统计完 $a=b=c$ 以及 a=b\;\or\;a=c\;\or\;b=c 后
利用 $\mu[u]\neq 0,\mu[v]\neq 0,[u,v]\le \max(A,B,C)$ 建边
权值设置为 $[u,v]$
然后跑一下三元环计数即可，时间降为 $O(m\sqrt m)$ ，$m$ 不会很大

✅

const int N = 5e5 + 10;

namespace Number {
        bool ntp[N];
        vector<int> prime;
        int mu[N];
        inline void Sieve () {
                mu[1] = ntp[0] = ntp[1] = 1;
                for (int i = 2; i < N; i ++) {
                        if (!ntp[i]) prime.push_back(i), mu[i] = -1;
                        for (int j = 0; j < prime.size() && i * prime[j] < N; j ++) {
                                ntp[i * prime[j]] = 1;
                                if (i % prime[j] == 0) break;
                                mu[i * prime[j]] = -mu[i];
                        }
                }
        }
} using namespace Number;

const int M = 1e7 + 10;
struct Edge {
        int nxt, to;
        int val;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to, int val) {
        edge[++cnt] = {head[from], to, val};
        head[from] = cnt;
}

inline int gcd (int a, int b) { return b ? gcd(b, a % b) : a; }

inline void Solve () {
        int A, B, C; cin >> A >> B >> C;

        int mx = max({A, B, C}), mn = min({A, B, C});
        for (int i = 1; i <= mx; i ++) head[i] = 0; cnt = 0;
        vector<ll> fa(mx + 1, 0), fb(mx + 1, 0), fc(mx + 1, 0);
        for (int x = 1; x <= A; x ++) for (int i = x; i <= A; i += x) fa[x] += A / i;
        for (int x = 1; x <= B; x ++) for (int i = x; i <= B; i += x) fb[x] += B / i;
        for (int x = 1; x <= C; x ++) for (int i = x; i <= C; i += x) fc[x] += C / i;

        ll res = 0;

        for (int i = 1; i <= mn; i ++) if (mu[i]) res += mu[i] * mu[i] * mu[i] * fa[i] * fb[i] * fc[i];

        vector<tuple<int, int, int> > graph;
        vector<int> deg(mx + 1, 0);
        for (int g = 1; g <= mx; g ++) {
                for (int i = 1; 1ll * i * g <= mx; i ++) {
                        if (!mu[i * g]) continue;
                        for (int j = i + 1; 1ll * i * j * g <= mx; j ++) {
                                if (!mu[i * j * g]) continue;
                                if (gcd(i, j) != 1) continue;
                                int u = i * g, v = j * g, lcm = i * j * g;
                                res += mu[v] * mu[v] * mu[u] * (fa[v] * fb[lcm] * fc[lcm] + fa[lcm] * fb[v] * fc[lcm] + fa[lcm] * fb[lcm] * fc[v]);
                                res += mu[u] * mu[u] * mu[v] * (fa[u] * fb[lcm] * fc[lcm] + fa[lcm] * fb[u] * fc[lcm] + fa[lcm] * fb[lcm] * fc[u]);
                                deg[u] ++; deg[v] ++;
                                graph.push_back({u, v, lcm});                               
                        }
                }
        }

        for (auto [u, v, w] : graph) {
                if (deg[u] > deg[v]) {
                        add_Edge(u, v, w);
                } else if (deg[u] == deg[v]) {
                        add_Edge(min(u, v), max(u, v), w);
                } else {
                        add_Edge(v, u, w);
                }
        }
        vector<int> vis(mx + 1, 0);
        for (int a = 1; a <= mx; a ++) {
                for (int i = head[a]; i; i = edge[i].nxt) vis[edge[i].to] = edge[i].val;
                for (int i = head[a]; i; i = edge[i].nxt) {
                        int b = edge[i].to;
                        int val1 = edge[i].val;
                        for (int j = head[b]; j; j = edge[j].nxt) {
                                int c = edge[j].to;
                                int val2 = edge[j].val;
                                if (vis[c]) {
                                        int val3 = vis[c];
                                        res += mu[a] * mu[b] * mu[c] * (
                                                fa[val1] * fb[val2] * fc[val3] + 
                                                fa[val1] * fb[val3] * fc[val2] +
                                                fa[val2] * fb[val1] * fc[val3] + 
                                                fa[val2] * fb[val3] * fc[val1] +
                                                fa[val3] * fb[val1] * fc[val2] + 
                                                fa[val3] * fb[val2] * fc[val1]
                                        );
                                }
                        }
                }
                for (int i = head[a]; i; i = edge[i].nxt) vis[edge[i].to] = 0;
        }

        cout << res % 1000000007 << endl;
}

int main () {
        Sieve();
        ios::sync_with_stdio(false);
        int cass; cin >> cass; while (cass --) {
                Solve();
        }
}

---

洛谷P6055_GCD

🔗

💡

$\begin{aligned}&\sum\limits_{i=1}^N\sum\limits_{j=1}^N\sum\limits_{p=1}^{\left \lfloor \frac Nj\right \rfloor}\sum\limits_{q=1}^{\left \lfloor \frac Nj\right \rfloor}[gcd(i,j)=1][gcd(p,q)=1]\\=&\sum\limits_{i=1}^N\sum\limits_{j=1}^N\sum\limits_{p=1}^N\sum\limits_{q=1}^N[gcd(i,j)=1]j[gcd(p,q)=j]\\=&\sum\limits_{i=1}^N\sum\limits_{p=1}^N\sum\limits_{q=1}^N[gcd(i,p,q)=1]\end{aligned}$
令$f(k)=\sum\limits_{i=1}^N\sum\limits_{p=1}^N\sum\limits_{q=1}^N[gcd(i,p,q)=k]$
$F(k)=\sum\limits_{i=1}^N\sum\limits_{p=1}^N\sum\limits_{q=1}^N[k|gcd(i,p,q)]$
设$i'=\frac ik,p'=\frac pk,q'=\frac qk$进行枚举倍数
则$\begin{aligned}F(k)=\sum\limits_{i'=1}^{\left \lfloor \frac Nk\right \rfloor}\sum\limits_{p'=1}^{\left \lfloor \frac Nk\right \rfloor}\sum\limits_{q'=1}^{\left \lfloor \frac Nk\right \rfloor}1=\left \lfloor \frac Nk\right \rfloor^3\end{aligned}$
根据$f(k)=\sum\limits_{k\mid d}\mu(\frac dk)F(d)$
设$d'=\frac dk,d=d'k$枚举倍数
$f(k)=\sum\limits_{d'=1}^{\left \lfloor \frac Nk\right \rfloor}\mu(d')F(d'k)=\sum\limits_{d'=1}^{\left \lfloor \frac Nk\right \rfloor}\mu(d')\left \lfloor \frac N{d'k}\right \rfloor^3$
本题让求$f(1)=\sum\limits_{d'=1}^N\mu(d')\left \lfloor \frac N{d'}\right \rfloor^3$
那么公式出来了，剩下的就是杜教筛数论分块乱搞了

✅

const ll N = 2e6 + 10;
const ll mod = 998244353;
namespace Number {
        bool notprime[N];
        vector<ll> prime;
        ll mu[N], sum[N];
        inline void Sieve () {
                mu[1] = notprime[1] = notprime[0] = 1;
                for ( ll i = 2; i < N; i ++ ) {
                        if ( !notprime[i] ) prime.push_back(i), mu[i] = -1;
                        for ( ll j = 0; j < prime.size() && i * prime[j] < N; j ++ ) {
                                notprime[i * prime[j]] = 1;
                                if ( i % prime[j] == 0 ) break;
                                mu[i * prime[j]] = -mu[i];
                        }
                }
                for ( ll i = 1; i < N; i ++ ) sum[i] = (sum[i - 1] + mu[i]) % mod;
        }
        inline ll g ( ll k, ll x ) { return k / (k / x); }

        map<ll, ll> S;
        inline ll SUM ( ll x ) {
                if ( x < N ) return sum[x];
                if ( S[x] ) return S[x];
                ll res = 1;
                for ( ll L = 2, R; L <= x; L = R + 1 ) {
                        R = min ( x, g(x, L) );
                        res = (res - (R - L + 1) * SUM(x / L) % mod + mod) % mod;
                } return S[x] = res;
        }
} using namespace Number;

int main () {
        Sieve();
        ll n, res = 0; cin >> n;
        for ( ll l = 1, r; l <= n; l = r + 1 ) {
                r = g(n, l);
                res = (res + (SUM(r) - SUM(l - 1) + mod) % mod * (n / l) % mod * (n / l) % mod * (n / l) % mod) % mod;
        }
        cout << res << endl;
}

---

ICPC吉林站2020H_Curious

🔗

💡

题目大意是给定一个序列 $\{a\}$
每一次询问给定一个 $x$
问 $\sum\limits_{i=1}^n\sum\limits_{j=1}^n[(a_i,a_j)=x]$
我们可以感性地想到这一题 $\sum\limits_{i=1}^n\sum\limits_{j=1}^n[(i,j)=k]$
想到我们后面在处理 $F(k)=\sum\limits_{i=1}^n\sum\limits_{j=1}^n[k\mid(i,j)]$ 时使用的是让 $i$ 和 $j$ 都是枚举的是 $k$ 的倍数
从而得到 $F(k)=\left\lfloor\frac nk\right\rfloor^2$
其实也就是 $n$ 以下 $k$ 的倍数个数的平方
而我们此时也可以使用这个
我们预处理一个数组 $\{A\}$ ，其中 $A[i]$ 表示对于 $\{a\}$ 中是 $i$ 倍数的个数
这个可以通过对 $\{a\}$ 埃氏筛 $O(nlogn)$ 地得到
那么我们的 $F(k)=A[k]^2$
$f(k)=\sum\limits_{d=1}^{\left\lfloor\frac mk\right\rfloor}\mu(d)A[d\times k]^2$
然后什么都不用，暴力跑一遍这个式子就行了

✅

const int N = 1e5 + 10;
int a[N], vis[N];
int n, m, k;
ll A[N];

namespace Number {
        ll mu[N];
        bool not_prime[N];
        vector<int> prime;

        inline void Sieve () {
                mu[1] = 1;
                not_prime[0] = not_prime[1] = 1;
                for ( int i = 2; i < N; i ++ ) {
                        if ( !not_prime[i] ) 
                                mu[i] = -1,
                                prime.push_back(i);
                        for ( int j = 0; j < prime.size() && i * prime[j] < N; j ++ ) {
                                not_prime[i * prime[j]] = 1;
                                if ( i % prime[j] == 0 ) break;
                                mu[i * prime[j]] = -mu[i];
                        } 
                }
        }
        inline int g ( int x, int k ) { return x / (x / k); }
} using namespace Number;

int main () { Sieve();
        int cass; scanf("%d", &cass); while ( cass -- ) {
                scanf("%d%d%d", &n, &m, &k);
                for ( int i = 0; i < n; i ++ ) scanf("%d", &a[i]), vis[a[i]] ++; // 记录a[i]出现次数
                for ( int i = 1; i <= m; i ++ ) {
                        for ( int j = i; j <= m; j += i ) {
                                A[i] += vis[j]; // 预处理{a}中i的倍数的个数
                        }
                }
                while ( k -- ) {
                        int x; scanf("%d", &x);
                        ll res = 0;
                        for ( int i = 1; i <= m / x; i ++ ) res += mu[i] * A[i * x] * A[i * x]; // 跑柿子
                        printf("%lld\n", res);
                }
                for ( int i = 0; i <= m; i ++ ) A[i] = vis[i] = 0; // 清空
        }
}

---