概率DP

#

---

洛谷P1769_淘汰赛制

🔗

💡

一个普通的概率 $dp$ ，考虑每一次对战的胜者的概率
胜者需要由两个人对决得出，对于一个人每一次的对战，能对战的人是有一定的范围的
即对于当前赛区为 $[l,r]$ ，如果 $i$ 是在左半赛区，那么它会对战右半赛区的胜者，否则对战左半赛区的胜者
比赛就是一棵二叉树，这个 $[l,r]$ 是可以通过深度唯一确定的，故 $dp[u][deep]$ 表示 $u$ 作为深度为 $deep$ 的节点的胜者的概率
那么如果一个赛区是 $[a,b]$ ，一个赛区是 $[c,d]$ ，且 $u$ 在第一个赛区深度为 $deep$ ，则对于这次就要累加上所有的 $\sum\limits_{i=c}^d p[u][i]*dp[u][deep+1]*dp[i][deep+1]$ ，$\in$ 的意思是属于哪个赛区的胜者，$deep$ 已经能唯一确定，故不需要参数
如果 $u$ 在第二个赛区，累加 $\sum\limits_{i=a}^b p[u][i]*dp[u][deep+1]*dp[i][deep+1]$
用记忆化搜索对所有的 $dp[i][1]$ 求一遍，然后维护一个最大值即可

✅

bool vis[2010][20];
double dp[2010][20];
int n, N;
double p[2010][2010];

inline double dfs (int u, int deep, int L, int R) {
    if (vis[u][deep]) return dp[u][deep]; vis[u][deep] = 1;
    if (deep == n + 1) return dp[u][deep] = 1;
    int MID = (L + R) / 2;
    if (L <= u && u <= MID) for (int i = MID + 1; i <= R; i ++) {
        dp[u][deep] += p[u][i] * dfs(u, deep + 1, L, MID) * dfs(i, deep + 1, MID + 1, R);
    }
    if (MID + 1 <= u && u <= R) for (int i = L; i <= MID; i ++) {
        dp[u][deep] += p[u][i] * dfs(i, deep + 1, L, MID) * dfs(u, deep + 1, MID + 1, R);
    }
    return dp[u][deep];
}

int main () {
    scanf("%d", &n);
    N = 1 << n;
    for (int i = 1; i <= N; i ++) {
        for (int j = 1; j <= N; j ++) {
            int x; scanf("%d", &x);
            p[i][j] = 1.0 * x / 100;
        }
    }

    for (int i = 1; i <= N; i ++) 
        dfs(i, 1, 1, N);
    
    double mxv = 0; int mxi = 0;
    for (int i = 1; i <= N; i ++) {
        if (mxv - dp[i][1] < -1e-6) {
            mxi = i;
            mxv = dp[i][1];
        }
    }
    printf("%d\n", mxi);
}

---

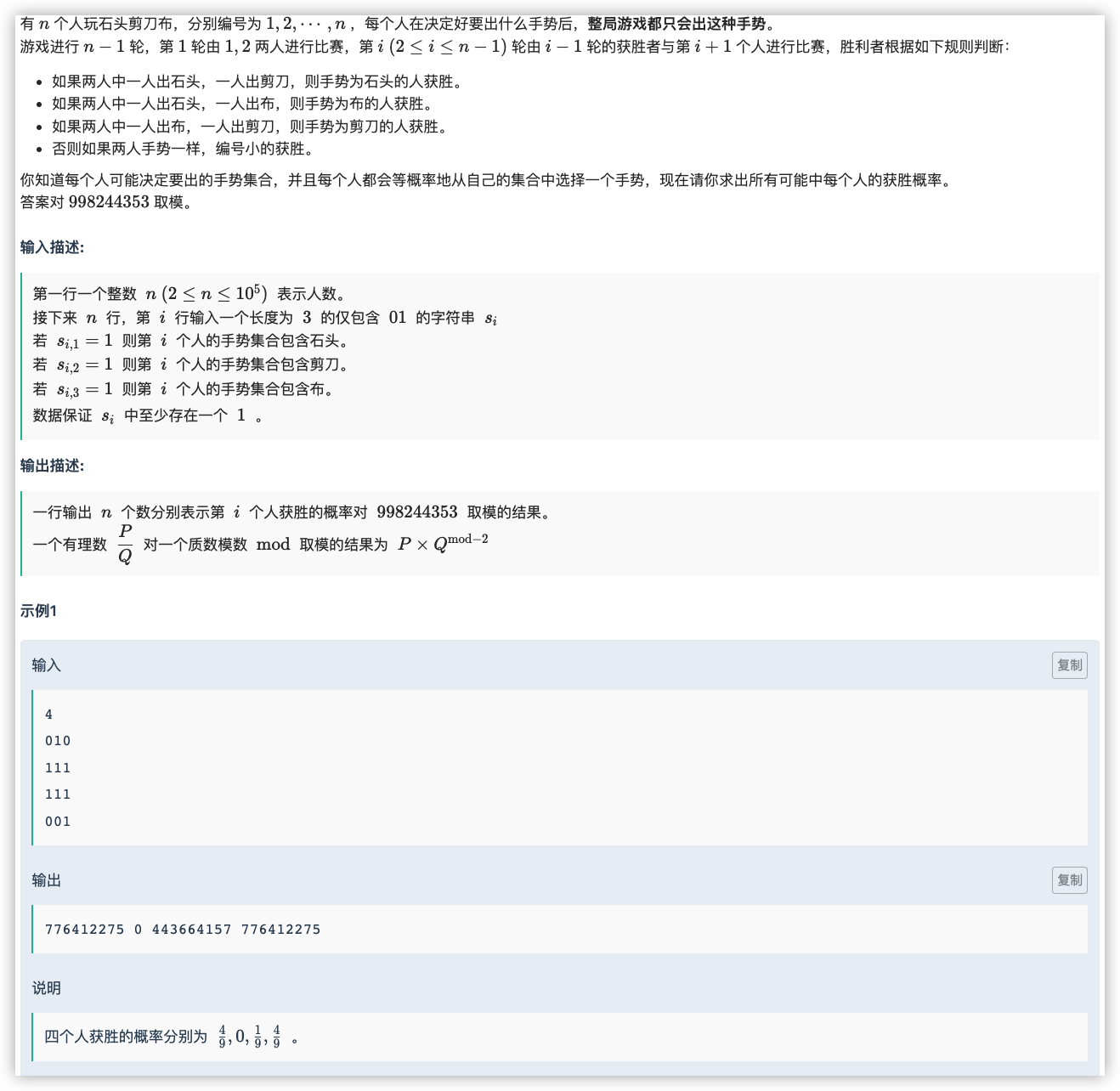
牛客挑战赛59B_游戏

🔗

💡

考虑第 $i$ 个人在什么条件下才可以取胜

首先他如果出石头，后面的可以遇到出石头的也可以遇到出剪刀的
即所有的 $j>i$ ，$j$ 必须平局或者败给 $i$
所有的 $j<i$ ，$j$ 必须败给 $i$
那么对于前者我们做三个后缀积表示后缀出 $12/23/13$ 的可能性积
然后三个前缀 $dp$ 表示 $[1,i]$ 出 $1/2/3$ 赢到 $i$ 的概率和

dp1[i] = dp1[i - 1] * (a1[i] + a2[i]) + a1[i] * dp2[i - 1]
dp2[i] = dp2[i - 1] * (a2[i] + a3[i]) + a2[i] * dp3[i - 1]
dp3[i] = dp3[i - 1] * (a3[i] + a1[i]) + a3[i] * dp1[i - 1]

dp1[i] = dp1[i - 1] * (a1[i] + a2[i]) + a1[i] * dp2[i - 1]
dp2[i] = dp2[i - 1] * (a2[i] + a3[i]) + a2[i] * dp3[i - 1]
dp3[i] = dp3[i - 1] * (a3[i] + a1[i]) + a3[i] * dp1[i - 1]

转移方式为：$[1,i-1]$ 赢过 $i$ ，他们可以让 $i$ 选一样的或者输给 $[1,i-1]$ 的 ，$i$ 赢过 $[1,i-1]$ 那么 $[1,i-1]$ 只能输给 $i$

dp1[i] = dp1[i - 1] * (a1[i] + a2[i]) + a1[i] * dp2[i - 1]
dp2[i] = dp2[i - 1] * (a2[i] + a3[i]) + a2[i] * dp3[i - 1]
dp3[i] = dp3[i - 1] * (a3[i] + a1[i]) + a3[i] * dp1[i - 1]

那么对于 $i$ 赢的情况就可以用上面说的情况做解了

✅

int main () {
        int n; cin >> n;
        vector<string> s(n); for (string &i : s) cin >> i;
        vector<modint> a1(n + 2, 0), a2(n + 2, 0), a3(n + 2, 0);
        vector<modint> suf12(n + 2, 0), suf13(n + 2, 0), suf23(n + 2, 0);
        for (int i = 1; i <= n; i ++) {
                int num = 0; for (char j : s[i - 1]) num += j == '1';
                for (int j = 0; j < 3; j ++) {
                        if (j == 0)       a1[i] = (modint)(s[i - 1][j] == '1') / num;
                        else if (j == 1)  a2[i] = (modint)(s[i - 1][j] == '1') / num;
                        else              a3[i] = (modint)(s[i - 1][j] == '1') / num;
                }
        }
        suf12[n + 1] = suf23[n + 1] = suf13[n + 1] = 1;
        for (int i = n; i >= 1; i --) {
                suf12[i] = suf12[i + 1] * (a1[i] + a2[i]);
                suf13[i] = suf13[i + 1] * (a1[i] + a3[i]);
                suf23[i] = suf23[i + 1] * (a2[i] + a3[i]);
        }

        vector<modint> dp1(n + 2, 0), dp2(n + 2, 0), dp3(n + 2, 0);
        dp1[0] = dp2[0] = dp3[0] = 1;
        for (int i = 1; i <= n; i ++) {
                if (i == 1) {
                        dp1[i] = a1[i];
                        dp2[i] = a2[i];
                        dp3[i] = a3[i];
                        continue;
                }
                dp1[i] = dp1[i - 1] * (a1[i] + a2[i]) + a1[i] * dp2[i - 1];
                dp2[i] = dp2[i - 1] * (a2[i] + a3[i]) + a2[i] * dp3[i - 1];
                dp3[i] = dp3[i - 1] * (a3[i] + a1[i]) + a3[i] * dp1[i - 1];
        }
        for (int i = 1; i <= n; i ++) {
                modint res = 0;
                if (a1[i] > 0) res += dp2[i - 1] * a1[i] * suf12[i + 1];
                if (a2[i] > 0) res += dp3[i - 1] * a2[i] * suf23[i + 1];
                if (a3[i] > 0) res += dp1[i - 1] * a3[i] * suf13[i + 1];
                cout << res << " ";
        }
}

---