迭代加深DFS

#

---

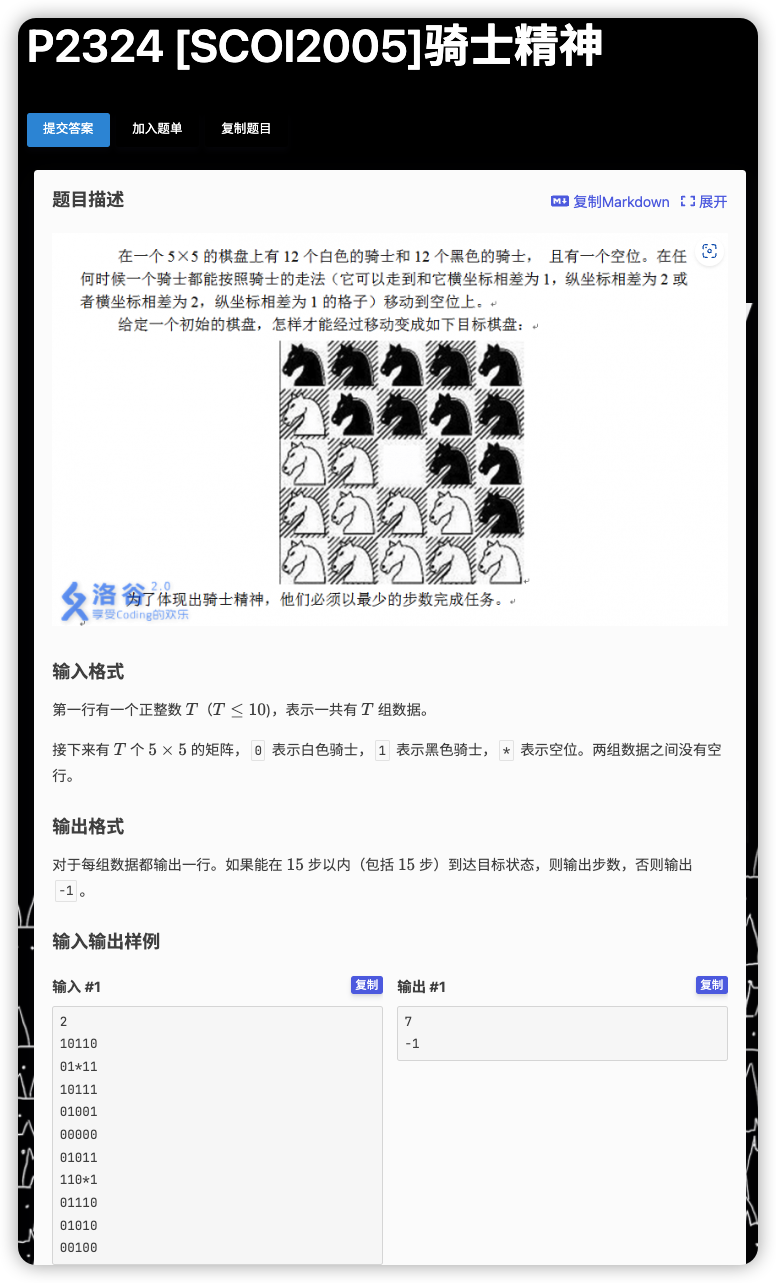
洛谷P2324_骑士精神

🔗

💡

这个看起来就很 $bfs$ ，结构体存矩阵然后跑到第一个满足的停止，但是内存费得离谱，相当于在原有基础上乘了个 $25$ ，那么这种需要 $bfs$ 的效果但是不用 $bfs$ 的内存的搜索采用迭代加深 $DFS$
while (!flag) dfs(maxstep ++);
就是看当前的一个和目标矩阵的差异值，如果这个差异值过大的话就剪枝掉，即差异值大于剩余步数就剪
然后枚举上界 $[0,15]$ 在第一个可以判断到可行上界后输出上界
如果一直没有可行上界就输出 $-1$

✅

int dx[] = {1, 1, 2, 2, -1, -1, -2, -2};
int dy[] = {2, -2, 1, -1, 2, -2, 1, -1};

int target[5][5]; // 目标矩阵
int a[5][5], b[5][5]; // 当前矩阵，原始矩阵
inline int diff () { // 当前矩阵与目标矩阵的差异值
    int res = 0;
    for (int i = 0; i < 5; i ++) {
        for (int j = 0; j < 5; j ++) {
            res += target[i][j] != a[i][j];
        }
    }
    return res;
}

bool flag = false;
inline void dfs (int x, int y, int stp, int lim) {
    if (flag) return;
    int dif = diff();
    if (dif == 0) { // 成功了
        flag = true;
        return;
    }
    if (dif > lim - stp + 1) return; // 剩余步数不够变的
    if (stp == lim) return; // 不能再走了
    for (int i = 0; i < 8; i ++) {
        int nx = x + dx[i];
        int ny = y + dy[i];
        if (nx < 0 || ny < 0 || ny >= 5 || nx >= 5) continue;
        swap(a[x][y], a[nx][ny]);
        dfs(nx, ny, stp + 1, lim);
        swap(a[x][y], a[nx][ny]);
    }
}

inline void Solve () {
    int x, y;
    for (int i = 0; i < 5; i ++) {
        for (int j = 0; j < 5; j ++) {
            char c; cin >> c;
            if (c == '1') b[i][j] = 1;
            else if (c == '0') b[i][j] = 0;
            else {
                b[i][j] = -1;
                x = i, y = j;
            }
        }
    }  

    flag = false;
    for (int lim = 0; lim <= 15; lim ++) {
        for (int i = 0; i < 5; i ++) {
            for (int j = 0; j < 5; j ++) {
                a[i][j] = b[i][j];
            }
        }
        dfs(x, y, 0, lim);
        if (flag) {
            cout << lim << endl;
            return;
        }
    }

    cout << "-1\n";
}

int main () {
    ios::sync_with_stdio(false);
    cin.tie(0);

    target[0][0] = 1; target[0][1] = 1; target[0][2] = 1;  target[0][3] = 1; target[0][4] = 1;
    target[1][0] = 0; target[1][1] = 1; target[1][2] = 1;  target[1][3] = 1; target[1][4] = 1;
    target[2][0] = 0; target[2][1] = 0; target[2][2] = -1; target[2][3] = 1; target[2][4] = 1;
    target[3][0] = 0; target[3][1] = 0; target[3][2] = 0;  target[3][3] = 0; target[3][4] = 1;
    target[4][0] = 0; target[4][1] = 0; target[4][2] = 0;  target[4][3] = 0; target[4][4] = 0;

    int cass; cin >> cass; while ( cass -- ) {
        Solve ();
    }
}

---