高等数学

#

---

求极限

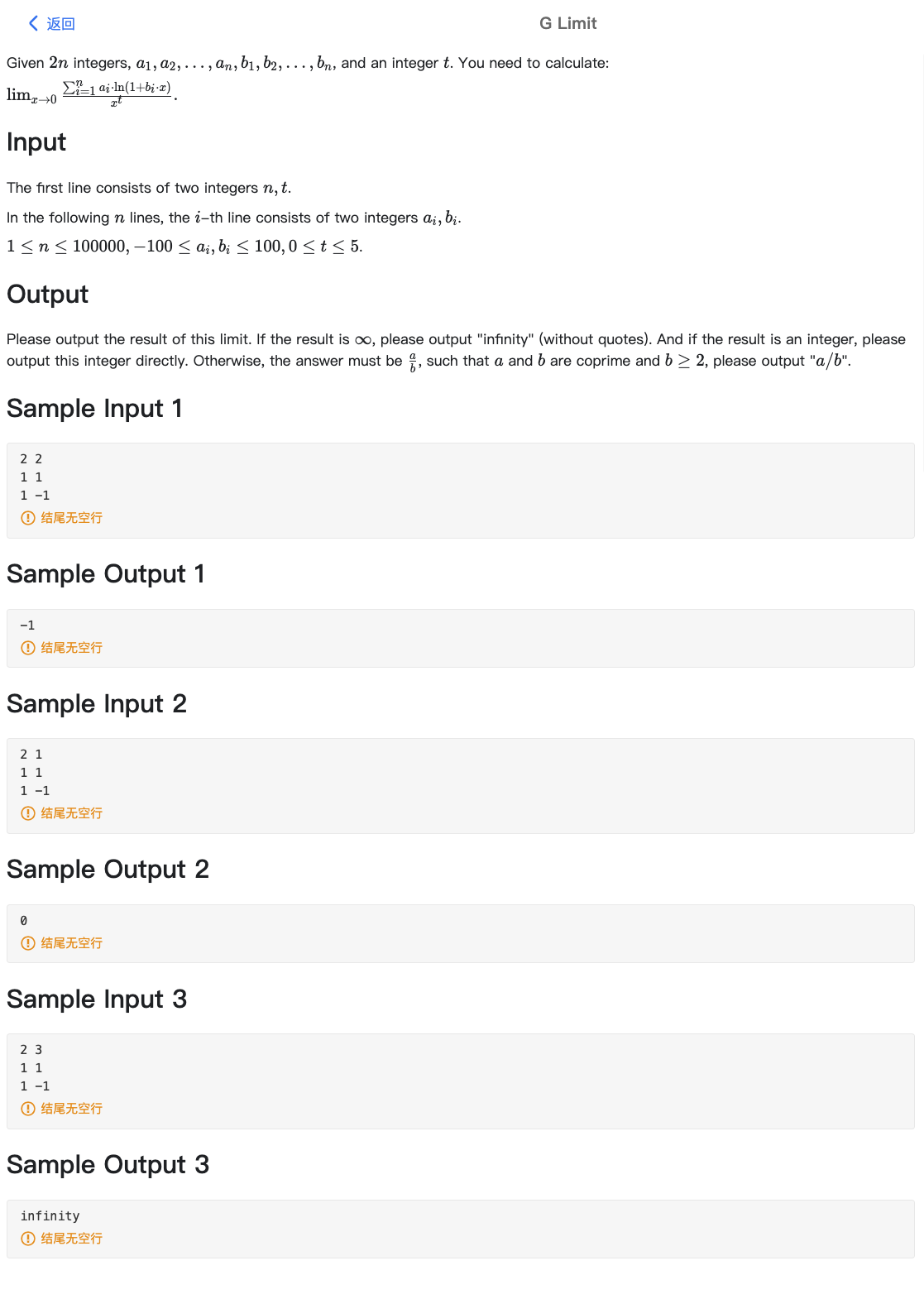
ICPC2021网络赛(2)G_Limit

🔗

💡

首先根据泰勒展开可得

我们想找指数最小的第一个系数不为0的项
如果它的指数，可以求系数
如果，就输出
如果，就输出

那么对于第项也就是的时候，每一对可以选出作为系数
所以分子可以枚举
在指数时，如果遇到系数不为，首先判断是否为
如果，满足条件，跳出循环可以开始求系数（分数，up和down）
如果就说明存在指数比t小且系数不为0的，那么就是

如果系数一直为且，那么最大的项也要比小，所以输出

✅

#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
#define ll long long
 
using namespace std;
 
inline ll ksm ( ll a, ll b ) {
        ll res = 1;
        while ( b ) {
                if ( b & 1 ) res = res * a;
                a = a * a;
                b >>= 1;
        }
        return res;
}
inline ll gcd ( ll a, ll b ) {
        return b ? gcd ( b, a % b ) : a;
}

int main () {
        ll n, t; cin >> n >> t;
        ll a[n], b[n];
        for ( ll i = 0; i < n; i ++ ) cin >> a[i] >> b[i];

        ll up = 0, down = 0;
        for ( ll j = 1; ; j ++ ) {
                if ( j > t ) { cout << "0"; return 0; } // 最大的项比x^t小
                up = 0, down = j;
                for ( ll i = 0; i < n; i ++ ) up += a[i] * ksm(b[i], j);
                if ( j % 2 == 0 ) up *= -1;
                if ( up ) { // 系数不为0
                        if ( j < t ) { cout << "infinity"; return 0; } // 最大的项比x^t大且存在  
                        break; // 否则开始求系数
                }
        }
        ll d = gcd ( llabs(up), llabs(down) );
        up /= d; down /= d; // 约分
        if ( up % down == 0 ) cout << up / down; // 直接除来求
        else {
                if ( up * down < 0 ) cout << "-"; // 异号，负号提出
                cout << up << "/" << down;
        }
}

---