kruskal重构树

#

---

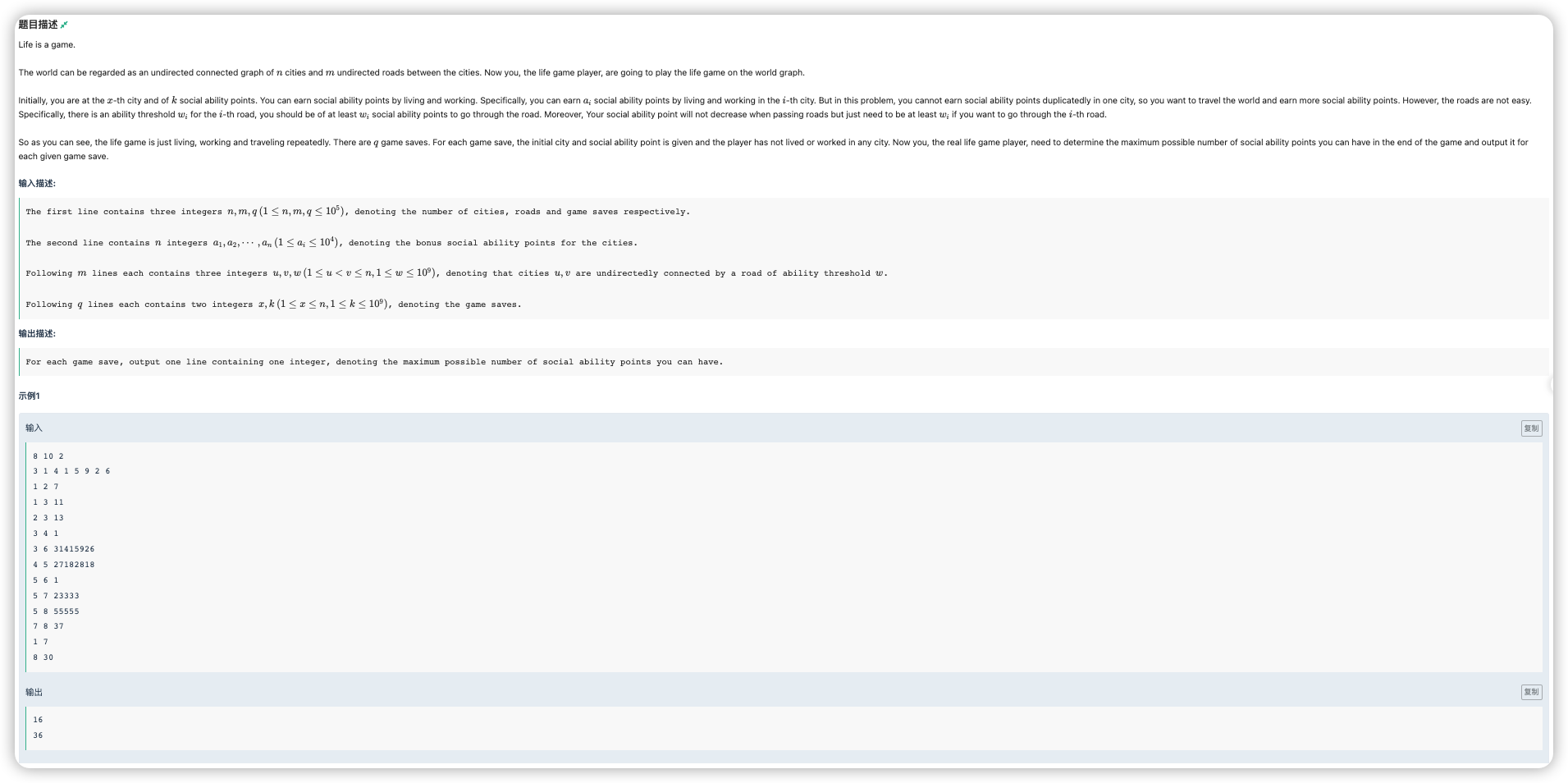
ICPC2021上海H_LifeIsAGame

🔗

💡

为了尽可能多拿有价值的点，走的路径权值肯定是希望比较小的
这就和最小生成树很像了
那么快速得到从 $x$ 能走到的点，我们想知道从 $x$ 出发的最后能走到的边界，而在生成树上这样考虑试着转化成重构树
发现 $x$ 在原图走可以转化为 $x$ 往上跳，每跳一步就可以收集另一部分的点权变成子树权值和
树上往上跳能跳的最大步数可以用倍增去解决，倍增维护区间左端点跳到右端点所付出代价（-(边权-子树权值和)）的最大值，当给出的 $k$ 满足不了时，就从能跳到的右边界继续向上跳，从而用二进制得到一个精确的能跳到的位置

✅

const int N = 3e5 + 10;
const int M = 1e6 + 10;
struct Dsu {
    vector<int> f;
    inline Dsu (int n) {
        f.resize(n + 1);
        for (int i = 0; i <= n; i ++) f[i] = i;
    }
    inline int find (int x) {return x == f[x] ? x : f[x] = find(f[x]);}
    inline void merge (int x, int y) {
        x = find(x);
        y = find(y);
        if (x == y) return;
        f[x] = y;
    }
    inline bool check (int x, int y) {
        x = find(x);
        y = find(y);
        return x == y;
    }
};
int n, m, q;
int a[N];
struct node {
    int u, v, w;
    inline friend bool operator < (node a, node b) {
        return a.w < b.w;
    }
};

int w[N];
int fa[N][40];
int ct[N][40];

inline void Solve (int x, int k) {
    while (x != 2 * n - 1) {
        int t = x;
        for (int j = 20; j >= 0; j --) {
            if (ct[x][j] + k >= 0) {
                x = fa[x][j];
                break;
            }
        }
        if (x == t) break;
    }
    cout << a[x] + k << endl;
}
signed main () {
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i ++) cin >> a[i];
    vector<node> v(m);
    for (node &it : v) cin >> it.u >> it.v >> it.w;

    int pt_idx = n;
    Dsu dsu(2 * n);
    sort(v.begin(), v.end());
    for (node it : v) {
        int itu = dsu.find(it.u);
        int itv = dsu.find(it.v);
        if (itu == itv) continue;
        w[++pt_idx] = it.w;
        dsu.merge(itu, pt_idx); dsu.merge(itv, pt_idx);
        fa[itu][0] = pt_idx;
        fa[itv][0] = pt_idx;
        a[pt_idx] += a[itu] + a[itv];
    } w[0] = 2e9 + 10;

    for (int i = 1; i <= 2 * n; i ++) 
        ct[i][0] = a[i] - w[fa[i][0]];
    for (int j = 1; j <= 20; j ++) {
        for (int i = 1; i <= 2 * n; i ++) {
            fa[i][j] = fa[fa[i][j - 1]][j - 1];
            ct[i][j] = min(ct[i][j - 1], ct[fa[i][j - 1]][j - 1]);
        }
    } 

    while (q --) {
        int x, k; cin >> x >> k;
        Solve(x, k);
    }
}

---