子集和DP

#

---

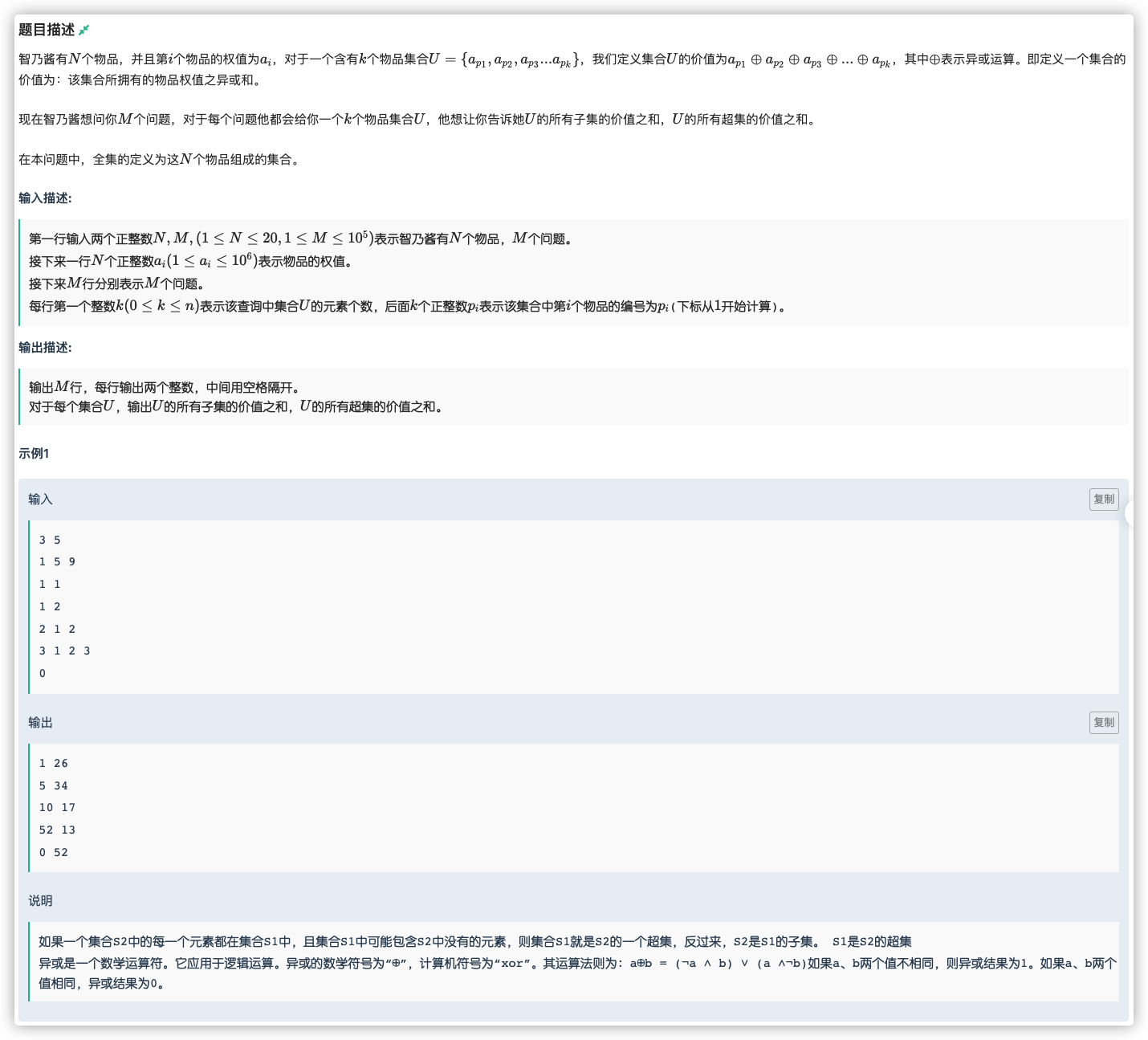
牛客NC225630_智乃酱的子集与超集

🔗

💡

一个 $0/1$ 的 $sosdp$
那么我们可以将维度压缩为一个二进制数字
枚举状态然后枚举物品，将物品的价值压入初始的前缀和后缀和数组内
枚举物品然后枚举状态，pre 和 suf 分别正着更新反着更新

询问结果的时候我们找出所有 $\{p\}$ 位置上为 $1$ 形成的 $01$ 串的 suf 和 pre 即可

✅

const int N = 25;
const int S = 1 << N;

int n, m;
int a[N];
ll pre[S], suf[S];

int main () {
        ios::sync_with_stdio(false);

        cin >> n >> m;
        for ( int i = 0; i < n; i ++ ) cin >> a[i];
        for ( int s = 0; s < (1 << n); s ++ ) {
                int sum = 0;
                for ( int i = 0; i < n; i ++ ) {
                        if ( s & (1 << i) ) sum ^= a[i];
                }
                pre[s] = suf[s] = sum;
        }
        for ( int i = 0; i < n; i ++ ) {
                for ( int s = 0; s < (1 << n); s ++ ) {
                        if ( s & (1 << i) ) pre[s] += pre[s ^ (1 << i)];
                        else                suf[s] += suf[s ^ (1 << i)];
                }
        }
        while ( m -- ) {
                int k; cin >> k;
                int s = 0;
                for ( int i = 0; i < k; i ++ ) {
                        int p; cin >> p;
                        s |= (1 << (p - 1));
                }
                cout << pre[s] << " " << suf[s] << endl;
        }
}

---

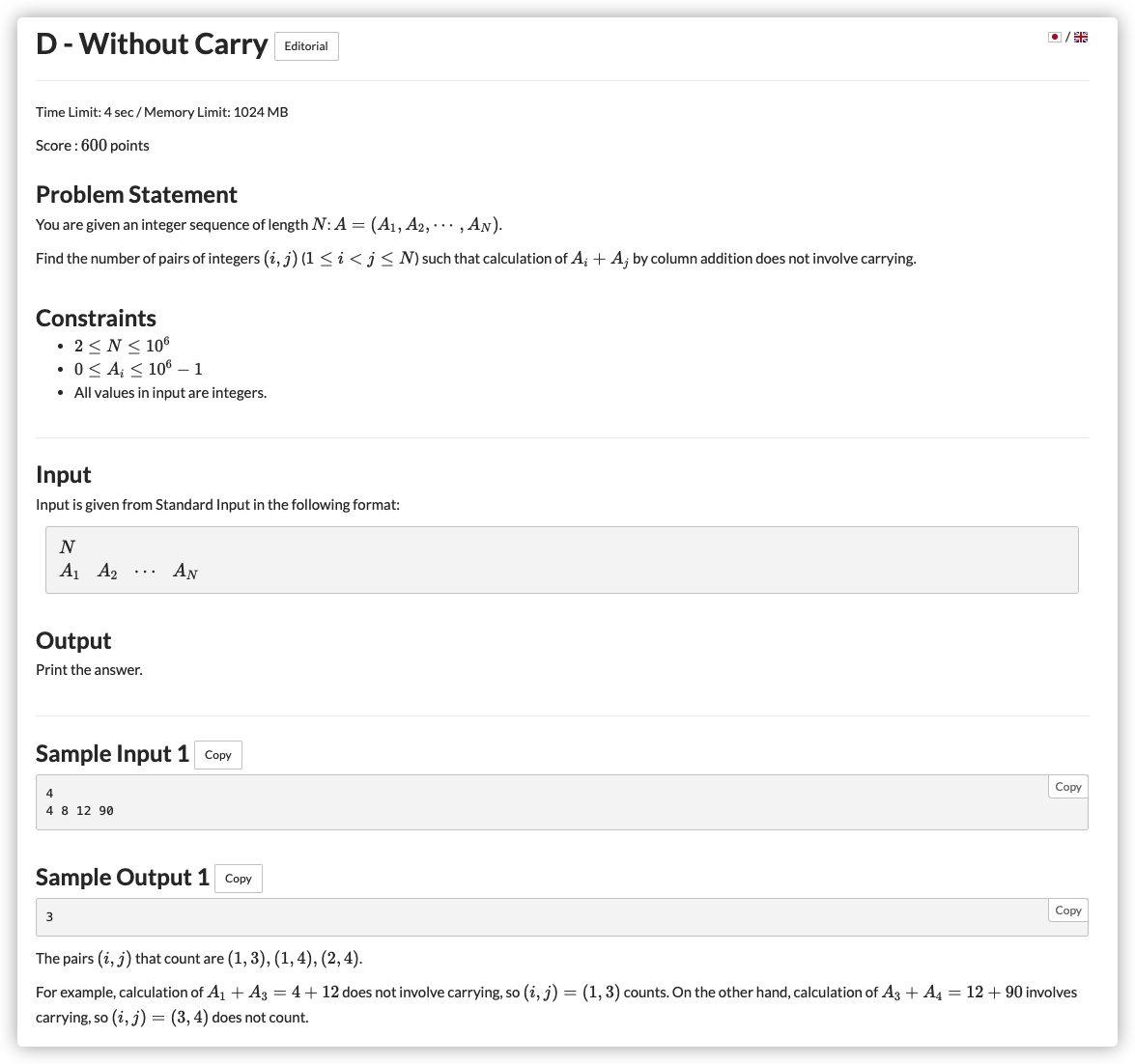
ARC136D_WithoutCarry

🔗

💡

对于数 $X$ 每一个数位 $x$ ，都有一个边界 $9-x$，与这个数能配对的数要满足所有数位均不大于边界
那么开六维 $dp$ ，初始每一位匹配每一个数位都让它 $+1$
即 $dp_{num_0,num_1,num_2,num_3,num_4,num_5}+1$

然后用高维前缀和的方式进行更新
那么每次满足条件的必然存在于 $dp_{9-num_0,9-num_19-num_29-num_39-num_49-num_5}$ 这个六维空间内

我们累加，注意如果当前枚举的数本身也在这个维空间内要减去
然后让结果 $/2$ 即可

✅

int n;
int num[1000005][6];
ll dp[11][11][11][11][11][11];

int main () {
        ios::sync_with_stdio(false);
        cin >> n;
        for ( int i = 0; i < n; i ++ ) {
                string s; cin >> s;
                reverse(s.begin(), s.end());
                for ( int j = 0; j < s.size(); j ++ ) num[i][j] = s[j] - '0';
                dp[num[i][0]][num[i][1]][num[i][2]][num[i][3]][num[i][4]][num[i][5]] ++;
        }

        # define rep(i,a,b) for ( int i = a; i <= b; i ++ )
        rep(a, 0, 9) rep(b, 0, 9) rep(c, 0, 9) rep(d, 0, 9) rep(e, 0, 9) rep(f, 0, 9) 
                dp[a + 1][b][c][d][e][f] += dp[a][b][c][d][e][f];
        rep(a, 0, 9) rep(b, 0, 9) rep(c, 0, 9) rep(d, 0, 9) rep(e, 0, 9) rep(f, 0, 9) 
                dp[a][b + 1][c][d][e][f] += dp[a][b][c][d][e][f];
        rep(a, 0, 9) rep(b, 0, 9) rep(c, 0, 9) rep(d, 0, 9) rep(e, 0, 9) rep(f, 0, 9) 
                dp[a][b][c + 1][d][e][f] += dp[a][b][c][d][e][f];
        rep(a, 0, 9) rep(b, 0, 9) rep(c, 0, 9) rep(d, 0, 9) rep(e, 0, 9) rep(f, 0, 9) 
                dp[a][b][c][d + 1][e][f] += dp[a][b][c][d][e][f];
        rep(a, 0, 9) rep(b, 0, 9) rep(c, 0, 9) rep(d, 0, 9) rep(e, 0, 9) rep(f, 0, 9) 
                dp[a][b][c][d][e + 1][f] += dp[a][b][c][d][e][f];
        rep(a, 0, 9) rep(b, 0, 9) rep(c, 0, 9) rep(d, 0, 9) rep(e, 0, 9) rep(f, 0, 9) 
                dp[a][b][c][d][e][f + 1] += dp[a][b][c][d][e][f];


        ll res = 0;
        for ( int i = 0; i < n; i ++ ) {
                res += dp[9 - num[i][0]][9 - num[i][1]][9 - num[i][2]][9 - num[i][3]][9 - num[i][4]][9 - num[i][5]];
                if ( num[i][0] < 5 && num[i][1] < 5 && num[i][2] < 5 && num[i][3] < 5 && num[i][4] < 5 && num[i][5] < 5 ) res --;
        }
        cout << res / 2 << endl;
}

---

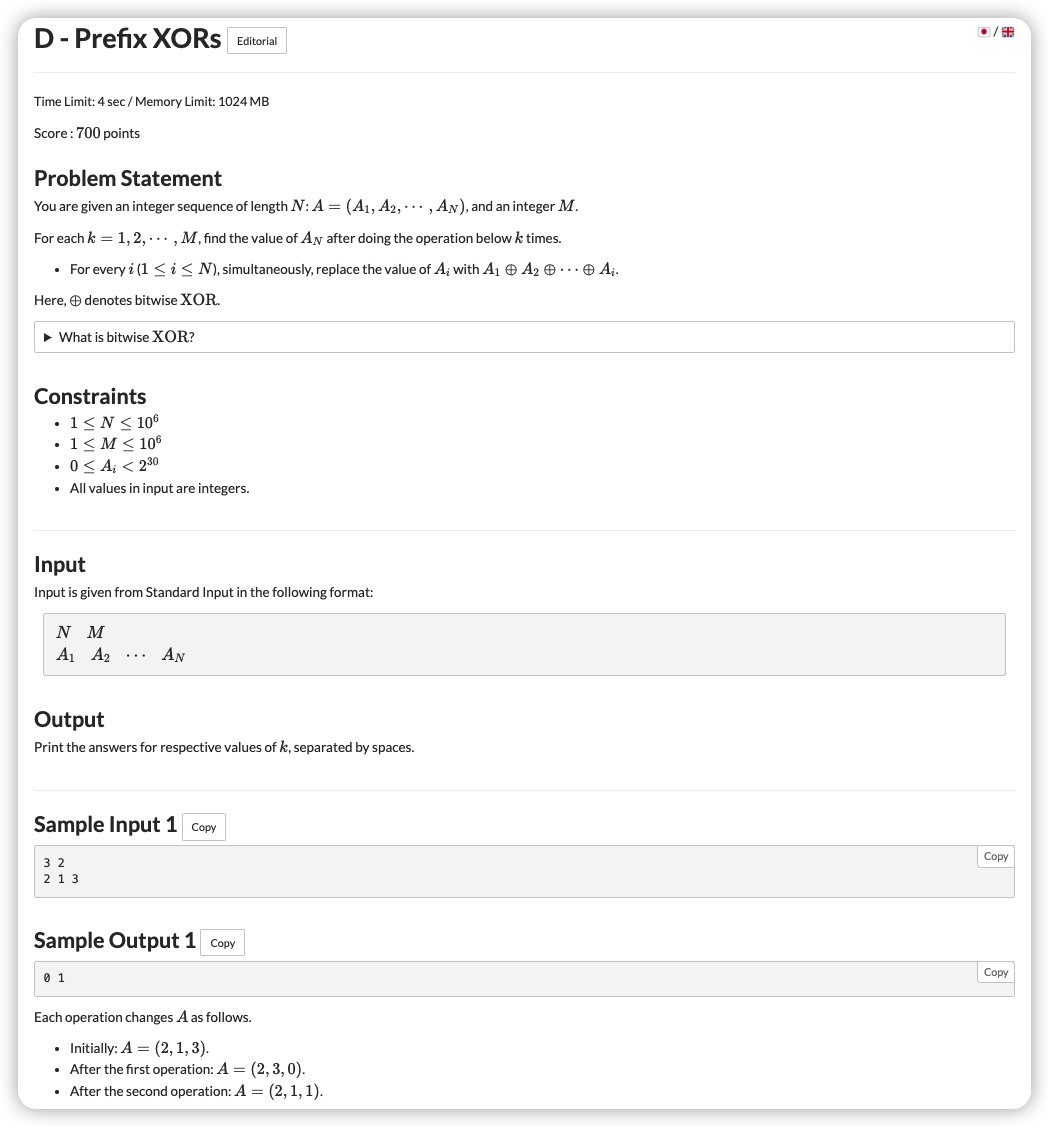
ARC137D_PrefixXORs

🔗

💡

一行为前一行的前缀，那么便可想到杨辉三角
在杨辉三角中，我们计算出第 $i$ 个数在第 $k$ 次的使用次数为 $\binom{n-i+k-1}{k-1}$
考虑异或次数为奇数时才会产生作用，要考虑奇偶性，组合数奇偶性便是 $Lucas$ 定理

好的思路在这里断了 看完题解之后才发现是要用 $Lucas$ 定理进行初始化子集和 $dp$
卢卡斯： $(n-i+k-1)\&(k-1)=(k-1)\Longrightarrow (n-i)\&(k-1)=0$
令 $s$ 为不小于 $max(n,m)$ 的第一个 $2$ 的幂
那么我们可以推出 $(s-1)^(n-i-1)$ 是最后一个存在 $a_i$ 的状态
由于 $sum_n$ 里面的 $a[1\to n]$ 的系数是反着来的 ，我们就也是倒着 $sosdp$
就是让 $1$ 的位置推到 $0$ 的位置即可

✅

const int N = (1 << 20) + 10;
int a[N], dp[N];
 
int main () {
        cin.tie(0)->sync_with_stdio(0);
        cin.exceptions(cin.failbit);
 
        int n, k; cin >> n >> k;
        read_Array(a, 0, n - 1);
 
        int s = 1, bit = 0;
        while ( s < max(n, k) ) s <<= 1, bit ++;
 
        for ( int i = 0; i < n; i ++ ) dp[(s - 1) ^ (n - i - 1)] = a[i];
 
        for ( int i = 0; i < bit; i ++ ) {
                for ( int j = 0; j < s; j ++ ) {
                        if ( j & (1 << i) ) dp[j ^ (1 << i)] ^= dp[j];
                }
        }
        
        print_Array(dp, ' ', 0, k - 1);
}

---