Chivas-Regal

二分

#

# 洛谷P1462_通往奥格瑞玛的道路

# 🔗

# 💡

二分答案，check() 可以通过删点来解决
在不走 f[x]>midf[x]>mid 的情况下，即提前标记 vis[x]=truevis[x]=true ，看看最短路是多少
和血量 bb 比较一下

# ✅

const int N = 1e4 + 10;
const int M = 1e5 + 10;

int n, m; ll b;
ll f[N];

bool vis[N];
ll dis[N];

struct Edge {
        int nxt, to;
        ll val;
} edge[M];
int head[N], cnt;
inline void add_Edge ( int from, int to, ll val ) {
        edge[++cnt] = { head[from], to, val };
        head[from] = cnt;
}

struct node { int id; ll dis; inline friend bool operator < ( node a, node b ) { return a.dis > b.dis; } };
inline bool Check ( ll x ) {
        for ( int i = 1; i <= n; i ++ ) {
                if ( f[i] <= x ) vis[i] = false;
                else             vis[i] = true;
                dis[i] = 1e18;
        }
        priority_queue<node> pque;
        pque.push({1, 0});
        dis[1] = 0;
        while ( !pque.empty() ) {
                node cur = pque.top(); pque.pop();
                if ( vis[cur.id] ) continue; vis[cur.id] = true;
                for ( int i = head[cur.id]; i; i = edge[i].nxt ) {
                        int to = edge[i].to;
                        if ( dis[to] > dis[cur.id] + edge[i].val && !vis[to] ) {
                                dis[to] = dis[cur.id] + edge[i].val;
                                pque.push({to, dis[to]});
                        }
                }
        }
        return dis[n] < b;
}

int main () {
        scanf("%d%d%lld", &n, &m, &b);
        for ( int i = 1; i <= n; i ++ ) scanf("%lld", &f[i]);
        for ( int i = 1; i <= m; i ++ ) {
                int x, y; ll z; scanf("%d%d%lld", &x, &y, &z);
                add_Edge(x, y, z);
                add_Edge(y, x, z);
        }

        ll l = 0, r = 1000000005;
        if ( Check(r) == false ) {
                puts("AFK");
                return 0;
        }

        ll res = r;
        while ( l <= r ) {
                int mid = (l + r) >> 1;
                if ( Check(mid) ) res = mid, r = mid - 1;
                else l = mid + 1;
        }
        printf("%lld\n", res);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

# 洛谷P1663_山

# 🔗

# 💡

思考什么样的点才可以被所有地方看见
在所有山坡直线上方的点
那么我们对于一个 yy ，可以求出它与所有山坡的交点
利用交点我们可以得到对于每个山坡，它能被看见的话，xx 可在的区间
利用二分答案，每一个 check() 是：对于所有 xx 可以被看到的区间是否有交集

# ✅

struct node {
        double k, b;
} l[5010];
pair<double, double> p[5010];

int n;

inline bool check ( double y ) {
        double L = -1e10, R = 1e10;
        for ( int i = 0; i < n - 1; i ++ ) {
                if ( l[i].k == 0 ) {
                        if ( l[i].b > y ) return false;
                } else {
                        double x0 = (y - l[i].b) / l[i].k, y0 = y;
                        if ( l[i].k < 0 ) L = max(L, x0);
                        else              R = min(R, x0);
                }
        }
        return L <= R;
}

int main () {
        cin >> n;
        for ( int i = 0; i < n; i ++ ) {
                cin >> p[i].first >> p[i].second;
                if ( i ) {
                        l[i - 1].k = (p[i].second - p[i - 1].second) / (p[i].first - p[i - 1].first);
                        l[i - 1].b = p[i].second - l[i - 1].k * p[i].first;
                } 
        }
        double l = 0, r = 1e10;
        while ( r - l > 1e-6 ) {
                double mid = (l + r) / 2;
                if ( check(mid) ) r = mid;
                else              l = mid;
        }
        printf("%.3f\n", l);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

# 洛谷P1704_寻找最优美做题曲线

# 🔗

# 💡

既然 [p][p] 是必须出现在 LISLIS 中的
那么我们可以找到 [1→n][1\to n] 中一定不会出现在 LISLIS 中的，删去
即对于 j:p[i−1]→p[i]j:p[i-1]\to p[i] c[p[i−1]]≥c[j]c[p[i-1]]\ge c[j] 或 c[j]≥c[p[i]]c[j]\ge c[p[i]] 的都不行
一看数据范围用二分法算 LISLIS
每次遇见 p[i]p[i] 后都一定会进行 push_back()

# ✅

const int N  = 5e5 + 10;
int n, k;
int p[N], c[N];
bool del[N];

int main () {
        ios::sync_with_stdio(false);
        cin >> n >> k;
        for ( int i = 1; i <= k; i ++ ) cin >> p[i];
        for ( int i = 1; i <= n; i ++ ) cin >> c[i];

        sort ( p + 1, p + 1 + k );
        for ( int i = 2; i <= k; i ++ ) {
                if ( c[p[i]] <= c[p[i - 1]] ) {
                        cout << "impossible" << endl;
                        return 0;
                }
        }


        for ( int j = 1; j < p[1]; j ++ ) if ( c[j] >= c[p[1]] ) del[j] = true;
        for ( int j = p[k] + 1; j <= n; j ++ ) if ( c[j] <= c[p[k]] ) del[j] = true;
        for ( int i = 2; i <= k; i ++ ) {
                for ( int j = p[i - 1] + 1; j < p[i]; j ++ ) {
                        if ( c[j] <= c[p[i - 1]] || c[j] >= c[p[i]] ) 
                                del[j] = true;
                }
        }

        vector<int> vec;
        for ( int i = 1; i <= n; i ++ ) {
                if ( del[i] ) continue;
                if ( vec.empty() || vec.back() < c[i] ) vec.push_back(c[i]);
                else vec[lower_bound(vec.begin(), vec.end(), c[i]) - vec.begin()] = c[i];
        }
        cout << vec.size() << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

# 洛谷P1768_天路

# 🔗

# 💡

带环的图很难求最长环
可以想一想能不能判断一个数是否为答案

考虑若 resres 是最后的结果
那么必然所有的环均满足

∑V∑P≤res∑V≤res×∑Pres×∑P−∑V≥0\begin{aligned} \frac{\sum V}{\sum P}&\le res\\ \sum V&\le res\times \sum P\\ res\times \sum P-\sum V&\ge 0 \end{aligned}

这样权值大小就很明显了，在最大值中找到最小的也是二分答案的标志
使用密度二分，每次对边权重新赋值 val=mid×p−vval=mid\times p-v
如果具有环 res×∑P−∑V<0res\times\sum P-\sum V\lt 0 那么说明还没有到最大值
否则的话可能比最大值要大
那么就是判断是否有负环，如果有的话就说名具有环满足上面的不等式，这个便是 check()

要注意可能会有不连通的情况，我们可以建立超级源点连接所有的边
这里 BFS 版 SPFASPFA 会寄， DFS 版勉强过

# ✅

const int N = 7010;
const int M = 40010;

struct Edge {
        int nxt, to;
        int v, p;
        double val;
} edge[M];
int head[N], cnt;
inline void add_Edge ( int from, int to, int v, int p ) {
        edge[++cnt] = { head[from], to, v, p };
        head[from] = cnt;
}
int n, m;


bool vis[N];
double dis[N];

inline bool has_Neg ( int x ) {
        vis[x] = true;
        for ( int i = head[x]; i; i = edge[i].nxt ) {
                int to = edge[i].to;
                if ( dis[to] > dis[x] + edge[i].val ) {
                        dis[to] = dis[x] + edge[i].val;
                        if ( vis[to] ) return true;
                        if ( has_Neg(to) ) return true;
                }
        }
        vis[x] = false;
        return false;
}

int main () {
        scanf("%d%d", &n, &m);       
        for ( int i = 0; i < m; i ++ ) {
                int a, b, c, d; scanf("%d%d%d%d", &a, &b, &c, &d);
                add_Edge(a, b, c, d);
        }
        for ( int i = 1; i <= n; i ++ ) add_Edge(0, i, 0, 0);

        double l = 0, r = 7000000;
        while ( r - l > 1e-6 ) {
                double mid = (l + r) / 2;
                for ( int i = 1; i <= cnt; i ++ ) edge[i].val = mid * edge[i].p - edge[i].v;
                for ( int i = 0; i <= n; i ++ ) vis[i] = 0, dis[i] = 100000000;
                dis[0] = 0;
                has_Neg(0) ? l = mid : r = mid;
        }
        if ( l == 0 ) {
                puts("-1");
                return 0;
        }
        printf("%.1f\n", l);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

# 洛谷P1800_software

# 🔗

# 💡

两个限制，即模块11和模块22的完成数要达到 mm
但是没有对应的价值，那么我们可以令一个模块的完成数作为价值，一个作为限制
那么开 dpdp
dp[i][j]dp[i][j] 表示前 ii 个人完成 jj 个模块11下最多能完成多少个模块22
由于时间固定出每个物品的价值（完成物品体积个模块11后又能完成多少个模块22），那么就是枚举时间，枚举物品，枚举背包容积，再枚举物品容积
这是一个 O(n4)O(n^4) 的复杂度
但是考虑一下随着时间增大， dp[n][m]dp[n][m] 肯定是单调递增的，那么时间使用二分答案判断 dp[n][m]dp[n][m] 是否 ≥m\ge m

# ✅

const int N = 110;
const int M = 110;

int n, m;
int a[N], b[N];

int dp[N][M];

inline bool Check ( int tim ) {
        memset(dp, -0x3f3f3f3f, sizeof dp);
        dp[0][0] = 0;
        for ( int i = 1; i <= n; i ++ ) {
                for ( int j = 0; j <= m; j ++ ) {         // 一共做了 j 个模块1
                        for ( int k = 0; k <= j; k ++ ) { // 第 i 个人做 k 个模块1
                                int time_else = tim - k * a[i];
                                if ( time_else >= 0 )
                                        dp[i][j] = max(dp[i][j], dp[i - 1][j - k] + time_else / b[i]);
                        }
                }
        }
        return dp[n][m] >= m;
}

int main () {
        ios::sync_with_stdio(false);
        cin >> n >> m;
        for ( int i = 1; i <= n; i ++ ) cin >> a[i] >> b[i];
        int l = 1, r = 100000;
        while ( l <= r ) {
                int mid = (l + r) >> 1;
                if ( Check(mid) ) r = mid - 1;
                else l = mid + 1;
        }
        cout << l << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

# 洛谷P1948_TelephoneLinesS

# 🔗

20220714170902

# 💡

以最大的那一条边做价值，经典二分答案的套路了
check(x) 表示路径上是否可以走不超过 kk 条边权 ≥x\ge x 的边，这些边可以免费
在此我们希望路径上大于等于 xx 的越少越好，那就以 [val≥x][val\ge x] 做权值，只有 11 和 00 来跑最短路
最终 dis[n]dis[n] 则是从 11 到 nn 最少有几个边权 ≥x\ge x 的边
如果这个数量 ≤k\le k 了说明我们还可以继续往 xx 小了找，否则要放松范围往 >x>x 了找
最后二分出来的结果就是答案

# ✅

const int N = 1003;
const int M = 20004;
struct Edge {
        int nxt, to, val;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to, int val) {
        edge[++cnt] = {head[from], to, val};
        head[from] = cnt;
}

int dis[N];// 1->i最少有多少个 长度>x的边
int vis[N];
int n, p, k;

struct node {
        int id, val;
        inline friend bool operator < (node a, node b) {
                return a.val > b.val;
        }
};
inline bool check (int x) {
        for (int i = 1; i <= n; i ++) dis[i] = 0x3f3f3f3f, vis[i] = 0;
        dis[1] = 0;
        priority_queue<node> pque;
        pque.push({1, 0});
        while (!pque.empty()) {
                int u = pque.top().id; pque.pop();
                if (vis[u]) continue; vis[u] = 1;
                for (int i = head[u]; i; i = edge[i].nxt) {
                        int v = edge[i].to;
                        int d = edge[i].val >= x;
                        if (dis[v] > dis[u] + d) {
                                dis[v] = dis[u] + d;
                                pque.push({v, dis[v]});
                        }
                }
        }
        return dis[n] <= k;
}

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        cin >> n >> p >> k;
        for (int i = 0; i < p; i ++) {
                int u, v, w; cin >> u >> v >> w;
                add_Edge(u, v, w);
                add_Edge(v, u, w);
        }
        int l = 0, r = 1000000, res = 1000001;
        while (l <= r) {
                int mid = (l + r) >> 1;
                if (check(mid)) res = mid, r = mid - 1;
                else l = mid + 1;
        }
        if (res == 0) res = 1;
        else if (res == 1000001) res = 0;
        cout << res - 1 << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

# 洛谷P2323_公路修建问题

# 🔗

# 💡

因为答案是一个数值且要最小，所以具有单调性
且具有很多限制，如果给定一个数值我们可以很好地得出是否可以完成指标（ kk 个 c1c1 ，还要完成可以构建生成树
那么我们利用这个限制，去二分答案求解，check() 可以通过删边来解决
每次用 x=midx=mid 去 check()check() 先扫一遍尽可能去把 c1<=xc1<=x 的道路都建上
满足了 kk 个边了再去看看生成树可不可以

# ✅

const int N = 2e4 + 10;
int n, k, m;

namespace UnionSet {
        int nod[N];
        inline void Init () { for ( int i = 0; i <= n; i ++ ) nod[i] = i; }
        inline int Find ( int x ) { return x == nod[x] ? x : Find(nod[x]); }
        inline void Merge ( int x, int y ) { int fx = Find(x), fy = Find(y); if ( fx != fy ) nod[fx] = fy; }
        inline bool is_Similar ( int x, int y ) { int fx = Find(x), fy = Find(y); return fx == fy; }
} using namespace UnionSet;

struct Edge {
        int a, b, c1, c2;
} e[N];

inline bool Check ( int x ) {
        Init();
        int cntk = 0, cnt = 0;
        for ( int i = 0; i < m; i ++ ) {
                if ( e[i].c1 <= x ) {
                        if ( !is_Similar(e[i].a, e[i].b) ) 
                                Merge(e[i].a, e[i].b),
                                cntk ++,
                                cnt ++;
                }
                if ( cnt == n - 1 ) {
                        return cntk >= k;
                }
        }
        if ( cntk < k ) return false;
        for ( int i = 0; i < m; i ++ ) {
                if ( e[i].c2 <= x ) {
                        if ( !is_Similar(e[i].a, e[i].b) ) 
                                Merge(e[i].a, e[i].b),
                                cnt ++;
                }
                if ( cnt == n - 1 ) break;
        }
        return cnt == n - 1;
}

int main () {
        scanf("%d%d%d", &n, &k, &m);
        for ( int i = 0; i < m; i ++ ) scanf("%d%d%d%d", &e[i].a, &e[i].b, &e[i].c1, &e[i].c2);
        int l = 1, r = 30000;
        int res = 30000;
        while ( l <= r ) {
                int mid = (l + r) >> 1;
                if ( Check(mid) ) res = mid, r = mid - 1;
                else l = mid + 1;
        }
        
        printf("%d\n", res);
        Init();

        int cnt = 0, cntk = 0;
        for ( int i = 0; i < m; i ++ ) {
                if ( e[i].c1 <= res ) {
                        if ( !is_Similar(e[i].a, e[i].b) ) 
                                Merge(e[i].a, e[i].b),
                                cntk ++,
                                cnt ++,
                                printf("%d 1\n", i + 1);
                }
                if ( cnt == n - 1 ) return 0;
        }
        for ( int i = 0; i < m; i ++ ) {
                if ( e[i].c2 <= res ) {
                        if ( !is_Similar(e[i].a, e[i].b) ) 
                                Merge(e[i].a, e[i].b),
                                cnt ++,
                                printf("%d 2\n", i + 1);
                }
                if ( cnt == n - 1 ) return 0;
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76

# 洛谷P2754_家园 / 星际转移问题

# 🔗

20221113203951

# 💡

如果就是正常平面上画一个图，会发现出现绕环的情况，也就是对于一条航母路线，是一个环，这样就会导致环上两个点同时接收流量的情况出现，而正常来看是有时间存在的
既然存在时间，那就多加一条时间线，而对于相同的节点，在不同时刻是存在不同的状态，它们不是一个点
故一个时间开 n+2n+2 个节点（nn 个空间站和地月球），那么就在 ii 时刻，jj 航母可以用 S[j][i%sz[j]]S[j][i\%sz[j]] 与 S[j][(i+1)%sz[j]]S[j][(i+1)\%sz[j]] 相连，容量就是该航母容量 r[j]r[j]
而且相邻时刻下，同一个节点的人是可以留在这个点的，就对每一个时刻的每一个节点向下一个时刻的该节点传递一个 ∞\infty 的容量
那么为了研究 00 到 tt 时间，能运走多少人，开 t+1t+1 个时刻进行上面的操作，然后就需要源点向每一个时刻的地球都挂 ∞\infty 个人，然后让每一时刻的月球连向汇点容量为 ∞\infty ，tt 时间内能运走的人数就是总流量
这只是能判断出来这么长时间能运多少，这是一个判定条件，且时间越长能运的越多
故开二分

# ✅

const int N = 15, M = 25, K = 55;
struct Edge {
    int nxt, to, flow;
} edge[N * K * N * N + 10];
int head[N * K * N + 10], cnt;
inline void add_Edge (int from, int to, int flow) {
    edge[++cnt] = {head[from], to, flow};
    head[from] = cnt;
    edge[++cnt] = {head[to], from, 0};
    head[to] = cnt;
}
inline void init_Edge () {
    memset(head, 0, sizeof head);
    cnt = 1;
}

int deep[N * K * N + 10], aim;
inline bool bfs (int S, int T) {
    aim = T;
    memset(deep, 0, sizeof deep);
    deep[S] = 1; queue<int> que;
    que.push(S);
    while (!que.empty()) {
        int u = que.front(); que.pop();
        for (int i = head[u]; i; i = edge[i].nxt) {
            int v = edge[i].to;
            if (edge[i].flow && !deep[v]) {
                deep[v] = deep[u] + 1;
                que.push(v);
            }
        }
    }
    return deep[T];
}
inline int dfs (int u, int fl) {
    if (u == aim) return fl;
    int f = 0;
    for (int i = head[u]; i && fl; i = edge[i].nxt) {
        int v = edge[i].to;
        if (deep[v] == deep[u] + 1 && edge[i].flow) {
            int x = dfs(v, min(fl, edge[i].flow));
            edge[i].flow -= x;
            edge[i ^ 1].flow += x;
            fl -= x;
            f += x;
        }
    }
    if (!f) deep[u] = -2;
    return f;
}
inline int dicnic (int S, int T) {
    int ret = 0;
    while (bfs(S, T)) ret += dfs(S, 0x3f3f3f3f);
    return ret;
}

vector<int> path[M];
int h[M], sz[M];
int n, m, k;

int S, T;
int mat[N * K][N];
inline bool Check (int x) {
    init_Edge();
    for (int i = 0; i + 1 < x; i ++) {
        for (int j = 1; j <= m; j ++) {
            int u = path[j][i % sz[j]];
            int v = path[j][(i + 1) % sz[j]];
            add_Edge(mat[i][u], mat[i + 1][v], h[j]);
        }
        for (int j = 0; j <= n + 1; j ++) 
            add_Edge(mat[i][j], mat[i + 1][j], 0x3f3f3f3f);
    }
    for (int i = 0; i < x; i ++) 
        add_Edge(S, mat[i][0], 0x3f3f3f3f),
        add_Edge(mat[i][n + 1], T, 0x3f3f3f3f);
    int mxf = dicnic(S, T);
    return mxf >= k;
}

int main () {
    for (int i = 0; i < N * K; i ++) for (int j = 0; j < N; j ++) mat[i][j] = i * N + j;
    S = N * K * N;
    T = S + 1;

    scanf("%d%d%d", &n, &m, &k);
    for (int i = 1; i <= m; i ++) {
        scanf("%d%d", &h[i], &sz[i]);
        for (int j = 1; j <= sz[i]; j ++) {
            int x; scanf("%d", &x);
            path[i].push_back(x == -1 ? n + 1 : x);
        }
    }

    int l = 1, r = N * K - 1, res = 0x3f3f3f3f;
    while (l <= r) {
        int mid = (l + r) >> 1;
        if (Check(mid)) res = mid, r = mid - 1;
        else l = mid + 1;
    }
    printf("%d\n", res == 0x3f3f3f3f ? 0 : res - 1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102

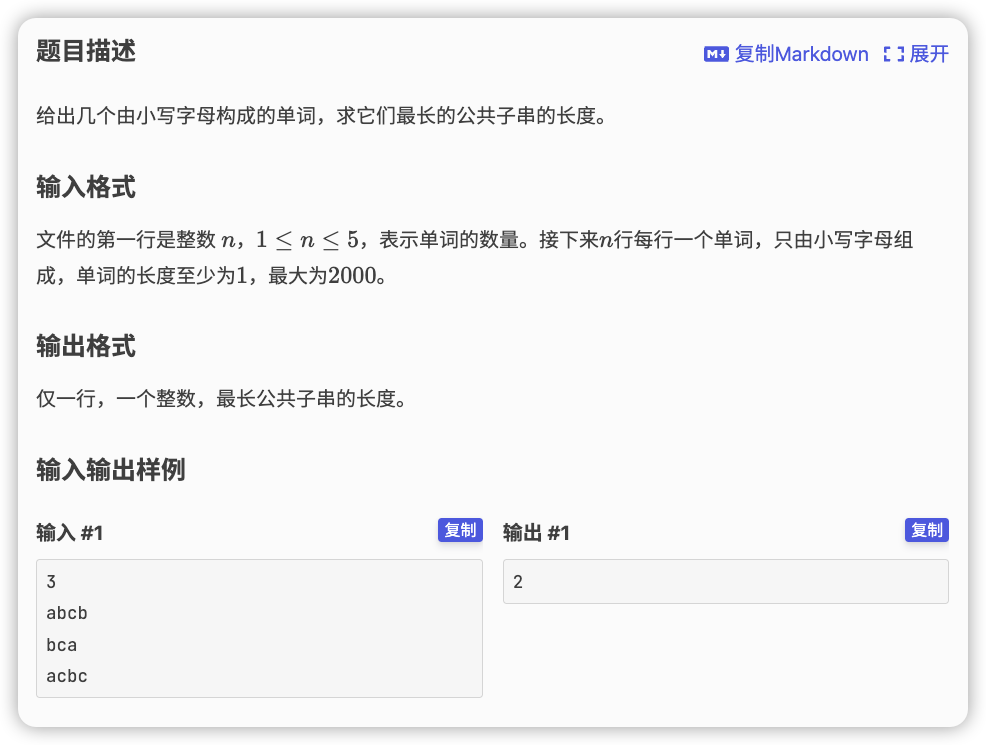
# 洛谷P5546_公共串

# 🔗

20220904182920

# 💡

20002000 初始可以想一个高复杂度的
这个数据量看来似乎可以将所有的子串全部枚举出来了
存储的时候如果存储所有子串空间不够，考虑压缩为 hashhash 数值存储
n≤5n \le 5 可以直接用 mapmap 将 keykey 设置为 hashhash 值，将 valval 设置为二进制表示在哪个字符串中出现过
第 ii 个串的所有子串全部与上 2i2^i 最后扫描所有子串看看是否够 2n−12^n-1 ，够的话代表在所有字符串中均出现过，维护最大值
这样分析一下复杂度 O(5n2logn)O(5n^2logn) 有点大了，优化一下
求最长公共子串应该要注意到这个“最”字，可以看一下是否存在单调性
可以发现，如果 abcdefgabcdefg 为公共子串，那么 abcdefabcdef 也为公共子串
这就证明检查公共子串的长度是否存在是存在 0101 单调性的
于是直接二分答案即可，复杂度为 O(5nlognlogn)O(5nlognlogn) 的

# ✅

const int N = 2e3 + 10;
const ll mod1 = 2000000011;
const ll mod2 = 3000000019;
const int HASH1 = 20023;
const int HASH2 = 20011;
ll h1[N], h2[N];
ll sum1[10][N], sum2[10][N];
inline ll query1 (int l, int r, int op) {
    return ((sum1[op][r] - sum1[op][l - 1] * h1[r - l + 1] % mod1) % mod1 + mod1) % mod1;
}
inline ll query2 (int l, int r, int op) {
    return ((sum2[op][r] - sum2[op][l - 1] * h2[r - l + 1] % mod2) % mod2 + mod2) % mod2;
}
inline pair<ll, ll> query (int l, int r, int op) {
    return {query1(l, r, op), query2(l, r, op)};
}

int n;
int len[10];
inline bool Check (int x) {
    map<pair<ll, ll>, int> mp;
    for (int i = 0; i < n; i ++) {
        for (int j = 1; j + x - 1 <= len[i]; j ++) {
            mp[query(j, j + x - 1, i)] |= 1 << i;
            if (mp[query(j, j + x - 1, i)] == (1 << n) - 1) return true;
        }
    }
    return false;
}

char str[10][N];
int main () {
    h1[0] = h2[0] = 1;
    for (int i = 1; i < N; i ++) h1[i] = h1[i - 1] * HASH1 % mod1, h2[i] = h2[i - 1] * HASH2 % mod2;

    cin >> n;
    for (int i = 0; i < n; i ++) {
        cin >> (str[i] + 1);
        len[i] = strlen(str[i] + 1);
        for (int j = 1; j <= len[i]; j ++) {
            sum1[i][j] = (sum1[i][j - 1] * HASH1 % mod1 + str[i][j]) % mod1;
            sum2[i][j] = (sum2[i][j - 1] * HASH2 % mod2 + str[i][j]) % mod2;
        }
    }

    int l = 1, r = 2000, res = 0;
    while (l <= r) {
        int mid = (l + r) >> 1;
        if (Check(mid)) res = mid, l = mid + 1;
        else r = mid - 1;
    }
    cout << res << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

# 洛谷P5657_格雷码

# 🔗

# 💡

一道二分观察的好题
(感觉没有涉及到位运算的思想鸭（逃

因为每一次都是将整个序列的长度*2
是一个以 2 为基数按规律构造的序列
那么可以想 log(n) 怎么操作

好好观察一下，将当前固定出的序列分半（记为这是第x次分半
可以看出，在x位上，原段的两半呈现一半为1一半为0，如果上一步是选择右边的一半，那么左1右0，否则左0右1

根据这个规律，我们就可以二分地写出来了

# ✅

int main () {
        ios::sync_with_stdio(false);
        ll n; cin >> n;
        ll k; cin >> k;
        ll l = 0, r = (1ll << n) - 1;
        bool where; //false: lft, true: rgt
        while ( n -- ) {
                ll mid = (l + r) >> 1;
                if ( k <= mid ) cout << 0 + where, r = mid, where = false;
                else            cout << 1 - where, l = mid + 1, where = true;
        }
}
1
2
3
4
5
6
7
8
9
10
11
12

# 牛客2022寒假算法基础集训营5A_疫苗小孩

# 🔗

# 💡

统计字符串中为 00 的位置 {ps}\{ps\} 后
我们枚举每个起始点 ps[i]ps[i]
对 ps[i]ps[i] 去找离 ps[i]+kps[i]+k 最近的左右两点，满足的统计一下 maxmax
然后对该左右两点分别去找最近的 ps+kps+k 的左右两点，满足的统计一下 maxmax
即：
i{pos01{pos011pos012pos02{pos021pos022i\left\{\begin{aligned} pos01\left\{\begin{aligned}pos011\\pos012\end{aligned}\right.\\ pos02\left\{\begin{aligned}pos021\\pos022\end{aligned}\right. \end{aligned}\right.

# ✅

ll k, w, q; 
inline ll calc ( ll a, ll b ) { // 计算 a->b 的提升值
        return w - llabs(b - a - k) * q;
}

int main () {
        ios::sync_with_stdio(false);

        ll n; string s; cin >> n >> s;
        cin >> k >> w >> q;
        vector<ll> ps;
        for ( int i = 0; i < s.size(); i ++ ) {
                if ( s[i] == '0' ) ps.push_back(i);
        }
        ll res = 0;
        for ( int i = 0; i < ps.size(); i ++ ) {
                ll pos02 = lower_bound(ps.begin(), ps.end(), ps[i] + k) - ps.begin();
                ll pos01 = pos02 - 1;
                if ( pos02 != ps.size() && pos02 > i ) res = max(res, calc(ps[i], ps[pos02]));
                if ( pos01 != ps.size() && pos01 > i ) res = max(res, calc(ps[i], ps[pos01]));

                if ( pos02 != ps.size() && pos02 > i ) {
                        ll disi02 = calc(ps[i], ps[pos02]);
                        ll pos022 = lower_bound(ps.begin(), ps.end(), ps[pos02] + k) - ps.begin();
                        ll pos021 = pos022 - 1;
                        if ( pos022 != ps.size() && pos022 > pos02 ) res = max(res, disi02 + calc(ps[pos02], ps[pos022]));
                        if ( pos021 != ps.size() && pos021 > pos02 ) res = max(res, disi02 + calc(ps[pos02], ps[pos021]));
                }
                if ( pos01 != ps.size() && pos01 > i ) {
                        ll disi01 = calc(ps[i], ps[pos01]);
                        ll pos012 = lower_bound(ps.begin(), ps.end(), ps[pos01] + k) - ps.begin();
                        ll pos011 = pos012 - 1;
                        if ( pos012 != ps.size() && pos012 > pos01 ) res = max(res, disi01 + calc(ps[pos01], ps[pos012]));
                        if ( pos011 != ps.size() && pos011 > pos01 ) res = max(res, disi01 + calc(ps[pos01], ps[pos011]));
                }
        }
        cout << res << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

# ABC236E_AverageAndMedian

# 🔗

# 💡

二分求平均数是一个经典的密度二分

一个位置可以选或者不选，但是不能有两个相邻的不选
这个我们可以感觉到 dpdp 就可以推出来

平均数
问题在于： 在不同选中数量下，一个数对平均数的贡献是不同的
但是我们求总值是很好求的
这个就奠定了我们可以给出一个平均数 ave 来判断能否获得比这个平均数更大的值
每一个数的贡献就变成了 x-ave
只要最终贡献大于 0 ，我们就可以说能造出来
通过这个编写一个 check ，过程中采用 dpdp 的解法去递推，判断最终结果即可

中位数
有了上一个问题做支撑
我们也可以想到这个可以尝试用二分去解决
根上一个不同的是，我们在设置期望中位数 mid 后，每一个数的贡献不同了
思考中位数的命名性质，我们只要求出 “比 mid 大的数的个数” 减去 “比 mid 小的数的个数” 的差
如果这个差大于 00 ，那么就说明我们可以造出比它更高的中位数

两个 check 搭建完毕，可以二分了

# ✅

const int N = 1e5 + 10;
int n;
int a[N];
 
double f[2][N]; // 0:不选i，1:选i
inline bool Check1 ( double ave ) {
        for ( int i = 1; i <= n; i ++ ) {
                f[1][i] = max(f[1][i - 1] + 1.0 * a[i] - ave, f[0][i - 1] + 1.0 * a[i] - ave);
                f[0][i] = f[1][i - 1];
        }
        return max(f[1][n], f[0][n]) > 0;
}
inline void Solve1 () {
        double l = 0, r = 1e9;
        while ( l - r < -1e-6 ) {
                double mid = (l + r) / 2;
                if ( Check1(mid) ) l = mid;
                else r = mid;
        }
        printf("%.4f\n", l);
}
 
double g[2][N]; // 0:不选i，1:选i
inline bool Check2 ( int mid ) {
        for ( int i = 1; i <= n; i ++ ) {
                g[1][i] = max(g[1][i - 1] + (a[i] >= mid ? 1 : -1), g[0][i - 1] + (a[i] >= mid ? 1 : -1) );
                g[0][i] = g[1][i - 1];
        }
        return max(g[1][n], g[0][n]) > 0;
}
inline void Solve2 () {
        int l = 0, r = 1e9;
        int res = 0;
        while ( l <= r ) {
                int mid = (l + r) / 2;
                if ( Check2(mid) ) l = mid + 1, res = mid;
                else r = mid - 1;
        }
        printf("%d\n", res);
}
 
int main () {
        scanf("%d", &n);
        for ( int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
        Solve1();
        Solve2();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

# AcWing2694_最长公共子序列

# 🔗

# 💡

LCS是个动态规划问题，但我们可以用DP的思想贪过去

因为a中每个数只出现过一次，所以在这道题里面，我们可以将问题转化为一个LIS问题

首先设置一个数组id[]用来存入a数组里面的每个出现的数的下标

然后将b数组转化为b'数组，即b'[i] = id[b[i]]用来表示：b数组中当前数在a数组中对应的下标

那么要想b中的某个序列在a中也是其中的序列

就需要我们得到的这个b'中的某个子序列，在a中出现过就行了，同时要保证在a中的下标是顺序的

所以问题可以转化为求b'数组的最长上升子序列

具体LIS问题求法可以看 -> 这里 (opens new window)

我们发现这个数据范围是1e61e6的，所以我们采用贪心+二分优化，时间复杂度O(nlogn)

# ✅

const int N = 1e6 + 10;

int id[N], n;
vector<int> vec;

int main(){
    read(n);
    for(int i = 1, x; i <= n; i ++)  read(x), id[x] = i;
    for(int i = 1, x; i <= n; i ++){ read(x);
        if(!id[x]) continue;//注意：如果没出现过那就不要加进去了
        if(vec.empty() || vec.back() < id[x]) vec.push_back(id[x]);
        else                                  vec[lower_bound(vec.begin(), vec.end(), id[x]) - vec.begin()] = id[x];
    }write(vec.size());
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# CCPC2017哈尔滨站L_ColorATree

# 🔗

20221113224431

# 💡

AA 操作是子树最少选 yy个
BB 操作是非子树最少选 yy 个，想办法把 BB 移植成 AA 的格式，那么就是子树最多选 allsum−yallsum-y 个，这样就是一个区间的向上递归满足的问题
我们在判断一个 allsumallsum 是否可行时，将其进行区间嵌套 dfsdfs 到 11 也就是根节点，看看 11 的范围内是否存在 allsumallsum ，如果存在说明可行
且可以看出来黑点从少到多的可行判断是存在单调性的，所以对 allsumallsum 二分即可

# ✅

const int N = 1e5 + 10;
const int M = N << 1;
struct Edge {
    int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to) {
    edge[++cnt] = {head[from], to};
    head[from] = cnt;
}
int sz[N];
inline void dfs_Pre (int u, int fa) {
    sz[u] = 1;
    for (int i = head[u]; i; i = edge[i].nxt) {
        int v = edge[i].to;
        if (v == fa) continue;
        dfs_Pre(v, u);
        sz[u] += sz[v];
    }
}

int n, m1, m2;
pair<int, int> A[N], B[N];
pair<int, int> limit[N];

inline pair<int, int> intersect (pair<int, int> a, pair<int, int> b) {
    return {max(a.first, b.first), min(a.second, b.second)};
}
inline void dfs (int u, int fa) {
    pair<int, int> limu = {0, 1};
    for (int i = head[u]; i; i = edge[i].nxt) {
        int v = edge[i].to;
        if (v == fa) continue;
        dfs(v, u);
        limu.first += limit[v].first;
        limu.second += limit[v].second;
    }
    limit[u] = intersect(limit[u], limu);
}

inline bool check (int x) {
    for (int i = 1; i <= n; i ++) limit[i] = {0, sz[i]};
    for (int i = 1; i <= m1; i ++) limit[A[i].first].first = max(limit[A[i].first].first, A[i].second);
    for (int i = 1; i <= m2; i ++) limit[B[i].first].second = min(limit[B[i].first].second, x - B[i].second);
    dfs(1, 0);
    for (int i = 1; i <= n; i ++) if (limit[i].first > limit[i].second) return false;
    if (limit[1].first <= x && x <= limit[1].second) return true;
    return false;
}

inline void Solve () {
    scanf("%d", &n);

    for (int i = 1; i <= n; i ++) head[i] = 0; cnt = 0;

    for (int i = 1; i < n; i ++) {
        int u, v; scanf("%d%d", &u, &v);
        add_Edge(u, v);
        add_Edge(v, u);
    }
    dfs_Pre(1, 0); bool flag = true;
    scanf("%d", &m1);
    for (int i = 1; i <= m1; i ++) {
        scanf("%d%d", &A[i].first, &A[i].second);
        if (A[i].second > sz[A[i].first]) flag = false;
    }
    scanf("%d", &m2);
    for (int i = 1; i <= m2; i ++) {
        scanf("%d%d", &B[i].first, &B[i].second);
        if (B[i].second > n - sz[B[i].first]) flag = false;
    }
    if (!flag) {
        puts("-1");
        return;
    }

    int l = 0, r = n, res = n;
    while (l <= r) {
        int mid = (l + r) >> 1;
        if (check(mid)) res = mid, r = mid - 1;
        else l = mid + 1;
    }
    printf("%d\n", res);
}

int main () {
    int cas; scanf("%d", &cas); while (cas --) {
        Solve();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90

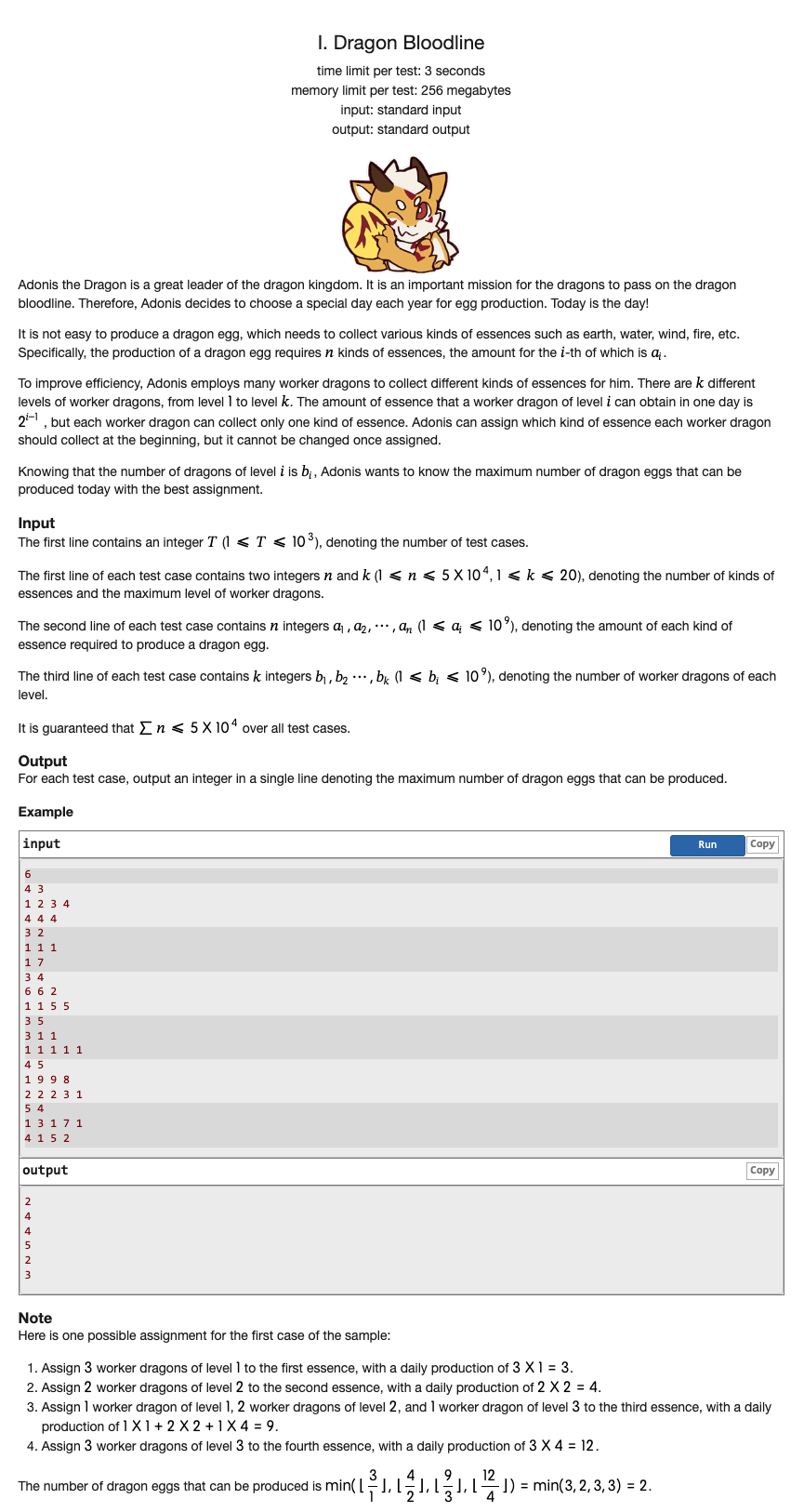
# CCPC2022威海站I_DragonBloodline

# 🔗

20221113221710

# 💡

由于我们很难求得最多能满足多少套食物，但是我们可以判定是否可以满足 xx 套食物即材料 ii 用 xa[i]xa[i] 个
这个判定是会随着 xx 存在单调性的，故使用二分答案
在 checkcheck 里面分配时，从效率高的龙开始往效率低的龙枚举，2j2^j 效率的龙首先分给所有 a[i]≥2ja[i]\ge 2^j 的材料 ⌊a[i]2j⌋\left\lfloor\frac{a[i]}{2^j}\right\rfloor 个，当然数量总和不能超过龙数，如果最后还有剩余的，分给最多的几个材料一个材料一份
到最后判断一下是否所有材料都被给占满了即可

# ✅

const int N = 5e5 + 10;
int n, k;
__int128_t a[N], b[N], tb[N], c[N];
 
inline bool check (__int128_t x) {
    for (int i = 0; i < k; i ++) b[i] = tb[i];
    for (int i = 1; i <= n; i ++) c[i] = x * a[i];
    for (int i = k - 1; i >= 0; i --) {
        for (int j = 1; j <= n; j ++) {
            if (c[j] <= 0) continue;
            __int128_t cos = min(b[i], c[j] / (1 << i));
            b[i] -= cos;
            c[j] -= cos * (1 << i);
        }
        if (n < b[i]) nth_element(c + 1, c + 1 + n, c + 1 + n, [&](int e, int f){return e > f;});
        else nth_element(c + 1, c + 1 + b[i], c + 1 + n, [&](int e, int f){return e > f;});
        for (int j = 1; j <= b[i] && j <= n; j ++) {
            c[j] -= 1 << i;
        }
    }
    for (int i = 1; i <= n; i ++) if (c[i] > 0) return false;
    return true;
}
inline void Solve () {
    scanf("%d%d", &n, &k);
    for (int i = 1; i <= n; i ++) {
        int x; scanf("%d", &x);
        a[i] = x;
    }
    for (int i = 0; i < k; i ++) {
        int x; scanf("%d", &x);
        tb[i] = x;
    }
 
    ll l = 0, r = 2e15, res = 0;
    while (l <= r) {
        ll mid = (l + r) >> 1;
        if (check(mid)) res = mid, l = mid + 1;
        else r = mid - 1;
    }
    printf("%lld\n", res);
}
 
int main () {
    int cass; scanf("%d", &cass); while (cass --) {
        Solve ();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

# CodeForces1141G_PrivatizationOfRoadsInTreeland

# 🔗

20220517153827

# 💡

首先根据鸽巢原理，如果一个点接了 xx 条边，我们有 yy 个公司，当 x>yx>y 时，这个点必会被两个相同公司的边连接。
那么我们判断最少需要用多少个公司就有方法了，由于每个点的 xx 是固定的也就是 degideg_i ，我们最多坏点个数也是确定的，且公司越多坏点越少，单调性也有了，那么可以直接二分出来。
对于 check(mid) 的时候，我们去看有多少个点的度数 >mid>mid 也就是有多少个坏点，如果有超过 kk 个坏点，那么就是 false ，否则是 true

那么染色的方式就比较多了，思考一下省事点就是 dfsdfs ，一个点连接向儿子的边的公司，在与连接父亲的边的公司不同的情况下尽量不重复地去选即可

# ✅

const int N = 2e5 + 10;
const int M = N << 1;
struct Edge {
        int nxt, to, id;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to, int id) {
        edge[++cnt] = {head[from], to, id};
        head[from] = cnt;
}
 
int du[N];
int n, m;
int res, col[M];
 
inline bool Check (int val) {
        int num = 0;
        for (int i = 1; i <= n; i ++) num += du[i] > val; // 坏点就 +1 
        return num <= m;
}
inline void col_Dfs (int u, int fa) {
        int colidx = 0;
        int colgrand; for (int i = head[u]; i; i = edge[i].nxt) if (edge[i].to == fa && fa != -1) colgrand = col[edge[i].id];
        for (int i = head[u]; i; i = edge[i].nxt) {
                int v = edge[i].to; if (v == fa) continue;
                if (colidx == colgrand) colidx = (colidx + 1) % res; // 与连接父亲的边的公司不同
                col[edge[i].id] = colidx;
                col_Dfs(v, u);
                colidx = (colidx + 1) % res;
        }
}
 
int main () {
        scanf("%d%d", &n, &m);
        for (int i = 1; i < n; i ++) {
                int u, v; scanf("%d%d", &u, &v);
                add_Edge(u, v, i);
                add_Edge(v, u, i);
                du[u] ++, du[v] ++;
        }
 
        int l = 1, r = n - 1; res = r;
        while (l <= r) {
                int mid = (l + r) >> 1;
                if (Check(mid)) res = mid, r = mid - 1;
                else l = mid + 1;
        }
 
        col_Dfs(1, -1);
        printf("%d\n", res);
        for (int i = 1; i < n; i ++) printf("%d ", col[i] + 1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

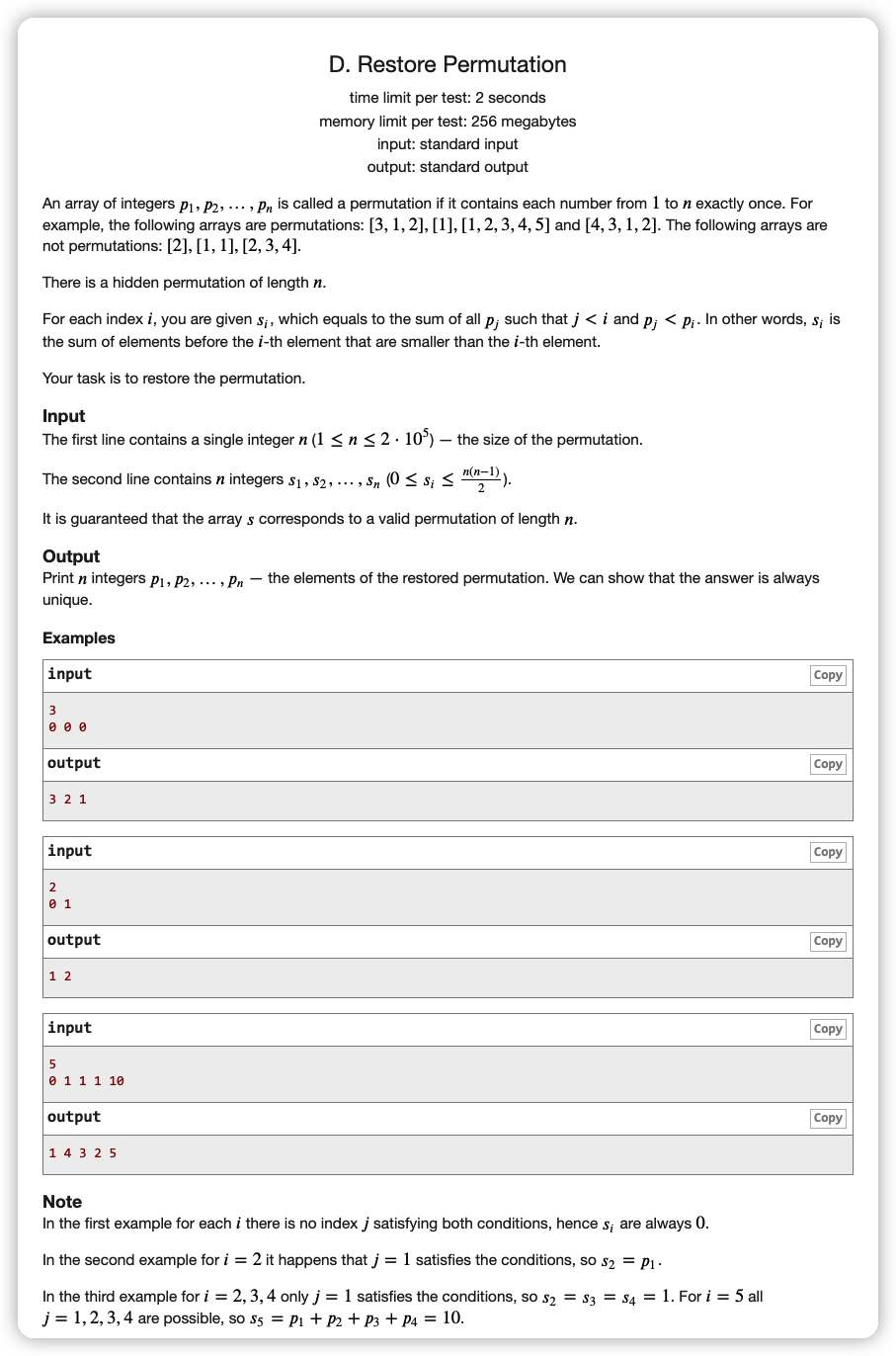
# CodeForces1208D_RestorePermutation

# 🔗

20220517151604

# 💡

拿到题肯定先是正着看，发现正着看了话也就是能确定 aa 连续的相同的位置，它们对应的排列数是单调递减的。还有就是第一个非 00 的位置是前面 00 的部分位置上的数的累加和。别的没什么性质了，思路断了，考虑倒着看。

首先对于第三个样例，最后一个位置 10=1+2+3+410=1+2+3+4 ，这个位置一定是 55 。然后倒数第二个位置 1=11=1 ，这个位置可以选 2,3,42,3,4 ，由于如果选了 33 了话这里 a[i]a[i] 还要加一个 22 ，因为 22 在前面，所以说明是选前缀 sum[x−1]≥a[i]sum[x-1]\ge a[i] 的数 xx，这里 [sum][sum] 是指除掉后面确定的数后 剩余的数的前缀和。

这样就很明确了，我们有一个数组 [b][b] ，其中如果 b[i]b[i] 被后面的位置确定了那么就是 00 ，如果没有那么 b[i]=ib[i]=i ，然后 [sum][sum] 是 [b][b] 的前缀和
我们倒着枚举 ii ，在 [1,n][1,n] 中二分出来 b[x]≠0b[x]\neq 0 且 sum[x−1]≥a[i]sum[x-1]\ge a[i] 的位置 ，然后将 b[x]b[x] 设置为 00 并且更新 [sum][sum]
这里这两个更新操作如果暴力操作都会很费时间，可以使用线段树或树状数组进行更新，查询也是。

# ✅

const ll N = 5e5 + 10;
 
ll t[N];
inline ll lowbit (ll x) { return x & -x; }
inline void update (ll id, ll c) {
        while (id < N) t[id] += c, id += lowbit(id);
}
inline ll query (ll id) {
        ll res = 0;
        while (id > 0) res += t[id], id -= lowbit(id);
        return res;
}
 
ll n, a[N], p[N];
 
int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);
        
        cin >> n;
        for (ll i = 1; i <= n; i ++) cin >> a[i], update(i, i);
 
        for (ll i = n; i >= 1; i --) {
                ll l = 1, r = n, res = n;
                while (l <= r) {
                        ll mid = (l + r) >> 1;
                        ll qm = query(mid - 1);
                        if (query(mid) - qm == 0) { // 注意如果 mid 不存在，那么要根据 sum 直接调整区间
                                if (qm > a[i]) {
                                        r = mid - 1;
                                } else {
                                        l = mid + 1;
                                }
                        } else { // 如果存在， qm=a[i]时说明找到了便可直接 break
                                if (qm > a[i]) r = mid - 1;
                                else if (qm == a[i]) { res = mid; break; }
                                else l = mid + 1;
                        }
                } 
                p[i] = res;
                update(res, -res);
        }
        for (ll i = 1; i <= n; i ++) cout << p[i] << " ";
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

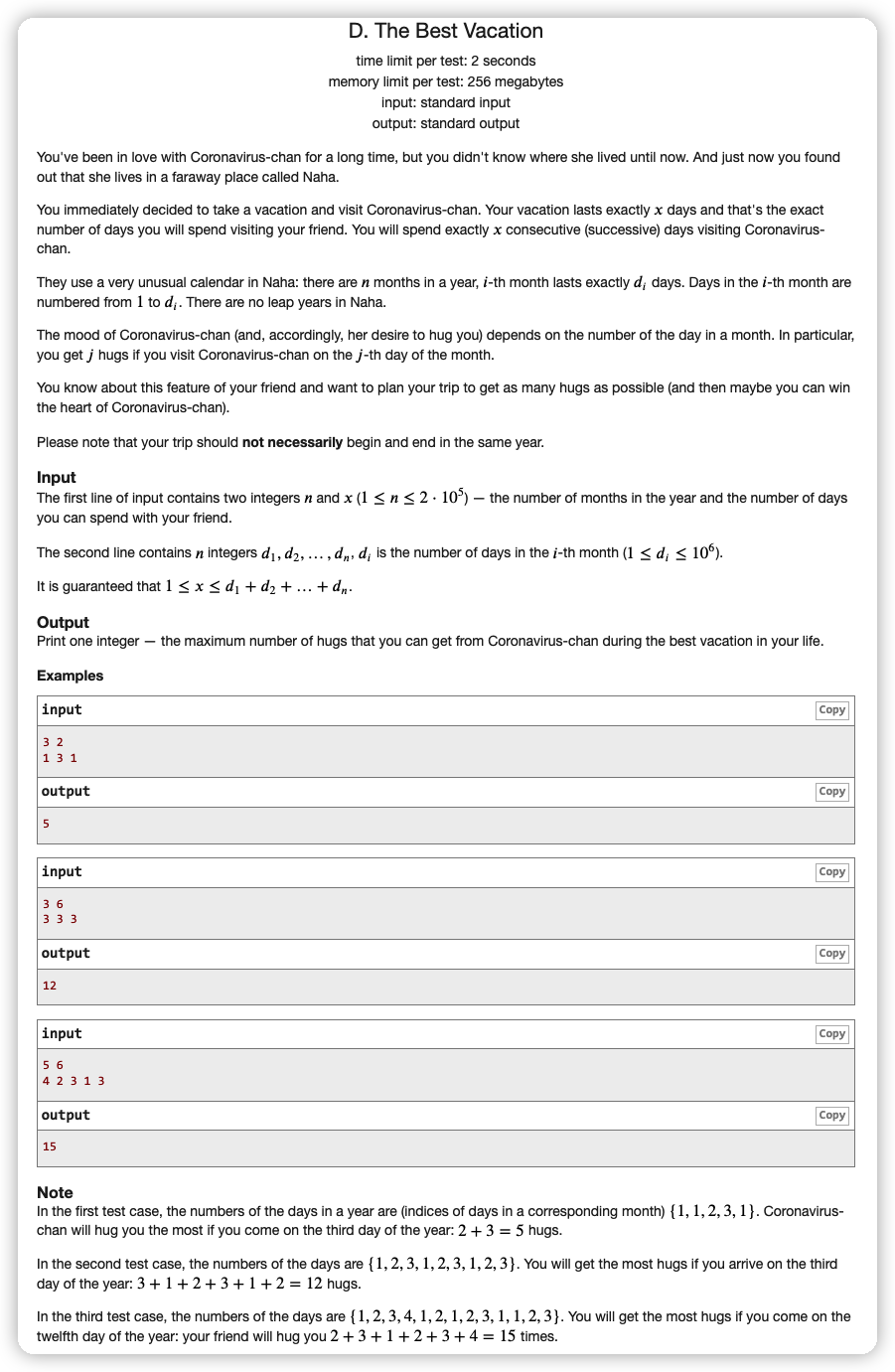
# CodeForces1358D_TheBestVacation

# 🔗

20220517155203

# 💡

首先能分析出来的信息是，左端点一定存在于某一个块的某一个位置上，右端点也能通过左端点快速求出来。
那么我们可以枚举每一个块，看看左端点在这个块内的哪个位置可以让答案最大。
当左端点从一个块的位置 LL 往右移动一个位置，右端点也要移动一个位置，其价值变化为 −L+R-L+R ，这里 L,RL,R 都是块内位置
那么把加减情况列出来：
−1−2−3−4−5−6−7…+3+4+5+1+2+3+1…=+2+2+2−3−3−3−6…\begin{aligned} &-1-2-3-4-5-6-7\dots\\ &+3+4+5+1+2+3+1\dots\\ =&+2+2+2-3-3-3-6\dots \end{aligned}
思考一下就能看出来在加减上存在单调性，因为如果出现 R=1R=1 ，那么 RR 将会再也追不上 LL ，那么一定是先加后减（当然也可能不加），所以我们可以二分 LL 求出来最后一个加的数≥\ge减的数的位置
这样也就是我们在这个块内答案的峰值
然后维护一下每一个块我们求出来 LL 所得的 calc(L,R) 的最大值即可

# ✅

# define int ll // 雾
 
int n, m;
int d[200005];
int sum[200005];
int val[200005];
 
// pair<int, int> 第first个块的第second个
 
inline int toint (pair<int, int> x) { // 将二维位置换成一维
        return sum[x.first - 1] + x.second;
} 
inline pair<int, int> topair (int x) { // 将一维位置换成二维
        pair<int, int> res;
        res.first = lower_bound(sum + 1, sum + 1 + n, x) - sum; // 找出第一个大于等于 x 的块
        res.second = x - sum[res.first - 1];
        return res;
}
 
inline pair<int, int> get_r (pair<int, int> l) { // 对于二维的 l，用区间长度 m 求出二维的 r
        int intr = toint(l) + m - 1;
        if (intr > sum[n]) intr -= sum[n]; // 注意这是一个环， r 有可能会绕到前面
        return topair(intr);
}
inline int calc (pair<int, int> L, pair<int, int> R) { // 计算二维下 l->r 的值
        if (R.first == L.first) {
                return (L.second + R.second) * (R.second - L.second + 1) / 2;
        } else if (R.first > L.first) {
                int mid = val[R.first - 1] - val[L.first];
                int l = (L.second + d[L.first]) * (d[L.first] - L.second + 1) / 2;
                int r = (1 + R.second) * R.second / 2;
                return l + mid + r;
        } else {
                int mid = (val[n] - val[L.first]) + (val[R.first - 1]);
                int l = (L.second + d[L.first]) * (d[L.first] - L.second + 1) / 2;
                int r = (1 + R.second) * R.second / 2;
                return l + mid + r;
        }
}
 
 
signed main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);
 
        cin >> n >> m;
        for (int i = 1; i <= n; i ++) 
                cin >> d[i], 
                sum[i] = sum[i - 1] + d[i], 
                val[i] = val[i - 1] + d[i] * (d[i] + 1) / 2;
 
        int RES = 0;
        for (int i = 1; i <= n; i ++) {
                int l = 1, r = d[i], res = 1;
                while (l <= r) {
                        int mid = (l + r) >> 1;
                        if (get_r({i, mid}).second < mid) r = mid - 1;
                        else l = mid + 1, res = mid;
                }
                RES = max(RES, calc({i, res}, get_r({i, res})));
        }
        cout << RES << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

# CodeForces1486D_MaxMedian

# 🔗

20220401083639

# 💡

套路地看一眼是二分中位数，我们用分数规划对其进行重新赋值
≥mid\ge mid 为 11 ，其余为 00 ，做前缀和 sum
这样的话我们评判一个区间能否比中位数大就仅看 sum[r]≥sum[l−1]sum[r]\ge sum[l-1]
套路出来这一点之后，我们就可以维护一个前缀的最小值，但是这个前缀必须是要在 i−ki-k 之前的
维护出来后每次对 sum[i]sum[i] 和 min(sum)min(sum) 进行比较，如果出现 sum[i]≥min(sum)sum[i]\ge min(sum) 的情况就以为着 checkcheck 成功

# ✅

const int N = 2e5 + 10;
int n, k;
int a[N];
 
int b[N];
inline bool Check ( int x ) {
        set<int> vis;
        bool flag = false;
        for ( int i = 1; i <= n; i ++ ) {
                if ( i - k >= 0 ) vis.insert(b[i - k]);
 
                if ( a[i] < x ) b[i] = b[i - 1] - 1;
                else b[i] = b[i - 1] + 1;
 
                if ( vis.size() && *vis.begin() < b[i] ) flag = true;
        }
        return flag;
}
 
int main () {
        cin.tie(0)->sync_with_stdio(0);
        cin.exceptions(cin.failbit);
 
        cin >> n >> k;
        for ( int i = 1; i <= n; i ++ ) cin >> a[i];
 
        int l = 1, r = 200005, res = l;
        while ( l <= r ) {
                int mid = (l + r) >> 1;
                if ( Check(mid) ) l = mid + 1, res = mid;
                else r = mid - 1;
        }
        cout << res << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

# CodeForces1490G_OldFloppyDrive

# 🔗

20220517161350

# 💡

画一个图来辅助分析一下

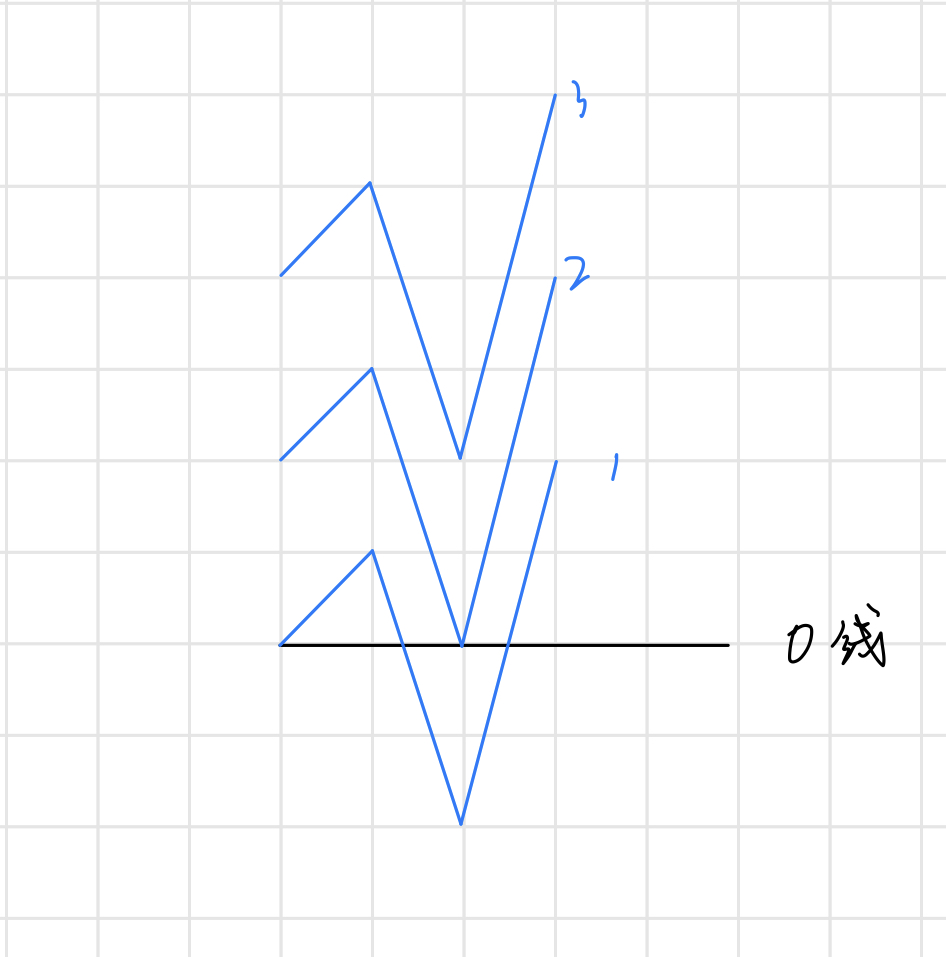
IMG_0918

图中蓝线为每一轮的走势
如果 ∑i=1nai>0\sum\limits_{i=1}^na_i>0 了话，这个线是一点点向上平移的
如果设置一个前缀和 sum[i]sum[i] ，那么如果第 tt 轮 [sum][sum] 的最大值 mx+(t−1)×sum[n]mx+(t-1)\times sum[n] 大于等于我们查询的值了话，这一轮就一定是可以满足情况的

对于查询 xx
是哪一轮可以做到，我们把上面的公式 mx+(t−1)×sum[n]≥xmx+(t-1)\times sum[n]\ge x 变化一下直接做除法就可以 O(1)O(1) 求得
问题在于是在这一轮中哪一个位置可以做到，我们可以求一个前缀和 [sum][sum] 的前缀 [mx][mx] ，这个前缀 [mx][mx] 是具有单调性的，我们既然要求第一个 mx[i]≤xmx[i]\le x 的位置，可以直接二分
不过要注意提前特判一下达不到的情况

# ✅

const int N = 2e5 + 10;
int n, m;
ll a[N], sum[N], mxsum[N];
ll mx;
 
inline void Solve () {
        cin >> n >> m; mx = -1e18;
        for (int i = 1; i <= n; i ++) 
                cin >> a[i], 
                sum[i] = sum[i - 1] + a[i],
                mx = max(mx, sum[i]),
                mxsum[i] = max(mxsum[i - 1], sum[i]);
 
        while (m --) {
                ll ned; cin >> ned;
                if (mx < ned && sum[n] <= 0) { // 要往上走但每做一轮都会往下跑
                        cout << "-1 ";
                        continue;
                } else if (ned <= mx) { // 就在第一轮
                        int l = 1, r = n, res = n;
                        while (l <= r) {
                                int mid = (l + r) >> 1;
                                if (mxsum[mid] >= ned) res = mid, r = mid - 1;
                                else l = mid + 1;
                        }
                        cout << res - 1 << " ";
                } else {
                        ll ret_t = (ned - mx) / sum[n] + ((ned - mx) % sum[n] != 0); // 看看要做几轮
                        int l = 1, r = n, res = n; 
                        while (l <= r) {
                                int mid = (l + r) >> 1;
                                if (mxsum[mid] + ret_t * sum[n] >= ned) res = mid, r = mid - 1;
                                else l = mid + 1;
                        }
                        cout << ret_t * n + res - 1 << " ";
                } 
        } cout << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

# CodeForces1512D_CorruptedArray

# 🔗

# 💡

在b排列中我们想舍弃一个数，然后将排列的前n个数的和等于第n+1个数，我们只需要求出整个b排列的sum，然后去寻找sum减去哪个数再/2可以在其中找到（而且不能是当前减去的那个数），删去的那个数为x，找到的那个数为b[n+1]

# ✅

void solve()
{
    vector<ll> b;//b排列
    ll n;
    ll sum = 0;//排列的和
    cin >> n;
    for (ll i = 0; i < n + 2; i++)
    {
        ll x;
        cin >> x;
        b.push_back(x);
        sum += x;
    }
    sort(b.begin(), b.end());//排序，方便二分
    for (ll i = 0; i < b.size(); i++)
    {
        ll cur_sum = sum - b[i];
        if (cur_sum & 1)//奇数不再操作，因为无法准确/2
            continue;
        cur_sum /= 2;
        if (!binary_search(b.begin(), b.end(), cur_sum))//找不到的就不再操作
            continue;
        int con=b[i];//记录一下删掉的是哪个，下面两行有用
        b.erase(b.begin() + i, b.begin() + i + 1);
        if (!binary_search(b.begin(), b.end(), cur_sum))//唯一一个小坑点，可能会因为找到的数是当前的数，而当前的数又被删掉了
        {
            b.insert(b.begin()+i,con);//若删掉就再放回去，这次操作不能满足，continue了
            continue;
        }
        ll id = lower_bound(b.begin(), b.end(), cur_sum) - b.begin();//寻找我们应该设为b[n+1]的数
        b.erase(b.begin() + id, b.begin() + id + 1);//删掉这个数
        for (ll j = 0; j < b.size(); j++)//此时我们就只有n个数了，就是a的排列
        {
            cout << b[j] << " ";
        }
        return;
    }
    cout << "-1" << endl;//循环完了也找不到能满足的，就"-1"
}
int main()
{
    int cass;
    each_cass(cass)
    {
        solve();
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

# CodeForces1530C_Persuit

# 🔗

https://codeforces.com/contest/1530/problem/C

# 💡

一步一步向后走的话，很多模拟细节很难维护，而且走的次数会很多
我们需要在 n 的后面找到一个满足条件的数
而且要尽可能小
这种大范围找数的题型可以用二分
写个check函数判断一下就可以开始二分了

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'

#define CHIVAS_ int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
//#define map unordered_map

#define _int(a) int a; cin >> a
#define  _ll(a) ll a; cin >> a
#define _char(a) char a; cin >> a
#define _string(a) string a; cin >> a
#define _vectorInt(a, n) vector<int>a(n); cin >> a
#define _vectorLL(a, b) vector<ll>a(n); cin >> a

#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cass = inputInt(); cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
template<typename T>             vector<T>& operator--            (vector<T> &v){for (auto& i : v) --i;            return  v;}
template<typename T>             vector<T>& operator++            (vector<T> &v){for (auto& i : v) ++i;            return  v;}
template<typename T>             istream& operator>>(istream& is,  vector<T> &v){for (auto& i : v) is >> i;        return is;}
template<typename T>             ostream& operator<<(ostream& os,  vector<T>  v){for (auto& i : v) os << i << ' '; return os;}
inline int inputInt(){int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);}
inline void outInt(int X){if(X<0) {putchar('-'); X=~(X-1);}int s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline ll inputLL(){ll X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1); }
inline void outLL(ll X){if(X<0) {putchar('-'); X=~(X-1);}ll s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}

int n;

inline bool check(deque<int> da, deque<int> db, int x){
        for(int i = n + 1; i <= x; i ++){
                da.push_back(100); db.push_front(0);
        }
        int los = x / 4;
        while(los --) da.pop_front(), db.pop_front();
        int suma = 0, sumb = 0;
        for(int i = 0; i < da.size(); i ++) suma += da[i], sumb += db[i];
        return suma >= sumb;
}

inline void solve(){
        n = inputInt();
        deque<int> da, db;
        for(int i = 0; i < n; i ++) da.push_back(inputInt());
        for(int i = 0; i < n; i ++) db.push_back(inputInt());
        sort(ALL(da)); sort(ALL(db));
        
        int r = n * 10, l = n;
        while(l <= r){
                int mid = (l + r) >> 1;
                if(check(da, db, mid)) r = mid - 1;
                else l = mid + 1;
        }cout << r - n + 1 << endl;
}
int main(){
        int cass;
        EACH_CASE(cass){
                solve();
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117

# CodeForces1611F_ATMAndStudents

# 🔗

# 💡

看到这个题首先会想一段区间会被前缀影响也会被后缀影响，那么我们可以采用区间求解的形式

由于收益的累加是从前往后的，所以我们建立一个前缀和 {sum}\{sum\} 表示从 11 到 ii 这一段的总收益为 sum[i]sum[i]
如果我们选 [l,r][l,r] 这一段，因为不看前面的收益了，所以从 ll 到 xx 的准确收益会是 sum[x]−sum[l−1]sum[x]-sum[l-1]
而这一段能否被选择的关键在于这一段准确收益的最小值是否低于ss

好了， {sum}\{sum\} 的区间最小值，可以开一个 STST 表

for ( int i = 1; i <= n; i ++ ) st[i][0] = sum[i];

inline void Build () {
        int k = 32 - __builtin_clz(n) - 1;
        for ( int j = 1; j <= k; j ++ ) {
                for ( int i = 1; i + (1 << j) - 1 <= n; i ++ ) {
                        st[i][j] = min ( st[i][j - 1], st[i + (1 << (j - 1))][j - 1] );
                }
        }
}
inline ll Query ( int l, int r ) {
        int k = 32 - __builtin_clz(r - l + 1) - 1;
        return min ( st[l][k], st[r - (1 << k) + 1][k] );
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

那么如何确定最多能选多长的区间呢？
由于区间长度的行于不行单调递增
那么可以采用二分区间长度，对每一个二分到的区间长度下的区间最小值（准确收益下的）逐一判断
如果不可行说明我们这个选的太长了，应该跑小的那一半，否则跑大的那一半

inline bool this_MinInLen ( int len ) {
        for ( int i = 1; i + len - 1 <= n; i ++ ) {
                ll cur = Query ( i, i + len - 1 );
                if ( s + (cur - sum[i - 1]) >= 0 ) { // cur-sum[i-1]：准确收益
                        if ( len > res.second - res.first + 1 ) res = {i, i + len - 1};
                        return true;
                }
        }
        return false;
}


int l = 1, r = n;
while ( l <= r ) {
        int mid = ( l + r ) >> 1;
        if ( this_MinInLen(mid) ) l = mid + 1;
        else                      r = mid - 1;
}
this_MinInLen ( l );
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

时间复杂度： O(nlogn)O(nlogn)

# ✅

const int N = 2e5 + 10;
ll a[N], sum[N];
ll st[N][100];
int n;
ll s;
pair<int, int> res;

inline void Build () {
        int k = 32 - __builtin_clz(n) - 1;
        for ( int j = 1; j <= k; j ++ ) {
                for ( int i = 1; i + (1 << j) - 1 <= n; i ++ ) {
                        st[i][j] = min ( st[i][j - 1], st[i + (1 << (j - 1))][j - 1] );
                }
        }
}
inline ll Query ( int l, int r ) {
        int k = 32 - __builtin_clz(r - l + 1) - 1;
        return min ( st[l][k], st[r - (1 << k) + 1][k] );
}
inline bool this_MinInLen ( int len ) {
        for ( int i = 1; i + len - 1 <= n; i ++ ) {
                ll cur = Query ( i, i + len - 1 );
                if ( s + (cur - sum[i - 1]) >= 0 ) {
                        if ( len > res.second - res.first + 1 ) res = {i, i + len - 1};
                        return true;
                }
        }
        return false;
}

inline void Solve () {
        res = {0, -1};

        cin >> n >> s;
        for ( int i = 1; i <= n; i ++ ) {
                cin >> a[i];
                sum[i] = sum[i - 1] + a[i];
                st[i][0] = sum[i];
        }

        Build ();

        int l = 1, r = n;
        while ( l <= r ) {
                int mid = ( l + r ) >> 1;
                if ( this_MinInLen(mid) ) l = mid + 1;
                else                      r = mid - 1;
        }
        this_MinInLen ( l );
        
        if ( res.first <= res.second ) cout << res.first << " " << res.second << endl;
        else                           cout << -1 << endl;
}

int main () {
        ios::sync_with_stdio(false);
        int cass; cin >> cass; while ( cass -- ) {
                Solve ();
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

# CodeForces1622C_SetOrDecrease

# 🔗

20220309214915

# 💡

两个操作

  • 令 ai=aja_i=a_j
  • 令 ai−1a_i-1

分析一下这两个操作，对于操作一，我们肯定是贪心地想让 ai=min[a]a_i=min[a] ，并且是优先让最大的 =min[a]=min[a]
对于操作二，我们肯定为了让操作一的收益更高，让最小的 −1-1
我们先令一个 down=∑i=1nai−kdown=\sum\limits_{i=1}^na_i-k ，这样我们就是想让通过最少的步数让减去的值 ≤down\le down

注意到一个性质，随着操作数的增大，我们减去的值可以越来越大，具备单调性

发现两个操作对于操作总数 xx 的增减是相反的
并且如果有 oneone 次操作一，twotwo 次操作二，就一定是先来 oneone 次操作一再来 twotwo 次操作二
那么操作一没必要对一个位置上的数反复赋值，所以操作一最多有 min(x,n−1)min(x,n-1) 次，最少有 00 次
这个我们枚举操作一的次数就可以 O(n)O(n) 地求出每一种操作分配情况下，我们所能减去的最大值

既然这个非常容易，那么就二分操作次数去获得答案即可

# ✅

inline bool check ( ll x, const vector<ll> a, const ll down ) {
        ll cur = 0;
        for ( ll i = a.size() - 1; i >= max(1ll, (ll)a.size() - x); i -- ) cur += a[i] - a[0];

        ll two = min(x, (ll)a.size() - 1);
        ll one = x - two;
        if ( cur + one + two * one >= down ) return true;

        for ( ll i = max(1ll, (ll)a.size() - x); i < a.size(); i ++ ) {
                cur -= a[i] - a[0];
                two --;

                one = x - two;
                if ( cur + one + two * one >= down ) return true;
        }
        return one >= down;
}

inline void Solve () {
        ll n, k; cin >> n >> k;
        ll down = 0;
        vector<ll> a(n); for ( ll &i : a ) cin >> i, down += i;
        down -= k;
        sort(a.begin(), a.end());

        ll l = 0, r = 1e15, res = 1e15;
        while ( l <= r ) {
                ll mid = (l + r) >> 1;
                if ( check(mid, a, down) ) res = mid, r = mid - 1;
                else l = mid + 1;
        }
        cout << res << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

# CodeForces1623C_BalancedStoneHeaps

# 🔗

20220309220125

# 💡

既然想让每一个都比答案 resres 大，那我们分配时肯定是贪心地让后面的在不低于 resres 的情况下尽可能向前分配
我们令 b[i]b[i] 为第 ii 个位置上获取的值，后面的向前分配我们就可以倒着走，显然由于题上让从前往后走，那么我们前面的不能利用后面给的，但是可以考虑自己能往前分配多少
ai−giv×3+bi≥res→giv≤ai+bi−x3a_i-giv\times3+b_i\ge res\rightarrow giv\le\frac{a_i+b_i-x}{3}
giv≤ai3giv\le \frac{a_i}{3}
在 resres 的限制下，肯定是 resres 越大越难得
所以我们可以二分答案进行求解

# ✅

inline bool check ( int x, const vector<ll> a ) {
        vector<ll> b(a.size());
        vector<ll> aa = a;
        for ( int i = aa.size() - 1; i >= 2; i -- ) {
                if ( aa[i] + b[i] - x < 0 ) return false;
                ll giv = min(aa[i] + b[i] - x, aa[i]) / 3;
                aa[i] -= giv * 3;
                b[i - 1] += giv;
                b[i - 2] += giv * 2;
        }
        for ( int i = 0; i < aa.size(); i ++ ) {
                if ( aa[i] + b[i] < x ) return false;
        } 
        return true;
}

inline void Solve () {
        int n; cin >> n;
        vector<ll> a(n); for ( auto &i : a ) cin >> i;
        int l = 0, r = 1000000000;
        int res = 0;
        while ( l <= r ) {
                int mid = (l + r) >> 1;
                if ( check(mid, a) ) l = mid + 1, res = mid;
                else r = mid - 1;
        }
        cout << res << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# CodeForces1632D_NewYearConcert

# 🔗

# 💡

思索一下，如果我们对一个从 ii 开始的前缀可以发现存在这样 gcd=l−r+1gcd=l-r+1 的，那么我们可以在 ii 的位置加一个很大的质数从而隔断 ii 到 11 的位置
这样我们后面的任意一个位置到达 ii 都会变成 gcd=1gcd=1 ，我们要从 l=i+1l=i+1 之后进行判断即可
所以隔断后我们在后面枚举 ii 时只需要判断 ∑j=l+1i[gcd=i−j+1]\sum\limits_{j=l+1}^i[gcd=i-j+1] 是否 ≥1\ge 1 即是否存在
注意一下单调性，对于固定的右端点，区间越长 gcdgcd 不会越来越大，同时区间长度越来越大，他们两个呈相遇状
那么我们找这个满足 gcd(a[j→i])=i−j+1gcd(a[j\rightarrow i])=i-j+1 就可以采用二分左端点的形式

  • 如果 gcd(a[j→i])<i−j+1gcd(a[j\rightarrow i])<i-j+1 说明我们枚举的太长了，应该让左端点往右走
  • 如果 gcd(a[j→i])>i−j+1gcd(a[j\rightarrow i])>i-j+1 就说明要往左走
  • 如果 gcd(a[j→i])=i−j+1gcd(a[j\rightarrow i])=i-j+1 就说明找到了，存在这样的位置，我们对 ii 进行隔断然后让答案 +1+1 即可

注意中间存在区间查询 gcdgcd 的操作，可以使用 stst 表预处理

# ✅

const int N = 2e5 + 10;
ll st[N][25];
ll a[N];
ll n;

inline ll gcd ( ll a, ll b ) { return b ? gcd(b, a % b) : a; }
inline void Build(){ // 构建ST
        for ( int i = 1; i <= n; i ++ ) st[i][0] = a[i];
        ll k = 32 - __builtin_clz(n) - 1;
        for (ll j = 1; j <= k; j ++) {
                for (ll i = 1; i + (1 << j) - 1 <= n; i ++) {
                        st[i][j] = gcd(st[i][j - 1],st[i + (1 << (j - 1))][j - 1]);
                }
        }
}
ll Query(ll l, ll r){ // 查询
        ll k = 32 - __builtin_clz(r - l + 1) - 1;
        return gcd(st[l][k], st[r - (1 << k) + 1][k]);
}

inline int check ( ll p, ll i ) {
        ll qry = Query(p, i);
        if ( qry < i - p + 1 ) return -1;
        else if ( qry == i - p + 1 ) return 0;
        return 1;
}

inline void Solve () {
        cin >> n;
        for ( int i = 1; i <= n; i ++ ) cin >> a[i];
        Build();
        int l = 1, res = 0; // 隔断后面的第一个位置，答案
        for ( int i = 1; i <= n; i ++ ) {
                int R = i;
                int L = l;
                bool flg = 0;
                while ( L <= R ) {
                        int mid = (L + R) >> 1;
                        if ( check(mid, i) == 0) {
                                flg = true;
                                break;
                        } 
                        if ( check(mid, i) == 1 ) R = mid - 1;
                        else L = mid + 1;
                }
                if ( flg ) {
                        l = i + 1;
                        res ++;
                }
                cout << res << " ";
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

# HDU2022多校(3)B_BossRush

# 🔗

20220727221905

# 💡

在限制条件下找最值，注意到随着值的变大，限制是从满足不了到满足的，这是一个单调性，考虑二分。
选取一个值 xx ，找到最优的填技能的方式
注意到 n≤18n\le 18 ，用状态表示，对于同一种选择技能的状态，花费的时间 altalt 是固定的，即里面所有 11 的 cdcd 总和对 xx 取 minmin 。那么我下一步选择第 ii 个技能能放出来的伤害也能得知，即 ∑j=1min(cdi,x−alt)d[i]j\sum\limits_{j=1}^{min(cd_i,x-alt)}d[i]_j ，这个可以前缀和预处理出来。
既然我们要伤害最大，那么用 dp[S]dp[S] 存储状态 SS 的伤害，在每一次选取新技能的时候维护 dp[S∣2i]=max(dp[S]+sum[i][min(cdi,x−alt)])dp[S|2^i]=max(dp[S]+sum[i][min(cd_i,x-alt)]) 即可
最后看最大伤害是否满足限制（大于等于 HH）是对于选定值 xx 的单调性，依次进行二分答案。

# ✅

int n;
ll H;
int t[20], len[20];
ll d[20][100005];
ll sum[20][100005];
ll alt[1000006];

ll dp[1000006];
inline bool check (int T) {
        for (int S = 0; S < (1 << n); S ++) dp[S] = -1;
        dp[0] = 0;
        ll res = 0;
        for (int S = 0; S < (1 << n); S ++) {
                if (dp[S] < 0) continue;
                if (dp[S] >= H) return 1;
                int cT = T - alt[S];
                if (cT <= 0) continue;
                for (int i = 0; i < n; i ++) {
                        if (S >> i & 1) continue;
                        dp[S | (1 << i)] = max(dp[S | (1 << i)], dp[S] + sum[i][min(len[i], cT)]);
                        res = max(res, dp[S | (1 << i)]);
                }
        }
        return res >= H;
}

inline void Solve () {
        memset(alt, 0, sizeof alt);

        cin >> n >> H;
        for (int i = 0; i < n; i ++) {
                cin >> t[i] >> len[i];
                for (int j = 1; j <= len[i]; j ++) {
                        cin >> d[i][j];
                        sum[i][j] = sum[i][j - 1] + d[i][j];
                }
        }

        for (int S = 0; S < (1 << n); S ++) {
                for (int i = 0; i < n; i ++) {
                        if (S >> i & 1) alt[S] += t[i];
                }
        }

        int l = 0, r = 1e9, res = 1e9;
        while (l <= r) {
                int mid = (l + r) >> 1;
                if (check(mid)) res = mid - 1, r = mid - 1;
                else l = mid + 1;
        }
        cout << (res == 1e9 ? -1 : res) << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

# ICPC2020上海站D_Walker

# 🔗

# 💡

给定一条路，两个人的位置，两个人的速度，怎么样最快走完这条路

如果考虑左左，左右，右左，右右这样会很麻烦，要根据速度还要考虑相遇点
相遇最好，每个人都能做出贡献
那么我们根据相遇入手

首先要考虑一个人走完全程的情况
然后是相遇点
1.相遇完不扭头
2.相遇完扭头

相遇完不扭头很好计算，就直接对向走到头即可
相遇完扭头我们可以二分一下 p1,p2 中间的相遇点
对每个相遇点我们求一下两个人全部走完自己路程的最小用时
其实有了相遇点这个就会很好求，就是每个人已经固定了要走的 l 和 r 了，在 l,r 内走需要 (min(p-l,r-p)+(r-l))/v
所以在这里我们不需要考虑一个人左走还是右走，程序会用 min 判断

我们二分一百次之后的中点就已经很确定了，每次维护一下花费时间的最小值即可

# ✅

inline double LRTime ( double l, double r, double v, double p ) {
        return (min(p - l, r - p) + (r - l)) / v;
}

inline void Solve () {
        double n, p1, v1, p2, v2; 
        cin >> n >> p1 >> v1 >> p2 >> v2;

        if ( p1 > p2 ) swap(p1, p2), swap(v1, v2);

        double res = min(LRTime(0, n, v1, p1), LRTime(0, n, v2, p2));
        res = min(res, max((n - p1) / v1, p2 / v2));

        double l = p1, r = p2;
        for ( int i = 0; i < 100; i ++ ) {
                double mid = (l + r) / 2;
                double res1 = LRTime(0, mid, v1, p1);
                double res2 = LRTime(mid, n, v2, p2);

                res = min(res, max(res1, res2));
                if ( res1 > res2 ) r = mid;
                else l = mid;
        }

        printf("%.10f\n", res);
}

int main () {
        ios::sync_with_stdio(false);

        ll cass; cin >> cass; while ( cass -- ) {
                Solve();
        }
        
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

# ICPC2021台湾省赛E_EatCoin

# 🔗

# 💡

首先我们化简一下问题
第 dd 天算法会消耗 pp ，获得 qd5qd^5
也就是若算法可以执行，那么将获得 −p+qd5-p+qd^5
若开始前有 xx ，执行 yy 天后会成为 x−py+q∑i=1yi5x-py+q\sum\limits_{i=1}^yi^5
我们要让这个值 ≥1099\ge10^{99}
同时要保证 ∀j∈[0,y],x−pj+q∑i=1ji5≥p\forall j\in[0,y],x-pj+q\sum\limits_{i=1}^ji^5\ge p ，不然就继续不了算法了，（左侧如果开始上升那么就可以保证了

我们求 ∑i=1ji5\sum\limits_{i=1}^ji^5 可以用求自然数幂和 (opens new window)的方式进行拉格朗日插值，这里 kk 不大，所以就是常数复杂度
我们求 xx 可以使用第二个限制进行二分
求 yy 可以使用第一个进行二分

数很大，开java的BigInteger

# ✅

public class Main{
        static int N = 100;
        static BigInteger zero = BigInteger.ZERO;
        static BigInteger one = BigInteger.ONE;
        static BigInteger two = BigInteger.valueOf(2);
        static BigInteger six = BigInteger.valueOf(6);
        static BigInteger ten = BigInteger.TEN;
        static BigInteger five = BigInteger.valueOf(5);

        static BigInteger ksm ( BigInteger a, BigInteger b ) {
                BigInteger res = one;
                while ( b.compareTo(zero) == 1 ) {
                        if ( b.mod(two).compareTo(one) == 0 ) {
                                res = res.multiply(a);
                        } a = a.multiply(a);
                        b = b.divide(two);
                } return res;
        }
        static BigInteger[] fac = new BigInteger[N];
        static BigInteger[] pre = new BigInteger[N];
        static BigInteger[] suf = new BigInteger[N];
        static BigInteger pownk ( BigInteger n, int k ) {
                BigInteger y = zero, up = zero, down = zero, res = zero;
                fac[0] = pre[0] = suf[k + 3] = one;
                for ( int i = 1; i <= k + 2; i ++ ) {
                        pre[i] = pre[i - 1].multiply(n.subtract(BigInteger.valueOf(i)));
                        fac[i] = fac[i - 1].multiply(BigInteger.valueOf(i));
                }
                for ( int i = k + 2; i >= 1; i -- ) {
                        suf[i] = suf[i + 1].multiply(n.subtract(BigInteger.valueOf(i)));
                }
                for ( int i = 1; i <= k + 2; i ++ ) {
                        y = y.add(ksm(BigInteger.valueOf(i), BigInteger.valueOf(k)));
                        up = pre[i - 1].multiply(suf[i + 1]);
                        down = fac[i - 1].multiply(fac[k + 2 - i]).multiply(((k - i) & 1) > 0 ? zero.subtract(one) : one);
                        res = res.add(y.multiply(up).divide(down));
                }
                return res;
        }
        static BigInteger q, p;
        static BigInteger x, y;

        static boolean check ( BigInteger j ) {
                BigInteger a = x.subtract(p.multiply(j)).add(q.multiply(pownk(j, 5)));
                BigInteger b = ksm(ten, BigInteger.valueOf(99));
                if ( a.compareTo(b) >= 0 ) return true;
                return false;
        }
        static boolean chk_x ( BigInteger xx ) {
                boolean flg = false;
                for ( Long i = Long.valueOf(0);; i ++ ) {
                        if ( xx.subtract(p.multiply(BigInteger.valueOf(i))).add(q.multiply(pownk(BigInteger.valueOf(i), 5))).compareTo(p) == -1 ) break;
                        if ( i > Long.valueOf(0) && xx.subtract(p.multiply(BigInteger.valueOf(i))).add(q.multiply(pownk(BigInteger.valueOf(i), 5))).compareTo(xx.subtract(p.multiply(BigInteger.valueOf(i - 1))).add(q.multiply(pownk(BigInteger.valueOf(i - 1), 5)))) == 1 ) { flg = true; break;}
                }
                return flg;
        }

        public static void main (String[] args) {
                Scanner input = new Scanner(System.in);
                p = input.nextBigInteger();
                q = input.nextBigInteger();
                x = p;
                y = zero;
                
                BigInteger l = zero, r = ksm(ten, BigInteger.valueOf(20));
                while ( l.compareTo(r) == -1 ) {
                        BigInteger mid = l.add(r).divide(two);
                        if ( chk_x(mid) ) r = mid;
                        else l = mid.add(one);
                }
                x = l;

                l = zero; r = ksm(ten, BigInteger.valueOf(30));
                while ( l.compareTo(r) == -1 ) {
                        BigInteger mid = l.add(r).divide(two);
                        if ( check(mid) ) r = mid;
                        else l = mid.add(one);
                }
                y = l;
                System.out.println(x + "\n" + y);
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82

# NCD2019A_HasanTheLazyJudge

# 🔗

# 💡

答案问我们在满足一定条件下的结果，要最优的
可以使用二分答案

我们对结果 lenlen 进行二分，思考这个答案如何进行 checkcheck

首先，这两条线的长度都至少为 len×2len\times2
我们设横线为 pp 竖线为 qq ，每条线都有 {a,b,pos}\{a,b,pos\} ，即端点、垂直坐标，我们枚举竖线，满足的情况应为 q.pos∈[p.a+len,p.b−len]q.pos\in[p.a+len,p.b-len] 且 q.pos∈[q.a+len,q.b−len]q.pos\in[q.a+len,q.b-len]，这个集合 α\alpha 是包含在集合 β:q.pos∈[p.a,p.b]\beta:q.pos\in[p.a,p.b] 中的，我们首先要满足 α\alpha 才能找 β\beta
我们可以把这两个情况用两种方式同步求

对于 β\beta，可以发现这三者有偏序关系，所以排序就可以解决
我们存入每个横线的 a+lena+len 和 b−lenb-len 以及竖线的 pospos ，将它们进行排序后进行遍历，如果当前遍历到的是横线的 aa ，就把这个横线的 pospos 存入，如果是 bb 就把这个横线的 pospos 弹出，这个可以用一个 multiset 来维护
如果遍历到的是 qq 的 pospos ，就是子集的求法
已知所有存在 multiset 中的 pospos 都是满足第一个集合的情况，我们在其中进行二分出满足 [q.a+len[q.a+len 这个子集的最左端，如果这个点也能满足 ≤q.b−len\le q.b-len 那么就说明可能存在比这个答案更大的情况，我们就 checkcheck 成功了

# ✅

onst int N = 1e5 + 10;

struct node {
        int a, b, pos;
        inline friend bool operator < ( node a, node b ) {
                if ( a.a != b.a ) return a.a < b.a;
                return a.b < b.b;
        }
} p[N], q[N];
int n, m;

inline bool Check ( int len ) {
        vector<node> vec;
        for ( int i = 0; i < n; i ++ ) {
                if ( p[i].b - p[i].a >= 2 * len ) 
                        vec.push_back({p[i].a + len, 1, p[i].pos}), // 优先满足区间的左端点
                        vec.push_back({p[i].b - len, 3, p[i].pos}); // 最后满足区间的右端点
        }
        for ( int i = 0; i < m; i ++ ) {
                if ( q[i].b - q[i].a >= 2 * len ) 
                        vec.push_back({q[i].pos, 2, i}); // 我们要尽可能在两个端点中间看看有没有 q[i].pos
        }
        sort ( vec.begin(), vec.end() );

        multiset<int> mst;
        for ( auto i : vec ) {
                if ( i.b == 1 ) mst.insert(i.pos);
                else if ( i.b == 3 ) mst.erase(mst.find(i.pos));
                else {
                        auto id = mst.lower_bound(q[i.pos].a + len); // 找子集合的区间左端点
                        if ( id == mst.end() ) continue; // 找不到
                        if ( *id <= q[i.pos].b - len ) return true;  // 这个也能满足子集合的区间右端点
                }
        }
        return false;
}

inline void Solve () {
        cin >> n >> m;
        for ( int i = 0, x, y, z; i < n; i ++ ) cin >> x >> y >> z, p[i] = {min(x, y), max(x, y), z};
        for ( int i = 0, x, y, z; i < m; i ++ ) cin >> x >> y >> z, q[i] = {min(x, y), max(x, y), z};

        int l = 0, r = 5e4;
        int res = 0;
        while ( l <= r ) {
                int mid = (l + r) >> 1;
                if ( Check(mid) ) l = mid + 1, res = mid;
                else r = mid - 1;
        }
        cout << res << endl;
}

int main () {
        ios::sync_with_stdio(false);
        int cass; cin >> cass; while ( cass -- ) {
                Solve ();
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

# POJ3579_Median

# 🔗

http://poj.org/problem?id=3579

# 💡

一个比较妙的二分题
首先我们获得差值的中位数
而差值之间又无太大的关系
所以我们利用中位数的性质
在个数上做文章

而本题中个数上操作的方法就是：二分找出所处差值在中间的元素
check函数：枚举的差值，用a[i]-x然后upperbound遍历出比他小的数的个数和总差值数目(n*(n-1)/2)的关系
然后在这层关系上二分缩l和r即可

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/

//#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '<br>'

#define CHIVAS_ int main()
#define _REGAL exit(0)
#define SP system("pause")
#define IOS ios::sync_with_stdio(false)

//#define map unordered_map

#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cass = inputInt(); cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

/*
template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal <vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i])MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal <vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i])MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
template<typename T> vector<T>& operator-- (vector<T> &v){for (auto& i : v) --i; return v;}
template<typename T> vector<T>& operator++ (vector<T> &v){for (auto& i : v) ++i; return v;}
template<typename T> istream& operator>>(istream& is, vector<T> &v){for (auto& i : v) is >> i; return is;}
template<typename T> ostream& operator<<(ostream& os, vector<T> v){for (auto& i : v) os << i << ' '; return os;}
*/inline int inputInt(){int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);}
inline void outInt(int X){if(X<0) {putchar('-'); X=~(X-1);}int s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline ll inputLL(){ll X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1); }
inline void outLL(ll X){if(X<0) {putchar('-'); X=~(X-1);}ll s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}

const int N = 1e5 + 10;
ll a[N], n, npr;

inline int check ( ll x ) {
        ll cnt = 0;
        for ( ll i = 1; i <= n; i ++ ) {
                cnt += upper_bound( a + 1, a + 1 + n, a[i] - x) - (a + 1);
        }
        return cnt < npr / 2 + 1;
}

inline void solve(){
        for ( int i = 1; i <= n; i ++ ) a[i] = inputLL(); sort(a + 1, a + 1 + n);

        int l = 0, r = a[n] - a[1];
        while ( l <= r ) {
                ll mid = (l + r) >> 1;
                if ( check (mid) ) r = mid - 1;
                else l = mid + 1;
        }
        outInt(r); puts("");
}

CHIVAS_{
        while ( scanf("%lld", &n) == 1 ) {
                npr = (n - 1) * n / 2;
                solve();
        }
        _REGAL;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
Last Updated: 11/17/2025, 8:46:26 PM

暴力优化