最短路

Chivas-Regal

#

# 洛谷P1027_Car的旅行路线

# 🔗

# 💡

其实刚开始想的是一个dp的解法
想着全排列一下然后从a到b每一个城市四个点由上一个城市四个点跑火车和跑飞机推过来
想到时间复杂度过不去， $\inline O(n\times n!)$
然后~~这一看不就是个图论吗~~
建好边然后四个点各跑一次 $\inline Dijkstra$
从 $\inline a$ 城市的四个点到 $\inline b$ 城市的四个点一共 $\inline 16$ 种走法选最短的就行了...

# ✅

const int N = 15;
const int NN = 100;
const int M = 1e6;
const double eps = 1e-9;

struct Contry {
        double x[4], y[4];
        double T;
} cty[N];
int n, a, b;
double t;

namespace Map {
        struct Edge {
                int nxt, to;
                double val;
        } edge[M];
        int head[M], cnt;
        inline void add_Edge ( int from, int to, double val ) {
                edge[ ++ cnt ] = { head[from], to, val };
                head[from] = cnt;
        }
} using namespace Map;

namespace ShortestPath {
        struct node {
                int id;
                double dis;
                inline friend bool operator < (node a, node b) {
                        return a.dis > b.dis;
                }
        };
        double dis[NN]; bool vis[NN];
        inline void Dijkstra ( int id ) {
                for ( int i = 0; i < NN; i ++ ) dis[i] = 0x3f3f3f3f, vis[i] = 0;
                priority_queue<node> pque;
                dis[id] = 0;
                pque.push({id, dis[id]});
                while ( pque.size() ) {
                        node stt = pque.top(); pque.pop();
                        if ( vis[stt.id] ) continue; vis[stt.id] = 1;
                        for ( int i = head[stt.id]; i; i = edge[i].nxt ) {
                                int to = edge[i].to;
                                if ( dis[to] - dis[stt.id] - edge[i].val >= eps ) {
                                        dis[to] = dis[stt.id] + edge[i].val;
                                        pque.push({to, dis[to]});
                                }
                        }
                }
        }
} using namespace ShortestPath;

inline double Dis ( double x1, double y1, double x2, double y2 ) {
        double dirx = x1 - x2;
        double diry = y1 - y2;
        return sqrt ( dirx * dirx + diry * diry );
}

inline void Solve() {
        cin >> n >> t >> a >> b;
        for ( int i = 1; i <= n; i ++ ) {
                cin >> cty[i].x[0] >> cty[i].y[0]; 
                cin >> cty[i].x[1] >> cty[i].y[1]; 
                cin >> cty[i].x[2] >> cty[i].y[2]; 
                double ds01 = (cty[i].x[0] - cty[i].x[1]) * (cty[i].x[0] - cty[i].x[1]) + (cty[i].y[0] - cty[i].y[1]) * (cty[i].y[0] - cty[i].y[1]);
                double ds02 = (cty[i].x[0] - cty[i].x[2]) * (cty[i].x[0] - cty[i].x[2]) + (cty[i].y[0] - cty[i].y[2]) * (cty[i].y[0] - cty[i].y[2]);
                double ds12 = (cty[i].x[2] - cty[i].x[1]) * (cty[i].x[2] - cty[i].x[1]) + (cty[i].y[2] - cty[i].y[1]) * (cty[i].y[2] - cty[i].y[1]);
                if ( ds01 + ds02 == ds12 ) cty[i].x[3] = cty[i].x[1] + cty[i].x[2] - cty[i].x[0], cty[i].y[3] = cty[i].y[1] + cty[i].y[2] - cty[i].y[0];
                if ( ds01 + ds12 == ds02 ) cty[i].x[3] = cty[i].x[0] + cty[i].x[2] - cty[i].x[1], cty[i].y[3] = cty[i].y[0] + cty[i].y[2] - cty[i].y[1];
                if ( ds02 + ds12 == ds01 ) cty[i].x[3] = cty[i].x[0] + cty[i].x[1] - cty[i].x[2], cty[i].y[3] = cty[i].y[0] + cty[i].y[1] - cty[i].y[2];
                cin >> cty[i].T;
        }
        for ( int i = 1; i <= n; i ++ ) {
                for ( int i1 = 0; i1 < 4; i1 ++ ) {
                        for ( int i2 = 0; i2 < 4; i2 ++ ) {
                                if ( i1 == i2 ) continue;
                                add_Edge ( i * 4 + i1, i * 4 + i2, Dis(cty[i].x[i1], cty[i].y[i1], cty[i].x[i2], cty[i].y[i2]) * cty[i].T );
                        }
                }
                for ( int j = 1; j <= n; j ++ ) {
                        if ( i == j ) continue;
                        for ( int ii = 0; ii < 4; ii ++ ) {
                                for ( int jj = 0; jj < 4; jj ++ ) {
                                        add_Edge ( i * 4 + ii, j * 4 + jj, Dis(cty[i].x[ii], cty[i].y[ii], cty[j].x[jj], cty[j].y[jj]) * t );
                                }
                        }
                }
        }
        double res = 0x3f3f3f3f;
        for ( int i = 0; i < 4; i ++ ) {
                Dijkstra(a * 4 + i);
                for ( int j = 0; j < 4; j ++ ) res = min ( res, dis[b * 4 + j] );
        }
        printf("%.1f\n", res);
}

int main () {
        int cass; cin >> cass; while ( cass -- ) Solve ();
}

# 洛谷P1070_道路游戏

# 🔗

# 💡

想不出来去看了题解，一堆单调队列(2021/11/09: 没学过)题解，然后就看到了一个题解说用SPFA能过
~~真是小刀划屁股给👴开了眼~~

然后想了半天发现雀食是这么回事
这是一个要转移最优解的问题
而每一次转移都是从一个已有的优解转移出一个新的优解，这份转移价值就是你在这个时间哪个工场买了机器人跑几次
可以发现时间与时间之间还有制约关系，就是你a时间买了个机器人让它跑b次那么你一定会在a+b时间继续抉择
就相当于a时间和a+b时间连了个边

（那不就最短路更新了？
由于会出现负权，我们要使用 $\inline SPFA$
我们使用基本的bfs，队内塞时间点，每次对一个时间点枚举一下此时选择哪个工厂造使用多长时间的机器人
由于会推到另一个时间点，我们设置类似于最段路的best数组，和是否在队内的inq数组
对下一个时间点本身的best和它是否在队内决定吧更不更新和入不入队

在时间p和总时间m和spfa的优化下不会太长时间

# ✅

#include <iostream>
#include <queue>
#include <cstring>


#define ll long long

using namespace std;

const int N = 1e3 + 10;
const int M = 1e3 + 10;
int n, m, p;
int pth[N][N];
int dty[N];

int best[M]; // best[i]: i时刻的最多钱数
bool inq[M]; // inq[i] : i时刻在队里面没有

int main () {
        ios::sync_with_stdio(false);
        memset ( best, -0x3f3f3f3f, sizeof best );
        cin >> n >> m >> p;
        for ( int i = 0; i < n; i ++ ) for ( int j = 0; j < m; j ++ ) cin >> pth[i][j];
        for ( int i = 0; i < n; i ++ ) cin >> dty[i];

        int res = -0x3f3f3f3f;
        queue<int> que; // 存的是时间
        que.push(0); best[0] = 0;
        while ( que.size() ) {
                int cur_time = que.front(); que.pop(); inq[cur_time] = false; // 当前时间
                res = max ( res, best[cur_time] );
                for ( int dtyid = 0; dtyid < n; dtyid ++ ) {                                // 选择哪个工厂买机器人
                        int getmoney = -dty[dtyid];                                         // 获得钱数
                        for ( int sttm = 1; sttm <= p && sttm + cur_time <= m; sttm ++ ) {  // 设置多长时间
                                getmoney += pth[(dtyid + sttm - 1) % n][(cur_time + sttm - 1) % m]; 

                                int nxt_time = cur_time + sttm;             // 新产生的时间
                                int nxt_money = best[cur_time] + getmoney;  // 新产生的钱数
                                if ( best[nxt_time] < nxt_money ) {         // 有更优的方案
                                        best[nxt_time] = nxt_money;         // 更新一下
                                        if ( !inq[nxt_time] )               // 如果不在队列里面那么更新不起递推作用，要放进去
                                                que.push(nxt_time),
                                                inq[nxt_time] = true;
                                }
                        }
                }
        }
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

# 洛谷P1119_灾后重建

# 🔗

# 💡

这个题就是最短路加上点更新
由于问我们的点比较随机加上点数比较少

考虑到 $\inline Floyd$ 的更新机制就是以点为中转
那么我们可以直接使用其 $\inline Dp$ 思想进行更新
出现一个点时，所有以它为中转的点都可以更新一下看看
如果问的两个点都不在时间内或者中间无法转移
那么就输出-1
否则就是 $\inline Floyd$ 的那个数组

# ✅

const int N = 1e4 + 10;
int dis[N][N];
int t[N], n, m, q;

vector<int> tims[N]; // tims[i]: 时间i的时候已经建成的村庄集合

int main () {
        cin >> n >> m;
        for ( int i = 0; i < n; i ++ ) cin >> t[i], tims[t[i]].push_back(i);
        for ( int i = 0; i < n; i ++ ) {
                for ( int j = 0; j < n; j ++ ) {
                        if ( i == j ) dis[i][j] = 0;
                        else          dis[i][j] = 0x3f3f3f3f;
                }
        }
        for ( int i = 0; i < m; i ++ ) {
                int a, b, c; cin >> a >> b >> c;
                dis[a][b] = dis[b][a] = c;
        }


        function<void(int)> update = [&]( int x ) { // 点更新
                for ( int i = 0; i < n; i ++ ) {
                        for ( int j = 0; j < n; j ++ ) {
                                if ( dis[i][j] > dis[i][x] + dis[x][j] ) 
                                        dis[i][j] = dis[j][i] = dis[i][x] + dis[x][j];
                        }
                }
        };

        int curtime = 0, q; 
        cin >> q;
        while ( q -- ) {
                int x, y, tm; cin >> x >> y >> tm;
                while ( curtime <= tm ) {
                        for ( auto i : tims[curtime] ) update ( i );
                        curtime ++;
                }
                if ( t[x] > tm || t[y] > tm || dis[x][y] == 0x3f3f3f3f ) cout << "-1" << endl;
                else                                                     cout << dis[x][y] << endl;
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

# 洛谷P2761_软件补丁问题

# 🔗

# 💡

有一次操作的用时，要算总最短用时，思考最短路
操作看成一个点到另一个点的连边，而确定不同点的方式就是错误状态
看一下总错误数不大，而且数据很敏感那么就去状态压缩，错误为 $1$ ，正确为 $0$
每一个点都是一个错误状态，一共 $2^n$ 个错误状态，每一个操作都是状态与状态的连边，我们的目的是求全错到全对的最短路
看一下什么样的两个状态 $u,v$ 可以连边

$u$ 包含 $b1[i]$ 的所有错误，即 $u|b1[i]=u$
$u$ 不包含 $b2[i]$ 的任何错误，即 $u|b2[i]=u+b2[i]$
$u$ 修正 $f1[i]$ 的错误，即将 $1$ 的位置置为 $0$ ，那么就是 $u\&\stackrel{\_\_\_\_\_}{f1[i]}$
再补上 $f2[i]$ 的错误，即 $u\&\stackrel{\_\_\_\_\_}{f1[i]}|f2[i]$

好了边有了，跑最短路就行了

# ✅

const int N = 2e6 + 10;

int n, m;
int b1[101], b2[101], f1[101], f2[101], tim[101];
char b[25], f[25];

int dis[N], vis[N];
struct node {
    int id, val;
    inline friend bool operator < (node a, node b) {
        return a.val > b.val;
    }
};

int main () {
    scanf("%d%d", &m, &n);
    for (int i = 0; i < n; i ++) {
        scanf("%d%s%s", &tim[i], b, f);
        for (int j = 0; j < m; j ++) {
            if (b[j] == '+') b1[i] |= 1 << j;
            else if (b[j] == '-') b2[i] |= 1 << j;
        }
        for (int j = 0; j < m; j ++) {
            if (f[j] == '-') f1[i] |= 1 << j;
            else if (f[j] == '+') f2[i] |= 1 << j;
        }
    }

    memset(dis, 0x3f, sizeof dis);
    priority_queue<node> pque;
    pque.push({(1 << m) - 1, 0}); 
    dis[(1 << m) - 1] = 0;
    vis[(1 << m) - 1] = 1;
    while (!pque.empty()) {
        int u = pque.top().id; pque.pop();
        for (int i = 0; i < n; i ++) {
            if ((u | b1[i]) == u && (u | b2[i]) == u + b2[i]) {
                int v = u & (~f1[i]) | f2[i];
                if (dis[v] > dis[u] + tim[i]) {
                    dis[v] = dis[u] + tim[i];
                    if (!vis[v]) pque.push({v, dis[v]}), vis[v] = 1;
                }
            }
        }
    }
    printf("%d\n", dis[0] == 0x3f3f3f3f ? 0 : dis[0]);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

# 洛谷P4568_飞行路线

# 🔗

# 💡

看到有一个很基础的类似 $dp$ 转移的东西，那就是再开一维记录用了几次免费
对于 $[u][i]$ ，可以转移的方式为

$[v][i]=[u][i]+edge.val$
$[v][i+1]=[u][i]$

保证 $i\le k$ ，也可以视作拆点，即一个点被拆成 $k$ 种状态，那么最后统计一下 $t$ 的 $[0,k]$ 状态下的最小值即可

# ✅

const int N = 1e4 + 10;
const int M = 1e5 + 10;

struct Edge {
    int nxt, to, val;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to, int val) {
    edge[++cnt] = {head[from], to, val};
    head[from] = cnt;
} 

struct node {
    int id, val;
    inline friend bool operator < (node a, node b) {
        return a.val > b.val;
    }
};
int n, m, k;
int s, t;
int dis[N][20];
int vis[N][20];
inline int tonumber (int u, int id) {
    return u * 20 + id;
}
inline pair<int, int> tostatus (int number) {
    return {number / 20, number % 20};
}
inline void Dijkstra () {
    memset(dis, 0x3f, sizeof dis);
    dis[s][0] = 0;
    priority_queue<node> pque;
    pque.push({tonumber(s, 0), 0});
    while (!pque.empty()) {
        int u = tostatus(pque.top().id).first;
        int id = tostatus(pque.top().id).second;
        pque.pop();
        if (vis[u][id]) continue; vis[u][id] = 1;
        for (int i = head[u]; i; i = edge[i].nxt) {
            int v = edge[i].to;
            if (id <= k && dis[v][id] > dis[u][id] + edge[i].val) {
                dis[v][id] = dis[u][id] + edge[i].val;
                pque.push({tonumber(v, id), dis[v][id]});
            }
            if (id + 1 <= k && dis[v][id + 1] > dis[u][id]) {
                dis[v][id + 1] = dis[u][id];
                pque.push({tonumber(v, id + 1), dis[v][id + 1]});
            }
        }
    }
}

inline void Solve () {
    scanf("%d%d%d%d%d", &n, &m, &k, &s, &t);
    for (int i = 0; i < m; i ++) {
        int u, v, w; scanf("%d%d%d", &u, &v, &w);
        add_Edge(u, v, w);
        add_Edge(v, u, w);
    }
    Dijkstra();
    int res = 0x3f3f3f3f;
    for (int i = 0; i <= k; i ++) {
        res = min(res, dis[t][i]);
    }
    printf("%d\n", res);
}

int main () {
    ios::sync_with_stdio(false);
    cin.tie(0);

    int cass = 1; while (cass --) {
        Solve ();
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

# ABC237E_Skiing

# 🔗

# 💡

~~这道题出题人可能没想到没卡住数据，便有了一群佬赛后疯狂提交原代码TLE~~

赛中傻瓜版

看到图，看到最长路，看到负权，啥也不说试一手 SPFA ，过了
~~代码太过傻瓜就不发了~~

当时比赛时候也是在想SPFA竟然没有被卡，赛后出题人也是不负众望让人去思考了一波正解
注意一下边权是由于高度差产生的
如果一条路只走下坡路，那么高度差就是每个点的边权和
但是走上坡路边权会形成两倍高度差的负数
如果这个是一倍，那么我们依然可以直接通过高度差求得答案
毕竟你上坡失去的快乐，下坡会给你补回来

所以我们可以把一倍的上坡单独提出来
在这个基础上跑“以快乐减小值为边权”的最短路，这个是非负的，直接 Dijkstra 即可
让从 $1$ 到每个点走的上坡路都尽可能少
让 $1$ 到 $i$ 走的上坡路的量成为 $dis[i]$
这样的话我们最后统计 “高度差 $-dis[i]$ ” 的最大值即可

# ✅

const ll N = 2e5 + 10;
const ll M = 4e5 + 10;

struct Edge {
        ll nxt, to;
        ll val;
} edge[M];
ll head[N], cnt;
inline void add_Edge ( ll from, ll to, ll val ) {
        edge[++cnt] = { head[from], to, val };
        head[from] = cnt;
}
ll n, m;
ll h[N];

ll dis[N];
bool vis[N];
struct node {
        ll id, val;
        inline friend bool operator < ( node a, node b ) {
                return a.val > b.val;
        }
};
inline void Dijkstra () {
        for ( int i = 0; i <= n; i ++ ) dis[i] = 0x3f3f3f3f,vis[i] = 0;
        priority_queue<node> pque;
        dis[1] = 0; pque.push({1, 0});
        while ( pque.size() ) {
                node cur = pque.top(); pque.pop();
                if ( vis[cur.id] ) continue; vis[cur.id] = 1;
                for ( int i = head[cur.id]; i; i = edge[i].nxt ) {
                        int to = edge[i].to;
                        if ( dis[to] > dis[cur.id] + edge[i].val ) {
                                dis[to] = dis[cur.id] + edge[i].val; 
				pque.push({to, dis[to]});
                        }
                }
        }
}


int main () {
        scanf("%lld%lld", &n, &m);
        for ( ll i = 1; i <= n; i ++ ) scanf("%lld", &h[i]);
        for ( ll i = 1; i <= m; i ++ ) {
                ll a, b; scanf("%lld%lld", &a, &b);
                // 只考虑上坡路
                add_Edge(a, b, max(0ll, h[b] - h[a]));
                add_Edge(b, a, max(0ll, h[a] - h[b]));
        }
        Dijkstra();
        ll res = 0;
        for ( ll i = 1; i <= n; i ++ ) {
                res = max(res, h[1] - h[i] - dis[i]);
        }
        printf("%lld\n", res);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

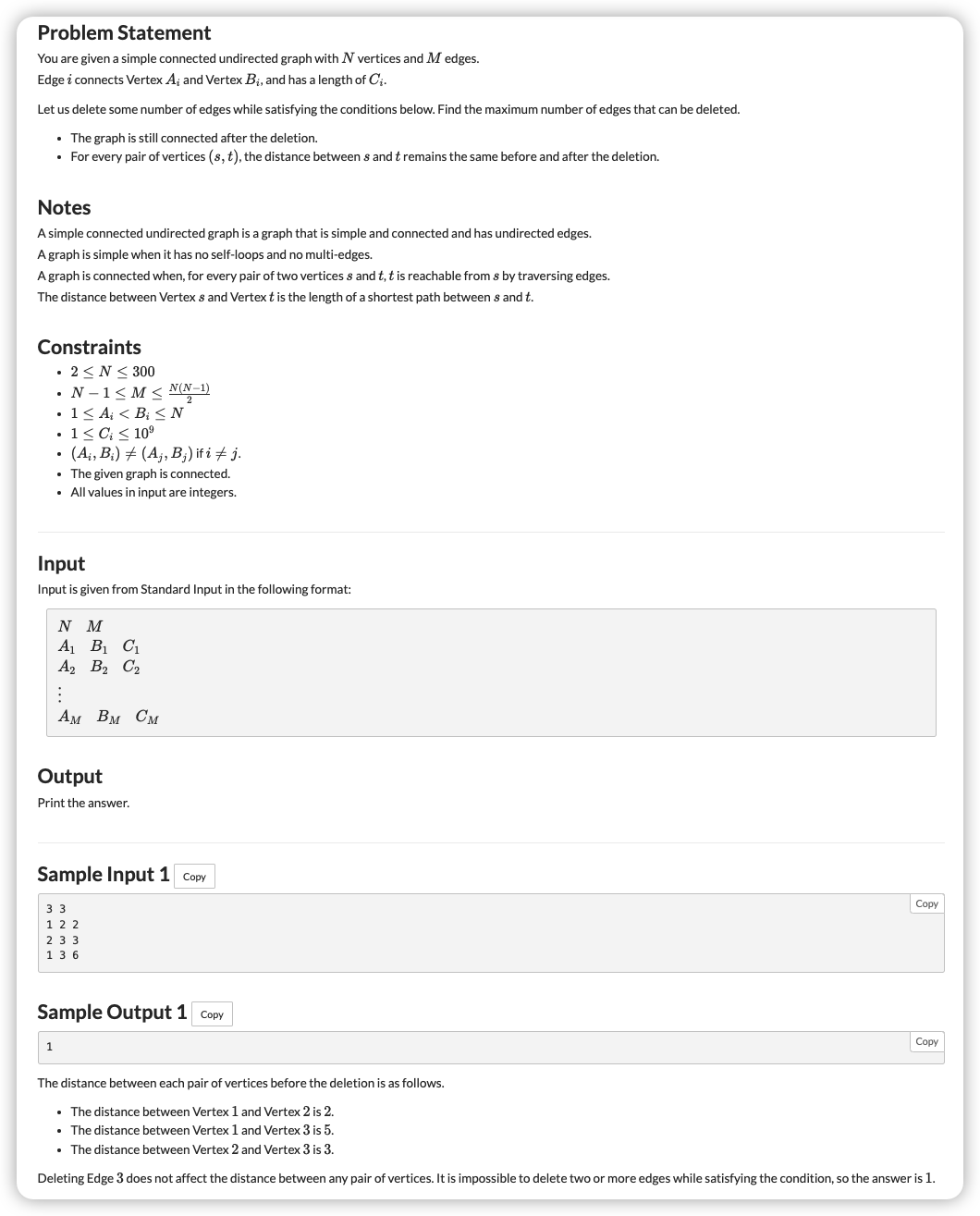
# ABC243E_EdgeDeletion

# 🔗

# 💡

$N$ 很小，这个关注出来是想让我们走 $n^3$ 的
考虑什么是我们不需要的边，即可以被替代的边
$Floyd$ 的更新操作
如果一条边可以被别的已知的边更新的话，那么这条边就没必要
走一遍把边的编号存入 $set$ 然后 $m-sz$ 即为答案

# ✅

const int N = 310;
int n, m;
ll dis[N][N];
int id[N][N];
set<int> st;
 
int main () {
        scanf("%d%d", &n, &m);
        for ( int i = 1; i <= n; i ++ ) for ( int j = 1; j <= n; j ++ ) dis[i][j] = 1e15;
        for ( int i = 1; i <= m; i ++ ) {
                int a, b, c; scanf("%d%d%d", &a, &b, &c);
                dis[a][b] = dis[b][a] = c;
                id[a][b]  = id[b][a]  = i;
        }
        for ( int k = 1; k <= n; k ++ ) {
                for ( int i = 1; i <= n; i ++ ) {
                        for ( int j = 1; j <= n; j ++ ) {
                                if ( dis[i][j] >= dis[i][k] + dis[k][j] ) {
                                        if ( id[i][j] ) st.insert(id[i][j]);
                                        dis[i][j] = dis[i][k] + dis[k][j];
                                }
                        }
                }
        }
        printf("%d\n", (int)st.size());
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

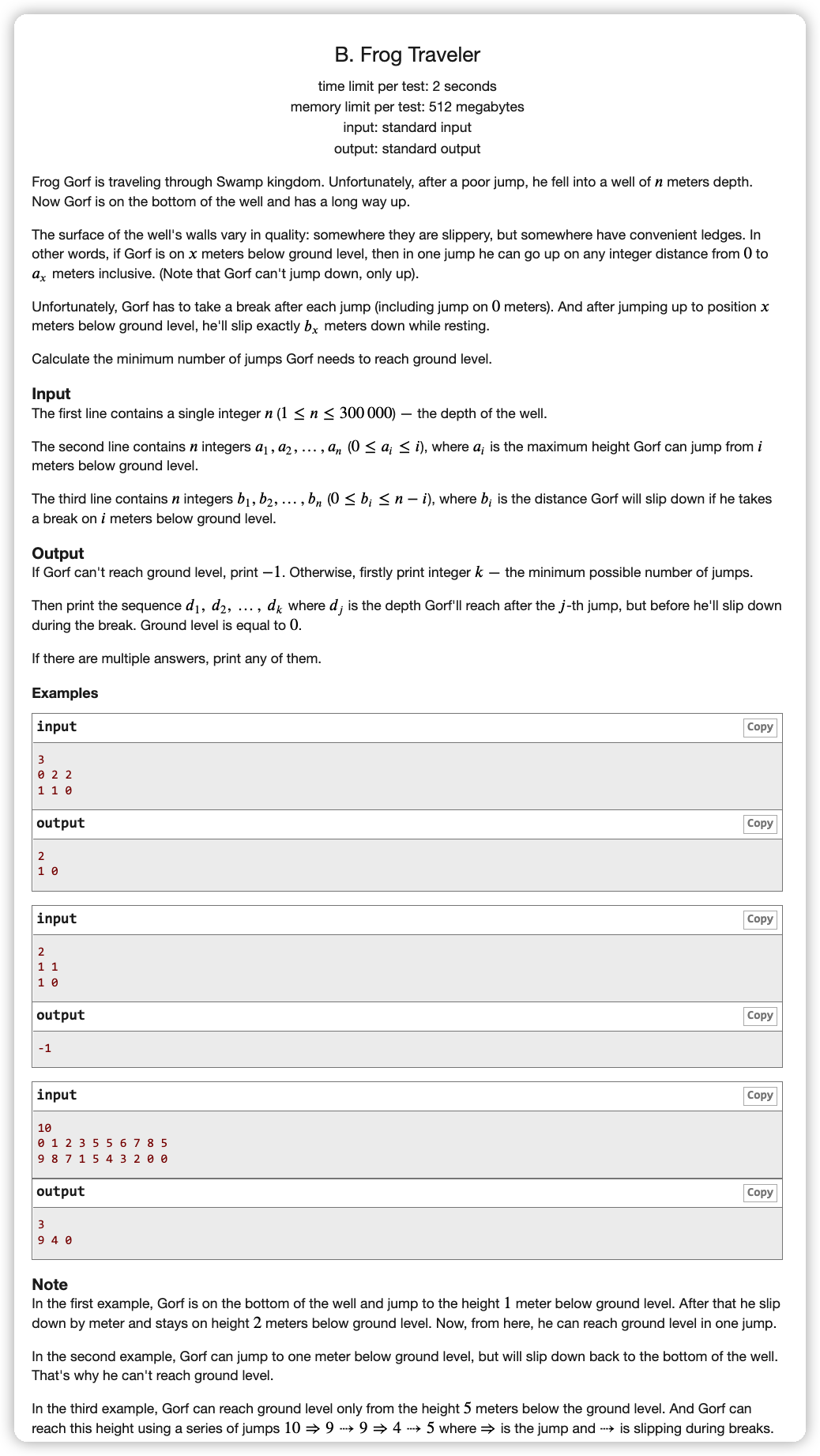
# CodeForces1601B_FrogTraveler

# 🔗

# 💡

分析这个问题
首先这个问题是一个类似于最短路的问题，我们要跳最少的次数到达目的地，需要更新
同时这个问题也要维护路径，需要记录最短路前驱

如果把它按最短路单纯地连边的话，边数可能会到达 $\frac{n^2}{2}$ ，非常大，时间空间都过不去
注意到一个点可以跑的点是它后面连续的一段点，考虑到其实 $dijkstra$ 就是一个 $dp$ 的转移，那么用线段树区间修改进行这个 $dp$ 的转移操作

但是注意到有一个下滑的过程，由于我们要使用这个连续的下标，我们就要在用 $a_i$ 时，用 $i$ 这个点的最短距离 $+1$ 更新 $[i+b_i-a_{i+b_i},i+b_i-1]$
因为我们路径记录的都是下滑之前的路径点，所以标记这次更新是用 $i$ 更新的即可
所以我们要有一个双关键字的懒标记，一个关键字是更新的距离，另一个则是更新出第一个关键字的出发点
线段树懒标记往下推的时候，需要考虑需不需要更改这两个关键字，而当子树的 $l=r$ 了话，就代表我们推到底了，如果将距离更新为更短了，就要直接修改 $pre[l]$

# ✅

const int N = 3e5 + 10;
const int inf = 0x3f3f3f3f;
 
int pre[N]; // 最短路的前驱
struct node {
        int val;
        pair<int, int> lazy;
} t[N << 2];
inline void pushUp (int rt) {
        t[rt].val = max(t[rt << 1].val, t[rt << 1 | 1].val);
}
inline void pushDown (int l, int r, int rt) {
        if (t[rt].lazy.first == inf) return;
        node &fa = t[rt], &ls = t[rt << 1], &rs = t[rt << 1 | 1];
        // 更短的话，更新的原因点也要修改
        if (ls.lazy.first > fa.lazy.first) ls.lazy = fa.lazy;
        if (rs.lazy.first > fa.lazy.first) rs.lazy = fa.lazy;
        int mid = (l + r) >> 1;
        // 叶子节点，如果需要更新的话就把 pre 更新了
        if (mid - l + 1 == 1) { 
                if (ls.val > fa.lazy.first) {
                        pre[l] = fa.lazy.second;
                        ls.val = fa.lazy.first;
                }
        } else {       
                ls.val = min(ls.val, fa.lazy.first);
        }
        if (r - mid == 1) {
                if (rs.val > fa.lazy.first) {
                        pre[r] = fa.lazy.second;
                        rs.val = fa.lazy.first;
                }
        } else {
                rs.val = min(rs.val, fa.lazy.first);
        }
        fa.lazy = {inf, -1};
}
inline void Build (int l, int r, int rt) {
        t[rt] = {inf, {inf, -1}};
        if (l == r) return;
        int mid = (l + r) >> 1;
        Build(l, mid, rt << 1);
        Build(mid + 1, r, rt << 1 | 1);
}
inline void Update (int a, int b, int c, int id, int l, int r, int rt) {
        if (a <= l && r <= b) {
                if (t[rt].lazy.first > c) t[rt].lazy = {c, id};
                // 同理，叶子结点要看情况直接更新 pre
                if (l == r) {
                        if (t[rt].val > c) {
                                t[rt].val = c;
                                pre[l] = id;
                        }
                } else {
                        t[rt].val = min(t[rt].val, c);
                }
                return;
        }
        pushDown(l, r, rt);
        int mid = (l + r) >> 1;
        if (a <= mid) Update(a, b, c, id, l, mid, rt << 1);
        if (b > mid) Update(a, b, c, id, mid + 1, r, rt << 1 | 1);
        pushUp(rt);
}
inline int Query (int id, int l, int r, int rt) {
        if (l == r) return t[rt].val;
        pushDown(l, r, rt);
        int mid = (l + r) >> 1;
        if (id <= mid) return Query(id, l, mid, rt << 1);
        else return Query(id, mid + 1, r, rt << 1 | 1);
}
 
 
int a[N], b[N], n;
int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);
 
        cin >> n;
        for (int i = 1; i <= n; i ++) cin >> a[i];
        for (int i = 1; i <= n; i ++) cin >> b[i];
 
        Build(0, n, 1);
        Update(n, n, 0, n + 1, 0, n, 1);
 
        for (int i = n; i >= 1; i --) {
                int ti = i + b[i];
                // 用当前所在点的最短路 去 更新下滑过后的点所能跑到的区间，并记录这次更新是当前所在点更新的
                if (a[ti]) Update(ti - a[ti], ti - 1, Query(i, 0, n, 1) + 1, i, 0, n, 1);
        }
        for (int i = 0; i <= n; i ++) Query(i, 0, n, 1); // 懒标记全推下去
 
        if (t[1].val == inf) {
                cout << "-1\n";
                return 0;
        }
        cout << t[1].val << endl;
        vector<int> res;
        int cur = 0;
        while (pre[cur] != n + 1) {
                res.push_back(cur);
                cur = pre[cur];
        }
        reverse(res.begin(), res.end());
        for (auto i : res) cout << i << " ";
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106

# CodeForces1611E1_EscapeTheMaze(easyversion)

# 🔗

# 💡

玩家想抓到Vlad，Vlad想逃脱
每一个玩家往上跑，Vlad往下跑
如果一个点Vlad先到了玩家才到，那么玩家是赶不上Vlad的

所以应该预处理出来玩家到达每一个节点的最短时间 $\inline \{tim\}$
然后让Vlad往下跑，如果一个点玩家会先到，那么Vlad就不能走这个点
看看有没有一种方法让Vlad到达叶子节点

那么问题的关键就在处理 $\inline \{tim\}$ 数组上了
这个可以想到最短路的更新方式，以所有玩家为起始点入队进行 $\inline BFS$
如果 $\inline to$ 点的 $\inline tim[to]$ 被 $\inline tim[x]+1$ 更新了，那么就入队，一个一个向上更新

# ✅

int n, k;
const int N = 2e5 + 10;
const int M = 4e5 + 10;
int a[N];
bool flag;

namespace Tree {
        int head[M], cnt;
        struct Edge {
                int nxt, to;
        } edge[M];

        inline void add_Edge ( int from, int to ) {
                edge[ ++ cnt ] = { head[from], to };
                head[from] = cnt;
        }

        int dep[N];
        int tim[N];
        inline void Init () {
                for ( int i = 0; i <= n; i ++ )
                        head[i] = 
                        dep[i]  = 0,
                        tim[i] = 0x3f3f3f3f;
                cnt = 0;
                flag = false;
        }

        inline void pre_Dfs ( int x, int fath ) { // 处理 {dep}
                if ( x != 1 ) dep[x] = dep[fath] + 1;
                for ( int i = head[x]; i; i = edge[i].nxt ) {
                        int to = edge[i].to;
                        if ( to == fath ) continue;
                        pre_Dfs ( to, x );
                }
        }

        inline void pre_Bfs () { // 最短路处理 {tim}
                queue<int> que;
                for ( int i = 0; i < k; i ++ ) 
                        que.push(a[i]),
                        tim[a[i]] = 0;

                while ( que.size() ) {
                        int x = que.front(); que.pop();
                        for ( int i = head[x]; i; i = edge[i].nxt ) {
                                int to = edge[i].to;
                                if ( dep[to] > dep[x] ) continue; // 要往上跑
                                if ( tim[to] > tim[x] + 1 ) // 更新就入队
                                        tim[to] = tim[x] + 1,
                                        que.push(to);
                        }
                }
        }

        inline void Solve_Dfs ( int x, int fath ) { // 求答案看看往哪搜
                if ( dep[x] >= tim[x] || flag ) return; // 先到了

                bool has_son = false;
                for ( int i = head[x]; i; i = edge[i].nxt ) {
                        int to = edge[i].to;
                        if ( to == fath ) continue;
                        Solve_Dfs ( to, x );
                        has_son = true;
                }
                if ( !has_son ) flag = true;
        }

} using namespace Tree;



inline void Solve () {
        scanf("%d%d", &n, &k); Init();
        for ( int i = 0; i < k; i ++ ) scanf("%d", &a[i]);
        for ( int i = 0, x, y; i < n - 1; i ++ )
                scanf("%d%d", &x, &y),
                add_Edge ( x, y ),
                add_Edge ( y, x );
        pre_Dfs ( 1, 1 );
        pre_Bfs ();
        Solve_Dfs ( 1, 1 );
        if ( flag ) puts("YES");
        else        puts("NO");
}

int main () {
        int cass; scanf("%d", &cass); while ( cass -- ) {
                Solve ();
        }
}

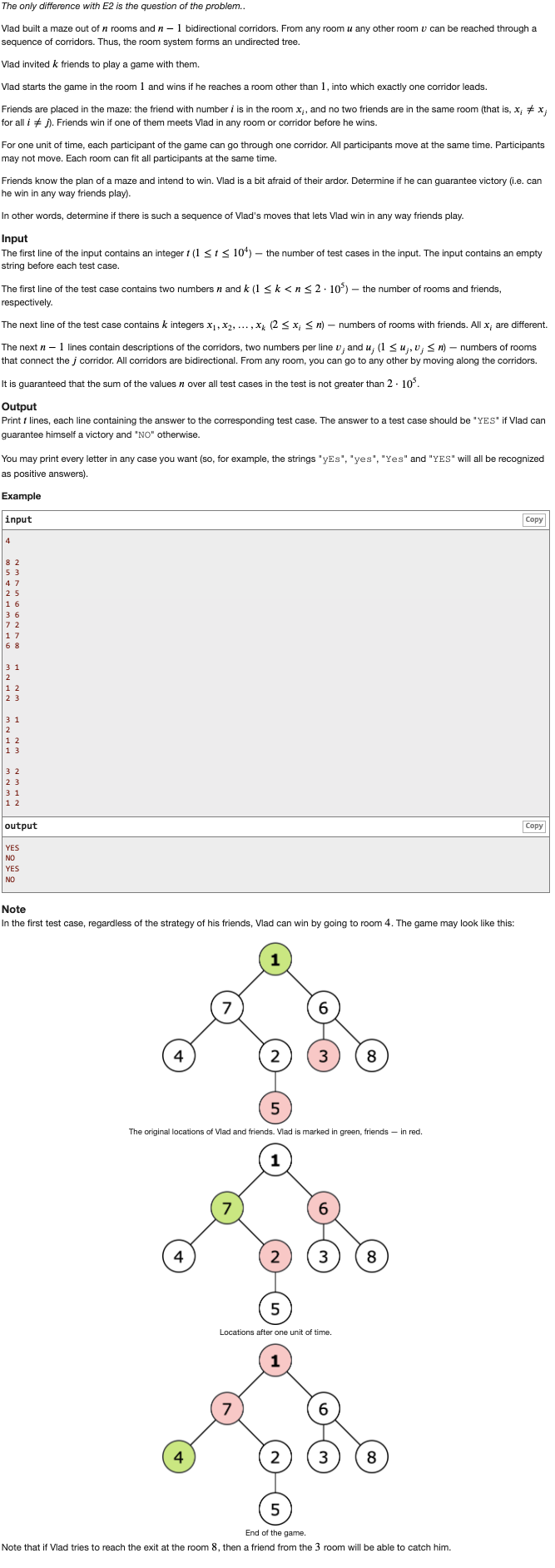
# CodeForces1611E2_EscapeTheMaze(hardversion)

# 🔗

# 💡

和这个题没什么大区别，就是任务稍微改了一下而已

如果Vlad可以逃脱，那么谁都抓不住他，输出-1
否则能抓住他的就是在最后一个dfs中看一下Vlad走的时候会被断多少次
因为每个人最多会断它一次，因为从上往下走的时候不会有多次相邻一个点

# ✅

int n, k;
const int N = 2e5 + 10;
const int M = 4e5 + 10;
int a[N];
bool flag;
int can_catch; // 可以抓住的
 
namespace Tree {
        int head[M], cnt;
        struct Edge {
                int nxt, to;
        } edge[M];
 
        inline void add_Edge ( int from, int to ) {
                edge[ ++ cnt ] = { head[from], to };
                head[from] = cnt;
        }
 
        int dep[N];
        int tim[N];
        inline void Init () {
                for ( int i = 0; i <= n; i ++ )
                        head[i] = 
                        dep[i]  = 0,
                        tim[i] = 0x3f3f3f3f;
                cnt = can_catch = 0;
                flag = false;
        }
 
        inline void pre_Dfs ( int x, int fath ) {
                if ( x != 1 ) dep[x] = dep[fath] + 1;
                for ( int i = head[x]; i; i = edge[i].nxt ) {
                        int to = edge[i].to;
                        if ( to == fath ) continue;
                        pre_Dfs ( to, x );
                }
        }
 
        inline void pre_Bfs () {
                queue<int> que;
                for ( int i = 0; i < k; i ++ ) 
                        que.push(a[i]),
                        tim[a[i]] = 0;
 
                while ( que.size() ) {
                        int x = que.front(); que.pop();
                        for ( int i = head[x]; i; i = edge[i].nxt ) {
                                int to = edge[i].to;
                                if ( dep[to] > dep[x] ) continue;
                                if ( tim[to] > tim[x] + 1 )
                                        tim[to] = tim[x] + 1,
                                        que.push(to);
                        }
                }
        }
 
        inline void Solve_Dfs ( int x, int fath ) {
                if ( flag ) return;
                if ( dep[x] >= tim[x] ) {can_catch ++; return;}
 
                bool has_son = false;
                for ( int i = head[x]; i; i = edge[i].nxt ) {
                        int to = edge[i].to;
                        if ( to == fath ) continue;
                        Solve_Dfs ( to, x );
                        has_son = true;
                }
                if ( !has_son ) flag = true;
        }
 
} using namespace Tree;
 
 
 
inline void Solve () {
        scanf("%d%d", &n, &k); Init();
        for ( int i = 0; i < k; i ++ ) scanf("%d", &a[i]);
        for ( int i = 0, x, y; i < n - 1; i ++ )
                scanf("%d%d", &x, &y),
                add_Edge ( x, y ),
                add_Edge ( y, x );
        pre_Dfs ( 1, 1 );
        pre_Bfs ();
        Solve_Dfs ( 1, 1 );
        if ( flag ) puts("-1");
        else        printf("%d\n", can_catch);
}
 
int main () {
        int cass; scanf("%d", &cass); while ( cass -- ) {
                Solve ();
        }
}

# HDUOJ1217_Arbitrage

# 🔗

https://acm.dingbacode.com/showproblem.php?pid=1217

# 💡

判断是否有负环
使用Bellman-Ford算法
松弛操作完之后判断还能不能松弛
朴素就能过

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'

#define CHIVAS_ int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
//#define map unordered_map

#define _int(a) int a; cin >> a
#define  _ll(a) ll a; cin >> a
#define _char(a) char a; cin >> a
#define _string(a) string a; cin >> a
#define _vectorInt(a, n) vector<int>a(n); cin >> a
#define _vectorLL(a, b) vector<ll>a(n); cin >> a

#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cin >> cass; cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

template<typename T> inline void Read(T &x){T f = 1; x = 0;char s = getchar();while(s < '0' || s > '9'){if(s == '-') f = -1; s = getchar();}while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}x*=f;}
template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
template<typename T>             vector<T>& operator--            (vector<T> &v){for (auto& i : v) --i;            return  v;}
template<typename T>             vector<T>& operator++            (vector<T> &v){for (auto& i : v) ++i;            return  v;}
template<typename T>             istream& operator>>(istream& is,  vector<T> &v){for (auto& i : v) is >> i;        return is;}
template<typename T>             ostream& operator<<(ostream& os,  vector<T>  v){for (auto& i : v) os << i << ' '; return os;}
template<typename T> inline void read(T &f) { f = 0; T fu = 1; char c = getchar();while (c < '0' || c > '9') { if (c == '-') { fu = -1; } c = getchar(); }while (c >= '0' && c <= '9') { f = (f << 3) + (f << 1) + (c & 15); c = getchar(); }f *= fu;}
template<typename T> inline void write(T x) { if(x < 0) x = ~(x - 1), putchar('-'); if(x > 9) write(x / 10); putchar(x % 10 + '0'); }


const int M = 1000, N = 100;
string fr[M], to[M];
double val[M];
map<string, double> dis;
int n, m;
int cas = 0;

inline void Init(){
        for(int i = 0; i < M; i ++){
                val[i] = 1;
                fr[i] = to[i] = "";
        }
}

inline void DrawMap(){
        for(int i = 0; i < n; i ++){
                string s; cin >> s;
                dis[s] = 1;
        }
        cin >> m;
        for(int i = 0; i < m; i ++){
                cin >> fr[i] >> val[i] >> to[i];
        }
}

inline void BellmanFord(){
        cout << "Case " << ++cas << ": ";
        for(int k = 1; k <= n - 1; k ++){
                for(int i = 0; i < m; i ++){
                        dis[to[i]] = MAX(dis[fr[i]] * val[i], dis[to[i]]);
                }
        }
        for(int i = 0; i < m; i ++){
                if(dis[to[i]] < dis[fr[i]] * val[i]){
                        puts("Yes");
                        return;
                }
        }puts("No");
}

CHIVAS_{
        while(cin >> n, n){
                Init();
                DrawMap();
                BellmanFord();
        }
        _REGAL;
}

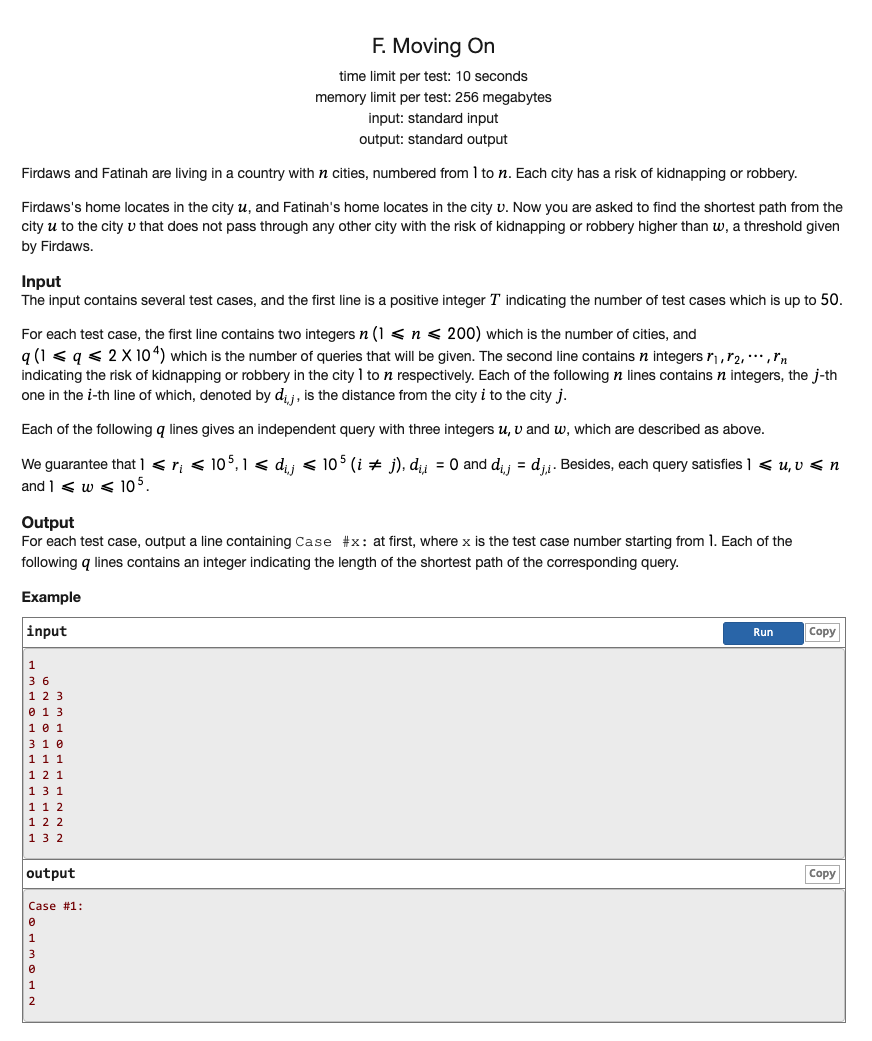
# ICPC2018银川F_MovingOn

# 🔗

# 💡

首先看见 $n\le 200$ 且点权的种数也就只有 $n$ 个，故想到使用分层最短路，分层进行 $floyd$ 看看哪些可以转移哪些不可以，发现总复杂度是 $n^4$ 太大了
不过分析一下 $floyd$ 的优点是插入，我们可以在求答案的时候动态插点，让限制下的都插入成为中转点就可以了
所以对点权排序，对询问按限制排序（离线处理）
在每次询问前，将这个限制下的点递进式插入进 $floyd$ 中，然后直接给答案赋值即可

# ✅

const int N = 210;

int dis[N][N];
int n;
struct node {
    int id, val;
} a[N];

inline void insert (int mid) {
    for (int u = 1; u <= n; u ++) {
        for (int v = 1; v <= n; v ++) {
            dis[u][v] = min(dis[u][v], dis[u][mid] + dis[mid][v]);
        }
    }
}


struct Query {
    int id, s, t, w;
} q[20004];
int Q;
int res[20004];

int casid;
void Solve () {
    printf("Case #%d:\n", ++casid);
    scanf("%d%d", &n, &Q);
    for (int i = 1; i <= n; i ++) scanf("%d", &a[i].val), a[i].id = i;
    sort(a + 1, a + 1 + n, [&](node x, node y) { return x.val < y.val; });

    memset(dis, 0x3f, sizeof dis);
    for (int i = 1; i <= n; i ++) {
        for (int j = 1; j <= n; j ++) {
            scanf("%d", &dis[i][j]);
        }
    }
    for (int i = 1; i <= Q; i ++) {
        q[i].id = i;
        scanf("%d%d%d", &q[i].s, &q[i].t, &q[i].w);
    }
    sort(q + 1, q + 1 + Q, [&](Query x, Query y) {return x.w < y.w;});

    int idxpoint = 1;
    for (int i = 1; i <= Q; i ++) {
        while (idxpoint <= n && a[idxpoint].val <= q[i].w) {
            insert(a[idxpoint].id);
            idxpoint ++;
        }
        res[q[i].id] = dis[q[i].s][q[i].t];
    }
    for (int i = 1; i <= Q; i ++) printf("%d\n", res[i]);
    
}
int main () { 
    int cass; scanf("%d", &cass); while (cass --) {
        Solve();
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

基环树特殊图