线段树分裂合并

#

---

洛谷P1600_天天爱跑步

🔗

💡

这依旧是一个路径操作问题，但是由于时间戳的存在，路径上每一个点都要更新为不一样的值
但是这些值是连续的，所以考虑使用参照系的方法去更新
路径操作，首选树上差分，那么参照点会有三个，即对于一条 $s\to t$ 的路径来说，参照点为 $s,t,lca(s,t)$ 这三个点可以选
最终我们是要求这条路径上的任意一点 $p$ ，因为这条路径可以对其中的点做贡献
分类讨论一下：
$1.$ $p$ 在 $s\to lca$ 这一段：$deep_s+w_p=deep_p \Rightarrow \color{red}{deep_s=deep_p-w_p}$
$2.$ $p$ 在 $lca\to t$ 这一段：$(deep_s-deep_{lca})+(deep_p-deep_{lca})=w_p\Rightarrow\color{red}{2deep_{lca}-deep_s=deep_p+w_p}$
公式有了，每个点都做权值线段树，并修改路径时按上面两条进行树上差分即可

注意，减的时候值域可能为负导致线段树$RE$ ，所以我们将值域向右偏移 $n$

✅

const int N = 3e5 + 10;
const int M = N * 2;

struct Edge {
        int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to) {
        edge[++cnt] = {head[from], to};
        head[from] = cnt;
}
int fa[N], sz[N], son[N], top[N], dep[N];
inline void dfs_TreeDivide1 (int u, int fath) {
        fa[u] = fath;
        sz[u] = 1;
        son[u] = 0;
        dep[u] = dep[fath] + 1;
        for (int i = head[u]; i; i = edge[i].nxt) {
                int v = edge[i].to;
                if (v == fath) continue;
                dfs_TreeDivide1(v, u);
                sz[u] += sz[v];
                if (sz[v] > sz[son[u]]) son[u] = v;
        }
}
inline void dfs_TreeDivide2 (int x, int topx) {
        top[x] = topx;
        if (son[x]) dfs_TreeDivide2(son[x], topx);
        for (int i = head[x]; i; i = edge[i].nxt) {
                if (edge[i].to != fa[x] && edge[i].to != son[x])
                        dfs_TreeDivide2(edge[i].to, edge[i].to);
        }
}
inline int Lca (int x, int y) {
        while (top[x] != top[y]) {
                if (dep[top[x]] < dep[top[y]]) swap(x, y);
                x = fa[top[x]];
        }
        return dep[x] < dep[y] ? x : y;
}

struct node {
        int l, r;
        int val;
} t[N * 100];
int root[N], tot;
inline void pushUp (int rt) {
        t[rt].val = t[t[rt].l].val + t[t[rt].r].val;
}
inline void Update (int id, int c, int l, int r, int &rt) {
        if (!rt) rt = ++tot;
        if (l == id && id == r) {
                t[rt].val += c;
                return;
        }
        int mid = (l + r) >> 1;
        if (id <= mid) Update(id, c, l, mid, t[rt].l);
        else Update(id, c, mid + 1, r, t[rt].r);
        pushUp(rt);
}
inline int Query (int id, int l, int r, int rt) {
        if (l == id && id == r) return t[rt].val;
        int mid = (l + r) >> 1;
        if (id <= mid) return Query(id, l, mid, t[rt].l);
        else return Query(id, mid + 1, r, t[rt].r);
}
inline void Merge (int &x, int y, int l, int r) {
        if (!x || !y) x |= y;
        else if (l == r) t[x].val += t[y].val;
        else {
                int mid = (l + r) >> 1;
                Merge(t[x].l, t[y].l, l, mid);
                Merge(t[x].r, t[y].r, mid + 1, r);
                pushUp(x);
        }
}

int n, m;
int w[N];
int res[N];

inline void dfs_Res (int u) {
        for (int i = head[u]; i; i = edge[i].nxt) {
                int v = edge[i].to;
                if (v == fa[u]) continue;
                dfs_Res(v);
                Merge(root[u], root[v], 1, n << 1);
        }
        if (w[u] && n + dep[u] + w[u] <= 2 * n) {
                res[u] += Query(n + dep[u] + w[u], 1, n << 1, root[u]);
        } res[u] += Query(n + dep[u] - w[u], 1, n << 1, root[u]);
}

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);
        
        cin >> n >> m;
        for (int i = 1; i < n; i ++) {
                int u, v; cin >> u >> v;
                add_Edge(u, v);
                add_Edge(v, u);
        }
        dfs_TreeDivide1(1, 0);
        dfs_TreeDivide2(1, 1);

        for (int i = 1; i <= n; i ++) cin >> w[i];
        for (int i = 1; i <= m; i ++) {
                int x, y; cin >> x >> y;
                int lca = Lca(x, y);
                Update(n + dep[x], 1, 1, n << 1, root[x]);
                Update(n + dep[lca] * 2 - dep[x], 1, 1, n << 1, root[y]);
                Update(n + dep[x], -1, 1, n << 1, root[lca]);
                if (lca != 1) Update(n + dep[lca] * 2 - dep[x], -1, 1, n << 1, root[fa[lca]]);
        }

        dfs_Res(1);

        for (int i = 1; i <= n; i ++) cout << res[i] << " ";
        cout << endl;
}

---

洛谷P3201_梦幻布丁

🔗

💡

下标维护颜色想了想不知道怎么实现，于是可以考虑颜色维护下标
每个颜色构建一棵线段树，每个节点维护值为该区间内的连续区间个数，颜色变换即为线段树合并
但是考虑到这样往上 pushup 时有可能因为中间区间合并而需要加完减一
那么就再维护这个区间最左端为该颜色的下标和最右端为该颜色的下标 $lst,rst$
我们在 pushup 时特判一下，看看左子树的 $rst$ 和右子树的 $lst$ 的差，如果为 $1$ ，说明它两个是连续的，就加上左右子树值后减一，否则不减

而且每一次查询的时候都跑一遍很慢，注意到修改都是只修改一个颜色，那么我们动态地改变 $res$ 的值即可

✅

const int N = 1e6 + 10;
const int M = 1e5 + 10;

struct node {
        int l, r;
        int val;
        int lst, rst;
} t[M * 100];
int root[N], cnt;

inline void pushUp (int rt) {
        t[rt].lst = t[t[rt].l].lst ? t[t[rt].l].lst : t[t[rt].r].lst;
        t[rt].rst = t[t[rt].r].rst ? t[t[rt].r].rst : t[t[rt].l].rst;
        t[rt].val = t[t[rt].l].val + t[t[rt].r].val - (t[t[rt].l].rst + 1 == t[t[rt].r].lst);
}
inline void Update (int id, int l, int r, int &rt) {
        if (!rt) rt = ++cnt;
        if (l == r) {
                t[rt].lst = t[rt].rst = id;
                t[rt].val = 1;
                return;
        }
        int mid = (l + r) >> 1;
        if (id <= mid) Update(id, l, mid, t[rt].l);
        else Update(id, mid + 1, r, t[rt].r);
        pushUp(rt);
}
inline void Merge (int &x, int y, int l, int r) {
        if (!x || !y) {
                x |= y;
        } else if (l == r) {
                t[x].lst = t[x].rst = l;
                t[x].val = 1;
        } else {
                int mid = (l + r) >> 1;
                Merge(t[x].l, t[y].l, l, mid);
                Merge(t[x].r, t[y].r, mid + 1, r);
                pushUp(x);
        }
}

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);
        
        int res = 0;

        int n, m; cin >> n >> m;
        for (int i = 1; i <= n; i ++) {
                int x; cin >> x;
                res -= t[root[x]].val;
                Update(i, 1, n, root[x]);
                res += t[root[x]].val;
        }
        
        while (m --) {
                int op; cin >> op;
                if (op == 1) {
                        int x, y; cin >> x >> y;
                        if (x == y) continue;
                        res -= t[root[x]].val + t[root[y]].val;
                        Merge(root[y], root[x], 1, n);
                        root[x] = 0;
                        res += t[root[y]].val;
                } else {
                        cout << res << endl;
                }
        }
}

---

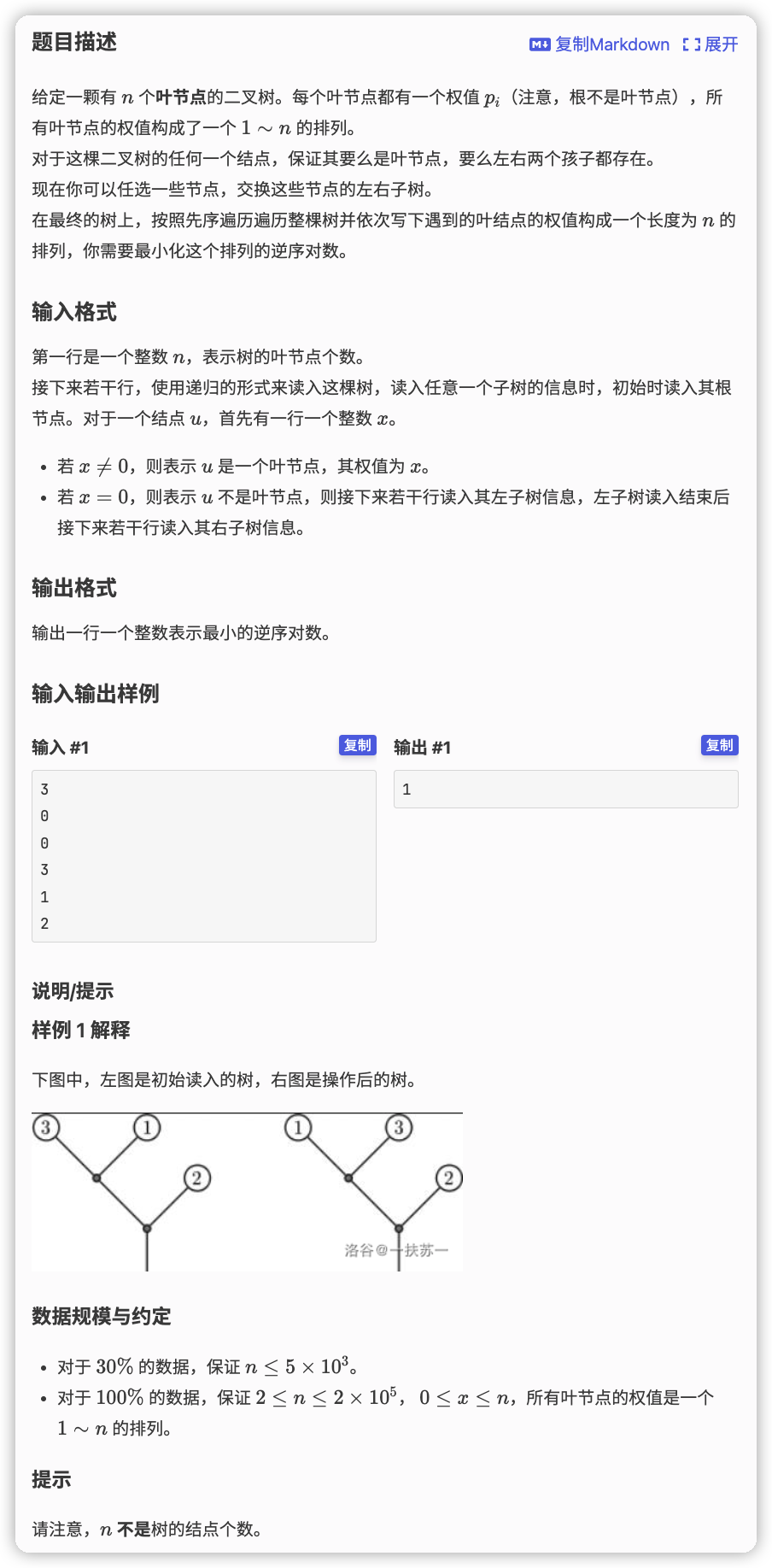
洛谷P3521_ROT-TreeRotations

🔗

💡

考虑交换子树后的叶子逆序对，相当于整体交换其中的叶子
那么我们每一个节点都存一个子树叶子的权值线段树，查询的时候直接查左子树的每一个数对应右子树的每一个比它大的数的个数 与 右子树的每一个数对应左子树每一个比它大的数的个数，答案累加最小值，然后把这两棵权值线段树合并给父亲即可
但是注意到，如果我们每一个节点都对于一棵子树的所有内容都去查询一遍另一棵子树比它大的个数，时间复杂度是 $O(nlognlogn)$ ，考虑优化
其实不需要在每次合并前都每一个数查一下，读入树图下左子树在前右子树在后，每个节点的权值线段树中左子树大于右子树，那么每次合并之前计算一下“左儿子权值线段树下的右子树个数”与“右儿子权值线段树下左子树的个数”的乘积，便是当前合并下所产生的逆序对
如果交换，则是把上面的左右儿子反过来
那么每次合并时按上述方法记录一个交换前的逆序对数量，与交换后的逆序对数量，让 $res$ 累加最小值即可

✅

const int N = 8e5 + 10;
const int M = N;
struct Edge {
        int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to) {
        edge[++cnt] = {head[from], to};
        head[from] = cnt;
}

int node_idx;
int is_leaf[N];
inline void Read_Tree (int fa) {
        int u; cin >> u;
        node_idx ++;
        if (~fa) add_Edge(fa, node_idx);
        if (!u) {
                int t = node_idx;
                Read_Tree(t);
                Read_Tree(t);
        } else {
                is_leaf[node_idx] = u;
        }
}

int n;
ll res, num1, num2;
struct SegmentTreeNode {
        int l, r;
        int val;
} t[N * 100];
int root[N], tot;
inline void pushUp (int rt) {
        t[rt].val = t[t[rt].l].val + t[t[rt].r].val;
}
inline void Merge (int &x, int y, int l, int r) {
        if (!x || !y) {
                x |= y;
                return;
        }
        if (l == r) {
                t[x].val += t[y].val;
                return;
        }
        num1 += 1ll * t[t[x].r].val * t[t[y].l].val;
        num2 += 1ll * t[t[y].r].val * t[t[x].l].val;
        int mid = (l + r) >> 1;
        Merge(t[x].l, t[y].l, l, mid);
        Merge(t[x].r, t[y].r, mid + 1, r);
        t[x].val += t[y].val;
}
inline void Update (int id, int c, int l, int r, int &rt) {
        if (!rt) rt = ++tot;
        if (l == id && id == r) {
                t[rt].val += c;
                return;
        }
        int mid = (l + r) >> 1;
        if (id <= mid) Update(id, c, l, mid, t[rt].l);
        else Update(id, c, mid + 1, r, t[rt].r);
        pushUp(rt);
}

inline void dfs_Res (int u) {
        if (is_leaf[u]) {
                Update(is_leaf[u], 1, 1, n, root[u]);
                return;
        }
        vector<int> v_node;
        for (int i = head[u]; i; i = edge[i].nxt) {
                v_node.push_back(edge[i].to);
                dfs_Res(edge[i].to);
        }

        num1 = num2 = 0;
        Merge(root[u], root[v_node[0]], 1, n);
        Merge(root[u] ,root[v_node[1]], 1, n);

        res += min(num1, num2);
}

int main () {
        ios::sync_with_stdio(false);
        cin.tie(0);
        
        cin >> n;
        Read_Tree(-1);
        dfs_Res(1);
        cout << res << endl;
}

---