整除相关

Chivas-Regal

#

# 因数、素数

# 洛谷P1128_求正整数

# 🔗

# 💡

唯一分解定理
如果 $\inline x$ 可以被质因数分解为 $\inline x=p_1^{a_1}\times p_2^{a_2}\times p_3^{a_3}\times ...\times p_k^{a_k}$
则 $\inline x$ 的因数个数为 $\inline (a_1+1)\times (a_2+1)\times (a_3+1)\times ...\times (a_k+1)$

解题思路
这个题很对应这个定理
~~所以定理应该能很快想到吧（是吧是吧~~

现在给出的是因数个数 $\inline n$ ，那么我们利用公式贪心地反推一下不就好了吗？
我们第一反应肯定能想到可以对 $\inline n$ 分解质因数 $\inline \{a\}$
那么每一个质因数 $\inline a$ 都可以有一个 $\inline ksm(p,a-1)$ 来构造我们要求的这个数 $\inline m$
根据贪心，我们肯定希望越大的质因数 $\inline a$ 去与越小的质数 $\inline p$ 凑数，这样可以使得 $\inline m$ 更小
这样的基础共识就是 $\inline m=p_1^{(a_1-1)}\times p_2^{(a_2-1)}\times p_3^{(a_3-1)}\times...\times p_{sz}^{(a_{sz}-1)}$

而由于大质数的变化性会很大我们可以考虑合并某两个因数 $\inline a_i=a_i\times&space;a_j$
例如如果给你 $\inline n=16$
我们可以分解成 $\inline 2*2*2*2$ ，此时 $\inline m=2^1*3^1*5^1*7^1=210$
而考虑合并一下一个因数给第一个 $\inline 2$ ，此时 $\inline m=2^3*3^1*5^1=120$
会变得更小

所以我们可以枚举我们可不可以在 $\inline i$ 的基础上乘上 $\inline j$ ，也就是把 $\inline a[j]$ 合并给 $\inline a[i]$ 同时 $\inline a[j]$ 删掉且整体 $\inline sz--$
看看这样做会不会更小更优如果更优的话就和合并掉，然后继续进行这套操作

数很大要开高精，这里直接拿 $\inline BigInteger$ 写了
（由于计算了一下对 $\inline n$ 分解后本身就是 $\inline log$ 级别的，我们最多合并 $\inline \frac{(logn + 1)logn}2$ 次，所以时间复杂度最高的为 $\inline log(n)^2$ ，然后 $\inline Java$ 学的也不好，就啥都开暴力了（逃

# ✅

import java.lang.reflect.Array;
import java.math.BigDecimal;
import java.math.BigInteger;
import java.util.*;

public class Main {
        static int N = 100010;
        static Vector<BigInteger> prime = new Vector<BigInteger>();
        static Vector<Integer> intprime = new Vector<Integer>();
        static boolean[] notprime = new boolean[N];

        static BigInteger one = BigInteger.ONE;
        static BigInteger two = BigInteger.valueOf(2);
        static BigInteger zero = BigInteger.ZERO;
        static BigInteger ten = BigInteger.TEN;

        public static void Sieve () { // 线性筛
                notprime[0] = notprime[1] = true;
                for ( int i = 2; i < N; i ++ ) {
                        if ( !notprime[i] ) {
                                prime.add(BigInteger.valueOf(i));
                                intprime.add(i);
                        }
                        for ( int j = 0; j < intprime.size() && i * intprime.elementAt(j) < N; j ++ ) {
                                notprime[i * intprime.elementAt(j)] = true;
                                if ( i % intprime.elementAt(j) == 0 ) break;
                        }
                }
        }
        public static BigInteger ksm ( BigInteger a, BigInteger b ) { // 快速幂
                BigInteger res = BigInteger.ONE;
                while ( b.compareTo(zero) == 1 ) {
                        if ( b.mod(two).compareTo(one) == 0 ) res = res.multiply(a);
                        a = a.multiply(a);
                        b = b.divide(two);
                }
                return res;
        }
        public static void main ( String[] args ) {
                Scanner input = new Scanner(System.in);
                Sieve();
                BigInteger n = input.nextBigInteger();

                BigInteger[] dv = new BigInteger[100]; // 对n分解的质因数数组
                int sz = 0; // 数组长度
                for ( int i = 0; i < prime.size() && BigInteger.valueOf(i).multiply(BigInteger.valueOf(i)).compareTo(n) <= 0; i ++ ) {
                        while ( n.mod(prime.elementAt(i)).compareTo(zero) == 0 ) {
                                n = n.divide(prime.elementAt(i));
                                dv[sz ++] = prime.elementAt(i);
                        }
                }
                if ( n.compareTo(one) == 1 ) dv[sz ++] = n;

                for ( int i = 0; i < sz; i ++ ) { // 降序排个序（冒泡儿（逃
                        for ( int j = i + 1; j < sz; j ++ ) {
                                if ( dv[i].compareTo(dv[j]) == -1 ) {
                                        BigInteger tmp = dv[i];
                                        dv[i] = dv[j];
                                        dv[j] = tmp;
                                }
                        }
                }

                boolean flag = true;
                while ( flag ) {
                        flag = false; // false为这一趟没有a[j]可以给a[i]合并
                        BigInteger res = one;
                        for ( int i = 0; i < sz; i ++ ) { // 计算一下本身结果
                                res = res.multiply(ksm(prime.elementAt(i), dv[i].subtract(one)));
                        }
                        for ( int i = 0; i < sz; i ++ ) {
                                for ( int j = i + 1; j < sz; j ++ ) {
                                        dv[i] = dv[i].multiply(dv[j]); // a[j]乘给a[i]
                                        int idx = 0;
                                        BigInteger cur = one; // 计算这次剪掉a[j]后的结果
                                        for ( int k = 0; k < j; k ++ ) cur = cur.multiply(ksm(prime.elementAt(idx ++), dv[k].subtract(one)));
                                        for ( int k = j + 1; k < sz; k ++ ) cur = cur.multiply(ksm(prime.elementAt(idx ++), dv[k].subtract(one)));
                                        if ( cur.compareTo(res) == -1 )  { // 如果结果小于本身的，那就直接跳出循环开始找下一层
                                                flag = true;
                                                sz --; for ( int k = j; k < sz; k ++ ) dv[k] = dv[k + 1]; // 把 dv[j] 删掉 
                                                break;
                                        }
                                        dv[i] = dv[i].divide(dv[j]); // 否则的话就再把a[j]还回去
                                }
                                if ( flag ) {
                                        break;
                                }
                        }
                }

                BigInteger res = one; // 最终结果再算一下（复制粘贴上面的代码
                for ( int i = 0; i < sz; i ++ ) {
                        res = res.multiply(ksm(prime.elementAt(i), dv[i].subtract(one)));
                }
                System.out.println(res);
                input.close();
        }
}

# 洛谷P1445_樱花

# 🔗

# 💡

这个柿子比较难看，我们化简一下
$\inline \begin{aligned}\frac1x+\frac1y&=\frac1{n!}\\yn!+xn!&=xy\\xy-(x+y)n!&=0\\n!^2-(x+y)n!+xy&=n!^2\\(x+n!)(y+n!)&=n!^2\end{aligned}$

令 $\inline A=x+n!,\;B=y+n!$
则 $\inline AB=n!^2$
$\inline A$ 是整数则 $\inline x$ 也是整数， $\inline B$ 同理
只要 $\inline A$ 是 $\inline n!^2$ 的因数，那么 $\inline B$ 也会是 $\inline n!^2$ 的因数
那么这道题就变成了求 $\inline n!^2$ 因数的个数

由唯一分解定理我们知道，若 $\inline n=\prod\limits_{p|n}p^a$
那么 $\inline n$ 的因数个数就是 $\inline \prod\limits_{p|a}(a+1)$

由于是求 $\inline n!^2$ 的因数
我们可以对 $\inline 1\rightarrow&space;n$ 的每一个数都分解一下质因数
然后让 $\inline a$ 乘 $\inline 2$
再唯一分解定理进行求解即可

# ✅

const int mod = 1e9 + 7;
const int N = 1e6 + 10;

namespace Number {
        bool not_prime[N];
        vector<ll> prime;
        inline void Sieve () {
                not_prime[0] = not_prime[1] = 1;
                for ( int i = 2; i < N; i ++ ) {
                        if ( !not_prime[i] ) prime.push_back(i);
                        for ( ll j = 0; j < prime.size() && i * prime[j] < N; j ++ ) {
                                not_prime[i * prime[j]] = 1;
                                if ( i % prime[j] == 0 ) break;
                        }
                }
        }
} using namespace Number;



ll mp[N], n;

int main () {
        Sieve (); cin >> n;
        for ( int i = 1; i <= n; i ++ ) {
                int x = i;
                for ( int j = 0; j < prime.size() && prime[j] * prime[j] <= x; j ++ ) {
                        while ( x % prime[j] == 0 ) 
                                mp[prime[j]] += 2, 
                                x /= prime[j];
                }
                if ( x > 1 ) 
                        mp[x] += 2;
        }
        ll res = 1;
        for ( int i = 1; i <= n; i ++ ) res = res * (mp[i] + 1) % mod;
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

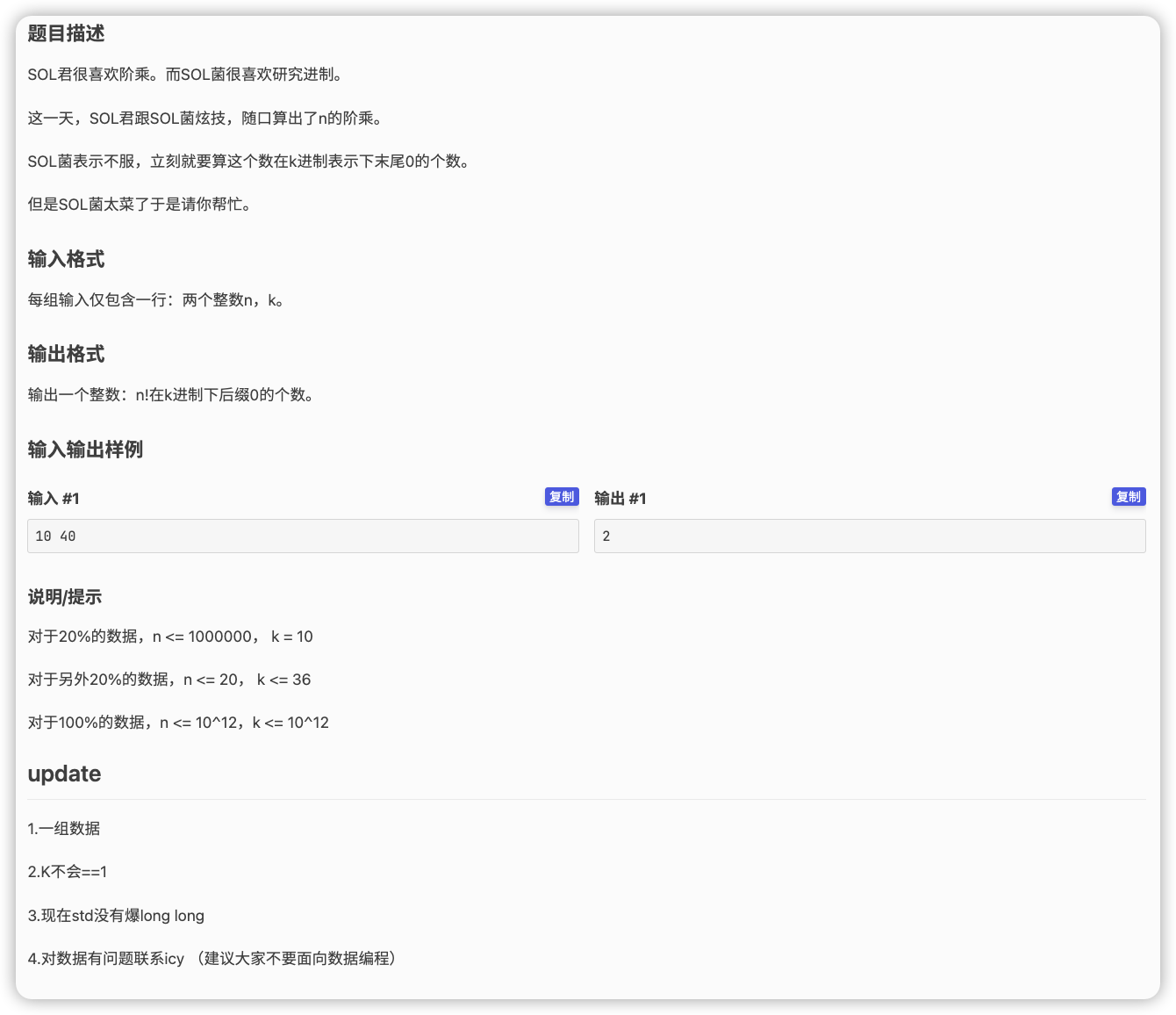
# 洛谷P3927_一道中档题Factorial

# 🔗

# 💡

一个数 $k$ 进制下末尾 $0$ 的数量，参考 $10$ 进制下末尾 $0$ 的数量的计算方式：统计 $2$ 和 $5$ 的数量
即需要知道待转换的数可以通过质因数拼成 $k$ 的几次方
现将 $k$ 分解为 $\prod\limits_{i} p_i^{a_i}$ ，那么对于每一个 $p_i$ 都要知道 $n!$ 中有几个 $p_i$ ，如果有 $b_i$ 个，可以通过它拼成 $\left\lfloor\frac{b_i}{a_i}\right\rfloor$ 个 $k$ 的幂，但是最终拼成数量是要靠他们一起维护的，故求所有的 $p_i$ 这个数量的最小值

对于一个 $p_i$ 的求法可以算有几个 $p_i^1$ 的倍数，有几个 $p_i^2$ 的倍数，设对于每一个 $p_i^j$ $n$ 以下有 $c_j$ 个倍数，则结果为 $\sum\limits_{j}c_j$ ，直接埃氏筛将第一层换成幂即可，对于每一个统计的 $p_i^j$ ，累加 $\left\lfloor\frac{n}{p_i^j}\right\rfloor$

# ✅

ll n, k; cin >> n >> k;

vector<pair<ll, ll> > need;
for (ll i = 2; i * i <= k; i ++) {
    if (k % i == 0) {
        ll num = 0;
        while (k % i == 0) {
            num ++;
            k /= i;
        }
        need.push_back({i, num});
    }
}
if (k > 1) need.push_back({k, 1});


ll res = 1e18;
for (auto [v, num] : need) {
    ll cur = 0;
    for (__int128_t i = v; i <= n; i *= v) {
        cur += n / i;
    }
    res = min(res, cur / num);
}

cout << res << endl;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

# 牛客2022寒假算法基础集训营4J_区间合数的最小公倍数

# 🔗

# 💡

$lcm(a,b)=\frac{a\times b}{(a,b)}$
本题需要注意，模意义下是无法 $gcd$ 的
即 $gcd(a,b)\neq gcd(a\%m,b)$
那么我们考虑 $gcd$ 的本质
即挑出 $a$ 和 $b$ 的所有共同的质因数的乘积
那么我们实时存入 $res$ 的所有质因数
然后与当前的合数质因数进行比对求解 $gcd$
求解的过程中顺便将当前的合数压缩下去再让 $res$ 直接乘
到最后需要将当前合数的质因数融入 $res$ 的质因数

# ✅

namespace primeNumber {
        const ll N = 3e4 + 10;
        vector<ll> prime;
        bool notprime[N];
        inline void Sieve () {
                notprime[0] = notprime[1] = 1; 
                for ( ll i = 2; i < N; i ++ ) {
                        if ( !notprime[i] ) prime.push_back(i);
                        for ( ll j = 0; j < prime.size() && i * prime[j] < N; j ++ ) {
                                notprime[i * prime[j]] = 1;
                                if ( i % prime[j] == 0 ) break;
                        }
                }
        }
} using namespace primeNumber;

ll l, r;
const ll mod = 1000000007;

inline ll gcd ( ll a, ll b ) { return b ? gcd(b, a % b) : a; }
inline ll ksm ( ll a, ll b ) { ll res = 1; while ( b ) { if ( b & 1 ) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv ( ll x ) { return ksm(x, mod - 2); }


int main () {
        ios::sync_with_stdio(false);

        Sieve();
        vector<ll> ntp;
        cin >> l >> r;
        for ( ll i = l; i <= r; i ++ ) {
                if ( !notprime[i] ) continue;
                ntp.push_back(i);
        }
        if ( !ntp.size() ) {
                cout << "-1" << endl;
                return 0;
        }
        ll res = ntp[0];
        
        // 分解 ntp[0]
        map<ll, ll> divres;
        ll tt = res;
        for ( ll j = 0; j < prime.size() && prime[j] * prime[j] <= tt; j ++ ) {
                while ( tt % prime[j] == 0 ) divres[prime[j]] ++, tt /= prime[j];
        }
        if ( tt > 1 ) divres[tt] ++;

        for ( ll i = 1; i < ntp.size(); i ++ ) {
                // 分解 ntp[i]
                map<ll, ll> divi;
                ll tmp = ntp[i];
                for ( ll j = 0; j < prime.size() && prime[j] * prime[j] <= tmp; j ++ ) {
                        while ( tmp % prime[j] == 0 ) divi[prime[j]] ++, tmp /= prime[j];
                }
                if ( tmp > 1 ) divi[tmp] ++;

                // 缩小 ntp[i]
                for ( auto kk : divi ) {
                        ll k = kk.first;
                        ntp[i] /= ksm(k, min(divi[k], divres[k]));
                }

                // 计算 lcm
                res = res * ntp[i] % mod;

                // 融合 res 质因数
                for ( auto kk : divi ) {
                        if ( kk.second > divres[kk.first] ) divres[kk.first] += kk.second - divres[kk.first];
                }
        }
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

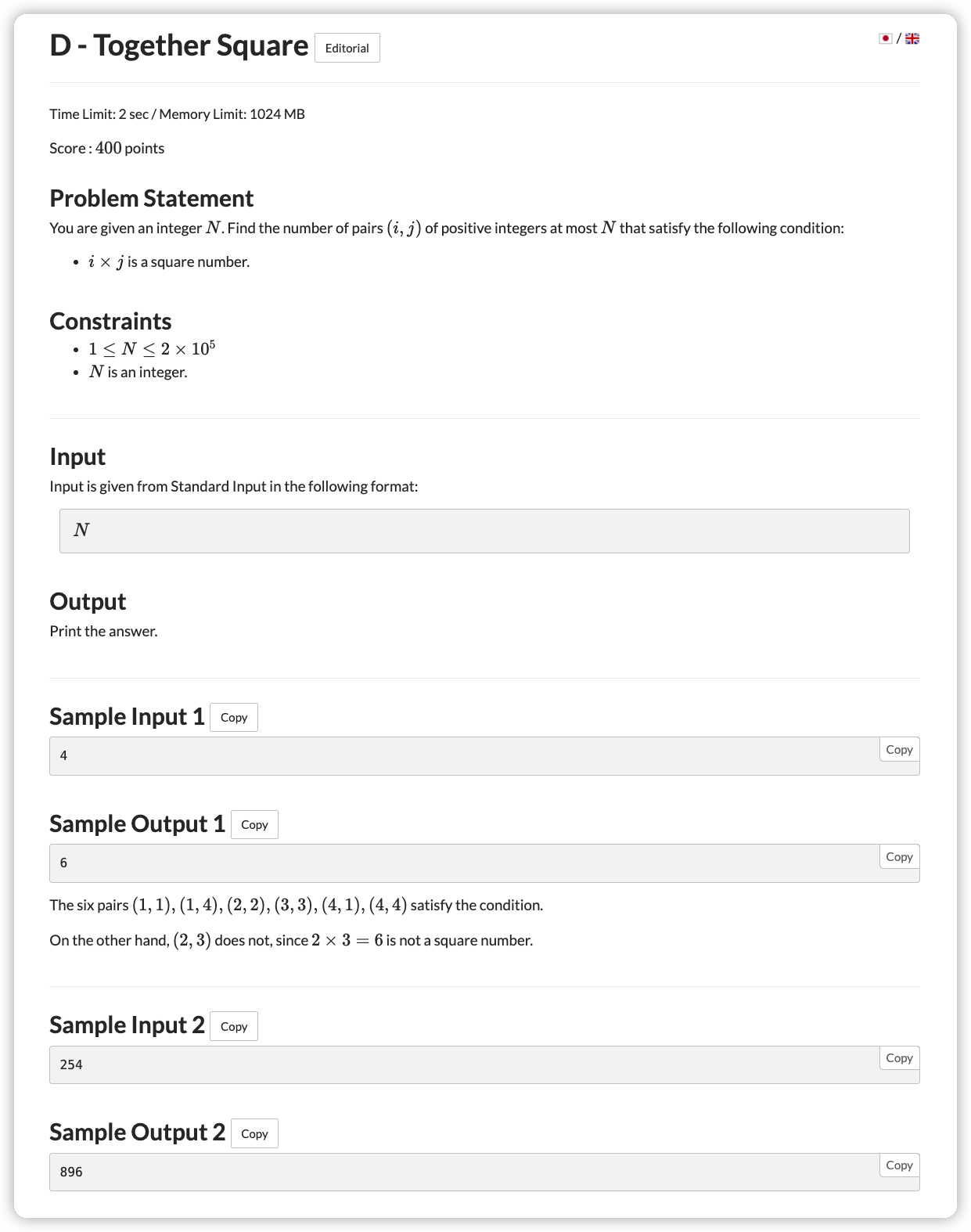
# ABC254D_TogetherSquare

# 🔗

# 💡

首先应该考虑到的是，偶数个质因子可以自己成为一个平方数
那么对于 $i$ ，我们对每个质因子去掉最大的偶数个后成为 $i'$ ，对于 $j$ ，我们进行同样的操作形成 $j'$
如果要 $i\times j$ 是平方数，那么 $i'=j'$ ，因为要保证剩下的单个质因子一一对应
所以我们对于 $[1,n]$ 中的每一个数 $i$ 都让 $num[i']+1$
这样我们在最后就可以对 $i'$ 相同的数进行配对了

# ✅

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);
 
        int n; cin >> n;
        map<int, int> mp;
        for (int i = 1; i <= n; i ++) {
                int ii = i;
                for (int j = 2; j * j <= ii; j ++) {
                        int iii = ii;
 
                        int cnt = 0;
                        while (iii % j == 0) iii /= j, cnt ++;
                        int eve_cnt = cnt / 2 * 2;
                        iii = ii;
                        while (eve_cnt --) ii /= j;
                }
                mp[ii] ++;
        }
 
        ll res = 0;
        for (auto i : mp) {
                res += 1ll * i.second * i.second;
        }
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

# ABC254F_RecangleGCD

# 🔗

# 💡

注意到如果是直接每一个位置受到两个数组影响的 $gcd$ 很难去优化
所以我们想让 $a_i+b_j$ 变成 $a_i$ 或者 $b_j$ 这样的
这里是加，我们就要用一个减，考虑 $gcd$ 有减法的性质： $gcd(x,y)=gcd(x,x-y)$
那么用其推一下普通的式子看看
$\begin{aligned} &\gcd\limits_{i=1}^2\gcd\limits_{j=1}^2(a_i+b_j)\\ =&\gcd(\gcd(a_1+b_1,a_1+b_2),\gcd(a_2+b_1,a_2+b_2))\\ =&\gcd(\gcd(a_1+b_1,b_1-b_2),\gcd(a_2+b_1,b_1-b_2))\\ =&\gcd(a_1+b_1,a_2+b_1,b_1-b_2)\\ =&\gcd(a_1+b_1,b_1-b_2,a_1-a_2) \end{aligned}$ 这样就消掉了
朴素下来就是：对于查询 $[h1,h2,w1,w2]$ ，我们计算 $\gcd(a_{h1}+b_{w1},\gcd\limits_{i=h1+1}^{h2}(a_i-a_{i-1}),\gcd\limits_{i=w1+1}^{w2}(b_i-b_{i-1}))$ 即可
后面两个 $\gcd$ 可以直接区间查询

# ✅

const int N = 2e5 + 10;
 
int n, q;
int st[2][N][30];
int a[N], b[N];
 
inline int gcd (int a, int b) { return abs(b ? gcd(b, a % b) : a); }
inline void Build () {
        int k = 32 - __builtin_clz(n) - 1;
        for (int j = 1; j <= k; j ++) {
                for (int i = 1; i + (1 << j) - 1 <= n; i ++) {
                        st[0][i][j] = gcd(st[0][i][j - 1], st[0][i + (1 << (j - 1))][j - 1]);
                        st[1][i][j] = gcd(st[1][i][j - 1], st[1][i + (1 << (j - 1))][j - 1]);
                }
        }
}
inline int Query (int l, int r, int op) {
        int k = 32 - __builtin_clz(r - l + 1) - 1;
        return gcd(st[op][l][k], st[op][r - (1 << k) + 1][k]);
}
 
int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);
 
        cin >> n >> q;
        for (int i = 1; i <= n; i ++) cin >> a[i], st[0][i][0] = a[i] - a[i - 1];
        for (int i = 1; i <= n; i ++) cin >> b[i], st[1][i][0] = b[i] - b[i - 1];
 
        Build();
 
        while (q --) {
                int h1, h2, w1, w2; cin >> h1 >> h2 >> w1 >> w2;
                int res = a[h1] + b[w1];
                if (h1 < h2) res = gcd(res, Query(h1 + 1, h2, 0));
                if (w1 < w2) res = gcd(res, Query(w1 + 1, w2, 1));
                cout << res << endl;
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

# CodeForces1445C_Division

# 🔗

https://codeforces.com/problemset/problem/1445/C

# 💡

既然a是x的倍数，x就一定可以是a变来的，b不能是x的因数，就转化为了探究a和b关系的一道题。
b不能是x的因数，则保证了x中不能有b的所有(相同也算)质因数，所以x是由a除掉b的某个质因数的一部分得来的。
于是我们对b拆解质因数，并在a除这种质因数时判断除到什么程度了a不是b的倍数，最大的就是x

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'

#define CHIVAS_ int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
//#define map unordered_map

#define _int(a) int a; cin >> a
#define  _ll(a) ll a; cin >> a
#define _char(a) char a; cin >> a
#define _string(a) string a; cin >> a
#define _vectorInt(a, n) vector<int>a(n); cin >> a
#define _vectorLL(a, b) vector<ll>a(n); cin >> a

#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cass = inputInt(); cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
template<typename T>             vector<T>& operator--            (vector<T> &v){for (auto& i : v) --i;            return  v;}
template<typename T>             vector<T>& operator++            (vector<T> &v){for (auto& i : v) ++i;            return  v;}
template<typename T>             istream& operator>>(istream& is,  vector<T> &v){for (auto& i : v) is >> i;        return is;}
template<typename T>             ostream& operator<<(ostream& os,  vector<T>  v){for (auto& i : v) os << i << ' '; return os;}
inline int inputInt(){int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);}
inline void outInt(int X){if(X<0) {putchar('-'); X=~(X-1);}int s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline ll inputLL(){ll X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1); }
inline void outLL(ll X){if(X<0) {putchar('-'); X=~(X-1);}ll s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}

void solve()
{
        ll a = inputLL(), b = inputLL();
        vector<ll> vec; //存放质因数
        if (a < b) {     //特殊情况，不需要分了，已经满足了
                outLL(a), puts("");
                return;
        }
        ll cur_b = b; //替代b
        for (ll i = 2; i * i <= cur_b; i++){
                if (cur_b % i) continue;
                while (cur_b % i == 0) cur_b /= i;
                vec.push_back(i);
        }
        if (cur_b > 1) vec.push_back(cur_b);
        ll ans = 0; //记录结果并维护最大值
        for (ll i = 0; i < (ll)vec.size(); i++){
                ll x = a;
                //若a是b的倍数，a把b的某个质因数除完(非最优)就不是它的倍数了，看看除到第几个就不是了
                while (x % vec[i] == 0 && x % b == 0) x /= vec[i];
                ans = max(ans, x);
        }
        outLL(ans);
}
CHIVAS_{
        int cass;
        EACH_CASE(cass){
                solve();
        }
        _REGAL;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118

# CodeForces1593D2_HalfOfSame

# 🔗

# 💡

这道题是让一半的数一样
那么就在差值上做文章

首先还是个特判，如果已经有一半以上都是一样的话那么就是-1
然后枚举基点是谁
对基点以后的数求一下他们与基点的差值
0特殊记录一下因为这代表与基点相同的点，并塞到一个计数变量cnt内

对每个差值统计一下因数k，因为每个因数都可以让这个差值变成0
枚举的过程中，如果出现一个因数出现的个数+cnt超过一半了，那么就维护一下答案的最大值
但要记得也去统计另一个因数dir/k并且满足条件了话就维护

# ✅

const int N = 300;
int a[N], dir[N];
map<int, int> mp;

inline void Solve() {
        mp.clear();
        int n; cin >> n;
        for ( int i = 0; i < n; i ++ ) cin >> a[i], mp[a[i]] ++;
        for ( int i = 0; i < n; i ++ ) if ( mp[a[i]] >= n / 2 ) { cout << "-1" << endl; return; }
        sort ( a, a + n );
        
        int res = -1;

        for ( int i = 0; i < n / 2 + 1; i ++ ) {
                int samecnt = 0; mp.clear();
                for ( int j = i; j < n; j ++ ) {
                        samecnt += a[j] == a[i];
                        dir[j] = a[j] - a[i];
                }
                for ( int j = i; j < n; j ++ ) {
                        if ( dir[j] == 0 ) continue;
                        for ( int k = 1; k * k <= dir[j]; k ++ ) {
                                if ( dir[j] % k == 0 ) {
                                        mp[k] ++;
                                        if ( mp[k] + samecnt >= n / 2 ) res = max ( res, k );
                                        if ( k * k != dir[j] ) {
                                                mp[dir[j] / k] ++;
                                                if ( mp[dir[j] / k] + samecnt >= n / 2 ) res = max ( res, dir[j] / k );
                                        } 
                                }
                        }
                }
        }        
        cout << res << endl;
}

int main () {
        ios::sync_with_stdio(false);
        ll cass; cin >> cass; while ( cass -- ) {
                Solve();
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

# DaimayuanOnlineJudge131_最大公约数

# 🔗

# 💡

如果分成 $k$ 段，第 $i$ 段的和是 $sum[i]$ ，他们的最大公因数为 $p$ ，说明 $p|sum[1],p|sum[2],...,p|sum[k]$ ，说明 $p|\sum sum[i]$ ，说明 $p|SUM$
同时另一条线是，如果令 $pre[i]$ 表示 $i$ 的前缀和，分段的和也就是他们分段之间的相邻差，相邻差是 $p$ 的倍数说明它们模 $p$ 同余
所以答案是 $SUM$ 的因数之一，每一个因数最多可分段数为模 $k$ 相等的 $pre[i]$ 中最多的数量
打个表发现 $SUM$ 的因数不会非常多，故统计完所有的因数后可以对每一个因数都跑一遍，拿 $map$ 存余数，最后可以统计出来每一个因数最多可以分割的段数 $times[]$
然后求 $k$ 的答案时，找到最大的因数 $i$ ，满足 $times[i]\ge k$

# ✅

const int N = 2010;
int n;
ll a[N], pre[N], sum;
int times[N];

int main () {
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++) 
        scanf("%lld", &a[i]),
        pre[i] = pre[i - 1] + a[i],
        sum += a[i];
    
    vector<ll> sep;
    for (int i = 1; 1ll * i * i <= sum; i ++) {
        if (sum % i == 0) {
            sep.push_back(i);
            if (i != sum / i) sep.push_back(sum / i);
        }
    }
    sort(sep.begin(), sep.end());

    for (int i = 0; i < sep.size(); i ++) {
        map<ll, int> mp;
        for (int j = 1; j <= n; j ++) mp[pre[j] % sep[i]] ++;
        for (auto it : mp) times[i] = max(times[i], it.second);
    }
    for (int k = 1; k <= n; k ++) {
        for (int i = sep.size() - 1; i >= 0; i --) {
            if (times[i] >= k) {
                printf("%lld\n", sep[i]);
                break;
            }
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

# HDU2021多校(6)1_YesPrimeMinister

# 🔗

# 💡

首先分析一下等差数列求和公式： $\frac{(l+r)*(r-l+1)}{2}$
如果正数超过两项，则必然会产生一个因数，所以只有正数三项不行

先考虑一项：
1.就是n是质数的情况，就输出1
然后考虑两项：
2.首先是只有两个数，即(n-1)+n和(n+1)+n有一个是质数，就可以输出2
3.然后是正数部分多出来两个数，就是从i=n+1开始往后找，如果i+(i+1)是质数，就需要i*2+1长度的数列

然后考虑暴力数列和为一项：
4.可以预处理出来素数表后，找出第一个比n大的质数p，这个答案是p*2

在非1、2情况下拿3和4出的答案进行比较，输出较小的那个

# ✅

namespace primeNumber {
        const int N = 5e7 + 10;
        vector<int> prime;
        bool notprime[N];
        inline void Sieve () {
                notprime[0] = notprime[1] = 1; 
                for ( int i = 2; i < N; i ++ ) {
                        if ( !notprime[i] ) prime.push_back(i);
                        for ( int j = 0; j < prime.size() && i * prime[j] < N; j ++ ) {
                                notprime[i * prime[j]] = 1;
                                if ( i % prime[j] == 0 ) break;
                        }
                }
        }
} using namespace primeNumber;

inline void Solve () {
        int n; cin >> n;
        if ( n > 0 && notprime[n] == 0 ) { cout << 1 << endl; return; } 
        if ( n > 0 && (notprime[n + n + 1] == 0 || notprime[n + n - 1] == 0) ) { cout << 2 << endl; return; }

        int res = prime[upper_bound(prime.begin(), prime.end(), abs(n)) - prime.begin()] * 2;
        for ( int i = abs(n) + 1; i * 2 + 1 < N; i ++ ) {
                if ( notprime[i * 2 + 1] == 0 ) { cout << min(res, i * 2 + 1) << endl; return;}
        }
        cout << res << endl;
}

int main () {
        ios::sync_with_stdio(false);
        Sieve();
        int cass; cin >> cass; while ( cass -- ) {
                Solve();
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

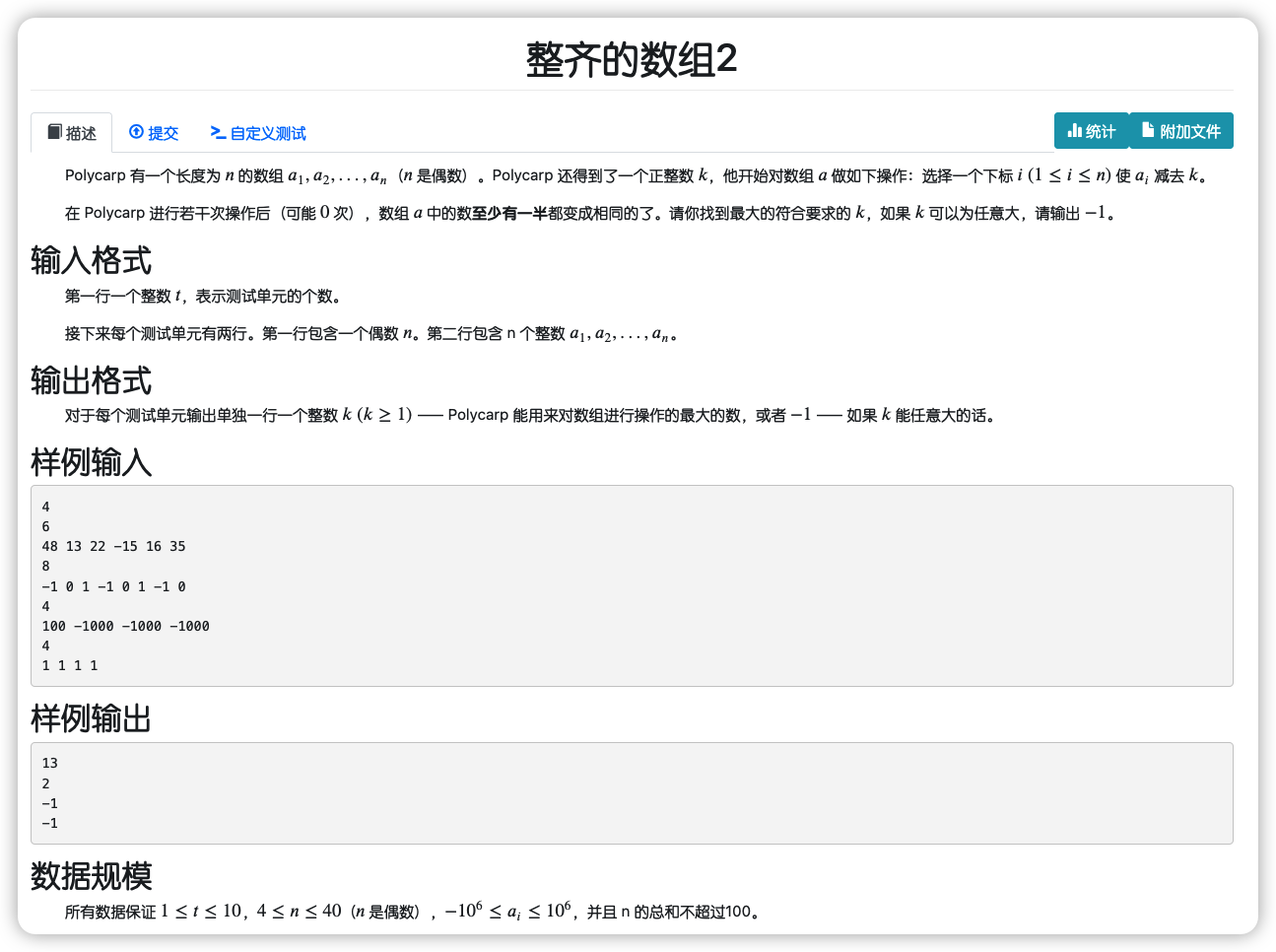
# NamomoCamp2022春季div1每日一题_整齐的数组2

# 🔗

# 💡

思考 $a,b$ 每次减 $k$ 什么条件才有可能减到相同
即 $a-b\equiv0(mod\;k)$ ，也是 $a\equiv b(mod\;k)$
那么我们去收集一下每个 $a_i-a_j$ 的因数
对每个因数统计 $a_i\% k$ 的个数
如果出现一个个数 $\ge \frac n2$
那么就意味着可以选这个因数
走完所有的我们收集的因数维护最大值即可

# ✅

const int N = 50;
int n;
int a[N];
int num[2000006];

inline void Solve () {
        cin >> n;
        for ( int i = 1; i <= n; i ++ ) cin >> a[i];
        sort ( a + 1, a + 1 + n ); a[0] = a[1];
        for ( int i = 1; i <= n; i ++ ) a[i] -= a[0] - 1;

        set<int> dif_set;
        for ( int i = 1; i <= n; i ++ ) {
                for ( int j = i + 1; j <= n; j ++ ) {
                        if ( a[j] == a[i] ) continue;
                        int dif = a[j] - a[i];
                        for ( int p = 1; p * p <= dif; p ++ ) {
                                if ( dif % p == 0 ) 
                                        dif_set.insert(p),
                                        dif_set.insert(dif / p);
                        }
                }
        }
        dif_set.insert(2000001);

        int res = -1e6;
        for ( int k : dif_set ) {
                for ( int i = 1; i <= n; i ++ ) num[a[i] % k] ++;
                bool flag = false;
                for ( int i = 1; i <= n; i ++ ) {
                        if ( num[a[i] % k] >= n / 2 ) flag = true;
                        num[a[i] % k] = 0;
                }
                if ( flag ) res = k;
        }
        if ( res == 2000001 ) cout << "-1\n";
        else cout << res << "\n";
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

# 欧拉函数

# 洛谷P2158_仪仗队

# 🔗

https://www.luogu.com.cn/problem/P2158

# 💡

每个能被看到的点的gcd(x, y) = 1

将正方形分成两个三角形
对于每个三角形
寻找互质数即可
所以
$res=\sum\limits_1^{n-1}phi(i)\quad*2+1$

# ✅

#pragma region
/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <utility>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'

#define CHIVAS int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
#define map unordered_map

#define PB(x) push_back(x)
#define ALL(a) ((a).begin(),(a).end())
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cin >> cass; cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? gcd(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}

#pragma endregion

//全局变量
#pragma region
const int maxn = 40010;
bool isprime[maxn];
int prime[maxn];
int phi[maxn];
int cnt = 0;
#pragma endregion

//主体------------------------------------------

inline void GET_PHI(){
    phi[1] = 1;
    for(int i = 2; i <= maxn; i ++){
        if(!isprime[i]) prime[++cnt] = i, phi[i] = i - 1;
        for(int j = 1; j <= cnt && i * prime[j] <= maxn; j ++){
            isprime[i * prime[j]] = true;
            if(i % prime[j] == 0){
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            }else phi[i * prime[j]] = phi[i] * (prime[j] - 1);
        }
    }
}

CHIVAS{
    GET_PHI();
    int n; cin >> n;
    int res = 0;
    for(int i = 1; i < n; i ++) res += phi[i];
    cout << (n == 1? 0 : (res << 1 | 1)) << endl;
    _REGAL;
}

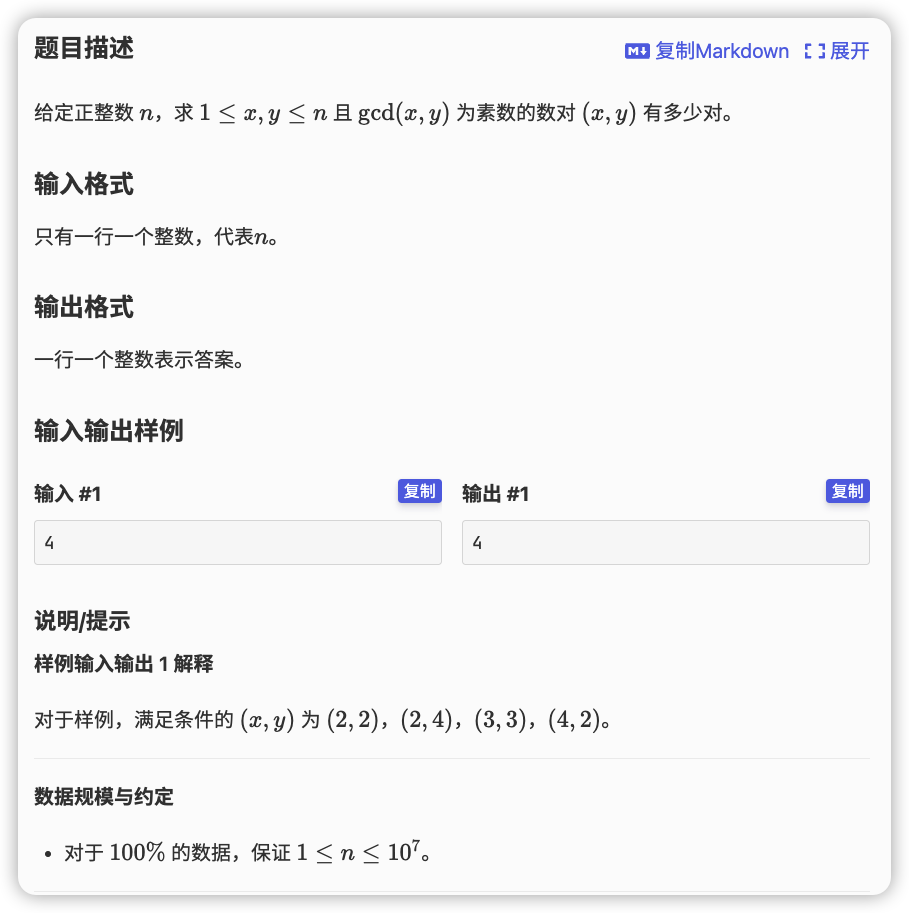
# 洛谷P2398_GCDSUM

# 🔗

# 💡

$\begin{aligned}&\sum\limits_{i=1}^n\sum\limits_{j=1}^ngcd(i,j)\\=&\sum\limits_{k=1}^nk\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}[gcd(i,j)=k]\\=&\sum\limits_{k=1}^nk\sum\limits_{i=1}^{\left\lfloor\frac nk\right\rfloor}\sum\limits_{j=1}^{\left\lfloor\frac nk\right\rfloor}[gcd(i,j)=1]\end{aligned}$

在转化完之后变成了在 n / k 内求两个数互质的个数
那么可以利用欧拉函数，不重复地计算任选两个数互质的个数，即1~n/k的phi和
由于每个数的区间都一样所以会重复，就是将当前答案*2，减去重复的(1,1)
对每一个结果乘k累加

当然每次求1~n/k的phi和都可以预先前缀和处理一下

# ✅

namespace Number {
        const ll N = 2e6 + 10;
        bool notprime[N];
        ll phi[N];
        vector<ll> prime;
        ll sum[N];

        inline void Sieve () {
                notprime[1] = notprime[0] = phi[1] = 1;
                for ( ll i = 2; i < N; i ++ ) {
                        if ( !notprime[i] ) 
                                prime.push_back(i),
                                phi[i] = i - 1;
                        for ( ll j = 0; j < prime.size() && i * prime[j] < N; j ++ ) {
                                notprime[i * prime[j]] = 1;
                                if ( i % prime[j] == 0 ) { phi[i * prime[j]] = phi[i] * prime[j]; break; }
                                else                     phi[i * prime[j]] = phi[i] * (prime[j] - 1);
                        }
                }
                for ( ll i = 1; i < N; i ++ ) sum[i] = sum[i - 1] + phi[i];
        }
} using namespace Number;

int main () {
        ios::sync_with_stdio(false); Sieve ();
        ll n; cin >> n;
        ll res = 0;
        for ( ll k = 1; k <= n; k ++ ) {
                res += k * (sum[n / k] * 2 - 1);
        }
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

# 洛谷P2568_GCD

# 🔗

# 💡

公式转化：

$\begin{aligned} &\sum\limits_{i=1}^n\sum\limits_{j=1}^n[(i,j)\in p]\\ =&\sum\limits_{d\in p}\sum\limits_{i=1}^n\sum\limits_{j=1}^n[(i,j)=d]\\ =&\sum\limits_{d\in p}\sum\limits_{i=1}^{\frac nd}\sum\limits_{j=1}^{\frac nd}[(i,j)=1] \end{aligned}$
注意到后面这两重连加很像欧拉函数的意义，让 $j$ 枚举到 $i$ ，就是欧拉函数了
不过需要乘二表示 $ij$ 谁大谁小都可以，但是 $i=j=1$ 的情况乘二贡献也被乘了二，所以还要再减一
即
$\sum\limits_{d\in p}(2\sum\limits_{i=1}^{\frac nd}\phi(i)-1)$
其中 $\sum\limits_{i=1}^{\frac nd}\phi(i)$ 预处理一下前缀和或者从小到大动态累加（ $d$ 从大到小）

# ✅

const int N = 1e7 + 10;
bool ntp[N];
ll phi[N];
vector<int> prime;
inline void Sieve () {
        phi[1] = ntp[0] = ntp[1] = 1;
        for (int i = 2; i < N; i ++) {
                if (!ntp[i]) prime.push_back(i), phi[i] = i - 1;
                for (int j = 0; j < prime.size() && i * prime[j] < N; j ++) {
                        ntp[i * prime[j]] = 1;
                        if (i % prime[j] == 0) {
                                phi[i * prime[j]] = phi[i] * prime[j];
                                break;
                        }
                        phi[i * prime[j]] = phi[i] * (prime[j] - 1);
                }
        }
}
int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);
        Sieve();
        
        int n; cin >> n;
        
        ll sum = 0; int idx = 0;
        ll res = 0;
        for (int i = upper_bound(prime.begin(), prime.end(), n) - prime.begin() - 1; i >= 0; -- i) {
                int d = prime[i];
                while (idx < n / d) sum += phi[++idx];
                res += sum * 2 - 1;
        }
        cout << res << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

# 洛谷P3601_签到题

# 🔗

# 💡

首先要清楚 $i$ 以下不与 $i$ 互质的数的个数为 $i-\phi(i)$
那么问题就是 $\frac{(l+r)(r-l+1)}{2}-\sum\limits_{i=l}^r\phi(i)$
注意到 $r-l\le 10^6$ 这肯定是想让我们求出来这里面的所有欧拉函数
一个常识是 $\le\sqrt{r}$ 的素数可以分解 $[l,r]$ 内的所有质因子（这也是 $\sqrt{n}$ 可以求 $n$ 的质因数的道理）
所以先筛出来 $\le 10^6$ 的所有质数，然后埃氏筛去跑一遍 $[l,r]$ ，进行欧拉函数的求解
注意可能含有大质数，所以最后要单独跑一遍 $[l,r]$ 看看有没有除完所有的小质数后没有到 $1$ 的数，如果有就说明有大质因数，再用这个质数求一下它的欧拉函数即可
最后暴力累加

# ✅

const int N = 1e6 + 10;

vector<int> prime;
bool ntp[N];
inline void Sieve () {
    ntp[0] = ntp[1] = 1;
    for (int i = 2; i < N; i ++) {
        if (!ntp[i]) prime.push_back(i);
        for (int j = 0; j < prime.size() && 1ll * i * prime[j] < N; j ++) {
            ntp[i * prime[j]] = 1;
            if (i % prime[j] == 0) break;
        }
    }
}

ll num[N];
ll phi[N];

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    Sieve();

    ll l, r; cin >> l >> r;    
    for (ll i = l; i <= r; i ++) {
        num[i - l] = i;
        phi[i - l] = i;
    }

    for (int p : prime) {
        for (ll j = (l + p - 1) / p * p; j <= r; j += p) {
            phi[j - l] = phi[j - l] / p * (p - 1);
            while (num[j - l] % p == 0) num[j - l] /= p;
        }
    }
    for (ll i = l; i <= r; i ++) {
        if (num[i - l] > 1) {
            phi[i - l] = phi[i - l] / num[i - l] * (num[i - l] - 1);
        }
    }

    ll res = (l + r) * (r - l + 1) / 2;
    for (ll i = l; i <= r; i ++) {
        res -= phi[i - l];
    }
    cout << res % 666623333 << endl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

# 牛客2022寒假算法基础集训营1D_牛牛做数论

# 🔗

# 💡

对于题目中给的 $\frac{\phi(n)}{n}$ 得出这个函数不会到达 $1$

对于第二问，我们让他越逼近 $1$ 越好，所以我们肯定选 $n$ 以下最大的质数
对于第一问
思考一下欧拉函数积性函数的性质和除法结合： $\frac{\phi(n\times m)}{n\times m}=\frac{\phi(n)}{n}\times\frac{\phi(m)}{m}$ 当且仅当 $gcd(n,m)=1$
由于他们的乘积在互质下越来越小，所以我们选所有 $n$ 以下的质数，让它们相乘不超过 $n$ 即可

暴力就可以写

# ✅

inline bool is_Prime ( ll x ) {
        for ( ll i = 2; i * i <= x; i ++ ) {
                if ( x % i == 0 ) {
                        return false;
                }
        }
        return true;
}

int main () {
        ios::sync_with_stdio(false);
        ll cass; cin >> cass; while ( cass -- ) {
                ll n; cin >> n;
                if ( n == 1 ) {
                        cout << "-1" << endl;
                } else {
                        ll mx_prime = n;
                        for ( ; mx_prime >= 2; mx_prime -- ) if ( is_Prime(mx_prime) ) break;
                        ll mul_prime = 1;
                        for ( int i = 2; i <= n; i ++ ) {
                                if ( is_Prime(i) ) {
                                        if ( mul_prime * i <= n ) mul_prime *= i;
                                        else break;
                                }
                        }
                        cout << mul_prime << ' ' << mx_prime << endl;
                }
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

# CodeForces1654D_PotionBrewingClass

# 🔗

# 💡

在本题中，如果可以确定一个数，那么别的数也就出来了
注意到这是一个树

第一遍 $DFS$ :
那么我们可以设计一个根节点，然后通过将路上的分子乘起来从而确定根节点的值
考虑到要最小，所以我们可以最后的时候通过求所有数的 $gcd$ 来化简
但是这是一个带模的数，所以我们需要通过 map 存每个数的质因数来让我们最后可以求出来 $gcd$

第二遍 $DFS$ :
我们已经有了根节点的值，那么可以通过乘分数的方式推出来所有数的值
但这一遍 $DFS$ 还有一个要做的事情就是确定 $gcd$ ，那么要通过求得所有的数的质因数来确定
打表出来所有的 map 不合适，map复制是 $O(nlogn)$ 的时间复杂度，但是 $DFS$ 的回溯特性，可以只设计一个 map ，然后在每一层操作完向下递推后将操作复原
每一个 $DFS$ 节点都取一下 $d$ 的最小值也不现实
后面 $d$ 的质因数可能会非常多，但是考虑到在和分母约分的过程中会让 $gcd$ 质因数变少，可以在一个 map 路上和分母约分的时候化简 $gcd$ 的质因数表即可

路上累加所有的 res_map ，最后再除一下 $gcd$ 的质因数表组成的数即可

# ✅

const int N = 2e5 + 10;
const int M = 4e5 + 10;
const int mod = 998244353;
inline ll ksm ( ll a, ll b ) { ll res = 1; while ( b > 0 ) { if ( b & 1 ) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv ( ll x ) { return ksm(x, mod - 2); }

namespace primeNumber {
        vector<int> prime;
        bool notprime[N];
        inline void Sieve () {
                notprime[0] = notprime[1] = 1; 
                for ( int i = 2; i < N; i ++ ) {
                        if ( !notprime[i] ) prime.push_back(i);
                        for ( int j = 0; j < prime.size() && i * prime[j] < N; j ++ ) {
                                notprime[i * prime[j]] = 1;
                                if ( i % prime[j] == 0 ) break;
                        }
                }
        }
} using namespace primeNumber;
vector<pair<int, int> > factor_table[N]; // 每个数的质因数表
ll invv[N];
inline void main_Pre () { // 预处理逆元与质因数表
        Sieve(); invv[1] = inv(1);
        for ( int i = 2; i < N; i ++ ) {
                int tmp = i;
                for ( int j = 0; prime[j] * prime[j] <= tmp; j ++ ) {
                        if ( tmp % prime[j] == 0 ) {
                                int num = 0;
                                while ( tmp % prime[j] == 0 ) num ++, tmp /= prime[j];
                                factor_table[i].push_back({prime[j], num});
                        }
                }
                if ( tmp > 1 ) factor_table[i].push_back({tmp, 1});
                invv[i] = inv(i);
        }
}
inline void Division ( map<int, int> &mp, int val ) { // 质因数表为mp的数 除val
        for ( auto [x, y] : factor_table[val] ) 
                mp[x] -= y;
}
inline void Multiply ( map<int, int> &mp, int val ) { // 质因数表为mp的数 乘val
        for ( auto [x, y] : factor_table[val] ) 
                mp[x] += y;
}
inline ll toNumber ( map<int, int> mp ) { // 返回质因数表为mp的数
        ll res = 1;
        for ( auto [x, y] : mp ) res = res * ksm(x, y) % mod;
        return res;
}
inline ll mul_Fraction ( ll x, ll up, ll down ) { // x * 分数(up/down)
        return x * up % mod * invv[down] % mod;
}

struct Edge {
        int nxt, to;
        int up, down;
} edge[M];
int head[N], cnt;
inline void add_Edge ( int from, int to, int up, int down ) {
        edge[++cnt] = { head[from], to, up, down };
        head[from] = cnt;
}

// ------------------------------------------------------------------------------------------------------------------------------------------------

ll res_val[N]; // 所有数的值
map<int, int> res_map; // 所有数的值的质因数表
inline void DFS ( int u, int fa ) {
        for ( int i = head[u], v = edge[i].to; i; i = edge[i].nxt, v = edge[i].to ) { if ( v == fa ) continue;
                DFS(v, u);
                Multiply(res_map, edge[i].up);
        }
}


map<int, int> gcd_map; // 最大公因数的质因数表

inline void getRES ( int u, int fa ) {
        for ( int i = head[u], v = edge[i].to; i; i = edge[i].nxt, v = edge[i].to ) { if ( v == fa ) continue;
                int up = edge[i].down, down = edge[i].up; 

                Multiply(res_map, up);
                Division(res_map, down);

                for ( auto [x, y] : factor_table[down] ) gcd_map[x] = min(gcd_map[x], res_map[x]);
                res_val[v] = mul_Fraction(res_val[u], up, down);
                getRES(v, u);

                Division(res_map, up);
                Multiply(res_map, down);
        }
};

inline void Solve () {
        int n; scanf("%d", &n);
        for ( int i = 1; i < n; i ++ ) {
                int u, v, up, down;
                scanf("%d%d%d%d", &u, &v, &up, &down);
                function <int(int, int)> gcd = [&gcd](int a, int b) { return b ? gcd(b, a % b) : a; };
                int d = gcd(up, down); up /= d, down /= d;
                add_Edge(u, v, up, down);
                add_Edge(v, u, down, up);
        }

        DFS(1, 0);
        res_val[1] = toNumber(res_map);
        gcd_map = res_map; 
        getRES(1, 0); 

        ll gcd_res = toNumber(gcd_map), iv_gcd_res = inv(gcd_res);       
        ll RES = 0; for ( int i = 1; i <= n; i ++ ) RES = (RES + res_val[i] * iv_gcd_res % mod) % mod;
        printf("%lld\n", RES); 

        for ( int i = 0; i <= n; i ++ ) head[i] = 0; cnt = 0;
        gcd_map.clear(); res_map.clear();
}

int main () {
        main_Pre(); 
        int cass; scanf("%d", &cass); while ( cass -- ) {
                Solve ();
        }
}

# HDUOJ2588_GCD

# 🔗

https://acm.dingbacode.com/showproblem.php?pid=2588

# 💡

我们可以转化一下, $gcd(i,n)=a\Longrightarrow gcd(\frac ia,\frac na)=1$
我们枚举的是 n 的大于等于 m 的因子(a)
此时在这个位置上个数就是 $\phi(\frac na)$
由于因数都是成对出现的，所以我们只需遍历一边因子，即从 1 到 $\sqrt{n}$ 即可

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'

#define CHIVAS_ int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
//#define map unordered_map

#define _int(a) int a; cin >> a
#define  _ll(a) ll a; cin >> a
#define _char(a) char a; cin >> a
#define _string(a) string a; cin >> a
#define _vectorInt(a, n) vector<int>a(n); cin >> a
#define _vectorLL(a, b) vector<ll>a(n); cin >> a

#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cass = inputInt(); cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
template<typename T>             vector<T>& operator--            (vector<T> &v){for (auto& i : v) --i;            return  v;}
template<typename T>             vector<T>& operator++            (vector<T> &v){for (auto& i : v) ++i;            return  v;}
template<typename T>             istream& operator>>(istream& is,  vector<T> &v){for (auto& i : v) is >> i;        return is;}
template<typename T>             ostream& operator<<(ostream& os,  vector<T>  v){for (auto& i : v) os << i << ' '; return os;}
inline int inputInt(){int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);}
inline void outInt(int X){if(X<0) {putchar('-'); X=~(X-1);}int s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline ll inputLL(){ll X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1); }
inline void outLL(ll X){if(X<0) {putchar('-'); X=~(X-1);}ll s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}

inline ll phi(ll x){ // 数比较大，直接求
        ll res = x;
        for(ll i = 2; i * i <= x; i ++){
                if(x % i == 0) res -= res / i;
                while(x % i == 0) x /= i;
        }
        if(x > 1) res -= res / x;
        return res;
}

CHIVAS_{
        int cass;
        EACH_CASE(cass){
                ll n = inputLL(), m = inputLL();
                ll res = 0;
                for(ll i = 1; i * i <= n; i ++){
                        if(n % i) continue;
                        if(i >= m) res += phi(n / i); // 枚举大于m的n的倍数
                        if(n / i >= m && i * i != n) res += phi(i); // 枚举大于m的n的倍数
                }
                outLL(res); puts("");
        }
        _REGAL;
};

# POJ1284_PrimitiveRoots

# 🔗

http://poj.org/problem?id=1284

# 💡

原根的一个知识点
每个数x的原根个数为phi[phi[x]]

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <utility>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'

#define CHIVAS int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
#define map unordered_map

#define PB(x) push_back(x)
#define ALL(a) ((a).begin(),(a).end())
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cin >> cass; cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? gcd(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}

#pragma endregion

//全局变量
#pragma region
const int maxn = 70000;
int cnt = 0;
int phi[maxn];
int prime[maxn];
int isprime[maxn];

#pragma endregion

//主体------------------------------------------

inline void GET_PHI(){
    phi[1] = 1;
    for(int i = 2; i <= maxn; i ++){
        if(!isprime[i]) prime[++cnt] = i, phi[i] = i - 1;
        for(int j = 1; j <= cnt && i * prime[j] <= maxn; j ++){
            isprime[i * prime[j]] = 1;
            if(i % prime[j] == 0){
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            }else phi[i * prime[j]] = phi[i] * (prime[j] - 1);
        }
    }
}

CHIVAS{
    ll n;
    GET_PHI();
    while(cin >> n) cout << phi[phi[n]] << endl;
    _REGAL;
}

# POJ2407_Relatives

# 🔗

http://poj.org/problem?id=2407

# 💡

欧拉函数的模板
只需要求欧拉值即可

# ✅

#pragma region
/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <utility>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'

#define CHIVAS int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
#define map unordered_map

#define PB(x) push_back(x)
#define ALL(a) ((a).begin(),(a).end())
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cin >> cass; cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? gcd(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}

#pragma endregion

//全局变量
#pragma region

#pragma endregion

//主体------------------------------------------

inline int PHI(ll n){
    ll res = n;
    for(ll i = 2; i * i <= n; i ++){
        if(n % i == 0){
            res = res * (i - 1) / i;
            while(n % i ==0 ) n /= i;
        }
    }
    if(n > 1) res = res * (n - 1) / n;
    return res;
}

CHIVAS{
    ll n;
    while(cin >> n, n) cout << PHI(n) << endl;
    _REGAL;
}

# POJ2478_FareySequence

# 🔗

http://poj.org/problem?id=2478

# 💡

每个数以自己为分母时可以有phi[x]个数互质成立
所以求2 ~ n的phi和即可

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <utility>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'

#define CHIVAS int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
#define map unordered_map

#define PB(x) push_back(x)
#define ALL(a) ((a).begin(),(a).end())
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cin >> cass; cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? gcd(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}

#pragma endregion

//全局变量
#pragma region
const int maxn = 1e6 + 10;
ll phi[maxn];
ll isprime[maxn];
ll prime[maxn];
ll cnt = 0;
#pragma endregion

//主体------------------------------------------

inline void GET_PHI(){
    phi[1] = 1;
    for(ll i = 2; i <= maxn; i ++){
        if(!isprime[i]) prime[++cnt] = i, phi[i] = i - 1;
        for(ll j = 1; j <= cnt && i * prime[j] <= maxn; j ++){
            isprime[i * prime[j]] = 1;
            if(i % prime[j] == 0){
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            }else phi[i * prime[j]] = phi[i] * (prime[j] - 1);
        }
    }
}

CHIVAS{
    GET_PHI();
    ll n;
    while(cin >> n, n){
        ll res = 0;
        for(int i = 2; i <= n; i ++) res += phi[i];
        cout << res << endl;
    }
    _REGAL;
}

# POJ2773_Happy2006

# 🔗

http://poj.org/problem?id=2773

# 💡

需要了解到的一个性质：
gcd(a, b) = gcd(a + b * T, b) = gcd(a, b + a * T)
其中T为周期，
利用周期的性质，
我们可以很轻松地把k排除n以内的数
并在计数时从n * T + 1开始计算

虽然是暴力，但是优化了时间

# ✅

#pragma region
/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <utility>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'

#define CHIVAS int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
#define map unordered_map

#define PB(x) push_back(x)
#define ALL(a) ((a).begin(),(a).end())
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cin >> cass; cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? gcd(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}

#pragma endregion

//全局变量
#pragma region
const int maxn = 1e6 + 10;
ll phi[maxn];
ll isprime[maxn];
ll prime[maxn];
ll cnt = 0;
#pragma endregion

//主体------------------------------------------

inline void GET_PHI(){
    phi[1] = 1;
    for(ll i = 2; i <= maxn; i ++){
        if(!isprime[i]) prime[++cnt] = i, phi[i] = i - 1;
        for(ll j = 1; j <= cnt && i * prime[j] <= maxn; j ++){
            isprime[i * prime[j]] = 1;
            if(i % prime[j] == 0){
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            }else phi[i * prime[j]] = phi[i] * (prime[j] - 1);
        }
    }
}

CHIVAS{GET_PHI();
    ll n, k;
    while(cin >> n >> k){
        ll T = k / phi[n];//周期数
        k %= phi[n];//这T个周期以外还有多少个，优化时间的精髓
        if(k == 0) T --, k = phi[n];//能整除要抠出来一组T
        for(ll i = n * T + 1; ; i ++){
            if(GCD(i, n) == 1) k --;
            if(k == 0){
                cout << i << endl;
                break;
            }
        }
    }
    _REGAL;
}

# POJ3090_VisibleLatticePoints

# 🔗

http://poj.org/problem?id=3090

# 💡

就是入门题那个仪仗队
只不过这里n++而已

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <utility>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'

#define CHIVAS int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
#define map unordered_map

#define PB(x) push_back(x)
#define ALL(a) ((a).begin(),(a).end())
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cin >> cass; cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? gcd(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}

#pragma endregion

//全局变量
#pragma region
const int maxn = 1e3 + 10;
ll phi[maxn];
ll isprime[maxn];
ll prime[maxn];
ll cnt = 0;
int cas_id = 0;
#pragma endregion

//主体------------------------------------------

inline void GET_PHI(){
    phi[1] = 1;
    for(ll i = 2; i <= maxn; i ++){
        if(!isprime[i]) prime[++cnt] = i, phi[i] = i - 1;
        for(ll j = 1; j <= cnt && i * prime[j] <= maxn; j ++){
            isprime[i * prime[j]] = 1;
            if(i % prime[j] == 0){
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            }else phi[i * prime[j]] = phi[i] * (prime[j] - 1);
        }
    }
}

inline void solve(){
    ll n, res = 0; cin >> n; n ++;
    for(int i = 1; i < n; i ++) res += phi[i];
    res = (res << 1 | 1);
    cout << ++cas_id << " " << n - 1 << " " << res << endl;
}

CHIVAS{
    GET_PHI();
    int cass;
    EACH_CASE(cass){
        solve();
    }
    _REGAL;
}

# Question_phi

# 🔗

给出若干个正整数 $n$ ，请你求出最小的 $m$ ，使得 $\phi(m)\ge n$ 。

# 💡

首先要很容易想到一个性质：x为素数时， $\phi(x)=x-1$
而n后面的第一个素数肯定能满足 $\phi\ge n$
根据素数分布规则来看，我们完全可以从 $n$ 向后找，从 n 到大于n的第一个素数这个范围内会有满足条件的数
且时间复杂度能过去

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'

#define CHIVAS_ int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
//#define map unordered_map

#define _int(a) int a; cin >> a
#define  _ll(a) ll a; cin >> a
#define _char(a) char a; cin >> a
#define _string(a) string a; cin >> a
#define _vectorInt(a, n) vector<int>a(n); cin >> a
#define _vectorLL(a, b) vector<ll>a(n); cin >> a

#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cass = inputInt(); cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
template<typename T>             vector<T>& operator--            (vector<T> &v){for (auto& i : v) --i;            return  v;}
template<typename T>             vector<T>& operator++            (vector<T> &v){for (auto& i : v) ++i;            return  v;}
template<typename T>             istream& operator>>(istream& is,  vector<T> &v){for (auto& i : v) is >> i;        return is;}
template<typename T>             ostream& operator<<(ostream& os,  vector<T>  v){for (auto& i : v) os << i << ' '; return os;}
inline int inputInt(){int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);}
inline void outInt(int X){if(X<0) {putchar('-'); X=~(X-1);}int s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline ll inputLL(){ll X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1); }
inline void outLL(ll X){if(X<0) {putchar('-'); X=~(X-1);}ll s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}

const int N = 1e6 + 10;
int phi[N], isprime[N];
vector<int> prime;

inline void GET_PHI(){
        isprime[0] = isprime[1] = 1, phi[1] = 1;
        for(int i = 2; i < N; i ++){
                if(!isprime[i]) prime.push_back(i), phi[i] = i - 1;
                for(int j = 0; j < prime.size() && i * prime[j] < N; j ++){
                        isprime[i * prime[j]] = 1;
                        if(i % prime[j] == 0){
                                phi[i * prime[j]] = phi[i] * prime[j];
                                break;
                        }else   phi[i * prime[j]] = phi[i] * (prime[j] - 1);
                }
        }
}

CHIVAS_{GET_PHI();
        int cass;
        EACH_CASE(cass){
                int n = inputInt();
                for(int i = n; ; i ++){
                        if(phi[i] >= n){
                                outInt(i); puts("");
                                break;
                        }
                }
        }
}

# README

📕【模板】欧拉函数

# 🔗

https://acm.dingbacode.com/contests/contest_showproblem.php?pid=1007&cid=1019

# 💡

学习传送门 (opens new window)

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'

#define CHIVAS_ int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
//#define map unordered_map

#define _int(a) int a; cin >> a
#define  _ll(a) ll a; cin >> a
#define _char(a) char a; cin >> a
#define _string(a) string a; cin >> a
#define _vectorInt(a, n) vector<int>a(n); cin >> a
#define _vectorLL(a, b) vector<ll>a(n); cin >> a

#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cass = inputInt(); cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
template<typename T>             vector<T>& operator--            (vector<T> &v){for (auto& i : v) --i;            return  v;}
template<typename T>             vector<T>& operator++            (vector<T> &v){for (auto& i : v) ++i;            return  v;}
template<typename T>             istream& operator>>(istream& is,  vector<T> &v){for (auto& i : v) is >> i;        return is;}
template<typename T>             ostream& operator<<(ostream& os,  vector<T>  v){for (auto& i : v) os << i << ' '; return os;}
inline int inputInt(){int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);}
inline void outInt(int X){if(X<0) {putchar('-'); X=~(X-1);}int s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline ll inputLL(){ll X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1); }
inline void outLL(ll X){if(X<0) {putchar('-'); X=~(X-1);}ll s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}

const int N  = 32770;
ll phi[N];
vector<ll> prime;
ll isprime[N];

inline void GET_PHI(){//欧拉筛打表
        phi[1] = 1; isprime[1] = isprime[0] = 1;
        for(ll i = 2; i < N; i ++){
                if(!isprime[i]) prime.push_back(i), phi[i] = i - 1;
                for(ll j = 0; j < prime.size() && i * prime[j] < N; j ++){
                        isprime[i * prime[j]] = 1;
                        if(i % prime[j] == 0) { phi[i * prime[j]] = phi[i] * prime[j]; break; } //定理：对于i % j == 0，有phi[i * j] = phi[i] * j
                        phi[i * prime[j]] = phi[i] * (prime[j] - 1); //积性函数性质：如果gcd(i, j) == 1, phi[i * j] = phi[i] * phi[j]。在这里j为质数，所以有phi[i] * phi[j] = phi[i] * (j - 1)
                }
        }
}

inline void solve(){
        ll n = inputInt();
        outLL(phi[n]); puts("");
}
CHIVAS_{GET_PHI();
        int cass;
        EACH_CASE(cass){
                solve();
        }
        _REGAL;
}

# 欧拉降幂

# HDUOJ5728_PowMod

# 🔗

https://acm.dingbacode.com/showproblem.php?pid=5728

# 💡

问题可拆解成两个子问题（子过程）

解K
由于 n 无平方因子，所以 n 唯一分解成几个质因子之后，每个质因子 p 都与别的互质

即：
$\phi(p*\frac np)=\phi(p)*\phi(\frac np)$

设
$\sum\limits_{n=1}^m\phi(i,n)=f(n,m)$

$\sum\limits_{n=1}^m\phi(i,n)=\phi(p)\sum\limits_{i=1}^m\phi(i,\frac np)+\sum\limits_{i=1}^{\frac mp}\phi(i,n)$ $\Rightarrow f(n,m)=\phi(p)*f(\frac np, m)+f(n, \frac mp)$
递归降幂
用
$a^b=a^{b%\phi(n)+\phi(n)}(mod\quad n)$ 递归一层层降幂
递归出口是 phi = 1

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'

#define CHIVAS_ int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
//#define map unordered_map

#define _int(a) int a; cin >> a
#define  _ll(a) ll a; cin >> a
#define _char(a) char a; cin >> a
#define _string(a) string a; cin >> a
#define _vectorInt(a, n) vector<int>a(n); cin >> a
#define _vectorLL(a, b) vector<ll>a(n); cin >> a

#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cass = inputInt(); cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
template<typename T>             vector<T>& operator--            (vector<T> &v){for (auto& i : v) --i;            return  v;}
template<typename T>             vector<T>& operator++            (vector<T> &v){for (auto& i : v) ++i;            return  v;}
template<typename T>             istream& operator>>(istream& is,  vector<T> &v){for (auto& i : v) is >> i;        return is;}
template<typename T>             ostream& operator<<(ostream& os,  vector<T>  v){for (auto& i : v) os << i << ' '; return os;}
inline int inputInt(){int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);}
inline void outInt(int X){if(X<0) {putchar('-'); X=~(X-1);}int s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline ll inputLL(){ll X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1); }
inline void outLL(ll X){if(X<0) {putchar('-'); X=~(X-1);}ll s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}

const int N = 1e7 + 10, mod = 1e9 + 7;
int phi[N], isprime[N];
int sum[N];
vector<int> prime;

inline void GET_PHI () {
        isprime[0] = isprime[1] = 1, phi[1] = 1;
        for ( int i = 2; i < N; i ++ ) {
                if ( !isprime[i] ) prime.push_back(i), phi[i] = i - 1;
                for ( int j = 0; j < prime.size() && i * prime[j] < N; j ++ ) {
                        isprime[i * prime[j]] = 1;
                        if ( i % prime[j] == 0 ) {
                                phi[i * prime[j]] = phi[i] * prime[j];
                                break;
                        }else   phi[i * prime[j]] = phi[i] * (prime[j] - 1);
                }
        }
        for ( int i = 1; i < N; i ++ ) sum[i] = (sum[i - 1] + phi[i]) % mod;
}

inline ll GET_K ( int n, int m ) { //解K
        //把f ( n, m )换回累加phi的形式，会得到三个特判，也能成为递归出口
        if ( m < 1 ) return 0;
        if ( m == 1 ) return phi[n];
        if ( n == 1 ) return sum[m];

        if ( phi[n] == n - 1 ) return (GET_K(1, m) * phi[n] % mod + GET_K(n, m / n)) % mod; // 质数，没必要查因子了
        for ( int i = 2; i * i <= n; i ++ ){ // 质因子拆解
                if ( n % i ) continue;
                return (phi[i] * GET_K(n / i, m) % mod + GET_K(n, m / i)) % mod;
        }
}

inline ll ksm ( ll a, ll b, ll mod ) {
        ll res = 1;
        while ( b ) {
                if ( b & 1 ) res = res * a % mod;
                a = a * a % mod;
                b >>= 1;
        }return res;
}

inline ll get(ll k, ll p){ // 递归降层幂
        if ( p == 2 ) return k & 1;
        return ksm ( k, get ( k, phi[p] ) + phi[p], p );
}

CHIVAS_{GET_PHI();
        int n, m, p;
        while ( scanf ( "%d%d%d", &n, &m, &p ) == 3 ) {
                ll k = GET_K ( n, m );
                outLL ( get ( k, p ) ); puts("");
        }
        _REGAL;
};

# README

# 🔗

https://www.luogu.com.cn/problem/P5091

# 💡

学习传送门 (opens new window)

# ✅

/*
           ________   _                                              ________                              _
          /  ______| | |                                            |   __   |                            | |
         /  /        | |                                            |  |__|  |                            | |
         |  |        | |___    _   _   _   ___  _   _____           |     ___|   ______   _____   ___  _  | |
         |  |        |  __ \  |_| | | | | |  _\| | | ____|          |  |\  \    |  __  | |  _  | |  _\| | | |
         |  |        | |  \ |  _  | | | | | | \  | | \___           |  | \  \   | |_/ _| | |_| | | | \  | | |
         \  \______  | |  | | | | \ |_| / | |_/  |  ___/ |          |  |  \  \  |    /_   \__  | | |_/  | | |
Author :  \________| |_|  |_| |_|  \___/  |___/|_| |_____| _________|__|   \__\ |______|     | | |___/|_| |_|
                                                                                         ____| |
                                                                                         \_____/
*/
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>

#define G 10.0
#define LNF 1e18
#define EPS 1e-6
#define PI acos(-1.0)
#define INF 0x7FFFFFFF

#define ll long long
#define ull unsigned long long

#define LOWBIT(x) ((x) & (-x))
#define LOWBD(a, x) lower_bound(a.begin(), a.end(), x) - a.begin()
#define UPPBD(a, x) upper_bound(a.begin(), a.end(), x) - a.begin()
#define TEST(a) cout << "---------" << a << "---------" << '\n'

#define CHIVAS_ int main()
#define _REGAL exit(0)

#define SP system("pause")
#define IOS ios::sync_with_stdio(false)
//#define map unordered_map

#define _int(a) int a; cin >> a
#define  _ll(a) ll a; cin >> a
#define _char(a) char a; cin >> a
#define _string(a) string a; cin >> a
#define _vectorInt(a, n) vector<int>a(n); cin >> a
#define _vectorLL(a, b) vector<ll>a(n); cin >> a

#define PB(x) push_back(x)
#define ALL(a) a.begin(),a.end()
#define MEM(a, b) memset(a, b, sizeof(a))
#define EACH_CASE(cass) for (cass = inputInt(); cass; cass--)

#define LS l, mid, rt << 1
#define RS mid + 1, r, rt << 1 | 1
#define GETMID (l + r) >> 1

using namespace std;

template<typename T> inline T MAX(T a, T b){return a > b? a : b;}
template<typename T> inline T MIN(T a, T b){return a > b? b : a;}
template<typename T> inline void SWAP(T &a, T &b){T tp = a; a = b; b = tp;}
template<typename T> inline T GCD(T a, T b){return b > 0? GCD(b, a % b) : a;}
template<typename T> inline void ADD_TO_VEC_int(T &n, vector<T> &vec){vec.clear(); cin >> n; for(int i = 0; i < n; i ++){T x; cin >> x, vec.PB(x);}}
template<typename T> inline pair<T, T> MaxInVector_ll(vector<T> vec){T MaxVal = -LNF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_ll(vector<T> vec){T MinVal = LNF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<T, T> MaxInVector_int(vector<T> vec){T MaxVal = -INF, MaxId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MaxVal < vec[i]) MaxVal = vec[i], MaxId = i; return {MaxVal, MaxId};}
template<typename T> inline pair<T, T> MinInVector_int(vector<T> vec){T MinVal = INF, MinId = 0;for(int i = 0; i < (int)vec.size(); i ++) if(MinVal > vec[i]) MinVal = vec[i], MinId = i; return {MinVal, MinId};}
template<typename T> inline pair<map<T, T>, vector<T> > DIV(T n){T nn = n;map<T, T> cnt;vector<T> div;for(ll i = 2; i * i <= nn; i ++){while(n % i == 0){if(!cnt[i]) div.push_back(i);cnt[i] ++;n /= i;}}if(n != 1){if(!cnt[n]) div.push_back(n);cnt[n] ++;n /= n;}return {cnt, div};}
template<typename T>             vector<T>& operator--            (vector<T> &v){for (auto& i : v) --i;            return  v;}
template<typename T>             vector<T>& operator++            (vector<T> &v){for (auto& i : v) ++i;            return  v;}
template<typename T>             istream& operator>>(istream& is,  vector<T> &v){for (auto& i : v) is >> i;        return is;}
template<typename T>             ostream& operator<<(ostream& os,  vector<T>  v){for (auto& i : v) os << i << ' '; return os;}
inline int inputInt(){int X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1);}
inline void outInt(int X){if(X<0) {putchar('-'); X=~(X-1);}int s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}
inline ll inputLL(){ll X=0; bool flag=1; char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}if(flag) return X;return ~(X-1); }
inline void outLL(ll X){if(X<0) {putchar('-'); X=~(X-1);}ll s[20],top=0;while(X) {s[++top]=X%10; X/=10;}if(!top) s[++top]=0;while(top) putchar(s[top--]+'0');}

ll a, m;
string s;
ll b = 0;
//  a^{s} (mod m) <=> a^{b} (mod m)

inline ll phi(ll x){
        ll xx = x;
        ll res = x;
        for(ll i = 2; i * i <= xx; i ++){
                if(x % i == 0){
                        res -= res / i;
                        while(x % i == 0) x /= i;
                }
        }
        if(x != 1) res -= res / x;
        return res;
}

inline ll ksm(){
        ll res = 1;
        while(b){
                if(b & 1) res = res * a % m;
                a = a * a % m;
                b >>= 1;
        }return res;
}

CHIVAS_{
        cin >> a >> m >> s;
        ll phi_m = phi(m), flag = 0;
        for(ll i = 0; i < s.size(); i ++){
                b = b * 10 + s[i] - '0';
                if(b > phi_m) flag = 1, b %= phi_m; // 一边转一边判断有没有 phi(m) 大
        }
        b += (flag && GCD(a, m) != 1) * phi_m; // 三个情况全满足了，nice
        cout << ksm();
        _REGAL;
};

欧拉反演博弈论