优先队列

#

---

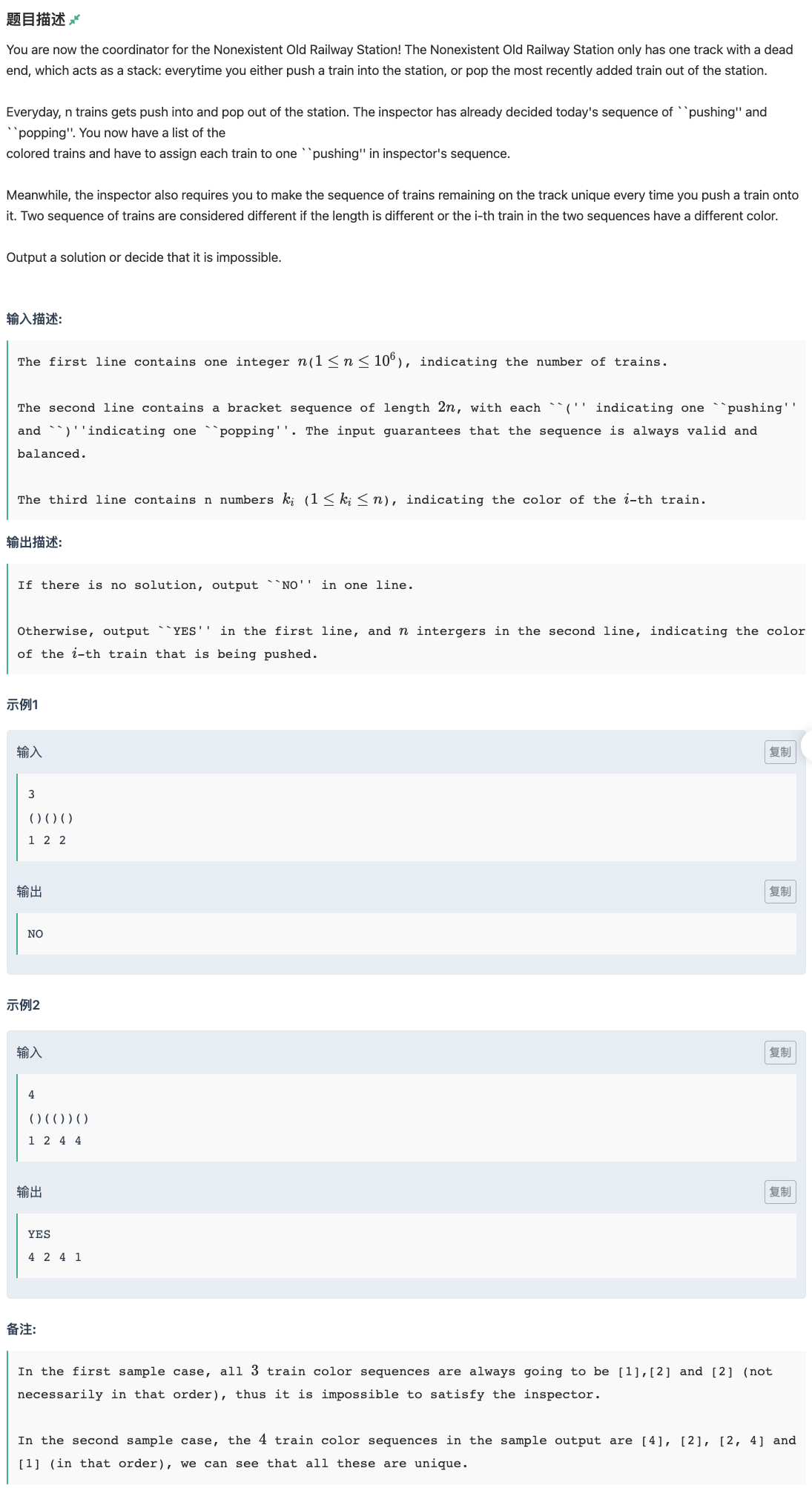
牛客2021多校(10)F_TrainWreck

🔗

💡

本题重在模型的搭建
首先对于一个括号字符串 "(()())"，我们可以很容易地知道一个括号的的"子同一级的括号"不可用一样的
那么我们可以得到一个树模型，每个节点的编号是我们自定的
而这个节点的子节点就是一个括号的子同一级括号

问题转化为：对于每一个节点，它的子节点们不能使用相同的数
所以，我们要尽可能地在更浅的地方将重复数量多的用完
那么我们可以使用map对每个数存入数量后，把他们打到优先队列里面
然后每次遍历到一个节点后，对这个节点的子节点进行选数
我们可以从优先队列里面每次选出该节点的子节点个数个前面的数
如果选不出来这么多，就"NO"了
如果可以，就一个个映射上去就行了
选完数再把每个数的数量-1，再倒回优先队列即可

✅

#include <unordered_map>
#include <iostream>
#include <vector>
#include <queue>
#include <map>

using namespace std;


struct cmp{ // 重载一下pair的运算符
	bool operator()(pair<int, int>& p1, pair<int, int>& p2){
		return p1.second <= p2.second;
	}
};

const int N = 1e6 + 10;
struct Edge { int nxt, to; } edge[N]; // 前向星
int head[N], cnt; // 前向星
int n, a[N], fath[N]; // 输入个数，输入的数，每个节点的父亲节点
unordered_map<int, int> mp; // 存数的个数
priority_queue<pair<int, int>, vector<pair<int, int> >, cmp> pque; // .first = 数， .second = 数的个数
int res[N]; // 结果序列
string s; // 输入的括号


inline void Init () { cnt = 0; for ( int i = 0; i < N; i ++ ) head[i] = -1; }
	
inline void Add_Edge ( int from, int to ) { edge[++cnt] = {head[from], to}; head[from] = cnt; }
	
inline void BFS ( ) {
	queue<int> que; que.push(0); // 从一个虚拟源总根节点开始
	while ( que.size() ) {
		int x = que.front(); que.pop();
		vector<pair<int, int> > lose; // 存放优先队列前几个
		
		for ( int i = head[x]; ~i; i = edge[i].nxt ) { 
			int to = edge[i].to; que.push(to);
			if ( pque.size() ) // 如果还有数，就放进去
				lose.push_back(pque.top()), 
				res[to] = lose.back().first, 
				pque.pop(); 
			else	          // 如果没有不同的了，就"NO"
				puts("NO"), 
				exit(0);
		}
			
		for ( auto i : lose ) { // 再把提出来的这些导回去
			i.second --;
			if ( i.second ) pque.push(i);
		} 
	}
}


int main () {

#ifndef ONLINE_JUDGE
	freopen("in.in", "r", stdin);
#endif
	
	cin >> n >> s;
	for ( int i = 0; i < n; i ++ ) 
		cin >> a[i],
		mp[a[i]] ++; // 统计一下数的个数
	for ( auto i : mp )
		pque.push({i.first, i.second}); // 整体导入优先队列
	
	Init(); int cur_fath = 0 /*表当时重定义的倒数第二层节点*/, cur_son = 1 /*表当时重定义的最后一层节点*/;
	for ( auto i : s ) {
		if ( i == '(' ) 
			Add_Edge(cur_fath, cur_son),
			fath[cur_son] = cur_fath, // 把son和fath对应一下，以便遇见')'后cur_fath点回去一层
			cur_fath = cur_son ++;
		else cur_fath = fath[cur_fath]; // 回去一层
	}
	BFS ();
	
	puts("YES");
	for ( int i = 1; i <= n; i ++ )
		cout << res[i] << " ";
}

---

HDU2021多校(6)5_Median

🔗

💡

首先可以想到由于每一块都是子序列
所以顺序不必要
每一个数都可以选取比它大的不做中位数的数的数量最多比比它小的不做中位数的数的数量多一个，至少两边相等
那么首先是两个数两个数匹配给他们中间的一个中位数保持稳定
那么在剩下一些数时，这一些数最多可以每一个分配一个给比他们小的中位数
因为这些中位数右侧数的个数可以+1

那么这就是一个对项相消的问题
我们把每一个不做中位数的连续的数的数量提出

比如：n=5，选取3、5做中位数，那么就是剩下[1,2],[4]这两个块
对这些块进行对项相消，贪心地让每一个块都尽量用完
那么可以用优先队列每次消我们定义关系中大的那两个进行消除，套一个结构体两个元素分别表示这个块的数个数和这个块前面有几个中位数
我们定义的关系是：如果这个块前面的每个中位数都吃掉这个块内的一个元素，剩下的个数进行比较

每次优先队列提出两个块消一下，如果还有数就塞回去
最后看一下剩下的那个块能不能被前面的中位数吃完

✅

struct node { int val, op; /*个数，前面有几个中位数*/inline friend bool operator < (node a, node b) { return a.val - a.op < b.val - b.op; } };

const int N = 1e5 + 10;
int a[N], n, m;

inline void Solve () {
        scanf("%d%d", &n, &m);
        priority_queue<node> pque;
        for ( int i = 0; i < m; i ++ ) cin >> a[i];
        sort ( a, a + m );
        for ( int i = 0; i < m; i ++ ) {
                if ( i == 0     && a[i] > 1 )   pque.push({a[i] - 1, 0});
                if ( i == m - 1 && a[i] < n )   pque.push({n - a[i], m});
                if ( i && a[i] > a[i - 1] + 1 ) pque.push({a[i] - a[i - 1] - 1, i});
        }
        while ( pque.size() >= 2 ) {
                node fir = pque.top(); pque.pop();
                node sec = pque.top(); pque.pop();
                fir.val --; sec.val --;
                if ( fir.val ) pque.push(fir);
                if ( sec.val ) pque.push(sec);
        } 
        if ( !pque.size() ) puts("YES");
        else {
                node x = pque.top();
                if ( x.val - x.op > 0 ) puts("NO");
                else                    puts("YES");
        }
}

int main () {
        int cass; scanf("%d", &cass); while ( cass -- ) {
                Solve();
        }
}

---

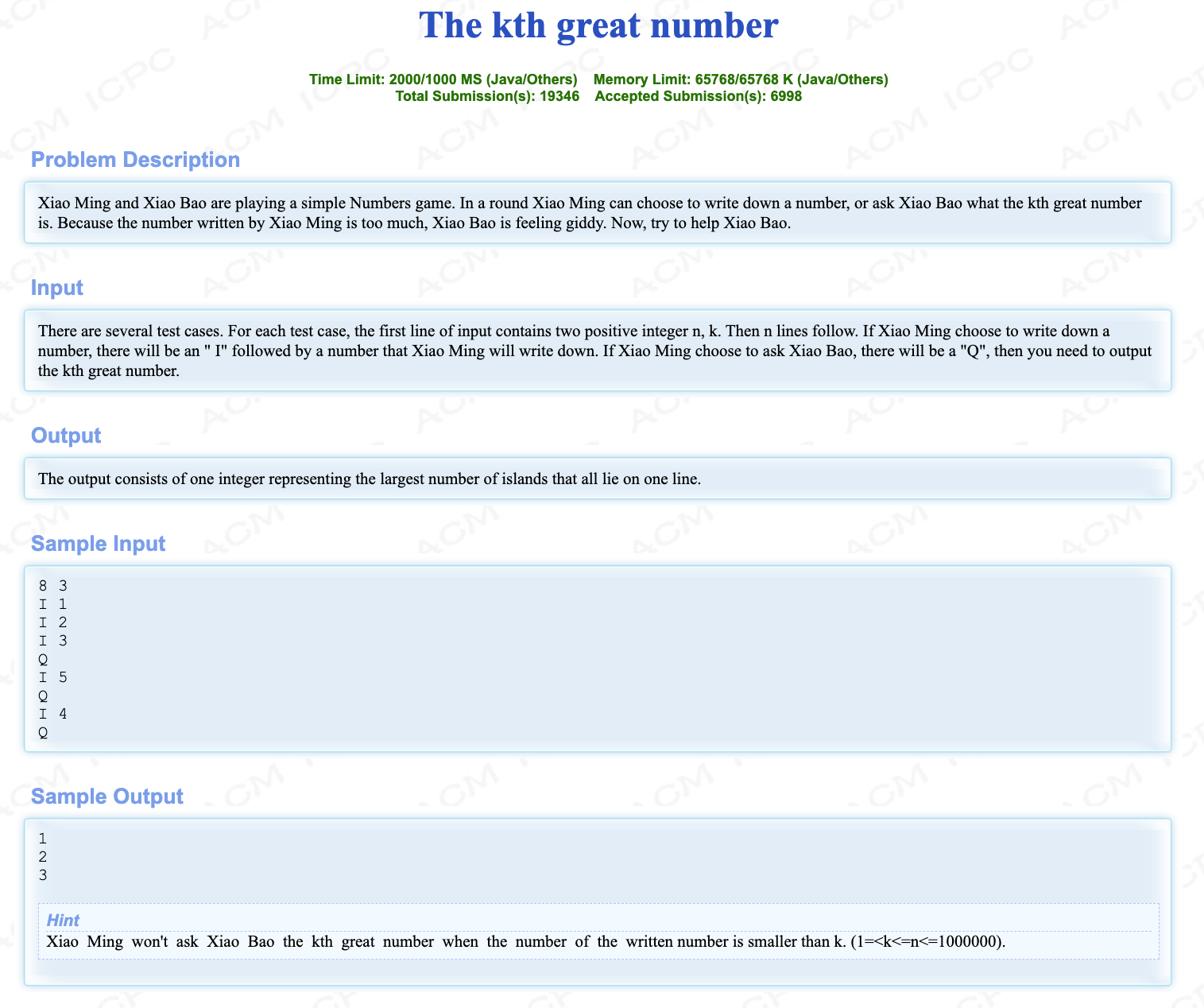
ICPC2011大连6_TheKthGreatNumber

🔗

💡

插入也是很费时的，反正m之后的用不到
就实时存储实时pop就行

✅

#pragma region
#pragma GCC optimize(3,"Ofast","inline")
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define eps 1e-6
#define PI acos(-1.0)
#define ll long long
#define INF 0x7FFFFFFF
#define Regal exit(0)
#define Chivas int main()
#define pb(x) push_back(x)
#define SP system("pause")
#define Max(a,b) ((a)>(b)?(a):(b))
#define Min(a,b) ((a)<(b)?(a):(b))
#define IOS ios::sync_with_stdio(false)
#define mm(a, b) memset(a, b, sizeof(a))
#define each_cass(cass) for (cin>>cass; cass; cass--)
#define test(a) cout << "---------" << a << "---------" << '\n'
 
using namespace std;
#pragma endregion

//全局变量
#pragma region
int n, m;
priority_queue<int, vector<int>, greater<int> > pque;
#pragma endregion

Chivas{
    IOS;
    while(scanf("%d%d", &n, &m) == 2){
        
        while(pque.size()) pque.pop();

        for(int i = 0; i < n; i ++){
            getchar();
            char op; scanf("%c", &op);
            if(op == 'I'){
                int x; scanf("%d", &x);
                pque.push(x);
                if(pque.size() > m) pque.pop();
            }else{
                printf("%d\n", pque.top());
            }
        }
    }
    Regal;
}

---

POJ2833_FenceRepair

🔗

http://poj.org/problem?id=2833

💡

分析样例说明中的构造方式
每次选取最小的两个（证明方式可以联想到三角形定理）
每次选取其中最小的两个拼一起再压入堆内
如果堆长度=1就break

✅

#pragma region
#pragma GCC optimize(3,"Ofast","inline")
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define eps 1e-6
#define PI acos(-1.0)
#define ll long long
#define INF 0x7FFFFFFF
#define Regal exit(0)
#define Chivas int main()
#define pb(x) push_back(x)
#define SP system("pause")
#define Max(a,b) ((a)>(b)?(a):(b))
#define Min(a,b) ((a)<(b)?(a):(b))
#define IOS ios::sync_with_stdio(false)
#define mm(a, b) memset(a, b, sizeof(a))
#define each_cass(cass) for (cin>>cass; cass; cass--)
#define test(a) cout << "---------" << a << "---------" << '\n'
 
using namespace std;
#pragma endregion

//全局变量
#pragma region
int n; 
priority_queue<int, vector<int>, greater<int> > pque;
#pragma endregion


Chivas{
    IOS;
    cin >> n;
    for(int i = 0; i < n; i++){
        int x; cin >> x;
        pque.push(x);
    }

    ll res = 0;
    while(pque.size() > 1){
        int fir = pque.top(); pque.pop();
        int sec = pque.top(); pque.pop();

        pque.push(fir + sec);
        res += fir + sec;
    }

    cout << res << endl;

    Regal;
}

---

POJ2833_TheAverage

🔗

http://poj.org/problem?id=2833

💡

两个堆分别存最大的n1个数和最小的n2个数
计算非这俩堆内的元素和

✅

#pragma region
#pragma GCC optimize(3,"Ofast","inline")
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define eps 1e-6
#define PI acos(-1.0)
#define ll long long
#define INF 0x7FFFFFFF
#define Regal exit(0)
#define Chivas int main()
#define pb(x) push_back(x)
#define SP system("pause")
#define Max(a,b) ((a)>(b)?(a):(b))
#define Min(a,b) ((a)<(b)?(a):(b))
#define IOS ios::sync_with_stdio(false)
#define mm(a, b) memset(a, b, sizeof(a))
#define each_cass(cass) for (cin>>cass; cass; cass--)
#define test(a) cout << "---------" << a << "---------" << '\n'
 
using namespace std;
#pragma endregion

//全局变量
#pragma region
int n, n1, n2; 
priority_queue<int, vector<int>, greater<int> > pque1;
priority_queue<int> pque2;
#pragma endregion

Chivas{
    IOS;
    while(scanf("%d%d%d", &n1, &n2, &n) == 3){

        if((!n) && (!n1) && (!n2)) break;
        
        ll res = 0;
        ll cnt_res = n - n1 - n2;

        for(int i = 0; i < n; i ++){
            int x; scanf("%d", &x); res += x;
            pque1.push(x); pque2.push(x);
            if(pque1.size() > n1) pque1.pop();
            if(pque2.size() > n2) pque2.pop();
        }

        while(pque1.size()) res -= pque1.top(), pque1.pop();
        while(pque2.size()) res -= pque2.top(), pque2.pop();

        printf("%.6f\n", res * 1.0 / cnt_res);
    }
    Regal;
}

---