链表

#

---

洛谷P2391_白雪皑皑

🔗

💡

看一下题，什么鬼就是一个 $set$ 吧，再看一眼数据量，要么每次 $O(1)$ 操作，要么总复杂度不高
总复杂度很容易想到 $O(n)$
这种覆盖性质的染色问题，基本上都是倒着染，每染一个之后就不看这个点了
这种删除、不遍历的操作可以使用链表来解决
但是考虑到如果确定操作 $[l,r]$ 了话，从哪里开始呢，找了话还是要 $log$ ？
思考了一下也就是说我们用链表删除后，这个点的后继在之后的操作不会被修改了，所以我们没法找到它的存在后继
但是每一块被删除的部分，一定有一个最后被删的元素，其前驱后继就是这一块所有点的前驱后继
这种认贼作父（啊不是）的操作，就是并查集的根啊

所以我们开一个标记记录是否存在，再开一套并查集
在删除一个点的时候，我们看它前后是否有删除的点，如果有，就让它们的并查集根认作这个即将删除的点
然后在操作时，对于 $l$ 更改为它并查集根的后继，$r$ 更改为它并查集根的前驱
然后让 $l$ 一直按链表向后跑并不断删除访问过的点直到 $r$ 即可

✅

const int N = 1000006;

int n, m, p, q;

struct node { int pre, nxt; } a[N];
int fa[N], vis[N], res[N];
inline int find (int x) { return x == fa[x] ? x : fa[x] = find(fa[x]); }

inline void del (int x) {
    a[a[x].nxt].pre = a[x].pre;
    a[a[x].pre].nxt = a[x].nxt;

    int fx = find(x);
    if (vis[x - 1]) {
        int fxd1 = find(x - 1);
        fa[fxd1] = fx;
    }
    if (vis[x + 1]) {
        int fxa1 = find(x + 1);
        fa[fxa1] = fx;
    }
    vis[x] = 1;
}

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n >> m >> p >> q;
    for (int i = 1; i <= n; i ++) {
        fa[i] = i;
        a[i].pre = i - 1;
        a[i].nxt = i + 1;
    }

    for (int i = m; i >= 1; i --) {
        int l = ((ll)i * p + q) % n + 1;
        int r = ((ll)i * q + p) % n + 1;
        if (l > r) swap(l, r);
        l = vis[l] ? a[find(l)].nxt : l;
        r = vis[r] ? a[find(r)].pre : r;
        while (l <= r) {
            res[l] = i;
            int tmp = l;
            l = a[l].nxt;
            del(tmp);
        }
    }   

    for (int i = 1; i <= n; i ++) cout << res[i] << endl;
}

---

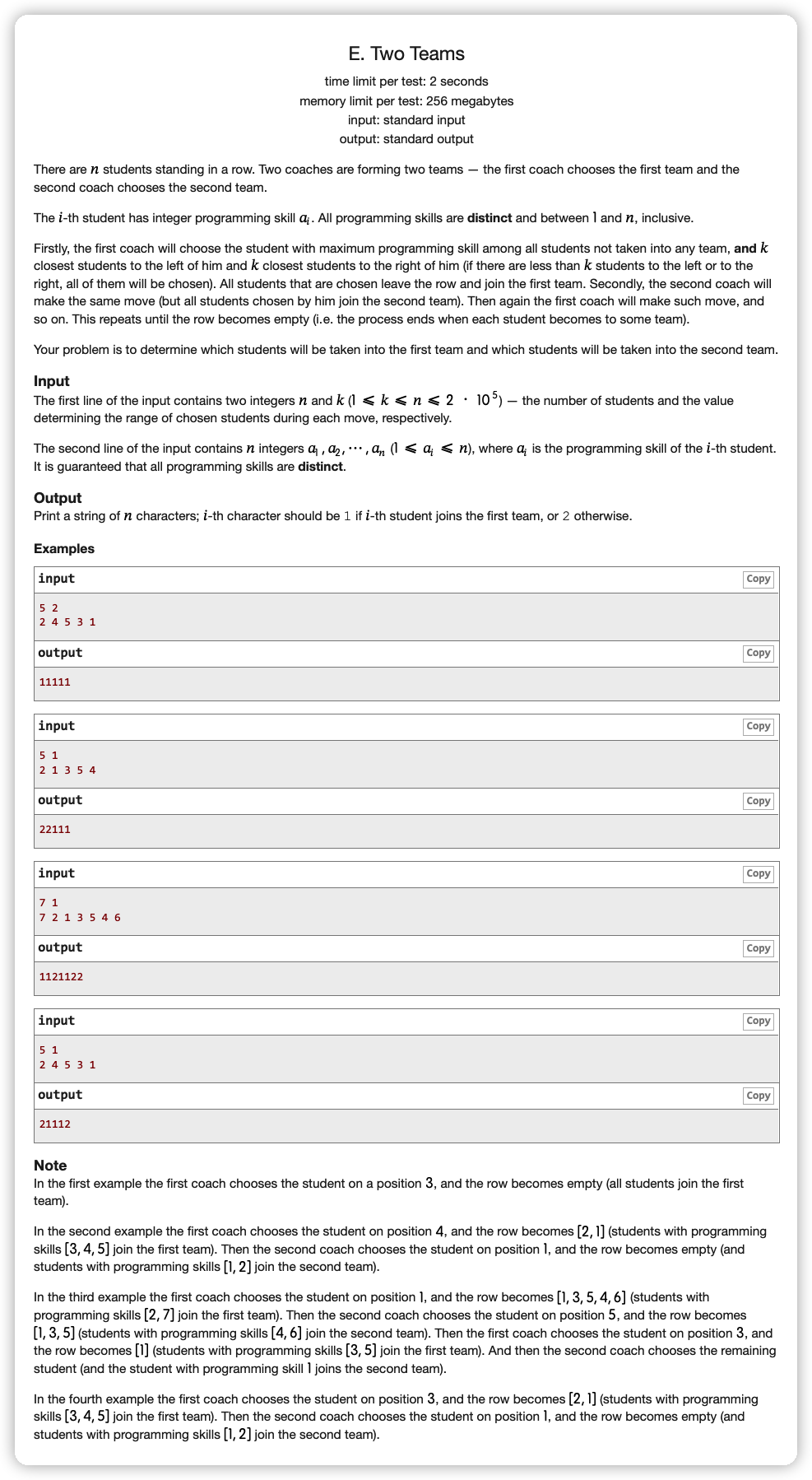
CodeForces1154E_TwoTeams

🔗

💡

每次找出最大的，不难
按顺序删去不到 $2k$ 个，不难
这不是暴力 $O(n)$ 吗？很怪，再看看。哦删除之后合并的问题没想到
顺序..删除..合并...，这不就是链表的几个特性吗
由于我们还要找到最大的下标，所以手写链表进行删除与合并
最大值一定是向下减的，所以我们记录谁有答案之后，先确定最大值是 $n$ ，然后每次操作完向下走到第一个没有答案的
时间复杂度 $O(n)$

✅

const int N = 2e5 + 10;
int n, k, a[N], id[N];
int nxt[N], pre[N]; // 链表节点前驱后继
int res[N];
 
int mxv, mxi;
inline int get_MaxId () {
        while (res[mxi]) mxv --, mxi = id[mxv];
        return mxi;
}
 
int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);
 
        cin >> n >> k;
        for (int i = 1; i <= n; i ++) {
                cin >> a[i];
                id[a[i]] = i;
                nxt[i] = i + 1;
                pre[i] = i - 1;
                if (a[i] == n) mxi = i, mxv = n;
        }
 
        int nn = n;
        int tim = 1;
        while (nn) {
                int ths = get_MaxId();
                int kk = k + 1;
                int i = ths;
                while (kk -- && i != n + 1) {
                        res[i] = tim;
                        // 删除与合并
                        nxt[pre[i]] = nxt[i];
                        pre[nxt[i]] = pre[i];
                        nn --;
                        i = nxt[i];
                }
                kk = k;
                i = pre[ths];
                while (kk -- && i != 0) {
                        res[i] = tim;
                        // 删除与合并
                        nxt[pre[i]] = nxt[i];
                        pre[nxt[i]] = pre[i];
                        nn --;
                        i = pre[i];
                }
                tim = 3 - tim;
        }
 
        for (int i = 1; i <= n; i ++) cout << res[i];
}

---

CodeForces1482D_Playlist

🔗

💡

先不急着把所有的可能会碰见的两点都预处理出来
先预处理第一轮会删除的两点，即相邻的 $(i,j)$ 满足 $(a[i],a[j])=1$ 的
为了避免时间浪费，使用 $map$ 存储，可以快速得到我们这一轮要进行删除的点
然后去进行删点操作，对于相邻的三个点 $(i,j,k)$ ，我们先删除了 $j$ ，此时 $i,k$ 相邻，去判断一下 $(a[i],a[k])$ 是否等于 $1$ ，如果等于的话，将 $mp[i]$ 的值换成 $k$ ，如果不等于的话，那么就传进一个待删除的数组里面（因为遍历 $map$ 过程中是不能删除当前键的）
此时 $j$ 不存在了，直接删除掉 $mp[j]$ ，然后走下一个（要删除 $k$ 都是下一轮的事情了）
当然我们的相邻关系也要发生改变，可以用链表记录后继是谁
由于最多删 $n$ 个，所以带上 $map$ 复杂度为 $O(nlogn)$

有一个细节要处理，就是如果我们当前 $map$ 里面有一个点对，并且这个点对是 $(1,1)$ ，如果不进行特判就会死循环，这里特判一下如果满足就将 $1$ 加入答案然后 break

✅

const int N = 1e5 + 10;
int n, nxt[N], pre[N], a[N];
map<int, int> mp;

inline int gcd (int a, int b) {return b ? gcd(b, a % b) : a;}
inline void del (int i) { // 删除 i
        nxt[pre[i]] = nxt[i];
        pre[nxt[i]] = pre[i];
        mp.erase(i);
}

inline void Solve () {
        cin >> n;
        for (int i = 1; i <= n; i ++) cin >> a[i];

        mp.clear();
        for (int i = 1; i <= n; i ++) {
                if (gcd(a[i], a[i == n ? 1 : i + 1]) == 1) {
                        mp[i] = i == n ? 1 : i + 1;
                }
                nxt[i] = i + 1;
                pre[i] = i - 1;
        }
        nxt[n] = 1;
        pre[1] = n;

        vector<int> res;
        while (mp.size()) {
                if (mp.size() == 1 && mp.begin()->first == mp.begin()->second) {
                        res.push_back(mp.begin()->first);
                        break;
                }
                vector<int> delnum; // 待删除数组
                for (auto &it : mp) {
                        res.push_back(it.second);
                        del(it.second);
                        if (gcd(a[it.first], a[nxt[it.second]]) == 1) { // 与后继形成新的点对，修改
                                it.second = nxt[it.second];
                        } else { // 形成不了，加入待删除数组
                                delnum.push_back(it.first);
                        }
                }
                for (int i : delnum) mp.erase(i);
        }

        cout << res.size() << " ";
        for (int i : res) cout << i << " ";
        cout << endl;
}

---