矩阵树定理

#

---

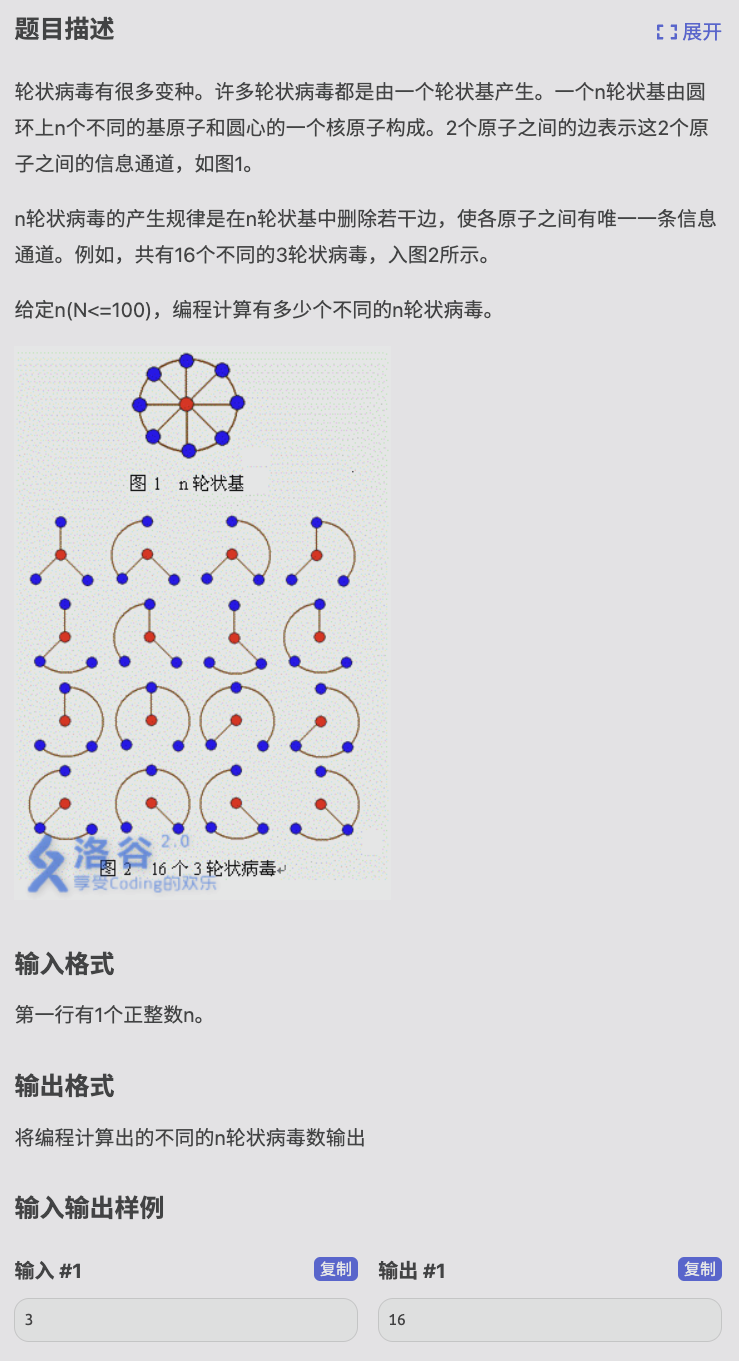
洛谷P2144_轮状病毒

🔗

💡

无向图统计生成树个数
设一圈是1~n号点，中心是n+1号点，就连一圈边，然后每个点还要与n+1号点相连
利用矩阵树定理构建行列式，然后高斯消元求一下行列式即可
（答案过大爆longlong，Java出击

✅

public class Main {
        static BigInteger [][] a = new BigInteger[110][110];
        static int n;
        public static void add ( int x, int y ) {
                a[x][y] = a[x][y].subtract(BigInteger.ONE);
                a[y][x] = a[y][x].subtract(BigInteger.ONE);
                a[x][x] = a[x][x].add(BigInteger.ONE);
                a[y][y] = a[y][y].add(BigInteger.ONE);
        }
        public static BigInteger Gauss ( int n ) {
                BigInteger res = BigInteger.ONE;
                for ( int i = 1; i <= n; i ++ ) {
                        for ( int ii = i + 1; ii <= n; ii ++ ) {
                                while ( a[ii][i].compareTo(BigInteger.ZERO) != 0 ) {
                                        BigInteger d = a[i][i].divide(a[ii][i]);
                                        for ( int j = i; j <= n; j ++ ) {
                                                a[i][j] = a[i][j].subtract(d.multiply(a[ii][j]));
                                                BigInteger tmp = a[i][j];
                                                a[i][j] = a[ii][j];
                                                a[ii][j] = tmp;
                                        }
                                        res = BigInteger.ZERO.subtract(res);
                                }
                        }
                        res = res.multiply(a[i][i]);
                        if ( res.compareTo(BigInteger.ZERO) == 0 ) return BigInteger.ZERO;
                }
                return res;
        }
        public static void main (String[] args) {
                for ( int i = 0; i < 110; i ++ ) for ( int j = 0; j < 110; j ++ ) a[i][j] = BigInteger.ZERO;
                Scanner cin = new Scanner(System.in);
                n = cin.nextInt();
                for ( int i = 1; i <= n; i ++ ) {
                        add((i % n) + 1, (i + 1) % n + 1);
                        add((i % n) + 1, n + 1);
                }
                System.out.println(Gauss(n));
        }
}

---

洛谷P4111_小Z的房间

🔗

💡

两两能到达的房间连边
求无向图生成树个数
对每一个单位重新编号，然后进行连边
可以采用每一个点如果能向右连就向右连，能向下连就向下连，可以防止重复
使用矩阵树定理建行列式
高斯消元求一下行列式sz-1阶行列式即可即可

✅

const int N = 15, M = 105;
const int mod = 1e9;
char s[N][N];
int id[N][N], a[M][M];
int n, m;

inline void add ( int x, int y ) {
	-- a[x][y];
	-- a[y][x];
	++ a[x][x];
	++ a[y][y];
}
inline int Gauss ( int n ) {
	int res = 1;
	for ( int i = 1; i <= n; i ++ ) { // 在(i, i)上进行消元
		for ( int ii = i + 1; ii <= n; ii ++ ) { // 将(ii, i)变成0
			while ( a[ii][i] ) {
				int d = a[i][i] / a[ii][i];
				for ( int j = i; j <= n; j ++ )
					a[i][j] = (a[i][j] - (ll)d * a[ii][j] % mod + mod) % mod,
					swap ( a[i][j], a[ii][j] );
				res = -res;
			}
		}
		res = (ll)res * a[i][i] % mod;
		if ( res == 0 ) return 0;
	}
	return (res % mod + mod) % mod;
}


int main () {
	cin >> n >> m;
	for ( int i = 1; i <= n; i ++ ) cin >> (s[i] + 1);
	int idx = 0;
	for ( int i = 1; i <= n; i ++ ) for ( int j = 1; j <= m; j ++ ) if ( s[i][j] == '.' ) id[i][j] = ++ idx;
	for ( int i = 1; i <= n; i ++ ) for ( int j = 1; j <= m; j ++ ) if ( s[i][j] == '.' ) {
		if ( id[i - 1][j] ) add ( id[i][j], id[i - 1][j] );
		if ( id[i][j - 1] ) add ( id[i][j], id[i][j - 1] );
	}
	cout << Gauss ( idx - 1 ) << endl;
	return 0;
}

---

洛谷P4336_黑暗前的幻想乡

🔗

💡

每条公路只能给一个公司构造
如果多个公司建造这条路
那么就是我们重复考虑的地方
重复，计数，可以想到容斥原理
我们可以二进制枚举一下让哪些公司来建边
每一次的结果就是这套方案的生成树个数

然后容斥地加减，最后得到每条边一个公司建造的结果

✅

const ll M = 100;
const ll mod = 1e9 + 7;
ll a[M][M];
ll n, m;

inline void add ( ll x, ll y ) {
        -- a[x][y];
        -- a[y][x];
        ++ a[x][x];
        ++ a[y][y];
}
inline ll Gauss ( ll n ) {
        ll res = 1;
        for ( ll i = 1; i <= n; i ++ ) { // 在(i, i)上进行消元
                for ( ll ii = i + 1; ii <= n; ii ++ ) { // 将(ii, i)变成0
                        while ( a[ii][i] ) {
                                ll d = a[i][i] / a[ii][i];
                                for ( ll j = i; j <= n; j ++ )
                                        a[i][j] = (a[i][j] - (ll)d * a[ii][j] % mod + mod) % mod,
                                                swap ( a[i][j], a[ii][j] );
                                res = -res;
                        }
                }
                res = (ll)res * a[i][i] % mod;
                if ( res == 0 ) return 0;
        }
        return (res % mod + mod) % mod;
}

vector<pair<ll, ll> > vec[M];

int main () {
        cin >> n;
        for ( ll i = 0; i < n - 1; i ++ ) {
                cin >> m;
                for ( ll j = 0, x, y; j < m; j ++ ) {
                        cin >> x >> y;
                        vec[i].push_back({x, y});
                }
        }
        ll res = 0;
        for ( ll num = 0; num < (1ll << (n - 1)); num ++ ) {
                for ( ll i = 0; i < M; i ++ ) for ( ll j = 0; j < M; j ++ ) a[i][j] = 0;
                ll cnt = 0;
                for ( ll i = 0; i < n - 1; i ++ ) {
                        if ( num & (1 << i) ) {
                                cnt ++;
                                for ( auto j : vec[i] ) add(j.first, j.second);
                        }
                }
                if ( (n - cnt) & 1 ) res = (res + Gauss(n - 1)) % mod;
                else res = (res - Gauss( n - 1 ) + mod) % mod;
        }
        cout << res << endl;
        return 0;
}

---

洛谷P4821_生成树

🔗

💡

无向图+生成树个数
对内圈每一个节点编一个号，外面的五边形多出来的三个点设一个计数器进行编号
对连的边用矩阵树定理构造行列式
然后高斯消元解行列式即可

✅

const int N = 105, M = 505;
const int mod = 2007;
int a[M][M];
int n, m;

inline void add ( int x, int y ) {
	-- a[x][y];
	-- a[y][x];
	++ a[x][x];
	++ a[y][y];
}
inline int Gauss ( int n ) {
	int res = 1;
	for ( int i = 1; i <= n; i ++ ) { // 在(i, i)上进行消元
		for ( int ii = i + 1; ii <= n; ii ++ ) { // 将(ii, i)变成0
			while ( a[ii][i] ) {
				int d = a[i][i] / a[ii][i];
				for ( int j = i; j <= n; j ++ )
					a[i][j] = (a[i][j] - (ll)d * a[ii][j] % mod + mod) % mod,
					swap ( a[i][j], a[ii][j] );
				res = -res;
			}
		}
		res = (ll)res * a[i][i] % mod;
		if ( res == 0 ) return 0;
	}
	return (res % mod + mod) % mod;
}


int main () {
	int cass;
	for ( cin >> cass; cass; cass -- ) {
		for ( int i = 0; i < M; i ++ ) for ( int j = 0; j < M; j ++ ) a[i][j] = 0;
		cin >> n;
		int idx = n + 1;
		for ( int i = 1; i < n; i ++ ) {
			add ( i, idx );
			add ( idx, idx + 1 ); 
			add ( idx + 1, idx + 2 );
			add ( idx + 2, i + 1 );
			add ( i, i + 1 );
			idx += 3;
		}
		add ( n, idx );
		add ( idx, idx + 1 );
		add ( idx + 1, idx + 2 );
		add ( idx + 2, 1 ); 
		add ( n, 1 );
		idx += 2;
		cout << Gauss ( idx - 1 ) << endl;

	}
	return 0;
}

---