树上启发式合并

Chivas-Regal

#

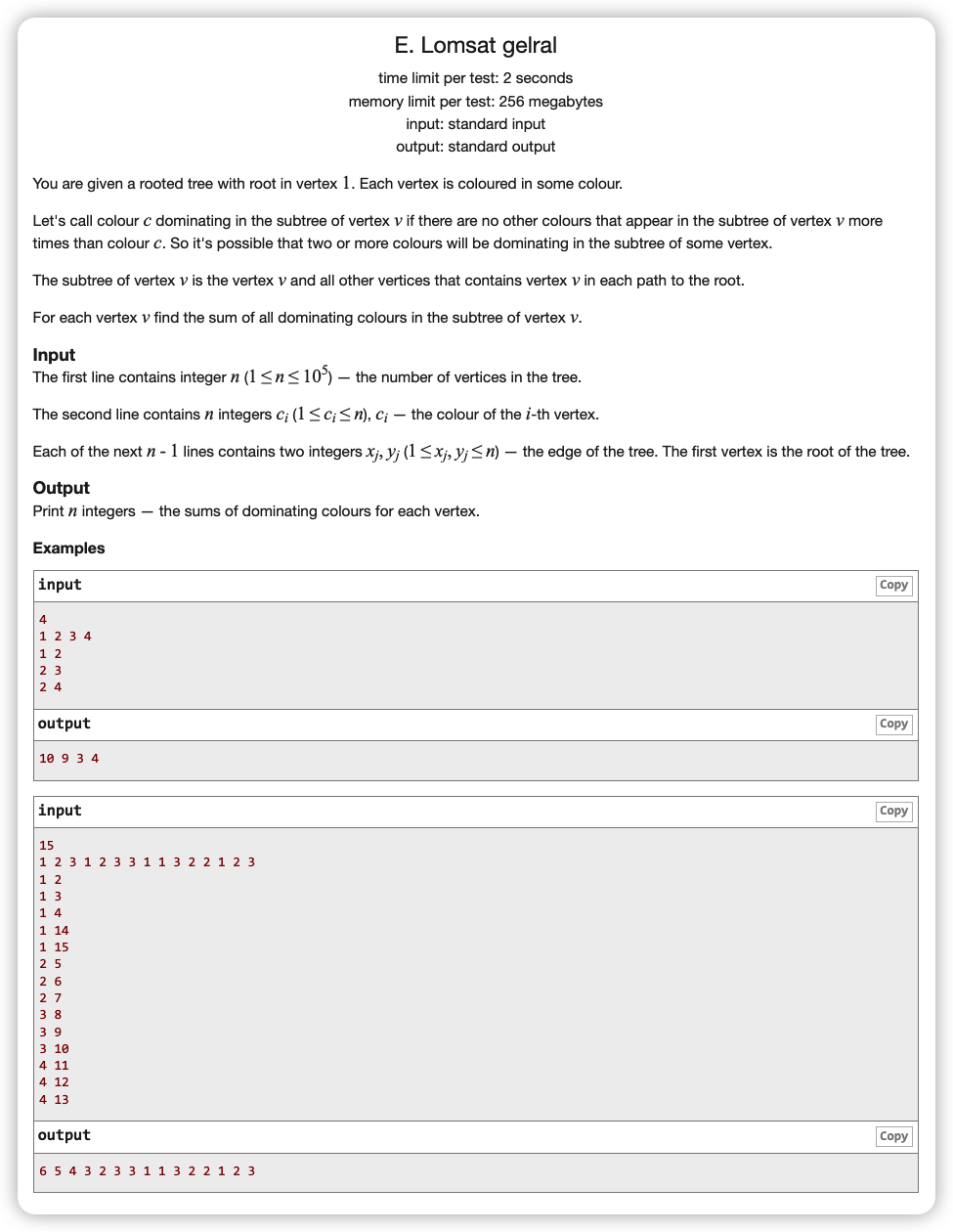
# CodeForces600E_LomsatGelral

# 🔗

# 💡

本题为模板题，知识点与伪代码看这里 (opens new window)
本题 $AC$ 代码已批注释

# ✅

const int N = 1e5 + 10;
const int M = 2e5 + 10;
struct Edge {
        int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge ( int from, int to ) {
        edge[++cnt] = { head[from], to };
        head[from] = cnt;
}

int n, col[N], num[N];

int son[N], sz[N];
inline void pre_Son ( int u, int fa ) { // todo: 预处理出重儿子
        sz[u] = 1; son[u] = 0;
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fa ) continue;
                pre_Son(v, u);
                sz[u] += sz[v];
                if ( sz[v] > sz[son[u]] ) son[u] = v;
        }
}

int flag;
ll max_num, max_col, res[N];
inline void dfs_Count ( int u, int fa, int val ) { // todo: 暴力处理出 flag 节点之外的所有点从而得到的答案
        num[col[u]] += val;
        if ( num[col[u]] > max_num ) // 更新最大颜色
                max_num = num[col[u]],
                max_col = col[u];
        else if ( num[col[u]] == max_num ) // 同数量颜色要累加
                max_col += col[u];
        
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fa || v == flag ) continue;
                dfs_Count(v, u, val);
        }
}

inline void dfs_Main ( int u, int fa, bool keep ) { // todo: 树上启发式合并
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fa || v == son[u] ) continue;
                dfs_Main(v, u, false); // 先递归轻儿子
        }
        if ( son[u] ) dfs_Main(son[u], u, true), flag = son[u]; // 递归重儿子

        dfs_Count(u, fa, 1); // 暴力统计所有轻儿子树
        res[u] = max_col;
        flag = 0;
        if ( !keep ) { // 这是个轻节点，删除它的所有贡献信息
                dfs_Count(u, fa, -1); 
                max_num = max_col = 0; // 它对最大值的贡献也要删除
        }
}


int main () {
        scanf("%d", &n);
        for ( int i = 1; i <= n; i ++ ) scanf("%d", &col[i]);
        for ( int i = 1; i < n; i ++ ) {
                int u, v; scanf("%d%d", &u, &v);
                add_Edge(u, v);
                add_Edge(v, u);
        }

        pre_Son(1, 0);
        dfs_Main(1, 0, 1);

        for ( int i = 1; i <= n; i ++ ) printf("%lld ", res[i]);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

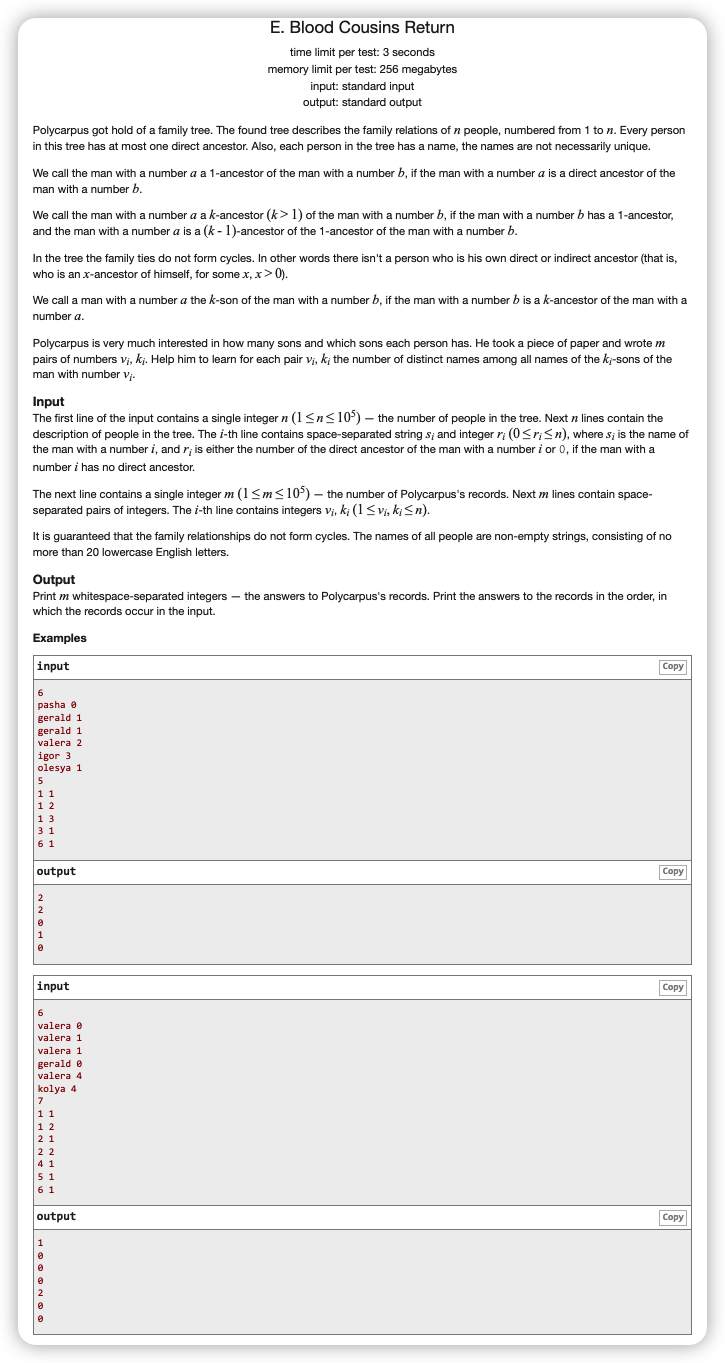
# CodeForces246E_BloodCousinsReturn

# 🔗

# 💡

注意到 $v$ 的 $k$ 儿子和 $v$ 的深度是相对的
那么我们就固定完深度后，查找 $dep_v+k$ 的深度的不同名字个数即可
考虑在树上启发式合并的主体递归内，到一个点后我们去找完它的轻儿子后，就收集了整棵子树的信息
这样其实可以开一个 map 去存放不同深度下的节点名称
即在 dfs_Count(u, fa) 内，令 map[dep[u]][col[u]] ++ 即可
在删除子树信息的时候若 map[dep[u]][col[u]] = 0 就删掉这个名字
这样在我们的主体递归内，在关于 $u$ 的所有问题都可以直接在对应的深度下求 map[].size() 即可

# ✅

const int N = 1e5 + 10;
const int M = 2e5 + 10;

struct Edge {
        int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge ( int from, int to ) {
        edge[++cnt] = { head[from], to };
        head[from] = cnt;
}

int son[N], fa[N], sz[N], dep[N];
inline void dfs_Son ( int u, int fath ) {
        fa[u] = fath;
        sz[u] = 1;
        dep[u] = dep[fath] + 1;
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fath ) continue;
                dfs_Son(v, u);
                sz[u] += sz[v];
                if ( sz[son[u]] < sz[v] ) son[u] = v;
        }
}

int n, q;
string name[N];
struct Query {
        int k;
        int id;
};
vector<Query> g[N];
int res[N]; 

map<string, int> nameson[N];
int flag;

inline void dfs_Count ( int u, int ope ) {
        if ( ope == 1 ) {
                nameson[dep[u]][name[u]] ++;
        } else {
                nameson[dep[u]][name[u]] --;
                if ( !nameson[dep[u]][name[u]] ) nameson[dep[u]].erase(name[u]);
        }
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fa[u] || v == flag ) continue;
                dfs_Count(v, ope);
        }
}

inline void dfs_Main ( int u, bool keep ) {
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fa[u] || v == son[u] ) continue;
                dfs_Main(v, false);
        }
        if ( son[u] ) dfs_Main(son[u], true), flag = son[u];

        dfs_Count(u, 1); flag = 0;
        for ( auto [k, id] : g[u] ) {
                if ( dep[u] + k > n ) continue;
                res[id] = nameson[dep[u] + k].size();
        }

        if ( !keep ) dfs_Count(u, -1);
}

int main () {
        cin.tie(0)->sync_with_stdio(0);
        cin.exceptions(cin.failbit);

        cin >> n; vector<int> in(n + 1, 0);
        for ( int i = 1; i <= n; i ++ ) {
                int fath; cin >> name[i] >> fath;
                if ( fath == 0 ) continue;
                in[i] ++;
                add_Edge(fath, i);
        }
        
        for ( int i = 1; i <= n; i ++ ) if ( !in[i] ) dfs_Son(i, 0);
        
        cin >> q;
        for ( int i = 1; i <= q; i ++ ) {
                int v, k; cin >> v >> k;
                g[v].push_back({k, i});
        }

        for ( int i = 1; i <= n; i ++ ) if ( !in[i] ) dfs_Main(i, false);

        for ( int i = 1; i <= q; i ++ ) cout << res[i] << "\n";
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93

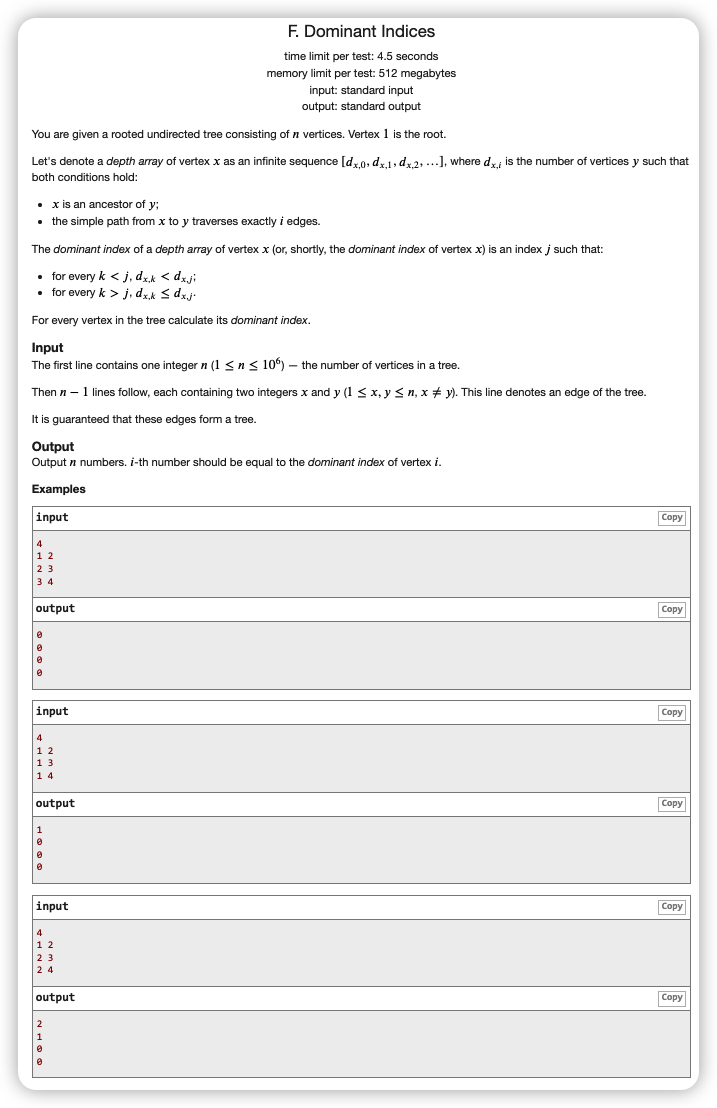
# CodeForces1009F_DominantIndices

# 🔗

# 💡

考虑好两个条件
$a<x<b,\;d_{v,a}<d_{v,x}\le d_{v,b}$
这就是在说让我们在 $v$ 的子树内，找到节点个数最多的深度，如果有多个深度节点个数相同且最多，选择最小的深度
那么就在 dfs_Count() 下维护一下每个深度的节点最小数量和该深度编号即可

# ✅

const int N = 1e6 + 10;
const int M = 2e6 + 10;

struct Edge {
        int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge ( int from, int to ) {
        edge[++cnt] = { head[from], to };
        head[from] = cnt;
}

int son[N], sz[N], out[N], dep[N];
inline void dfs_Son ( int u, int fa ) {
        sz[u] = 1;
        son[u] = 0;
        dep[u] = dep[fa] + 1;
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fa ) continue;
                dfs_Son(v, u);
                sz[u] += sz[v];
                if ( sz[v] > sz[son[u]] ) son[u] = v;
                out[u] ++;
        } 
} 

int flag;
int dep_num[N];

int mxid = 0, mxval = 1; 
int res[N];
inline void dfs_Count ( int u, int fa, int ope ) {
        dep_num[dep[u]] += ope;
        if ( mxval < dep_num[dep[u]] ) {
                mxval = dep_num[dep[u]];
                mxid = dep[u];
        } else if ( mxval == dep_num[dep[u]] && mxid > dep[u] ) {
                mxid = dep[u];
        } 
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fa || v == flag ) continue;
                dfs_Count(v, u, ope);
        }
}

inline void dfs_Main ( int u, int fa, bool keep ) {
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fa || v == son[u] ) continue;
                dfs_Main(v, u, false);
        }
        if ( son[u] ) dfs_Main(son[u], u, true);

        flag = son[u]; dfs_Count(u, fa, 1); flag = 0;
        res[u] = mxid;

        if ( !keep ) {
                dfs_Count(u, fa, -1);
                mxid = 0;
                mxval = 1;
        }
}

int main () {
        cin.tie(0)->sync_with_stdio(0);
        cin.exceptions(cin.failbit);

        int n; cin >> n;
        for ( int i = 1; i < n; i ++ ) {
                int u, v; cin >> u >> v;
                add_Edge(u, v);
                add_Edge(v, u);
        }  
        dfs_Son(1, 0);
        dfs_Main(1, 0, true);
        for ( int i = 1; i <= n; i ++ ) {
                if ( res[i] == 0 ) cout << "0\n";
                else               cout << res[i] - dep[i] << "\n";
        }

# CodeForces375D_TreeAndQueries

# 🔗

# 💡

我们在对个数加减时可以正确保留一个重链的颜色个数集
注意一下查询
这个查询是查询个数比 $k$ 大的数，如果我们统计完每次做查询的时候往后扫每一个颜色一定超时
但是这样看来对于个数来说算是一个线性的区间查询
那么可以直接在 dfs_Count 统计时统计数字个数，顺带将该个数插入线段树内
然后在查询时直接查询 $k\to N$ 的区间和即可

# ✅

const int N = 1e5 + 10;
const int M = 2e5 + 10;

namespace SegmentTree { 
        int t[N << 2];
        inline void PushUp ( int rt ) {
                t[rt] = t[rt << 1] + t[rt << 1 | 1];
        }
        inline void Update ( int id, int c, int l = 1, int r = N, int rt = 1 ) {
                if ( l == id && id == r ) {
                        t[rt] += c;
                        return;
                }
                if ( l > id || id > r ) return;
                int mid = (l + r) >> 1;
                Update(id, c, l, mid, rt << 1);
                Update(id, c, mid + 1, r, rt << 1 | 1);
                PushUp(rt);
        }
        inline int Query ( int a, int l = 1, int r = N, int rt = 1 ) {
                if ( r < a ) return 0;
                if ( a <= l ) return t[rt];
                int mid = (l + r) >> 1;
                return Query(a, l, mid, rt << 1) + Query(a, mid + 1, r, rt << 1 | 1);
        }
}

struct Edge {
        int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge ( int from, int to ) {
        edge[++cnt] = { head[from], to };
        head[from] = cnt;
}

int n, col[N], num[N], q;

int son[N], sz[N];
inline void dfs_Son ( int u, int fa ) {
        son[u] = 0;
        sz[u] = 1;
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fa ) continue;
                dfs_Son(v, u);
                sz[u] += sz[v];
                if ( sz[son[u]] < sz[v] ) son[u] = v;
        }
}

int flag;
int res[N];
inline void dfs_Count ( int u, int fa, int ope ) {
        if ( num[col[u]] ) SegmentTree::Update(num[col[u]], -1);
        num[col[u]] += ope;
        if ( num[col[u]] ) SegmentTree::Update(num[col[u]], 1);
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fa || v == flag ) continue;
                dfs_Count(v, u, ope);
        }
}

vector<pair<int, int> > g[N]; // val, id

inline void dfs_Main ( int u, int fa, bool keep ) {
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fa || v == son[u] ) continue;
                dfs_Main(v, u, false);
        }
        if ( son[u] ) dfs_Main(son[u], u, true);
        flag = son[u]; dfs_Count(u, fa, 1); flag = 0;

        for ( auto [down, id] : g[u] ) {
                res[id] = SegmentTree::Query(down);
        }

        if ( !keep ) dfs_Count(u, fa, -1);
}

int main () {
        scanf("%d%d", &n, &q);
        for ( int i = 1; i <= n; i ++ ) scanf("%d", &col[i]);
        for ( int i = 1; i < n; i ++ ) {
                int u, v; scanf("%d%d", &u, &v);
                add_Edge(u, v);
                add_Edge(v, u);
        }
        for ( int i = 1; i <= q; i ++ ) {
                int v, k; scanf("%d%d", &v, &k);
                g[v].push_back({k, i});
        }
        
        
        dfs_Son(1, 0); 
        dfs_Main(1, 0, true);
        
        for ( int i = 1; i <= q; i ++ ) {
                printf("%d\n", res[i]);
        }
}

# CodeForces570D_TreeRequests

# 🔗

# 💡

注意一下回文串是左右对称结构，但是奇数回文串我们倒是可以将中间插入一个数
这就意味着我们如果能组成回文串，那么当前统计的数量内，最多只能有一个奇数个数
看到这依旧是按层级来的，那么我们就每一层维护一个 set 专门存放对应层内的奇数数字
在查询时，如果该层 size 大于 $1$ 的话那么就无法构成，否则可以

# ✅

const int N = 5e5 + 10;
const int M = N * 2;
 
struct Edge {
        int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge ( int from, int to ) {
        edge[++cnt] = { head[from], to };
        head[from] = cnt;
}
 
char s[N]; int num[700];
vector<pair<int, int> > g[N]; // k,id
 
int dep[N], son[N], sz[N];
inline void dfs_Pre ( int u, int fa ) {
        dep[u] = dep[fa] + 1;
        son[u] = 0, sz[u] = 1;
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fa ) continue;
                dfs_Pre(v, u);
                sz[u] += sz[v];
                if ( sz[son[u]] < sz[v] ) son[u] = v;
        }
}
 
int flag;
set<char> odd[N];
bool res[N];
inline void dfs_Count ( int u, int fa, int op ) {
        if ( odd[dep[u]].count(s[u]) ) odd[dep[u]].erase(s[u]);
        else odd[dep[u]].insert(s[u]);
        num[s[u]] += op;
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fa || v == flag ) continue;
                dfs_Count(v, u, op);
        }
}
 
inline void dfs_Main ( int u, int fa, bool keep ) {
        for ( int i = head[u]; i; i = edge[i].nxt ) {
                int v = edge[i].to;
                if ( v == fa || v == son[u] ) continue;
                dfs_Main(v, u, false);
        }
        if ( son[u] ) dfs_Main(son[u], u, true);
        flag = son[u]; dfs_Count(u, fa, 1); flag = 0;
 
        for ( auto [k, id] : g[u] ) {
                res[id] = odd[k].size() <= 1;
        }
 
        if ( !keep ) dfs_Count(u, fa, -1);
}
 
int main () {
        int n, q; scanf("%d%d", &n, &q);
        for ( int i = 2; i <= n; i ++ ) {
                int f; scanf("%d", &f);
                add_Edge(i, f);
                add_Edge(f, i);
        }
        scanf("%s", s + 1);
        for ( int i = 1; i <= q; i ++ ) {
                int u, k; scanf("%d%d", &u, &k);
                g[u].push_back({k, i});
        }
 
        dfs_Pre(1, 0);
        dfs_Main(1, 0, true);
 
        for ( int i = 1; i <= q; i ++ ) {
                puts(res[i] ? "Yes" : "No");
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78

差分约束 kruskal重构树