组合数学

#

---

排列组合

洛谷P1066_2^k进制数

🔗

💡

我们先打一个 进制和 进制的对应表看看

表格

k	进制	进制	进制
1
	1	1	1
	2	10	10
	3	11	11
	4	100	100
	5	101	101
	6	110	110
	7	111	111
	8	1000	1000
	9	1001	1001
	10	1010	1010
	11	1011	1011
	12	1100	1100
	13	1101	1101
	14	1110	1110
	15	1111	1111
	16	10000	10000
	17	10001	10001
	18	10010	10010
	19	10011	10011
	20	10100	10100
	21	10101	10101
	22	10110	10110
	23	10111	10111
	24	11000	11000
	25	11001	11001
	26	11010	11010
	27	11011	11011
	28	11100	11100
	29	11101	11101
	30	11110	11110
	31	11111	11111
	32	100000	100000
	33	100001	100001
	34	100010	100010
	35	100011	100011
	36	100100	100100
	37	100101	100101
	38	100110	100110
	39	100111	100111
	40	101000	101000
	41	101001	101001
	42	101010	101010
	43	101011	101011
	44	101100	101100
	45	101101	101101
	46	101110	101110
	47	101111	101111
	48	110000	110000
	49	110001	110001
	50	110010	110010
	51	110011	110011
	52	110100	110100
	53	110101	110101
	54	110110	110110
	55	110111	110111
	56	111000	111000
	57	111001	111001
	58	111010	111010
	59	111011	111011
	60	111100	111100
	61	111101	111101
	62	111110	111110
	63	111111	111111
64	1000000	1000000
65	1000001	1000001
66	1000010	1000010
67	1000011	1000011
68	1000100	1000100
69	1000101	1000101
70	1000110	1000110
71	1000111	1000111
72	1001000	1001000
73	1001001	1001001
74	1001010	1001010
75	1001011	1001011
76	1001100	1001100
77	1001101	1001101
78	1001110	1001110
79	1001111	1001111
80	1010000	1010000
81	1010001	1010001
82	1010010	1010010
83	1010011	1010011
84	1010100	1010100
85	1010101	1010101
86	1010110	1010110
87	1010111	1010111
88	1011000	1011000
89	1011001	1011001
90	1011010	1011010
91	1011011	1011011
92	1011100	1011100
93	1011101	1011101
94	1011110	1011110
95	1011111	1011111
96	1100000	1100000
97	1100001	1100001
98	1100010	1100010
99	1100011	1100011
100	1100100	1100100
2
	1	1	1
	2	2	10
	3	3	11
	4	10	100
	5	11	101
	6	12	110
	7	13	111
	8	20	1000
	9	21	1001
	10	22	1010
	11	23	1011
	12	30	1100
	13	31	1101
	14	32	1110
	15	33	1111
	16	100	10000
	17	101	10001
	18	102	10010
	19	103	10011
	20	110	10100
	21	111	10101
	22	112	10110
	23	113	10111
	24	120	11000
	25	121	11001
	26	122	11010
	27	123	11011
	28	130	11100
	29	131	11101
	30	132	11110
	31	133	11111
	32	200	100000
	33	201	100001
	34	202	100010
	35	203	100011
	36	210	100100
	37	211	100101
	38	212	100110
	39	213	100111
	40	220	101000
	41	221	101001
	42	222	101010
	43	223	101011
	44	230	101100
	45	231	101101
	46	232	101110
	47	233	101111
	48	300	110000
	49	301	110001
	50	302	110010
	51	303	110011
	52	310	110100
	53	311	110101
	54	312	110110
	55	313	110111
	56	320	111000
	57	321	111001
	58	322	111010
	59	323	111011
	60	330	111100
	61	331	111101
	62	332	111110
	63	333	111111
64	1000	1000000
65	1001	1000001
66	1002	1000010
67	1003	1000011
68	1010	1000100
69	1011	1000101
70	1012	1000110
71	1013	1000111
72	1020	1001000
73	1021	1001001
74	1022	1001010
75	1023	1001011
76	1030	1001100
77	1031	1001101
78	1032	1001110
79	1033	1001111
80	1100	1010000
81	1101	1010001
82	1102	1010010
83	1103	1010011
84	1110	1010100
85	1111	1010101
86	1112	1010110
87	1113	1010111
88	1120	1011000
89	1121	1011001
90	1122	1011010
91	1123	1011011
92	1130	1011100
93	1131	1011101
94	1132	1011110
95	1133	1011111
96	1200	1100000
97	1201	1100001
98	1202	1100010
99	1203	1100011
100	1210	1100100
3
	1	1	1
	2	2	10
	3	3	11
	4	4	100
	5	5	101
	6	6	110
	7	7	111
	8	10	1000
	9	11	1001
	10	12	1010
	11	13	1011
	12	14	1100
	13	15	1101
	14	16	1110
	15	17	1111
	16	20	10000
	17	21	10001
	18	22	10010
	19	23	10011
	20	24	10100
	21	25	10101
	22	26	10110
	23	27	10111
	24	30	11000
	25	31	11001
	26	32	11010
	27	33	11011
	28	34	11100
	29	35	11101
	30	36	11110
	31	37	11111
	32	40	100000
	33	41	100001
	34	42	100010
	35	43	100011
	36	44	100100
	37	45	100101
	38	46	100110
	39	47	100111
	40	50	101000
	41	51	101001
	42	52	101010
	43	53	101011
	44	54	101100
	45	55	101101
	46	56	101110
	47	57	101111
	48	60	110000
	49	61	110001
	50	62	110010
	51	63	110011
	52	64	110100
	53	65	110101
	54	66	110110
	55	67	110111
	56	70	111000
	57	71	111001
	58	72	111010
	59	73	111011
	60	74	111100
	61	75	111101
	62	76	111110
	63	77	111111
64	100	1000000
65	101	1000001
66	102	1000010
67	103	1000011
68	104	1000100
69	105	1000101
70	106	1000110
71	107	1000111
72	110	1001000
73	111	1001001
74	112	1001010
75	113	1001011
76	114	1001100
77	115	1001101
78	116	1001110
79	117	1001111
80	120	1010000
81	121	1010001
82	122	1010010
83	123	1010011
84	124	1010100
85	125	1010101
86	126	1010110
87	127	1010111
88	130	1011000
89	131	1011001
90	132	1011010
91	133	1011011
92	134	1011100
93	135	1011101
94	136	1011110
95	137	1011111
96	140	1100000
97	141	1100001
98	142	1100010
99	143	1100011
100	144	1100100

可以发现几个有趣的事情：
$1.$ $2^k$ 进制对于 $2$ 进制的进位极限在 $2^k$ 进制表示的最高位上呈这样的排列

k=1	1,1,1,1,1,1,...
k=2	1,3,1,3,1,3,...
k=3	1,3,7,1,3,7,...

那么我们可以从中推出

k=x	$2^0-1,2^1-1,2^2-1,...2^x-1,2^0-1,2^1-1,2^2-1,....,2^x-1....$

$2.$ $2^k$ 进制下，在这个排列里面，一次循环 $2^k$ 进制会进一位

对于题目，我们走完这个排列中 个数就可以结束了
我们枚举最高位的数字 ，可知在一次循环中我们 进制的位数时不变的
且如果 是 的幂次，即 那么就说明我们走过了排列中的一个数也就是在 进制下进了一位
而我们想要在最高位 数字为 时后面低位有多少种构造方式，可以通过 预处理一下

但是我们这个是计算了 进制下的所有可行位数，最后还要按要求减掉 位的

这里上 高精

✅

public class Main {

        static BigInteger zero = BigInteger.ZERO;
        static BigInteger one = BigInteger.ONE;
        static BigInteger two = BigInteger.valueOf(2);
        static BigInteger six = BigInteger.valueOf(6);
        static BigInteger ten = BigInteger.TEN;

        static int N = 1000;
        static BigInteger[][] dp = new BigInteger[N][N];
        static int k, w;

        public static void Get_Dp () {
                for ( int i = 0; i < N; i ++ ) for ( int j = 0; j < N; j ++ ) dp[i][j] = zero;
                for ( int i = 1; i < (1 << k); i ++ ) dp[1][i] = one;
                for ( int i = 2; i < (1 << k); i ++ ) {
                        for ( int j = 2; j < (1 << k); j ++ ) dp[i][1] = dp[i][1].add(dp[i - 1][j]);
                        for ( int j = 2; j < (1 << k); j ++ ) dp[i][j] = dp[i][j - 1].subtract(dp[i - 1][j]);
                }
        }
        public static int lowbit ( int x ) { return x & (-x); }
        public static void main (String[] args) {
                Scanner input = new Scanner(System.in);
                k = input.nextInt();
                w = input.nextInt(); int tmp = w;
                Get_Dp();

                int num = 1;
                BigInteger res = zero;
                boolean flag = false;
                while ( true ) {
                        for ( int i = 1; i < (1 << k); i ++ ) {         // 枚举最高位
                                res = res.add(dp[num][i]);              // num个数字，最高位是i的构造方式
                                if ( lowbit(i + 1) == i + 1 ) w --;     // 是排列中的一个数，进了一位
                                if ( w == 0 ) { flag = true; break; }   // 进到头了
                        }
                        if ( flag ) break;
                        num ++;
                }

                w = tmp;
                for ( int i = 1; i < (1 << k); i ++ ) { // 减去(2^k)长度为1的串
                        res = res.subtract(dp[1][i]);
                        if ( lowbit(i + 1) == i + 1 ) w --;
                        if ( w == 0 ) break;
                }
                System.out.println(res);
                input.close();
        }
}

---

洛谷P2290_树的计数

🔗

💡

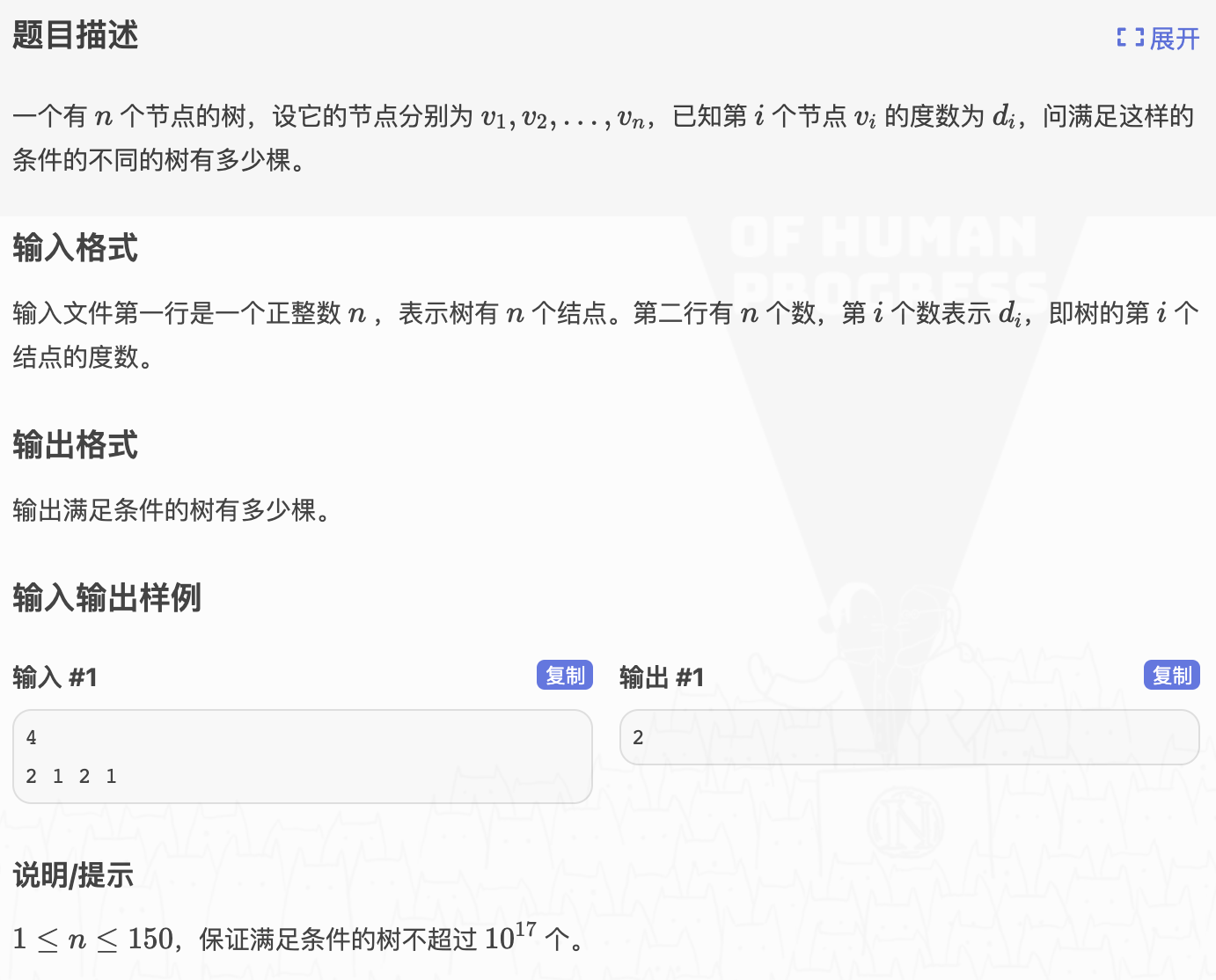
直接根据Prufer编码性质3推论进行这个式子的计算
不过需要特判很多地方
1.如果节点数为1，输入的点度数只能是一个0
2.如果节点数不为1，有一个节点度数是0就不行
3.如果节点数不为1，才行

这些特判判掉之后就进行计算即可
要开高精

✅

public class Main {
        public static BigInteger one = BigInteger.ONE;
        public static BigInteger zero = BigInteger.ZERO;
        public static BigInteger two = BigInteger.valueOf(2);
        public static BigInteger ten = BigInteger.TEN;
        
        static int N = 200;
        static BigInteger[] f = new BigInteger[N];
        public static void get_F () {
                f[0] = one;
                for ( int i = 1; i < N; i ++ ) {
                        f[i] = f[i - 1].multiply(BigInteger.valueOf(i));
                }
        }
        static int n;
        static int[] d = new int[N];
        static int sumd = 0;

        public static void main ( String[] args ) {
                get_F();
                Scanner input = new Scanner(System.in);
                n = input.nextInt();
                for ( int i = 0; i < n; i ++ ) {
                        d[i] = input.nextInt();
                        sumd += d[i] - 1;
                }
                if ( n == 1 ) {
                        if ( d[0] == 0 ) System.out.println(1);
                        else             System.out.println(0);
                        return;
                }
                if ( sumd != n - 2 ) {
                        System.out.println(0);
                        return;
                }
                for ( int i = 0; i < n; i ++ )
                        if ( d[i] == 0 ) {
                                System.out.println(0);
                                return;
                        }

                BigInteger up = f[n - 2];
                BigInteger down = one;
                for ( int i = 0; i < n; i ++ ) down = down.multiply(f[d[i] - 1]);
                if ( down.compareTo(zero) != 0 ) System.out.println(up.divide(down));
                else                             System.out.println(0);

                input.close();
        }
}

---

洛谷P2606_排列计数

🔗

💡

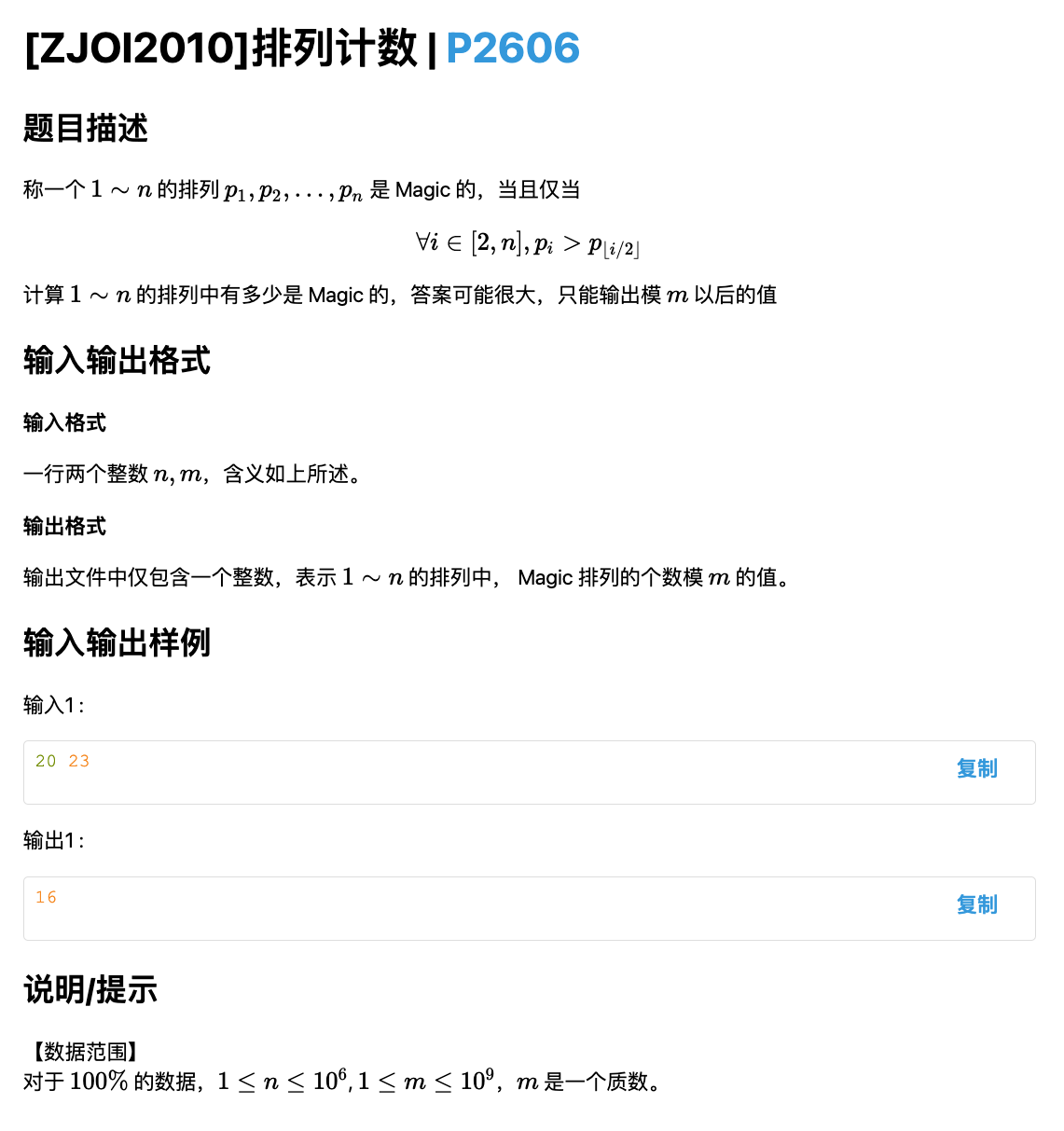
看到这个约束条件
我们可以构建出一棵二叉树
从 开始，我们有 个节点，可以选择 放入二号子树，其余放入三号子树
通俗地说，就是 放入左子树，其余放入右子树
这样就是

注意模数可能很小，所以我们需要用 定理

✅

const int N = 3e6 + 10;

int n, mod;

inline ll ksm ( ll a, ll b ) { ll res = 1; while ( b ) { if ( b & 1 ) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv ( ll x ) { return ksm(x, mod - 2); }
ll fac[N]; inline void get_Fac () { fac[0] = 1; for ( int i = 1; i < N; i ++ ) fac[i] = fac[i - 1] * i % mod; }
inline ll C ( ll n, ll m ) { 
        if ( n < m )   return 0;
        if ( n < mod ) return fac[n] * inv(fac[n - m]) % mod * inv(fac[m]) % mod; 
        return C ( n / mod, m / mod ) * C ( n % mod, m % mod ) % mod;
}

namespace Tree {
        ll sz[N];
        inline void get_Sz ( ll x ) {
                sz[x] = 1;
                if ( x * 2 <= n )     get_Sz ( x * 2 ),     sz[x] += sz[x * 2];
                if ( x * 2 + 1 <= n ) get_Sz ( x * 2 + 1 ), sz[x] += sz[x * 2 + 1];
        }
        inline ll dfs ( ll x ) {
                if ( x > n ) return 1; 
                return C ( sz[x] - 1, sz[2 * x] ) * dfs ( 2 * x ) % mod * dfs ( 2 * x + 1 ) % mod;
        }
} using namespace Tree;

int main () { 
        cin >> n >> mod;
        get_Fac (); get_Sz ( 1 );
        cout << dfs ( 1 ) << endl;
}

---

洛谷P3048_CowIDsS

🔗

💡

由于数从小到大，首先考虑跳过一些长度的数
对于长度 $x$ ，我们将一个 $1$ 拿出来放到第一个位置，后面的 $x-1$ 个位置放置 $k-1$ 个 $1$ 有 $C_{x-1}^{k-1}$ 中分布方式
那么就可以通过这样一步步对 $N$ 减小来固定出答案的长度是多少
然后剩下了 $N$ 个排名，考虑每一位如果放了 $1$ 会提升多少排名，我们只要让排名提升到等于 $N$ 即可
至于每一位放置 $1$ 提升的排名，令 $n-i$ 为后面的位置数，$one$ 为剩下还没有放置的 $1$ 的个数
那么提升的排名为 $C_{n-i}^{one}$
如果这个数比 $N$ 小的话就让 $N$ 减去它就行了，并且剩余未放置的 $1$ 的个数减一

✅

inline int C (int n, int m) {
        if (m < 0 || n < m) return 0;
        if (m == 0 || n == m) return 1;
        int res = 1;
        int idx = 1;
        for (int i = m + 1; i <= n; i ++) {
                res *= i;
                while (idx <= n - m && res % idx == 0) {
                        res /= idx;
                        ++ idx;
                }
        }
        return res;
}

int main () {
        int N, K; scanf("%d%d", &N, &K);
        N --;
        int n = K - 1, m = 0;
        int Cnm = C(n, m);
        while (N - Cnm >= 0) {
                N -= Cnm; 
                ++ n, ++ m;
                Cnm = C(n, m);
        }
        int one = n - m;

        putchar('1');
        for (int i = 1; i <= n; ++ i) {
                int cur = C(n - i, one);
                if (cur <= N) {
                        N -= cur;
                        putchar('1');
                        one --;
                } else {
                        putchar('0');
                }
        } 
}

---

洛谷P3904_三只小猪

🔗

💡

根据图片就能看出，$n$ 个不同的小猪放到 $m$ 个相同的房间里面，这不就是球盒模型吗？
看到数据量大力 $\begin{Bmatrix}n\\m\end{Bmatrix}$
（不过要开高精就是了

✅

public class Main{
        static int N = 2005;
        static BigInteger zero = BigInteger.ZERO;
        static BigInteger one = BigInteger.ONE;
        static BigInteger two = BigInteger.valueOf(2);
        static BigInteger six = BigInteger.valueOf(6);
        static BigInteger ten = BigInteger.TEN;
        static BigInteger five = BigInteger.valueOf(5);
        static BigInteger[][] s = new BigInteger[100][100];
        public static void main(String[] args) {
                Scanner input = new Scanner(System.in);
                int n = input.nextInt(), m = input.nextInt();
                for (int i = 0; i <= n; i ++) for (int j = 0; j <= m; j ++) s[i][j] = zero;
                for (int i = 1; i <= n; i ++) {
                        for (int j = 1; j <= i; j ++) {
                                if (j == i || j == 1) s[i][j] = one;
                                else s[i][j] = BigInteger.valueOf(j).multiply(s[i - 1][j]).add(s[i - 1][j - 1]);
                        }
                }
                System.out.println(s[n][m]);
                input.close();
        }
}

---

洛谷P3937_Changing

🔗

💡

分析第 $a_{t,i}$ 的转移关系
$\begin{aligned} &1a_{t,i}\\ =&1a_{t-1,i}+1a_{t-1,i+1}\\ =&1a_{t-2,i}+2a_{t-2,i+1}+1a_{t-2,i+2}\\ =&1a_{t-3,i}+3a_{t-3,i+1}+3a_{t-3,i+2}+1a_{t-3,i+3}\\ ... \end{aligned}(mod\;2)$
换句话说 $a_{t,k}=a_{t-1,k}+a_{t-1,k+1}$ 这个式子就很容易让人联想到杨辉三角
那么可以推出来式子 $a_{t,k}=\sum\limits_{i=0}^tC_t^ia_{0,k+i}$
等于说如果 $C_t^i=1$ 那么 $a_{0,k+i}$ 就会产生贡献
模 $2$ 的杨辉三角考虑 Sierpinski三角形推出来的杨辉三角与进制关系 (opens new window)
可以发发现当 $t\&i=i$ 时 $a_{k+i}$ 是有贡献的，加上即可
最后看答案的奇偶性

✅

int n, t, k;
inline int add (int x, int y) {return (x + y) % n;}

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        cin >> n >> t >> k; k --;
        vector<int> a(n); for (int i = 0; i < n; i ++) cin >> a[i];

        int res = 0;
        for (int i = 0; i <= t; i ++) {
                if ((t | i) == t) res ^= a[add(k, i)];
        }
        cout << res << endl;
}

---

洛谷P4562_游戏

🔗

💡

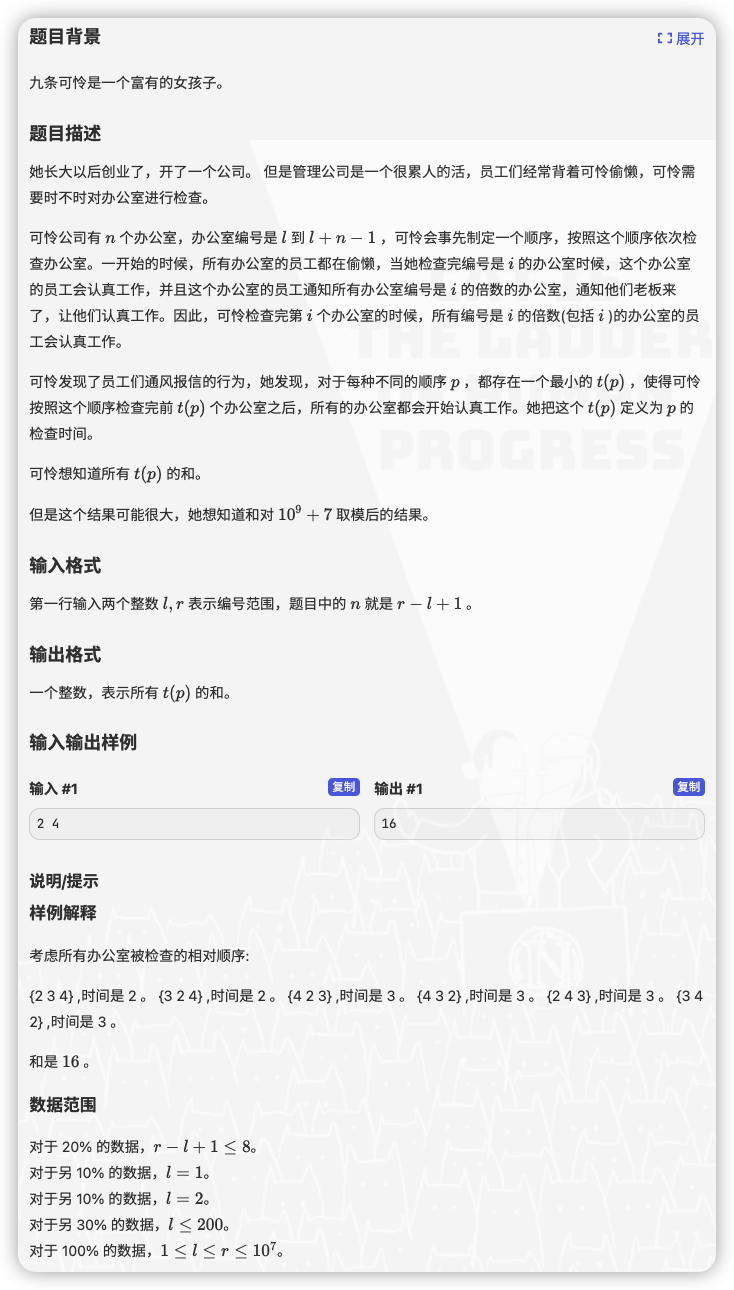
分析一波题意，$t(p)$ 就是对于排列 $p$ ，没有因子的数出现的最后位置

那么我们将所有数分为
$div_1$：无因子的数的数量
$div_2$：有因子的数的数量
这个可以通过埃氏筛求得

对于答案，考虑贡献，即为对于每一个位置 $i$，求它能作为 $t(p)$ 的排列数量 $num$
那么答案便是 $\sum\limits_i(i\times num)$

对于 $num$ 的求法:

• 我们让 $div_1$ 其中一个卡在第 $i$ 个位置
• 其余的 $div_1-1$ 个数在 $[1,i)$ 里面任意分布
• 这里我们只是考虑了位置。还要考虑方案数 所以 $div_1,div_2$ 也都要全排列一下

那么 $num=1\times \binom{i-1}{div_1-1}\times (div_1!)\times (div_2!)$

由于前 $i$ 个位置要存放完 $div_1$ 个数，所以 $i\in[div_1,n]$
所以答案为

$$\sum\limits_{i=div_1}^n(1\times\binom{i-1}{div_1-1}\times (div_1!)\times (div_2!)\times i)$$

✅

const int N = 1e7 + 10;
const int mod = 1e9 + 7;

inline ll ksm (ll a, ll b) { ll res = 1; while (b) { if (b & 1) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv (ll x) { return ksm(x, mod - 2); }

ll f[N], ivf[N];
inline void Pre () {
        f[0] = 1;
        for (int i = 1; i < N; i ++) f[i] = f[i - 1] * i % mod;
        ivf[N - 1] = inv(f[N - 1]);
        for (int i = N - 2; i >= 0; i --) ivf[i] = ivf[i + 1] * (i + 1) % mod;
}
inline ll C (int n, int m) {
        return f[n] * ivf[m] % mod * ivf[n - m] % mod;
}

bool vis[N];

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        Pre();

        int l, r; cin >> l >> r;
        int n = r - l + 1;

        int div1 = 0, div2 = n;
        for (int i = l; i <= r; i ++) {
                if (!vis[i]) {
                        div1 ++;
                        div2 --;
                        for (int j = i + i; j <= r; j += i) vis[j] = true;
                }
        }

        ll res = 0;
        for (int i = div1; i <= n; i ++) {
                res += C(i - 1, div1 - 1) * f[div1] % mod * f[div2] % mod * i % mod;
                res %= mod;
        }
        cout << res << endl;
}

---

洛谷P4912_情侣？给我烧了！

🔗

💡

一个核心为求错位全排列的问题
首先去算有 $k$ 个匹配上的方案数
选择 $k$ 对情侣，选择 $k$ 个位置，情侣进行全排列即 $k!$ ，每对情侣左右顺序可以互换 $2^k$ ，剩下 $(n-k)$ 对情侣进行可男男、女女、男女、女男的错位全排列 $ep[n-k]$
即：$res[k]=C_n^kC_n^k(k!)2^kep[n-k]$

接下来是考虑这个 $ep[k]$ 是怎么求的
第一排选择同性：
$k$ 个人有 $k(k-1)$ 种选择方式
如果ta们的对象进行匹配，则在剩下的 $k-1$ 排中选择一排可以左右交坐，然后剩余的 $k-2$ 对情侣进行错位匹配，即 $2(k-1)ep[k-2]$
如果他们的对象不进行匹配，那么把他们的对象看做一对情侣，则剩下有 $k-1$ 对情侣，即 $ep[k-1]$
该种选择方法有 $2k(k-1)(ep[k-1]+2(k-1)ep[k-2])$
第一排坐异性：
选择方式依然是有 $k(k-1)$ 种方式
推导过程不变，则也是有 $2k(k-1)(ep[k-1]+2(k-1)ep[k-2])$
得到：$ep[k]=4k(k-1)(ep[k-1]+2(k-1)ep[k-2])$
将其预处理出来之后直接用上面的 $res[k]$ 公式即可

✅

const int mod = 998244353;
const int N = 1e3 + 10;
ll f[N], ivf[N];
ll ep[N];


inline ll ksm (ll a, ll b) { ll res = 1; while (b) { if (b & 1) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv (ll x) { return ksm(x, mod - 2); }
inline ll C (int n, int m) { return f[n] * ivf[n - m] % mod * ivf[m] % mod; }
inline ll A (int n, int m) { return f[n] * ivf[n - m] % mod; }
inline void Pre () {
        f[0] = 1;
        for (int i = 1; i < N; i ++) f[i] = f[i - 1] * i % mod;
        ivf[N - 1] = inv(f[N - 1]);
        for (int i = N - 2; i >= 0; i --) ivf[i] = ivf[i + 1] * (1ll * i + 1) % mod;

        ep[0] = 1; ep[1] = 0;
        for (int i = 2; i < N; i ++) ep[i] = 4ll * i % mod * (i - 1) % mod * ((ep[i - 1] + 2ll * (i - 1) % mod * ep[i - 2]) % mod) % mod;
}

inline void Solve () {
        int n; cin >> n;
        for (int i = 0; i <= n; i ++) {
                cout << C(n, i) * C(n, i) % mod * f[i] % mod * ksm(2, i) % mod * ep[n - i] % mod << endl;
        }
}

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        Pre();
        int cass; cin >> cass; while (cass --) {
                Solve ();
        }
}

---

洛谷P4936_Agent1

🔗

💡

AB两队，每队必出一个人
我们可以枚举每队谁必出，然后为了保证 我们让每队出的两个人中间的数必不出，两侧的数选出
这样的话就是
这是一个 的柿子，我们优化一下

好了，这么一个 的柿子就出来了

✅

cout << (n * ksm(2, n - 1) % mod - (ksm(2, n) + mod - 1) % mod + mod) % mod << endl;

---

洛谷P4981_父子

🔗

💡

整个寝室的关系图很容易看成一棵树
而且是一棵n个人轮流当根的树
对于每一个人当祖先，根据prufer编码性质有种树
而n个人当祖先就是

✅

const int mod = 1e9 + 9;
inline ll ksm ( ll a, ll b ) {
        ll res = 1;
        while ( b ) {
                if ( b & 1 ) res = res * a % mod;
                a = a * a % mod;
                b >>= 1;
        }
        return res;
}

int main () {
        int cass;
        for ( cin >> cass; cass; cass -- ) {
                int n; cin >> n;
                cout << ksm ( n, n - 1 ) << endl;
        }
        return 0;
}

---

洛谷P5377_鸽鸽的分割

🔗

💡

点和面通过建模为立体几何想欧拉公式：

$$F=E-V+2$$

其中 $F$ 为分割块数， $E$ 为边数， $V$ 为点数
$V=$ 原本点数 $+$ 任取四个点连线相交 $=n+\binom{n}{2}$
$E=$ 弧 $+$ 原本点之间相连 $+$ 连线交点分割出两条边 $=n+\binom{n}{2}+2\times\binom{n}{4}$
注意在立体几何上多了一个面为圆外的面，要减去一

✅

int main() {
    int n;

    while (scanf("%d", &n) != EOF) {
        int Cn4 = n * (n - 1) * (n - 2) * (n - 3) / 24;
        int Cn2 = n * (n - 1) / 2;
        int E = n + Cn2 + 2 * Cn4;
        int V = n + Cn4;
        printf("%d\n", E - V + 2 - 1);
    }
}

---

洛谷P6162_四角链

🔗

💡

每一个数 $x$ 可以填的数字一定是 $x$ 减去前面选中的数的个数

我们先来尝试一个 $O(n^2)$ 的算法
令 $dp[n][m]$ 表示前 $n$ 个位置选了 $m$ 个填数
那么对于 $n$ 可以填数，$dp[n][m]+\quad (n-m+1)\times dp[n-1][m-1]$
也可以不填数，$dp[n][m]+\quad dp[n-1][m]$
也就是说 $dp[n][m]=dp[n-1][m]+(n-m+1)\times dp[n-1][m-1]$
可以感觉到这个东西就是一个项带了系数的组合数递推，很像第二类斯特林数 $\begin{Bmatrix}n\\m\end{Bmatrix}=\begin{Bmatrix}n-1\\m-1\end{Bmatrix}+m\begin{Bmatrix}n-1\\m\end{Bmatrix}$
只不过系数带错了位置且不是结尾，那么我们让 $n$ 上升 $1$ ，同时系数要变成 $m$ ，那么就让 $m$ 变成 $(n+1)-m$ ，也就是说 $dp[n][m]=\begin{Bmatrix}n+1\\n+1-m\end{Bmatrix}$
发现这样转移过来就是 $\begin{Bmatrix}n+1\\n+1-m\end{Bmatrix}=\begin{Bmatrix}n\\n-m\end{Bmatrix}+(n-m+1)\times \begin{Bmatrix}n\\n+1-m\end{Bmatrix}$
和第二类斯特林数的公式一样了
那么我们就是 $O(n)$ 地求一下 $\begin{Bmatrix}n+1\\n+1-m\end{Bmatrix}$ 即可

$\begin{Bmatrix}n\\m\end{Bmatrix}=\sum\limits_{i=0}^m\frac{(-1)^{m-i}i^n}{i!(m-i)!}$

✅

const int mod = 998244353;
const int N = 1e6 + 10;

inline ll ksm (ll a, ll b) { ll res = 1; while (b) { if (b & 1) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv (ll x) { return ksm(x, mod - 2); }

ll f[N], ivf[N];
inline void Pre () {
        f[0] = 1;
        for (int i = 1; i < N; i ++) f[i] = f[i - 1] * i % mod;
        ivf[N - 1] = inv(f[N - 1]);
        for (int i = N - 2; i >= 0; i --) ivf[i] = ivf[i + 1] * (i + 1) % mod;
}
inline ll S (int n, int m) {
        ll res = 0;
        for (int i = 0; i <= m; i ++) {
                (res += ((m - i) & 1 ? -1ll : 1ll) * ksm(i, n) % mod * ivf[i] % mod * ivf[m - i] % mod) %= mod;
                res = (res + mod) % mod;
        }
        return res;
}

int main () {      
        cin.tie(nullptr);
        Pre();
        int n, k; cin >> n >> k; n --;
        cout << S(n + 1, n + 1 - k);
}

---

牛客2022国庆集训派对day3G_Subsequence1

🔗

💡

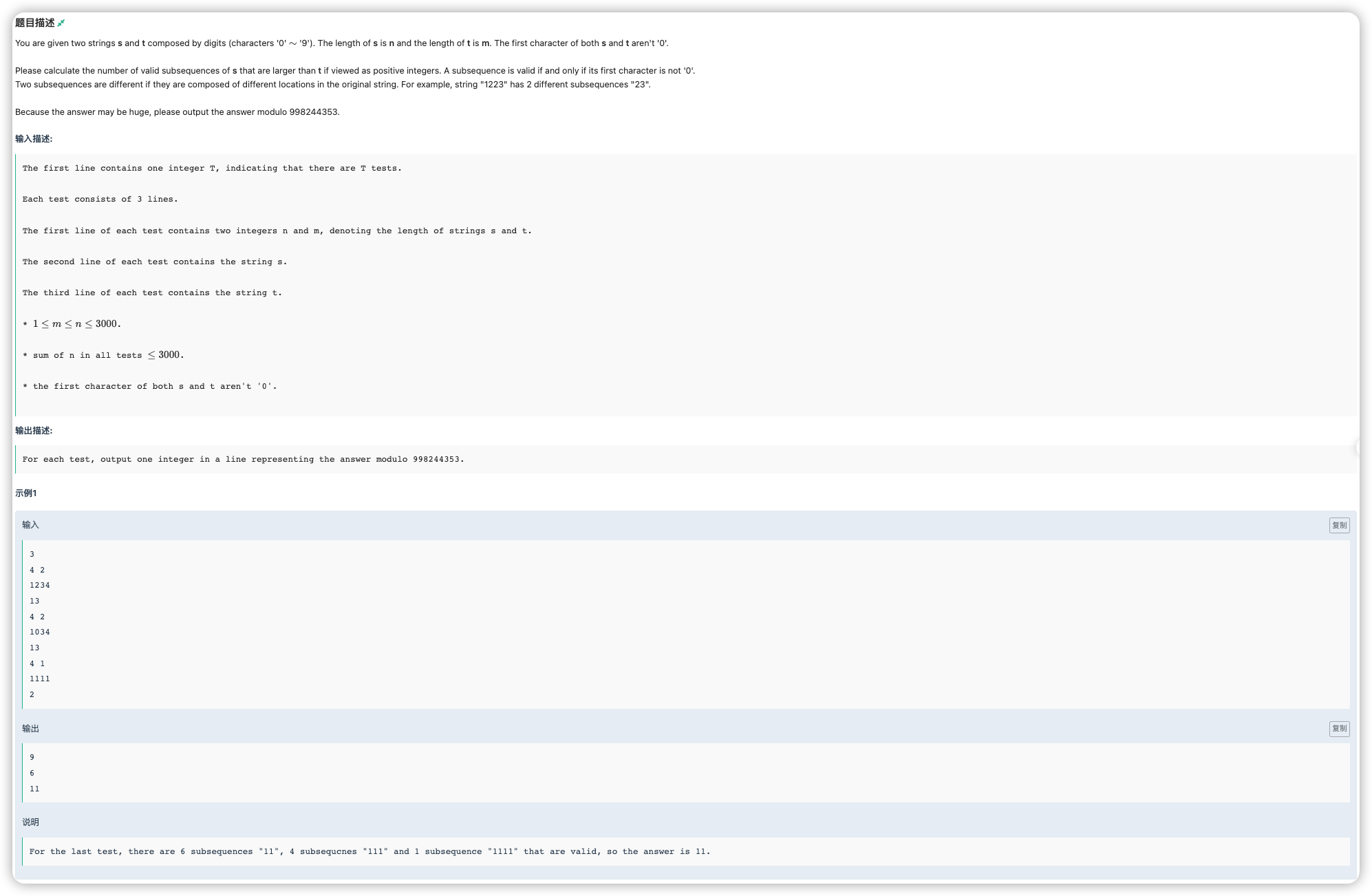
如果在 $s$ 中要获得和 $t$ 同长度的串，那么就是一个同长子序列的字典序偏序计数问题了
令 $s_s$ 表示 $s$ 的子序列，我们要看在哪一位让 $s_s>t$ ，这之后的是可以随便选的
如果 $s_i>t_j$ ，那么就需要计一个 $s$ 在 $i$ 前面能找到多少个与 $t[1,j-1]$ 可以匹配上的子序列
这个用一个 $dp$ 来实现，$dp[i][j]$ 表示 $s$ 在前 $i$ 位能匹配上 $t[1,j]$ 的子序列数量
$dp[i][]$ 用 $dp[i-1][]$ 来转移，枚举 $i-1$ 匹配了多少个，那么如果 $s_i=t_j$ ，$dp[i][j+1]$ 加上 $dp[i-1][j]$ ，然后正常继承关系为 $dp[i][j]+dp[i-1][j]$
处理好这个 $dp$ 后，看哪一位 $s_i>t_j$ ，找到后答案累加 $\binom{n-i}{m-j}\times dp[i-1][j-1]$ 即可，即表示前面都匹配上，后面随便选

当然最后也要加上长度超过 $m$ 的子序列数量，为 $\sum\limits_{i=m+1}n\binom{n-j}{i-1}$
由于不能有前导 $0$ ，就对于长度 $i$ 时，枚举一下 $s_j$ 是否为 $0$ ，如果为 $0$ ，说明以它开头的都不可以选，减去 $\binom{n-j}{i-1}$

✅

const int N = 3010;
const int mod = 998244353;
int f[N], ivf[N];
inline int C (int n, int m) {
    if (m > n) return 0;
    return (ll)f[n] * ivf[m] % mod * ivf[n - m] % mod;
}
inline int ksm (int a, int b) {
    int res = 1;
    while (b) {
        if (b & 1) res = 1ll * res * a % mod;
        a = 1ll * a * a % mod;
        b >>= 1;
    }
    return res;
}
inline int inv (int x) { return ksm(x, mod - 2); }

int n, m;
string s, t;
int dp[N][N];

inline void Solve () {
    int res = 0;
    cin >> n >> m >> s >> t;
    s = "0" + s;
    t = "0" + t;

    dp[0][0] = 1;
    
    for (int i = 1; i <= n; i ++) {
        for (int j = 0; j <= m; j ++) {
            if (j + 1 <= m && s[i] == t[j + 1]) {
                (dp[i][j + 1] += dp[i - 1][j]) %= mod;
            }
            (dp[i][j] += dp[i - 1][j]) %= mod;
        }
        for (int j = 1; j <= m; j ++) {
            if (s[i] > t[j]) {
                res += (ll)C(n - i, m - j) * dp[i - 1][j - 1] % mod;
                res %= mod;
            }
        }  
    }

    for (int i = 0; i <= n; i ++) for (int j = 0; j <= m; j ++) dp[i][j] = 0;

    for (int i = m + 1; i <= n; i ++) {
        (res += C(n, i)) %= mod;
        for (int j = 1; j <= n; j ++) {
            if (s[j] == '0') {
                res = ((res - C(n - j, i - 1)) % mod + mod) % mod;
            }
        }
    }
    cout << res << endl;
}

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    f[0] = 1;
    for (int i = 1; i < N; i ++) f[i] = (ll)f[i - 1] * i % mod;
    ivf[N - 1] = inv(f[N - 1]);
    for (int i = N - 2; i >= 0; i --) ivf[i] = (ll)ivf[i + 1] * (i + 1) % mod;

    int cass; cin >> cass; while ( cass -- ) {
        Solve ();
    }
}

---

牛客2022寒假算法基础集训营4G_子序列权值乘积

🔗

💡

考虑每个数作为 $min$ 和 $max$ 出现的次数
分成这么两类

• 自己这个数在整个序列中只出现一次
• 自己这个数在整个序列中出现任意次

对于第一类：
我们找出比自己大的数的个数设置为 gre，比自己小的设置为 les
由于可以选或者不选，所以 $x$ 个数就有 $2^x$ 种方案
那么这类情况做出的贡献为 $a^{2^{les}}\times a^{2^{gre}}$

对于第二类：
首先我们自己有 $b$ 个，然后依旧是比自己大的数的个数设置为 gre，比自己小的设置为 les
自己至少要选两个，别的选或者不选
那么贡献为 $a^{(2^b-1-b)\times 2^{les}}\times a^{(2^b-1-b)\times 2^{gre}}$

有一个细节是取模的时候指数不应是取 $10^9+7$
而是根据欧拉降幂取 $\phi(10^9+7)=10^9+6$

本题线段树解法请看这里 (opens new window)

✅

ll a[200005];
const ll mod = 1e9 + 7;
const ll powmod = 1e9 + 6;
inline ll ksm ( ll a, ll b, ll mod = 1e9 + 7 ) { ll res = 1; while ( b ) { if ( b & 1 ) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
map<ll, ll> num;

int main () {
        ios::sync_with_stdio(false);
        ll n; cin >> n;
        for ( ll i = 0; i < n; i ++ ) {
                cin >> a[i];
                num[a[i]] ++;
        }
        sort ( a, a + n ); a[n] = 0x3f3f3f3f;
        ll res = 1;
        for ( ll i = 0; i < n; i ++ ) {
                ll les = lower_bound(a, a + n + 1, a[i]) - a;
                ll gre = n - (upper_bound(a, a + n + 1, a[i]) - a);
                res = res * ksm(a[i], ksm(2, les, powmod)) % mod; 
                res = res * ksm(a[i], ksm(2, gre, powmod)) % mod;
        }
        for ( auto i : num ) {
                res = res * ksm(
                                i.first % mod, 
                                (((ksm(2, i.second, powmod) - 1 - i.second) % powmod + powmod) % powmod) * ksm(2, lower_bound(a, a + n + 1, i.first) - a, powmod)
                        ) % mod;
                res = res * ksm(
                                i.first % mod,
                                (((ksm(2, i.second, powmod) - 1 - i.second) % powmod + powmod) % powmod) * ksm(2, n - (upper_bound(a, a + n + 1, i.first) - a), powmod)
                        ) % mod;       
        }
        cout << res << endl;
}

---

牛客练习赛80B_卷积

🔗

💡

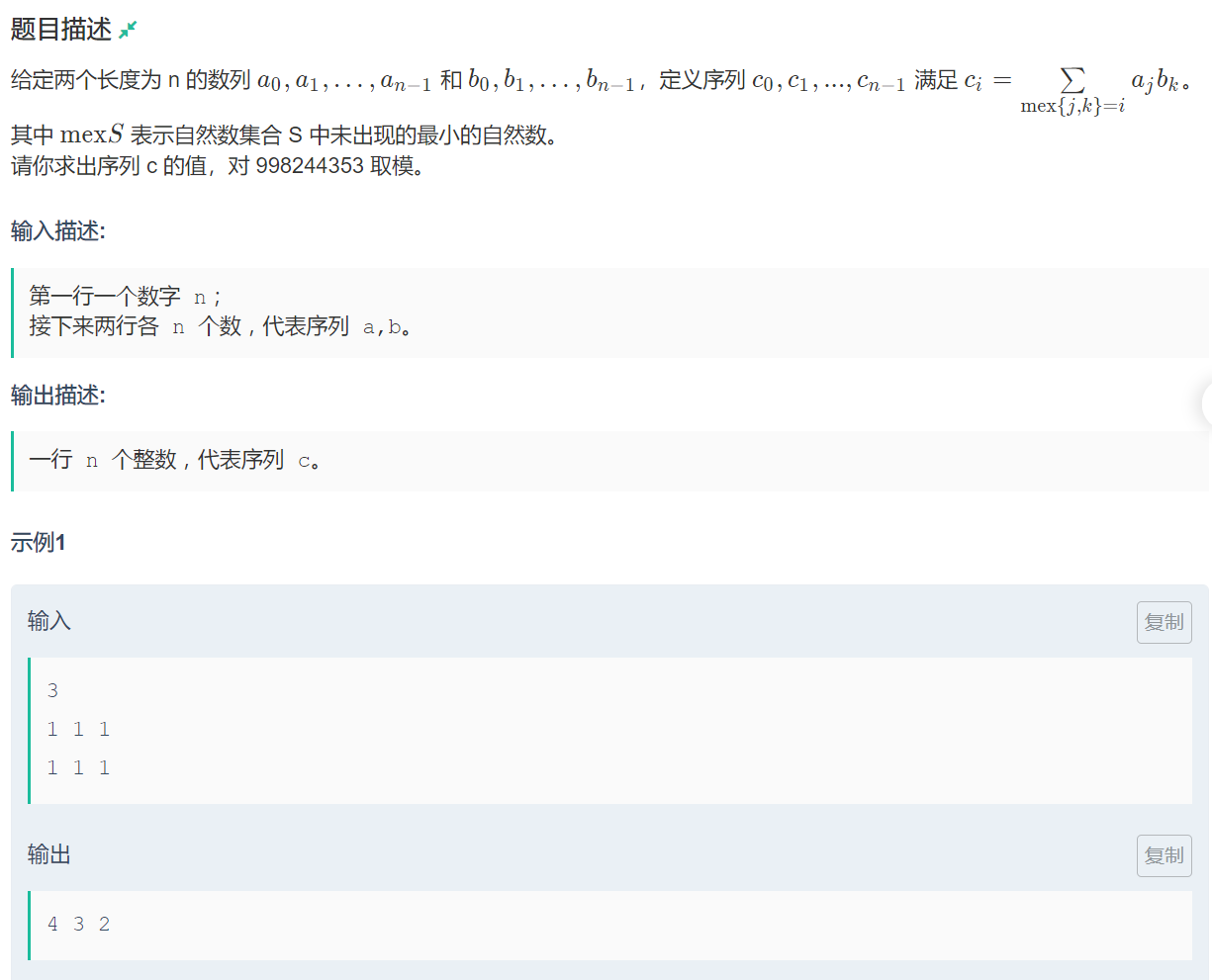
既然要mex，那么：
在i=0时，a[1 ~ (n-1)]*b[1 ~ (n-1)]都可行
在i=1时，a[0]*b[0 ~ (n-1)]与b[0]*a[0 ~ (n-1)]都可行
在i=2时，只有a[1]*b[0]和a[0]*b[1]可行
从i=3开始，任何数都不满足，所以都是0
而对于区间和时我们只需记录前缀和就行了，相减时要加上一个mod防止结果为负

✅

const int maxn = 1e5 + 100;
const ll mod = 998244353;
ll a[maxn];
ll b[maxn];
ll sum_a[maxn] = {0};//a的前缀和
ll sum_b[maxn] = {0};//b的前缀和
ll n;
int main()
{
    scanf("%lld", &n);
    for (int i = 1; i <= n; i++)
        scanf("%lld", &a[i]), sum_a[i] = (sum_a[i - 1] + a[i]) % mod;
    for (int i = 1; i <= n; i++)
        scanf("%lld", &b[i]), sum_b[i] = (sum_b[i - 1] + b[i]) % mod;
    for (int i = 1; i <= n; i++)//这里计数都+1，方便统计sum_a[0]与sum_b[0]
    {
        if (i == 1)
            printf("%lld", (sum_a[n] + mod - sum_a[1]) * (sum_b[n] + mod - sum_b[1]) % mod);
        else if (i == 2)
            printf("%lld",  (a[1] * (sum_b[n] + mod - sum_b[0]+mod-b[2]) % mod + b[1] * (sum_a[n] + mod - sum_a[0]+mod-a[2]) % mod +mod- /*去重*/a[1] * b[1] % mod)%mod);
        else if (i == 3)
            printf("%lld", (a[1] * b[2] % mod + a[2] * b[1] % mod) % mod);
        else
            printf("%lld", 0ll);
        if (i != n)
            printf(" ");
    }
    return 0;
}

---

牛客练习赛98D_SonString

🔗

💡

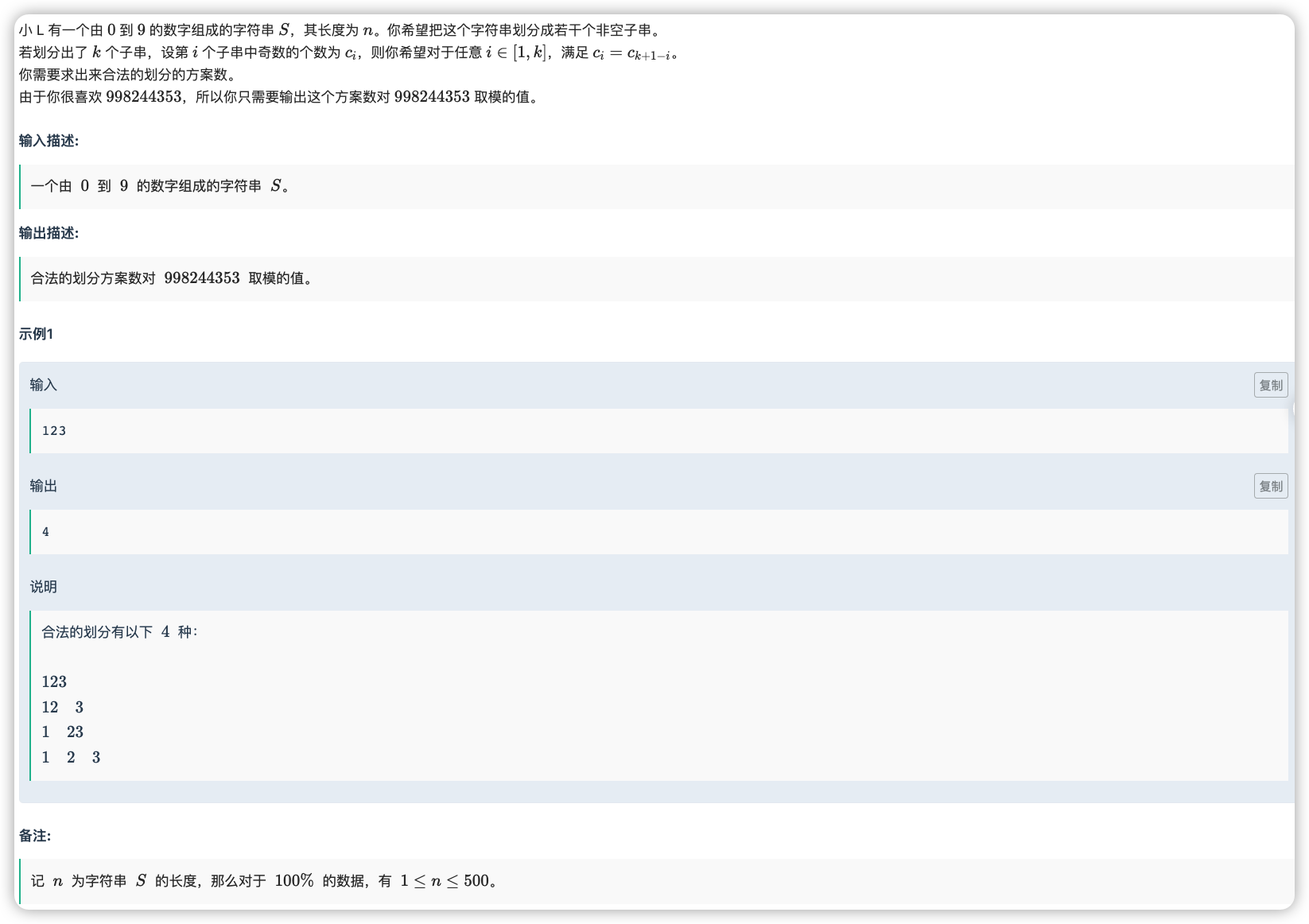
由于是连续数列的瓜分，考虑一下隔板法
那么需要考虑的就是两个相邻奇数的偶数之间要存在多少个隔板，同时相对应的是它对称的两个奇数之间的偶数的隔板数要一样
我们存一下奇数的位置
通过两个奇数的位置可以快速得到这两个奇数之间有多少个偶数，与其对称的奇数信息
由于存在乘法原理的转移关系，那么我们令 $dp[i]$ 表示转移到第 $i$ 个奇数有多少种方案数
第 $i-1$ 到第 $i$ 个奇数之间设存在 $f1$ 个偶数，对称有 $f2$ 个偶数
那么除了第一位有 $f1$ 种插法之外，别的都有 $f1+1$ 种插法
所以
$dp[0]=\sum\limits_{j=0}^{min(f1,f2)}\binom{f1}{j}\binom{f2}{j}$
$dp[i]=dp[i-1]\times\sum\limits_{j=0}^{min(f1,f2)+1}\binom{f1+1}{j}\binom{f2+1}{j}$

注意如果有偶数个奇数的情况了话，我们中间两个奇数之间的偶数（设有 $num$ 个）是没有算过的，而这些偶数可以随便插板，也就是 $dp[mid]\times2^{num}$
而且奇数个数是 $0$ 个也要特殊处理一下，同理 $2^{n-1}$

✅

const int mod = 998244353;


inline ll ksm (ll a, ll b) { ll res = 1; while (b > 0) { if (b & 1) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv (ll x) { return ksm(x, mod - 2); }

int f[510], ivf[510];
inline ll C (int n, int m) {
        if (n < m) return 0;
        return 1ll * f[n] * ivf[n - m] % mod * ivf[m] % mod;
}

ll dp[510];
int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        string s; cin >> s;
        int n = s.size();

        f[0] = 1;
        for (int i = 1; i <= n; i ++) 
                f[i] = 1ll * f[i - 1] * i % mod;
        ivf[n] = inv(f[n]);
        for (int i = n - 1; i >= 0; i --) 
                ivf[i] = 1ll * ivf[i + 1] * (i + 1) % mod;
        
        vector<int> id1;
        for (int i = 1; i <= n; i ++) 
                if ((s[i - 1] - '0') % 2 == 1) 
                        id1.push_back(i);

        if (id1.size() == 0) {
                cout << ksm(2, n - 1) << endl;
                return 0;
        } 

        for (int i = 0; i < id1.size() / 2 + (id1.size() % 2); i ++) { // 枚举一半
                if (i == 0) {
                        int f1 = id1[i] - 1;
                        int f2 = n - id1.back();
                        for (int j = 0; j <= min(f1, f2); j ++) {
                                dp[i] += C(f1, j) * C(f2, j) % mod;
                                dp[i] %= mod;
                        }
                } else {        
                        int f1 = id1[i] - id1[i - 1] - 1;
                        int f2 = id1[id1.size() - i] - id1[id1.size() - i - 1] - 1;
                        for (int j = 0; j <= min(f1, f2) + 1; j ++) {
                                dp[i] += dp[i - 1] * C(f1 + 1, j) % mod * C(f2 + 1, j) % mod;   
                                dp[i] %= mod;
                        }
                }
        } 

        if (id1.size() % 2 == 0) {
                int num = id1[id1.size() / 2] - id1[id1.size() / 2 - 1];
                cout << dp[id1.size() / 2 - 1] * ksm(2, num) % mod;
        } else {
                cout << dp[id1.size() / 2] << endl;
        }
}

---

牛客练习赛99D_礼物

🔗

💡

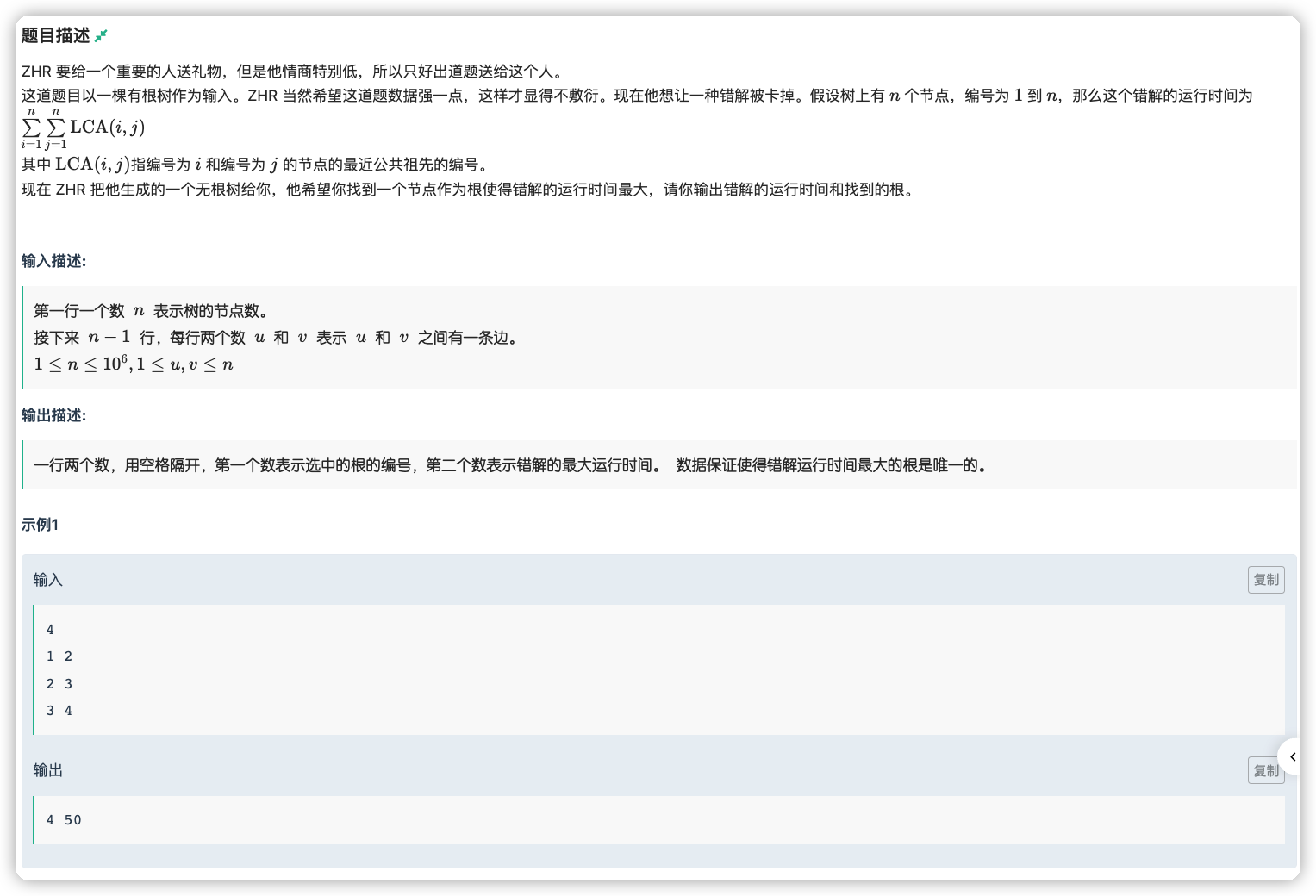
如果给定根是谁，那么会很好算，一个点被当做 $LCA$ 的次数为

• 每个子树所有点与其他子树的所有点互相配对的方案数：$\sum\limits_{v\in son_u}sz_v\times(sz[u]-1-sz[v])$
• 每个子树所有点与 $u$ 互相配对：$\sum\limits_{v\in son_u}sz[v]$

但问题是现在没有给根
不过我们如果固定出来了一个根了，将根从 $u$ 推到其中一个子节点 $v$ 后答案的变化是可以快速求得的
即将 $LCA$ 为 $u$ 的换为 $LCA$ 为 $v$ 的情况，那么就是 $v$ 的子树所有点与非 $v$ 的子树的所有点， $sz[v]\times (n-sz[v])$ ，将他们乘的权值改为 $v$ 即可
这个可以通过每次传入一个以父节点为根时的参数，将根从父节点换为本次遍历节点，并维护最大值

✅

const int N = 1e6 + 10;
const int M = N * 2;
struct Edge {
        int nxt, to;
} edge[M];
int head[N], cnt;
inline void add_Edge (int from, int to) {
        edge[++cnt] = {head[from], to};
        head[from] = cnt;
}
int n;
int sz[N];
ll resv, resid;

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        cin >> n;
        for (int i = 0; i < n - 1; i ++) {
                int u, v; cin >> u >> v;
                add_Edge(u, v);
                add_Edge(v, u);
        }

        function<ll(int, int)> dfs = [&](int u, int fa) ->ll {
                ll cur = 0;
                sz[u] = 1;
                for (int i = head[u]; i; i = edge[i].nxt) {
                        int v = edge[i].to;
                        if (v == fa) continue;
                        cur += dfs(v, u);
                        sz[u] += sz[v];
                }
                int sum = 0;
                for (int i = head[u]; i; i = edge[i].nxt) {
                        int v = edge[i].to;
                        if (v == fa) continue;
                        cur += 1ll * sz[v] * (sum + 1) * u;
                        sum += sz[v];
                }
                return cur;
        };

        function<void(int, int, ll)> find_Root = [&](int u, int fa, ll cur) ->void {
                if (fa != -1) { // 换根
                        cur -= 1ll * sz[u] * (n - sz[u]) * fa;
                        cur += 1ll * sz[u] * (n - sz[u]) * u;
                        if (cur > resv) resid = u, resv = cur;
                } else resid = u, resv = cur;

                for (int i = head[u]; i; i = edge[i].nxt) {
                        int v = edge[i].to;
                        if (v == fa) continue;
                        find_Root(v, u, cur);
                }
        };

        find_Root(1, -1, dfs(1, -1));
        cout << resid << " " << resv * 2 + 1ll * n * (n + 1) / 2 << endl;
}

---

牛客挑战赛58B_清新题

🔗

💡

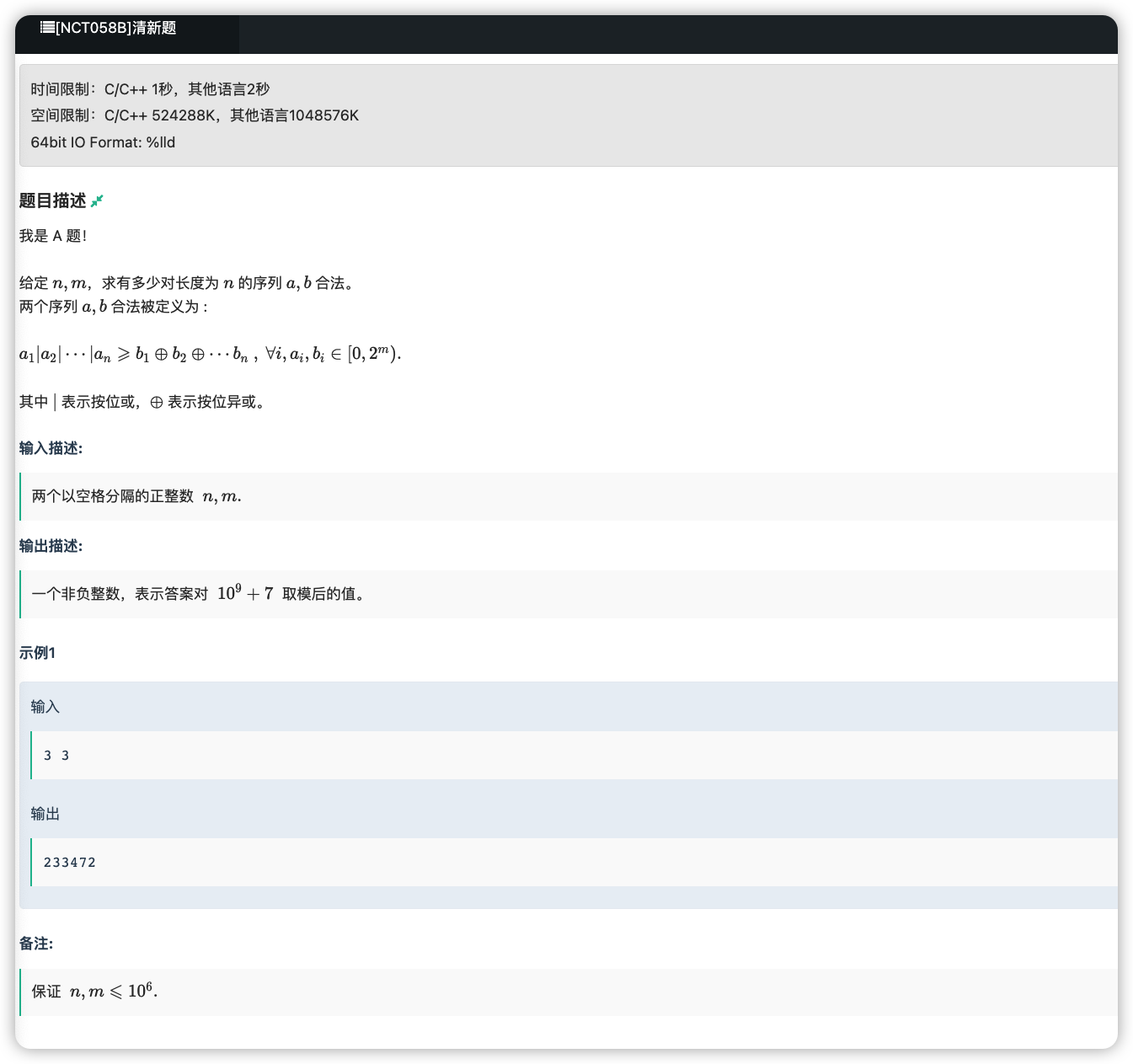
首先考虑左 $>$ 右的方案数
同位数二进制大小可以看作字典序，即如果因为第 $i$ 位导致左大于右，则：前相同，该位大，后随意

首先预处理出 $n$ 个数选偶数个为 $chosev$ ，奇数个为 $chosod$

前相同：
左 $1$ 右 $1$ ：左 $n$ 个数至少有一个要选 $1$ 即 $2^n-1$ ，右侧 $n$ 个数选奇数个即 $chosod$
左 $0$ 右侧 $0$ ，左侧不选为 $1$ ，右侧选偶数个即 $chosev$
每一位均是如此，所以令方案数 $^{i-1}$

该位大：
左为 $1$ ，即 $2^n-1$ 右为 $0$ ，即 $chosev$

后随意：
即每一位是 $2^n$ 共有 $m-i$ 位为 $(2^{2\times n})^{m-i}$

最后要加上所有数均相等的情况，即前相同中每一位方案数 $^m$

✅

const int mod = 1e9 + 7;
inline ll ksm ( ll a, ll b ) { ll res = 1; while ( b ) { if ( b & 1 ) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv ( ll x ) { return ksm(x, mod - 2); }
 
ll f[1000006];
inline void pre_F () {
        f[0] = 1;
        for ( int i = 1; i < 1000006; i ++ ) f[i] = f[i - 1] * i % mod;
}
inline ll C ( ll n, ll m ) {
        return f[n] * inv(f[m]) % mod * inv(f[n - m]) % mod;
}
 
int main () { pre_F();
        ll n, m; cin >> n >> m;
 
        ll chosod = 0, chosev = 0;
        for ( int i = 0; i <= n; i ++ ) {
                if ( i & 1 ) (chosod += C(n, i)) %= mod;
                else (chosev += C(n, i)) %= mod;
        }
 
        ll ksm2nsub1 = ((ksm(2, n) - 1) % mod + mod) % mod;
 
        ll res = ksm((ksm2nsub1 * chosod % mod + chosev) % mod, m);
        for ( int i = 1; i <= m; i ++ ) {       
                res += ksm((ksm2nsub1 * chosod % mod + chosev) % mod, i - 1) 
                       * ksm2nsub1 % mod * chosev % mod
                       * ksm(ksm(2, 2 * n), m - i) % mod;
                res %= mod;
        }
        cout << res << endl;
}

---

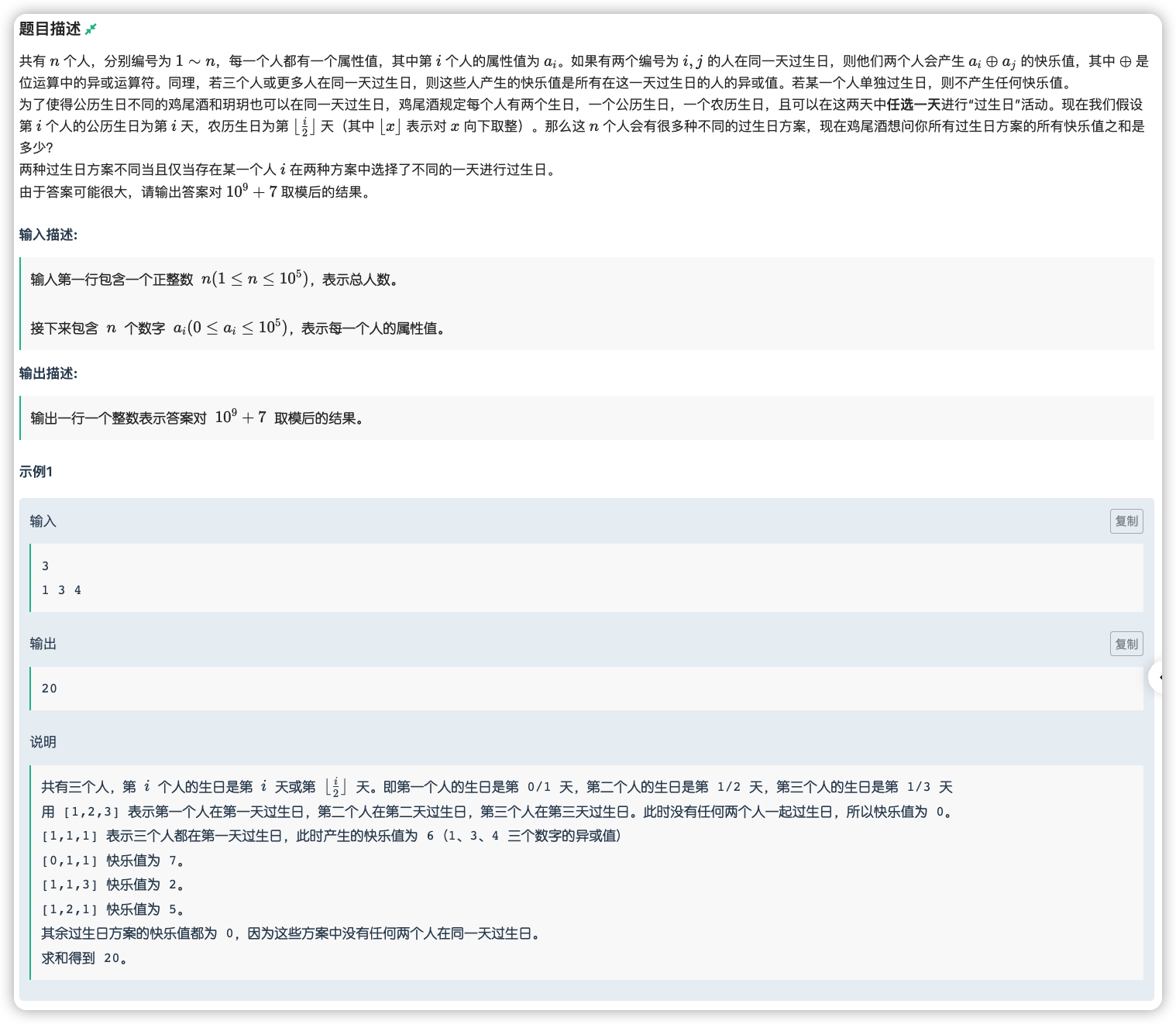
牛客小白月赛50D_生日

🔗

💡

首先要注意到的是，选第 $i$ 天过生日的人只可能有 $i,2i,2i+1$ 这三个
那么也就是说，我们可以对每一天维护一个权值集
第 $i$ 天的权值即为它的权值集的异或和乘上 $2$ 的“别的不确定的人数”次方 如果说里面有两个人会选它，那么就是 $(a_i\oplus a_{2i})\times2^{n-2}$
如果有三个人会选它，那么就需要分开计算一下有两个人选和有三个人选的情况了
即 $((a_i\oplus a_{2i})+(a_i\oplus a_{2i+1})+(a_{2i}\oplus a_{2i+1}))\times 2^{n-2}$
与 $(a_i\oplus a_{2i}\oplus a_{2i+1})\times 2^{n-3}$

✅

const int mod = 1e9 + 7;
inline ll ksm (ll a, ll b) {
        ll res = 1;
        while (b) {
                if (b & 1) res = res * a % mod;
                a = a * a % mod;
                b >>= 1;
        }
        return res;
}
vector<ll> g[100005];

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        int n; cin >> n;
        vector<int> a(n + 1); for (int i = 1; i <= n; i ++) cin >> a[i];

        for (int i = 1; i <= n; i ++) {
                g[i / 2].push_back(a[i]);
                g[i].push_back(a[i]);
        }

        ll res = 0;
        for (int i = 0; i <= n; i ++) {
                if (g[i].size() <= 1) continue;
                ll cur = 0;
                if (g[i].size() == 2) {
                        cur = (g[i][0] ^ g[i][1]) % mod * ksm(2, n - 2) % mod;
                } else {
                        cur += ((g[i][0] ^ g[i][1]) + (g[i][1] ^ g[i][2]) + (g[i][0] ^ g[i][2])) % mod * ksm(2, n - 3) % mod;
                        cur += (g[i][0] ^ g[i][1] ^ g[i][2]) % mod * ksm(2, n - 3) % mod;
                        cur %= mod;
                }
                res += cur;
                res %= mod;
        }
        cout << res << endl;

}

---

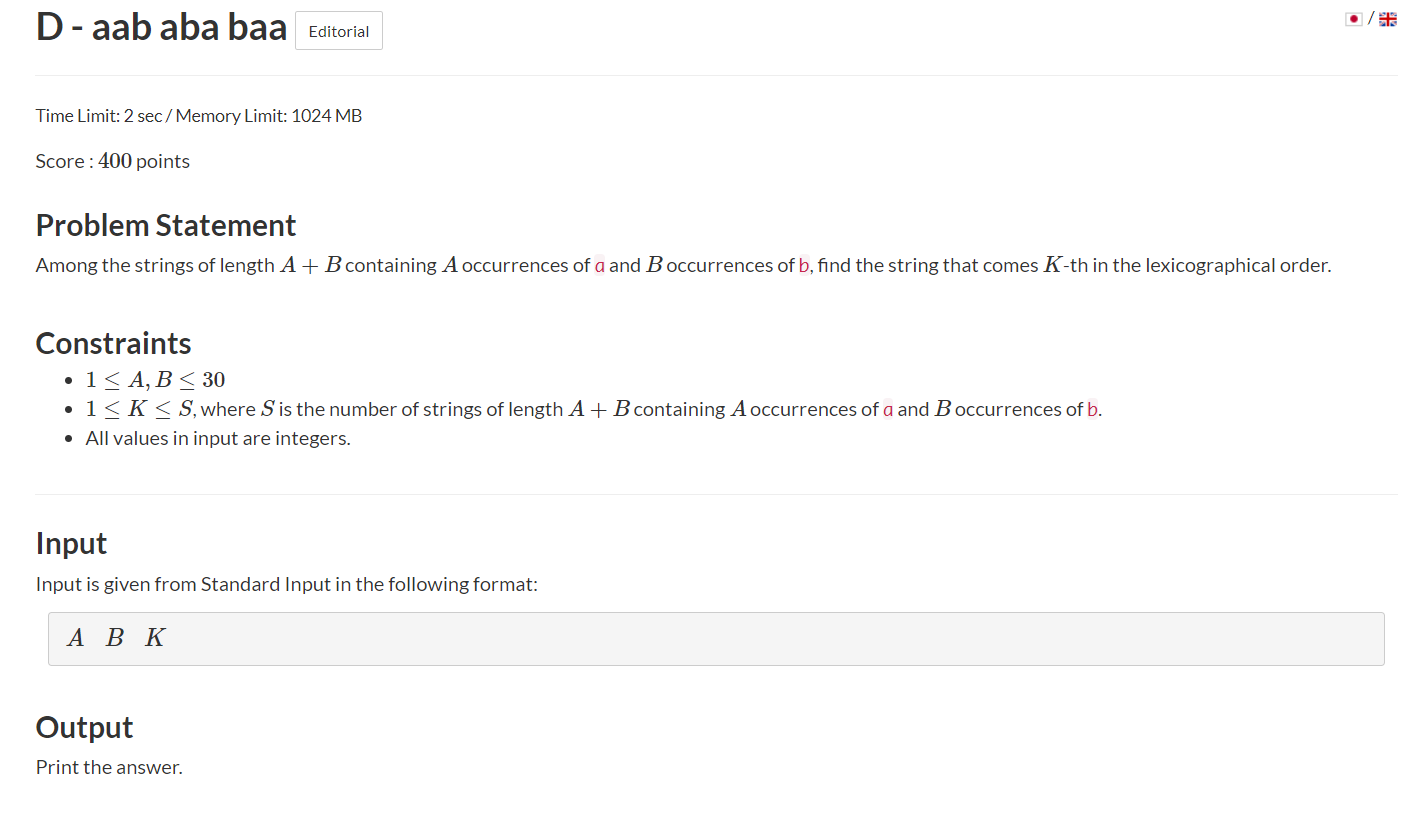
ABC202D_aabababaa

🔗

💡

拿到这道题
刚开始我其实是想转化为二进制看变化的
因为如果把'a'视作1，'b'视作0，每次向后推一个字典序其实就是减去一个数
但是有很多处理地方不知道怎么办
放弃了，虽然不对，但不得不说确实是一种好的思维拓展方向

正解来了：
操作数过大的时候我们考虑跳步
分析字典序性质
发现每个位置都有两种存放方式：
要么存a要么存b
这取决于k的剩余值

这个位置放a是对k没有影响的
因为k是寻找第几个字典序最小的

而放b的话我们要知道我们跳了几步也就是减了多少个k
确定方式是假设这里放a（比放b小1）我们后面能构造出的字符串数量
一想这不是组合数吗？
我们想在剩下的（a + b - 1）个位置随意放置（a - 1）个'a'
所以跳的步数是C(a + b - 1, a - 1)

流程： 在k>1时（因为我们字典序从头开始找的，所以要少用一个k）：
如果k > C(a + b - 1, a - 1)，那么这一步是可以放'b'来跳步的
否则，不能跳步，老老实实放'a'吧
在最后，我们构造出后面没有构造的最小字符串：先放完a，再放完b

✅

ll c[65][35];

inline void get_C(){//杨辉三角构建组合数
        for(int i = 0; i < 65; i ++) c[i][0] = 1;
        for(int i = 0; i < 65; i ++){
                for(int j = 1; j <= i && j < 35; j ++){
                        c[i][j] = c[i - 1][j] + c[i - 1][j - 1];
                }
        }
}


inline void solve(){get_C();
        _ll(a); _ll(b); _ll(k);
        string res;
        while(k > 1){
                if(k > c[b + a - 1][a - 1]){ k -= c[b + a - 1][a - 1]; //可以跳步
                        b --; //放了'b'，b的数量就减1
                        res += "b";
                }else{
                        a --;//放了'a'，a的数量就减1
                        res += "a";
                }
        }
        for(int i = 0; i < a; i ++) res += "a";
        for(int i = 0; i < b; i ++) res += "b";
        cout << res << endl;
}

CHIVAS{
        solve();
        _REGAL;
}

---

AcWing2418_光之大陆

🔗

💡

我们先将题意抽象出来
相当于给定n个点，分成任意块，每块都是个环，让这些环连通

环与环的之间连通可以prufer编码的性质 ^(n-2)直接得到
问题就是分成块的问题
对于i个点，我们要考虑每一个点的归属
我们分成j块，我们考虑k个点的归属
那么我们要递推i-1个点中选k-1个点： dp[i][j] = (dp[i][j] + dp[i - k][j - 1] * c[i - 1][k - 1]
因为每一块可以旋转环，所以要乘阶乘

最后统计一下分成1～n块的方案数

✅

const int N = 210;
ll g[N];
ll dp[N][N];
ll c[N][N];
ll n, mod;

inline void Pre () {
        for ( int i = 0; i < N; i ++ ) {
                for ( int j = 0; j <= i; j ++ ) {
                        if ( j == 0 ) c[i][j] = 1;
                        else          c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
                } 
        }
        g[1] = 1, g[3] = 3;                                                                                                                     
        for ( int i = 4; i < N; i ++ ) g[i] = g[i - 1] * i % mod;
}

int main () {
        cin >> n >> mod; Pre();
        dp[0][0] = 1;
        for ( int i = 1; i <= n; i ++ ) { // 总共i个点
                for ( int j = 1; j <= i; j ++ ) { // 分成j块
                        for ( int k = 1; k <= i - j + 1; k ++ ) { // 要枚举k个看看怎么分配
                                dp[i][j] = (dp[i][j] + dp[i - k][j - 1] * c[i - 1][k - 1] * g[k] % mod) % mod;
                        }
                }
        }
        ll res = g[n - 1], p = 1; // p: prufer定理后面要乘的数
        for ( int k = 2; k <= n; k ++ ) {
                res = ( res + dp[n][k] * p % mod ) % mod;
                p = p * n % mod;
        }
        cout << res << endl;
}

---

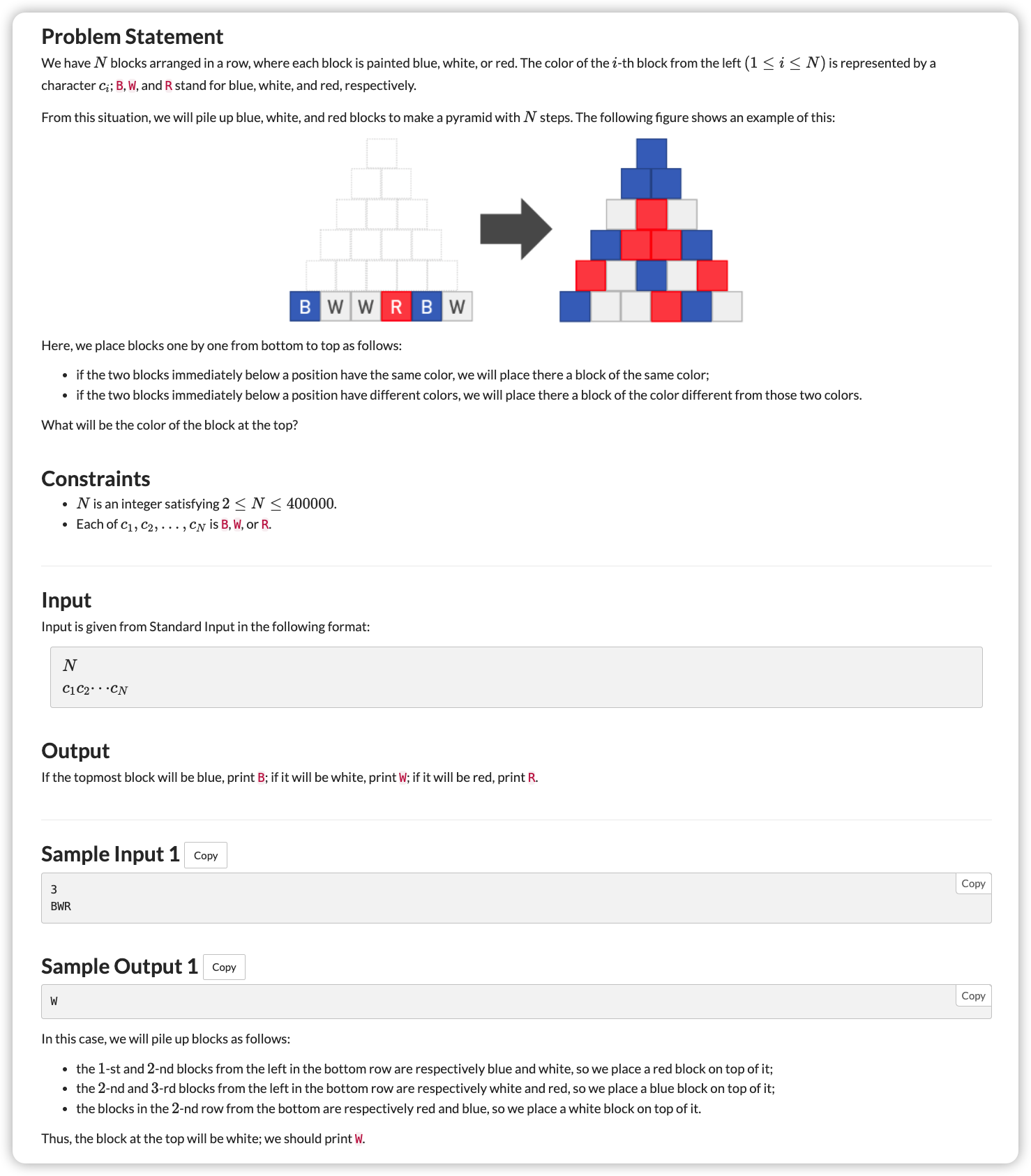
ARC117C_TricolorPyramid

🔗

💡

就三种颜色来回变，将其转换成 $(0,1,2)(mod\;3)$
一个颜色与其下面两个有关系，将关系图画出来

	0	1	2
0	0	2	1
1	2	1	0
2	1	0	2

发现和相同的两对，其值也相同，其和的负值与最终值差 $3$ ，也可以看做是 $target\equiv -(x+y)(mod\;3)$
令最后一行为 $a,b,c,d,e$
推上去为
$a+4b+6c+4d+e\\ -a-3b-3c-d\quad -b-3c-3d-e\\ a+2b+c\quad b+2c+d\quad c+2d+e\\ -a-b\quad -b-c\quad -c-d\quad -d-e\\ a\quad b\quad c\quad d\quad e$
如果令字符 $c$ 的权值为 $w_c$ ，权值为 $v$ 的字符为 $c_v$
得到第一行为 $c[(-1)^{n-1}\sum\limits_{i=0}^{n-1}\binom{n-1}{i}w[s_i]]$

不过由于模数很小，不能直接阶乘求组合数，不然很容易出现无逆元无法除的情况
但由于模数很小，可以用 $Lucas$ 快速求解，且求单个组合数的过程中不用取模

✅

inline int Comb (int a, int b, int mod) {
    if (a < b) return 0;
    if (a == b) return 1;
    if (b > a - b) b = a - b;
    int res = 1;
    for (int i = 0; i < b; i ++) res = res * (a - i);
    for (int i = 0; i < b; i ++) res = res / (b - i);
    return res % mod;
}
inline int Lucas (int n, int m, int mod) {
    int res = 1;
    while (n && m && res) {
        res = 1ll * res * Comb(n % mod, m % mod, mod) % mod;
        n /= mod;
        m /= mod;
    }
    return res;
}


int n;
string s;

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n >> s;

    int res = 0;
    for (int i = 0; i < n; i ++) {
        res += (s[i] == 'B' ? 0 : (s[i] == 'W' ? 1 : 2)) * Lucas(n - 1, i, 3) % 3;
        res %= 3;
    }
    if (n % 2 == 0) res = (-res + 3) % 3;
    cout << (res == 0 ? 'B' : (res == 1 ? 'W' : 'R')) << endl;
}

---

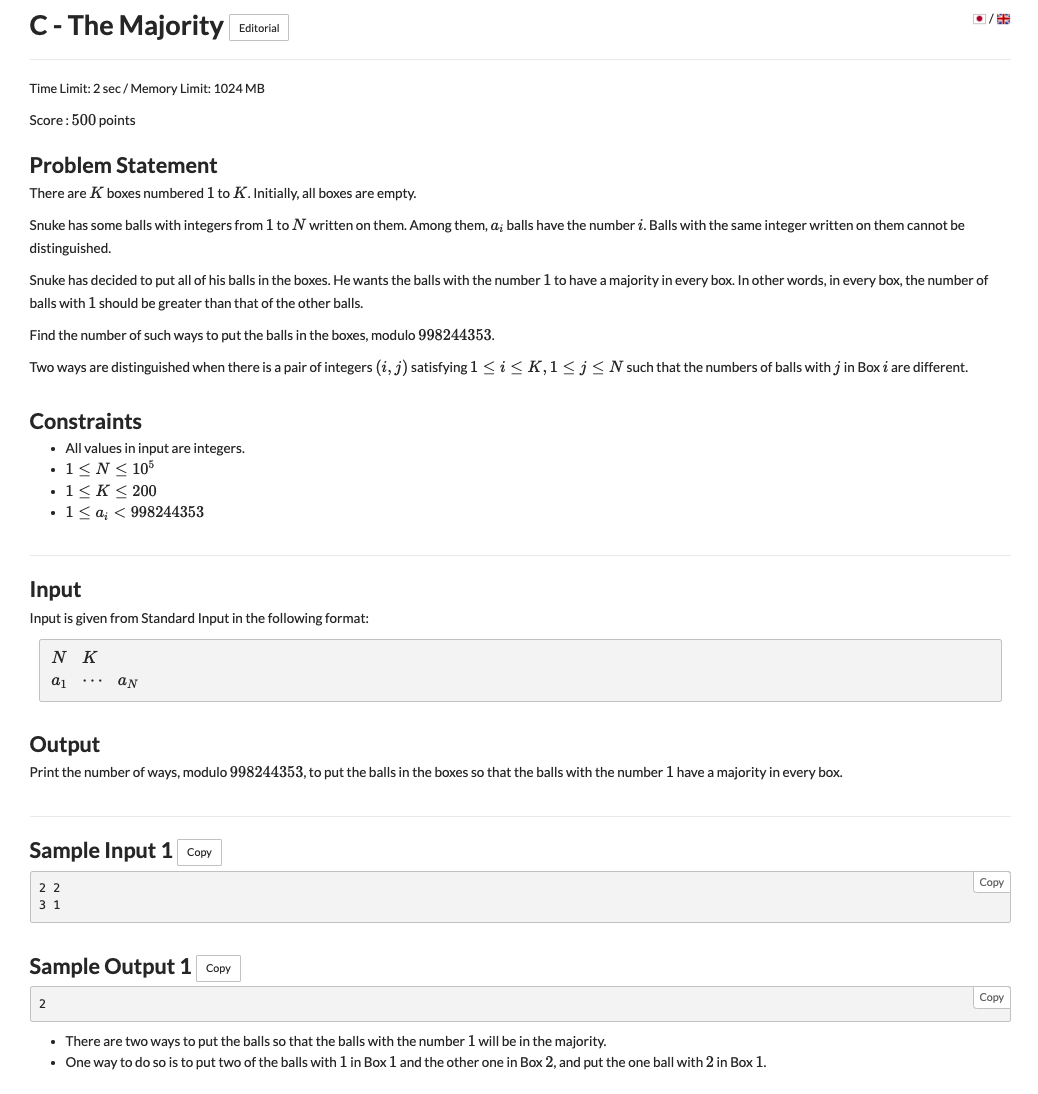
ARC134C_TheMajority

🔗

💡

可以这样想，要想数字是 $1$ 的球个数严格大于别的数字的球个数
我们可以先给每一个盒子都铺上数字是 $1$ 的球，然后每往一个盒子里面放一个 $1$ 就跟着放一个别的

那么我们可以将这些球分成两类物品
数字不是 $1$ 的球和数字是 $1$ 的球两两配对形成物品 $a$ ，有 $\alpha$ 个
剩余的数字是 $1$ 的球每个都是物品 $b$ ，有 $\beta$ 个

我们要先给每个盒子都铺上物品 $b$ ，不能有空盒子
对于 球盒模型情况四 (opens new window)，方案数为 $\begin{pmatrix}\alpha-1\\\beta-1\end{pmatrix}$
之后对于物品 $b$ ，注意同数字的球之间是相同的，而不同数字的球是不同的，放置的时候盒可空
那么我们要对于每一个 $i$ 和 $1$ 拼接物品的数量 $a_i$ 计算一次 球盒模型情况三 (opens new window)，方案数为 $\prod\limits_{i=2}^n\begin{pmatrix}a_i+m-1\\m-1\end{pmatrix}$

故答案为

$$\begin{pmatrix}\alpha-1\\\beta-1\end{pmatrix}\prod\limits_{i=2}^n\begin{pmatrix}a_i+m-1\\m-1\end{pmatrix}$$

另外，对于 $m$ 比较小但是 $n$ 比较大的组合数，我们可以用分子分母约分之后的方式进行计算

inline ll C ( ll n, ll m ) {
        ll res = 1;
        for ( ll i = 0; i < m; i ++ ) res = res * (n - i) % mod;
        return res * inv[m] % mod;
}

✅

const int N = 1e5 + 10;
const int K = 210;
const int mod = 998244353;

ll inv[N];

inline ll Ksm ( ll a, ll b ) { ll res = 1; while ( b ) { if ( b & 1 ) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll Inv ( ll x ) { return Ksm(x, mod - 2); }
inline void get_I () {
        inv[0] = Inv(1);
        for ( int i = 1; i < K; i ++ ) 
                inv[i] = inv[i - 1] * Inv(i) % mod;
}
inline ll C ( ll n, ll m ) {
        ll res = 1;
        for ( ll i = 0; i < m; i ++ ) res = res * (n - i) % mod;
        return res * inv[m] % mod;
}

ll n, k;
ll a[N];
ll one, els; // 数字1的个数，别的数字的个数
ll res;
int main () {
        get_I();
        ios::sync_with_stdio(false);

        cin >> n >> k;
        for ( int i = 1; i <= n; i ++ ) {
                cin >> a[i];
                if ( i == 1 ) one += a[i];
                else els += a[i];
        }
        if ( one - els < k ) {
                cout << 0 << endl;
                return 0;
        }

        res = C(one - els - 1, k - 1);
        for ( int i = 2; i <= n; i ++ ) res = res * C(a[i] + k - 1, k - 1) % mod;
        cout << res << endl;
}

---

ARC136B_TripleShift

🔗

💡

考虑进行一次操作会产生什么影响
三个不同的数数往后转一次
逆序对 $\pm2$
三个数存在两个相同的
逆序对改变可以包揽所有的

那么考虑两个数组的逆序对奇偶即可
同奇偶性必然可以
不同奇偶性若存在相同的数也可以
否则不行

✅

int n;
int a[5010], b[5010];
int numa[5010];
int mxnum = 0;
 
int main () {
        ios::sync_with_stdio(false);
 
        cin >> n;
        for ( int i = 1; i <= n; i ++ ) cin >> a[i], numa[a[i]] ++, mxnum = max(mxnum, numa[a[i]]);
        for ( int i = 1; i <= n; i ++ ) {
                cin >> b[i];
                if ( numa[b[i]] == 0 ) {
                        cout << "No" << endl;
                        return 0;
                }
                numa[b[i]] --;
        }
        int reva = 0;
        for ( int i = 1; i <= n; i ++ ) {
                for ( int j = 1; j < i; j ++ ) {
                        reva += a[j] > a[i];
                }
        }
        int revb = 0;
        for ( int i = 1; i <= n; i ++ ) {
                for ( int j = 1; j < i; j ++ ) {
                        revb += b[j] > b[i];
                }
        }
        if ( reva % 2 == revb % 2 || mxnum >= 2 ) {
                cout << "Yes" << endl;
        } else {
                cout << "No" << endl;
        }
}

---

ICPC2019南京B_ChessBoard

🔗

💡

第二张图的说服性很强，就是我们每次不能在已有矩阵 $a*b(a\le 2,b\le 2)$ 的前提下，往一个方向开两步，不然会出现同行同列要往回收出现空边的情况（分析第二个图）
开一步的话可以选四个角，选一个方向开，本身有 $n-1+m-1$ 种开法，调 $n-1$ 个位置开行，故答案为 $4\times \binom{n+m-2}{n-1}$
特判 $m=1$ 和 $n=1$

✅

inline void Solve () {
    int n, m; cin >> n >> m;
    if (n == 1) {
        cout << 1 + (m != 1) << endl;
    } else if (m == 1) {
        cout << 1 + (n != 1) << endl;
    } else {
        cout << 4ll * C(n + m - 2, n - 1) % mod << endl;
    }
}

---

CodeForces340C_TouristProblem

🔗

💡

这个是看每一对的贡献
首先每一个数和 $0$ 的差出现的次数为后面别的数的全排列，即 $(n-1)!$
其次每两个数的差出现的次数依然是 $(n-1)!$，可以只看做大减小，然后出现的次数乘 $2$
在对 $[a]$ 排序后
分子为 $(\sum\limits_{i=1}^na_i(n-1)!)+(2\sum\limits_{i=1}^n\sum\limits_{j=i+1}^n(a_j-a_i)(n-1)!)$
分母为 $n!$
初步化简后：
分子为 $(\sum\limits_{i=1}^na_i)+(2\sum\limits_{i=1}^n\sum\limits_{j=i+1}^n(a_j-a_i))$
分母为 $n$
后面那个两重循环可以直接用前缀和化简，即 $\sum\limits_{i=1}^n(a_i\times(i-1)-pre\_sum)$

✅

inline ll gcd (ll a, ll b) {
        return b ? gcd(b, a % b) : a;
}
 
int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);
 
        int n; cin >> n;
        vector<ll> a(n); for (ll &i : a) cin >> i;
        sort(a.begin(), a.end());
 
        ll up = 0, down = n;
        ll pre_sum = 0;
        for (int i = 0; i < n; i ++) {
                up += (a[i] * i - pre_sum) * 2;
                up += a[i];
                pre_sum += a[i];
        }
        ll d = gcd(up, down);
        up /= d;
        down /= d;
        cout << up << " " << down << endl;
}

---

CodeForces1609E_IntercityTravelling

🔗

💡

对于每一段作为每一个疲劳值，用排列组合求一个贡献次数

研究第二个样例
第一段：
作为 $a_1$ ：
贡献次数为后面的断点数任选即 $2^3$
第二段：
作为 $a_1$ ：
贡献次数为占了前面一个断点后前面的剩余断点数任选即 $2^0$ ，乘上后面的断点数任选即 $2^2$
作为 $a_2$ ：
贡献次数为后面的断点数任选即 $2^2$
第三段：
作为 $a_1$ ：
贡献次数为占了前面一个断点后前面的剩余断点数任选即 $2^1$ ，乘上后面的断点数任选即 $2^1$
作为 $a_2$ ：
贡献次数为占了前面一个断点后前面的剩余断点数任选即 $2^0$ ，乘上后面的断点数任选即 $2^1$
作为 $a_3$ ：
贡献次数为后面的断点数任选即 $2^1$
第四段：
作为 $a_1$ ：
贡献次数为占了前面一个断点后前面的剩余断点数任选即 $2^2$ ，乘上后面的断点数任选即 $2^0$
作为 $a_2$ ：
贡献次数为占了前面一个断点后前面的剩余断点数任选即 $2^1$ ，乘上后面的断点数任选即 $2^0$
作为 $a_3$ ：
贡献次数为占了前面一个断点后前面的剩余断点数任选即 $2^0$ ，乘上后面的断点数任选即 $2^0$
作为 $a_1$ ：
贡献次数为后面的断点数任选即 $2^0$

划分下来即：
$(2^3+3\times 2^2)a_1+\\(2^2+2\times 2^1)a_2+\\(2^1+1\times2^0)a_3+\\(2^0)a_4$
每一个 $a_i$ 最前面的是第 $i$ 段使用它的贡献次数，后面有 $n-i$ 个断点，所以是 $2^{n-i}次$ 。而后面的则是第 $i$ 段之后的 $(n-i)$ 个段使用它，指数是互补的（左加右减），即 $2^{n-i-1}次$
则答案为 $\sum\limits_{i=1}^n2^{n-i}+(n-i)2^{n-i-1}$

✅

const int mod = 998244353;
inline ll ksm (ll a, ll b) { if (b < 0) return 0; ll res = 1; while (b) { if (b & 1) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv (ll x) { return ksm(x, mod - 2); }
 
int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);
 
        int n; cin >> n;
        vector<ll> a(n + 1); for (int i = 1; i <= n; i ++) cin >> a[i];
 
        ll res = 0;
        for (int i = 1; i <= n; i ++) {
                res += (ksm(2, n - i) + (n - i) * ksm(2, n - i - 1) % mod) % mod * a[i] % mod;
                res %= mod;
        }
        cout << res << endl;
}

---

CodeForces1371E1_Asterism（Easy Version）

🔗

💡

一个排列数问题
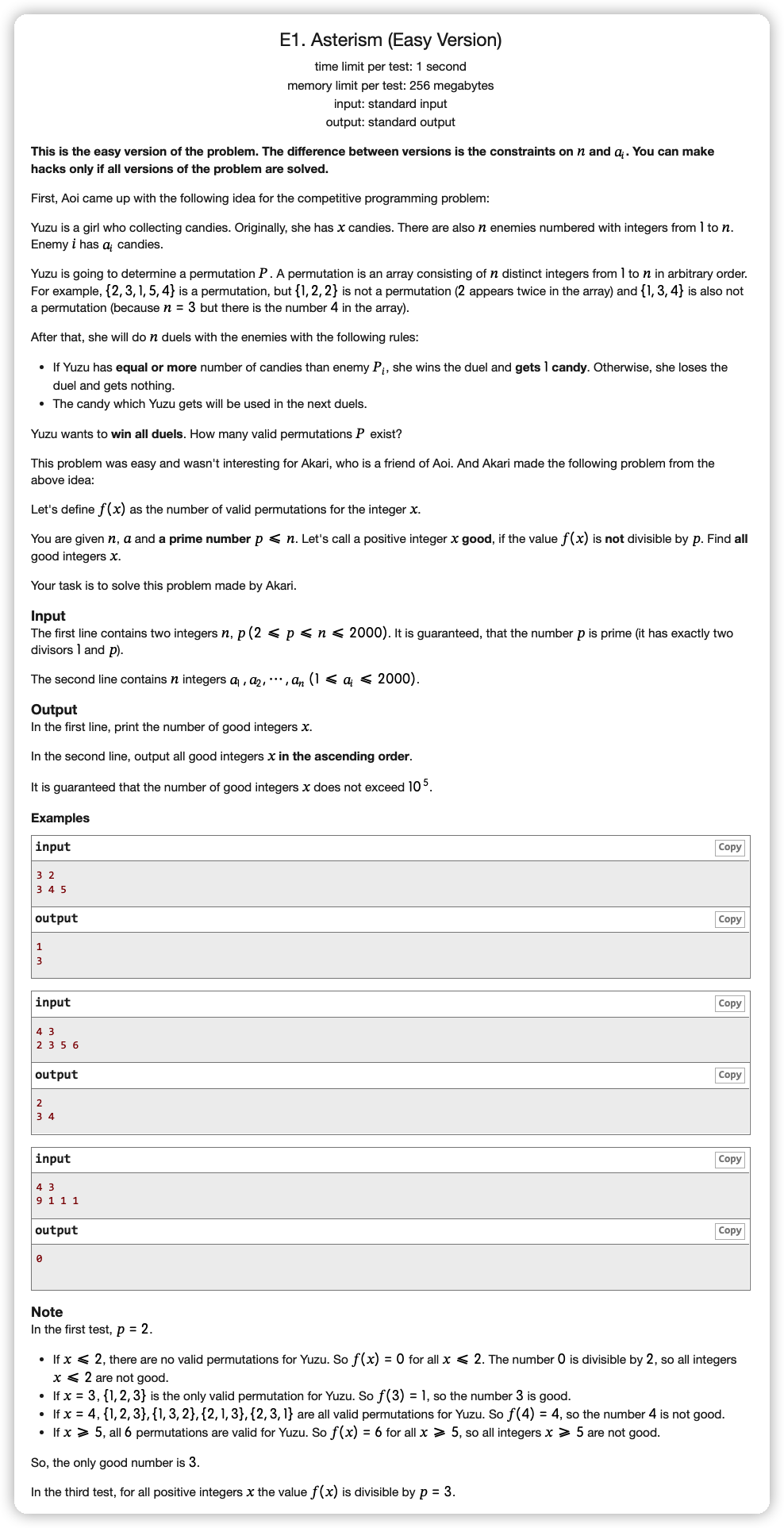
注意到对于 $f(x)$ ，从 $0\to n-1$ 的位置手里的糖数是 $x\to x+n-1$
则每一个位置应都有一些怪兽可以放置，且是升序的，并且能放在 $x$ 位置上的怪兽，也一定能放在 $x+10$ 的位置上，这是一个包含的
现在就是看如果有 $i$ 颗糖，可以应付几只怪兽，由此预处理出来 $[b]$
我们在求 $f(x)$ 时，对于有 $i$ 颗糖的时候，我们这里可以放 $b_i$ 个怪兽，但是之前过了 $i-x$ 个怪兽了，所以要减去。让这些进行累乘即可，公式表示为：

$$f(x)=\prod\limits_{i=x}^{x+n-1}b_i-(i-x)$$

在这里面判断是否存在 $b_i-(i-x)\equiv 0(mod\;p)$ 即可

✅

const int N = 4100;
int n, p;
int a[N], b[N];

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        cin >> n >> p;
        for (int i = 0; i < n; i ++) cin >> a[i];
        
        sort(a, a + n);
        for (int i = max(0, a[n - 1] - n + 1); i <= a[n - 1] + n - 1; i ++) b[i] = upper_bound(a, a + n, i) - a;
        vector<int> res;
        for (int x = max(0, a[n - 1] - n + 1); x <= a[n - 1]; x ++) {
                for (int i = x; i <= x + n - 1; i ++) {
                        if ((b[i] - (i - x)) % p == 0) goto end;
                }
                res.push_back(x);
                end:;
        }

        cout << res.size() << endl;
        for (int i : res) cout << i << " ";
}

---

CodeForces1371E1_Asterism（Hard Version）

🔗

💡

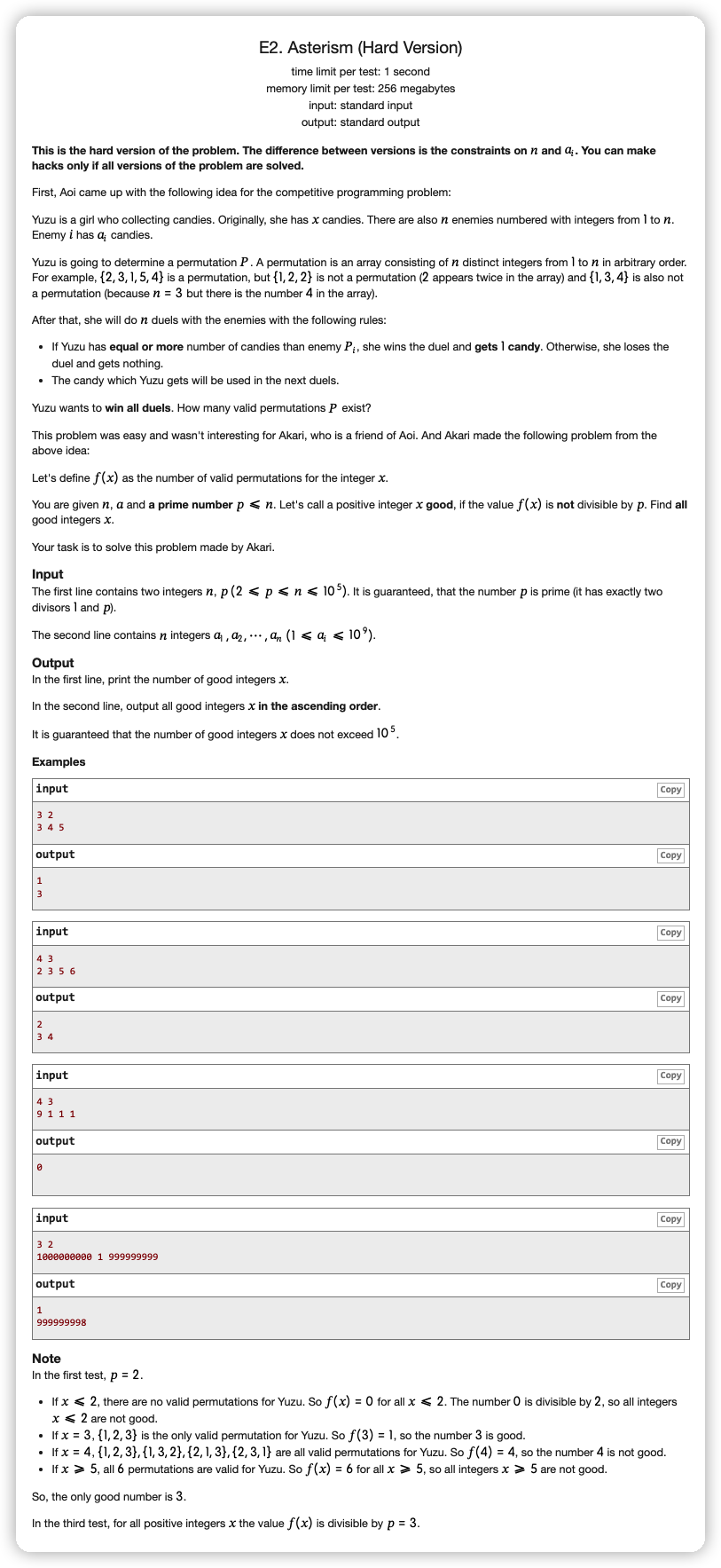
根据上面的思路有：
判断是否 $b_i-(i-x)\equiv 0(mod\;p)$
可转化为判断是否 $i-b_i\equiv x(mod\;p)$
这里 $i-b_i$ 可以直接预处理存一下，即存 $(i-b_i)\%p$ ，然后在枚举 $x$ 时判断 $x\%p$ 是否存过即可
但是注意到轮数不互通，因为转化之后的公式为 $f(x)=\prod\limits_{i=x}^{x+n-1}x-(i-b_i)$ ，我们枚举的是 $x$ ，当 $x+1$ 后，上一轮的 $i=x$ 就不能用了
所以我们可以先存入第一轮，然后在判断完一个 $x$ 是否能用后，将 $i=x$ 时的 $i-b_i$ 删去，加入下一轮的 $i-b_i$ ，即 $i=x+n$ 时的
这样判断下去就行了

✅

const int N = 1e5 + 10;
int n, p;
int a[N];
inline int sub (int a, int b) { return ((a - b) % p + p) % p; }
 
int vis[N];
 
int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);
 
        cin >> n >> p;
        for (int i = 0; i < n; i ++) cin >> a[i];
 
        sort(a, a + n);
 
        for (int i = a[n - 1] - n + 1; i <= a[n - 1]; i ++) {
                vis[sub(i, upper_bound(a, a + n, i) - a) % p] ++;
        }
 
        vector<int> res;
        for (int x = max(0, a[n - 1] - n + 1); x <= a[n - 1]; x ++) {
                if (!vis[x % p]) res.push_back(x);
                vis[sub(x, upper_bound(a, a + n, x) - a) % p] --; // 删除 i=x 的记录
                vis[sub(x + n, upper_bound(a, a + n, x + n) - a) % p] ++; // 加入 i=x+n 的记录
        }
        cout << res.size() << endl;
        for (int i : res) cout << i << " ";
}

---

CodeForces1422C_Bargain

🔗

💡

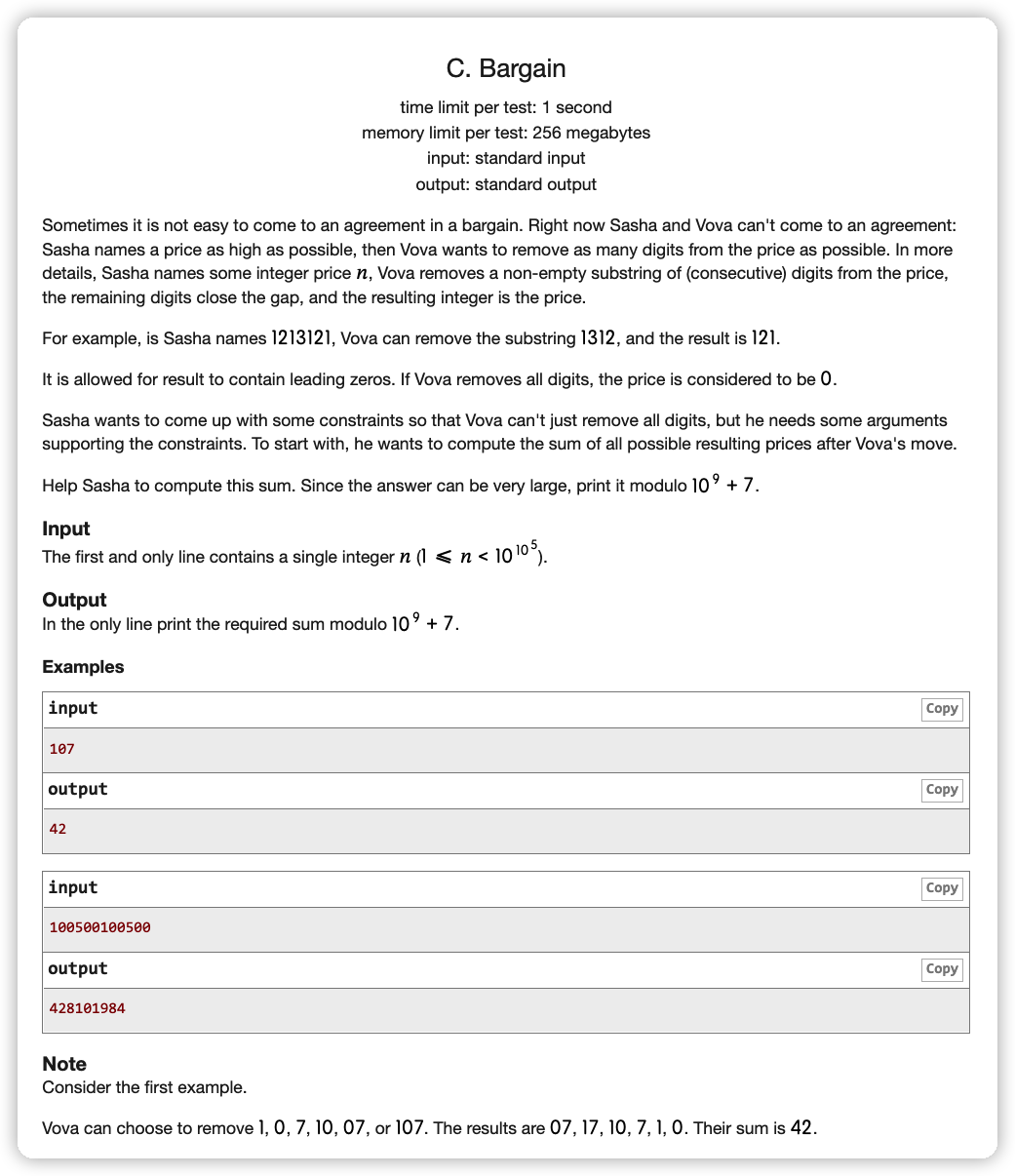
这种对数进行操作，算所有结果的和的，直接算每一个数做出贡献的次数
但是由于我们可以删一位后面的数，它所在的位数会发生改变，所以我们要算的是它作为第几位所做出的贡献是多少

对第 $k$ 位的数 $x$ 做一下分类讨论：
作为第 $1$ 位：后面全删
作为第 $2$ 位：后面删到剩 $1$ 个
作为第 $3$ 位：后面删到剩 $2$ 个
$...$
作为第 $k$ 位：前面删任意子段
如果数有 $n$ 位，那么第 $k$ 位作为 $[1,k-1]$ 位的贡献为 $a_k\times (k-1)(k-2)...321$ 这样的数，我们可以预处理出来一个 $1,21,321,4321,...$ 这样的数组 \_dots321
而作为第 $k$ 位的贡献次数，前面有 $n-k$ 个数，所以有 $\binom{n-k}{2}$ 种子段截取方式，再乘上它对应的位数即 $10^{k}$ ，则贡献是 $a_k\times \binom{n-k}{2}10^k$

由于上面说的是“位”不是“下标”
则转换为下标的最终结果为：

$$\sum\limits_{i=1}^n(\binom{i-1}{2}10^{n-i}+\_dots321_{n-i})s_i$$

✅

const ll N = 1e5 + 10;
const ll mod = 1e9 + 7;
inline ll ksm (ll a, ll b) { ll res = 1; while (b) { if (b & 1) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv (ll x) { return ksm(x, mod - 2); }

ll _dots321[N];
ll pw10[N];
ll iv2;

int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        _dots321[0] = 0;
        _dots321[1] = 1;
        for (int i = 2; i < N; i ++) _dots321[i] = (_dots321[i - 1] * 10 % mod + 1) % mod;
        for (int i = 2; i < N; i ++) _dots321[i] = (_dots321[i - 1] * 10 % mod + _dots321[i]) % mod;
        pw10[0] = 1;
        for (int i = 1; i < N; i ++) pw10[i] = pw10[i - 1] * 10 % mod;
        iv2 = inv(2);


        ll res = 0;

        string s; cin >> s; s = "0" + s;
        ll n = s.size() - 1;
        for (int i = n; i >= 1; i --) {
                ll pre = 1ll * (i - 1) * i % mod * iv2 % mod * pw10[n - i] % mod;
                res += (pre + _dots321[n - i]) % mod * (s[i] - '0') % mod;
                res %= mod;
        }
        cout << res << endl;
}

---

CodeForces1536B_AdvertisingAgency

🔗

💡

我们从上向下取数，最多能取的个数取决于：我们需要多少个跟第k个数相等的数ned、跟第k个数相等的数的个数num。
这两个得到还是比较容易的，就考验了写码的严谨性，而这个个数明显是组合数，值为(num!) / (ned!) / ((num-ned)!)并取模
解组合数有两种方式：
1.杨辉三角递推法（1000*1000）的时间复杂度
2.在结果上做运算：求逆元

✅

const ll mod = 1e9 + 7;
int cass;
ll n, k;

ll qpow(ll a,ll b){//ksm
    ll ans = 1;
    while(b){
        if(b&1)
            ans = ans * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return ans%mod;
}

ll Inv(ll a,ll p){//逆元
    return qpow(a, p - 2);
}

void solve(){
    vector<ll> vec;
    cin >> n >> k;
    for (int i = 0,x; i < n; i++){
        cin >> x;
        vec.push_back(x);
    }
    sort(vec.begin(), vec.end(), greater<ll>());//合并出最大数，就要降序int cur = k;
    map<int, ll> mp;//mp[i]表i的出现次数
    for (int i = 0; i < vec.size(); i++)
    {
        if(mp[vec[i]]==0)
            mp[vec[i]] = 1;
        else
            mp[vec[i]]++;
    }
    k--;//我们从0开始存的，第k个的下标为k-1
    ll num = mp[vec[k]];//第k个数有多少个
    ll ned = 0;//我们需要多少个第k个数
    for (int i = k; i >= 0; i--){
        if(i==0||vec[i]!=vec[i-1]){
            ned = k - i + 1;
            break;
        }
    }

    //前面的小坑结束了，开始组合数取模
    ll on = 1;//分子
    for (int i = ned + 1; i <= num; i++)
        on = on * i % mod;
    ll dn = 1;//分母
    for (int i = 1; i <= num - ned; i++)
        dn = dn * i % mod;
    cout << on * Inv(dn, mod) % mod << endl;
}

int main()
{
    each_cass(cass){
        solve();
    }
    return 0;
}

---

CodeForces1557C_MoamenAndXOR

🔗

思路一

💡

首先把整个个k位数画成一个的矩阵
然后对于每一列，也就是个数的每一位
如果全了话，有一个就是。
偶数个了话，奇数个

得到两条性质：
n为奇数时： 这一位最多在含有偶数个的时候与和异或相等，都是
n为偶数时： 这一位在全时，，。而在全以下的偶数个时，

那么有两类解决方案：
n为奇数时：
每一位最多只能相等，就是在每一位都有偶数个或者全的情况下
所以我们对每一位的n个数字进行排列组合，设偶数个和全的组合情况累加为
那么答案就是

n为偶数时：
每一位可以是相等，就是在每一位在非全且有偶数个的情况下，设为
当前位还可以大于，就是在这一位(设为)全的情况下，那么前面的所有位都可以任意个组合，方案有个
所以这一位就是要递推，答案是

✅

const int N = 2e5 + 10;
const int mod = 1e9 + 7;
ll f[N];

inline void Get_F () {
        f[0] = 1;
        for ( int i = 1; i < N; i ++ ) 
                f[i] = f[i - 1] * i % mod;
}
inline ll ksm ( ll a, ll b ) {
        ll res = 1;
        while ( b > 0 ) {
                if ( b & 1 ) res = res * a % mod;
                a = a * a % mod;
                b >>= 1;
        }
        return res;
}
inline ll C ( ll a, ll b ) {
        return f[a] * ksm(f[b], mod - 2) % mod * ksm(f[a - b], mod - 2) % mod;
}

inline void solve () {
        ll n, k; cin >> n >> k;

        ll has_Eve = 0; for ( ll i = 0; i < n; i += 2 ) has_Eve = (has_Eve + C(n, i)) % mod;
        if ( n & 1 ) {
                cout << ksm ( has_Eve + 1, k) << endl; // 每一位都是要么选偶数个要么全选，只有这样才能相等
        } else {
                ll res = 1;
                for ( ll i = 1; i <= k; i ++ ) {
                        res = res * has_Eve % mod;                 // 第i位不全是1 -- 前一位满足的方案数乘它
                        res = (res + ksm(ksm(2, n), i - 1)) % mod; // 第i位全是1 -- 前面的可以随意搞
                }
                cout << res << endl;
        }
}

int main () {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif
        Get_F();
        int cass;
        for ( cin >> cass; cass; cass -- ) {
                solve();
        }
}

思路二

💡

和 清新题 思路解法一样，使用对于每一位考虑前相同，此位大，后随意的方式
首先预处理出 $one\_one$ 和 $zero\_zero$ 表示左右均为 $0$ 和 $1$ 的方案数
前相同即 $(one\_one+zero\_zero)^{i-1}$
此位大就是这一位左侧为 $1$ 右侧为 $0$ ，当且仅当 $n$ 为偶数时可以
后随意就 $2^{k-i}$
最后加上所有相同即 $(one\_one+zero\_zero)^k$

✅

const int mod = 1e9 + 7;
 
inline ll ksm ( ll a, ll b ) { ll res = 1; while ( b ) { if ( b & 1 ) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv ( ll x ) { return ksm(x, mod - 2); }
ll f[200005];
inline ll C ( ll n, ll m ) { return f[n] * inv(f[m]) % mod * inv(f[n - m]) % mod; }
 
inline void Solve () {
        ll n, k; cin >> n >> k;
        
        ll one_one = n % 2;
        ll zero_zero = 0;
        for ( int i = 0; i <= n; i += 2 ) {
                zero_zero += C(n, i);
                zero_zero %= mod;
        } if ( n % 2 == 0 ) zero_zero --, zero_zero = (zero_zero % mod + mod) % mod;
 
        ll res = ksm((one_one + zero_zero) % mod, k);
        for ( int i = 1; i <= k; i ++ ) {
                res += ksm((one_one + zero_zero) % mod, i - 1)
                       * (n % 2 == 0) % mod
                       * ksm(ksm(2, n), k - i) % mod;
                res %= mod;
        }
        cout << res << endl;
}
 
int main () {
        cin.tie(0)->sync_with_stdio(0);
        cin.exceptions(cin.failbit);
        f[0] = 1; for ( int i = 1; i < 200005; i ++ ) f[i] = f[i - 1] * i % mod;
        int cass; cin >> cass; while ( cass -- ) {
                Solve ();
        }
}

---

CodeForces1594B_SpecialNumbers

🔗

💡

对一个b进行分割
首先看一下按顺序的排列情况：
0 (1)
1 0+1 (2)
2 0+2 1+2 0+1+2 (4)
3 0+3 1+3 2+3 0+1+3 0+2+3 1+2+3 0+1+2+3 (8)
...
首先想到对b进行查找，看看是存在于哪一组（设为bas）中
然后b -= (1ll << bas)
可以发现剩下的也就是被拆过之后的值，可以继续进行分割，然后查找
那么每次 res 也就是加上 a^bas，直到b被拆到0

✅

const int mod = 1e9 + 7;

inline ll ksm ( ll a, ll b ) {
	ll res = 1;
	while ( b ) {
		if ( b & 1 ) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}

inline void Solve() {
	ll a, b; cin >> a >> b;
	ll res = 0;
	while ( b > 0 ) {
		ll bas = 0, sum = 0;
		while ( sum + (1ll << bas) < b ) {
			sum += (1ll << bas);
			bas ++;
		}
		res = (res + ksm(a, bas)) % mod;
		b -= (1ll << bas);
	}
	cout << res << endl;

}

int main () {
	int cass; cin >> cass; while ( cass -- ) {
		Solve();
	}
        return 0;
}

---

CodeForces1594E1_Rubik'sCubeColoring(easyversion)

🔗

💡

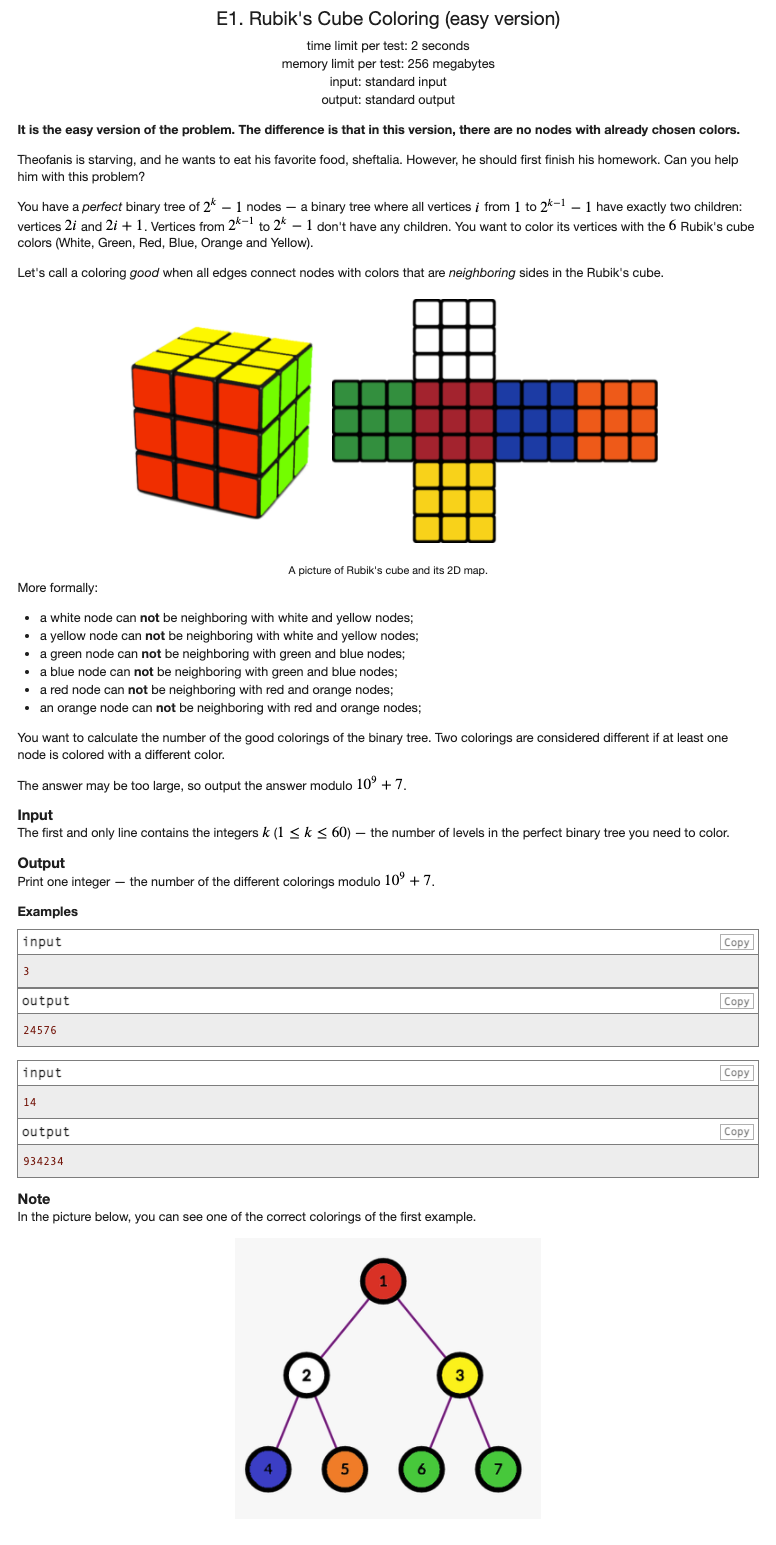
首先应该能很快想到，只有祖先节点有6种颜色可以选，那么对于每个有父节点的节点，他们都只能选四个
一共有个节点
那么答案公式就是

此时k不过60所以我们也没有必要用快速幂求指数
如果非要用的话，模数要选择，因为根据欧拉定理，指数取模时在时要取

✅

const int mod = 1e9 + 7;

inline ll ksm ( ll a, ll b ) {
	ll res = 1;
	while ( b ) {
		if ( b & 1 ) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}

int main () {
	ll n; cin >> n;
	cout << 6 * ksm(4, (1ll << n) - 2) % mod << endl;
        return 0;
}

---

CodeForces1644D_CrossColoring

🔗

💡

这个是要能对结果进行分区再组合
求出我们可以向下移动的次数 can_dwn 和可以向右移动的次数 can_rgt

首先我们要找到真正可以移动的部分
即 $s[i]!=s[i+1]$ 的位置（第一个拐角
先求出彻底包含第一个拐角之后的路径的行数 r 和列数 c
那么
第一个部分是我们一直向右移动可以多覆盖的面积：$can\_rgt\times c$
第二个部分是我们一直向下移动可以多覆盖的面积：$can\_dwn\times r$
第三个部分是我们开始时覆盖的面积：$s.size()+1$
第四个部分是我们右下角的面积：$can\_dwn\times can\_rgt$

将这四部分加在一起即可

✅

inline void Solve () {
        int n; cin >> n; n --;
        string s; cin >> s;
        ll rgt = 0, dwn = 0;
        for ( int i = 0; i < s.size(); i ++ ) {
                rgt += s[i] == 'R';
                dwn += s[i] == 'D';
        }
        ll canr = n - rgt;
        ll cand = n - dwn;
 
        string tmp = s; sort ( tmp.begin(), tmp.end() );
        if (tmp[0] == tmp.back()) {
                cout << n + 1 << endl;
                return;
        }
 
        int id = 0;
        for ( int i = 0; i < s.size(); i ++ ) {
                if ( s[i] != s[i + 1] ) {
                        id = i;
                        break;
                }
        }
        rgt = dwn = 1;
        for ( int i = id + 1; i < s.size(); i ++ ) rgt += s[i] == 'R', dwn += s[i] == 'D';
 
 
        ll dwn_num = rgt * cand;
        ll rgt_num = dwn * canr;
        cout << canr * cand + s.size() + 1 + dwn_num + rgt_num << endl;
}

---

CodeForces1649E_TylerAndStrings

🔗

💡

考虑一个没有任何限制的情况
若存在 $cnt[i]$ 个 $i$ ，构造出不同的数列的方案数 $=\frac{(\sum\limits_{i=1}^Ncnt[i])!}{\prod\limits_{i=1}^Ncnt[i]!}$
这里我们要让字典序 $a<b$
那么也就是说必须要含一串相同的前缀，然后对于第一个非前缀的位置，让 $a[i]<b[i]$
枚举从第 $i$ 个为第一个非同前缀的位置

• 前面由于相同，方案数为 $1$
• 第 $i$ 个位置可以选的数的个数为小于 $b[i]$ 的数的个数
• 后面可以随意排列，为 $(n-i)!$
• 最后要除 $\prod\limits_{i=1}^Ncnt[i]!$

考虑一个递进的记录，这样可以防止每次我们要重新对每一个数算 $\prod\limits_{i=1}^Ncnt[i]!$ 与 $\sum\limits_{j=1}^{b[i]-1}cnt[j]$

$ifac,fac$ 都可以提前预处理
前者可以维护一个 $div\_permutation=\frac{1}{\prod\limits_{i=1}^Ncnt[i]!}$ ，每次使 $cnt[b[i]]-1$ 时意味着要少除一个 $cnt[b[i]]$ ，那么让 $div\_permutation\times cnt[b[i]]$ 即可
后者可以用树状数组去记录

✅

const int N = 2e5 + 10;
const int mod = 998244353;
struct modint{ /*.....*/ };
# define mi modint

int n, m;
int a[N], b[N];
int cnt[N];
 
int t[N];
inline int lowbit ( int x ) { return x & -x; }
inline void Update ( int x, int c ) {
        while ( x < N ) t[x] += c, x += lowbit(x);
}
inline mi Query ( int x ) {
        mi res = 0;
        while ( x > 0 ) res += t[x], x -= lowbit(x);
        return res;
}
 
mi fac[N], ifac[N];
 
int main () {
        fac[0] = ifac[0] = 1;
        for ( int i = 1; i < N; i ++ ) fac[i] = fac[i - 1] * i, ifac[i] = ifac[i - 1] / i;
 
 
        scanf("%d%d", &n, &m);
        for ( int i = 1; i <= n; i ++ ) scanf("%d", &a[i]), cnt[a[i]] ++, Update(a[i], 1);
        for ( int i = 1; i <= n; i ++ ) scanf("%d", &b[i]);
 
        mi div_permutation = 1;
        for ( int i = 1; i < N; i ++ ) div_permutation *= ifac[cnt[i]];
 
        mi res = 0;
        bool flag = true;
        for ( int i = 1; i <= min(n, m); i ++ ) {
                res += Query(b[i] - 1) * fac[n - i] * div_permutation;
                div_permutation *= cnt[b[i]];
                cnt[b[i]] --;
 
                if ( cnt[b[i]] < 0 ) {
                        flag = false;
                        break;
                }
 
                Update(b[i], -1);
        }       
        if ( flag && n < m ) res += 1;
 
        printf("%d", res);
}

---

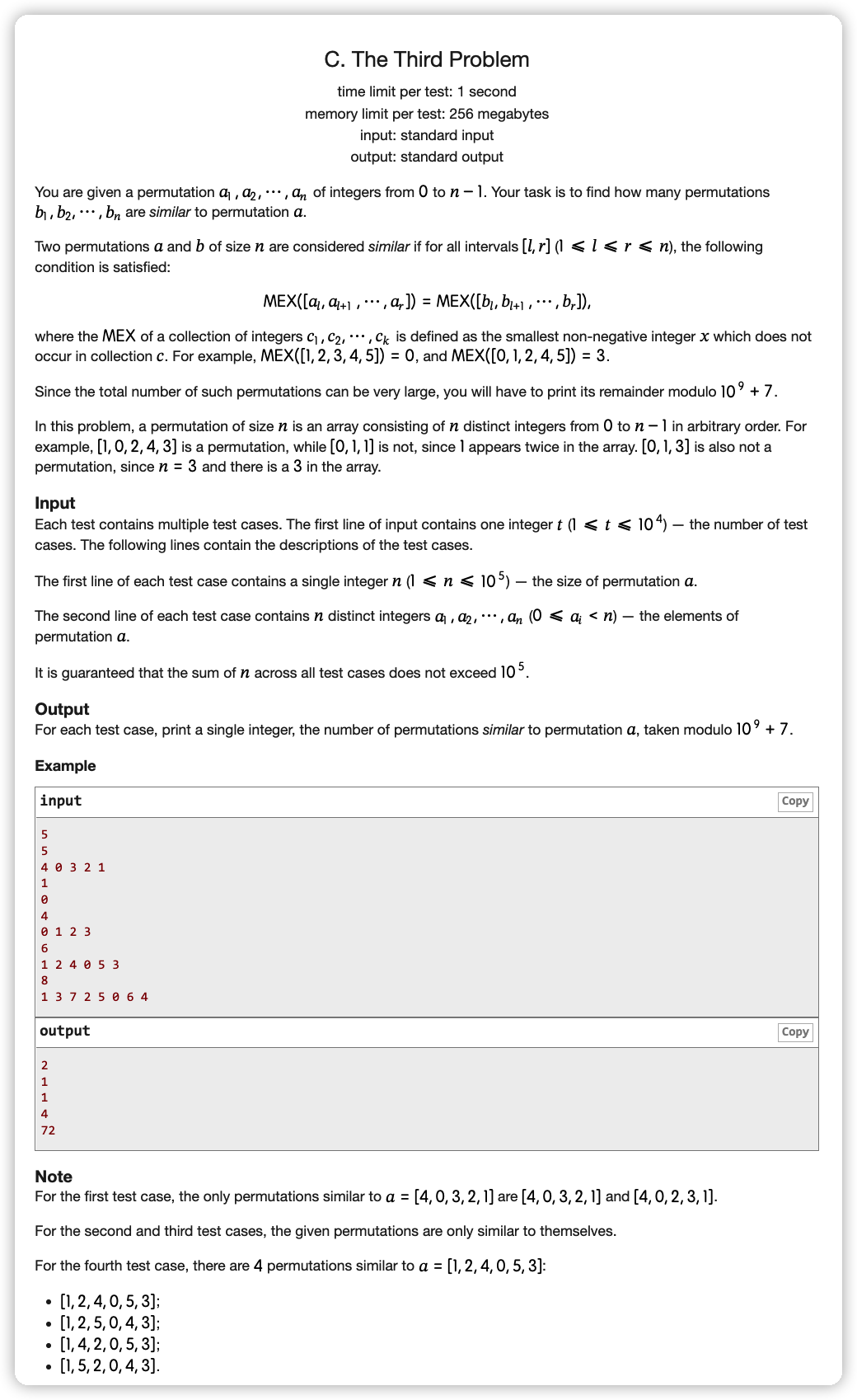
CodeForces1699C_TheThirdProblem

🔗

💡

首先 $0、1$ 的位置一定是固定的，因为要通过 $0、1$ 的 $[l,r]$ 确定出来 $mex=2$
所以可以往数值从 $1,2,3,4,5,...$ 考虑的方式着手
考虑这样的序列 $[0,2,3,4,1]$ ，其中对于 $x\in\{2,3,4\}$ 怎么摆都不会影响 $[l=1,r=5]$ 也不会影响 $1$ 到 $x$ 和 $0$ 到 $x$ 形成的 $mex[l,r]$ ，因为稳定上升 $mex$ 的区间已经固定了，里面的数值不管怎么摆都不会影响这个 $mex[l,r]$
而如果考虑 $[0,3,4,1,2]$ ，由于 $2$ 会让 $[l,r]$ 向外更新，所以由 $0,1,2$ 固定的区间 $[l=1,r=5]$ 是固定的，那么 $2$ 的位置也是固定的

在往上同理，得到这样一个性质：
如果对于当前扫描的 $x$ 在 $[l,r]$ 内，则 $[l,r]$ 内的空位都可以供 $x$ 选择
如果对于当前扫描的 $x$ 不在 $[l,r]$ 内，则 $x$ 是固定的，同时向外扩张 $[l,r]$
用这个性质求解即可

✅

inline void Solve () {
        int n; cin >> n;
        int l, r;
        vector<int> id(n);
        vector<int> a(n); for (int i = 0; i < n; i ++) {
                cin >> a[i];
                id[a[i]] = i;
                if (!a[i]) l = r = i;
        }
        ll res = 1;
        for (int i = 1; i < n; i ++) {
                if (id[i] < l || id[i] > r) l = min(l, id[i]), r = max(r, id[i]);
                else res = res * (1ll * r - l + 1 - i) % mod;
        }
        cout << res << endl;
}

---

HDU2021多校7D_LinkWithBalls

🔗

💡

两步都走到我想象不到的地方...

两个都有限制，即奇数 $2x-1$ 要求是选 $x$ 的倍数，偶数 $2x$ 要选不超过 $x$
考虑限制和限制取并集能否变得没有限制，发现将选 $x$ 的倍数和不超过 $x-1$ 的两个块合并到一个块，则对于这个块是任选任意数量的
合并的块为：$1,(2,3),(4,5),...,(2n-2,2n-1),2n$
前 $n$ 个都是任选，最后一个块是可以选不超过 $n$ 个
那么首先有一个式子就是枚举最后一个块选 $i$ 个，然后前 $m-i$ 个相同的东西分配进 $n$ 个不同的块内
即 $\sum\limits_{i=0}^{min(n,m)}C_{m-i+n-1}^{n-1}$

这个式子时间复杂度过不去，需要优化
看到这是一个总量连续的求和
在组合数的杨辉三角求解里面，$C_{n-1}^{m-1}=C_n^m-C_{n-1}^m$ 也是一个连续的东西，拿这个套一个基础的式子看看
$C_{n-1}^{m-1}+C_{n-2}^{m-2}=C_n^m-C_{n-1}^m+C_{n-1}^m-C_{n-2}^m=C_n^m-C_{n-2}^m$
而推的原式为 $C_{m+n-1}^{n-1}+C_{m+n-2-1}^{n-1}+...+C_{m+n-min(n,m)-1}^{n-1}$
就可以进行化简为 $C_{m+n}^n-C_{m+n-min(n,m)-1}^n$
最终式子已出，$O(1)$ 算即可

✅

const int mod = 1e9 + 7;
const int N = 2e6 + 10;
inline int ksm (int a, int b) {
    int res = 1;
    while (b) {
        if (b & 1) res = (ll)res * a % mod;
        a = (ll)a * a % mod;
        b >>= 1;
    }
    return res;
}
inline int inv (int x) {return ksm(x, mod - 2);}

int f[N], ivf[N];
inline int C (int n, int m) {
    if (n < m) return 0;
    return (ll)f[n] * ivf[n - m] % mod * ivf[m] % mod;
}

int main () {
    f[0] = 1;
    for (int i = 1; i < N; i ++) f[i] = (ll)f[i - 1] * i % mod;
    ivf[N - 1] = inv(f[N - 1]);
    for (int i = N - 2; i >= 0; i --) ivf[i] = (ll)ivf[i + 1] * (i + 1) % mod;

    int t; scanf("%d", &t); while (t --) {
        int n, m; scanf("%d%d", &n, &m);
        printf("%d\n", (C(m + n, n) - C(m - min(n, m) + n - 1, n) + mod) % mod);
    }
}

---

HDU2021多校8E_SeparatedNumber

🔗

💡

一共要放置不超过 $k-1$ 块隔板
首先根据经典组合数套路贡献次数，我们求 $a_i$ 乘 $10^j$ 时的贡献
如果 $i+j=n$ ，那么 $i+j$ 的后面放隔板是正常的，故最多还可以放 $k-1$ 块，一共有 $n-j-1$ 个空
如果 $i+j<n$ ，最多还能放 $k-2$ 块，有 $n-j-1$ 个空
公式即为 $\sum\limits_{i=1}^na_i\sum\limits_{j=0}^{n-i}10^j\sum\limits_{\alpha=0}^{k-1-[j\neq n-i]}C_{n-j-1-[j\neq n-i]}^{\alpha}$
拆一下变成 $\sum\limits_{i=1}^na_i\left\{\begin{aligned}\sum\limits_{j=0}^{n-i-1}10^jF_{n-j-2}^{k-2}\\10^{n-i}F_{n-j-1}^{k-1}\end{aligned}\right.$ 由于组合数是预处理，那么后面这一个看着像前缀和的也预处理
令 $F_n^m=\sum\limits_{i=0}^mC_n^i$
$F_n^m=F_n^{m-1}+C_n^m$ 且 $C_n^m=C_{n-1}^{m-1}+C_{n-1}^m$
推到 $\sum$ 里面，由于前缀中除了该位置，每一个都是用了两次，故 $F_n^m=2F_{n-1}^m-C_{n-1}^m$
这样根据上面的式子我们只需要预处理出 $F_{[]}^{k-1}$ 和 $F_{[]}^{k-2}$ 即可
那么在求的时候还有一个困难就是在第一类求解里面还有一个累加符号
发现在倒着推的时候 $n-i-1$ 是递增的，且第 $i$ 项只比第 $i+1$ 项多了 $10^{n-i-1}F_{n-(n-i-1)-2}^{k-2}$ ，别的都没变，于是第一类可以倒着求然后不断累加上新增的值，可以视作一个后缀
第二类就直接算即可

✅

const int mod = 998244353;
inline int ksm (int a, int b) {
    int res = 1;
    while (b) {
        if (b & 1) res = (ll)res * a % mod;
        a = (ll)a * a % mod;
        b >>= 1;
    }
    return res;
}
inline int inv (int x) {return ksm(x, mod - 2);}

const int N = 1e6 + 10;

int f[N], ivf[N];
inline int C (int n, int m) {
    if (n < m) return 0;
    return (ll)f[n] * ivf[m] % mod * ivf[n - m] % mod;
}

char s[N];
int a[N];

int Fkd1[N], Fkd2[N];
int pw10[N];

inline void Solve () {
    int k; scanf("%d", &k);
    scanf("%s", s + 1);
    int n = strlen(s + 1);
    for (int i = 1; i <= n; i ++) a[i] = s[i] - '0';

    if (k == 1) {
        int res = 0;
        for (int i = 1; i <= n; i ++) res = ((ll)res * 10 % mod + a[i]) % mod;
        printf("%d\n", res);
        return;
    }

    Fkd1[0] = Fkd2[0] = 1;
    for (int i = 1; i < N; i ++) 
        Fkd1[i] = (Fkd1[i - 1] * 2 % mod - C(i - 1, k - 1) + mod) % mod,
        Fkd2[i] = (Fkd2[i - 1] * 2 % mod - C(i - 1, k - 2) + mod) % mod;
    
    int sum_fkd2 = 0;
    int res = 0;
    for (int i = n; i >= 1; i --) {
        if (n - i - 1 >= 0) {
            (sum_fkd2 += (ll)pw10[n - i - 1] * Fkd2[n - (n - i - 1) - 2] % mod) %= mod;
        }
        int num = ((ll)pw10[n - i] * Fkd1[n - (n - i) - 1] % mod + sum_fkd2) % mod;
        (res += (ll)a[i] * num % mod) %= mod;
    }
    printf("%d\n", res);
}


int main () {
    f[0] = 1;
    for (int i = 1; i < N; i ++) f[i] = (ll)f[i - 1] * i % mod;
    ivf[N - 1] = inv(f[N - 1]);
    for (int i = N - 2; i >= 0; i --) ivf[i] = (ll)ivf[i + 1] * (i + 1) % mod;
    pw10[0] = 1;
    for (int i = 1; i < N; i ++) pw10[i] = (ll)pw10[i - 1] * 10 % mod;

    int cass; scanf("%d", &cass); while (cass --) {
        Solve();
    }
}

---

ICPC2018南京站J_PrimeGame

🔗

💡

刚拿到这个题是想着怎么去优化式子，在想用什么数据结构，但是区间问题的时候就很难看一个区间是否存在一个数，这样的话还要再开一个复杂度
看一下问的是什么，“对于所有区间，出现的不同质因数和”，加和是以一个质因数出没出现为单位的，那就分开考虑质因数，累加每一个质因数的贡献（经典组合套路
首先将所有质数出现的所有位置统计一遍
对于质数 $p$ 的出现位置：$a,b,c,d$
它所贡献的次数为 $a\times(b-a)+(b-a)\times(c-b)+(d-c)\times(n+1-d)$
按这种方式一个质数贡献的次数为 $a_0=0,a_{sz+1}=n+1,\sum\limits_{i=1}^{sz}(a_i-a_{i-1})(a_{i+1}-a_i)$

✅

const int N = 1e6 + 10;
bool ntp[N];
int mnp[N];
vector<int> p;
vector<int> id[N];

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    ntp[0] = ntp[1] = 1;
    for (int i = 2; i < N; i ++) {
        if (!ntp[i]) p.push_back(i), mnp[i] = i;
        for (int j = 0; j < p.size() && 1ll * i * p[j] < N; j ++) {
            ntp[i * p[j]] = 1;
            mnp[i * p[j]] = p[j];
            if (i % p[j] == 0) break;
        }
    }

    for (int i = 2; i < N; i ++) id[i].push_back(0);
    int n; cin >> n;
    for (int i = 1; i <= n; i ++) {
        int x; cin >> x;
        while (x > 1) {
            id[mnp[x]].push_back(i);
            x /= mnp[x];
        } 
    } 
    for (int i = 2; i < N; i ++) id[i].push_back(n + 1);

    ll res = 0;
    for (int i = 2; i < N; i ++) {
        id[i].erase(unique(id[i].begin(), id[i].end()), id[i].end());
        for (int j = 1; j + 1 < id[i].size(); j ++) {
            res += 1ll * id[i][j] * (id[i][j + 1] - id[i][j]);
        }
    }
    cout << res << endl;
}

---

ICPC2020上海站G_Fibonacci

🔗

💡

fibonacci数列每第三个数一定是偶数
那么 n/3 求一下偶数的个数 eve 偶数和所有数相乘都是偶数 res = eve * n 但是不能和自己组合 res -= eve
偶数内部两两组合也多加了一次，要减去 res -= eve * (eve - 1) / 2

✅

int main () {
        ios::sync_with_stdio(false);

        ll n; cin >> n;
        ll eve = n / 3;
        ll res = eve * n - eve;
        res -= eve * (eve - 1) / 2;
        cout << res << endl;
}

---

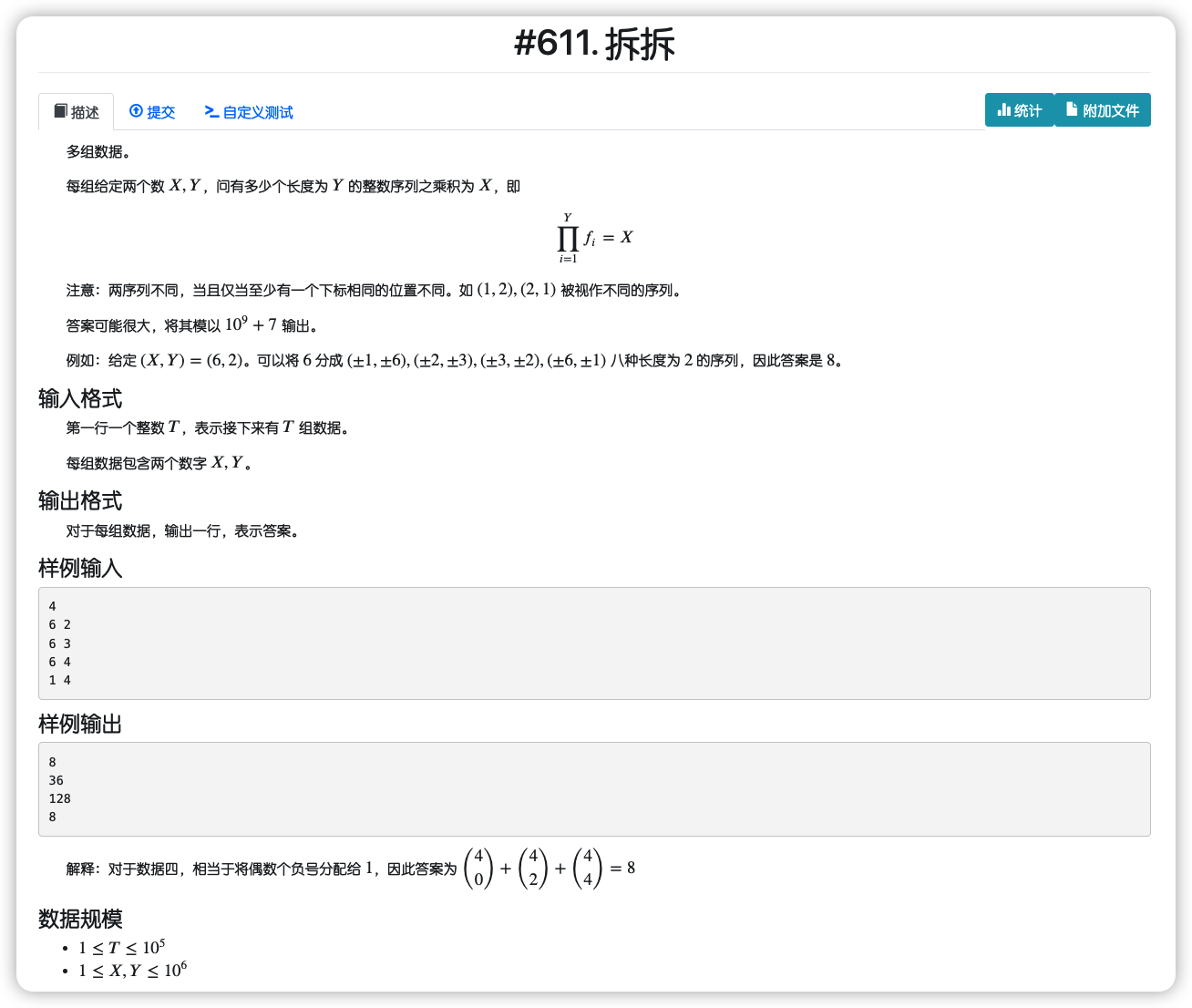
NamomoCamp2022春季div1每日一题_拆拆

🔗

💡

我们分解质因子

$$x=p_1^{a_1}\times p_2^{a_2}\times\dots\times p_k^{a_k}$$

由于每个因数不同且独立，对这个问题转化一下其实也就是将 $a_i$ 个 $p_i$ 放入 $y$ 个盒子内，球盒模型下表达式为 $\binom{a_i+y-1}{y-1}$
利用乘法原理得到结果
正数是要在 $y$ 中偶数个作为负数，即 $2^{y-1}$
让结果乘上这个数即可

但是这道题时间卡的紧，考虑优化（看到了一堆黑科技

快速拆分质因数

int ntp[N], prime[N], idx;
inline void Sieve () {
        ntp[1] = 1;
        for ( int i = 2; i < N; i ++ ) {
                if ( !ntp[i] ) prime[idx ++] = i, ntp[i] = i;
                for ( int j = 0; j < idx && 1ll * i * prime[j] < N; j ++ ) {
                        if ( !ntp[i * prime[j]] ) {
                                ntp[i * prime[j]] = prime[j];
                        }
                        if ( i % prime[j] == 0 ) break;
                }
        }
}

vector<int> table; // x 的质因数的指数表
int lst = ntp[x], t = 1;
x /= ntp[x];
while ( ntp[x] > 1 ) {
        if ( ntp[x] == lst ) {
                t ++;
        } else {
                table.push_back(t);
                lst = ntp[x];
                t = 1;
        }
        x /= ntp[x];
}
if ( lst > 1 ) table.push_back(t);

int ntp[N], prime[N], idx;
inline void Sieve () {
        ntp[1] = 1;
        for ( int i = 2; i < N; i ++ ) {
                if ( !ntp[i] ) prime[idx ++] = i, ntp[i] = i;
                for ( int j = 0; j < idx && 1ll * i * prime[j] < N; j ++ ) {
                        if ( !ntp[i * prime[j]] ) {
                                ntp[i * prime[j]] = prime[j];
                        }
                        if ( i % prime[j] == 0 ) break;
                }
        }
}

vector<int> table; // x 的质因数的指数表
int lst = ntp[x], t = 1;
x /= ntp[x];
while ( ntp[x] > 1 ) {
        if ( ntp[x] == lst ) {
                t ++;
        } else {
                table.push_back(t);
                lst = ntp[x];
                t = 1;
        }
        x /= ntp[x];
}
if ( lst > 1 ) table.push_back(t);

令 npt[i] 表示筛出来 $i$ 不是质数的最小质因数
然后让 $x$ 不断 $x/ntp[x]$ 即可得到所有的质因数

int ntp[N], prime[N], idx;
inline void Sieve () {
        ntp[1] = 1;
        for ( int i = 2; i < N; i ++ ) {
                if ( !ntp[i] ) prime[idx ++] = i, ntp[i] = i;
                for ( int j = 0; j < idx && 1ll * i * prime[j] < N; j ++ ) {
                        if ( !ntp[i * prime[j]] ) {
                                ntp[i * prime[j]] = prime[j];
                        }
                        if ( i % prime[j] == 0 ) break;
                }
        }
}

vector<int> table; // x 的质因数的指数表
int lst = ntp[x], t = 1;
x /= ntp[x];
while ( ntp[x] > 1 ) {
        if ( ntp[x] == lst ) {
                t ++;
        } else {
                table.push_back(t);
                lst = ntp[x];
                t = 1;
        }
        x /= ntp[x];
}
if ( lst > 1 ) table.push_back(t);

快速求阶乘逆元

ivf[n] = inv(f[n]);
for ( int i = n - 1; i >= 0; i -- ) ivf[i] = ivf[i + 1] * (i + 1) % mod;

ivf[n] = inv(f[n]);
for ( int i = n - 1; i >= 0; i -- ) ivf[i] = ivf[i + 1] * (i + 1) % mod;

利用大阶乘做分母，然后向前化简

ivf[n] = inv(f[n]);
for ( int i = n - 1; i >= 0; i -- ) ivf[i] = ivf[i + 1] * (i + 1) % mod;

✅

const int N = 2e6 + 10;
const int mod = 1e9 + 7;

inline ll ksm ( ll a, ll b ) { ll res = 1; while ( b ) { if ( b & 1 ) res = res * a % mod; a = a * a % mod; b >>= 1; } return res; }
inline ll inv ( ll x ) { return ksm(x, mod - 2); }

namespace Number {
        int ntp[N], prime[N], idx;
        inline void Sieve () {
                ntp[1] = 1;
                for ( int i = 2; i < N; i ++ ) {
                        if ( !ntp[i] ) prime[idx ++] = i, ntp[i] = i;
                        for ( int j = 0; j < idx && 1ll * i * prime[j] < N; j ++ ) {
                                if ( !ntp[i * prime[j]] ) {
                                        ntp[i * prime[j]] = prime[j];
                                }
                                if ( i % prime[j] == 0 ) break;
                        }
                }
        }
        ll f[N], ivf[N];
        inline void get_F () {
                f[0] = 1;
                for ( int i = 1; i < N; i ++ ) f[i] = f[i - 1] * i % mod;
                ivf[N - 1] = inv(f[N - 1]);
                for ( int i = N - 2; i >= 0; i -- ) ivf[i] = ivf[i + 1] * (i + 1) % mod;
        }
} using namespace Number;

inline ll C ( int n, int m ) {
        return f[n] * ivf[m] % mod * ivf[n - m] % mod;
}

inline void Solve () {
        int x, y; cin >> x >> y;

        vector<int> table;
        int lst = ntp[x], t = 1;
        x /= ntp[x];
        while ( ntp[x] > 1 ) {
                if ( ntp[x] == lst ) {
                        t ++;
                } else {
                        table.push_back(t);
                        lst = ntp[x];
                        t = 1;
                }
                x /= ntp[x];
        }
        if ( lst > 1 ) table.push_back(t);

        ll res = 1;
        for ( int i : table ) res = res * C(i + y - 1, y - 1) % mod;
        res = res * ksm(2, y - 1) % mod;
        cout << res << "\n";
}

int main () {
        cin.tie(0)->sync_with_stdio(0);
        cin.exceptions(cin.failbit);

        Sieve(); get_F();

        int cass; cin >> cass; while ( cass -- ) {
                Solve ();
        }
}

---

POJ3734_Blocks

🔗

💡

首先生成函数想一波，把这四个砖的生成函数乘起来得到 发现啥也不啥，告辞
组合数想一波
其实就是分成两部分，一部分一定是偶数，一部分无所谓，偶数那一部分分成两份偶数，无所谓那一部分分成两份无所谓
块砖选偶数个有 种，选任意个有 种
那么从这偶数个中选偶数个，再从另外任意个中选任意个，得到柿子

注意在 时 可能会出错，所以拿出来

我们解这个柿子就行了

✅

const int mod = 10007;

inline ll ksm ( ll a, ll b ) {
        ll res = 1;
        while ( b ) {
                if ( b & 1 ) res = res * a % mod;
                a = a * a % mod;
                b >>= 1;
        }
        return res;
}

int main () {
        int cass; cin >> cass; while ( cass -- ) {
               ll n; cin >> n;
               ll two_mi = ksm(2, n - 1);
               cout << (two_mi * (two_mi - 1) % mod + two_mi * 2 % mod) % mod << endl;
        }
}

---

生成函数

洛谷P6078_Sweets

🔗

💡

先根据题目构建生成函数

将生成函数乘起来
上面的可以变成一个多项式
看下面的

合并起来得到

对于 这一项：（系数设置为 )
那么这一项贡献为
由 可将 化成
即

那么答案为

对于取模，观察
将 ，取完模是比 要大的，那么这时就可以直接除 了

✅

int n, a, b;
int m[15];
map<int, int> g_mps;
vector<pair<int, int> > g; // first: 指数，second: 系数

const int mod = 2004;
ll MOD = mod;
ll fac = 1;
inline int C ( int n, int m ) {
        if ( n < m ) return 0;
        ll res = 1;
        for ( int i = n - m + 1; i <= n; i ++ ) res = res * i % MOD;
        return res / fac % mod;
}

int main () {
        cin >> n >> a >> b;
        for ( ll i = 1; i <= n; i ++ ) fac *= i;
        MOD *= fac;

        g_mps[0] = 1;
        for ( int i = 0; i < n; i ++ ) {
                cin >> m[i];
                vector<pair<int, int> > tmps; 
                for ( auto g_mp : g_mps ) {
                        tmps.push_back({g_mp.first, g_mp.second});
                        tmps.push_back({g_mp.first + m[i] + 1, -g_mp.second});
                }
                g_mps.clear();
                for ( auto tmp : tmps ) {
                        g_mps[tmp.first] += tmp.second;
                }
        }
        for ( auto g_mp : g_mps ) g.push_back({g_mp.first, g_mp.second});

        ll res = 0;
        for ( auto i : g ) {
                int k = i.first;
                res = ((res + (ll)i.second * (C(n + b - k, n) - C(n + a - k - 1, n) + mod) % mod) % mod + mod) % mod;
        }
        cout << res << endl;
}

---

牛客NC207746_背包

🔗

💡

我们对每一个物品一个生成函数多项式，同时根据下面这个结论将他们化简

对于等比 数列求和公式：
如果
那么
所以

对后面的求和并化简得到
展开得
根据二项式定理得到最后 的系数便是

那么就直接求

✅

const int mod = 1e9 + 7;
inline ll ksm ( ll a, ll b ) {
        ll res = 1;
        while ( b ) {
                if ( b & 1 ) res = res * a % mod;
                a = a * a % mod;
                b >>= 1;
        }
        return res;
}
inline ll inv ( ll x ) {
        return ksm ( x, mod - 2 );
}

int main () {
        ll n; cin >> n;
        ll a = n % mod, b = (n + 1) % mod, c = (n + 2) % mod;
        ll d = inv(6);
        cout << a * b % mod * c % mod * d % mod << endl;
}

---

HDUOJ1521_排列组合

🔗

http://acm.hdu.edu.cn/showproblem.php?pid=1521

💡

✅

#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define eps 1e-6
#define ll long long
#define INF 0x7FFFFFFF
#define Chivas int main()
#define Regal return 0
#define PI acos(-1.0)
#define pb(x) push_back(x)
#define SP system("pause")
#define mm(a, b) memset(a, b, sizeof(a))
#define fir(i, a, n) for (ll i = a; i <= n; i++)
#define rif(i, a, n) for (ll i = a; i >= n; i--)
#define each_cass(cass) for (scanf("%d", &cass); cass; cass--)

using namespace std;

const int maxn = 15;
double c1[maxn], c2[maxn];
ll num[maxn];
ll F[maxn];
ll n, m;

void Factorial(){
    F[0] = 1;
    for (int i = 1; i < maxn; i++)
        F[i] = F[i - 1] * i;
}

void init(){
    mm(c1, 0);
    mm(c2, 0);
    for (int i = 0; i <= num[1]; i++)
        c1[i] = 1.0 / F[i];
}

Chivas{
    Factorial();
    while (scanf("%lld%lld", &n, &m) == 2){
        for (int i = 1; i <= n; i++)
            scanf("%lld", &num[i]);
        init();
        for (int i = 2; i <= n; i++){
            for (int j = 0; j <= m; j++){
                for (int k = 0; k + j <= m && k <= num[i]; k++)
                    c2[j + k] += c1[j] / F[k];
            }
            for (int j = 0; j <= m; j++)
                c1[j] = c2[j], c2[j] = 0;
        }
        printf("%.0f\n", c1[m] * F[m]);
    }
    Regal;
}

---

HDUOJ1028_IgnatiusAndThePrincess3

🔗

http://acm.hdu.edu.cn/showproblem.php?pid=1028

💡

✅

#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define eps 1e-6
#define ll long long
#define INF 0x7FFFFFFF
#define PI acos(-1.0)
#define pb(x) push_back(x)
#define SP system("pause")
#define mm(a, b) memset(a, b, sizeof(a))
#define fir(i, a, n) for (int i = a; i <= n; i++)
#define rif(i, a, n) for (int i = a; i >= n; i--)
#define each_cass(cass) for (cin >> cass; cass; cass--)

using namespace std;

const int maxn = 200;
int c1[maxn];
int c2[maxn];

void init(){
    for (int i = 0; i < maxn; i++)
        c1[i] = 1, c2[i] = 0;
}

int main(){
    int n;
    while(cin>>n){
        init();
        for (int i = 2; i <= n; i++){//n-1次合并
            for (int j = 0; j <= n; j++)//第一个括号
                for (int k = 0; k + j <= n; k += i)//第二个括号
                    c2[j + k] += c1[j];
            for (int j = 0; j <= n; j++)//替换
                c1[j] = c2[j], c2[j] = 0;
        }
        cout << c1[n] << endl;
    }
    return 0;
}

---

HDUOJ1085_HoldingBin-LadenCaptive

🔗

http://acm.hdu.edu.cn/showproblem.php?pid=1085

💡

✅

#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define eps 1e-6
#define ll long long
#define INF 0x7FFFFFFF
#define PI acos(-1.0)
#define pb(x) push_back(x)
#define SP system("pause")
#define mm(a, b) memset(a, b, sizeof(a))
#define fir(i, a, n) for (ll i = a; i <= n; i++)
#define rif(i, a, n) for (ll i = a; i >= n; i--)
#define each_cass(cass) for (scanf("%d", &cass); cass; cass--)

using namespace std;

const int maxn = 100010;
int kind[4] = {0, 1, 2, 5};
int c1[maxn];
int c2[maxn];
int num[4];
int sum;

void init(){
    mm(c1, 0);
    mm(c2, 0);
    for (int i = 0; i <= sum; i++)
        c1[i] = 1, c2[i] = 0;
}

int main(){
    while (scanf("%d%d%d", &num[1], &num[2], &num[3]) == 3, num[1] || num[2] || num[3]){
        sum = num[1];
        init();
        for (int i = 2; i <= 3; i++){
            for (int j = 0; j <= sum; j++)
                for (int k = 0; k <= num[i] * kind[i]; k += kind[i])
                    c2[j + k] += c1[j];
            sum += num[i] * kind[i];
            for (int j = 0; j <= sum; j++)
                c1[j] = c2[j], c2[j] = 0;
        }
        for (int i = 0; i <= sum + 1; i++){
            if(!c1[i]){
                printf("%d\n", i);
                break;
            }
        }
    }
    return 0;
}

---

HDUOJ1398_SquareCoins

🔗

http://acm.hdu.edu.cn/showproblem.php?pid=1398

💡

✅

#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define eps 1e-6
#define ll long long
#define INF 0x7FFFFFFF
#define PI acos(-1.0)
#define pb(x) push_back(x)
#define SP system("pause")
#define mm(a, b) memset(a, b, sizeof(a))
#define each_cass(cass) for (cin >> cass; cass; cass--)

using namespace std;

const ll maxn = 1000;
ll c1[maxn];
ll c2[maxn];
ll a[1000];

void init(){
    for (ll i = 0; i < maxn; i++)
        c1[i] = 1, c2[i] = 0;
    for (ll i = 0; i < 1000; i++)
        a[i] = i * i;
}

int main(){
    ll n;
    while(scanf("%d",&n)==1,n){
        init();
        for (ll i = 2; i <= n; i++){
            for (ll j = 0; j <= n; j++)
                for (ll k = 0; k + j <= n; k += a[i])
                    c2[k + j] += c1[j];
            for (ll j = 0; j <= n; j++)
                c1[j] = c2[j], c2[j] = 0;
        }
        printf("%d\n", c1[n]);
    }
    return 0;
}

---

HDUOJ1709_TheBalance

🔗

http://acm.hdu.edu.cn/showproblem.php?pid=1709

💡

✅

#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define eps 1e-6
#define ll long long
#define INF 0x7FFFFFFF
#define PI acos(-1.0)
#define pb(x) push_back(x)
#define SP system("pause")
#define mm(a, b) memset(a, b, sizeof(a))
#define fir(i, a, n) for (ll i = a; i <= n; i++)
#define rif(i, a, n) for (ll i = a; i >= n; i--)
#define each_cass(cass) for (scanf("%d", &cass); cass; cass--)

using namespace std;

const int maxn = 100005;
int n;
int A[110];
int c1[maxn];
int c2[maxn];

void init(){
    mm(c1, 0);
    mm(c2, 0);
    c1[0] = c1[A[1]] = 1;
}

main(){
    while (scanf("%d", &n) == 1){
        int sum = 0;
        for (int i = 1; i <= n; i++)
            scanf("%d", &A[i]), sum += A[i];
        init();
        for (int i = 2; i <= n; i++){
            for (int j = 0; j <= sum; j++){
                for (int k = 0; k + j <= sum && k <= A[i]; k += A[i])
                    c2[abs(k - j)] += c1[j], c2[k + j] += c1[j];
            }
            for (int j = 0; j <= sum; j++)
                c1[j] = c2[j], c2[j] = 0;
        }

        vector<int> ans;
        for (int i = 0; i <= sum; i++){
            if(!c1[i]){
                ans.push_back(i);
            }
        }
        printf("%lu\n", ans.size());
        for (int i = 0; i < ans.size(); i++)
            printf("%d%c", ans[i], i == ans.size() - 1 ? '\n' : ' ');
    }
        return 0;
}

---

HDUOJ2152_Fruit

🔗

http://acm.hdu.edu.cn/showproblem.php?pid=2152

💡

✅

#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define eps 1e-6
#define ll long long
#define INF 0x7FFFFFFF
#define Chivas int main()
#define Regal return 0
#define PI acos(-1.0)
#define pb(x) push_back(x)
#define SP system("pause")
#define mm(a, b) memset(a, b, sizeof(a))
#define fir(i, a, n) for (ll i = a; i <= n; i++)
#define rif(i, a, n) for (ll i = a; i >= n; i--)
#define each_cass(cass) for (scanf("%d", &cass); cass; cass--)

using namespace std;

const ll maxn = 1e4 + 10;
ll n, m;
struct fruit{
    ll a;
    ll b;
    void read(){
        scanf("%lld%lld", &a, &b);
    }
} f[110];
ll c1[maxn];
ll c2[maxn];

void init(){
    mm(c1, 0);
    mm(c2, 0);
    for (ll i = f[1].a; i <= f[1].b; i++)
        c1[i] = 1;
}

Chivas{
    while (scanf("%lld%lld", &n, &m) == 2){
        for (ll i = 1; i <= n; i++)
            f[i].read();
        init();
        for (ll i = 2; i <= n; i++){
            for (ll j = 0; j <= m; j++){
                for (ll k = f[i].a; k + j <= m && k <= f[i].b; k++)
                    c2[j + k] += c1[j];
            }
            for (ll j = 0; j <= m; j++)
                c1[j] = c2[j], c2[j] = 0;
        }
        printf("%lld\n", c1[m]);
    }
    Regal;
}

---

容斥原理

洛谷P1450_硬币购物

🔗

💡

本题尝试生成函数 分， 优化还是 分...

看了眼时间，开始老老实实想背包
（不会吧 是极限而且不一定过？

提前给定的 一定有其用意，先拿完全背包预处理一下 数组
但是让多重背包，我们就容斥减掉不合法的
假设我们枚举第 个，此时我们如果预先拿走 个，那么之后的任意选择方式都是不合法的
此时不合法的也就是容积 的背包，我们减去
当然因为是容斥，所以我们还要加回来提前两个不合法，减掉提前三个不合法...

二进制枚举，观察时间复杂的， 很正常的时间

好家伙，容斥改完全背包为多重背包...

✅

#include <iostream>

#define ll long long

using namespace std;

const int N = 1e5 + 10;
int c[N], d[N], n;
ll dp[N];

inline void Solve () {
        for ( int i = 0; i < 4; i ++ ) cin >> d[i];
        cin >> n;
        ll res = dp[n];
        for ( int i = 0; i < (1 << 4); i ++ ) { // 枚举提前选哪些物品超过限制
                int cnt = 0; ll cur = 0;
                for ( int j = 0; j < 4; j ++ ) {
                        if ( i & (1 << j) ) {
                                cnt ++;
                                cur += (ll)c[j] * (d[j] + 1);
                        }
                }
                if ( cur > n || cur == 0 ) continue; // n以下没有不合法解 或者 全都不选不构成解也不构成不合法解
                if ( cnt & 1 ) res -= dp[n - cur];
                else           res += dp[n - cur];
        }
        cout << res << endl;
}

int main () {
        for ( int i = 0; i < 4; i ++ ) cin >> c[i]; 
        dp[0] = 1; for ( int i = 0; i < 4; i ++ ) for ( int j = c[i]; j < N; j ++ ) dp[j] += dp[j - c[i]]; 

        int cass; cin >> cass; while ( cass -- ) {
                Solve ();
        }
}

---

洛谷P3166_数三角形

🔗

💡

题目先说的全部，然后给了限制，按着它的顺序想就是用容斥。
本题是格点，我们将 $n,m$ 都 $+1$ 会更好看
首先所有的点为：$C_{nm}^3$
减去在同一条线上的情况：
$1.$ 与坐标轴平行：
$nC_m^3+mC_n^3$
$2.$ 与坐标轴不平行：
注意 $1\le N,M\le1000$ ，可以 $O(nm)$ 写
枚举两个点的纵坐标差 $i$ 与横坐标差 $j$ ，对于一对点是形成一个 $i\times j$ 的矩形
这个矩形对角线上除了顶点之外的点一共有 $gcd(i,j)-1$ 个

证明

令 $d=gcd(i,j)$ ，则不经过任何一个点的坐标差应为 $(\frac{i}{d},\frac{j}{d})$ ，这个点一共有 $d$ 个倍数，包含了一个顶点，应减去为 $d-1$

一个矩形有两个对角线，应乘 $2$
$n\times m$ 的矩形有 $(n-i)(m-j)$ 个这样的小矩形，乘上个数
则这一条应减去 $2\sum\limits_{i=1}^{n-1}\sum\limits_{j=1}^{m-1}(n-i)(m-j)(gcd(i,j)-1)$

则答案为：

$$C_{nm}^3-nC_m^3-mC_n^3-2\sum\limits_{i=1}^{n-1}\sum\limits_{j=1}^{m-1}(n-i)(m-j)(gcd(i,j)-1)$$

✅

inline ll gcd (ll a, ll b) { return b ? gcd(b, a % b) : a; }
int main () {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);

        ll n, m; cin >> n >> m;
        n ++, m ++;

        ll res = n * m * (n * m - 1) * (n * m - 2) / 6;
        
        res -= m * n * (n - 1) * (n - 2) / 6;
        res -= n * m * (m - 1) * (m - 2) / 6;
        for (ll i = 1; i < n; i ++) {
                for (ll j = 1; j < m; j ++) {
                        res -= 2ll * (gcd(i, j) - 1) * (n - i) * (m - j);
                }
        }

        cout << res << endl;
}

---

牛客2021多校(2)J_CountingTriangles

🔗

💡

很妙的题
要得到同色边三角形，只能枚举，且枚举两个点还不够，还要去检查第三个点是否合法
正难则反，从一个点出发不同色的两个边是可以直接算出来的
枚举 $u$ ，枚举 $u$ 出发的边，$cnt[i]$ 为颜色为 $i$ 的边数，则 $u$ 出发的不同色边为 $cnt[0]\times cnt[1]$ ，这就是两个边确定出来的三角形 ，让答案 $res$ 加上
最后会有重复的，需要 $res/2$
所有的三角形数量为从 $n$ 个点中选 $3$ 个点，那么同色边三角形数为 $C_n^3-res$

✅

namespace GenHelper
{
    unsigned z1,z2,z3,z4,b,u;
    unsigned get()
    {
        b=((z1<<6)^z1)>>13;
        z1=((z1&4294967294U)<<18)^b;
        b=((z2<<2)^z2)>>27;
        z2=((z2&4294967288U)<<2)^b;
        b=((z3<<13)^z3)>>21;
        z3=((z3&4294967280U)<<7)^b;
        b=((z4<<3)^z4)>>12;
        z4=((z4&4294967168U)<<13)^b;
        return (z1^z2^z3^z4);
    }
    bool read() {
      while (!u) u = get();
      bool res = u & 1;
      u >>= 1; return res;
    }
    void srand(int x)
    {
        z1=x;
        z2=(~x)^0x233333333U;
        z3=x^0x1234598766U;
        z4=(~x)+51;
      	u = 0;
    }
}
using namespace GenHelper;

int e[8001][8001];

int main () {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, seed; cin >> n >> seed;
    srand(seed);
    for (int i = 0; i < n; i ++) {
        for (int j = i + 1; j < n; j ++) e[i][j] = e[j][i] = read();
    }

    ll res = 0;
    for (int i = 0; i < n; i ++) {
        int num[2] = {0};
        for (int j = 0; j < n; j ++) {
            if (i != j) num[e[i][j]] ++;
        }
        res -= 1ll * num[0] * num[1];
    }
    res = res / 2 + 1ll * n * (n - 1ll) * (n - 2ll) / 6;

    cout << res << endl;
}

---

牛客2022寒假算法基础集训营K_智乃的C语言模除方程

🔗

💡

本题是让我们计数
让 $[l,r]$ 以 $p$ 为循环区间进行移动，看多少个模后存在于 $[L,R]$ 中
首先肯定是要看需不需要从 $0$ 的位置分开计算的

对于 $[L,R]$ 都在同一边的，我们可以想到用容斥， $calc(R)-calc(L-1)$ 这种
那么不在一边的我们要分开计算然后加起来

那么就将区间问题转化为前缀的点问题了
任务是求从 $x$ 到 $0$ 有多少个数模后为 $[l,r]$ ，上面在叙述问题时已经很明白了，这个计算循环节进行优化
以 $[0,p-1]$ 为循环节，每个循环节内计算 $[0,p-1]\cap[l,r]$ 的个数，然后循环 $\left\lfloor\frac xp\right\rfloor$ 次
多出来的就算一下 $[0,x\%p]\cap[l,r]$ 即可

相交区间长度我们写一个函数 get_intersection(a, b, c, d) 来计算
那么我们对于循环 x / p 次，每个循环有 get_intersection(0, p - 1, l, r) 个相交，加上 get_intersection(0, x % p, l, r) 这样去算
记得对 x 分奇偶

✅

ll P, l, r, L, R;

inline ll get_Intersection ( ll a, ll b, ll c, ll d ) {
        if ( c > b || d < a ) return 0;
        return min(b, d) - max(a, c) + 1;
}
inline ll Query ( ll bondry ) {
        if ( bondry < 0 ) 
                return (- bondry / P) * get_Intersection(- P + 1, 0, l, r) + get_Intersection(bondry % P, 0, l, r );
        else 
                return bondry / P * get_Intersection(0, P - 1, l, r) + get_Intersection(0, bondry % P, l, r);
}

int main () {
        ios::sync_with_stdio(false);

        cin >> P >> l >> r >> L >> R;
        P = llabs(P);
        if ( L <= 0 && R >= 0 ) 
                cout << Query(R) + Query(L) - Query(0) << endl; // 分开计算，多算了个 0
        else if ( L < 0 && R < 0 )
                cout << Query(L) - Query(R + 1) << endl; // 负数容斥
        else 
                cout << Query(R) - Query(L - 1) << endl; // 正数容斥
}

---

牛客练习赛92C_D与C

🔗

💡

真就看见计数想容斥呗
首先可以得到总边数 为
对于这些边数让两人一起放一共有 种情况，设为

如果 那么不管咋放都成立，直接输出 就行
否则看看两人没有公共边的情况
就是在 中选 个，再从 个中选 个
这样的答案就是

✅

#include <iostream>

#define ll long long

using namespace std;

const int mod = 1e9 + 7;
const int N = 1e6 + 10;

ll f[N];
inline void Get () {
        f[0] = 1;
        for ( ll i = 1; i < N; i ++ ) f[i] = f[i - 1] * i % mod;
}
inline ll ksm ( ll a, ll b ) {
        ll res = 1;
        while ( b ) {
                if ( b & 1 ) res = res * a % mod;
                a = a * a % mod;
                b >>= 1;
        }
        return res;
}
inline ll inv ( ll x ) { return ksm (x, mod - 2); }
inline ll C ( ll n, ll m ) {
        return f[n] * inv(f[m]) % mod * inv(f[n - m]) % mod;
}

int main () {
        Get();
        ll n, a, b; cin >> n >> a >> b;
        ll has_edge = n * (n - 1) / 2;
        ll has_situation = C(has_edge, a) * C(has_edge, b) % mod;
        if ( a + b >= has_edge ) cout << has_situation << endl;
        else {
                ll sub = C(has_edge, a) * C(has_edge - a, b) % mod;
                cout << (has_edge - sub + mod) % mod << endl;
        }
}

---

ABC221E_LEQ

🔗

💡

问题转化一下就是
从左向右，的贡献就是每个前面比它小的，在这个位置上的贡献为
由于区间长度总是参差不齐的
那么对于每个，我们都可以维护一个前缀贡献为
然后在的位置的时候的贡献容斥为即可，其中sum可以由树状数组的前缀得到
所以每次累加查询位置以前的总贡献，query(a[i]) * ksm(2, i)
然后在的位置上更新一下这个前缀贡献，update( a[i], ksm(ksm(2, i + 1), mod - 2) )

✅

#include <iostream>
#include <vector>
#include <algorithm>
#define ll long long
using namespace std;

const int N = 3e5 + 10;
const int mod = 998244353;
ll n, a[N];
vector<ll> nums;

inline ll ksm ( ll a, ll b ) {
	ll res = 1;
	while ( b ) {
		if ( b & 1 ) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}

namespace TreeArray {
	ll tr[N];
	inline ll lowbit ( ll x ) {
		return x & -x;
	}
	inline void update ( ll id, ll val ) {
		while ( id < N ) tr[id] = (tr[id] + val) % mod, id += lowbit(id);
	}
	inline ll query ( ll id ) {
		ll res = 0;
		while ( id > 0 ) res = (res + tr[id]) % mod, id -= lowbit(id);
		return res;
	}
} using namespace TreeArray;

int main() {
#ifndef ONLINE_JUDGE
	freopen("in.in", "r", stdin);
	freopen("out.out", "w", stdout);
#endif
	cin >> n;
	ll res = 0;
	for ( int i = 1; i <= n; i ++ ) 
		cin >> a[i],
		nums.push_back(a[i]);
	sort ( nums.begin(), nums.end() );
	nums.erase(unique(nums.begin(), nums.end()), nums.end());
	for ( int i = 1; i <= n; i ++ ) a[i] = lower_bound(nums.begin(), nums.end(), a[i]) - nums.begin() + 1;
	for ( int i = 1; i <= n; i ++ ) {
		res = (res + query(a[i]) * ksm(2, i) % mod) % mod;
		update (a[i], ksm(ksm(2, i + 1), mod - 2));	
	}
	cout << res << endl;
	return 0;
}

---

CCPC2021威海M_810975

🔗

💡

一个看起来就很典的容斥问题。
卡在 $k$ 上太难处理，于是令 $f(k)$ 表示最大连胜长度不低于 $k$ ，答案即为 $f(k+1)-f(k)$
对于 $f(k)$ 先安排一个长度为 $k$ 的连胜段，别的任意分配，假设这个段分配到 $a$ 位置，$b$ 位置又放了 $k$ 个胜场，而反过来又会重新计数一次，这就是容斥了。所以先计算排一个长度为 $k$ 的连续段剩下胜场随便排的数量，再减去排两个长度为 $k$ 的连续段剩下胜场随便排的数量，再加上排三个长度为 $k$ 的连续段剩下场数随便排的数量....
对于选 $i$ 个连胜段，先在剩下的 $n-ik$ 个场选 $n-m$ 个败场，在败场的 $n-m+1$ 个空中插 $i$ 个板子，有效防止了出现 $\checkmark\underline{\checkmark\checkmark...\checkmark}$ 和 $\underline{\checkmark\checkmark...\checkmark}\checkmark$ 的冲突。故计数为
$f(k)=\sum\limits_{i=1}^{ik<=m}(-1)^{i+1}\binom{n-m+1}{i}\binom{n-ik}{n-m}$
最后求一下 $f(k+1)-f(k)$
注意特判一下 $k=0$ ，不然会 $RE$

而对于 $g(k)$ 表示最大连胜长度不多于 $k$
有一个生成函数求 $g(k)$ 的思考方式
有 $n-m+1$ 个空，每个空最多放 $k$ 个，其生成函数为 $1+x+x^2+...+x^k$
对于所有的空合并起来就是 $(1+x+x^2+...+x^k)^{n-m+1}$ ，而最后要求有 $m$ 个胜场，返回这个多项式的幂的 $m$ 次项系数即可
这里就需要支持长多项式的多项式快速幂了（不会写）

✅

const int mod = 998244353;
const int N = 1e5 + 10;
int f[N], ivf[N];
inline int ksm (int a, int b) {
    int res = 1;
    while (b) {
        if (b & 1) res = 1ll * res * a % mod;
        a = 1ll * a * a % mod;
        b >>= 1;
    }
    return res;
}
inline int inv (int x) {return ksm(x, mod - 2);}
inline int C(int n, int m) {
    return 1ll * f[n] * ivf[m] % mod * ivf[n - m] % mod;
}

int n, m, k;
inline int Calc (int x) {
    int ret = 0;
    for (int i = 1; i * x <= m; i ++) {
        if (i & 1) ret += 1ll * C(n - m + 1, i) * C(n - i * x, n - m) % mod;
        else ret -= 1ll * C(n - m + 1, i) * C(n - i * x, n - m) % mod;
        ret = (ret % mod + mod) % mod;
    }
    return ret;
}


inline void Solve () {
    cin >> n >> m >> k;
    if (k == 0) {
        cout << (m == 0) << endl;
    } else {
        cout << ((Calc(k) - Calc(k + 1)) % mod + mod) % mod << endl;
    }
}

---

CodeForces451E_DevuAndFlowers

🔗

💡

这个数据量...
感觉母函数过不了，看了眼 想一下容斥

和多重背包超限一样
我们考虑这里面的总方案和不合法方案
如果箱子无限朵花，那么就是 种取法

即问：
那就是使用 个隔板将 个物品分割成 份
那就是有了 个位置可以用来放这 个隔板
方案数就是

不合法方案就是“你第 个箱子只有 朵花，但是你取了 朵花

那么我们如果直接强制在号箱子取 朵花，那么别的所有取法都不合法
这就是容斥的问题了，因为枚举会出现重复
所以就（奇数个箱子）-（偶数个箱子）

由于一开始给出的 可能很大，所以这里需要用 定理

✅

const int N = 30;
const int mod = 1e9 + 7;

namespace PermutationAndCombination {
        inline ll ksm ( ll a, ll b ) {
                ll res = 1;
                while ( b ) {
                        if ( b & 1 ) res = res * a % mod;
                        a = a * a % mod;
                        b >>= 1;
                }
                return res;
        }
        inline ll inv ( ll x ) { return ksm(x, mod - 2); }

        ll iv[N];
        inline void Get () {
                for ( int i = 1; i < N; i ++ ) iv[i] = inv(i);
        }
        inline ll C ( ll n, ll m ) {
                if ( n < m )   return 0;
                if ( n < mod ) {
                        ll res = 1;
                        for ( ll i = 1; i <= m; i ++ ) {
                                ll a = (n + i - m) % mod;
                                ll b = i % mod;
                                res = res * a % mod * iv[b] % mod;
                        }
                        return res;
                }
                return C ( n / mod, m / mod ) * C ( n % mod, m % mod ) % mod;
        }
} using namespace PermutationAndCombination;

ll a[N], n, s, res;
int main () {
        ios::sync_with_stdio(false);
        Get(); cin >> n >> s;
        for ( int i = 0; i < n; i ++ ) cin >> a[i];
        for ( int i = 0; i < (1 << n); i ++ ) {
                ll np = 1, cur = s;
                for ( int j = 0; j < n; j ++ ) {
                        if ( i & (1 << j) ) {
                                np = -np;
                                cur -= a[j] + 1; 
                        }
                }
                if ( cur < 0 ) continue;
                ll upd = C(cur + n - 1, n - 1);
                res = (res + np * upd) % mod;
        }
        cout << (res + mod) % mod << endl;
}

---

CodeForces979C_KuroAndWalkingRoute

🔗

💡

直接处理可以到达的点对很麻烦，要考虑很多种情况
那么可以容斥地减一下不能到达的点
即通过y再到达x即之后的点

既然是一棵树
那么就直接用"x的子树大小"乘"y的子树中不包含x的子树的大小总和"就是我们要减的值
即res = n * (n - 1) - son[x] * elsSon

可以再写一个判断判断子树中有没有x的函数
处理好son[]后，对y的子节点一个个判断并乘一下就行了

✅

const ll N = 3e5 + 10, M = N * 2;
ll n, X, Y;
ll res;
struct Edge { ll nxt, to; } edge [M]; ll head[M], cnt;

inline void add_Edge ( ll from, ll to ) {
        edge[ ++ cnt ] = { head[from], to };
        head[from] = cnt;
}
ll son[N], sonels;
inline void get_Sz ( ll x, ll fath ) {
        for ( ll i = head[x]; ~i; i = edge[i].nxt ) {
                ll to = edge[i].to;
                if ( to == fath ) continue;
                get_Sz ( to, x );
                son[x] += son[to];
        }
}
inline bool check ( ll x, ll fath ) {
        ll res = 1;
        if ( x == X ) res = 0;
        for ( ll i = head[x]; ~i; i = edge[i].nxt ) {
                ll to = edge[i].to;
                if ( to == fath ) continue;
                res *= check(to, x);
        }
        return res;
}

int main () {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif 
        memset ( head, -1, sizeof head );
        for ( ll i = 0; i < N; i ++ ) son[i] = 1;
        scanf("%lld%lld%lld", &n, &X, &Y);
        res = n * (n - 1);
        for ( ll i = 1; i < n; i ++ ) {
                ll a, b; cin >> a >> b;
                add_Edge ( a, b );
                add_Edge ( b, a );
        }
        get_Sz ( Y, -1 );
        for ( ll i = head[Y]; ~i; i = edge[i].nxt ) {
                sonels += check(edge[i].to, Y) * son[edge[i].to];
        }
        sonels ++;
        res -= son[X] * sonels;
        printf("%lld\n", res);
}

---

CodeForces1569C_JuryMeeting

🔗

💡

观察题目转换一下题目问题
即最大值的后面至少有一个可以让最大值最后一步和倒数第二步不在一起的数
那么如果最大值有两个，怎么搞都可以
如果最大值和次大值的差值大于1则怎么搞都不行
然后就是最大值和次大值差值为1的情况

获取一下所有的排列方式即
然后最大值在最后是不可以的，所以要减去
然后计算所有次大值都在最大值前面的情况

我们设置是最大值，是次大值，是出现的个数
最大值前面至少要留下，最多就是个
那么我们以遍历
将个数不记顺序地放入个空中
即
然后对这个数考虑顺序，对其余的个数考虑顺序
即都是阶乘
那么就有公式：

✅

#include <iostream>
#include <algorithm>
#include <map>
#include <cmath>
#include <vector>
#include <cstring>
#include <list>
using namespace std;
#define ll long long
const int N = 200005;
const ll mod = 998244353;

ll a[N];
ll f[N];
ll n;
map<ll, ll> num;
inline void get_F () {
        f[0] = 1;
        for ( int i = 1; i < N; i ++ ) {
                f[i] = f[i - 1] * i % mod;
        }
}
inline ll ksm ( ll a, ll b ) {
        ll res = 1;
        while ( b ) {
                if ( b & 1 ) res = res * a % mod;
                a = a * a % mod;
                b >>= 1;
        }
        return res;
}
inline ll C ( ll a, ll b ) { 
        return f[a] * ksm(f[b], mod - 2) % mod * ksm(f[a - b], mod - 2) % mod;
}
inline void solve () {
        num.clear();
        cin >> n;
        for ( int i = 0; i < n; i ++ ) 
                cin >> a[i],
                num[a[i]] ++;
        sort ( a, a + n, [] ( ll a, ll b ) { return a > b; } );
        
        if ( a[0] - a[1] > 1 ) { // 最后一个要自己一个连续减好多次
                cout << 0 << endl;
        } else if ( num[a[0]] > 1 ) { // 自己和自己顶，可以随便搞
                cout << f[n] << endl;
        } else {
                ll res = f[n]; // 初始化为所有的情况
                ll del = f[n - 1]; // 要删去的不符合的情况
                for ( int i = num[a[1]]; i <= n - 2; i ++ ) {
                        del = ( del + C(i, num[a[1]]) * f[num[a[1]]] % mod * f[n - 1 - num[a[1]]] % mod ) % mod;
                }
                cout << ( ( res - del ) % mod + mod) % mod << endl;
        }
}

int main () {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif
        get_F();
        ll cass; cin >> cass; while ( cass -- ) {
                solve();
        }
}

---

HDU2021多校(10)4_PtyHatesPrimeNumbers

🔗

💡

问题可以转化一下，由于自己也是自己的因数，所以就是问[1, n]内有多少个数不是前k个素数的倍数
这类计数问题很快联想到容斥

16个数，但是有1e5组数据
那么2^16 * 1e5就很难办了
但是2^8还是很好过的，那么可以对质数的组合乘积情况打表vec
对于前k个质数，k<=8，我们打1~8的容斥表
对于k>8，我们打9~16的容斥表
(由于容斥表中含1，即都不选，那么我们不需要使用n-vec[i]来计算不是前k素数倍数的个数）

k<=8
我们直接就容斥地res +-= n / vec[i]就行了
k>8
我们还要做一些处理
前八个素数的乘积是9699690
有个显然的性质就是：如果一个数x不是前八个素数的倍数，x%9699690也不会是前八个素数的倍数（同余
而9699690也不是非常大，所以我们可以继续预处理一下9699690以内不是前八个数的倍数的个数（前缀地处理
然后我们可以利用我们处理出来的信息，容斥x=“在n以内不是vec[i]的倍数的数中，也不是前8个数的倍数的情况”

这里我们可以采用枚举倍数的方式
n / vec[i]表示的是n以内从1开始的vec[i]的倍数
对这些倍数，[1, ..]相当于拆解完vec[i]这个质因数之后残余的数，且从1开始连续
这些数中我们可以求一下N的周期个数，每个周期有sum[N]个满足条件的数
然后剩余n / vec[i] % N，这里面有sum[n / vec[i] % N]个满足条件的数

容斥这些数就行了

✅

const int N = 9699690;
int prime[] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53}; // 前16个质数
vector<ll> a[20], b[20]; // 01枚举后，奇数个数的乘积情况和偶数哥的乘积情况
int sum[N + 10]; // sum[i] = [1, i]中不能被前八个质数整除的个数

inline void DFS ( int id, ll res, int cnt, int k ) { // 构造容斥数组（塞入1，不用取反数了
        if ( id > k ) {
                if ( cnt & 1 ) a[k].emplace_back(res);
                else           b[k].emplace_back(res);
                return; 
        }
        DFS ( id + 1, res * prime[id], cnt + 1, k );
        DFS ( id + 1, res,             cnt,     k );
}
inline void Pre () { // 预处理sum与容斥数组
        for ( int k = 1; k <= 16; k ++ ) {
                if ( k <= 8 ) DFS ( 1, 1, 0, k );
                else          DFS ( 9, 1, 0, k );
        }
        for ( int i = 1; i <= 8; i ++ ) for ( int j = prime[i]; j <= N; j += prime[i] ) sum[j] = 1; // 埃氏筛
        for ( int i = 1; i <= N; i ++ ) sum[i] = sum[i - 1] + (sum[i] == 0);
}
int main () {
        ios::sync_with_stdio(false); Pre();
        int cass; cin >> cass; while ( cass -- ) {
                ll n, k, res = 0;
                cin >> n >> k;
                if ( k <= 8 ) {
                        for ( auto i : a[k] ) res -= n / i; // 普通的容斥原理
                        for ( auto i : b[k] ) res += n / i;
                } else {
                        for ( auto i : a[k] ) res -= n / i / N * sum[N] + sum[n / i % N]; // 相当于枚举倍数，倍数有 n / i 个，在[1, n / i]中找N的周期与模N之后剩余的个数
                        for ( auto i : b[k] ) res += n / i / N * sum[N] + sum[n / i % N];
                }
                cout << res << endl;
        }
}

---

HDUOJ5776_sum

🔗

http://acm.hdu.edu.cn/showproblem.php?pid=5776

💡

✅

#pragma region
#pragma GCC optimize(3,"Ofast","inline")
#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <stack>
#include <queue>
#include <cmath>
#include <map>
#include <set>
#define G 10.0
#define LNF 1e18
#define eps 1e-6
#define PI acos(-1.0)
#define ll long long
#define INF 0x7FFFFFFF
#define Regal exit(0)
#define Chivas int main()
#define pb(x) push_back(x)
#define SP system("pause")
#define Max(a,b) ((a)>(b)?(a):(b))
#define Min(a,b) ((a)<(b)?(a):(b))
#define IOS ios::sync_with_stdio(false)
#define mm(a, b) memset(a, b, sizeof(a))
#define each(cass) for (cin>>cass; cass; cass--)
#define test(a) cout << "---------" << a << "---------" << '\n'
 
using namespace std;
#pragma endregion

//全局变量
#pragma region
string fro[100005];
string enn[100005];
int n, m;
vector<int> a;
map<int, int> vis;
int sum;
int cass;
#pragma endregion

inline void solve(){
    a.clear();
    vis.clear();
    sum = 0;
    cin >> n >> m;
    for(int i = 0, x; i < n; i ++){
        cin >> x;
        a.push_back(x);
    }
    for(int i = 0; i < n; i ++){
        sum = (sum + a[i]) % m;
        if(sum == 0){
            cout << "YES" << endl;
            return;
        }
        if(vis[sum]){
            cout << "YES" << endl;
            return;
        }
        vis[sum] = 1;
    }
    cout << "NO" << endl;
}

Chivas{
    each(cass){
        solve();
    }
    Regal;
}

---

HRBUST2414_格子染色计数

🔗

http://acm.hrbust.edu.cn/index.php?m=ProblemSet&a=showProblem&problem_id=2414

💡

设第a[i]种颜色不能用
那么我们在选k个数中，要求得的是

转化成容斥原理图得到的也就是

转化成公式就是

那么就开卢卡斯定理求解即可

✅

#include <iostream>
#define ll long long
using namespace std;

const int mod = 1e9 + 7;

ll inv[1000010]; // 预处理很重要

inline ll ksm ( ll a, ll b, ll p ) {
        ll res = 1;
        while ( b ) {
                if ( b & 1 ) res = res * a % p;
                a = a * a % p;
                b >>= 1;
        }
        return res;
}

inline void Init () {
        for ( ll i = 1; i < 1000010; i ++ ) inv[i] = ksm(i, mod - 2, mod);
}

inline ll C ( ll n, ll m, ll p ) {
        if ( m > n ) return 0;
        ll res = 1;
        for ( ll i = 1; i <= m; i ++ ) {
                ll a = (n + i - m) % p;
                ll b = i % p;
                res = res * (a * ksm(b, mod - 2, mod) % p) % p;
        }
        return res;
}

inline ll lucas ( ll n, ll m, ll p ) {
        if ( m == 0 ) return 1;
        return C( n % p, m % p, p ) * lucas ( n / p, m / p, p ) % p;
}

int main () {
        Init();
        int cass;
        for ( scanf("%d", &cass); cass; cass -- ) {
                ll n, m, k; scanf("%lld%lld%lld", &n, &m, &k);
                ll tmp = 1;
                ll res =  0;
                for ( int i = 1; i <= k; i ++ ) {
                        int flag = (k - i) % 2 == 0 ? 1 : -1; // 这一位该加该减
                        tmp = ((tmp * (k - i + 1)) % mod * inv[i]) % mod; // 不用每遍都lucas，推着用着即可
                        res = (res + flag * (i * ksm(i - 1, n - 1, mod) % mod) * tmp % mod + mod) % mod;
                }
                printf("%lld\n", res * lucas(m, k, mod) % mod);
        }
        return 0;
}

---

鸽笼原理

CodeForces577B_ModuloSum

🔗

💡

首先根据鸽笼原理
若 $m<=n$
对于前 $m$ 个数有 $m$ 个前缀和

• 存在 $0$ ，显然可以
• 不存在 $0$，$m$ 个数用 $sz\{1,2,\dots,m-1\}=m-1$ 个余数，必然有两重复，重复的前缀和构成的区间和为 $0$ ，也可以

若 $m>n$
那么 $n<m\le 1000$ ，则暴力跑一遍 $01$ 背包即可

✅

int n, m;
bool dp[2][1000];

int main () {
	ios::sync_with_stdio(false);
	cin >> n >> m;
	if ( m <= n ) {
		cout << "YES" << endl;
		return 0;
	}
	for ( int i = 1; i <= n; i ++ ) {
		int x; cin >> x; x %= m;
		memset(dp[i & 1], false, sizeof dp[i & 1]);
		dp[i & 1][x] = true;
		for ( int j = 0; j < m; j ++ ) {
			dp[i & 1][j]           |= dp[i - 1 & 1][j];
			dp[i & 1][(j + x) % m] |= dp[i - 1 & 1][j];
		} 
		if ( dp[i & 1][0] ) { cout << "YES"; return 0; }
	}
	cout << "NO";
}

---

NamomoCamp2022春季每日一题_选数

🔗

💡

$n$ 个数，范围很明显了，这里最多有 $n$ 个不同的模数
考虑前缀和，一共有 $n$ 个前缀和，如果出现 $0$ 那么就直接输出这个前缀即可
有可能没有 $0$ ，那么 $n$ 个前缀和要用 $n-1$ 个数就必然存在两个前缀和相同
相同的两个前缀和减出来的区间和为 $0$ ，也能满足

所以每次算前缀和，如果为 $0$ 直接输出，否则查看是否之前存在过这个前缀和，如果存在过，就从上一个该前缀和下标 $+1$ 一直到当前位置

✅

const int N = 1e5 + 10;
int n, a[N];
int id[N], sum;

int main () {
	ios::sync_with_stdio(false);
    
	cin >> n;
	for ( int i = 1; i <= n; i ++ ) {
		cin >> a[i];
		sum = (sum + a[i]) % n;
		if ( sum == 0 ) {
			cout << i << endl;
			for ( int j = 1; j <= i; j ++ ) cout << j << " ";
			cout << endl;
			return 0;
		}
		if ( id[sum] ) {
			cout << i - id[sum] << endl;
			for ( int j = id[sum] + 1; j <= i; j ++ ) cout << j << " ";
			return 0;
		}
		id[sum] = i;
	}
}

---