Sierpinski三角形

这个东西小时候见过，甚至还画过....

定义

Sierpinski三角形 是一种分形，是处理相似集的例子。

构造

正三角

将一个正三角形通过连接三条边上的中点分为相等的四部分，去掉中心那一部分，然后将其余三部分递归地重复这个操作进行构造。
如图我们访问过的递归部分为黑色三角形。

正方形

将一个正方形通过连接四条边上的中点分为四部分，去掉右下角那一部分，其余三部分按相同方式递归构造。

结论

Sierpinski三角形 与 杨辉三角

首先让我们来打印一个模 $2$ 意义下的杨辉三角形
黑色为模后等于 $0$ 的，白色为模后等于 $1$ 的

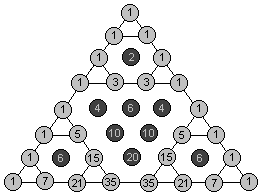
那么其实可以很明显看到杨辉三角形模 $2$ 依旧满足 Sierpinski三角形 的样子

证明

根据杨辉三角的组合数公式：$C_i^j=C_{i-1}^j+C_{i-1}^{j-1}$ 可以得到，每一个数只和上面相邻的两个有关系
那么我们只需要考虑哪一行全为奇数，通过这一行来作为分割线
分析组合数朴素公式 $C_i^j=\frac{i!}{j!(i-j)!}$ ，令 $l(i)$ 表示 $i$ 中 $2$ 的因数，也是作为 $2$ 进制下末尾 $0$ 的个数
已知 $l(n!)=\sum\limits_{i=0}^nl(i)$
则
$\begin{aligned}0=l(C_n^m)&=\sum\limits_{i=0}^nl(i)-\sum\limits_{i=0}^ml(i)-\sum\limits_{i=0}^{n-m}l(i)\\&=\sum\limits_{i=n-m+1}^nl(i)-\sum\limits_{i=0}^ml(i)\end{aligned}$
$\therefore \sum\limits_{i=0}^ml(i)=\sum\limits_{i=n-m+1}^nl(i)$
可以看出左侧表示的是 $[0,n]$ 中的前 $m$ 个数，右侧表示的是后 $m$ 个数，这说明我们要找一个具有对称性的 $n$
观察一下： $0_x\;1\;10\;11$ 发现 $n=2^x-1(x\in\N)$ 便可满足
说明 $2^x-1$ 行是作为分界线
由于左侧和右侧只能通过上面的 $1$ 传下来，则意味着我们将在下一部分的左侧和右侧各复制一遍上面的所有
所以形状满足，得证

Sierpinski三角形 与 进制

其实我们利用 $i\&j=j$ 画一个三角形，其形状依然满足 Sierpinski三角形 的样子

证明

已知在按位下，$ij$ 最高位会有四种可能性：
$i=1,j=0\\ i=1,j=1\\ i=0,j=0\\ i=0,j=1$
我们想去掉一位来满足这种图形，利用与运算，我们可以去掉第四种情况
即保证 $i$ 每一位 $\ge j$ 每一位
这样我们就可以递归地通过分成四份去掉一份的方式去枚举出来所有的情况
这与 Sierpinski三角形 的定义相同，得证

杨辉三角 与 进制

第 $i$ 行产生贡献的列 $j$ ，其二进制每一位下 $1$ 的集合是 $i$ 二进制每一位下 $1$ 的集合的子集，即 $i\&j=j$

证明

既然杨辉三角画出来的图形和按位与画出来的图形相同
那么可以得出结论 $C_i^j=[i\&j=j]$
并且这样看来，第 $i$ 行产生的贡献为 $\sum\limits_{j=0}^i[i\&j=j]$