虚树
# 前言
**有时我们会遇到很多点转移但同时又需要通过树遍历才能获取答案的问题。**比如说每次操作给你几个关键点,让你通过这些关键点维护的信息来回溯出整棵树的总信息,但是每组数据会有很多次操作,此时我们如果还是每次操作遍历一遍整棵树,时间复杂度过高
由于给定的关键点数量有限,且只有关键点会产生我们需要的信息,那么我们duck不必跑很多没有用的点
比如说给你一棵二叉树,询问的操作给的关键点全在最左边的一条树枝上,那么我们要是跑右边的树就会浪费很多时间
所以我们可以根据给定的关键点的位置和数量进行优化,即只考虑这些有必要去遍历来维护信息的点,对此有一个概念————虚树
# 虚树
# 概念
对一整棵树中我们需要去遍历的点建立出来一棵小树,在这棵小树上,我们每一次的转移操作都是有它一定的作用,而不是白白浪费时间,从而大大优化时间复杂度
需要遍历的点: 关键点, 关键点或者 之间的
# 思想要点
我们要获取到所有关键点两两点之间的 以及它们 的 ...,这个可以通过预处理实现,倍增、树连剖分..均可
我们如果每两个都要枚举一遍 ,就算每次求 是 也很花费时间
可以发现对于一条链,我们知道深度关系,同时一条链上一个点又是别的点的祖先(除了叶子节点
所以一条链可以很显然地通过深度来确定两两之间的关系
那么就可以使用一个栈,来维护整棵虚树的最右链来进行处理
# 建树流程
既然我们要维护右链,那么就需要一种绝对的从左到右的线性顺序 序
我们对所有关键点进行一次 序升序排序
然后按 序从小到大的顺序枚举关键点
由于关键点会按顺序入栈,所以栈从底到顶是一个从上到下的链
每次遍历到一个节点 会产生四种情况:
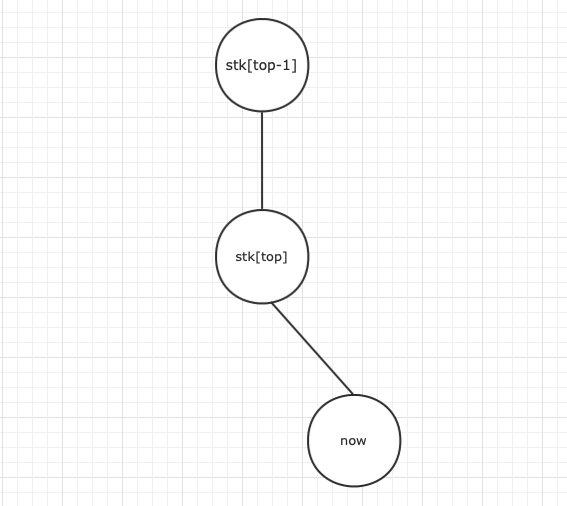
此时 是 的祖先的话,代表 在 的子树中,与栈中元素同在一条链上
那么就相当于扩了一个链,并不需要大量变动这条链
入栈- 在 与 中间
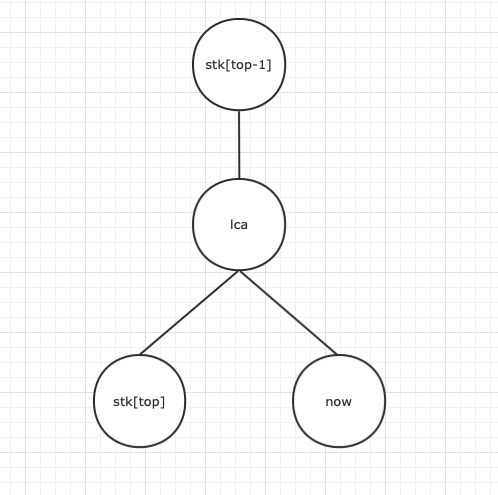
此时我们的 并不在最右链上了,就需要弹栈并将 和 依次加入
但是弹之前我们的这个栈的目的是为了建树,所以将 和 连边
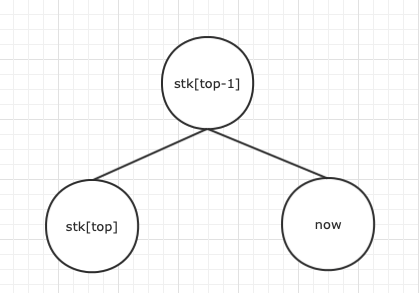
同样的, 并不能再作为右链结尾
所以弹出,同时让它和 建边
然后将 入栈
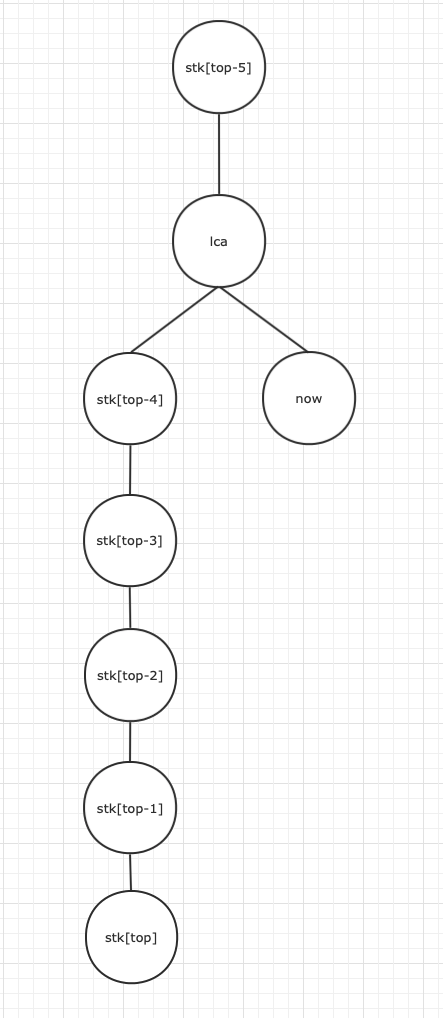
这种情况栈上面有多个元素都不可以作为右链
所以要一个个弹出,直到弹到上面三种情况为止
同时每弹出一次,都要让栈顶和栈倒数第二个建立虚树边
最后将整个右链加入虚树即可结束
这就是建树的规则流程了,下面给一个例子模拟
# 完整模拟
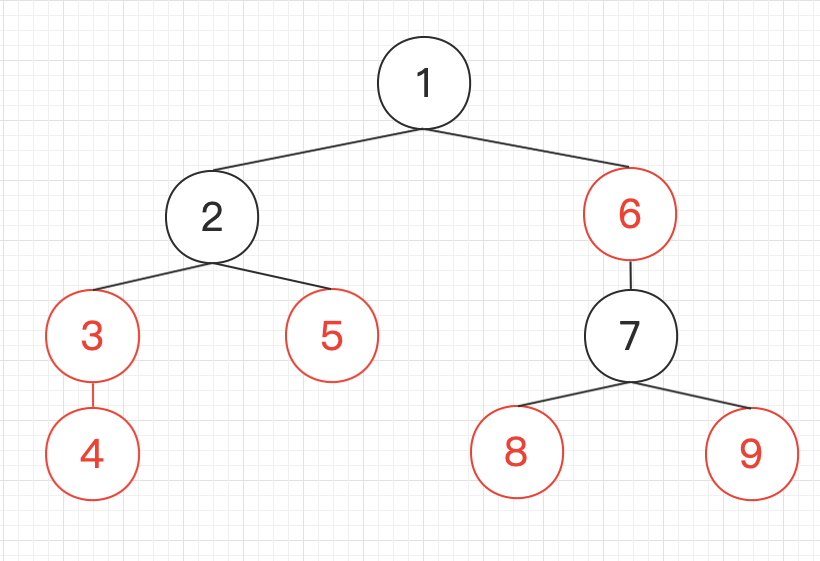 给定如上树,红色节点为所有的关键点,建立一个以关键点为核心的虚树(编号已按dfs序给出)
(下面橙色是栈,黑色是虚树)
给定如上树,红色节点为所有的关键点,建立一个以关键点为核心的虚树(编号已按dfs序给出)
(下面橙色是栈,黑色是虚树)
1.首先将节点 入栈,这样的话以1为哨兵可以防止空栈访问运行错误,更好处理
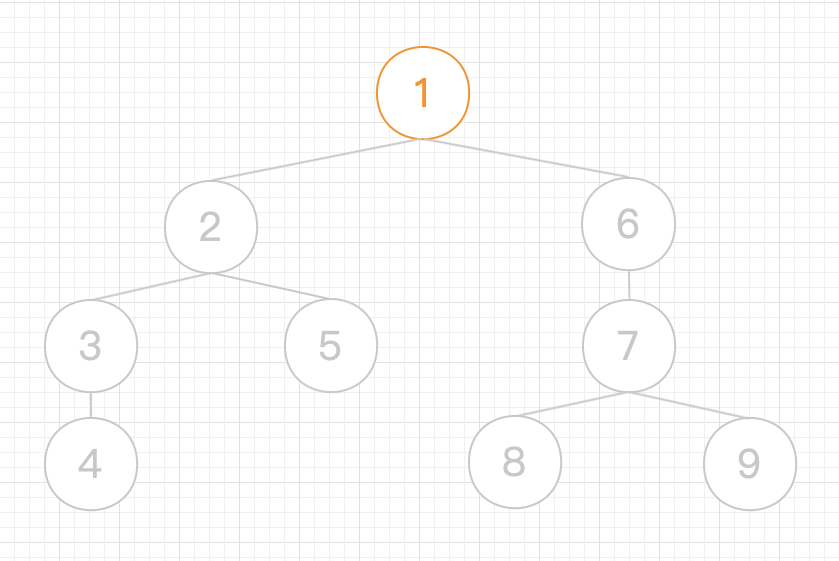
2.然后是 ,发现 是栈顶元素,所以 入栈
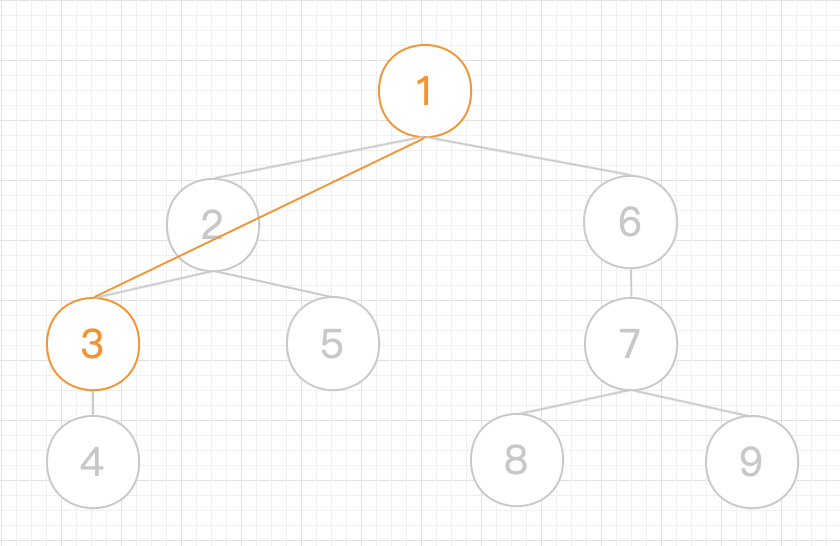
3.然后是 , 是栈顶元素,所以 入栈
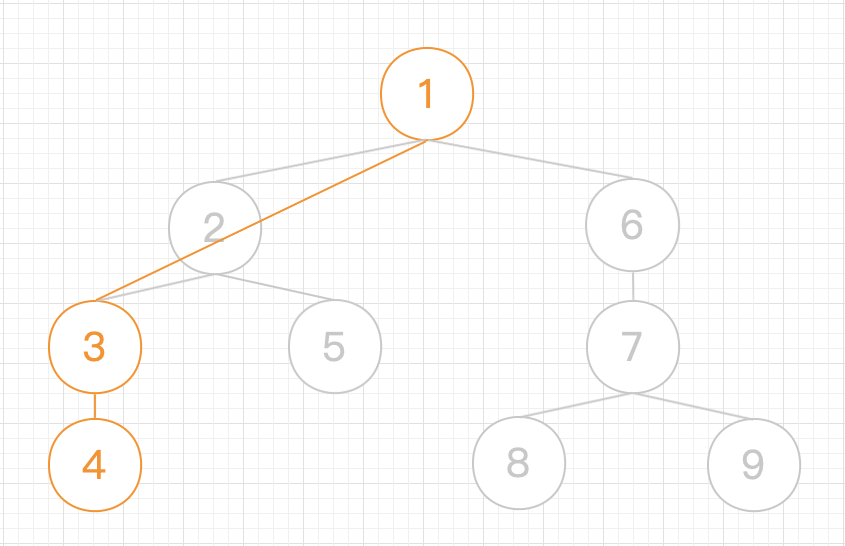
3.然后是 ,发现 ,所以 、 弹出,并且 与 、 与 连接虚树边,同时 , 入栈
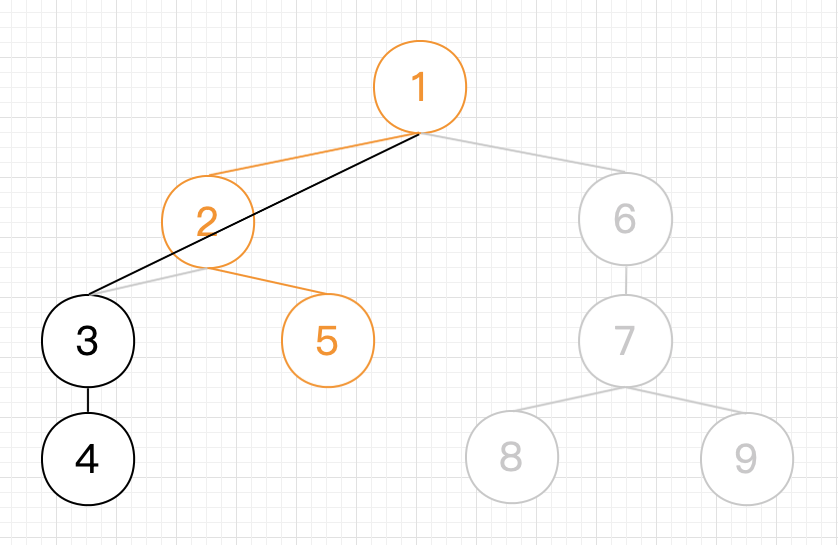
4.接着是 , ,所以 , 弹出,并且 与 、 与 连边,同时 入栈
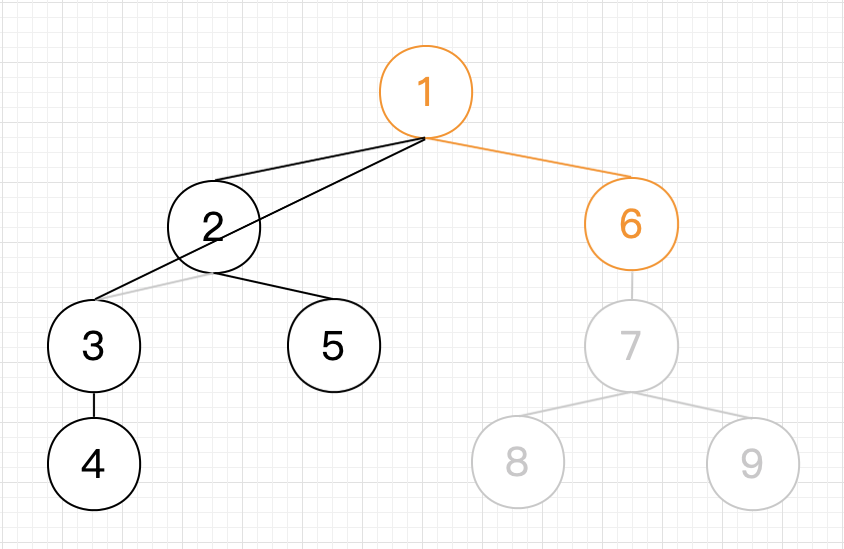
5.接着是 , ,所以 入栈
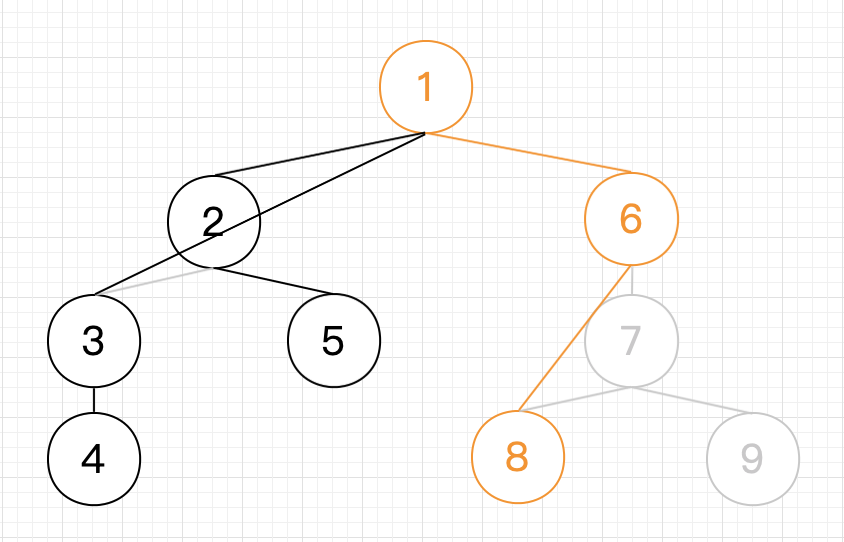
6.然后是 , , 弹出且与 连边, 和 依次入栈
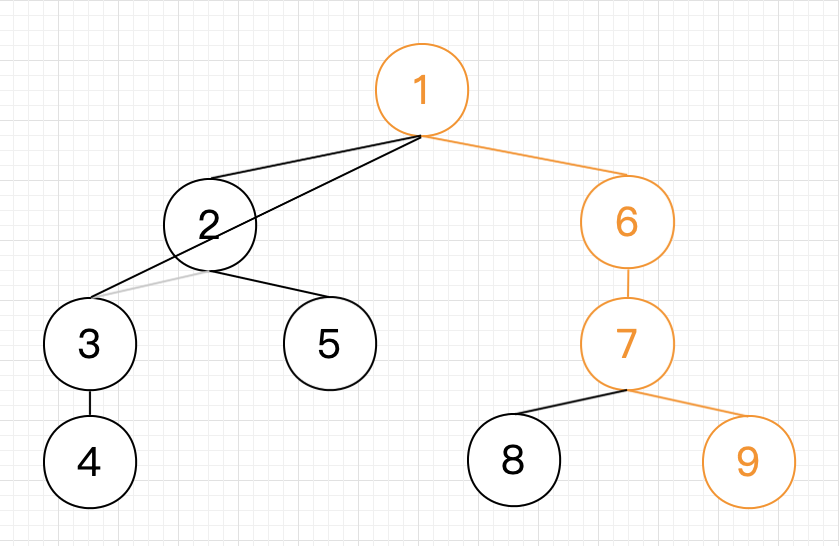
7.最后整条右链也就是栈中元素依次连边
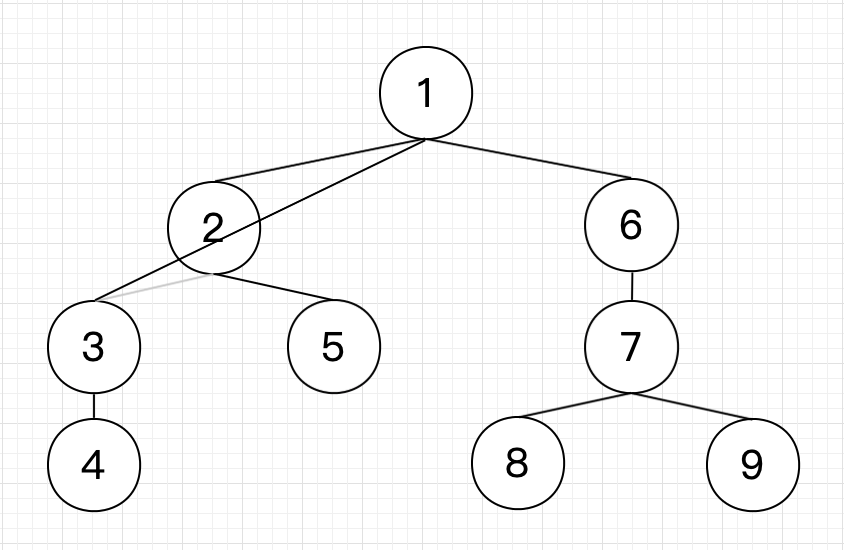
这样一棵虚树就建好了(是不是感觉没有少点,我想把所有情况都用上所以关键点有点多,但实际上在能用虚树解的题目中关键点不会非常多,不然它还不如告诉你所有点都关键了...(逃
# 算法框架
|--预处理树上倍增结构或者树链
|--遍历点
|----考虑四种情况
|----弹栈连边
|----该入栈道入栈
|--连接右链
# 程序演示
namespace VirtualTree {
int dfscnt = 1, dfn[N]; // dfs序
int dep[N]; // 深度
int fa[N][25]; // 父亲st表
int mxFa[N]; // 优化 -> i最多有mxFa[i]层祖先
ll minv[N]; // 1到i的最小边权是minv[i]
// 预处理fa[][],dfn[],minv[]
inline void dfs ( int pos ) {
int k;
for ( k = 0; fa[pos][k]; k ++ ) fa[pos][k + 1] = fa[fa[pos][k]][k];
mxFa[pos] = k;
dfn[pos] = dfscnt ++;
for ( int i = head[pos]; i; i = edge[i].nxt ) {
int to = edge[i].to;
if ( !dfn[to] )
dep[to] = dep[pos] + 1,
minv[to] = min ( minv[pos], edge[i].val ),
fa[to][0] = pos,
dfs ( to );
}
}
// st求LCA
inline int LCA ( int x, int y ) {
if ( dep[x] < dep[y] ) swap ( x, y );
for ( int i = mxFa[x]; i >= 0; i -- ) if ( dep[fa[x][i]] >= dep[y] ) x = fa[x][i];
if ( x == y ) return x;
for ( int i = mxFa[x]; i >= 0; i -- ) if ( fa[x][i] != fa[y][i] ) x = fa[x][i],
y = fa[y][i];
return fa[x][0];
}
int stk[N], top; // 单调栈
int lst[N]; // 查询的一套关键点
inline void build () {
sort ( lst + 1, lst + num + 1, [&]( int x, int y ) { return dfn[x] < dfn[y]; } ); // 按dfs序排序
stk[top = 1] = lst[1]; // 此时stk[0] = 0,dep[0] = 0,深度最小的哨兵
for ( int i = 2; i <= num; i ++ ) {
int now = lst[i];
int lca = LCA ( now, stk[top] );
while ( 1 ) {
if ( dep[lca] >= dep[stk[top - 1]] ) { // lca已在下面,应作为右链元素了
if ( lca != stk[top] ) { // top要删掉了
add_vEdge ( lca, stk[top] );
if ( lca != stk[top - 1] ) stk[top] = lca; // lca加入
else top --; // lca已有
}
break;
} else { // 一直弹直到lca在下面
add_vEdge ( stk[top - 1], stk[top] );
top --;
}
}
stk[ ++ top ] = now;
}
while ( --top ) add_vEdge ( stk[top], stk[top + 1] );
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
