网络流
# 割
将图分为两个点集,源点 位于点集 中,汇点 位于点集 中,割的大小为 到 的可行边数量(对于一个点集内的点可以不连通)
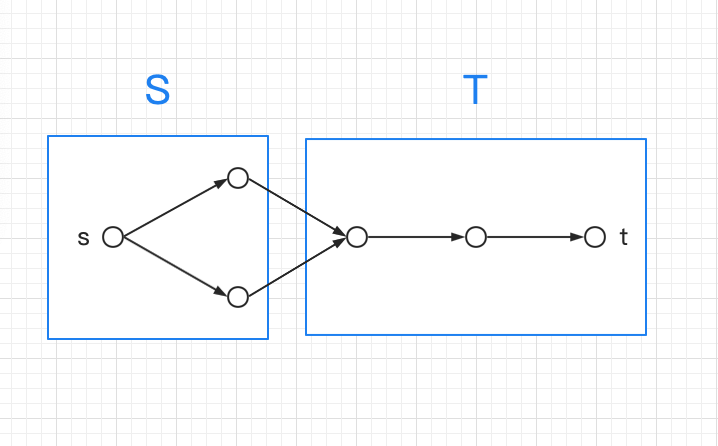
割的大小为
最多有多少条不相交路径
转移成判定问题:判定是否存在 条不相交路径
就是连通性证明
任意一对 割大小都不小于 ,因为 的路径必有至少一条边会从 到 ,若存在一对 割大小为 ,那么这条路必经,就不存在两条不想交路径
这就是 最小割问题(割掉最少的边,使图不连通)
# 残留网络
每一次找路都使用
在残留网络中将上一次找到的路径反着加入,没走过的边正着加入
本次 时要么走没有走过的边,要么纠正原先的一条边
初步:
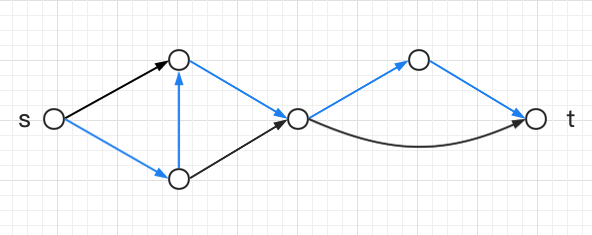
(蓝色的为找到的路径)
残留网络:
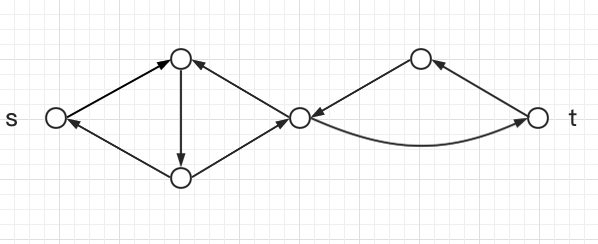
再走:
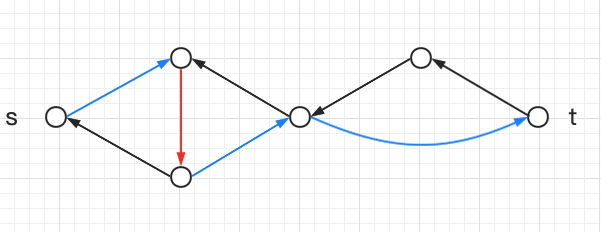
(其中红色的是它作为反边重复被走,是一条纠正边)
最终图:
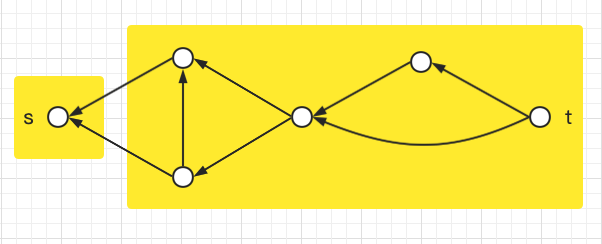
割的大小为 ,反过来后大小为
即第 步得到的残留网络为第 步走的图,用于前 步的纠正与寻找新路
在残留网络中找到一条路为原图新路,找不到新路则找过的路径数量为原图的割
证明
若找到 这 条路,走出 ,将 和 在不同路径上表示为不同状态
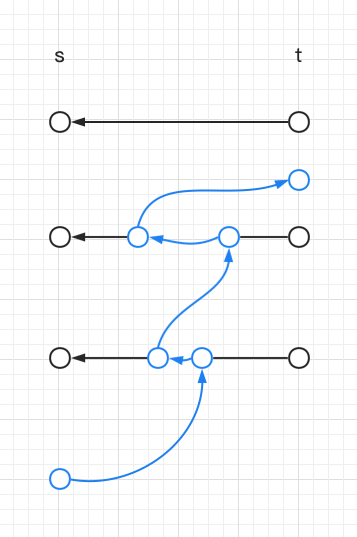
其中黑色的是残留网络,蓝色的是在残留网络上找到的新路,这里我们在原图中完全可以将纠正的边断开,黑色路径反回来,成为:
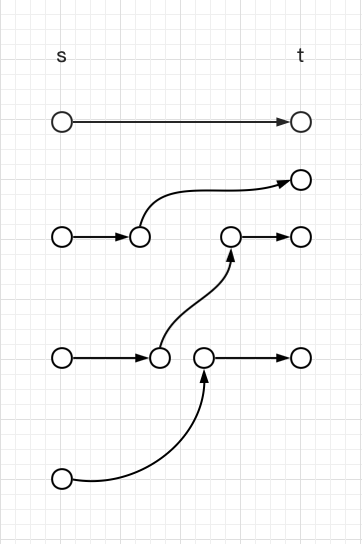
发现在本质上这就是四条不相交路径,若在此图的残留网络中找不到新路,说明原图正向边不能使该残留网络连通,那么最小割就是四
得证
所以从残留网络的利用中引出,最小割等于最大不相交路径数,也就是最大流。
# 最大流
这里说最为普遍的图:带权图
# 问题表示
一个比较明显地利用上面问题的做法,可以将一条边 的权 拆分,拆成 条权值为 的 边,不想交路径在图上的合并成为流。
且由于不允许存在拆分成大于 的路径数穿过 ,则 是路径 的 容量 。
同时易推得,如果 ,那么
若求最大流,可以表示成下面的形式:
令 最大
这就是网络流的原始线性规划表示
而新型的线性规划表示如下:
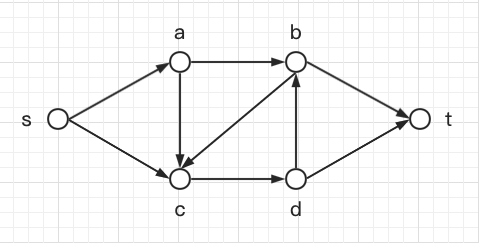
在这样一张图上,由于流量守恒
# dicnic算法解决
对于带权图,我们跑完一遍增广路之后得到的残留网络中跑的边要反向,那么我们可以直接让这条路上每一条的反边加上我们跑出来的流量,正边减去流量。
而增广路不能绕环,所以 算法先对残留网络进行分层,得到每一个点到 的最短路径 ,增广路的要求是这条路径上的 必须递增且连续的。
在分层图上找增广路的流程就是:从 出发,若边有流量且 比 高一层,那么继续向 找。
这样的复杂度有点说不过去了,毕竟这算是 暴力跑图了,这里有三个优化。
- 多路增广
- 当前弧优化
- 炸点
多路增广是说如果我们在跑完 的第一条边之后前面的流量还没有流满,那么就用剩下的流量空间去跑第二条边、第三条边...
当前弧优化是说如果我们现在跑的不是第一条边,说明第一条边已经尽自己所能去流了,在这次分层图上它之后就没什么用了,就直接让下一条边作为 的第一条边
炸点是说若当前点往下流的全都是 ,那么这个点在这次分层图上没有往后面跑的意义,将其 设为一个走不到的数就可以保证之后永远不走它了
这里是代码演示:
inline void bfs (int S, int T) {...} // 就是求一个边权为 1 的最短路,没有必要演示了
// 参数:
// 当前点为 u,到 u 之前剩余流量为 fl
// 变量:
// 从 u 出发的总流量为 f
// 目标节点为 v,<u,v> 反边为 edge[i ^ 1]
inline int dfs (int u, int fl) {
if (u == T) return fl;
int f = 0;
for (int i = head[u]; i && fl; i = edge[i].nxt) { // 多路增广
head[u] = i; // 当前弧优化
int v = edge[i].to;
if (edge[i].flow && deep[v] == deep[u] + 1) {
int x = dfs(v, min(fl, edge[i].flow));
edge[i].flow -= x;
edge[i ^ 1].flow += x;
fl -= x;
f += x;
}
}
if (!f) deep[u] = -2; // 炸点
return f;
}
inline int dicnic (int S, int T) {
int ret = 0;
while (bfs(S, T)) ret += dfs(S, 0x3f3f3f3f);
return ret;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 费用流
费用流说的都是 “最..费用最..流”
这里我们建边时要加一个费用信息,同时反边这个纠正边意味着我们不选择这些费用,就将反边的费用设为正边费用的相反数即可。
而这样最短路就不能使用普通的 来求了,而且存在负数的 费用,所以要跑一个 代替
然后在这样的最短路图上继续跑 即可
# 上下界网络流
# 无源汇可行流
为容量下界, 为容量上界, 为流量
要求
转化为
每条边的可行流就是在这个图上的边的流量加上其下界
但是碍于流量守恒,可能一个点的入边下界和小于出边下界和,减去的不一样多,在减过的图守恒但是补回来就不守恒了。
这里构建超级源点 ,超级汇点 ,如果 的入边下界和过大,补充一条 流量为入边下界和减去出边下界和,如果出边下界和过大,补充一条 流量为出边下界和减去入边下界和即可。
当 出发的边全部流满,说明满足了流量守恒,才有可行流。
# 有源汇的最大可行流
原源汇为 ,新源汇为 ,建图和上面一样,但要保证流量守恒的话,还要加上 容量为
令新图 的最大可行流为 , 的一个满流为 ,在找完 满流的残留网络上再找 的可行流为 (删掉 的边)
由 中 出边与 入边均已流满, 同样,故 一定不包含 出边与 入边,那么让 不守恒的因素 已经消失,则 与 一一对应,所以
故流程就是,按无源汇建图后,添加一条 的边,跑完 得到 的可行流下 的最大流,然后在残余网络中删去 的边(正反),再跑一遍 的最大流。
两次最大流相加就是答案。
