Prufer编码
# 序列
用于对无向无根树与一个数列的双射
# 树
# 步骤
找编号最小的叶节点
输出与这个叶节点相连的编号
删去这个叶节点
# 模拟
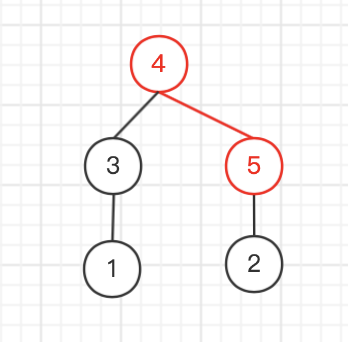
我们创建这样一棵树的 编码
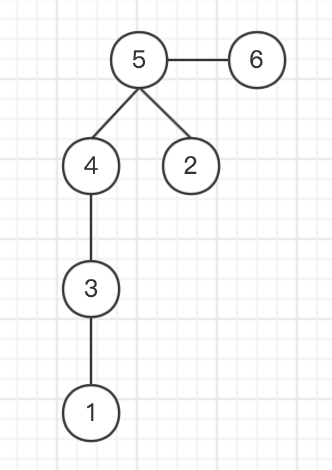
| 图示 | 找编号最小的叶节点 | 输出与该节点相连的编号 | 删去该叶节点 |
|---|---|---|---|
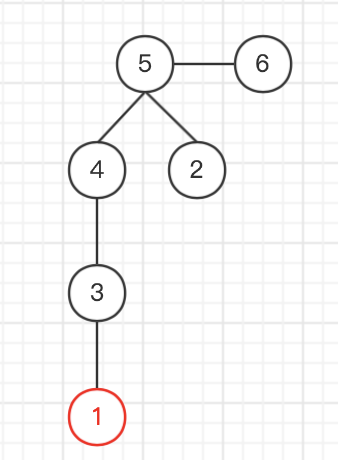 | |||
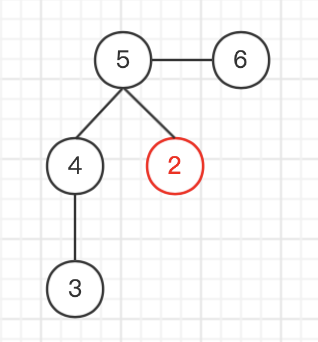 | |||
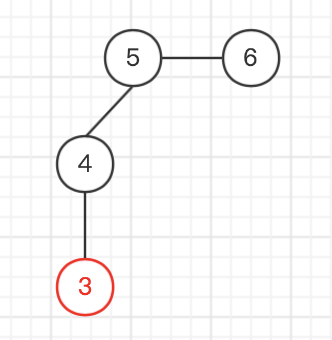 | |||
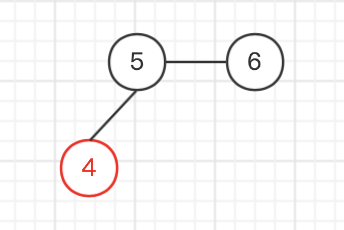 | |||
| 剩两个不输出 | |||
那么构造出来的 编码就是
# 线性构造
从小到大枚举 表示编号最小的度数为1的点
一旦走到一个度数为 的点,这个就是最小的叶节点,输出它的相连节点同时删除它
此时最多又暴露出一个点
,不用管,反正会继续向上枚举
, 本身就是最小的,新来了一个比 更小的,那么新叶节点就是最小的
# 程序
namespace Prufer {
int f[N]; // 每个节点的父亲节点
int d[N]; // 度数
int p[N]; // prufer编码
inline void Tree2Prufer () {
for ( int i = 1; i < n; i ++ )
cin >> f[i],
d[f[i]] ++;
for ( int i = 1, j = 1; i <= n - 2; j ++ ) {
while ( d[j] ) j ++; // 直到找到一个叶子结点
p[ i ++ ] = f[j]; // 这个叶子结点是最小的
while ( i <= n - 2 && /*在prufer范围内*/
-- d[p[i - 1]] == 0 && /*之前叶子结点删去后的度数*/
p[i - 1] < j ) /*满足这个点比上一个删去的叶子结点小*/
p[ i ++ ] = f[p[i - 1]]; // 新prufer是上一次删去的叶子节点的父亲
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 树
# 步骤 线性构造
根据已给的编码,我们可以得到每个节点有几个儿子
即除了最后一个点之外,每个点的儿子个数就是它在编码中的出现次数
我们可以模拟“ 树 ”的构造方式,只不过我们建树都是在确定一个(也就是上一种构造删边)时建边的
仍然从小到大枚举,当枚举到一个儿子个数为 的节点 时便是能确定这个是它在树中第一个删去的
同时也是第一个编码的子节点,那就说明</span style="color: red;">第一个编码就是 的父节点,于是建边
假装将这个小的叶子节点删去,那么就需要对 的子节点数量减
在“ 树 ”中我们删点后会出现的情况在这里也会出现
所以一样的流程进行判断即可
# 模拟
我们创建这么一个 编码的树
首先确定每个节点的子节点数量
| 节点 | 子节点数量 |
|---|---|
然后开始按上面说的模拟构造
| 节点-子节点数量 | 得到叶子结点 | 建树 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 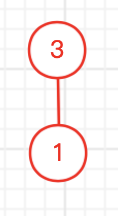 | |||||||||||||||
| 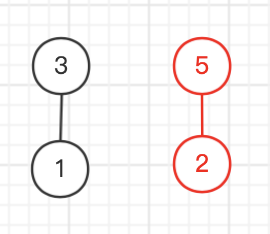 | |||||||||||||||
| 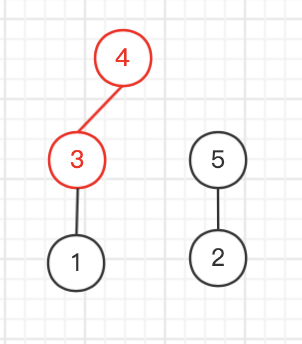 | |||||||||||||||
|  | |||||||||||||||
| 最后 连边 | 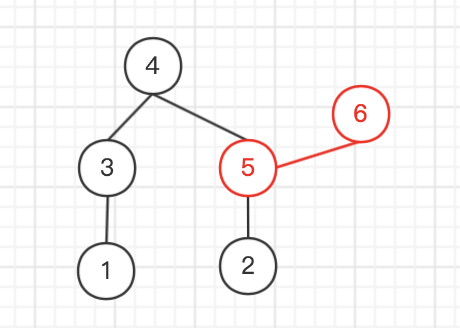 |
这样树就建出来了
# 程序
基本上就是上一种构造的反向构造,就不过多赘述了
namespace Prufer {
int f[N], d[N], p[N];
inline void Prufer2Tree () {
for ( int i = 1; i <= n - 2; i ++ )
cin >> p[i],
d[p[i]] ++;
p[n - 1] = n;
for ( int i = 1, j = 1; i < n; i ++, j ++ ) {
while ( d[j] ) j ++;
f[j] = p[i];
while ( i < n - 1 && -- d[p[i]] == 0 && p[i] < j ) f[p[i]] = p[i + 1], i ++;
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
# 性质
主要是使用下面几个性质实现树上计数
$1.$ $Prufer$ 编码与无根树形成双射
证明: 比较明显了, $Prufer$ 编码就是这么引出的 (也写不出反例了
一棵 个节点构成的无向完全图的生成树个数有 个
证明:
对于一个 编码,它每个位置能有 个数都可以选择,编码长度为
则总个数有 个放置方式
度数为 的节点在 编码中会出现 次
证明:
它的 个子节点要被删去,每次都会输出一次它,则一共有 次
对于一个已知度数序列 它可以形成的无根树数量为
证明:
长度为 的全排列有 个
由于每个 出现 次,则每个 会重复 次
在整个 全排列中去重 得到
别的性质还有待发掘...
