kurskal重构树

前置知识

• kruskal算法 (opens new window)
• LCA (opens new window)

定义

kruskal重构树是在kruskal算法构建最小生成树的基础上，构建出来的一棵新树。
在这棵树上，我们可以快速得到$[$ 最小的 $($ 两点之间路径上的最大边 $)$ $]$
这棵树的用法我们下面再说

流程

每个点首先看作是一个以自己为根节点的连通块

其余在 kruskal 算法的基础上多了一步

继承

• 对边按边权升序排序
• 遍历边，查看连接的两点是否位于同一连通块
  • 不同连通块 $\rightarrow$ 可以合并最小生成树可以建边，插入
  • 相同连通块，跳过
• 插入边达到 $n-1$ 条边，退出循环，否则继续第二步

补充

对于两个可以合并的节点 $(u,v)$ ，我们断开它们的边 $edge$
新建一个节点 $T$ ，作为它们各自连通块根结点的共同父亲
这个新节点的点权即是 $(u,v)$ 路径上的边权 $edge.val$

即：

变成了

例子

原图

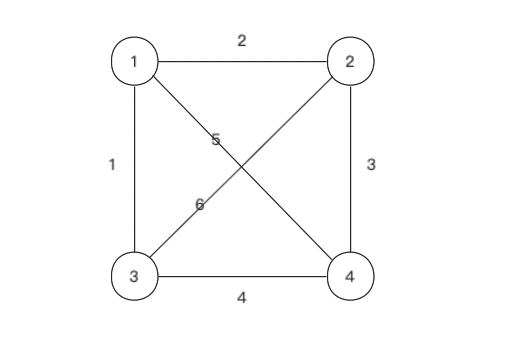
按边排序完为

• $1\stackrel{1}{\longleftrightarrow} 3$
• $1\stackrel{2}{\longleftrightarrow} 2$
• $2\stackrel{3}{\longleftrightarrow} 4$
• $3\stackrel{4}{\longleftrightarrow} 4$
• $1\stackrel{5}{\longleftrightarrow} 4$
• $2\stackrel{6}{\longleftrightarrow} 3$

开始操作

我们视新加的点是正方形，权值用 $[]$ 包裹

枚举边	是否合并	重构树
$1\stackrel{1}{\longleftrightarrow} 3$	$\checkmark$
$1\stackrel{2}{\longleftrightarrow} 2$	$\checkmark$
$2\stackrel{3}{\longleftrightarrow} 4$	$\checkmark$
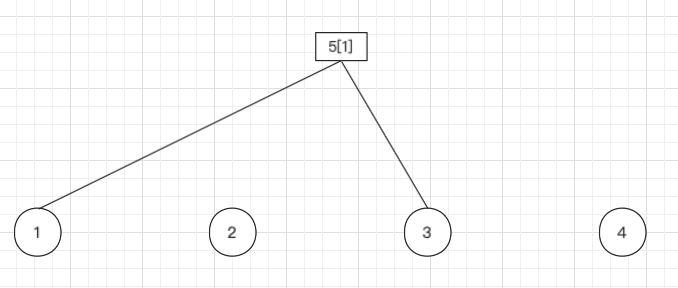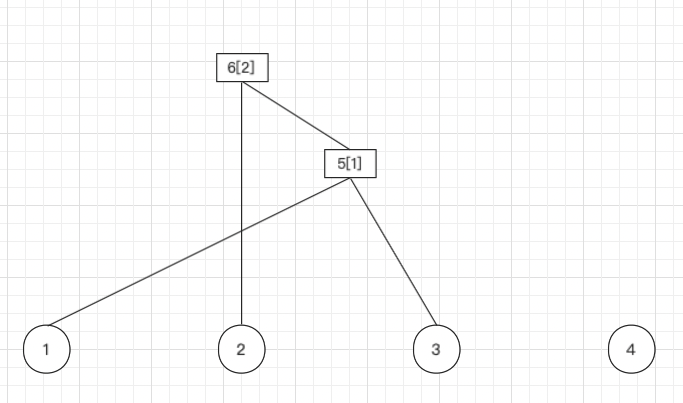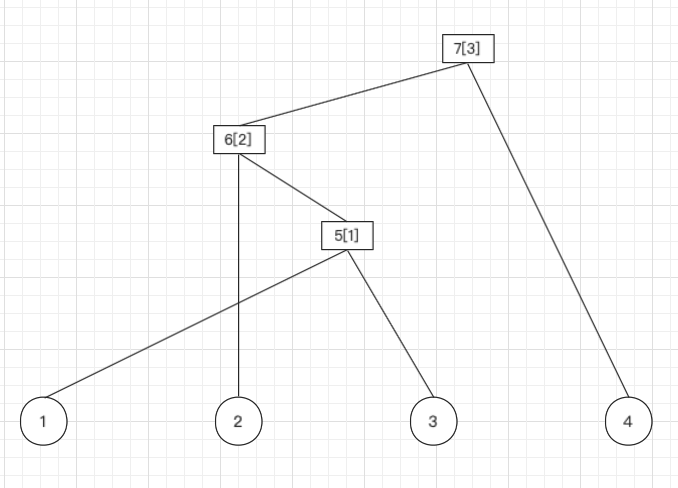break;

性质

• 树形为二叉树且是一棵完全二叉树性质1
• 除了叶子节点之外别的都有点权，且呈一个大根堆性质2
• 任意两点路径上边权最大值最小时为其 $LCA$ 的点权性质3

性质 $1$ 平平无奇，但是性质 $2,3$ 就有意思了
我们来简单说一下原因

按照 $kruskal$ 算法流程，我们枚举的边权会越来越大
而每个后面枚举到的边权，若是成立，必定是插在 某个叶子节点 或者 之前加过的点 的上面
叶子节点无权值这个由定义就可以知道
而之前加过的点它的点权一定是比当前点权小所以才先枚举
所以一条链是越来越小的，故成大根堆

考虑性质 $3$
每一个新加的点权都是最小生成树上的某条边权
而两个点间接相连是要经过他们在这里的 $LCA$ 的
又由于越往上权值越大，所以他们的 $LCA$ 就是最大的边权

作用

我们利用性质 $3$ 能很快得到 两个点路径上最大边权最小时应是多少

程序设计

以一道题为例吧 洛谷P1967_货车运输 (opens new window)

我们要走的路上限重要尽可能大，所以构建一棵最大生成树
在这个最大生成树上建立 $kruskal$ 重构树

首先我们建边、求LCA、并查集都要准备好

const int N = 1e5 + 10;
namespace Map {
        struct Edge {
                int nxt, to;
        }edge[N << 1];
        int  head[N << 1],  cnt = 0;
        inline void add_Edge ( int from, int to ) {
                edge[ ++ cnt ] = (Edge){ head[from], to };
                head[from] = cnt;
        }
} using namespace Map;

namespace TreeProblem {
        int dep[N];
        int fa[N][25];
        int mx_fa[N];
        inline void DFS ( int x, int fath ) {
                int k;
                for ( k = 0; fa[x][k]; k ++ ) fa[x][k + 1] = fa[fa[x][k]][k];
                mx_fa[x] = k;
                for ( int i = head[x]; i; i = edge[i].nxt ) {
                        int to = edge[i].to;
                        if ( to == fath ) continue;
                        dep[to] = dep[x] + 1;
                        fa[to][0] = x;
                        DFS(to, x);
                }
        }
        inline int LCA ( int x, int y ) {
                if ( dep[x] < dep[y] ) swap(x, y);
                for ( int i = mx_fa[x]; i >= 0; i -- ) if ( dep[fa[x][i]] >= dep[y] ) x = fa[x][i];
                if ( x == y ) return x;
                for ( int i = mx_fa[x]; i >= 0; i -- ) if ( fa[x][i] != fa[y][i] ) x = fa[x][i],
                                                                                   y = fa[y][i];
                return fa[x][0];
        }
} using namespace TreeProblem;

namespace UnionSet {
        int nod[N];
        inline int Find ( int x ) { return x == nod[x] ? x : nod[x] = Find(nod[x]); }
        // 后面这两个手写方便很多
} using namespace UnionSet;

然后建立一个点权值

int val[N];

打印完边后我们就排个序进行 $kruskal$ 算法即可
在可以合并的时候进行断边加点操作

sort ( nd, nd + m );
int num = 0; // 合并次数
for ( int i = 0; i < m; i ++ ) {
        int fx = Find(nd[i].u);
        int fy = Find(nd[i].v);
        if ( fx != fy ) {
                val[++ num + n] = nd[i].w; // 建立新点并给予点权
                // 两个根节点分别为新点的儿子
                add_Edge(num + n, fx);     
                add_Edge(num + n, fy);
                nod[fx] = nod[fy] = num + n;
        }
}

本题中两个点可能并不连通，所以我们 $DFS$ 要从每个不同的根节点去分别跑一次

bool vis[N]; // 记录这个根节点是否跑过了
for ( int i = 1; i <= n; i ++ ) {
        int fi = Find(i);
        if ( !vis[fi] ) 
                DFS(fi, fi),
                vis[fi] = 1;
        }

然后就剩一个查询了

cin >> q;
while ( q -- ) {
        int a, b; cin >> a >> b;
        int fa = Find(a), fb = Find(b);
        if ( fa != fb ) {
                cout << "-1" << endl;
        } else {
                cout << val[LCA(a, b)] << endl;
        }
}

设计完毕