FHQ-Treap

Chivas-Regal

# 前置知识：Treap

$Treap$ 者， $Tree+Heap$ 也。
$Tree$ 即二叉搜索树
$Heap$ 就是正常的堆

常见的 $Treap$ 通常使用二叉搜索树来维护值或者别的元素，使用堆来维护一个索引。
其索引是随机化的，这样也就使得随机性下满足树均匀二叉的期望非常大，也就是平衡。并且因为这个因素，在竞赛中随机化下的索引更难被卡掉，可以稳妥地分析时间复杂度。

且在二叉搜素树中要满足这样一个条件：左子树任意一点 $\le$ 当前点 $\le$ 右子树任意一点，也就是说其中序遍历是一个递增序列。

# FHQ-Treap

# 定义

开发于自 $11$ 年国家队队员范浩强的手中，可以被称为平衡树双子星。
它的核心操作是分裂合并。
分裂：按满足二叉搜索树的信息进行分裂，保证分裂出来的树都是连续的区间，并且两棵树分别满足二叉搜索树的性质。
合并：将两棵树进行合并，合并后依旧满足二叉搜索树的性质。
即树上的分裂合并，通过对树的分裂分出来我们要操作的树，结束操作后通过合并对其进行缝合。
由于二叉树下有 $log$ 层节点，则每次分裂合并都是 $logn$ 的时间复杂度

e.g.

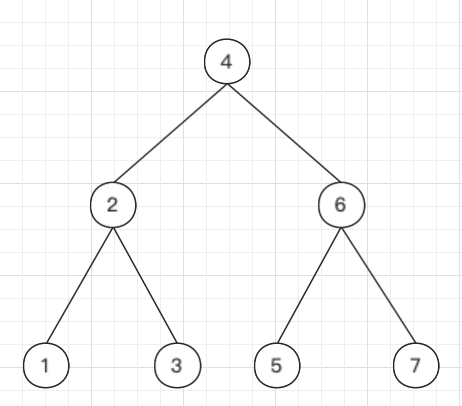
20220420100116
这样一棵树按 $2$ 分裂，即分裂出两棵树一棵值全部 $\le 2$ ，一棵全部 $>2$
也就是这样的颜色分区：
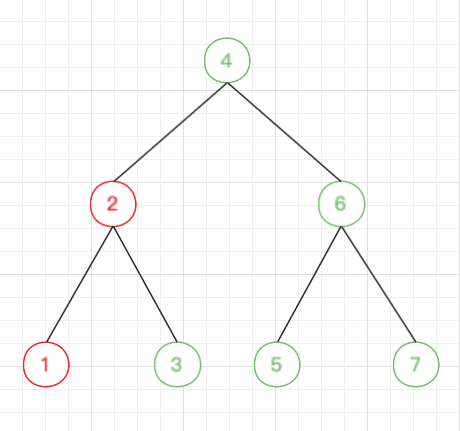
20220420100502
分裂后即为：
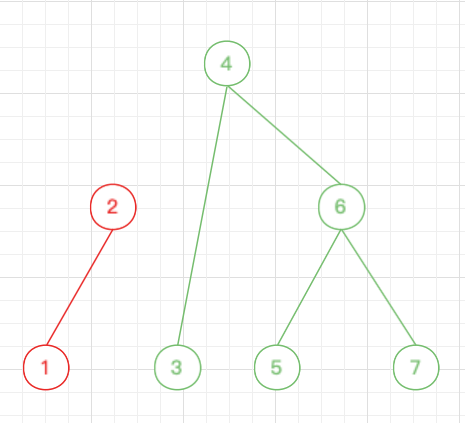
20220420100602

而其合并也就是将上述操作反过来进行即可

# 点值平衡树

# 节点信息

struct node {
        int l, r; // 左右子树
        int val, key; //值 和 索引

        DATA; // 要维护的信息，通常为 size ...

} fhq[N];

1
2
3
4
5
6
7

带上一个计数器 cnt 来对每一个新建立的节点进行编号
再用一个 root 表示树根编号

# 新节点

这个就如上面所说的
我们建立一个点，然后用计数器给一个下标过去
然后索引随机化一下即可（要开一下随机种子
最后要返回一下我们新建的下标

std::mt19937 rnd(233);
inline void newnode (int val) {
        fhq[++cnt] = {0, 0, val, (int)rnd()};
        /*
            * 信息初始化
            * 如 fhq[cnt].size = 1;
            * 如 fhq[cnt].min = val;
            * ...
        */
        return cnt;
}

1
2
3
4
5
6
7
8
9
10
11

# 信息更新

由于分裂合并之后，部分节点的子树会发生变化，所以我们每次递归完都要更新一下节点信息。
方式和线段树类似，都是一个向上更新，如果有类似于懒标记的东西的话还要进行 push_Down()

inline void Update (int now) { // 编号为 now 的树统计其子树的信息  
        // size:
        fhq[now].size = fhq[fhq[now].l].size + fhq[fhq[now].r].size + 1;
        // min:
        fhq[now].min = fhq[now].val;
        if (fhq[now].l) fhq[now].min = std::min(fhq[now].min, fhq[fhq[now].l].min);
        if (fhq[now].r) fhq[now].min = std::min(fhq[now].min, fhq[fhq[now].r].min);
}
inline void push_Down (int now) {
        // reverse:
        swap(fhq[now].l, fhq[now].r);
        fhq[fhq[now].l].reverse ^= 1;
        fhq[fhq[now].r].reverse ^= 1;
        fhq[now].reverse = false;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 分裂

这里就迎来了 $FHQ-Treap$ 最重要的操作之一分裂了。
在分裂中，需要一个向下移动的过程，走两棵树的边界，从而进行有效的分割。
我们可以传两个引用来表示我们的两棵树（左树右树）

如果向左走，那么我们只需要递归地去分裂左子节点，同时当前结点成为右树一部分，并且让当前节点左连下一个右树（详见上图中 $4\right2$ 的过程
如果向右走，和上面的其实也就是反过来了，递归地分裂右节点，同时当前节点成为左树一部分，并且让当前节点右连下一个左树

注意分裂会改变树的形状，所以要更新一下节点信息

inline void Split (int now, int val, int &x, int &y) {
        if (!now) {
                x = y = 0; // 出口，到了空节点，不存在左右树
        } else {
                if (val < fhq[now].val) { // 往左走
                        y = now;
                        Split(fhq[now].l, val, x, fhq[now].l);
                        Update(y);
                } else {
                        x = now;
                        Split(fhq[now].r, val, fhq[now].r, y);
                        Update(x);
                }
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 合并

合并操作就很直观，同时利用到我们的堆和二叉搜索树来缝补 $x$ 和 $y$ 。
首先也必然是一个递归向下的过程并且每次返回一个数字代表新合出来的节点编号。
由于 $x$ 必定是 $<y$ 的，那么只需要看两者的 $key$ 来确定哪个在上哪个在下

如果 $fhq[x].key$ 要更大，那么 $x$ 在上，同时由于 $y$ 每一个数值都比 $x$ 大，那么就意味着 $y$ 在 $x$ 的右下侧，应该让 $x$ 的右子树去合并 $y$
反之同理，如果 $fhq[y].key$ 更大，那么 $y$ 在上， $x$ 每一个数值小于 $y$ 意味着 $x$ 在 $y$ 的左下侧，应该让 $y$ 的左子树去合并 $x$

注意合并会改变树的形状，所以要更新一下节点信息

inline int Merge (int x, int y) {
        if (!x || !y) return x + y;
        if (fhq[x].key >= fhq[y].key) {
                fhq[x].r = Merge(fhq[x].r, y);
                Update(x);
                return x;
        } else {
                fhq[y].l = Merge(x, fhq[y].l);
                Update(y);
                return y;
        }
}

1
2
3
4
5
6
7
8
9
10
11
12

# 插入

我们插入 $val$ 时，按值分裂出两棵树 $x,y$
其中 $x$ 每一个节点值都 $\le val$ ， $y$ 每一个节点值都 $>val$
所以我们只需要建立一个新的值为 $val$ 的节点放在 $x$ 和 $y$ 中间，然后将三者压到一起

inline void Insert (int val) {
        int x, y;
        Split(root, val, x, y);
        root = Merge(Merge(x, newnode(val)), y);
}

1
2
3
4
5

# 删除

我们可以分出来一个完全是 $val$ 的树
即首先按 $val$ 将完整的树分裂出 $x,z$
然后按 $val-1$ 将 $x$ 分裂出 $x,y$
这样很显然 $y$ 就是完全是 $val$ 的树
我们删掉其中一个点，删掉根节点肯定最为方便
那么我们让 $y$ 成为自己左子树和右子树的并，就删掉了根节点
然后再把这三棵树合并在一起

inline void Delete (int val) {
        int x, y, z;
        Split(root, val, x, z);
        Split(x, val - 1, x, y);
        y = Merge(fhq[y].l, fhq[y].r);
        root = Merge(Merge(x, y), z);
}

1
2
3
4
5
6
7

# 值的排名

其实也就是找比 $val$ 小的数有几个
那么按 $val-1$ 分裂出来 $x,y$
然后获取 $x$ 的大小 $+1$ 即可

inline void Rank (int val) {
        int x, y;
        Split(root, val - 1, x, y);
        std::cout << fhq[x].size + 1 << "\n";
        root = Merge(x, y);
}

1
2
3
4
5
6

# 排名的值

有了排名，那么我们每次自然要根据左右子树的大小来确定往左走还是往右走
如果 $rnk<=fhq[fhq[now].l].size$ 证明左子树的数量够这个排名，自然要往左走
否则往右走，同时让排名减去左子树的大小 $+1$
直到当前排名等于左子树大小 $+1$

inline void Num (int rnk) {
        int now = root;
        while (now) {
                if (rnk == fhq[fhq[now].l].size + 1) break;
                if (rnk <= fhq[fhq[now].l].size) {
                        now = fhq[now].l;
                } else {
                        rnk -= fhq[fhq[now].l].size + 1;
                        now = fhq[now].r;
                }
        }
        std::cout << fhq[now].val << "\n";
}

1
2
3
4
5
6
7
8
9
10
11
12
13

# 前驱

问题具象出来其实也就是找比 $val$ 小的数中最大的数
那么按 $val-1$ 分裂，这样左子树必定是全部小于 $val$ 的
剩下的就是找其中最大的了，就一直往右子树走即可

inline void Pre (int val) {
        int x, y;
        Split(root, val - 1, x, y);
        int now = x;
        while (fhq[now].r) now = fhq[now].r;
        std::cout << fhq[now].val << "\n";
        root = Merge(x, y);
}

1
2
3
4
5
6
7
8

# 后继

和前驱一样，找右子树的最左边的点即可

inline void Suf (int val) {
        int x ,y;
        Split(root, val, x, y);
        int now = y;
        while (fhq[now].l) now = fhq[now].l;
        std::cout << t[now].val << "\n";
        root = Merge(x, y);
}

1
2
3
4
5
6
7
8

# 区间平衡树

即用二叉树来维护树大小，分裂时是按 $size$ 进行分裂

但要注意在建树的时候要按下标建树，让大下标合并到 $root$ 的右侧，才能保证中序遍历下是一个连续递增的下标。

# 分裂

传入一个 $siz$ ，按其分裂和上面求排名的值的思想一样
根据左右树大小来进行决定走左子树还是右子树
走左子树就往下传 $siz$
走右子树就往下传 $siz-fhq[fhq[now].l].size-1$

inline void Split (int now, int siz, int &x, int &y) {
        if (!now) {
                x = y = 0;
        } else {
                pushDown(now);
                if (t[t[now].l].size < siz) {
                        x = now;
                        Split(t[now].r, siz - t[t[now].l].size - 1, t[now].r, y);
                } else {
                        y = now;
                        Split(t[now].l, siz, x, t[now].l);
                }
                Update(now);
        }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 区间操作

这个和值操作的目标一样，就是要分裂出来一个树表示我们要操作的区间。
这里传入 l 和 r
那么按大小分裂出三个树： $x$ ， $y$ ， $z$
其中 $x$ 的大小为 $l-1$
其中 $y$ 的大小为 $r-l+1$
其中 $z$ 的大小为 $n-fhq[x].size-fhq[y].size$
这样很显然我们固定出来中间的这 $r-l+1$ 个节点也就是我们要操作的区间
操作后合并就行了

这里以文艺平衡树 (opens new window)中的反转为例

inline void Reverse (int l, int r) {
        int x, y, z;
        Split(root, l - 1, x, y);
        Split(y, r - l + 1, y, z);
        fhq[y].reverse ^= 1;
        root = Merge(Merge(x, y), z);
}

1
2
3
4
5
6
7

# 例题

洛谷P3369 【模板】普通平衡树
题目地址 (opens new window)

洛谷P3391 【模板】文艺平衡树
题目地址 (opens new window)

洛谷P3165 [CQOI2014]排序机械臂
题目地址 (opens new window)

树链剖分主席树