树分治

Chivas-Regal

# 分治

归并排序：递归左右分别排序，然后合并，是数组线性分治
点分治就是将数组的分治扩展到树上

# 点分治

# 主要问题

给定一个路径限制，求在这个限制下合法的路径

# 思想

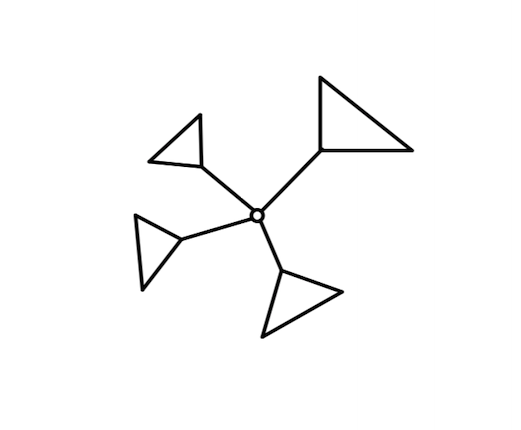
一个点上挂了几棵子树，子树内部问题递归去解，子树之间的问题进行合并

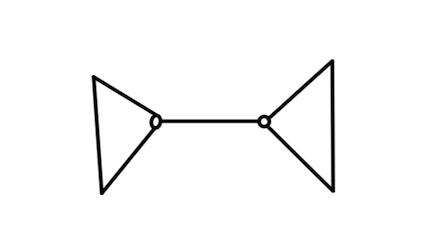
边分治：

用一个边进行拆分然后分别做

对于菊花图，边分治要分成 $n$ 层，而点分治可以分成 $logn$ 层（通过选重心）

重心的性质：每用重心拆分一层，最大连通块点数 $≤\frac n2$ ，也就是除 $2$

因此最多递归 $logn$ 层，最大连通块会成为 $1$
可以理解为，选定重心后每个块大小都不会太大，都 $≤\frac n2$

那么我们可以一层层地递归下去进行选边，时间复杂度也会大大缩小

# 过程

对于一个 $n$ 个点的树，总共有 $C^2_n$ 条路径
将路径分类:
1.两点都在一个子树内 $→$ 递归处理子树即可
2.其中一个点是重心(边界情况) $→$ 从重心开始向子树遍历，求子树内满足条件的点
3.两点不在一个子树内 $→$ 是子树间的问题，可以求完每个子树的节点后，进行不同子树节点之间按条件进行匹配

# 算法框架

|--求重心
|--删重心
|--分治
|----子树内递归
|----子树间合并
|----进入下一层

# 例题

例题1：AcWing252 树
题目地址 (opens new window)
题解地址 (opens new window)

例题2：AcWing264 权值
题目地址 (opens new window)
题解地址 (opens new window)

# 点分树

# 主要问题

给定一个点 $x$ 和一个点限制，求在这个限制内的所有点和 $x$ 之间的路径

# 思想

又叫动态点分治，主要还是通过点分治的思想

但在这里子树间问题可以通过一些算法直接求得，所以合并的过程可以直接求，那么就只需要构建一个递归方向
那么我们需要对这个树图建立一个结构，在这个结构下我们不需要对所有的子树构建重心
我们只需要在一步步锁定点 $x$ 的位置的时候，对重心一步步建立
那么就可以一次预处理存进所有的重心，存重心的结构被称为点分树，只不过每个子树的根节点是它的重心
然后我们就可以在锁定点 $x$ 的时候，子树间用算法就可以轻松求得，然后利用求到的递归方向，一层一层向下求子树间问题

# 过程

每一层可以将跨中心（也就是子树间问题）直接求得
然后向下锁定点 $x$

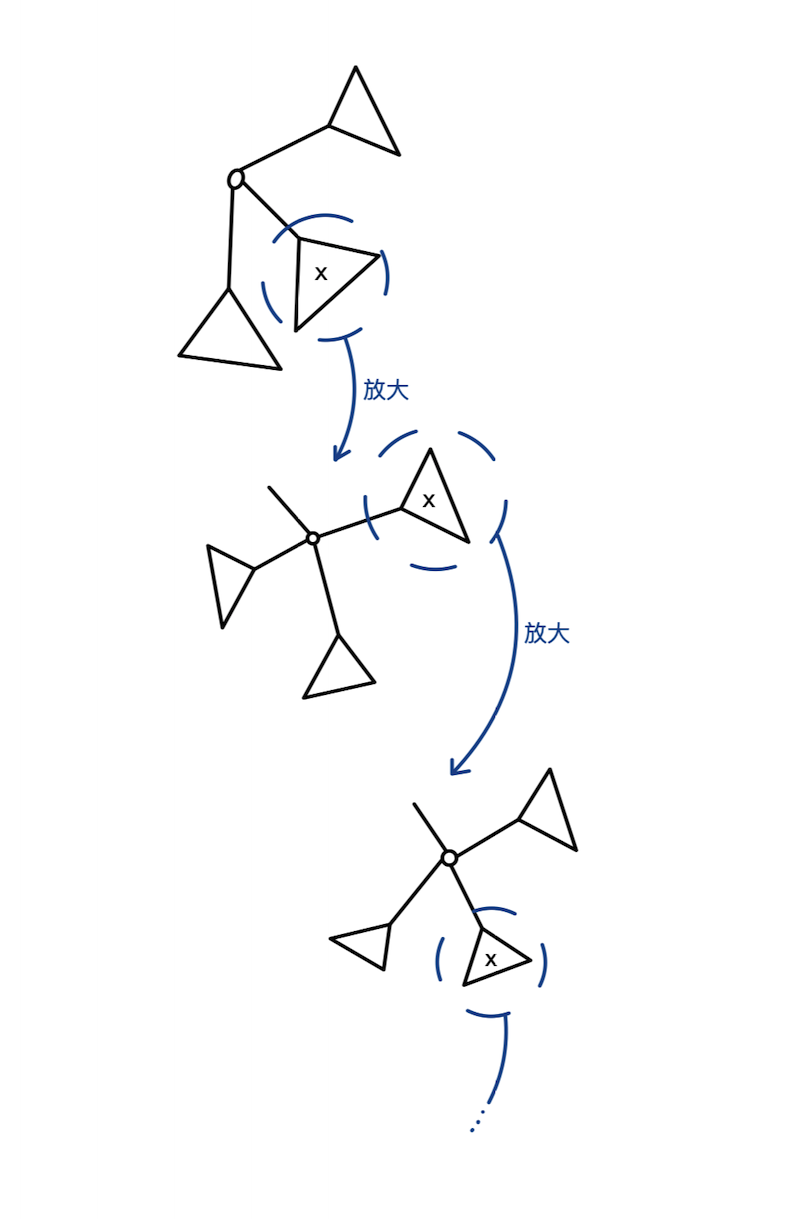
直到x就是这一层的重心，就直接暴力求得与其他子树中满足的点即可

# 算法框架

# 例题

AcWing2226 开店题目地址 (opens new window) 题解地址 (opens new window)

Prufer编码虚树