莫队算法

Chivas-Regal

# 普通莫队

# 问题类型

给定 $m$ 个查询操作，没有修改操作，每次查询 $[l,r]$ 有多少个不同的数

# 作用

可以解决区间离线问题的离线算法，如果在线可能会T掉
时间为 $O(nlogn)$ ，但可能会有出题人卡莫队

# 优化策略

# 双指针

给个数列有若干次询问 $[L,R]$ 的区间和（强制莫队）

解：开个数组

$0$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$
	$3$	$8$	$1$	$2$	$7$	$4$	$9$	$0$	$6$

若现在知道 $[2,5]$ 区间和为18
求 $[2,6]$ 的区间和 $\Rightarrow$ 加上第6项的值
求 $[2,4]$ 的区间和 $\Rightarrow$ 删掉第5项的值

朴素来看，对于区间 $[L, R]$ :

加上左边一格贡献: $add(--l)$
加上右边一格贡献: $add(++r)$
减去左边一格贡献: $sub(++l)$
减去右边一格贡献: $sub(--r)$

# 排序分块

若询问 $m$ 次， $[1,2],\;[n-1,n],\;[1,2],\;[n-1,n],\;[1,2].....$ ，上面的方法就变成了 $O(mn)$

可以改成 $[1,2],\;[1,2],\;[1,2],\;[n-1,n],\;[n-1,n]\;[n-1,n]...$

这样将距离较近的区间放在一起，时间复杂度变成 $O(n+m)$

# 算法架构

黑暗爆炸-1878《HH的项链》 (opens new window)

const int N = 1e4 + 10;
int pos[N];
int a[N];
int res[N];
int RES;
struct Q{
        int l, r, id;
}q[N];
int main () {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif
        // n m l r
        int n, m, l, r;
        cin >> n >> m >> l >> r;
        // 分块
        int len = sqrt(n);
        for ( int i = 1; i <= n; i ++ )
                cin >> a[i],
                pos[i] = i / len;
        // 询问
        for ( int i = 0; i < m; i ++ )
                cin >> q[i].l >> q[i].r,
                q[i].id = i;
        // 排序
        sort (q, q + m, [](Q x, Q y){
                return pos[x.l] == pos[y.l] ? x.r < y.r : pos[x.l] < pos[y.l];
        });
        // 初始化为开区间
        int l = 1, r = 0;
        for ( int i = 0; i < m; i ++ ) {
                // 左边太短了，l向左加一格
                while ( q[i].l < l ) Add ( -- l );
                // 右边太短了，r向右加一格
                while ( q[i].r > r ) Add ( ++ r );
                // 左边太长了，l向右减一格
                while ( q[i].l > l ) Sub ( ++ l );
                // 右边太长了，r向左减一格
                while ( q[i].r < r ) Sub ( -- r );
                // 记录答案
                res[q[i].id] = RES;
        }
        for ( int i = 0; i < m; i ++ )
                cout << res[i] << endl;
        return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

# 带修莫队

# 问题类型

多了个修改的版本问题，类似于时间

那么可以加一维记录时间戳
每次查询可以确定一下版本，即第 $k$ 次修改之后，第k+1次修改之前

# 指针移动

在同版本下的移动 $[l, r]$ 可以是普通莫队
在跳版本下移动 $[l, r, t]$ 要考虑两种情况
1.修改的数在区间外，不用理会
2.修改的数在区间内，计数减一下修改前的数，再加一下修改后的数

# 修改操作

可以把修改操作记录一个数组，每次修改的数组内存放这次修改的是什么数
那么在指针移动的时候我们只需要将原位置的数和修改后的数交换一下

# 排序优先级

$l$ 所在块编号， $r$ 所在块编号， $t$ 顺着递增块长为 $O(\sqrt[3]{nt})$

# 思想总结

带修莫队多了个时间戳的移动
也可以被视作第三个指针
其中可以做也是必做的优化就是我们再修改的的时候记录操作而不是直接修改，因为时间戳指针可能会来回折返，我们要知道下一步要改成什么
在移动时间戳时，走过某个修改时只需要将修改的值和原始值调换一下
如果在区间外也要交换，因为之后遍历 $[L,R]$ 也会走过去

# 算法架构

洛谷-P1903《[国家集训队]数颜色 / 维护队列》 (opens new window)

const int N = 1e4 + 10, M = 1e6 + 10;

int cnt[M], a[N], res[N], pos[N];
int n, m, len;
int nq, nm, RES;
struct Q{
	int l, r, t, id;
}qry[N];
struct M{
	int x, y;
}mdf[N];

inline void add ( int x ) {
	RES += ! cnt[x] ++;
}
inline void sub ( int x ) {
	RES -= ! -- cnt[x];
}

int main () {
	scanf("%d%d", &n, &m);
	for ( int i = 1; i <= n; i ++ )
		scanf("%d", &a[i]);
	for ( int i = 1; i <= m; i ++ ) {
		char op[2]; int x, y;
		scanf("%s%d%d", op, &x, &y);
		if ( op[0] == 'Q' ) ++ nq, qry[nq] = { x, y, nm, nq };
		else                ++ nm, mdf[nm] = { x, y };
	} 
	len = cbrt ((double)n * nm) + 1;
	for ( int i = 1; i <= m; i ++ ) 
		pos[i] = i / len;
	sort ( qry + 1, qry + 1 + nm, [&]( Q a, Q b ){
		if ( pos[a.l] != pos[b.l] ) return pos[a.l] < pos[b.l];
		if ( pos[a.r] != pos[b.r] ) return pos[a.r] < pos[b.r];
		if ( pos[a.r] & 1 ) return a.t > b.t;
		return a.t < b.t;		
	});
	
	for ( int L = 1, R = 0, T = 0, k = 1; k <= nq; k ++ ) {
		while ( L < qry[k].l ) sub ( a[L ++] );
		while ( L > qry[k].l ) add ( a[-- L] );
		while ( R < qry[k].r ) add ( a[++ R] );
		while ( R > qry[k].r ) sub ( a[R --] );
		while ( T != qry[k].t ) {
			if ( T < qry[k].t ) T ++;
			if ( L <= mdf[T].x && mdf[T].x <= R ) 
				sub ( a[mdf[T].x] ),
				add ( mdf[T].y );
			swap ( a[mdf[T].x], mdf[T].y );
			if ( T > qry[k].t ) T --;
		}
		res[qry[k].id] = RES;
	}
	for ( int i = 1; i <= nq; i ++ ) 
		printf("%d\n", res[i]);
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

# 回滚莫队

# 问题类型

给定一个数列，多个查询区间新定义的最大值
这种好增加不好删除的问题

我们可以全使用增加操作来进行跑指针

# 新遍历方法

我们在回滚莫队中一次考虑一整个块其中所有的询问 $l$ 在该块内点询问
这些询问 $r$ 递增

# 分类讨论

这样遍历时会出现两种情况：
1.开始时 $l$ 和 $r$ 在同一个块内
2.后面 $l$ 和 $r$ 不在同一个块内

情况1：
由于一个块内长度不超过 $\sqrt{n}$ ，所以直接暴力即可
但这波暴力是没有收益点，只能用来记一下答案，遍历完要清一下 $cnt[]$ 数组
情况2：
我们将查询的区间分为两部分
1.在 $l$ 所在的块内
对于这部分同样我们可以暴力解决，结束了也要清一下数组
2.不在 $l$ 所在的块内
这样的所有区间左端点都固定在 $l$ 的下一个块的第一个位置
这些区间遍历时只前进右端点
我们完全可以只使用莫队的 $add$ 操作来实现

# 思想总结

既然使用删除操作很麻烦，那么就不使用删除操作
对于一个短到一个块内的区间，直接使用暴力求解
对于跨区间的块，将其按左端点块编号分类之后，可以将同一类的每个区间分为左边的不到 $\sqrt{n}$ 的小区间和右边不断前进的大区间，左边暴力右边莫队即可解决问题

# 算法架构

洛谷-P5906《【模板】回滚莫队&不删除莫队》

const int N = 1e5 + 10;
int n, m, len;
int w[N], cnt[N];
ll res[N];
struct Q{
        int id, l, r;
}q[N];
vector<int> nums;

inline int get ( int x ) { return x / len;}

inline void add ( int x, ll &RES ) {
        cnt[x] ++;
        RES = max ( RES, (ll)cnt[x] * nums[x] );
}

int main () {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif
        scanf("%d%d", &n, &m); len = sqrt(n);
        for ( int i = 1; i <= n; i ++ ) 
                scanf("%d", &w[i]), 
                nums.push_back(w[i]);

        //离散化
        sort ( nums.begin(), nums.end() );
        nums.erase(unique(nums.begin(), nums.end()), nums.end());
        for ( int i = 1; i <= n; i ++ ) 
                w[i] = lower_bound(nums.begin(), nums.end(), w[i]) - nums.begin(); 
        
        // 询问读入与排序
        for ( int i = 0; i < m; i ++ ) {
                int l, r; scanf("%d%d", &l, &r);
                q[i] = {i, l, r};
        }
        
        sort ( q, q + m, [] ( Q a, Q b ) {
                if ( get(a.l) != get(b.l) ) return get(a.l) < get(b.l);
                return a.r < b.r;
        });

        // 遍历询问
        for ( int x = 0; x < m; ) {
                int y = x;
                while ( y < m && get(q[y].l) == get(q[x].l) ) y ++; // [x,y-1]的区间内都是.l相等的查询
                int right = get(q[x].l) * len + len - 1; // q[x].l所在的块的最后一个点

                // q[x].l和q[x].r在同一个块内，直接暴力求
                while ( x < y && q[x].r <= right ) { 
                        ll RES = 0; 
                        for ( int k = q[x].l; k <= q[x].r; k ++ ) add ( w[k], RES );
                        res[q[x].id] = RES;
                        for ( int k = q[x].l; k <= q[x].r; k ++ ) cnt[w[k]] --; // 回到更新前的数据状态
                        x ++;
                }
                
                // 求在不同块内的询问
                ll RES = 0;
                int i = right, j = right + 1; // 右端点和左端点
                while ( x < y ) {
                        while ( i < q[x].r ) add ( w[ ++ i ], RES ); // 右端点移动到正确的位置
                        ll backup = RES; // 备份一下
                        while ( j > q[x].l ) add ( w[ -- j ], RES ); // 左端点移动到正确的位置
                        res[q[x].id] = RES;
                        while ( j < right + 1 ) cnt[w[j ++]] --; // 左侧回到更新前的数据状态，因为左侧不删要重开
                        RES = backup; // 恢复备份
                        x ++;
                }
                memset ( cnt, 0, sizeof cnt ); // 进行下一部分的查询前要清空
        }
        for ( int i = 0; i < m; i ++ ) printf("%lld\n", res[i]);
        return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

# 树上莫队

# 问题类型

给一个无根普通树，若干询问，树的某条路径上一共有多少种不同权重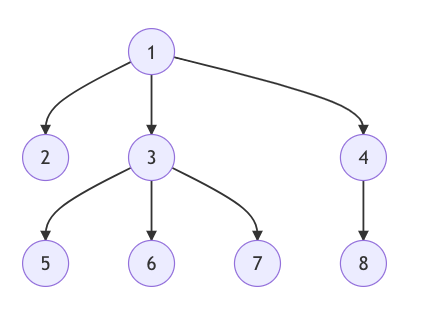权值：

1	2	3	4	5	6	7	8
45	2	9	1	8	5	7	7

树上的修改问题，可以变成一个线性区间修改问题
在这里可以使用欧拉序列

# 欧拉序列

# 构造方式

对树DFS一次，正序遍历到每个节点时记录一次，后序遍历再记录一次
比如上面的树可以变为 $1$ , $2$ , $2$ , $3$ , $5$ , $5$ , $6$ , $6$ , $7$ , $7$ , $3$ , $4$ , $8$ , $8$ , $4$ , $1$

# 性质

1.每个点进入写一次，离开写一次，共写两次
2.每次询问路径 $(x\rightarrow y)$ 选序列中x最开始(最后)出现的位置和y最开始出现的位置，只保留中间出现过一次的数

# 操作方式

两个数组
$first[u]$ 表示 $u$ 第一次出现的位置
$last[u]$ 表示 $u$ 第二次出现的位置
选 $x,y$ 满足 $x$ 在 $y$ 之前出现，即 $first[x]\lt first[y]$

# 分类讨论

$lca(x,y)=x$ ，则欧拉序列中 $first[x]\rightarrow first[y]$ 中间只出现一次的点对应 $x\rightarrow y$ 的路径（因为若出现0次说明没搜到，若出现两次说明进去搜了但是不存在
$lca(x,y)\neq x$ ，则路径对应欧拉序列中 $last[x]\rightarrow first[y]$ 中只出现一次的点以及 $lca(x,y)$ （因为最后的lca仍未回溯

# 指针移动

三个数组
$cnt[]$ 记录权值出现的个数
$st[]$ 记录序号出现的次数(0/1)，更新： $st[]^=1$
$res$ 实时记录答案

inline void add ( x ) {
        st[x] ^= 1;
        if ( st[x] == 0 ) res -= ! -- cnt[a[x]];
        else              res -= ! cnt[a[x]] --;
}

1
2
3
4
5

由于减去一个数也是异或1，所以一个 $add$ 就够用了

# 思想总结

对于一个树上问题，我们主要利用欧拉序列把它变成区间问题
然后对于欧拉序列性质（有关lca），我们可以得出我们每次要固定哪个区间和哪些数

# 算法架构

AcWing-2534 《树上计数2》 (opens new window)

const int N = 100010;

int n, m, len;
int w[N]; // 读入点权
struct Edge { int nxt, to; } edge[N]; int head[N], tot; 
int depth[N], f[N][16]; // 倍增lca那一套
int seq[N], top, first[N], last[N]; // 欧拉序列，当前位置出现的个数，最早出现的位置和最后出现的位置
int cnt[N], st[N], res[N]; // 权值不同个数，序号出现的个数（奇数/偶数），答案记录
int que[N]; // 宽搜队列
struct Qry {
        int id, l, r; // 第id个查询，查询区间是l, r
        int p; // 有无最近公共祖先
}q[N];
vector<int> nums; // 离散化
int RES; // 答案实时计数

inline void Add_Edge ( int from, int to ) {
        edge[ ++ tot ] = {head[from], to};
        head[from] = tot;
}

// -----------------------------------------------------------------求欧拉序列
inline void dfs ( int u, int father ) {
        seq[ ++ top ] = u;
        first[u] = top;
        for ( int i = head[u]; ~i; i = edge[i].nxt ) {
                int j = edge[i].to;
                if ( j != father ) dfs ( j, u );
        } 
        seq[ ++ top ] = u;
        last[u] = top;
}
// ---------------------------------------------------------------------------

// -------------------------------------------------------------------预处理倍增lca
inline int lca ( int a, int b ) {
        if ( depth[a] < depth[b] ) swap ( a, b );
        for ( int k = 15; k >= 0; k -- ) 
                if ( depth[f[a][k]] >= depth[b] ) 
                        a = f[a][k];
        if ( a == b ) return a;
        for ( int k = 15; k >= 0; k -- ) 
                if ( f[a][k] != f[b][k] ) 
                        a = f[a][k],
                        b = f[b][k];
        return f[a][0];
}

inline void bfs () {
        memset ( depth, 0x3f, sizeof depth );
        depth[0] = 0, depth[1] = 1;
        int hh = 0, tt = 0;
        que[0] = 1;
        while ( hh <= tt ) {
                int t = que[hh ++ ];
                for ( int i = head[t]; ~i; i = edge[i].nxt ) {
                        int to = edge[i].to;
                        if ( depth[to] > depth[t] + 1 ) {
                                depth[to] = depth[t] + 1;
                                f[to][0] = t;
                                for ( int k = 1; k <= 15; k ++ ) {
                                        f[to][k] = f[f[to][k - 1]][k - 1];
                                }
                                que[ ++ tt ] = to;
                        }
                }
        }
}
// ------------------------------------------------------------------------------------

// ----------------------------------------------------------------------------- 莫队操作
inline int get ( int x ) { return x / len; }

inline void add ( int x ) {
        st[x] ^= 1;
        if ( st[x] == 0 ) {
                cnt[w[x]] --;
                if ( !cnt[w[x]] ) RES --;
        } else {
                if ( !cnt[w[x]] ) RES ++;
                cnt[w[x]] ++;
        }
}
// ------------------------------------------------------------------------------------

int main () {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif
        // 读入数据并进行离散化
        scanf("%d%d", &n, &m);
        for ( int i = 1; i <= n; i ++ ) 
                scanf("%d", &w[i]), 
                nums.push_back(w[i]);
        sort ( nums.begin(), nums.end() );
        nums.erase(unique(nums.begin(), nums.end()), nums.end());
        for ( int i = 1; i <= n; i ++ ) {
                w[i] = lower_bound(nums.begin(), nums.end(), w[i]) - nums.begin();
        }

        // 建图
        memset(head, -1, sizeof head);
        for ( int i = 0; i < n - 1; i ++ ) {
                int a, b; scanf("%d%d", &a, &b);
                Add_Edge ( a, b );
                Add_Edge ( b, a );
        }

        // 求欧拉序列
        dfs ( 1, -1 );
        // 预处理最近公共祖先
        bfs ();
        
        // 询问
        for ( int i = 0; i < m; i ++ ) {
                int a, b; scanf("%d%d", &a, &b); 
                // 转移成线性区间问题
                if ( first[a] > first[b] ) swap ( a, b );
                int p = lca ( a, b );
                if ( a == p ) q[i] = {i, first[a], first[b]};
                else q[i] = {i, last[a], first[b], p};
        }

        // 分块排序
        len = sqrt ( top );
        sort ( q, q + m, [&]( Qry a, Qry b ) {
                if ( get(a.l) != get(b.l) ) return get(a.l) < get(b.l);
                if ( get(a.l) & 1 ) return a.r < b.r;
                else                return a.r > b.r;
        });
        
        // 莫队指针操作
        for ( int i = 0, L = 1, R = 0; i < m; i ++ ) {
                int id = q[i].id, l = q[i].l, r = q[i].r, p = q[i].p;
                while ( R < r ) add ( seq[ ++ R ] );
                while ( R > r ) add ( seq[ R -- ] );
                while ( L < l ) add ( seq[ L ++ ] );
                while ( L > l ) add ( seq[ -- L ] );
                if ( p ) add ( p ); // 如果x不是y的公共祖先的话要先加上再减去
                res[id] = RES;
                if ( p ) add ( p );
        }

        // 输出答案
        for ( int i = 0; i < m; i ++ ) 
                printf("%d\n", res[i]);

        return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150

# 二次离线莫队

# 问题类型

定义一个新的配对含义：两个数异或后二进制表示有 $k$ 个 $1$ 长度为 $n$ 的序列，一个 $k$ ， $m$ 次询问 $[l,r]$ 内有多少个数对配对
这类问题每次指针移动之后对数据的修改值非常难算

这类问题可以把一个问题推导成两个问题，一个问题使用莫队离线直接算出后，对另一个问题再拎出来离线算一次

# 遍历分类

对于 $[L,\;R\longrightarrow r]$

原是思想是 $R$ 向后移动并加入一个数，看加入的这个数对答案会不会产生什么价值或影响
在这里加入 $R+1$ 时，看 $R+1$ 这个位置上的数能和原区间内多少个元素产生配对

我们令 $S[R]$ 表示 $[1,R]$ 中多少个数与 $R+1$ 位置配对，则上问题的求法就是 $S[R]-S[L-1]$

设 $f[i]$ 表示 $w[1]~w[i]$ 中有多少个数与 $w[i+1]$ 配对，所以问题关键指向预处理 $f[i]$
设 $g[i]$ 表示前 $i$ 个数中有多少个与 $i$ 配对，则 $f[i]=g[w[i+1]]$
对于每次加入一个 $w[i$ 我们要寻找哪些数和 $i$ 配对，让他们的 $g()++$
所以我们要建一个数组存放所有存在 $k$ 个 $1$ 的数
要找 $w[i]\otimes x=y[i]\Rightarrow x=w[i]\otimes y[i]$ 遍历所有 $y[i]$ 得到 $g$ 要加的数，所以是对 $g[w[i]\otimes y[i]]++$
$g[i]$ 这么求，那么 $f[i]$ 也出来了

$\therefore S[R]=f[R]$
$S[L-1]$ 离线求

我们在推 $R\rightarrow r$ 时，每个数加进来都求一次 $S[L-1]$
那么就是 $[1,L-1]$ 每次都配对一下 $[R+1,r]$ 的数
可将这些问题拿出来，每个问题：某个固定前缀中，某个区间每个数和这个前缀中多少个数配对
从前往后求前缀即前缀是 $1$ 的哪些询问可以干掉， $2$ 的哪些询问可以干掉， $3$ 的，......
这些都可以离线做一遍出来

那么第一次离线得到 $S[R]$ ，再离线一次统一出 $S[L-1]$
注：每次求的 $S[R-S[L-1]]$ 是增量 $add$ 的数值

对于其他的分类讨论情况也同理

# 算法框架

【模板】莫队二次离线（第十四分块(前体)） (opens new window)

const int N = 100010;
int n, m, k, len;
int w[N];
ll res[N];
struct Q {
        int id, l, r;
        ll RES; // 先存一下，分成两次求得
} q[N];
struct Range { // 待解决问题
        int id, l, r;
        int t; // 判断要加还是减
};
vector<Range> range[N]; // 对于每个前缀可能会有多个询问区间
int f[N], g[N]; // 推的公式关系的需要的数组

inline int get ( int x ) { return x / len; }

inline int get_count ( int x ) { // 有多少个1
        int res = 0;
        while ( x ) res += x & 1, x >>= 1;
        return res;
}

int main () {
#ifndef ONLINE_JUDGE
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
#endif

        scanf("%d%d%d", &n, &m, &k);
        for ( int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
        
        // 存放所有有k个1的数
        vector<int> nums; 
        for ( int i = 0; i < 1 << 14; i ++ )
                if ( get_count(i) == k ) 
                        nums.push_back(i);
        
        // 初始化fg数组
        for ( int i = 1; i <= n; i ++ ) {
                for ( auto x : nums ) g[w[i] ^ x] ++; // 求当前新加的这个数（w[i]）对于哪些x是有影响的
                f[i] = g[w[i + 1]]; // 公式关系
        }

        // 读入询问，排序
        for ( int i = 0; i < m; i ++ ) {
                int l, r; cin >> l >> r;
                q[i] = {i, l, r};
        }
        len = sqrt ( n );
        sort ( q, q + m, [] ( Q a ,Q b ) {
                if ( get(a.l) != get(b.l) ) return get(a.l) < get(b.l);
                return a.r < b.r;
        });

        // 莫队
        for ( int i = 0, L = 1, R = 0; i < m; i ++ ) {

                // S_R - S_{L - 1}
                if ( R < q[i].r ) range[L - 1].push_back({i, R + 1, q[i].r, -1}); // [R + 1, r] 先不处理，加入询问
                while ( R < q[i].r ) q[i].RES += f[ R ++ ];

                // - ( S_{R - 1} - S_{L - 1} )
                if ( R > q[i].r ) range[L - 1].push_back({i, q[i].r + 1, R, 1}); // [r + 1, R] 先不处理， 加入询问
                while ( R > q[i].r ) q[i].RES -= f[ -- R ];

                // - ( S_R - S_L )
                if ( L < q[i].l ) range[R].push_back({i, L, q[i].l - 1, -1}); // [L, l - 1] 先不处理， 加入询问
                while ( L < q[i].l ) q[i].RES += f[L - 1] + !k, L ++; // 因为存的是[1, L - 1]有多少个与L配对，所以要多加个判断w_L是否配对(k!=0)

                if ( L > q[i].l ) range[R].push_back({i, q[i].l, L - 1, 1}); // [l, L - 1] 先不处理， 加入询问
                while ( L > q[i].l ) q[i].RES -= f[L - 2] + !k, L --;
        }

        // 整体求一下没求的部分
        memset ( g, 0, sizeof g );
        for ( int i = 1; i <= n; i ++ ) { // 枚举每个前缀
                for ( auto x : nums ) g[w[i] ^ x] ++; // 枚举所有满足要求的y
                for ( auto& rg : range[i] ) {
                        for ( int x = rg.l; x <= rg.r; x ++ )
                                q[rg.id].RES += g[w[x]] * rg.t;
                }
        }

        // 因为每次求的是增量，所以要累加前缀和
        for ( int i = 1; i < m; i ++ ) q[i].RES += q[i - 1].RES;
        for ( int i = 0; i < m; i ++ ) res[q[i].id] = q[i].RES;


        for ( int i = 0; i < m; i ++ ) printf("%lld\n", res[i]);
}

数位DP 三维偏序_CDQ分治