Chivas-Regal

最短路







回顾：链式前向星(邻接表的数组实现)

struct edge{ int nxt, to, dis; }edge[N];
int head[N];
int cnt = 0;

inline void add_edge(int from, int to, int val){
	edge[++cnt] = {head[from], to, val};
	head[from] = cnt;
}

inline void input(){
	for(int i = 1, x, y, z; i <= m; i ++){
		read(x); read(y); read(z);
		add_edge(x, y, z);
	}
}

inline void run(){
	for(int i = 1; i <= n; i ++){
		for(int k = head[k]; ~k; k = edge[k].nxt){
			//
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# DIJKSTRA

# 概念

迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。---《百度百科》

# 思想：

  • 按照最短路径长度递增的次序，依次求的——源点到其余各点到最短路径
  • 先求——最短的那条最短路径
  • 再求——第二短的最短路径
  • ......
  • 依次类推
  • ......
  • 最终求出所有的最短路径

# 算法变量

Dist[i]表示从起点到i点的最短路总权
Map[i][j]表示从i点到j点的距离权

算法图示 无向图的储存（邻接矩阵）

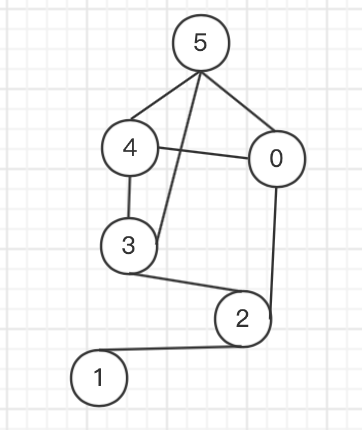转移后：
0 1 2 3 4 5
0 10 30 100
1 5
2 10 5 50
3 50 20 10
4 30 20 60
5 100 10 60

# dijkstra模拟求最短路

终点 Dist[i]
i=1 i=2 i=3 i=4 i=5
V1 INF INF INF INF INF
V2 10
V3 INF 60 50
V4 30 30
V5 100 100 90 60
Vj V2 V4 V3 V5

# 注意事项

如果无向图要建立反边 如果多条路要选择最短

# 松弛操作

if(Dis[x] + edge[i].val < Dis[edge[i].to]) 
	Dis[edge[i].to] = Dis[x] + edge[i].val,
	pque.push({edge[i].to, Dis[edge[i].to]});
1
2
3

其实就是看看从这个中转站转一下会不会更近

# 整体程序

int dis[N];
bool vis[N];
struct node {
        int id, val;
        inline friend bool operator < ( node a, node b ) {
                return a.val > b.val;
        }
};
inline void pre_Dijkstra () {
        for ( int i = 0; i <= n; i ++ ) dis[i] = 0x3f3f3f3f,vis[i] = 0;
        priority_queue<node> pque;
        dis[1] = 0; pque.push({1, 0});
        while ( pque.size() ) {
                node cur = pque.top(); pque.pop();
                if ( vis[cur.id] ) continue; vis[cur.id] = 1;
                for ( int i = head[cur.id]; i; i = edge[i].nxt ) {
                        int to = edge[i].to;
                        if ( dis[to] > dis[cur.id] + edge[i].val ) {
                                dis[to] = dis[cur.id] + edge[i].val; 
				pque.push({to, dis[to]});
                        }
                }
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# 补：记录路径

我们想用Dijkstra松弛的时候记录一下路径，可以设计每个点的前驱是哪个点
如果设计的是后继的话，由于一个点可能会更新很多个出发点发射出去的最短路
所以后继不能单独表示从出发点到谁的最短路，所以我们要倒着设置，也就是前驱

当然我们还想求到 xx 的哪一条边是最短路径的边
这个可以在设置一个数组，记录前向星的编号
无向图中由于每次加边都是成对加边，边的编号为奇数 ii 时，它和 i+1i+1 表示的是同一条边

int pre[N];        // pre[i]: i的前驱是pre[i]
int short_edge[N]; // short_edge[i]：到i点的边中，那一条边是最短路径的边

int to = edge[i].to;
if ( dis[to] > dis[cur.id] + edge[i].val ) {
	dis[to] = dis[cur.id] + edge[i].val; pque.push({to, dis[to]});
	pre[to] = cur.id;                       // cur.id -> to
	if ( i & 1 ) short_edge[to] = i;        // 记录是哪条边（正边）
	else         short_edge[to] = i - 1;    // 记录是哪条边（正边）
}
1
2
3
4
5
6
7
8
9
10

# 问题

作为最常用的最短路算法，对这个算法的很多问题进行思考

问题一

是否可以解决负环问题？

Answer

考虑这样一个图

由于我们顺序更新后 dis[1,3,4,5]dis[1,3,4,5] 均小于 dis[2]dis[2]
故 22 入队后，我们继续会走 3→4→53\to4\to5
这样 22 后面虽然更新过 44 但是 44 之前入过队并推导完毕，不会去更新 55
所以 55 的 disdis 错误为 11
所以不可以解决负环问题

问题二

是否可以求最长路？

Answer

可以看作将边权取反后跑最短路
负环最短路是错误的，所以正环最长路也是错误的，不能解决

问题三

是否可以解决无环负权图？

Answer

可以，但是首先要认清一个事情
该无环图不能有任何意义下的环，即强连通环和弱连通环
否则在问题一给出的图上使边从左到右即可
那么就是一个树图了，...其实 DFS() 就可以

# FLoyd(插点法，经典DP)

求任意两点的最短路

for(int k = 1; k <= n; k ++)        //插入点在外层循环很重要！
	for(int i = 1; i <= n; i ++)
		for(int j = 1; j <= n; j ++)
			dis[i][j] = MIN(dis[i][j], dis[i][k] + dis[k][j]);
1
2
3
4

# 算法思想

从i到j的只经过前k个点的最短路径

# 算法特点

简单、粗暴、易于实现、可以解决负权
且拥有独有的优势：
乍一看可能 O(n3)O(n^3) 的复杂度很难解决很多问题
但如果是动态多源最短路
我们每次加入新点的时候都可以在 O(n2)O(n^2) 的复杂度下完成所有点的更新

# 难点思考

三重循环是否可以任意交换顺序？
如果k放里面的话，我们在 MINMIN 更新中用到的 dis[i][k]dis[i][k]、dis[k][j]dis[k][j] 不一定是最优解，因为前面并没有更新过

# Bellman-Ford

//数据存储结构？
for(int k = 1; k < n; k ++){       //n - 1个阶段，每个阶段的效果？
	for(int i = 1; i <= m; i ++){  //每个阶段，对所有边尝试松弛
		dis[v[i]] = MIN(dis[v[i]], dis[u[i]] + w[i]);
	}
}
1
2
3
4
5
6

# 算法思想

一共 nn 个点，所构成最短一条最多 n−1n-1 条边
每次松弛都只能完善 mm 个中的一部分边
要想完善完所有 mm 条边
我们要对所有的边进行 n−1n-1 次松弛操作

# 算法特点：

简洁、可以解决负权负环的情况

其实并不一定需要 n−1n-1 轮，如果前面的点都没做过松弛操作，那么这一趟松弛操作并不会更新，就不需要继续进行（冒泡排序思想）

# 难点思考

如何检测是否存在负环？
如果在某两点内走会不断减权，那么就有负环

for(int k = 1; k <= n - 1; k ++)
	for(int i = 1; i <= m; i ++)
		dis[v[i]] = MIN(dis[v[i]], dis[u[i]] + w[i]);

//正常情况下，做了n-1趟松弛操作后整个图的最优解就稳定了，如果还有可以松弛的，就是负环
int flag = 0;
for(int i = 1; i <= m; i ++)
	if(dis[v[i]] > dis[u[i]] + w[i]) flag = 1;
if(flag) ... //有负环的情况
1
2
3
4
5
6
7
8
9

# Bellman_Ford算法队列优化（SPFA）

# 基本思想

每次仅对最短路程发生变化了的点的相邻边执行松弛操作
问题：如何知道当前哪些点的最短路程发生了变化呢？
方案：采用“队列“维护

# 具体操作

先把起点加进队列中，然后松弛和起点相连的所有边，如果松弛成功且该点不在队列中，那么就把这个点入队。然后依次取出队列中每一个点进行松弛，直到队列为空。

inline void SPFA(int u){
	que.push(u); vis[u] = 1;
	while(que.size()){
		int x = que.front(); que.pop(); vis[x] = 0;
		for(int i = head[x]; ~i; i = edge[i].nxt){
			int y = edge[i].to;
			if(dis[x] + edge[i].val < dis[y]){
				dis[y] = dis[x] + edge[i].val;
				if(!vis[y]) vis[y] = 1, que.push(y);
			}
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13

# 优缺点总结

DIJKSTRA
优点：大数据单源最短路求解
缺点：负环不能求
FLoyd
优点：擅长求任意两点最短路
缺点：时间复杂度高
Bellman-Ford(SPFA)
优点：求负环问题
缺点：最坏情况复杂度高

Last Updated: 10/14/2023, 7:51:49 PM

网络流