博弈论
# 博弈论
# 特点
- 两个以上玩家
- 状态为有限的集合
- 双方轮流操作
- 具有规则
- 有限次操作结束
- 有胜负
- 两人足够聪明
# 必定点
必胜(败)点:在该点进行操作的人必胜(败)
# 属性
所有终结点为必败点
每个必胜点至少有一个操作进入必败点
必败点只能走入必胜点
# 图示
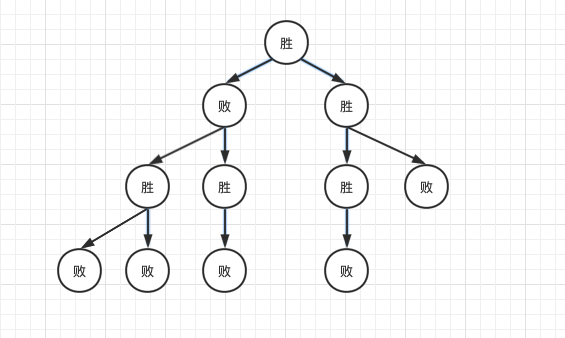
# 巴什博弈
人, 枚石子,双方轮流选取,不能拿或且不可拿超过 枚,没石子可拿的人就输了
这个问题由于两个人一定足够聪明,他们会有一种“跟着选”的策略
即:如果当前石子数为 的倍数,那么如果一个人拿了 个,那么第二个人只要跟着拿 个就一定可以赢
那么如果 是 的倍数,那么第一个人就一定会输
同时如果不是的话,第一个人可以把这 个石子变成 的倍数,他就一定可以获胜了
# 尼姆博弈
人,多堆石子,每个人选取其中一堆石子取走任意个石子
三堆石子分析
必败
必胜
必败
必败
# 尼姆和
按位的异或(上面是 )
其中 必败,否则必胜
证明:
例如三堆石子为
如果有方法令 变成 则必胜(属性 )
可以令第一个数变成 ,则
朴素做法:结果从前往后,第一个 上面一定是有奇数个 ,选择一行该位置为 的,这个位置变成 ,后面再遇到选取同行并取反
满足
如果任意方法都会让结果非 则必败(属性 )
本身已经是 平衡了,即任意位置都有偶数个
操作后必定会改变其中一列的 的个数成为奇数个,打破平衡使结果非 ,必败
满足
问题
| 判断先手输赢 | 根据起始状态的尼姆和 |
| 求先手拿石子可赢的方案数量 | 看尼姆和第一位 上面有多少个 ,因为不可以加石子 |
# 函数
节点的 值是不等于 后继节点的 值的最小非负整数
即:
其中 必败,否则必胜
证明:看巴什博弈(最多可以拿三个)
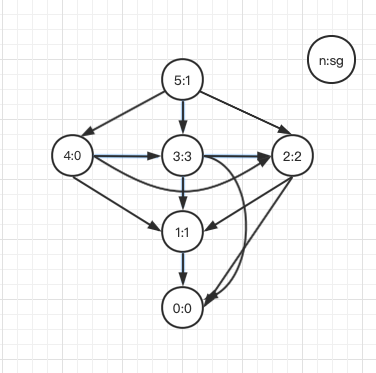 终结状态 必 ,非零必胜 (属性 )
终结状态 必 ,非零必胜 (属性 )
能转移到 的均必胜(属性 ),在 内必定不为
不能转移到 ,即必须转移到正整数,本身一定是 ,必败(属性 )
# 例
# 1
堆石子, 个。轮流拿石子,必拿但不超过三个。讨论先手的输赢
看作 个巴什博弈:
多用尼姆和与 函数相结合,全局输赢
本问题中讨论即 为 则先手必败,否则先手必胜
# 2
给定规则数 ,即可以拿走 个石子
给定情况数 ,每种情况有 堆牌,每堆 张,讨论每种情况的先手输赢
程序采用记忆化搜索
int n, m; // 规则数,情况数
int a[100]; // 规则
int sg[10001];
inline int SG ( int all ) {
bool vis[101] = {0};
for ( int i = 0; i < n; i ++ ) {
int remain = all - a[i]; // 剩余的石子数
if (remain < 0) break; // 少于0个不存在
if ( sg[remain] == -1 ) sg[remain] = SG(remain); // 继续递归子状态的sg值
vis[sg[remain]] = 1; // 子状态sg值标记一下
}
for ( int i = 0; ; i ++ ) if ( !vis[i] ) return i; // sg定义
}
int main () {
cin >> n;
for ( int i = 0; i < n; i ++ ) cin >> a[i];
sort(a, a + n); // 可以在sg内部选取拿走的石子数量上进行 break 优化
memset(sg, -1, sizeof sg);
sg[0] = 0;
cin >> m; while ( m -- ) {
int res_sg = 0;
int o; cin >> o; while ( o -- ) {
int x; cin >> x;
if ( x == -1 ) sg[x] = SG(x);
res_sg ^= sg[x];
}
if ( res_sg == 0 ) cout << "先手必败" << endl;
else cout << "先手必胜" << endl;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
